Differential Game Model of Resource Extraction with Continuous and Dynamic Updating

Abstract

This paper is devoted to a new class of differential games with continuous and dynamic updating. The direct application of resource extraction in a case of dynamic and continuous updating is considered. It is proved that the optimal control (cooperative strategies) and feedback Nash equilibrium strategies uniformly converge to the corresponding strategies in the game model with continuous updating as the number of updating instants converges to infinity. Similar results are presented for an optimal trajectory (cooperative trajectory), equilibrium trajectory and corresponding payoffs.

1 Introduction

The theory of differential games was established as a separate part of the game theory in the 50s. One of the first works in the field of differential games is considered to be the work of Isaacs [1], in which the problem of intercepting an airplane was formulated in terms of states and controls guided missile, and also derived the fundamental equation for defining a solution. The study of differential games started with the zero-sum differential games [2,3,4,5,6,7,8]. The motivation for studying the noncooperative differential game models was the problems involving several participants (players) having different goals or payoff functions and therefore acting individually. As an optimality principle in noncooperative differential games, the Nash equilibrium in open-loop or closed-loop form is mostly used [9,10,11,12].

Cooperative differential game models considered in the papers [13,14,15,16,17] are also of interest as they enable modeling the cooperative agreements. The theory of cooperative differential games studies the problem of constructing the terms of cooperative agreement, in particular cooperative strategies, corresponding trajectory, joint payoff along the cooperative trajectory, allocation rules of joint payoff among players, and time consistency property of the solution. Most of real-life conflicting processes evolve continuously in time, and their participants continuously receive updated information and adapt. For this kind of processes, an approach was proposed that allows constructing more realistic models, namely games with dynamic updating [18, 19] and games with continuous updating [20, 21].

Fundamental models discussed previously in differential game theory are related to the following: problems defined on a fixed time interval (players have all the information on a closed time interval) [10]; problems defined on an infinite time interval with discounting (players have information on an infinite time interval) [9]; problems defined on a random time interval (players have information on a given time interval, but the terminating instant is a random variable) [22]; and one of the first works in differential game theory is devoted to the pursuit-evasion game (payoff of the pursuer depends on the time of catching evaders) [6]. In all the above models and suggested solutions, it is assumed that players at the beginning of the game know all the information about the dynamics of game (motion equations) and about the preferences of players (payoff functions). However, this approach does not take into account the fact that in many real-life processes, players at the initial instant do not know all the information about the game. Thus, existing approaches cannot be directly used to construct a sufficiently large range of real life game-theoretic models. At each time instant information about the game structure updates, players receive information about motion equations and payoff functions. This new approach for the analysis of differential games via information updating provides a more realistic and practical alternative to the study of differential games.

Fig. 1

Each oval shows the information available to players at instant t, namely $[t, t+\overline{T}]$, where $\overline{T}$ is the time horizon

As shown in Fig. 1. In the game models with continuous updating, it is assumed that players

• (1) have information about the motion equations and payoff functions on the truncated time interval with length $\overline{T}$, which is called the information horizon,

• (2) continuously receive updated information about the motion equations and payoff functions and as a result continuously adapt to the updated information.

This class of problems till now was only studied in the papers [20, 21]. In the paper [20], the form of Hamilton–Jacobi–Bellman solution is presented for a case of continuous updating. In the paper [21], the explicit solution for a class of linear quadratic differential game models with continuous updating is presented.

In this paper, the detailed and practical solution for a differential game model of resource extraction with dynamic and continuous updating is presented. In this paper, the game model with continuous updating and corresponding results are presented for a classical differential game model of non-renewable resource extraction, proposed in [23] and further considered in [22, 24, 25]. Cooperative and noncooperative setting is considered and corresponding conclusions are drawn. Solution with continuous updating is obtained using the results from the paper [20], where the form of Hamilton–Jacobi–Bellman equations for continuous updating is derived.

In order to demonstrate the meaning of the continuous updating solution for a game model with resource extraction, the dynamic updating solution is used. Convergence results for a case of when the number of updating instants converges to infinity or when the length of updating interval converges to zero are presented. Convergence results are presented both for cooperative game model and noncooperative one, i.e., convergence results are presented for cooperative strategies and Nash equilibrium strategies and corresponding trajectories.

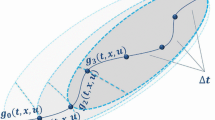
The class of games with dynamic updating was studied in the papers [18, 19, 26,27,28,29,30], where the authors laid the foundation for further study in the class of games with dynamic updating. It is assumed that the information about motion equations and payoff functions is updated in discrete time instants, and the interval on which players know the information is defined by the value of information horizon (Fig. 2).

Fig. 2

Each blue oval shows the information available to players over the interval $[t_0 + j \Delta t, t_0 + (j+1) \Delta t]$, namely $[t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}]$, $j = 0,\cdots ,l$, $l=\frac{T-t_0}{\Delta {t}}$. Color figure online

The results of numerical modeling are demonstrated in Python using NumPy and MatPlotLib libraries. For clarity, the results of numerical modeling for a large number of updating instants are presented, which demonstrates the convergence of optimal controls and corresponding trajectories in game model with dynamic updating to the constructed ones for the game model with continuous updating. The paper is structured as follows. In Sect. 2, the initial game model of non-renewable resource extraction is presented and corresponding solution is derived. In Sect. 3, the concept of truncated subgame is defined, with the help of which the behavior of players with dynamic updating (Fig. 3) is modeled. In Sect. 4, transition to the games with continuous updating is described. The results of a numerical simulation in Python are presented in Sect. 5. In Sect. 6, the conclusion is presented.

Fig. 3

Behavior of players in game with dynamic updating can be modeled using a set of truncated subgames $\bar{\Gamma }_j(x_{j,0}, t_0 + j \Delta t, t_0 + j \Delta t + \overline{T})$, $j = 0,\cdots ,l$, $l = \frac{T - t_0}{\Delta {t}}$

1.1 Initial Game Model

We will investigate the classical game theory model of resource extraction that was described in [23]. Here, the amount of resource directly depends on the rates of extraction, which are selected by the companies or players. The game involves n symmetric players (whose set of players is denoted by N) with utility functions depending on extraction rates $h_{i}(t, x, u_{i}) = \log {u_{i}}$. The game starts at the instant $t_{0}$ and terminates at T, i.e., the game is defined on the interval $[t_{0},T]$. The amount of resource at the beginning of the game is $x_{0}$.

We denote by $x(t) \in \mathbb {R}$ the amount of resource available for players at the instant t, and by $u_i(t, x)$, we denote the strategy of player $i \in N$, which is the resource extraction rate defined for any instant t and the amount of available resources in the system x. We will look for strategies in the class of feedback strategies, and we assume that $\forall {t}$, $u_i(t, x) \geqslant 0$ and $x(t)=0$ implies that $u_i(t, x)=0$. The amount of resource x(t) is a function of time t, which in the following way depends on the rates of extraction or strategies of players $u_i(t,x)$:

$$\begin{aligned}&\dot{x} = -\sum \limits _{i=1}^n u_i(t,x), \nonumber \\&x(t_0) = x_0. \ \end{aligned}$$

(1)

Payoff function of player $i \in N$ has the form:

$$\begin{aligned} K_i(x_0, T - t_0) = \int \limits _{t_0}^{T}\log (u_i(\tau ,x)) \textrm{d}\tau , i \in N. \end{aligned}$$

(2)

We assume that, for any n-tuple of strategies $u_1(\cdot ), \cdots , u_n(\cdot )$, the conditions of existence, uniqueness, and continuability of solution (1) are satisfied precisely as described in [31]. Taking into account the symmetry of players, we put $u(t,x)=u_i(t,x)$ for each $i \in N$.

In the next section, the calculation of optimal strategies (controls) is presented for two basic classes of differential games: cooperative differential games and noncooperative differential games.

1.2 Cooperative Differential Games

Consider the cooperative version of the non-renewable resource extraction game that was initially discussed in [23]. Here, players unite in grand coalition $S = N$ and acting as one player maximize the joint payoff. Corresponding optimal control problem is formulated in the following way:

$$\begin{aligned} \sum \limits _{i=1}^{n} K_i(x_0, T - t_0) = n \int \limits _{t_0}^{T}\log (u(\tau ,x))\textrm{d}\tau \rightarrow \max \limits _{u} \end{aligned}$$

(3)

$$\begin{aligned} \begin{aligned} \text {s.t.}\qquad&\dot{x}=-n{u(t,x)},\\&x(t_0)=x_0>0,\\&u(t,x)\geqslant 0,\\&x(t)\geqslant 0. \end{aligned} \end{aligned}$$

(4)

In order to solve the optimization problem (3), (4), we use the method of the dynamic programming principle proposed by Bellman in [32]. We define the value function as the maximum value of functional (2) in the subgame $\Gamma (x,T-t)$ starting at the instant t in the position x:

$$\begin{aligned} V(t,x) = \max \limits _{u}\left\{ \sum \limits _{i=1}^{n} K_i(x, T - t) \right\} = \max \limits _{u}\left\{ n\int \limits _{t}^{T}\log {u}(\tau ,x)\textrm{d}\tau \right\} . \end{aligned}$$

(5)

In the paper [32], it is proved that if there exists a continuously differentiable function V(t, x) satisfying the Hamilton–Jacobi–Bellman equation

$$\begin{aligned}{} & {} -V_t(t,x)=\max \limits _{u}\left\{ n \log {u} - n u V_x(t,x) \right\} , \nonumber \\{} & {} V(T,x)=0, \end{aligned}$$

(6)

then the control $u^*(t,x)$ determined by maximizing the right-hand side of (6) is optimal in the control problem (3), (4).

From the first-order extremum condition for (6), we obtain

$$\begin{aligned}u^*=\frac{1}{V_x(t,x)},\end{aligned}$$

and substitute in (6):

$$\begin{aligned}{} & {} V_t(t,x)=n\log {V_x(t,x)}+n, \\{} & {} V(T,x)=0. \end{aligned}$$

We define the value function in the form:

$$\begin{aligned}V(t,x)=A(t)\log {x}+B(t);\end{aligned}$$

then by substituting it in (6), we obtain

$$\begin{aligned}{} & {} \dot{A}(t)\log {x}+\dot{B}(t)=n\log {A(t)}-n\log {x}+n, \nonumber \\{} & {} A(T)=B(T)=0. \end{aligned}$$

(7)

The following functions are solutions of (7):

$$\begin{aligned} \begin{aligned} A(t)&=n(T-t),\\ B(t)&=-n(T-t)\log {n(T-t)}. \end{aligned} \end{aligned}$$

(8)

Finally, we obtain an expression for the value function:

$$\begin{aligned} V(t,x)=n(T-t)\log {\frac{x}{n(T-t)}}, t \in [t_0, T], \end{aligned}$$

(9)

and an expression for optimal control:

$$\begin{aligned} u^*(t,x) = \frac{1}{V_x(t,x)} = \frac{x}{n(T-t)}, \ t \in [t_0, T]. \end{aligned}$$

(10)

Substituting the optimal control to the motion equation (4), we obtain a differential equation for the trajectory corresponding to the optimal control:

$$\begin{aligned} \begin{aligned}&\dot{x}(t)=-\frac{x(t)}{T-t}, \\&x(t_0) = x_0. \end{aligned} \end{aligned}$$

(11)

Solution of Cauchy problem (11) has the form:

$$\begin{aligned} x^*(t)=x_0\frac{T-t}{T-t_0}, \ t \in [t_0, T]. \end{aligned}$$

(12)

Trajectory $x^*(t)$ and strategy (control) $u^*(t,x)$ are called cooperative.

Cooperative strategies along the cooperative trajectory have the form:

$$\begin{aligned} u^*(t,x^*) = \frac{x_0}{n(T-t_0)}, t \in [t_0, T]. \end{aligned}$$

(13)

In Fig. 4, the above solid line represents the cooperative trajectory $x^*(t)$ (12), and the longest solid line in the middle of Fig. 5 represents the corresponding optimal strategies (13) in the game of non-renewable resource extraction $\Gamma (x_0, T-t_0)$.

Fig. 4

Resulting cooperative trajectory $\hat{x}^*(t)$ given by (26) (the solid line in the middle) and cooperative trajectory in the initial game $x^*(t)$ given by (12) (the top line)

Fig. 5

Resulting cooperative strategies $\hat{u}^*(t,\hat{x}^*)$ given by (28) (the lines above and below the longest solid line in the middle) and cooperative strategies in the initial game $u^*(t,x^*)$ given by (13) (the longest solid line in the middle)

1.3 Noncooperative Differential Game Model

Consider a case when each player makes a decision about the amount of extracted resources ${u}_i(t,x)$ individually. As a principle of optimality, we use the feedback Nash equilibrium. We denote the payoff of player i in feedback Nash equilibrium $u^{\textrm{NE}}(t,x)=(u^{\textrm{NE}}_1(t,x), \cdots , u^{\textrm{NE}}_n(t,x))$ in the subgame $\Gamma (x,T-t)$ starting at time t in position x by

$$\begin{aligned} V_i(t,x) = \int \limits _{t}^{T}\log (u^{\textrm{NE}}_i(\tau ,x))\textrm{d}\tau \end{aligned}$$

(14)

$$\begin{aligned} \text {s.t.} \qquad&\dot{x}(t) = -\sum \limits _{i=1}^n u^{\textrm{NE}}_i(t,x), \nonumber \\&x(t) = x. \ \end{aligned}$$

(15)

To find the equilibrium strategies $u^{\textrm{NE}}_1(t,x), \cdots , u^{\textrm{NE}}_n(t,x)$, we also use the dynamic programming principle described in [9], corresponding system of Hamilton–Jacobi–Bellman equations:

$$\begin{aligned}&-V^i_t(t,x)=\max \limits _{u_i} \left\{ \log {u_i} - V^i_x(t,x) \left( u_i + \sum \limits _{k=1, \ k \ne i}^n u^{\textrm{NE}}_k \right) \right\} , \nonumber \\&V_i(T,x)=0, \ i \in N. \end{aligned}$$

(16)

In accordance with [9], if there exist continuously differentiable functions $V_i(t,x)$ satisfying (16), then $u_i^{\textrm{NE}}(t,x)$ is a feedback Nash equilibrium. We will look for a value function in the form:

$$\begin{aligned} V_i (t, x) = A_i (t) \,\textrm{log}\, {x} + B_i (t), \ i \in N. \end{aligned}$$

Fig. 6

Resulting equilibrium trajectory $\hat{x}^{\textrm{NE}}(t)$ given by (31) (the below solid line) and equilibrium trajectory in the initial game $x^{\textrm{NE}}(t)$ given by (12) (the above solid line)

By solving (16), we obtain the following form of value function:

$$\begin{aligned} V_i(t,x)=(T-t)\left( \log {\frac{x}{T-t}} - n + 1\right) , \ t\in [t_0, T], \ i \in N, \end{aligned}$$

(17)

Thus, the feedback Nash equilibrium has the form

$$\begin{aligned} u^{\textrm{NE}}_i(t,x)=\frac{x}{T-t}, \ t \in [t_0, T], \ i \in N, \end{aligned}$$

(18)

and corresponding trajectory $x^{\textrm{NE}}(t)$:

$$\begin{aligned} x^{\textrm{NE}}(t)=x_0\left( \frac{T-t}{T-t_0}\right) ^n, \ t \in [t_0, T]. \end{aligned}$$

(19)

Equilibrium strategies $(u^{\textrm{NE}}_1(t,x), \cdots , u^{\textrm{NE}}_n(t,x))$ along the trajectory $x^{\textrm{NE}}(t)$:

$$\begin{aligned} u^{\textrm{NE}}_i(t,x^{\textrm{NE}}) = x_0\frac{(T-t)^{n-1}}{(T-t_0)^n}, \ t \in [t_0, T], \ i \in N. \end{aligned}$$

(20)

In Fig. 6, the above solid line represents the feedback Nash equilibrium strategies $u^{\textrm{NE}}(t,x)$ (20), and the longest continuous solid line in the middle of Fig. 7 represents the corresponding equilibrium trajectory $x^{\textrm{NE}}(t)$ (19).

Fig. 7

Resulting equilibrium strategies $\hat{u}^{\textrm{NE}} (t,\hat{x}^{\textrm{NE}})$ given by (32) (the lines above and below the longest continuous solid line in the middle) and equilibrium strategies in the initial game $u^{\textrm{NE}}(t,x^{\textrm{NE}})$ given by (13) (the longest continuous solid line in the middle of the figure)

2 Game Model with Dynamic Updating

In papers [18, 19, 26,27,28,29,30], the method for constructing a game-theoretic model is described, where players have information about the game structure over a truncated interval and, based on this, make decisions. In order to model the behavior of players in the case, when information updates dynamically, the interval $[t_{0}, T]$ is split into l segments with length $\Delta {t} = \frac{T-t_0}{l}$ and the behavior of players on each segment $[t_0+j\Delta {t},t_0+(j+1)\Delta {t}]$, $j = 0, \cdots , l$ is modeled using the notion of truncated subgame:

Definition 1

Let $j=0, \cdots , l$. Truncated subgame $\bar{\Gamma }_j (x^j_0, t_0 + j\Delta t, t_0 + j\Delta t + \overline{T})$ is game defined on the interval $[t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}]$ as follows. On the interval $[t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}]$ payoff function, motion equation in the truncated subgame and initial game model $\Gamma (x_ {0}, T - t_0)$ coincide:

$$\begin{aligned} K^{j}_{i} (x_0^j, t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}; u_1, \cdots , u_n) = \int \limits _{t_0 + j \Delta {t}}^{t_0 + j \Delta {t} + \bar{T}} \log (u^j_i(\tau , x)) \textrm{d} \tau , \end{aligned}$$

(21)

$$\begin{aligned} \begin{aligned}&\dot{x} = - \sum \limits _{i = 1}^nu_i^j(t, x), \\&x(t_0 + j \Delta t) = x_0^j, \\&x(t) \geqslant 0,\\&u(t, x) \geqslant 0, \end{aligned} \end{aligned}$$

(22)

where $x_0^j = x_{j-1}(t_0 + j \Delta t)$ is the state of the previous truncated subgame $\bar{\Gamma }_{j-1}(x^{j-1}_0, t_0 + (j-1) \Delta t, t_0 + (j-1) \Delta t + \overline{T})$ at the updating instant $t = t_0 + j \Delta t$.

At any instant $t=t_0 + j \Delta {t}$ information about the process is updated, and players adapt to it. Such game models are called games with dynamic updating.

According to the approach described above, at any instant, players have or use truncated information about the game $\Gamma (x_0, T - t_0)$; therefore, the classical approaches for determining optimal strategies (cooperative and noncooperative) cannot be directly applied. In order to determine the solution for games with dynamic updating, we introduce the notion of resulting strategies.

Definition 2

Resulting strategies $\hat{u}(t,x) = (\hat{u}_1(t,x), \cdots , \hat{u}_n(t,x))$ of players in the game with dynamic updating have the form:

$$\begin{aligned} \{ \hat{u}(t,x) \}^{T}_{t = t_0} = {\left\{ \begin{array}{ll} u_{0}(t,x), \quad t \in [t_0, t_0 + \Delta t], \\ \qquad \quad \quad \quad \,\,\, \vdots \\ u_{j}(t,x), \quad t \in (t_0 + j\Delta t, t_0 + (j+1)\Delta t], \\ \qquad \qquad \quad \,\,\, \vdots \\ u_{l}(t,x), \quad t \in (t_0 + l\Delta t, t_0 + (l+1)\Delta t], \end{array}\right. } \end{aligned}$$

(23)

where $u_{j}(t,x) = (u^{j}_1(t,x), \cdots , u^{j}_n(t,x))$ are some fixed strategies chosen by the players in the truncated subgame $\bar{\Gamma }_j(x_{j,0}, t_0 + j \Delta t, t_0 + j \Delta t + \overline{T})$, $j = 0,\cdots ,l$.

The trajectory corresponding to the resulting strategies $\hat{u}(t,x)=(\hat{u}_1(t,x),\cdots ,\hat{u}_n(t,$ x)) is denoted by x(t) and is called the resulting trajectory.

2.1 Cooperative Game Model with Dynamic Updating

Firstly, consider a cooperative version of limited resource extraction game with dynamic updating. Since the structure of truncated subgame on each interval $[t_0+j\Delta {t},t_0+j\Delta {t}+\bar{T}]$ corresponds to the original game defined on the interval $[t_0, T]$, then the solution for each subgame j is defined in the similar way. The main difference is in model parameters; namely, $t_0 + j \Delta {t}$ is the initial instant of the subgame, $t_0 + j \Delta {t} + \overline{T}$ is the terminating instant of the subgame, and $x_0^j$ is the amount of resource at the beginning of truncated subgame. Thus, the cooperative strategies $u^*_j (x,t)$ for each subgame $\bar{\Gamma }_j(x^j_0, t_0 + j\Delta t, t_0 + j\Delta t + \overline{T})$ have the form

$$\begin{aligned} u^*_j(t,x)=\frac{x}{n(t_0+j\Delta {t}+\overline{T}-t)}, \ t \in [t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}], \end{aligned}$$

(24)

and the corresponding cooperative trajectory $x^*_j(t)$:

$$\begin{aligned} x^*_j(t)=x_0^j \frac{t_0+j\Delta {t}+\overline{T}-t}{\overline{T}}, \ t \in [t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}]. \end{aligned}$$

(25)

Note that $x_0^j$ depends on the value of trajectory in the previous truncated subgame $\bar{\Gamma }_j(x_{j,0}, t_0 + j \Delta t, t_0 + j \Delta t + \overline{T})$:

$$\begin{aligned} x_0^j=x_{j-1}(t_0+j\Delta {t}) \text {, where } x_0^0=x_0. \end{aligned}$$

Theorem 1

The resulting cooperative trajectory $\hat{x}^{*}(t)$ in the game model with dynamic updating has the following form:

$$\begin{aligned} \hat{x}^{*}(t){} & {} = x_0\left( 1-\frac{\Delta {t}}{\overline{T}}\right) ^j\frac{t_0+j\Delta {t}+\overline{T}-t}{\overline{T}}, \ t \in [t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}],\nonumber \\ \ j{} & {} =0, \cdots , l. \end{aligned}$$

(26)

Proof

In order to derive the explicit formula for the resulting trajectory using the formula (25), we need to define the parameter $x_0^j$ for any truncated subgame $\bar{\Gamma }_j(x_{j,0}, t_0 + j \Delta t, t_0 + j \Delta t + \overline{T})$.

Consider sections of the trajectory with numbers $j-1$ and j:

$$\begin{aligned} \begin{aligned}&x^{*}_{j-1}(t)=x_0^{j - 1}\frac{t_0+(j - 1)\Delta {t}+\overline{T}-t}{\overline{T}},\\&x^{*}_j(t)=x_0^j\frac{t_0+j\Delta {t}+\overline{T}-t}{\overline{T}}, \end{aligned} \end{aligned}$$

where $x_0^j=x^*_{j-1}(t_0+j\Delta {t})$, then the following holds:

$$\begin{aligned} \begin{aligned}&x_0^j = x_0^{j - 1}\left( 1 - \frac{\Delta {t}}{\overline{T}}\right) ,\\&x_0^{j} = x_0^{j - 2}\left( 1 - \frac{\Delta {t}}{\overline{T}}\right) ^2,\\&\qquad \qquad \qquad \vdots \\&x_0^{j} = x_0^0\left( 1 - \frac{\Delta {t}}{\overline{T}}\right) ^j.\\ \end{aligned} \end{aligned}$$

Taking into account $x_0^0=x_0$, we finally obtain (27):

$$\begin{aligned} x^j_0 = x_0\left( 1 - \frac{\Delta {t}}{\overline{T}}\right) ^n. \end{aligned}$$

(27)

By substituting (27) into (25), we obtain the formula (26):

$$\begin{aligned} \hat{x}^{*}(t){} & {} = x_0\left( 1-\frac{\Delta {t}}{\overline{T}}\right) ^j\frac{t_0+j\Delta {t}+\overline{T}-t}{\overline{T}}, \ t \in [t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}], \ \\ \ j{} & {} =0, \cdots , l. \end{aligned}$$

As a result, the cooperative strategies along the trajectory (26) have the form:

$$\begin{aligned} u^{*}_j(t,x^*_j)=\frac{x_0}{n\overline{T}}\left( 1-\frac{\Delta {t}}{\overline{T}}\right) ^j, t \in [t_0+j\Delta {t},t_0+j\Delta {t}+\bar{T}]. \end{aligned}$$

(28)

The resulting strategies $\hat{u}(t,x)$ (23) are denoted by $\hat{u}^{*}(t,x)$, and the corresponding resulting cooperative trajectory by $\hat{x}^*(t)$.

Figure 4 (Fig. 5) presents a comparison of resulting cooperative trajectory $\hat{x}^{*}(t)$ (26) (resulting cooperative strategies $\hat{u}^{*}(t)$ (28)) in the game with dynamic updating and cooperative trajectory $\hat{x}^{*}(t)$ (12) ($u^{*}(t)$ (13)) in the initial game with prescribed duration.

3 Noncooperative Game Model with Dynamic Updating

Consider now the noncooperative game model with dynamic updating, here it is assumed that players act individually. As in the initial game, we use the feedback Nash equilibrium as the optimality principle. Performing calculations similar to those in Sect. 2.1, we obtain

$$\begin{aligned} u^{\textrm{NE}}_j(t,x){=}\frac{x}{\overline{T}{+}j\Delta {t}{+}t_0{-}t}, \ t \in [t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}], j {=}0,\cdots ,l,\nonumber \\ \end{aligned}$$

(29)

$$\begin{aligned} x^{\textrm{NE}}_j(t){=}x_0^j\left( \frac{\overline{T}+j\Delta {t}+t_0-t}{\overline{T}}\right) ^n, \ t \in [t_0 + j \Delta t, t_0 + j \Delta t + \overline{T}], j {=}0,\cdots ,l.\nonumber \\ \end{aligned}$$

(30)

Theorem 2

The resulting equilibrium trajectory $\hat{x}^{\textrm{NE}}(t)$ in the game model with dynamic updating has the following form:

$$\begin{aligned} \hat{x}^{\textrm{NE}}(t){=} x_0\left( 1{-}\frac{\Delta {t}}{\overline{T}}\right) ^{jn}\left( \frac{t_0+j\Delta {t}{+}\overline{T}{-}t}{\overline{T}}\right) ^n, \ t \in [t_0 {+} j \Delta {t}, t_0 {+} (j{+}1) \Delta {t}].\nonumber \\ \end{aligned}$$

(31)

Proof

Proof is similar to the proof of Theorem 1.

The feedback Nash equilibrium strategies along the equilibrium trajectory $\hat{x}^{\textrm{NE}}(t)$ on the interval $t \in [t_0 + j \Delta {t}, t_0 + (j+1) \Delta {t}]$, $j = 0,\cdots , l$ have the form:

$$\begin{aligned} u^{\textrm{NE}}_j(t,x^{\textrm{NE}}_j(t))=x_0\left( 1-\frac{\Delta {t}}{\overline{T}}\right) ^{jn}\frac{(\overline{T}+j\Delta {t}+t_0-t)^{n-1}}{\overline{T}^n}. \end{aligned}$$

(32)

4 Game Model with Continuous Updating

Consider the case when the length of $\Delta t$ interval between the updating instants is negligibly small, in other words, information updates continuously in time. A class of games where information about the game structure is updated continuously in time, namely $\Delta {t}\rightarrow {0}$ or $l \rightarrow {\infty }$, is called the games with continuous updating.

In order to construct the resulting strategies and the resulting trajectory for a class of games with continuous updating in the general case, the application of classical approaches to dynamic programming, even for deriving the successive solutions to each truncated subgame, is not possible due to the infinite number of updating intervals $[t_0 + j \Delta t, t_0 + (j + 1) \Delta t]$, when $\Delta {t}\rightarrow {0}$. This class of problems till now was only studied in the papers [20, 21].

In this section, we apply the results of the paper [20], where the form of Hamilton–Jacobi–Bellman solution is presented for a case of continuous updating. Here, we will construct the cooperative strategies (10) (equilibrium strategies (18)) for a game model of resource extraction with continuous updating. Corresponding strategies will be denoted by $\tilde{u}^*(t, x)$ ($\tilde{u}^{\textrm{NE}}(t,x)$). Further we prove that these strategies are the resulting cooperative strategies (noncooperative strategies) in the game with dynamic updating, when $\Delta {t}\rightarrow {0}$, showing that these strategies are indeed the strategies with continuous updating.

Following the procedure described in the paper [20], in the first step, we consider the following game model $\Gamma (x, t, t + \overline{T})$, with an initial time t and a termination time $t + \overline{T}$:

$$\begin{aligned} K^{t}_{i} (x, t, t + \overline{T}; u^t_1, \cdots , u^t_n) = \int \limits _{t}^{t + \bar{T}} \log (u^t_i(\tau , x)) \textrm{d} \tau \end{aligned}$$

(33)

$$\begin{aligned} \begin{aligned} \text {s.t.} \qquad&\dot{x} = - \sum \limits _{i = 1}^nu_i^t(\tau , x), \\&x(t) = x, \\&x(t) \geqslant 0,\\&u(t,x)\geqslant 0, \end{aligned} \end{aligned}$$

(34)

where x is some starting position. Here, we suppose that the parameter t is a fixed constant. We will use the game model (33), (34) to construct the strategies for the games with continuous updating. According to the procedure presented in [20], we construct Hamilton–Jacobi–Bellman equations to find the cooperative (noncooperative) strategies, namely the optimal strategies (feedback Nash equilibrium). In order to do that, we need to define value function for this game model:

$$\begin{aligned} V(t,\tau ,x)= & {} \max \limits _{u^t}\left\{ \sum \limits _{i=1}^{n} K^t_i(x, t + \overline{T} - \tau ; u^t_1, \cdots , u^t_n) \right\} \nonumber \\= & {} \max \limits _{u^t}\left\{ n\int \limits _{\tau }^{t + \overline{T}}\log (u^t(\tau ,x))\textrm{d}\tau \right\} , \ \tau \in [t, t + \overline{T}] \end{aligned}$$

(35)

$$\begin{aligned} \Bigg ( V_i(t,\tau ,x)= & {} K^t_i(x, t + \overline{T} - \tau ; u^{t,\textrm{NE}}_1, \cdots , u^{t,\textrm{NE}}_n) \nonumber \\= & {} \int \limits _{\tau }^{t + \overline{T}} \log (u^{t,\textrm{NE}}_i(\tau ,x))\textrm{d}\tau , \ \tau \in [t, t + \overline{T}], \ i \in N \Bigg ), \end{aligned}$$

(36)

where the value function $V(t,\tau ,x)$ is the maximum value of total payoff of players (33) in the subgame $\Gamma (x, \tau , t + \overline{T})$, starting at the instant $\tau \in [t, t + \overline{T}]$ in the position x. (The value function $V_i(t,\tau ,x)$ is the payoff of player $i \in N$ in the feedback Nash equilibrium $u^{t,\textrm{NE}}(\tau ,x)=(u^{t,\textrm{NE}}_1(\tau ,x), \cdots , u^{t,\textrm{NE}}_n(\tau ,x))$ in the subgame $\Gamma (x, \tau , t + \overline{T})$ starting at the instant t in the position x.)

Using the approach described in Sect. 2.1, we can derive the corresponding Hamilton–Jacobi–Bellman equation to determine the cooperative strategies (feedback Nash equilibrium strategies):

$$\begin{aligned}&-V_{\tau }(t,\tau ,x)=\max \limits _{u^t}\left\{ n \log {u^t} - n u^t V_x(t,\tau ,x) \right\} , \nonumber \\&V(t, t + \overline{T}, x)=0 \end{aligned}$$

(37)

$$\begin{aligned}&\Bigg ( -V^i_{\tau }(t,\tau ,x)=\max \limits _{u^t}\left\{ n \log {u^t} - n u^t V^i_x(t,\tau ,x) \right\} , \nonumber \\&V(t,t + \overline{T},x)=0 \Bigg ). \end{aligned}$$

(38)

The technique for solving (37) and (38) is similar to the one used for classical control problems in Sect. 2.1. Therefore, in order to demonstrate the solution technique we will only present the solution for cooperative setting (37), i.e., determine the cooperative strategies $u^{t,*}(\tau ,x)$.

From the first-order extremum condition for (37), we obtain

$$\begin{aligned} u^{t,*}=\frac{1}{V_x(t, \tau ,x)}, \end{aligned}$$

and substitute in (37):

$$\begin{aligned}&V_t(t, \tau ,x)=n\log {V_x(t, \tau ,x)}+n,\\&V(t,t + \overline{T},x)=0. \end{aligned}$$

We define the value function in the form:

$$\begin{aligned} V(t,\tau ,x)=A(t,\tau )\log {x}+B(t,\tau ); \end{aligned}$$

then by substituting into (37), we obtain:

$$\begin{aligned}&\dot{A}_{\tau }(t,\tau )\log {x}+\dot{B}_{\tau }(t,\tau ) = n\log {A}(t,\tau )-n\log {x}+n, \nonumber \\&A(t, t + \overline{T})=B(t, t + \overline{T})=0. \end{aligned}$$

(39)

Solution of (39) is the functions:

$$\begin{aligned} \begin{aligned} A(t, \tau )&=n(t + \overline{T} - \tau ),\\ B(t, \tau )&=-n(t + \overline{T} - \tau )\log {n(t + \overline{T} - \tau )}, \ \tau \in [t, t + \overline{T}]. \end{aligned} \end{aligned}$$

(40)

Finally, we obtain an expression for the value function:

$$\begin{aligned} V(t,\tau ,x)=n(t + \overline{T} - \tau )\log {\frac{x}{n(t + \overline{T} - \tau )}}, \tau \in [t, t + \overline{T}], \end{aligned}$$

(41)

and an expression for the optimal control:

$$\begin{aligned} u^{t,*}(\tau ,x) = \frac{1}{V_x} = \frac{x}{n(t + \overline{T} - \tau )}, \ \tau \in [t, t + \overline{T}]. \end{aligned}$$

(42)

Control or strategy $u^{t,*}(\tau ,x)$ (42) is optimal in the game model $\Gamma (x, t, t + \overline{T})$, which is defined on the interval $[t, t + \overline{T}]$. Therefore, the strategy $u^{t,*}(\tau ,x)$ (42) for a fixed t is defined on the same interval, i.e., $[t, t + \overline{T}]$. But by changing the parameter t, we change the initial instant of the game $\Gamma (x, t, t + \overline{T})$ and therefore automatically change the interval on which the optimal control (feedback Nash equilibrium) is calculated. It is important to notice that the optimal control (42) explicitly depends on the parameter t as well as on the parameters $\overline{T}$ and $\tau$. Using $u^{t,*}(\tau ,x)$ (42), we construct the strategy that we will use to prove the convergence result. As it was mentioned above, we consider the problem where the information horizon moves as the time evolves. Suppose that at the instant t as a resulting strategy in the game with continuous updating we use $\tilde{u}^*(t,x) = u^{t,*}(\tau ,x)$, where $\tau = t$. It means that at any instant t players orient themselves or define the optimal strategies using the information on the interval $[t, t + \overline{T}]$. But as the time evolves, the information horizon shifts and at the instant $\bar{t}$ players orient themselves on the interval $[\bar{t}, \bar{t} + \overline{T}]$.

The same procedure can be performed for the equilibrium strategies, which we will denote by $\tilde{u}^{\textrm{NE}}(t,x)$:

$$\begin{aligned} \tilde{u}^*(t,x)=\frac{x}{n\overline{T}} \quad \left( \tilde{u}^{\textrm{NE}}(t,x)=\frac{x}{\overline{T}} \right) . \end{aligned}$$

(43)

Next thing we need to do is to show that the strategies constructed in this way are the strategies in the game with continuous updating, namely, in the case when interval between the updating instants $\Delta {t}\rightarrow {0}$ or, $l \rightarrow {\infty }$.

Theorem 3

When $\Delta {t}\rightarrow {0}$ or $l\rightarrow {\infty }$, the resulting strategies $\hat{u}^{*}(t,x)=\hat{u}^{*}_l(t,x)$ (28) ($\hat{u}^{\textrm{NE}}(t,x)=\hat{u}^{\textrm{NE}}_l(t,x)$ (29)) in the game with dynamic updating uniformly converge to $\tilde{u}^*(t,x)$ ($\tilde{u}^{\textrm{NE}}(t,x)$), which are the resulting strategies with continuous updating (43):

$$\begin{aligned} \hat{u}^{*}_l(t,x) \underset{[t_0,T]}{\rightrightarrows }\ \tilde{u}^{*}(t,x) \quad \left( \hat{u}^{\textrm{NE}}_l(t,x) \underset{[t_0,T]}{\rightrightarrows }\ \tilde{u}^{\textrm{NE}}(t,x) \right) . \end{aligned}$$

(44)

Proof

From the solution of initial game presented in Sect. 2, it follows that the strategy of player i in noncooperative game differs from the corresponding strategy only by the coefficient n; therefore, in the proof we present only the cooperative case.

We use the criterion for uniform convergence of sequence of functions $\hat{u}^{*}_l(t,x)$ as $l \rightarrow {\infty }$ to the function $\tilde{u}^{*}(t,x)$, where l is the number of updating instants:

$$\begin{aligned} \lim _{\Delta {t}\rightarrow {0}}\sup _{t \in [t_0,T]}|\hat{u}^{*}_l(t,x) - \tilde{u}^*(t,x)| = \lim _{l\rightarrow {\infty }}\sup _{t \in [t_0,T]}|\hat{u}^{*}_l(t,x) - \tilde{u}^*(t,x)| = 0. \end{aligned}$$

(45)

Suppose that the greatest value of difference $\hat{u}^{*}_l(t,x) - \tilde{u}^*(t,x)$ (45) belongs to the interval $[t_0+j\Delta {t},t_0+(j+1)\Delta {t}]$, then it is necessary to prove the following equality:

$$\begin{aligned} \lim _{\Delta {t}\rightarrow {0}}\sup _{t \in [t_0+j\Delta {t},t_0+(j+1)\Delta {t}]}|u^{*}_j(t,x) - \tilde{u}^*(t,x)| = 0. \end{aligned}$$

(46)

The greatest value of $\hat{u}^{*}_l(t,x) - \tilde{u}^*(t,x)$ can be achieved in three cases:

• (1) In the inner point of interval $(t_0 + j \Delta t, t_0 + (j + 1) \Delta t)$, then the extremum of difference (46) can be found using the first-order condition:

  $$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}(u^{*}_j(t,x) - \tilde{u}^*(t,x)){} & {} = \frac{\textrm{d}}{\textrm{d}t}\left( \frac{x}{n(\overline{T} + j\Delta {t} + t_0 - t)} - \frac{x}{n\overline{T}} \right) \\{} & {} = \frac{x}{n(\overline{T} + j\Delta {t} + t_0 - t)^2}. \end{aligned}$$

  Derivative does not reach zero on the interval $(t_0 + j \Delta t, t_0 + (j + 1) \Delta t)$, and it shows the strict monotonicity of difference function on the interval $(t_0 + j \Delta t, t_0 + (j + 1) \Delta t)$.

• (2) In the left-hand side of interval $[t_0 + j \Delta t, t_0 + (j+1) \Delta t]$, i.e., at the instant $t = t_0 + j\Delta {t}$:

  $$\begin{aligned}{} & {} \lim _{\Delta t \rightarrow {0}}|u^{*}_j(t_0 + j\Delta {t},x) - \tilde{u}^*(t_0 + j\Delta {t},x)| \\{} & {} = \lim _{\Delta t \rightarrow {0}}\left| \frac{x}{n(\overline{T} + j\Delta {t} + t_0 - (t_0 + j\Delta {t}))} - \frac{x}{n\overline{T}}\right| \\{} & {} = \lim _{\Delta t \rightarrow {0}}\left| \frac{x}{n\overline{T}} - \frac{x}{n\overline{T}}\right| = 0. \end{aligned}$$

• (3) In the right-hand side of interval $[t_0 + j \Delta t, t_0 + (j+1) \Delta t]$, i.e., at the instant $t = t_0 + (j+1)\Delta {t}$:

  $$\begin{aligned}{} & {} \lim _{\Delta t \rightarrow {0}}\left| u^{*}_j(t_0 + (j+1)\Delta {t},x) - \tilde{u}^*(t_0 + (j+1)\Delta {t},x)\right| \\{} & {} = \lim _{\Delta t \rightarrow {0}}\left| \frac{x}{n(\overline{T} + j\Delta {t} + t_0 - (t_0 + (j+1)\Delta {t}))} - \frac{x}{n\overline{T}}\right| \\{} & {} = \lim _{\Delta t \rightarrow {0}}\left| \frac{x}{n(\overline{T} - \Delta {t})} - \frac{x}{n\overline{T}}\right| = 0. \end{aligned}$$

The value of difference (46) within the interval does not exceed the values on the edges of interval, and on the left- and right-hand side the value of difference function tends to zero and as a result the value on the interval tends to zero.

In accordance with the criterion (45), the sequence of resulting controls $\hat{u}^{*}(t,x)=\hat{u}^{*}_l(t,x)$ with dynamic updating uniformly converges to the control $\tilde{u}^*(t,x)$ with continuous updating as $l\rightarrow {\infty }$.

Theorem 4

Cooperative trajectory in the game with dynamic updating $\hat{x}^*(t)=\hat{x}^*_l(t)$ uniformly converges to the trajectory in the game with continuous updating $\tilde{x}^*(t)$ for $\Delta {t}\rightarrow {0}$ or $l\rightarrow {\infty }$.

Proof

Notice that

$$\begin{aligned}{} & {} \hat{u}^{*}(t,x)= \hat{u}^{*}_l(t,x) = x\hat{u}^{*}(t,1),\\{} & {} \tilde{u}^{*}(t,x)=x\tilde{u}^{*}(t,1), \end{aligned}$$

then from the form of motion equation (22) for the case of dynamic updating, we obtain

$$\begin{aligned}{} & {} \frac{\textrm{d}\hat{x}^*_l}{\textrm{d}t}(t)=-nu^*(t,x)=-n\hat{x}^*_l\hat{u}^{*}(t,1),\\{} & {} \log {\hat{x}^*_l(t)} = -n \int \limits _{t_0}^t\hat{u}^{*}(\tau ,1)\textrm{d}\tau . \end{aligned}$$

In case of continuous updating:

$$\begin{aligned}{} & {} \frac{\textrm{d}\tilde{x}^*}{\textrm{d}t}(t)=-nu^*(t,x)=-n\tilde{x}^*(t)\tilde{u}^{*}(t,1),\\{} & {} \log {\tilde{x}^*(t)} = -n \int \limits _{t_0}^t\tilde{u}^{*}(\tau ,1)\textrm{d}\tau . \end{aligned}$$

From the properties of uniform convergence for strategies:

$$\begin{aligned} \hat{u}^{*}_l(t,x) \underset{[t_0,T]}{\rightrightarrows } \tilde{u}^{*}(t,x) \quad \Longrightarrow \quad n\int \limits _{t_0}^t\hat{u}^{*}_l(\tau ,x)\textrm{d}\tau \underset{[t_0,T]}{\rightrightarrows }\ n\int \limits _{t_0}^t\tilde{u}^{*}(\tau ,x)\textrm{d}\tau \nonumber \\ \quad \Longrightarrow \quad \exp \left\{ -n\int \limits _{t_0}^t\hat{u}^{*}_l(\tau ,x)\textrm{d}\tau \right\} \underset{[t_0,T]}{\rightrightarrows }\ \exp \left\{ -n\int \limits _{t_0}^t\tilde{u}^{*}(\tau ,x)\textrm{d}\tau \right\} . \end{aligned}$$

(47)

Since function $\textrm{e}^{-s}$ is bounded on the interval $s \in [0, \infty )$, then the following holds:

$$\begin{aligned} \hat{x}^{*}_l(t,x) \underset{[t_0,T]}{\rightrightarrows }\ \tilde{x}^{*}(t,x). \end{aligned}$$

(48)

Construct the resulting trajectory with continuous updating by substituting $\tilde{u}^*(t,x)$ ($\tilde{u}^{\textrm{NE}}(t,x)$) into the motion equation (1):

$$\begin{aligned} \begin{array}{l} \dot{x}=-\dfrac{x}{\overline{T}},\\ x(t_0)=x_0 \end{array} \quad \left( \begin{array}{l} \dot{x}=-n\dfrac{x}{\overline{T}}\\ x(t_0)=x_0 \end{array}\right) . \end{aligned}$$

(49)

Then, the corresponding solutions are the trajectories in the game with continuous updating:

$$\begin{aligned} \tilde{x}^*(t)={x_0}\textrm{e}^{-\frac{t-t_0}{\overline{T}}} \quad \left( \tilde{x}^{\textrm{NE}}(t)={x_0}\textrm{e}^{-n\frac{t-t_0}{\overline{T}}}\right) . \end{aligned}$$

(50)

The optimal strategies (feedback Nash equilibrium strategies) along the resulting trajectory in the game with continuous updating have the form:

$$\begin{aligned} \tilde{u}^*(t, \tilde{x}^*(t))=\frac{x_0}{n\overline{T}}\textrm{e}^{-\frac{t-t_0}{\overline{T}}} \quad \left( \tilde{u}^{\textrm{NE}}(t, \tilde{x}^{\textrm{NE}}(t))=\frac{x_0}{\overline{T}}{x_0}\textrm{e}^{-n\frac{t-t_0}{\overline{T}}}\right) . \end{aligned}$$

(51)

5 Numerical Simulation

Consider the results of numerical simulation for the game model of three symmetric players ($n = 3$) on the interval [0, 100], i.e., $t_0 = 0$, $T = 100$. At the initial instant $t_0 = 0$, the amount of resource is 2 000, i.e., $x_0 =$ 2 000. Suppose that for the case of a dynamic updating (the lines composed of a solid line and a dashed line in Figs. 8, 9, 10, 11), the intervals between updating instants are $\Delta t = 20$; therefore, $l = 5$. In Figs. 8, 10, the comparison of resulting strategies in the initial game with the prescribed duration (the top line) in the game with dynamic updating (the bottom line) and continuous updating (the middle line) for cooperative and noncooperative case is presented. In Figs. 9, 11, similar results are presented for the strategies.

Fig. 8

Resulting cooperative trajectory $\tilde{x}^{*}(t)$ given by (50) with continuous updating (solid line in the middle), resulting cooperative trajectory $\hat{x}^{*}(t)$ given by (26) with dynamic updating (solid line below) and cooperative trajectory in the initial game $x^{*}(t)$ given by (12) (solid line above)

Fig. 9

Resulting cooperative strategies $\tilde{u}^{*}(t)$ given by (43) with continuous updating (vertically inclined line), resulting cooperative strategies $\hat{u}^{*}(t)$ given by (28) with dynamic updating (lines that are horizontally above and below the longest solid line in the middle) and cooperative strategies in the initial game $u^*(t)$ given by (13) (the longest solid line in the middle of the horizontal direction)

Fig. 10

Resulting equilibrium trajectory $\tilde{x}^{\textrm{NE}}(t)$ given by (50) with continuous updating (the middle line), resulting equilibrium trajectory $\hat{x}^{\textrm{NE}}(t)$ given by (31) with dynamic updating (the below line) and equilibrium trajectory in the initial game $x^{\textrm{NE}}(t)$ given by (19) (the top line)

Fig. 11

Resulting equilibrium strategies $\tilde{u}^{\textrm{NE}}(t)$ given by (43) with continuous updating (continuous solid line from $(0, x_0/\overline{T})$ to (T, 0)), resulting equilibrium strategies in the initial game $u^{\textrm{NE}}(t)$ given by (20) (another continuous solid line from the vertical axis to (T, 0)), resulting equilibrium strategies $\hat{u}^{\textrm{NE}}(t)$ given by (32) with dynamic updating (the rest of the lines)

In order to demonstrate the results of Theorems 3 and 4 on convergence of resulting strategies and resulting trajectory, consider the simulation results for a case of frequent updating, namely $l=50$. Figures 12, 13, 14 and 15 represent the same solutions as in Figs. 8, 9, 10 and 11, but for the case, when $\Delta t = 2$. Therefore, convergence results are confirmed by the numerical experiments presented below.

Fig. 12

$\tilde{x}^{*}(t)$ given by (50) (red line), $\hat{x}^{*}(t)$ given by (26) (the bottom lines) and $x^{*}(t)$ given by (12) (the top line). Color figure online

Fig. 13

$\tilde{u}^{*}(t)$ given by (43) (continuous solid line from $(0, x_0/n\overline{T})$ to $(\infty , 0)$),$u^*(t)$ given by (13) (the longest continuous solid line in the horizontal direction) and $\hat{u}^{*}(t)$ given by (28) (other horizontal lines)

Fig. 14

$\tilde{x}^{\textrm{NE}}(t)$ given by (50) (the middle solid line), $x^{\textrm{NE}}(t)$ given by (19) (the top solid line) and $\hat{x}^{\textrm{NE}}(t)$ given by (31) (other lines)

Fig. 15

$\tilde{u}^{\textrm{NE}}(t)$ given by (43) (continuous solid line from $(0, x_0/\overline{T})$ to $(\infty , 0)$), $u^{\textrm{NE}}(t)$ given by (20) (another continuous solid line from the vertical axis to $(\infty , 0)$) and $\hat{u}^{\textrm{NE}}(t)$ given by (32) (other lines)

6 Conclusions

The optimal and feedback Nash equilibrium strategies for cooperative and noncooperative game models of non-renewable resource extraction with dynamic and continuous updating are constructed. The theorems are proved on the uniform convergence of resulting strategies and trajectories for $\Delta t \rightarrow 0$. Such a class of games has not been studied before, and the classical approaches of dynamic programming or the maximum principle cannot be applied to problems in which updating occurs continuously over time. In this regard, the results presented are valuable. We plan to study the construction of cooperative solution and study the property of time consistency. The obtained results are both fundamental and applied in nature, since they allow specialists from the applied field to use a new mathematical tool for more realistic modeling of conflict-controlled real-life processes.