Mars Trojan Orbits for Continuous Earth-Mars Communication

Abstract

This investigation selects orbits appropriate for a deep-space relay terminal to ensure continuous communication between Earth and Mars. Geometric constraints are derived and are used to evaluate the fitness of several periodic orbit families in the sun-Earth and sun-Mars circular-restricted three-body systems. It is determined that Mars Trojan orbits provide the best solution. Families of these orbits are presented and studied for stability in a multibody model. It is shown that with no station-keeping, appropriately chosen orbits satisfy the geometric telecommunication constraints for decades. Outbound transfer costs from Earth and orbit insertion costs are computed in both Keplerian and ephemeris-level multibody regimes. The use of an outbound Mars flyby significantly lowers the orbit insertion cost.

Introduction

Mars now hosts six operational orbiters,¹ two operational landers,² and should only expect its family of robotic explorers to grow in the future, due to the ongoing scientific interest in Mars’s geologic and climatic history and the potential for extinct or extant Martian life. Mars also remains a prime target for human exploration and colonization due to its stores of water ice and other resources necessary for human settlement. In the future, both robotic and human missions may return voluminous amounts of science data, high-definition images, streaming video, etc. As the number and complexity of missions grows, continuous, high-bandwidth communication with Earth will become highly desirable and perhaps, eventually, indispensable.

Communication between Earth and Mars degrades approximately every 26 months when the Earth-Mars line passes near or through the sun (see Table 1 and Fig. 1) [1]. The degradation in communication during these periods of solar conjunction brings command uplink and science downlink moratoriums, and critical events like aerobraking must be rescheduled. Also, below a frequency-dependent sun-Earth-probe (SEP) angle, radio-frequency (RF) navigation data become significantly noisier, eventually becoming ineffective. For surface vehicles lacking multiday autonomy, the command moratorium means these vehicles remain stationary and dormant for weeks [2]. Unplanned critical events occurring during solar conjunction, as when a spacecraft enters “safe mode” due to unforeseen circumstances, might permanently cripple the spacecraft without human intervention, for both surface and orbital missions.

Table 1 Earth-Mars solar conjunctions through Jan. 1, 2100

Fig. 1

Earth-Mars solar conjunction duration

During previous human missions in low Earth orbit and to the moon, reliable and constant communication with Earth has already proven beneficial. The most famous intervention occurred during the Apollo 13 lunar mission when, after an oxygen tank exploded on the service module, the problem-solving of ground support personnel enabled the safe return of crew after a post-anomaly flight of almost four days [3, 4]. During STS-114, enhanced inspection of the Space Shuttle, prompted by the disintegration of Columbia during reentry, revealed gap-filling material protruding between tiles of the orbiter’s thermal protection system. The protrusion was considered potentially hazardous due to the possibility for increased heating during reentry, so analysts conducted simulations to assess the aerothermodynamic implications of the protuberances to inform a recommended course of action [5]. After deciding to remove the most egregious gap fillers, mission controllers developed procedures to either remove or cut the fillers, including demonstration videos that were uplinked to the Shuttle [6]. The procedures enabled the crew to successfully remove the gap fillers and later safely reenter the atmosphere. Numerous other lesser-known anomalies, such as during the construction of the International Space Station when an astronaut during a spacewalk was coated in ammonia but advised by flight controllers with a plan to remove the coating [7], also demonstrate the utility of Earth-based intervention. Assistance during human spaceflight in the Earth-moon system is admittedly easier than at Mars where the one-way light time can rise above 22 minutes, but having a delayed response is clearly preferable to no response at all.

Most recent Mars missions communicate via X-band (8–12 GHz) [8]. At this frequency, the science downlink and command uplink moratoria are imposed when the SEP angle drops below about two to three degrees. For orbiters, tracking data for navigation purposes are noticeably noisier when the SEP angle drops below five degrees and are nearly useless when the SEP angle drops below three degrees. The actual minimum SEP angle where data are still useful is difficult to predict and is dependent on the transmission frequency, the presence of solar events, and the phase of the solar cycle [9].

Communication via Ka-band (26–40 GHz) is less susceptible to solar effects than via X-band and therefore represents an effective strategy in reducing the duration of communication blackout periods. With Ka-band, it may be possible to reliably communicate down to SEP angles of one degree [9]. While downlink via Ka-band is available at each complex of NASA’s Deep Space Network (DSN), uplink via Ka-band is currently limited to the Goldstone, California complex (though new Ka-band uplink capabilities are planned in the future for all three DSN complexes) [10, 11]. Moreover, Ka-band is more susceptible than X-band to corruption by Earth atmospheric weather like rain. Also, regardless of the communication frequency, periods of increased solar activity will increase the minimum allowable SEP angle.

An optical communication system enables higher bandwidth than an RF system and requires less mass, volume, and power than an RF system. Optical systems may provide an order of magnitude or greater increase in data rate with the same mass and power required for current RF systems [12]. Another perk of optical communication is that unlike RF bands, whose use is internationally regulated due to spectral congestion, optical frequencies are unregulated. The choice of an optical system, however, incurs months-long communication gaps at Mars because the minimum SEP angle for reliable communication may be 10 deg or more [13].

Given that the current X-band systems and the promising future optical systems incur a significant blackout period during solar conjunction, and given that any direct Earth-Mars communication system will fail when Mars is completely occulted by the sun (e.g. in 2023, 2038, and 2045), a limited number of studies have proposed using relay spacecraft to provide continuous communication during these periods. The concept of relay spacecraft placed at the triangular libration points throughout the solar system for the purpose of continuous communication with Earth was put forward by Strong in 1967 and 1972, with a focus chiefly on the triangular points of the sun-Earth system [14, 15]. Dealing specifically with the problem of continuous Earth-Mars communication, Howard in 1996 studied the attributes of a telecom system with large relay spacecraft placed in Earth-leading and Earth-trailing orbits [16]. Addressing the great distance between Mars and relays in Earth-like orbits or at the sun-Mars L₄ or L₅ points, Gangale proposed in 2005 to use a relay spacecraft in a Mars-like orbit allowing an unobstructed link to Earth and Mars during solar conjunction periods [17]. The relay spacecraft’s heliocentric orbit would have the same orbital period as Mars but different inclination and eccentricity, chosen so that the orbit’s path would appear as a ring around the sun-Mars line when viewed in a sun-Mars rotating reference frame. Orbit insertion costs, not evaluated in the study, could be prohibitive due to the high inclination required for even modest minimum SEM angles. In 2011, Macdonald et al. studied the potential for high-specific-impulse, low-thrust propulsion systems to maintain a relay spacecraft in a non-Keplerian orbit above Mars’s orbital plane [18]. This investigation estimated orbit maintenance requirements for both solar electric propulsion and hybrid solar sail systems, and considered a strategy to reduce energy needs by not continuously maintaining the relay geometry. Freeing the orbit shape from the confines of the heliocentric ellipse is an attractive possibility, but the lack of maturity of high-specific-impulse solar electric and solar sail technology, along with the required ongoing orbit maintenance, make this non-Keplerian option more problematic. Numerous other studies deal with the Earth-Mars communication problem conceptually, usually suggesting relays at L₄ and L₅, and other studies addressing Mars communication networks are focused on global visibility of the Martian surface and do not address the Earth-Mars conjunction issue.

The present study seeks an orbit that allows a single spacecraft to provide continuous Earth-Mars communication during solar conjunction by avoiding solar interference. It is assumed that communication from the surface of Mars can be routed through nearby orbiting spacecraft (like the Mars Reconnaissance Orbiter today) to the deep-space relay. This assumption removes the need to analyze the Martian surface visibility of the deep-space relay, and focuses this study on searching for and documenting the properties of orbits that satisfy the geometric constraints that enable continuous communication. The outbound transfer costs from Earth to the relay orbit will also be documented.

Geometry

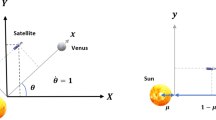
For communication between Earth and the relay spacecraft, the SEP angle must be greater than a specified minimum value, Φ. Due to relay spacecraft architecture limitations on receive and transmit power, the spacecraft must remain within a specified range of Mars while receiving and transmitting. It is preferable to maintain a long Earth-spacecraft leg rather than a long Mars-spacecraft leg since it is more practical to increase the size or power of Earth-based communications equipment than doing the same on the spacecraft or on Mars. Geometrically, these two main constraints define a “solar exclusion cone” and “Mars communication sphere” (Fig. 2). The solar exclusion cone, with its apex at the Earth and centerline defined by the Earth-sun line, establishes the region of space that the spacecraft must avoid during periods of Earth-Mars solar conjunction in order to function as a valid communication relay. The Mars-centered communication sphere defines the region within which the spacecraft must remain during solar conjunction periods. It is therefore desired to find orbits that situate the spacecraft within the Mars communication sphere but outside the solar exclusion cone and do so for multiple consecutive solar conjunction periods. This region is termed the comm zone.

Fig. 2

Geometric constraints

The geometric constraints limit the options for viable relay orbits. The solar exclusion cone imposes a minimum distance requirement on the trajectory if the spacecraft is to be visible to Earth and Mars during an entire solar conjunction period. Assuming a circular, coplanar solar system, and a coplanar spacecraft orbit, this minimum distance can be derived as a function of the minimum SEP angle.

At the commencement of the solar conjunction period, any spacecraft “behind” the Earth-Mars line will be outside the solar exclusion cone (Fig. 3). That is, any spacecraft with a geocentric position r such that $\boldsymbol {r} \cdot (\boldsymbol {\hat {h}}_{E} \times \boldsymbol {\hat {r}}_{EM_{0}}) > 0$ where $\boldsymbol {\hat {h}}_{E}$ is the direction of Earth’s angular momentum about the sun, and $\boldsymbol {\hat {r}}_{EM_{0}}$ is the Earth-Mars direction. Any relay spacecraft “ahead” of the Earth-Mars line (i.e. at a location of $\boldsymbol {r} \cdot (\boldsymbol {\hat {h}}_{E} \times \boldsymbol {\hat {r}}_{EM_{0}}) < 0$) must be at least a distance d away from Mars to be outside the solar exclusion region, as shown in Fig. 3. This distance can be derived in terms of known quantities by observing that

$$ \sin 2{\Phi} = \frac{d}{r_{EM_{0}}} $$

(1)

where $r_{EM_{0}}$ is the Earth-Mars distance at the commencement of the solar conjunction period. Solving for d gives

$$ \begin{array}{@{}rcl@{}} d &=& r_{EM_{0}}\sin2{\Phi} \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} d &=& 2 r_{EM_{0}}\sin{\Phi}\cos{\Phi} \end{array} $$

(3)

Similarly, at the termination of the solar conjunction period, any spacecraft behind the Earth-Mars line must have a Mars range of at least d, and any spacecraft ahead of the Earth-Mars line will be outside the solar exclusion cone. Because the spacecraft must provide relay communication continuously, the spacecraft-Mars distance must be greater than d at the beginning and end of the conjunction period. At the middle of the conjunction period, the spacecraft’s distance from Mars must be greater than $(r_{E} + r_{M})\sin \limits {\Phi }$.

Fig. 3

Planar solar exclusion zone geometry (sun-Earth rotating frame)

For a given Φ, the minimum distance d is a function of $r_{EM_{0}}$. By the law of sines, the initial Earth-Mars distance is given by

$$ r_{EM_{0}} = r_{M}\frac{\sin\beta}{\sin{\Phi}} $$

(4)

where the heliocentric radius of Mars, r_M, is constant by the circular solar system assumption, and β is the Earth-sun-Mars angle. The angle β is equivalent to π −Φ− α where α is the Earth-Mars-sun angle. By the law of sines, α is given by

$$ \sin\alpha = \frac{r_{E}}{r_{M}}\sin{\Phi} $$

(5)

where r_E is the constant heliocentric Earth radius. Since α is known, β is known; and since β is known, $r_{EM_{0}}$ is known. Thus, substituting Eqs. 4–5 into Eq. 3 gives the minimum Mars-spacecraft distance as

$$ \begin{array}{@{}rcl@{}} d &=& 2r_{M}\frac{\sin\beta}{\sin{\Phi}} \sin{\Phi}\cos{\Phi} \end{array} $$

(6)

$$ \begin{array}{@{}rcl@{}} d &=& 2r_{M}\sin({\Phi} + \alpha)\cos{\Phi} \end{array} $$

(7)

$$ \begin{array}{@{}rcl@{}} d &=& 2r_{M} \sin\left[ {\Phi} + \arcsin\left( \frac{r_{E}}{r_{M}}\sin{\Phi} \right)\right] \cos{\Phi} \end{array} $$

(8)

Figure 4 shows how the minimum Mars range varies for ${\Phi } \leqslant 15$ deg, for r_E = 1 AU and r_M = 1.5 AU. This result is useful when selecting a relay orbit since it eliminates many orbit candidates based on their proximity to Mars.

Fig. 4

Minimum Mars range

The angular offset between the sun-Mars line at the initial time and the final time is denoted 𝜃. To solve for 𝜃 in terms of known quantities, it is observed that 𝜃/2 and β are supplementary angles:

$$ \frac{\theta}{2} + \beta = \pi $$

(9)

Rewriting β in terms of Φ and α, and solving for 𝜃 gives

$$ \theta = 2({\Phi} + \alpha) $$

(10)

Substituting for α with Eq. 5 gives

$$ \theta = 2 \left[ {\Phi} + \arcsin\left( \frac{r_{E}}{r_{M}}\sin{\Phi}\right)\right] $$

(11)

Orbit Type Selection

The key criterion in the orbit selection process is that the spacecraft must be somewhere in the comm zone during the entirety of each Earth-Mars solar conjunction period. To satisfy this constraint, the orbit must pass at least once through the comm zone, and either remain in the comm zone for an extended duration, or re-enter it every Earth-Mars synodic period. Many trajectories could place the spacecraft in the comm zone for only one conjunction period, but such a single-use relay would likely not be cost-effective unless it was also repurposed for another mission. Using multiple spacecraft would broaden the choice of acceptable orbit families and is certainly worthy of further study, but only a single spacecraft is considered here.

Because repeatability of the relay geometry is required, periodic orbits are considered; because the communication endpoints are Mars and Earth, orbits are considered in the sun-Mars and sun-Earth systems. JPL’s Mission Operations and Navigation Toolkit Environment (Monte) [19, 20], used for trajectory design and spacecraft navigation operations, contains a database [21] of periodic orbits in the circular-restricted three-body problem (CRTBP). The database includes libration point, secondary-centered, and resonant orbit families for multiple planetary systems (e.g. Earth-moon, Saturn-Titan). For the present study, every orbit in every orbit family in the sun-Earth and sun-Mars systems in the database is evaluated as a candidate orbit for the relay spacecraft.

Table 2 shows the evaluation of each orbit family in the sun-Mars system. Due to this system’s low mass ratio of μ_M/(μ_S + μ_M) ≈ 3.2 × 10^− 7, orbits far from Mars are only weakly affected by its gravity and thus are essentially heliocentric ellipses in a non-rotating reference frame. Some well-known periodic orbit families at the collinear libration points (e.g. L₁ Lyapunov and L₂ halo) remain so near to Mars that the entire family exists within the solar exclusion cone and thus no individual orbit satisfies the problem’s geometric constraints. Other families, like Mars’s distant retrograde orbits, do include orbits that reach outside of the exclusion cone, but the periods of these orbits are essentially equal to Mars’s heliocentric orbit period, and are thus not useful for multiple solar conjunction periods. The only families satisfying the geometric and temporal constraints are the L₄ and L₅ long-period families [22, 23]. These orbits are planar, circumnavigate one triangular equilibrium point, and, in the sun-Mars circular-restricted system, have an orbital period over 1100 Earth years. Although these orbits do not remain permanently in the comm zone, the orbital period is so long that a spacecraft following such an orbit can remain in the comm zone well past the spacecraft’s expected lifespan. Figure 5 shows an example L₄ long-period orbit in the sun-Mars system with a period of 1240 Earth years. In this figure, the radial offset between the orbit and Mars’s orbit radius is amplified 20 times for visual clarity; if this were not done, the orbit at this scale appears as a single arc.

Table 2 Sun-Mars periodic orbit family evaluation

Fig. 5

Sun-Mars L₄ long-period orbit in sun-Mars rotating frame. The radial offset between the orbit and Mars’s orbital radius is amplified 20 times

A similar result follows for orbit families in the sun-Earth system. All families contain orbits that escape the solar exclusion cone, but few orbits enter the comm zone. Of those that do, none re-enter it in a time period commensurate with the Earth-Mars synodic period, and only the L₄ and L₅ long-period orbits enable a spacecraft to remain in the comm zone for extended time periods. Given that the minimum distance from Mars to its long-period orbits is less than the minimum distance from Mars to Earth’s long-period orbits, Mars long-period orbits are selected for further examination. If, however, the link distance between Mars and the relay spacecraft is acceptable for Earth long-period orbits, these may be preferred because the Earth departure and orbit insertion costs can be significantly reduced by using a multi-revolution outbound transfer.

An L₄ or L₅ long-period orbit can be thought of as a circular heliocentric orbit perturbed by Mars, leading to an oscillation in the angular offset relative to Mars. When a spacecraft on an L₄ orbit is nearest to Mars, the net force on the spacecraft contains a small component opposed to the spacecraft’s circular velocity about the system’s center of mass (see Fig. 6a). This anti-velocity component reduces the spacecraft’s orbital period and eventually causes the spacecraft to drift away from Mars. On the other hand, when the spacecraft is beyond L₄, the net force on the spacecraft contains a small component aligned with the spacecraft’s velocity and therefore acts to increase the spacecraft’s orbital period. The increased period means the spacecraft eventually begins to drift towards Mars. Because the mass ratio of the sun-Mars system is so low, the force perturbation relative to the force necessary for a circular orbit is small, and therefore the orbital period of the long-period orbits in the rotating frame is long. The degree of the perturbation is shown in Fig. 6b as the angle between the net force vector and the spacecraft’s position vector relative to the system’s center of mass (α in Fig. 6a). Even close to Mars (when 𝜃 is small in Fig. 6b), this angle is small and therefore the spacecraft’s circular orbit is only slightly perturbed. The angle’s magnitude is smaller beyond L₄, which means the spacecraft spends a majority of its time on the far side of L₄ relative to Mars.

Fig. 6

Sun-Mars CRTBP dynamics for spacecraft at Mars’s radius

Trojan Orbits

When the CRTBP model is upgraded to a multibody ephemeris model, no truly periodic orbits exist because the solar system geometry does not exactly repeat. Additionally, the eccentricity of Mars’s orbit ($\sim$0.1) imparts a per-revolution oscillation in the spacecraft’s angular offset from Mars. The L₄ and L₅ long-period orbits of the CRTBP are truly periodic; their quasi-periodic analogs in the ephemeris model are called Trojan orbits. In the context of this study, a Trojan orbit is any orbit with heliocentric energy similar to that of Mars, an orbital path similar to Mars’s heliocentric orbit, and a position always ahead of or behind Mars. Figure 7 shows an example Trojan orbit that initially leads Mars by 60 days and is propagated 1100 years. The one-Mars-year short-period oscillation is visible in the trajectory in Fig. 7a and is responsible for the yearly variation of the angular drift and Mars-distance visible in Fig. 7b–c.

Fig. 7

Sun-Mars L₄ Trojan orbit example in ephemeris model. The Trojan orbit initially leads Mars by 60 days and is propagated for 1100 Earth years

The initial state of a Trojan orbit can be obtained by taking Mars’s state at a different epoch, either in full or, while keeping the orbital energy fixed, varying other orbital elements. Figure 8 shows the first Mars year of multiple Trojan orbits in a multibody ephemeris model with initial states identical to Mars’s past and future states. The shape of each orbit when viewed in the sun-Mars rotating frame is due almost entirely to Mars’s orbital eccentricity. Each trajectory would be essentially a fixed point in the rotating frame if not for Mars’s orbital eccentricity.

Fig. 8

First Mars year of various Trojan orbits, with initial states equal to Mars’s past or future states, from − 50 days to + 50 days in 5 day increments

To function as a viable relay during Earth-Mars solar conjunction periods, a spacecraft following a Mars Trojan orbit must be offset far enough along Mars’s orbit that the SEP angle remains above the minimum allowed value for the entire conjunction period. Figure 9 shows the minimum duration by which a spacecraft must lead Mars in its orbit to satisfy the SEP angle constraint, calculated in both the simplified model—where Earth and Mars are assumed to have circular orbits with radii of 1 AU and 1.5 AU—and the ephemeris model—where the minimum offset satisfies the requirement for all conjunction periods in an Earth-Mars inertial repeat period of 15 years. For example, if the minimum allowed SEM and SEP angles are 5 deg, a spacecraft following an L₄ Trojan must lead Mars by at least 36 days. The difference between the required time offset as computed in the simplified and ephemeris models grows with increasing SEM angles due to the eccentricity of Mars’s orbit.

Fig. 9

Time-offset required for Mars-leading Trojan orbits in the simplified model and ephemeris model

Trojan orbits drift slowly enough that a spacecraft on a Trojan can remain, with no stationkeeping, within the visible communication zone for decades, which is most likely beyond the expected lifetime of the vehicle. The angular offset between the sun-Mars line and the sun-spacecraft line experiences a long-period oscillation due to Mars’s gravity, and a per-revolution oscillation due to Mars’s orbital eccentricity, since two points spaced equally in time along the same orbit will be farther apart near perihelion than near aphelion. For the present application, a given orbit is useful if it satisfies the geometric telecommunication constraints for decades. In the study and search for natural bodies following Mars Trojan orbits, orbital stability on the order of millions or billions of years is of interest. Some works note the existence of a few Mars Trojan asteroids and speculate on their origins and stability [24,25,26,27].

Figure 10 shows two examples of Trojan orbit drift. The angular and spatial drift of a Trojan initially leading Mars by 10 days are shown in Fig. 10a–b. The initial epoch corresponds to Mars’s 2020 perihelion, and the orbit is propagated for an Earth-Mars-Jupiter synodic period, taken as 47 years, under the gravitational influence of the sun and all major planets. Beginning with an initial angular offset between the sun-Mars and sun-spacecraft lines of under seven degrees, the offset eventually grows to 43 deg. Figure 10b shows a similar trend in the Mars-spacecraft distance. Over the first decade, the maximum spatial drift is less than 0.1 AU. The angular and spatial drift of a Mars-leading Trojan initially leading Mars by 30 days are shown in Fig. 10c–d. In this case, the magnitude of the per-orbit oscillation is similar to that of the first orbit when compared at equal angular offsets, but the long-period drift rate is only one quarter of the first orbit’s.

Fig. 10

Angular and spatial drift for example Trojan orbits

To more comprehensively understand the long-term stability of the Trojan orbit family, many Mars-leading Trojans are propagated and the maximum angular offset of the sun-spacecraft line relative to its initial location is documented. Both the initial epoch and the initial Trojan offset from Mars are parametrically varied. Given that Earth and Jupiter produce the most significant perturbations to the orbit, the initial epoch is varied from Mars’s 2020 perihelion over an entire Earth-Mars-Jupiter synodic period in 10-day increments, and each Trojan orbit is propagated for one Earth-Mars-Jupiter synodic period. The initial Trojan offset from Mars is varied from 10 to 50 days, in half-day increments. The results, shown in Fig. 11, indicate that, in general, the closer a Trojan begins to Mars, the faster it will drift away. For a given initial-time offset from Mars, the main factor in determining the maximum drift is Mars’s initial position in its orbit, which in turn dictates the initial spatial offset between Mars and the spacecraft. Little variation is observed across the Earth-Mars-Jupiter synodic period.

Fig. 11

Trojan orbit stability

Direct Trojan Transfers

The decadal stability of Trojans establishes this orbit family’s value for deep-space relay spacecraft. Any orbit’s utility, however, is also a function of the energy and time required to reach that orbit after launch. This section addresses the Trojan insertion cost for direct outbound elliptical transfers. A spacecraft following such a transfer departs Earth and targets a point in space on Mars’s orbit either leading or trailing the planet. When the spacecraft arrives, it performs a propulsive maneuver to match Mars’s orbital energy and perhaps more components of its state at that point in its orbit (Fig. 12). The cost of this transfer is estimated in the circular, coplanar conic model, the ephemeris conic model, and the ephemeris multibody model.

Fig. 12

Direct outbound transfer

Circular, Coplanar Conic Model

In the circular, coplanar conic model, the minimum-energy direct outbound transfer from Earth to a Mars Trojan orbit is a Hohmann transfer. The energy of such a transfer is

$$ \frac{(v_{0}^{+})^{2}}{2} - \frac{\mu_{s}}{r_{E}} = \frac{-\mu_{s}}{r_{E} + r_{M}} $$

(12)

where $v_{0}^{+}$ is the heliocentric speed immediately after Earth departure, μ_s is the gravitational parameter of the sun, and r_E and r_M are the heliocentric radii of Earth and Mars. Solving for the departure speed,

$$ v_{0}^{+} = \sqrt{2\mu_{s} \left( \frac{1}{r_{E}} - \frac{1}{r_{E} + r_{M}} \right) } $$

(13)

Since Earth’s orbit is assumed to be circular, the spacecraft’s speed relative to Earth at departure is

$$ v_{\infty} = \sqrt{2\mu_{s} \left( \frac{1}{r_{E}} - \frac{1}{r_{E} + r_{M}} \right) } - \sqrt{\frac{\mu_{s}}{r_{E}}} $$

(14)

Similarly, the difference between the speed needed to achieve the Trojan orbit and the heliocentric speed immediately before arrival is

$$ {\Delta} v = \sqrt{\frac{\mu_{s}}{r_{M}}} - \sqrt{2\mu_{s} \left( \frac{1}{r_{M}} - \frac{1}{r_{E} + r_{M}} \right) } $$

(15)

The transfer time from Earth to Trojan orbit insertion is

$$ \begin{array}{@{}rcl@{}} {\Delta} t &=& \frac{1}{2}\cdot 2\pi\sqrt{\frac{\left[\tfrac{1}{2}(r_{E}+r_{M})\right]^{3}}{\mu_{s}}} \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} {\Delta} t &=& \frac{\pi}{2}\sqrt{\frac{(r_{E}+r_{M})^{3}}{2\mu_{s}}} \end{array} $$

(17)

In computing the values of $v_{\infty }$, Δv, and Δt, it is important to consider variations in r_M, given that Mars’s heliocentric radius varies from about 1.38 AU to 1.67 AU. If the Earth’s heliocentric radius is taken as 1.0 AU (ignoring the variation between about 0.98 AU and 1.02 AU), Fig. 13 shows how the ideal transfer varies as a function of r_M. Since the outbound transfer is similar to an Earth-Mars transfer, the Earth departure energy and flight time are comparable to those of Earth-Mars transfers. However, since Mars is not nearby at orbit insertion, the Δv cost at arrival (2.1 km/s to 3.1 km/s) is higher than the cost of entering orbit around Mars.

Fig. 13

Ideal transfer characteristics

Ephemeris Conic Model

Because Mars’s orbital eccentricity is significant, it is necessary to retrieve Mars’s state from an ephemeris to accurately predict the transfer cost. The Earth-departure energy, Earth-departure declination, and orbit-insertion velocity impulse are computed for a range of Earth departure and Trojan orbit arrival dates. Favorable date combinations derived from these data are used later in this study to build an initial estimate for optimization in the multibody model, and in the design of a flight mission would be used to select a multi-week launch period. For each launch and arrival date pair, Lambert’s problem is solved between Earth and the Trojan orbit insertion point, a point leading or trailing Mars in its orbit. Transfers to Trojans are similar to Earth-Mars transfers but are unique and effectively represent a different Earth-Mars phasing. The characteristic contours (e.g. Earth-departure energy) of Trojan transfers are therefore shifted and warped relative to Earth-Mars transfers.

Figure 14 shows twice the Earth-departure energy (C₃), the departure declination, and the Trojan orbit insertion cost for a launch in 2022. The contours as a function of launch and arrival date are computed with minimum sun-Earth-Mars (SEM) angles (Φ) of 5 deg (representative of an X-band system), 10 deg and 15 deg (representative of an optical system). The minimum SEP angle, dictated by the spacecraft’s telecom architecture, determines the minimum angle between the sun-Mars and sun-spacecraft lines, and has a significant effect on the results. For example, a transfer during this launch opportunity with both C₃ < 10 km²/s² and Δv < 2.5 km/s is feasible for Φ = 10 deg, but not for Φ = 5 deg.

Fig. 14

Direct transfer contours of twice Earth-departure energy, Earth-departure declination, and orbit insertion cost

Ephemeris Multibody Model

Forces other than solar gravity were ignored when building transfers in the ephemeris conic model. The gravitational forces from the major planetary systems are now included in an end-to-end numerical simulation of the outbound transfer. This trajectory from Earth to the Trojan orbit is constructed with the Cosmic trajectory optimization system, which is part of Monte. In Cosmic, trajectory propagation begins at control points, and time and state continuity are enforced at intermediate patch points. This multiple-shooting method is well suited for the present problem since it is naturally defined with Earth and the Trojan orbit insertion point as terminal control points.

Since the analysis leading to Fig. 13 predicted launch energies comparable to typical Earth-Mars transfers but orbit insertion costs higher than the cost of entering orbit around Mars, the objective function for minimization is chosen to include only the orbit-insertion cost:

$$ J \equiv {\Delta} v $$

(18)

where ${\Delta }\boldsymbol {v} \equiv \boldsymbol {v}_{f} - \boldsymbol {v}_{f}^{*}$; v_f is the spacecraft velocity at the final time, t_f; $\boldsymbol {v}_{f}^{*} = \boldsymbol {v}_{M}(t_{f} + {\Delta } t)$ is the velocity of Mars at time t_f + Δt; and Δt is the desired time offset between Mars and the Trojan orbit. The free parameters are

$$ \boldsymbol{x}_{p} \equiv \left[\begin{array}{cc} \boldsymbol{v}_{\infty} \\ \theta_{B} \\ \boldsymbol{x}_{f} \end{array}\right]_{10 \times 1} $$

(19)

where $\boldsymbol {v}_{\infty }$ is the hyperbolic departure velocity, 𝜃_B is the departure B-plane angle [28], and x_f is the arrival state. The equality constraints require that the trajectory be continuous through the patch point and that the spacecraft achieves a final position along Mars’s orbit that exactly matches the future position of Mars:

$$ \boldsymbol{c} \equiv \left[\begin{array}{cc} \boldsymbol{x}_{i}^{+} - \boldsymbol{x}_{i}^{-} \\ \boldsymbol{r}_{f} - \boldsymbol{r}_{f}^{*} \end{array}\right]_{9 \times 1} = \boldsymbol{0} $$

(20)

where $\boldsymbol {x}_{i}^{-}$ and $\boldsymbol {x}_{i}^{+}$ represent the states immediately before and after the patch point (halfway along the transfer in time), and $\boldsymbol {r}_{f}^{*} = \boldsymbol {r}_{M}(t_{f} + {\Delta } t)$ is the position of Mars at time t_f + Δt.

An example transfer is optimized with an Earth departure date of September 1, 2022, a Trojan orbit arrival date of August 1, 2023, and a minimum SEP angle of five degrees, corresponding to a Trojan orbit leading Mars by 37 days at the arrival epoch. Based on the results of Fig. 14, the ephemeris conic model predicts an orbit-insertion cost of 2410 m/s. After optimizing the trajectory in the ephemeris multibody model with the multiple-shooting method described above, the resulting transfer, shown in Fig. 15, incurs a cost of 2408 m/s. The initial estimate by means of Lambert targeting is quite good in this case because the spacecraft remains in deep space after Earth departure, with no terminal close approach to Mars characteristic of typical Lambert targeting.

Fig. 15

Direct transfer and Trojan orbit in ephemeris multibody model. Duration of propagation is two Mars years after orbit insertion

Figure 15a shows the example transfer projected in the ecliptic plane in a non-rotating reference frame, and Fig. 15b shows the transfer projected in the sun-Mars plane in the rotating frame, with the orbit propagated two Mars years after insertion. Figures 15c–d show the distance to Mars and SEP angle for the transfer and first two Mars years of the relay orbit. Because in this case the spacecraft exactly matched Mars’s future state, its distance to Mars fluctuates between about 0.45 AU and 0.55 AU due almost entirely to Mars’s orbital eccentricity. The period of Earth-Mars solar conjunction where the SEM angle is less than five degrees is highlighted; as desired, the relay spacecraft maintains an SEP angle greater than five degrees during this period. The data rates achievable with a similar relay orbit for representative radio and optical systems are estimated in Reference [13].

Matching Mars’s future full state required an orbit-insertion cost of 2408 m/s in the example presented here. If instead only the orbit-insertion position and post-insertion period are constrained, the optimal cost for this example drops to 2174 m/s. The savings in Δv, however, is accompanied by increased orbital drift due to the out-of-plane motion, since the Trojan inclination isn’t constrained.

Trojan Transfers with Outbound Flyby

It is possible reduce the Trojan orbit insertion cost by using an outbound Mars flyby to boost the spacecraft’s heliocentric energy into a phasing orbit with a period different than Mars’s such that after one or more revolutions around the sun, the spacecraft will be offset from Mars by the desired amount where it can then propulsively enter the Trojan orbit (Fig. 16). The decreased cost is achieved by effectively “stealing” momentum from Mars. The Trojan orbit insertion maneuver is required to match only Mars’s orbital energy, but not Mars’s other orbital elements. The total cost of the this transfer is estimated in the circular, coplanar conic model, the ephemeris conic model, and the ephemeris multibody model.

Fig. 16

Outbound transfer with flyby and phasing orbit

Circular, Coplanar Conic Model

The total propulsive cost of Trojan orbit insertion with an outbound Mars flyby is estimated first in a circular, coplanar conic model, where the Earth-to-Mars leg is a Hohmann transfer. The energy of the outbound transfer from Earth is

$$ \frac{(v_{1}^{-})^{2}}{2} - \frac{\mu_{s}}{r_{M}} = \frac{-\mu_{s}}{r_{E} + r_{M}} $$

(21)

where $v_{1}^{-}$ is the heliocentric speed immediately before the Mars flyby. Solving for the pre-flyby speed,

$$ v_{1}^{-} = \sqrt{2\mu_{s} \left( \frac{1}{r_{M}} - \frac{1}{r_{E} + r_{M}} \right) } $$

(22)

If Δt represents the spacecraft’s desired time-offset relative to Mars, with Δt > 0 corresponding to a Mars-leading Trojan and Δt < 0 corresponding to a Mars-trailing Trojan, the period of the phasing orbit is

$$ T_{1}^{+} = T_{M} - {\Delta} t/n $$

(23)

where T_M is Mars’s orbital period and n is the number of circuits the spacecraft makes around the phasing orbit. The phasing orbit’s period, by Kepler’s Third Law, is

$$ T_{1}^{+} = 2\pi\sqrt{\frac{(a_{1}^{+})^{3}}{\mu_{S}}} $$

(24)

where $a_{1}^{+}$ represents the post-flyby semi-major axis. Substituting into Eq. 23 and solving for $a_{1}^{+}$ gives

$$ a_{1}^{+} = \left[ \mu_{S} \left( \frac{T_{M} - {\Delta} t/n}{2\pi}\right)^{2} \right]^{1/3} $$

(25)

The required heliocentric energy of the phasing orbit is

$$ -\frac{\mu_{S}}{2a_{1}^{+}} = \frac{(v_{1}^{+})^{2}}{2} - \frac{\mu_{S}}{r_{M}} $$

(26)

where the required post-flyby speed, $v_{1}^{+}$, is

$$ v_{1}^{+} = \sqrt{2\mu_{S}\left( \frac{1}{r_{M}} - \frac{1}{2a_{1}^{+}}\right)} $$

(27)

which is known since the post-flyby semi-major axis is given by Eq. 25.

In the zero-radius sphere of influence patched-conic model, the spacecraft’s energy relative to Mars is identical before and after the flyby. Through the rotation of the hyperbolic asymptote, however, the spacecraft’s heliocentric energy may be altered. The maximum available turning angle between the incoming and outgoing hyperbolic velocity relative to Mars is given by

$$ \delta_{avail} = 2 \arcsin \left( 1 + \frac{r_{p} v_{\infty}^{2}}{\mu_{M}} \right)^{-1} $$

(28)

where r_p is the spacecraft’s periapsis flyby radius, $v_{\infty }$ is the asymptotic speed relative to Mars, and μ_M is Mars’s gravitational parameter. By the law of cosines, the post-flyby speed is

$$ (v_{1}^{+})^{2} = {v_{M}^{2}} + v_{\infty}^{2} - 2 v_{M} v_{\infty} \cos\delta_{req} $$

(29)

where $v_{1}^{+}$ is given by Eq. 27, v_M is the heliocentric speed of Mars, and δ_req is the turning angle required to achieve a post-flyby speed of $v_{1}^{+}$. Solving for δ_req gives

$$ \delta_{req} = \arccos\left( \frac{{v_{M}^{2}} + v_{\infty}^{2} - (v_{1}^{+})^{2}}{2 v_{M} v_{\infty}}\right) $$

(30)

The actual turning angle is chosen to be

$$ \delta = \min(\delta_{req}, \delta_{avail}) $$

(31)

If the required turning angle is less than or equal to the maximum available turning angle, the flyby alone imparts the energy necessary to achieve the phasing orbit (Fig. 17a). If the required turning angle is greater than the maximum available turning angle, a propulsive maneuver is performed immediately after the flyby to achieve the required speed of $v_{1}^{+}$ (Fig. 17b). Therefore, the magnitude of the flyby maneuver is

$$ {\Delta} v_{1} = \left\{\begin{array}{ll} 0 & \text{if } \delta_{req} \leqslant \delta_{avail} \\ v_{1}^{+} - v_{1}^{+-} & \text{if } \delta_{req} > \delta_{avail} \end{array}\right. $$

(32)

where $v_{1}^{+-}$ is the heliocentric speed immediately after the flyby but before any maneuver is performed.

Fig. 17

Outbound flyby velocity diagrams

After one or more circuits on the phasing orbit, a propulsive maneuver is required for the spacecraft to enter the Trojan orbit, which by definition requires the spacecraft to achieve the same heliocentric energy as Mars. In all cases, the magnitude of this final maneuver is

$$ {\Delta} v_{2} = v_{M} - v_{1}^{+} $$

(33)

The total cost of the transfer is then simply

$$ {\Delta} v = {\Delta} v_{1} + {\Delta} v_{2} $$

(34)

The significant Δv savings enabled by this transfer method comes at the expense of increasing the outbound flight time by n ⋅ T_M −Δt, relative to the case where no outbound flyby is used. Additionally, the orbital elements of Mars are not matched exactly, resulting in a less stable Trojan orbit.

To understand how the total cost is affected by the time offset of the Trojan orbit relative to Mars, Mars’s heliocentric radius, and the number of phasing circuits, the cost is computed for several combinations of these parameters. With Mars in a circular orbit at its perihelion radius, Fig. 18a shows that at every Trojan orbit temporal offset the required flyby turning angle is less than the maximum allowed turning angle; therefore, the cost of the flyby maneuver is zero in each case, and the total cost equals the magnitude of the orbit insertion maneuver that occurs after one circuit around the phasing orbit. As the destination Trojan orbit’s temporal offset from Mars increases, the energy of the phasing orbit decreases, and therefore the required turning angle decreases, but also the difference between the phasing orbit’s energy and the Trojan orbit’s energy increases, resulting in a larger orbit insertion maneuver. With Mars halfway between its perihelion and aphelion radii, Fig. 18b shows that the desired turning angle is achieved when the offset from Mars is greater than about 35 days. Below this time, the flyby alone cannot endow the spacecraft with the post-flyby speed required for proper phasing. In these cases, the spacecraft performs a post-flyby maneuver to achieve the phasing orbit period. The magnitude of the orbit insertion maneuver approaches zero as the phasing orbit period approaches the period of Mars, because in that limiting case, the phasing orbit is the final orbit. With Mars at its aphelion radius, Fig. 18c shows that for every temporal offset considered, the spacecraft must perform a post-flyby maneuver.

Fig. 18

Flyby and orbit insertion cost in simplified conic model

Figure 18d–f show the flyby and insertion cost when the spacecraft completes two circuits along the phasing orbit (n = 2). In this scenario, the maximum available turning angle is unchanged since the spacecraft’s velocity relative to Mars at the flyby is unchanged. Thus, when δ_req > δ_avail, the total cost remains the same as the scenario where n = 1. However, completing an additional circuit of the phasing orbit means that the phasing orbit’s energy is closer to Mars’s orbital energy for a given temporal offset of the destination Trojan orbit. This means that the region where δ_req > δ_avail covers a greater range of temporal offsets, and where $\delta _{req} \leqslant \delta _{avail}$, the insertion cost increases more slowly than in the case where n = 1.

Ephemeris Conic Model

In the ephemeris conic model, the true positions of Earth and Mars are used, but the force model between encounters still includes only the gravity of the sun. This means the approach velocity’s orientation at Mars varies based on the Earth departure and Mars arrival epochs. In this scenario, the angle between Mars’s heliocentric velocity and the spacecraft’s post-flyby areocentric velocity is given by

$$ \cos\phi = \frac{{v_{M}^{2}} + v_{\infty}^{2} - (v_{1}^{+})^{2}}{2 v_{M} v_{\infty}} $$

(35)

The post-flyby areocentric velocity is

$$ \boldsymbol{v}_{\infty}^{+} = -v_{\infty} \cos\phi \boldsymbol{\hat{v}}_{M} - v_{\infty} \sin\phi \boldsymbol{\hat{h}} \times \boldsymbol{\hat{v}}_{M} $$

(36)

Since $\boldsymbol {v}_{\infty }^{-}$ is known and $\boldsymbol {v}_{\infty }^{+}$ can be calculated with Eq. 36, the required turning angle can be computed as

$$ \cos\delta_{req} = \frac{\boldsymbol{v}_{\infty}^{-} \cdot \boldsymbol{v}_{\infty}^{+}}{v_{\infty}^{2}} $$

(37)

With the maximum available turning angle given by Eq. 28, the actual turning angle is again chosen as $\delta = \min \limits (\delta _{req}, \delta _{avail})$. The costs of the flyby maneuver (if required) and the orbit-insertion maneuver are identical to those given by the formulation in the circular, coplanar conic model (Eqs. 32 and 33).

For a range of Earth departure and Mars arrival dates, the preceding results are used to compute the total mission Δv cost during four Earth-Mars launch opportunities in the 2020s (Fig. 19). With a single-circuit phasing orbit and a destination Trojan orbit leading Mars by 45 days, the minimum total Δv costs during the 2022, 2024, 2026, and 2028 launch opportunities are 750 m/s, 610 m/s, 580 m/s, and 840 m/s, respectively. Figure 19 also shows twice the Earth departure energy and the declination of the Earth departure asymptote in the EME2000 frame. The minimum values of C₃ during each launch opportunity are 13.8 km²/s², 11.1 km²/s², 9.2 km²/s², and 9.0 km²/s², respectively. Of course, the minimum values of C₃ and Δv don’t occur at the same departure/arrival date pair, so there is a trade between the energetic requirements of the launch vehicle and the spacecraft. For a specific launch vehicle and spacecraft architecture, the C₃ and Δv information could be integrated to produce an estimate of the maximum possible spacecraft mass delivered to the Trojan orbit.

Fig. 19

Flyby and orbit insertion cost in ephemeris conic model, for a single-circuit phasing orbit, and a Trojan orbit leading Mars by 45 days

Ephemeris Multibody Model

When optimizing transfers with an outbound flyby in the ephemeris multibody model, the cost function is chosen to be the sum of the flyby and orbit insertion maneuver magnitudes:

$$ J \equiv {\Delta} v_{1} + {\Delta} v_{2} $$

(38)

The free parameters are

$$ \boldsymbol{x}_{p} \equiv \left[\begin{array}{ccccccccccccccccccccc} \theta_{0} & & \phi_{0} & & v_{0} & & \xi_{0} & & {r_{p}}_{1} & & e_{1} & & i_{1} & & \omega_{1} & & {\Omega}_{1} & & {\Delta}\boldsymbol{v}_{1}^{\top} & & \boldsymbol{x}_{f}^{\top} \end{array}\right]_{1 \times 18}^{\top} $$

(39)

where 𝜃₀, ϕ₀, v₀, and ξ₀ represent the longitude, latitude, speed, and velocity azimuth at Earth departure; r_p1, e₁, i₁, ω₁, and Ω₁ represent the osculating periapsis radius, eccentricity, inclination, argument of periapsis, and longitude of the ascending node of the flyby orbit at Mars; Δv₁ represents the components of the flyby maneuver; and x_f is the full state immediately before Trojan orbit insertion. The final maneuver, Δv₂, is always chosen such that the post-maneuver heliocentric energy equals that of Mars. Periapsis state optimization variables have been used here rather than B-plane variables because it has been found through experience with Cosmic that multi-segment interplanetary optimization problems of this type are more well-behaved with the periapsis state parameterization. The constraints are

$$ \boldsymbol{c} \equiv \left[\begin{array}{cc} \boldsymbol{x}_{01}^{+} - \boldsymbol{x}_{01}^{-} \\ \boldsymbol{x}_{12}^{+} - \boldsymbol{x}_{12}^{-} \\ {\Delta}\theta_{2} - {\Delta}\theta_{*} \end{array}\right]_{13 \times 1} = \mathbf{0} $$

(40)

where the first two groups of constraints enforce continuity at the patch points, and the final constraint dictates the Mars-sun-spacecraft angle at arrival.

An example transfer with an outbound flyby is optimized with an Earth departure date of November 1, 2022, a flyby date of May 31, 2023, and a Trojan orbit arrival date of March 5, 2025, chosen in the low-Δv (and high-C₃) region predicted in Fig. 19a. Since in this formulation only the energy of Mars’s orbit is matched by the Trojan orbit, the offset from Mars is increased to 45 days to account for the additional spatial variation in the destination Trojan orbit. The initial estimate predicts a total cost of 672 m/s which includes a flyby maneuver of 70 m/s, which is less than the total cost in the ephemeris conic model, because the initial estimate here uses a maneuver at periapsis which is more efficient than the maneuver at the edge of the sphere of influence used in the ephemeris conic model. After optimizing the trajectory in the ephemeris multibody model, the resulting transfer, shown in Fig. 20, incurs a total cost of 604 m/s. Given the additional degrees of freedom in this formulation, the optimizer eliminated the flyby maneuver entirely. Table 3 shows the differences between the direct transfer and flyby transfer examples. Choosing Earth departure in later years like 2026 or 2028 would enable flyby transfers with low Δv and low C₃.

Fig. 20

Flyby transfer and Trojan orbit in ephemeris multibody model. Duration of propagation is two Mars years after orbit insertion

Table 3 Comparison of direct transfer and flyby transfer

Figure 20a shows the example transfer projected in the ecliptic plane in a non-rotating reference frame, and Fig. 20b shows the transfer projected in the sun-Mars plane in the rotating frame, with the orbit propagated two Mars years after insertion. Figures 20c–d show the distance to Mars and SEP angle for the transfer and first two Mars years of the relay orbit. The period of Earth-Mars solar conjunction where the SEM angle is less than five degrees is highlighted; as desired, the relay spacecraft maintains an SEP angle greater than five degrees during this period. Because the Trojan orbit elements don’t exactly match Mars’s orbital elements, the spacecraft’s drift relative to Mars is visible even after two Mars years.

Conclusions

Continuous communication between Earth and Mars is useful for human and robotic missions, and it may someday be essential with humans permanently living and working on the red planet. Moreover, as the number and complexity of missions to Mars increases, the need for increased uplink and downlink data rates will also increase. However, periods of Earth-Mars solar conjunction prevent reliable communication between the planets. For radio frequency systems, conjunctions prevent reliable two-way communication for days or weeks, depending on the signal frequency. For optical systems, which offer higher data rates, solar illumination interference constraints may preclude optical communication with Mars for several months.

In this study, the use of a single relay spacecraft was shown to be a viable option to provide continuous interplanet communication. A useful relay spacecraft must remain close enough to Mars to communicate effectively with Mars-based assets but far enough away to satisfy the off-solar pointing constraints during conjunction. Of all potential relay orbits studied, it was shown that only the families of long-period orbits at the triangular libration points of the sun-Mars and sun-Earth circular-restricted three-body systems satisfy the geometric constraints. Though the long-period orbits in the Martian system do not remain permanently in the viable communication region, their single-orbit period of over 1000 Earth years means that a spacecraft following such an orbit can maintain favorable communication geometry relative to Mars for decades. Trojan orbits, the quasi-periodic ephemeris-level counterparts of truly periodic long-period orbits in the CRTBP, were shown to deviate from the ideal orbits due, primarily, to the eccentricity of Mars’s orbit, but are still long-lived enough to serve as a useful trajectory for a telecommunication relay spacecraft.

As shown in simplified and high-fidelity dynamic models, direct outbound transfers from Earth to Mars Trojan orbits have similar launch energies and flight times as Earth-Mars transfers but higher insertion costs. Outbound transfers with an intermediate Mars flyby offer significant orbit-insertion savings versus direct transfers, in exchange for an increased flight time and a less stable Trojan orbit. Simplified models used to predict the Earth departure and orbit insertion costs of both direct and flyby transfers provided an excellent estimate of the cost as predicted in the high-fidelity ephemeris model.

Future mission concept studies should consider useful activities for the relay spacecraft during the downtime between Earth-Mars solar conjunction periods. If technically feasible and cost-effective, a spacecraft performing scientific observations in addition to its relay duties would undoubtedly increase the enthusiasm for such a mission. The spacecraft might observe the sun or search for natural bodies following Mars Trojan orbits.

Future trajectory design research on this topic could include study of the initial conditions of the Trojan orbit in order to extend its useful lifetime. Understanding a Trojan orbit’s stability as a function of its orbital elements—especially inclination—would also be valuable. Additionally, studying outbound transfers with a low-thrust propulsion system would likely show gains in the delivered mass of the relay spacecraft. Follow-on studies should also consider the orbit-insertion costs for Mars-trailing Trojans; the direct transfer costs will be similar to targeting Mars-leading Trojans, but outbound-flyby transfer costs could be significantly different given that the phasing orbit in this scenario would be more energetic than Mars’s orbit. Further useful analysis includes an assessment of the propellant mass required for orbit maintenance with a high-thrust or low-thrust propulsion system. Finally, multi-spacecraft relay strategies could be considered, providing redundancy and potentially increased data rates. One option for deployment would include two spacecraft co-manifested on the same launch vehicle that fly to Mars together and use different flybys to establish one in a Mars-leading Trojan and one in a Mars-trailing Trojan.

Future navigation research on this topic should include a study of the ability of the relay spacecraft to navigate solely with its optical system, therefore eliminating the need for an on-board radio-frequency system; the delivery requirements can likely be satisfied with optical ranging and astrometry measurements. Finally, it would also be useful to study the possibility of using the relay spacecraft to perform navigation of spacecraft in orbit near Mars, thus allowing Martian orbiters to continue regular science operations or critical mission operations like aerobraking during solar conjunction periods.