Nonequilibrium simulation analysis of the power dissipation and the pressure produced by TIG welding arcs

Abstract

The recently developed novel nonequilibrium model of TIG arcs is applied to study in detail the momentum balance and pressure establishment in the arc region and the power balance of the whole arc system. TIG configurations with two currents (100 and 200 A), two different cathode shapes (2-mm radius and vertex angles of 60^∘ and 30^∘), and an electrode distance of 5 mm are considered exemplary. The pressure analysis yields two regions of pressure in excess of atmospheric pressure below the cathode tip in front of the anode. The maximum values show weak dependence on the cathode vertex angles. The growth of the arc pressure with the arc current is predicted to be faster than quadratic. The analysis of the power budget shows the importance of the Joule heating term in the electron energy balance, which is the dominant mechanism in the vicinity of the cathode and the near surrounding while it is negative in the vicinity of the anode. The electric power deposited in the cathode space-charge sheath is a huge amount of the total power supply (40% at 200 A and 50% at 100 A) with a significant part of it being transferred to the plasma electrons.

1 Introduction

The significant progress in arc plasma modelling over the course of many years [1] and, in particular more recently, the nonequilibrium features included [2] in the advanced tungsten-inert gas (TIG) welding arc modelling give us rise to consider in more detail the characteristics of gas flow and power. The TIG arc provides not only the heat load but also the pressure exerted on the workpiece, which are of central importance for the weld properties.

The TIG arc configuration consists of a conically shaped cathode and a flat anode (the workpiece). The origin of the arc pressure is in the Lorentz force caused by the self-induced magnetic field [3] and the higher static gas pressure at the cathode tip than at the anode plate due to the divergent current distribution [4, 5]. The generated plasma jet towards the anode impinges on the anode and is than deflected to flow radially outwards. Arc pressure measurements have been performed to study the effects of the welding current, the geometry of the tungsten cathode, and the arc length [4, 6] in argon as a shielding gas. Numerical simulation of the arc pressure has been done in [7, 8]. However, an analysis of the terms in the momentum equation contributing to the formation of the arc pressure has not been considered. Since the flow conditions and the power dissipation strongly depend on the current density distribution in the TIG welding arc, a self-consistent description of the arc attachment on the electrodes is of major importance for the predictive capability of the arc model.

The nonequilibrium model applied for the present study [2, 9] is based on a fully nonequilibrium description of the arc plasma avoiding the assumptions of both thermal and ionization equilibria. It accounts for the properties of the space-charge sheaths adjacent to the electrodes and the two-directional interaction between the arc plasma and the electrodes. The novelty of this modelling approach allows us to gain deep insight into the arc properties.

The paper is organized as follows. The main features of the modelling approach are underlined in Section 2. Evaluation of the arc pressure and the terms of power dissipation is presented in Section 3. Concluding remarks and outlook for future work are given in Section 4.

2 Modelling approach

The modelling approach applied to study TIG arcs in argon at atmospheric pressure has been presented in detail in previous publications (see, e.g., [2, 9]). In this work, a summary will be given outlining its main features and expressions relevant to the present analysis.

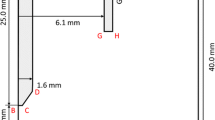
The schematic of the TIG arrangement is shown in Fig. 1. The cathode is a cylindrical rod made of ceriated tungsten (WC20) with a radius of 2 mm and a truncated tip of a conical shape. Vertex angles of 30^∘ and 60^∘ are considered for this study. The radius of the cathode tip is 0.2 mm. The anode is composed of a steel plate placed on a water-cooled plate made of copper and is perpendicular to the arc axis. The inter-electrode distance is 5 mm. Pure argon gas is fed through the nozzle with inner radius of 8 mm at a flow rate of 15 slpm. Since the configuration possesses axial symmetry, a two-dimensional geometry in the plane AHGE (28 mm × 30 mm) is employed.

Fig. 1

TIG arc configuration and solution area considered in the model

The modelling approach couples a magnetohydrodynamic (MHD) simulation of the arc, a description of the arc-electrode interaction, and the heat and current balances of the electrodes. The Navier-Stokes equation system for conservation of mass, momentum, energy, and species is coupled with the Maxwell equations, Ohm law, and the equation of state. The arc plasma containing electrons, atoms, and singly charged ions of argon is considered as quasi-neutral. Assumptions of thermal and ionization equilibrium are avoided. The MHD approach is valid not only in the arc column but also in the pre-sheath regions of the electrodes and in the arc fringes. Assuming a Maxwellian energy distribution, the electrons are characterized by a temperature T_e while the the atoms and ions are characterized by a common temperature T. Separate energy equations are solved for electrons and heavy particles with account for convective transport, thermal conduction, transport of enthalpy due to diffusive fluxes and thermal diffusion. Gain and loss of energy due to Joule heating, elastic and inelastic collisions, and radiation is considered.

The set of Navier-Stokes equations reads:

$$\begin{array}{@{}rcl@{}} \nabla\cdot\left( \rho\mathbf{u}\right)&=&0, \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}} \rho\left( \mathbf{u}\cdot\nabla\right)\mathbf{u}&=&\nabla\cdot\left( -p\tilde{I}+\tilde{\tau}\right)+\mathbf{F}_{L}, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \nabla\cdot\left( \frac{5}{2}n_{e} k_{B} T_{e} \mathbf{u}\right)&=& -\nabla\cdot\mathbf{J}_{\varepsilon}-\frac{e}{m_{e}}\mathbf{J}_{e}\cdot \mathbf{E} -Q^{el}_{e-n}\\&&-Q^{in}_{e-h}-Q_{rad}, \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} \nabla\cdot\left( \frac{5}{2}(n_{A}+n_{I}) k_{B} T_{h} \mathbf{u}\right)&=& -\nabla \cdot \mathbf{J}_{h}+\frac{e}{m_{I}}\mathbf{J}_{I}\cdot \mathbf{E} +Q^{el}_{e-h}, \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} \nabla \cdot \left( \rho \mathbf{u}Y_{i}+\mathbf{J}_{i}\right) &=&S_{i}. \end{array} $$

(5)

Here, $\rho ={\sum }_{i} n_{i}m_{i}$ denotes the mass density of the gas mixture, u is the flow velocity, Y_i is the mass fraction, n_i is the number density, and m_i is the mass of the species i, i = e,A,I for respectively electrons, argon atoms, and argon ions. $p={\sum }_{i} p_{i}$ denotes the total pressure, $\tilde {I}$—the identity matrix, $\tilde {\tau }$—the viscous stress tensor, and k_B—the Boltzmann constant. J_ε and J_h are the densities of energy flux of respectively electrons and heavy particles energy. These fluxes account for thermal conduction, transport of enthalpy by diffusive fluxes, and thermal diffusion. They are written as

$$\begin{array}{@{}rcl@{}} \mathbf{J}_{\varepsilon}&=&-\kappa_{e}\nabla T_{e}+\frac{5}{2}k_{B}T_{e}\left( 1+\frac{q^{01}}{q^{11}}\right)\mathbf{j}_{e}, \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} \mathbf{J}_{h}&=&-\kappa_{h}\nabla T_{h}+\frac{5}{2}k_{B}T_{h}(\mathbf{j}_{A}+\mathbf{j}_{I}). \end{array} $$

(7)

In Eqs. 6 and 7, $\mathbf {j}_{i}=\frac {\mathbf {J}_{i}}{m_{i}}$ denotes the particle flux of the species of mass m_i. The elements q⁰¹ and q¹¹ are expressed by the corresponding gas-kinetic cross-sections [10]. The densities of diffusive mass fluxes J_i are expressed using the Stefan-Maxwell equations [11] and the effective binary diffusion approach in a multi-component plasma according to Ramshaw [12] as follows:

$$ \mathbf{J}_{i}=\frac{Y_{i}}{z_{i}}\rho D_{i}\mathbf{G}_{i}-Y_{i} \sum\limits_{j} \frac{Y_{j}z_{j}}{\rho}D_{j}\mathbf{G}_{j}, $$

(8)

where D_i is the effective diffusion coefficient of species i, z_i is the ratio of the partial pressure of species i to the total pressure, and G_i is the volumetric driving force, accounting for gradients in the mass fractions Y_i of the species, pressure, and electron temperature and the drift of charges particles in the electric field E

$$ \mathbf{G}_{i}=-\nabla z_{i}+(Y_{i}-z_{i})\frac{\nabla p}{p}-\frac{\rho e}{p m_{i}}Y_{i}{C_{i}^{e}}\nabla T_{e}+\frac{Z_{i}e}{m_{i}}\rho_{i}\frac{\mathbf{E}}{p} $$

(9)

Notice that the mass fluxes must satisfy the condition J_e + J_I + J_A = 0. More details of the description can be found in [2].

In the equations of energy conservation (3) and (4), gain/loss of energy due to Joule heating ($\frac {e}{m_{e}}\mathbf {J}_{e}\cdot \mathbf {E}$, $\frac {e}{m_{I}}\mathbf {J}_{I}\cdot \mathbf {E}$), elastic ($Q^{el}_{e-n}$) and inelastic collisions ($Q^{in}_{e-h}$) between electrons and heavy particles, and radiation (Q_rad) are taken into account. The energy transferred by the electrons to the heavy particles in elastic collisions is given by [13]

$$ Q_{e-h}^{el}=\frac{3}{2}n_{e}k_{B}(T_{e}-T_{h})\frac{2m_{e}}{m_{A}}(\nu_{eA}+\nu_{eI}), $$

(10)

where ν_eA and ν_el denote the collision frequency of elastic collisions of electrons with atoms and ions.

The energy loss due to inelastic collisions of electrons with heavy particles is expressed as

$$ Q_{e-h}^{in}=n_{e}(n_{A}K^{ion}-n_{e}n_{I}K^{rec})\varepsilon_{I}, $$

(11)

whereby the reaction chemistry includes processes of ionization and three-body recombination with rate coefficients K^ion and K^rec including the contribution of the first excited state of the argon atom [14] according to the concept of prompt ionization once the atom becomes excited (ε_I= 11.65 eV).

The energy loss for electrons due to radiation, Q_rad, is expressed by means of the net emission coefficient reported in [15]. The transport parameters of the plasma are calculated in terms of the Chapman-Enskog theory with high order of approximation [16].

The electric field E and the self-induced magnetic field B are determined respectively by the generalized Ohm’s law and the Maxwell equation

$$\begin{array}{@{}rcl@{}} \mathbf{j}_{q}&=&\sigma\mathbf{E}+{\Delta}\mathbf{j}_{q}, \end{array} $$

(12)

$$\begin{array}{@{}rcl@{}} \nabla\times\frac{\mathbf{B}}{\mu_{0}}&=&\mathbf{j}_{q}, \end{array} $$

(13)

in which the magnetic vector potential A is introduced as B = ∇×A along with a gauge fixing. In Eqs. 12 and 13, j_q = eJ_I/m_I − eJ_e/m_e is the electric current density resulting from the mass fluxes of electrons and ions (see Eqs. 8 and 9). σ and μ₀ are respectively the electric conductivity of the plasma and the permeability of free space. Notice that the generalized Ohm’s law (12) relates a drift part (σE) and a diffusion part (Δj_q) of the electric current density. The general formulation of the mass fluxes in Eqs. 8 and 9 allows us to group the terms containing the dependence on the electric field into the drift part of the current density and to denote the coefficient of proportionality as the electrical conductivity σ. The remaining terms accounting for the species diffusion due to density, pressure, and temperature gradients are grouped into the diffusion part of the current density Δj_q. An effective electric field can be defined in a way that E_eff = E + Δj_q/σ and E_eff = −∇ϕ_eff, where an effective potential ϕ_eff is introduced similarly to the relation E = −∇ϕ between the drift electric field and the electric potential.

In addition, the conditions of quasi-neutrality, n_e = n_I, the equation of state of an ideal gas, and ${\sum }_{i} Y_{i}= 1$ are applied. Therefore, Eq. 5 is solved only for the ions and replaces the Saha equation in an equilibrium model. Notice that atmospheric pressure was set as a reference pressure when solving the hydrodynamic equations.

Equations 1 to 13 for the arc region are solved together with the heat and current balances of the electrodes. Proper boundary conditions are to be set at the external boundaries AB-BC-CD-DE-EF-GH (Fig. 1) and at the interfaces PB and OF between the arc region and the electrodes. Models for the space-charge sheathes are implemented at these interfaces. These models ensure the equality of the normal components of the electric current density and consider the energy transfer at the interfaces. Details of the space-charge sheath models which determine also the local space-charge potential as well as the boundary conditions for u, T_e, T_h, Y_I, j_q, and ϕ are formulated in [17] and given in detail in [2]. At the parts AP-PO-OH which build the symmetry axis, the corresponding variables have zero gradient. The temperature of heavy particles approaches the surface temperature of the walls. The temperature of the gas inflow and nozzle walls is set to 300 K and that at the base of the cathode (boundary AB) is 500 K. At the bottom of the anode, the temperature is set to 300 K to simulate a water cooling. Melting of the workpiece is not considered in the present work. The outer boundaries are electrically and magnetically insulated except the cathode base and the anode bottom on which electric potential is specified (the anode is grounded).

The model is realized on the computational platform COMSOL Multyphysics [18] which is based on the finite element method (FEM) with a computational domain of 5⋅ 10⁴–9⋅ 10⁴ mesh elements. The regions of the arc axis and close to the boundary between the electrodes and the plasma is resolved using a minimum element size of 2.5 μm.

In order to analyze the arc pressure and the power dissipation of the TIG arc, we will consider in detail Eqs. 2–4.

The Lorentz force in Eq. 2 is defined as F_L = j_q ×B. Applying Eq. 13, the Lorentz force can be resolved into two components

$$ \mathbf{F}_{L}=\frac{1}{\mu_{0}}\left( \mathbf{B}\cdot\nabla\right)\mathbf{B}-\nabla\left( \frac{B^{2}}{2\mu_{0}}\right). $$

(14)

The first term is the magnetic tension force and the second one represents the gradient of magnetic pressure. In the results below, a detailed analysis of the terms in the momentum (2) is given.

The terms in the equations of energy conservation (3) and Eq. 4 are obtained with the model for all radial and axial positions of the computational domain. In order to analyze the power balance inside the arc, spatial integrals of the terms in Eqs. 3 and 4, which are denoted as energy rates R(r,z), are evaluated by integration over the cross section of the arc.

$$ R_{c}(z)= 2\pi{\int}_{r_{s}}^{r_{e}} R(r,z) r dr. $$

(15)

In Eq. 15, r_e is the position of the outer radial border of the solution area. r_s is zero for all axial positions along the line PO (Fig. 1). The arc region around the cathode for axial positions above the cathode tip is treated in a similar way by setting r_s to the radial position of the cathode surface. The resulting terms R_c(z) have the meaning of cross-sectional energy rates in units of W/m. For the sake of easy reading, z = 0 corresponds to the axial position of the cathode tip, and z < 0 represents positions around the cathode body. Finally, the volume integrals of the terms in Eqs. 3 and 4 are evaluated to obtain the contributions of the various mechanisms to the power dissipation in the arc.

3 Results and discussion

A wide spectrum of characteristics of TIG arc plasmas generated in argon at atmospheric pressure between a conically shaped doped tungsten cathode and a flat anode made of steel or copper has been studied by means of the latest fully nonequilibrium model in recent authors’ publications (see, e.g., [9, 19, 20]). Temperatures of electrons and heavy particles and electric current density have been studied for different shapes of the cathode tip and various arc lengths. The electric field and potential obtained in account for diffusion currents (see Eq. 12 above) have been discussed in [21, 22]). The formation of a constricted arc attachment on the anode has been analyzed in relation to the macroscopic flow conditions and the evidence of thermal and ionization nonequilibrium in the anode region [19]. The presence of iron metal vapor released from a flat anode in the case of unforced air cooling has been considered in [20]. Analysis of the power budget in the TIG arc with a focus on the electron component has been considered in [22]. In the present work, we extend the previous studies and give a deep insight into the conservation of momentum and energy described by Eqs. 2, 3, and 4.

3.1 Analysis of the pressure and momentum balance

Figures 2 and 3 show the two-dimensional contour plots of the pressure in excess of atmospheric pressure for cathodes with cone angles of respectively 60^∘ and 30^∘. Streamlines indicate the gas flow. The pictures are mirrored with respect to the arc axis for better readability. Regions of increased pressure are observed close to the cathode tip end and in front of the anode. The pressure below the cathode tip has a maximum of about 500 Pa, while a maximum value of about 1400 Pa is seen near the anode. The corresponding maximum values are similar for vertex angles of 60^∘ and 30^∘, while the regions for 60^∘ are more extended. These results are related to the calculated temperature and current density distributions [20], according to which the temperature (T_e ≈ T_h) and the magnitude of the current density are a bit larger for a cone angle of 60^∘. For both values of the vertex angle, the arc is characterized by a very focused and a very hot arc core underneath the cathode tip. The pressure increase in front of the workpiece is related to the cathode jet impinging on it and the stagnation of the flow there illustrated by the streamlines. The radial extend and the pressure magnitude obtained in the present study are similar to those observed experimentally in [23] for a TIG arc at arc current of 200 A, arc length of 3 mm, and a cathode made of thoriated tungsten (45^∘, 1.6-mm radius). Extrapolated values of the measurements in [4] for 200 A and vertex angles of 60^∘ and 30^∘ refer to arc pressures of about 1500 Pa although for an arc length of 8 mm. Since the results for vertex angles of 60^∘ and 30^∘ show close similarity, the further analysis is performed only for 60^∘.

Fig. 2

Isocurves of the pressure in Pa and streamlines for the cathode with a 60^∘-tip at an arc current of 200 A

Fig. 3

Isocurves of the pressure in Pa and streamlines for the cathode with a 30^∘-tip at an arc current of 200 A

Figure 4 presents the pressure (in excess of atmospheric pressure), the shear stress, and the magnetic pressure (see Eqs. 2 and 14) on the surface of the workpiece as a function of the radial position. The shear stress for an axisymmetric model is expressed in cylindrical coordinates according to $\tau =\eta \sqrt {\frac {1}{2}[(2(\frac {\partial u}{\partial r})^{2}+ 2(\frac {\partial u}{\partial z}+\frac {\partial w}{\partial r})^{2}+ 2(\frac {\partial w}{\partial z})^{2}+ 4(\frac {u}{r})^{2}]}$ with u, w, and η representing respectively the radial and axial velocity components, and the dynamic viscosity [18]. Notice the different scales on the left and right site of the graph. The radial pressure profile is bell-shaped with a peak in the central point of impingement(r = 0), whereas the profiles of the shear stress and the magnetic pressure have zero-values in the center and off-axis maxima. Experimental data concerning the wall shear stress and magnetic pressure in TIG arcs are not reported sofar. Figure 5 shows the pressure (in excess of atmospheric pressure) on the workpiece as a function of the radial distance from the center for arc currents of 50 A, 100 A, and 200 A. The growth by a factor of five of the peak value is faster than quadratic with the arc current. This result differs from the linear dependence reported in [4] but is in fair agreement with those reported in [8], where a factor between five and six was predicted.

Fig. 4

Pressure p, shear stress τ, and magnetic pressure B²/μ₀ on the anode for arc current of 200 A, and a vertex angel of 60^∘ as a function of the radial position

Fig. 5

Pressure on the workpiece for arc currents of 50 A, 100 A, 200 A, and a vertex angel of 60^∘ as a function of the radial position

We consider now the equation of momentum conservation (2) in detail. In the region between the cathode tip and the anode plate, we virtually draw a series of line-outs, which are perpendicular to and cross the arc axis at positions z =5.1 mm, 4.3 mm, 2.3 mm, and 0.3 mm (see Fig. 2 for geometrical details). The axial positions under consideration allow one to look at the mechanisms of momentum conservation in the vicinity of the electrodes (the position z =5.1 mm is 0.2 mm away from the workpiece), in the plane across region of increased pressure in front of the workpiece (z =4.3 mm), and approximately in the middle plane of the arc (z =2.3 mm). The evaluated r- und z-components of the terms in Eq. 2 are plotted in Fig. 6 as a function of the radial distance from the arc axis (notice the different scales of the graphs for different axial positions).

Fig. 6

Radial behavior of the terms in the equation of momentum conservation (2) for arc current of 200 A, tip angle of 60^∘, and axial positions respectively z =5.1 mm (a), 4.3 mm (b), 2.3 mm (c), and 0.3 mm (d)

In the vicinity of the anode (workpiece) (Fig. 6a), the conservation of the r- and z-components of the momentum is covered by the gradients of the arc pressure and the stress tensor. The Lorentz force is of minor importance there. The terms, which account for the pressure and the stress tensor gradients and build the change of the momentum vector in the r-direction, are of opposite signs. For distances from the axis over ≈1 mm, the contribution of the stress tensor overtakes that of the radial pressure gradient so that the resulting term becomes negative. In contrast, the z-components of the pressure gradient and the stress tensor gradient are of the same sign and sum up to give the change of the z-component of the momentum. Close to the workpiece, the impinging flow looses its z-momentum component while the r-component strongly increases. This is the region where the streamlines change from vertical to horizontal ones (Fig. 2).

With increasing distance from the workpiece (Fig. 6b), the shear stress decreases. The negative contribution of the radial component of the Lorentz Force partially compensates the positive radial gradient of the stress tensor. The total of both contributions, being negative for radial positions below ≈2 mm and changing its sign beyond this position, and the dominant contribution of the radial pressure gradient, sum up to build the radial component of the momentum change. Although the z-component of the momentum change is dominated by the pressure gradient component, it includes ≈14 % contribution of the stress tensor gradient near the arc axis (r= 0–0.5 mm).

The situation is different near the middle of the arc (Fig. 6c), where the isolines of the pressure build their waistline. Here, the r-component of the Lorentz force has absolute values smaller but still comparable to that of the radial pressure gradient along the radius. Since these contributions are of opposite signs, the resulting r-component of the momentum change is positive with off axis maximum ≈0.5 mm away from the arc axis. The radial contribution of the stress tensor term is almost negligible. The balance of the z-component of the momentum is more complex. The pressure gradient is negative for radial positions up to ≈1.5 mm. The z-component of the Lorentz force is negative in the region under consideration. Its absolute value reaches a maximum at radial position r ≈2 mm and remains larger than the pressure gradient beyond that point. The gradient of the stress tensor is positive with appreciable values which overtake absolute value of the pressure gradient in the region r ≈0.14–0.4 mm.

In the vicinity of the cathode tip (Fig. 6d), significant changes in the r- and z- momentum components occur in a very narrow region (the radial extend is approximately ≈1 mm) due to the conical shape of the cathode tip. In radial direction, the contribution of the stress tensor gradient is of minor importance, whereas the pressure gradient and the Lorentz force are of opposite signs with local maxima at r ≈0.3 mm. The larger radial pressure gradient results in a positive change of the momentum component. In z-direction, the negative pressure gradient is the dominant component. The gradient of the stress tensor is negative on the axis and grows to reach a positive maximum value at r ≈0.3 mm. The z-component of the Lorentz force remains negative. It increases in absolute value to reach a maximum at r ≈0.5 mm.

The analysis of the terms in the equation of momentum conservation (2) shows the complex interplay between gradients of the pressure and the stress tensor, and the Lorentz force. The latter plays a minor role in the impingement region and its contribution increases upwards to become largest in the middle of the arc. Close to the cathode tip, the Lorentz force is important due to the high current density there. The conservation of momentum is strongly coupled to the conservation of energy through the temperatures and number densities of electrons and heavy particles, which constitute the total pressure. In the following, we analyze Eqs. 3 and 4 in order to gain insight into the mechanisms of power dissipation in the TIG arc.

3.2 Analysis of the power balance

Figures 7 and 8 show the terms appearing respectively in Eqs. 3 and 4 as a function of the radial position along the same line-outs as in Fig. 6. The results correspond to an arc current of 200 A and a tip angle of 60^∘.

Fig. 7

Radial behavior of the terms in the equation of energy conservation for electrons (3) for arc current of 200 A, tip angle of 60^∘. The axial positions of the line-outs are the same as in Fig. 6

Fig. 8

Radial behavior of the terms in the equation of energy conservation for heavy particles (4) for arc current of 200 A, tip angle of 60^∘. The axial positions of the line-outs are the same as in Fig. 6

In the vicinity of the anode (Fig. 7a), the Joule heating term ($-\frac {e}{m_{e}}\mathbf {J}_{e}\cdot \mathbf {E}$) is negative and therefore leads to cooling of the plasma electrons and decrease of the electron temperature. This is the effect of the diffusion current component in the generalized Ohm’s low (12). It has been shown by means of the nonequilibrium model [2] that the diffusive current density strongly increases in the vicinity of the anode. Therefore, the field-driven current density has to undergo a reversal in order to preserve charge conservation. A negative anode fall is therefore appearing. In the TIG arc arrangement considered here, the position of field reversal (maximum in the electric potential) is within 1 mm away from the anode [9]. Inelastic collisions (term $-Q^{in}_{e-h}$) lead to a large energy gain at almost all radial positions which results from low ionization near the anode. Elastic collisions ($-Q^{el}_{e-n}$) cause an electron energy loss because of the excess of T_e over T_h near the anode which is required to ensure that the electric conductivity is large enough to ensure the current transfer between the plasma and the relatively cold anode. Radiation losses (− Q_rad) play a role for radial positions below r ≈1.5 mm.

Moving towards the cathode (Fig. 7b, c, d), the Joule heating is turning to positive for all radial positions. Its importance continuously increases to dominance in the vicinity of the cathode. This results from the huge gradients of the electric potential there. The term of the elastic losses is negative at most of the radial positions as one would expect. This term is responsible for the important transfer of kinetic energy to the heavy particles and scales with the difference of the temperatures T_e − T_h. Positive values near to the arc axis, which represent an energy gain for the electrons, result here from a relatively small local excess of T_h over T_e. Inelastic collisions, ion recombination processes in particular, lead to a considerable energy gain for the electrons for all radial positions of the line-outs close to the anode (Fig. 7a, b). In the midplane of the arc and close to the cathode (Fig. 7c, d), this term becomes negative beyond r ≈1 mm. Appreciable amount of power is delivered by convective transport (term $\nabla \cdot \left (\frac {5}{2}n_{e} k_{B} T_{e} \mathbf {u}\right )$). Notice that contributions from radial and axial flow components are included in this term. In all cases, the electron energy flux (term −∇⋅J_ε), which accounts for the energy flux due to thermal conduction, transport of enthalpy due to diffusive fluxes, and thermal diffusion, is the dominant term and provides the balance of the remaining local energy excess or defect.

The results presented in Fig. 8 show that the heavy particles gain energy chiefly in elastic collisions. The Joule heating of ions by the electric field ($\frac {e}{m_{I}}\mathbf {J}_{I}\cdot \mathbf {E}$) is much less important. There are regions close to the arc axis (small r in Fig. 8a, c, d) and the entire radial distance in Fig. 8b, where the term representing elastic collisions takes negative values. This effect indicates a negative difference T_e − T_h. A look in the temperature distributions shows values of about −10 K. Significantly larger negative differences (∼− 1000 K) have been reported in [24]. The authors of [24] suggested that a part of the radiation losses could be assigned to the heavy particles in order to avoid this effect. Nevertheless, this approach has not been applied by others sofar. The contribution of the density of the energy flux of heavy particles (−∇⋅J_h) is of higher importance in the vicinity of the electrodes (Fig. 8a, d) than in the midplane of the arc.

To get a better insight into the overall energy balance of the electrons in the arc, a radial integration of the terms is applied. The axial behavior of the radially integrated terms of the energy balance of electrons and heavy particles according to Eq. 15 is presented in Figs. 9 and 10. The Joule heating is the strongest mechanism followed by inelastic collisions, the divergence of the flux of density of electron energy, and elastic collisions (Fig. 9a). The results show that the strongest heating of the electrons (and consequently of the arc plasma) by the electric field is localized near the cathode. The corresponding energy rate in the extended arc column (z ∼ 1–4 mm) is by a factor between two and three lower. Notice the large rate for Joule heating for z < 0. This is related to the spatial distribution of the current density. We have recently reported [20] that maximum normal current density is predicted on the inclined part of the cathode tip in an axial distance from the tip end z ∼−0.2 mm. Joule cooling of the electrons occurs near the anode (z ∼ 4.5–5 mm). The divergence of the electron energy flux compensates the inhomogeneous energy gain by the electric field to large extent. This term represents the energy transport from the front of the cathode to the near surrounding and vice versa, from the surrounding of the anode to the front of the anode (including transport in both radial and axial direction) in the integrated power balance. The term of elastic collisions is, after integration, negative for almost all axial positions. Inelastic collisions lead to an energy loss near the cathode and in the most of the arc column but to a considerable gain over the last 1.5 mm of the axial distance. The rate of radiation losses has a maximum at (z ≈ 4.5 mm).

Fig. 9

Radially integrated terms of the energy balance of electrons a and heavy particles b for an arc current of 200 A and a tip angle of 60^∘

Fig. 10

Radially integrated terms of the energy balance of electrons a and heavy particles b for an arc current of 100 A and a tip angle of 60^∘

The energy rates for heavy particles along the the axis (Fig. 9b) exhibit local maxima for axial positions with z < 0, which correspond to the maximum of current density (related to the Joule heating of electrons and ions) at the side of the cathode. The divergence of the density of energy flux of heavy particles is most important in front of the anode (z ∼ 3.5 − 5 mm) while the convective transport ($\nabla \cdot \left (\frac {5}{2}(n_{A}+n_{I}) k_{B} T_{h} \mathbf {u}\right )$) is important along the entire axis playing the role of gain or loss of energy. The behavior of the energy rates for an current density of 100 A is similar, though the region of increased values is narrower and the rates in the plasma column are lower by a factor of ∼2 than at an arc current of 200 A. The ratio of maximum values of the rates for Joule heating of electrons at 200 A and 100 A is however lower than two. We reported in a previous work [2] that the plasma properties (e.g., current density, electron, and heavy particle temperatures) in the vicinity of the cathode tip do not change much when the arc current is lowered. The size of the arc attachment area is smaller so that the current density remains large.

Integrating the terms appearing in the equations of energy conservation of electrons and heavy particles (3) and (4) over r and z, we get the power dissipation attributed to the individual mechanisms and the power budget of the TIG arc. These results are summarized in Table 1 together with the power dissipated in the electrodes and the electrode sheaths for arc currents of 200 A and 100 A. Additionally, the balances in percentages of the total electric power and the those of electron and heavy particles are given.

Table 1 Power deposition in the TIG arc

The total electric power of respectively 2673.9 W and 1243.7 W is supplied to the arc. In the 200 A arc, 39.8% of this power is deposited in the cathode sheath, from which about 28.7% is transferred to the electrons. (Notice that the power deposited in the cathode sheath is obtained by integrating the product of the local voltage drop in the space-charge sheath and the current density over the cathode surface.) The rest is heating the cathode. The charged particles in the arc column take about 59.5% of the electric power by Joule heating. The electrons lose 53.4% of their power income in elastic collisions, about 20.7% in inelastic collisions, and about 25.9% due to radiation. The convective transport is of minor importance for the global energy balance of the electrons.

The heavy particles gain almost 88.8% of their total energy in elastic collisions with the electrons, while the amount of 11.2% comes from Joule heating by the electric field. The power is transported chiefly by the heat conduction. Small amounts of the supplied power is dissipated in the cathode body. Notice the small amount of negative electric power resulting from the small negative voltage drop in the anode sheath. The results for an arc current of 100 A can be analyzed similarly. Notice that in this case 50.4% of the power supply is deposited in the cathode sheath from which 43% is going to the plasma electrons. We recall that in TIG arcs, the voltage drop in the cathode sheath decreases whereas the voltage drop in the arc column increases with increasing arc current [21].

4 Summary and outlook

This work presents a detailed analysis of the conservation of momentum and energy of electrons and heavy particles in TIG arcs. The results are obtained by means of the recently developed nonequilibrium model [2], which novel aspects lie in a general diffusion formulation of the plasma species transport, the generalized Ohm’s law, the consideration of the ionization regions in front of both electrodes within the arc plasma column, and in the self-consistent description of the bi-directional interaction between the arc plasma and the electrodes by means of boundary conditions accounting for the energy balance in the space-charge sheaths. The results of this analysis can be summarizes as follows.

Two regions of pressure in excess of atmospheric pressure are predicted in TIG arcs: the one is below the cathode tip (maximum value of about 500 Pa) and the other is in front of the anode (maximum value of about 1500 Pa). The latter is usually denoted as the arc pressure exerted on the workpiece. The corresponding maximum values are similar for vertex angles of 60^∘ and 30^∘, while the regions for 60^∘ are more extended. The pressure increase in front of the workpiece is related to the cathode jet impinging on it and the stagnation of the flow there. The radial pressure profile is bell-shaped with a peak in the central point of impingement, whereas the profiles of the shear stress and the magnetic pressure have zero-values in the center and off-axis maxima. The growth of the arc pressure with the arc current is predicted to be faster than quadratic.

The interplay between gradients of the pressure and the stress tensor, and the Lorentz force is very complex. The Lorentz force plays a minor role in the impingement region and its contribution increases upwards to become largest in the middle of the arc.

In the energy balance of the electrons, the Joule heating term is playing the most important role. It is dominant in the vicinity of the cathode and the near surrounding while it is negative in the vicinity of the anode due to the strong diffusion current. The electric power deposited in the cathode sheath is a huge amount of the total power supply (∼ 40% at 200 A and 50% at 100 A) with a significant part of it being transferred to the plasma electrons. The main loss of electron energy is due to elastic collisions with heavy particles followed by radiation and inelastic collisions (ionization and recombination). The heavy particles gain energy mostly in elastic collisions with the electrons and in a small extend by Joule heating of the ions, which is dissipated in the arc by heat conduction.

Forthcoming investigations based on the nonequilibrium model are aimed at analysis of the processes in metal-inert gas (MIG) welding arcs.