Determination of parameters of double-ellipsoidal heat source model based on optimization method

Abstract

To determine the parameters of the double-ellipsoidal heat source model (DEHSM) in welding simulations, a technique is developed to extract the parameters of weld pool shape from the simulation results. The technique is developed based on the knowledge of the isoparametric transformation and computer graphics, and its validity is verified by a graphic comparison. It is shown that the technique can effectively extract and reflect the shape of weld pools without interrupting the solution process of the DEHSM parameters. Second, using this technique in conjunction with the optimization method, an approach is proposed to determine the DEHSM parameters. Next, using the proposed method, the DEHSM parameters associated with four different welding conditions are determined. Finally, with these parameters, their corresponding weld widths and penetrations are compared with the measured ones. The results demonstrate that the proposed method can efficiently determine the DEHSM parameters with a relatively high accuracy.

1 Introduction

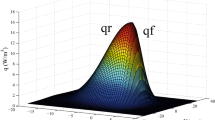
The double-ellipsoidal heat source model (DEHSM) [1], expressed by Eq. (1), utilizes two ellipsoidal heat sources (Fig. 1) to reflect the characteristics of steep and gentle welding temperature gradients in the front and rear of the heat source, respectively. The influence of arc stiffness on the penetration depth can also be considered by introducing a new parameter c. Thus, the DEHSM is especially applicable for the welding processes with large penetration depths, such as the groove welding and fillet welding.

$$ \Big\{{\displaystyle \begin{array}{l}{q}_f=\frac{6\sqrt{3}{f}_1Q}{\pi {a}_f bc\sqrt{\pi }}\exp \left(-3\frac{x^2}{a_f^2}\right)\exp \left(-3\frac{y^2}{b^2}\right)\exp \left(-3\frac{z^2}{c^2}\right)\\ {}{q}_r=\kern0.36em \frac{6\sqrt{3}{f}_2Q}{\pi {a}_r bc\sqrt{\pi }}\exp \left(-3\frac{x^2}{a_r^2}\right)\exp \left(-3\frac{y^2}{b^2}\right)\exp \left(-3\frac{z^2}{c^2}\right)\end{array}} $$

(1)

where q_f and q_r [W/m³] are the power density distributions inside the front and rear ellipsoids, respectively. Q represents the effective heat power [W], and Q = ηUI. Here, η, U, and I represent the efficiency, welding voltage [V], and current [A], respectively; a_f, a_r, b, and c represent geometric parameters of the front and rear ellipsoids [m]; x, y, and z are the local coordinates of the DEHSM [m]; and f₁ and f₂ denote the fractions of the heat power deposited in the front and rear half ellipsoids, respectively, and satisfying f₁ + f₂ = 2.

Fig. 1

Configuration of double-ellipsoidal heat source model

The DEHSM has been extensively used in numerical simulations of welding, such as gas shielded arc welding, submerged-arc welding, and electron beam welding. However, the determination of precise values of the DEHSM parameters is crucial for the simulation results of welding temperature [2], and it is also a prerequisite for obtaining precise simulation results of the welding residual stresses and distortions [3].

The procedure for determining the values of parameters of a welding heat source model (WHSM) commonly involves two aspects: (i) criteria for judging whether the values of the parameters are accurate, and (ii) a method for determining those values according to the criteria. In general, the criteria for verifying the values of the WHSM parameters can be classified into three categories: welding temperature, welding residual stress, and weld pool shape, as follows:

• 1. Determination of WHSM parameters according to the welding temperature [4,5,6,7]. This approach aims at making the simulated welding temperatures to be consistent with the measured ones. In this way, the welding temperature can be directly associated with the WHSM parameters. However, because of the significantly high temperature in the weld pool, the thermocouples must only be installed at a location away from the weld itself, where the welding temperatures are significantly high and the welding residual stresses are the most concerned.

• 2. Determination of WHSM parameters according to the welding residual stress [8]. According to this criterion, the simulated welding residual stresses are required to be in agreement with the measured ones. However, this method is seldom used because the lengthy computational time needed for simulating the welding residual stresses.

• 3. Determination of WHSM parameters of according to the weld pool shapes [9,10,11,12,13]. By this criterion, the WHSM parameters are adjusted repeatedly until the calculated weld pool shape is approximately identical to the actual one. This criterion is the widely used standard to verify the values of the WHSM parameters owing to its high accuracy and efficiency. Therefore, in this study, this criterion is also employed to determine the DEHSM parameters.

According to the criteria above, the methods for determining the WHSM parameters can be generally divided into three categories: trial and error, regression analysis, and intelligent computing.

The trial and error method [6, 14, 15] determines the WHSM parameters through experience. Therefore, its efficiency and accuracy are heavily dependent on experience, which may result in extensive tentative calculations and lengthy computation time.

The regression analysis method generally consists of two steps [9, 10, 14,15,16]. In the first step, several samples of WHSM parameters are calculated with regard to weld pool shapes. Then, a regression analysis method is used to establish an explicit expression of those parameters about the shape parameters of weld pool. When the explicit expression is obtained, the WHSM parameters can be directly calculated with the weld pool shape parameters.

To date, several studies have been conducted to determine the WHSM parameters by using a regression analysis method. Wang et al. [13] assumed that the DEHSM was made up of several point heat sources, and calculated the distribution of welding temperature by using a theoretical formula proposed by Rosenthal [16]. Subsequently, the authors established an expression of the DEHSM parameters with respect to weld width (W) and penetration (D). However, the prediction error of their expression can reach up to 30%; thus, further improvement may be necessary for obtaining more accurate results. Li and Lu [11] established an expression of the DEHSM parameters with respect to W and D for submerged-arc welding. After that, Guo et al. [12] carried out a similar study for CO₂-gas shielded welding. Rouquette et al. [17] performed a nonlinear least square analysis to predict the parameters of a Gauss heat source model for electron beam welding. Jia et al. [18] investigated the effects of the DEHSM parameters on W, D, and the maximum welding temperature (T_p). Subsequently, the multiple regression and partial least squares regression method were both used to establish the expressions of the DEHSM parameters with respect to the weld pool shape parameters.

Using the regression analysis method, when the parameters of a weld pool are known, the WHSM parameters can be easily obtained with the regression expression. However, for a given regression expression, it is only applicable for a specific weld joint which is deposited by a specific welding process. If the welding process or dimensions of weldment change, a series of parametric analyses is required again for deriving a new regression expression. For example, the formula established by Li and Lu [11] can only be suitable for the butt joint with a dimension of 600 mm × 300 mm × 22 mm and deposited under the welding condition of 1000 A and 32 V. Certainly, more parameters can be introduced into the regression formulas to solve this problem, such as geometric parameters and welding process parameters. Nonetheless, this will also greatly raise the number of the parametric analyses and increase the complexity of the regression formulas.

To overcome the limitation of the regression analysis method, Li and Lu [19] employed intelligent computing techniques, i.e., the artificial neural network and support vector machine [19], to predict the DEHSM parameters without the limitations of the welding processes. However, this method has two shortcomings as follows.

• 1. A large number of samples of various welding process parameters with regard to W and D are required. In a previous study [19], 18 measurements were performed to obtain the samples of W and D under different values of welding voltage (U) and current (I); however, the measurements of the W and D require complex processes, such as grinding, polishing, and acid etching.

• 2. In general, this approach can only be used for the weldments with specific dimensions. For example, all 18 samples of W and D used in the previous study [19] were obtained from one type of weldment, and all the weldments had a specific dimension of 600 mm × 300 mm × 16 mm; therefore, the intelligent computing techniques based on these samples are only applicable for the welded joints with the same dimension. For taking into consideration the weldment dimensions, more measurements of W and D versus various welding processes are required.

To address the above-mentioned problems, an approach based on optimization methods was developed in this study to determine the DEHSM parameters. In the proposed method, neither extensive parametric analyses nor large amount of samples of W and D were required. Moreover, when the W and D of a weld joint are known, the DEHSM parameters can be determined automatically by the proposed method, without the limitations of weld dimensions and welding conditions.

2 Numerical simulation of welding temperature

2.1 Parametric modeling of butt joint

Taking the butt joint shown in Fig. 2 as an example, for its finite element model to be suitable for different welding conditions, the butt joint was modeled parametrically with the ANSYS parametric design language. The ANSYS parametric design language is a scripting language very similar to FORTAN but can only be compiled in ANSYS. The butt weld was modeled with first-order hexahedral elements (SOLID70). For the radiative and convective boundary conditions to be defined effectively, a layer of surface effect element (SURF152) was overlaid on the surface of the finite element model.

Fig. 2

Finite element model of butt weld

A grid convergence study was performed and demonstrated that relatively fine meshes were required through the thickness of the plate in or adjacent to the weld. For the 16-mm-thick plate used, 16 layers of elements were required through thickness to achieve a relatively accurate result of welding temperature in the weld areas. The size of elements located in these areas is less than 1 mm × 1 mm × 4 mm. In the areas away from the weld, the welding temperature gradient is significantly smaller. Therefore, coarse meshes, with sizes greater than 4 mm, were adopt to reduce the numbers of degrees of freedoms. The element size used in the longitudinal direction of the specimen is 4 mm. All the meshes are defined as first-order hexahedral elements, and every element has a single degree of freedom, temperature, at each node.

2.2 Governing equation and boundary conditions

The governing equation for transient heat transfer analysis is given by:

$$ k{\nabla}^2T\left(x,y,z,t\right)+q\left(x,y,z,t\right)=\rho c\frac{\partial T}{\partial t}\left(x,y,z,t\right) $$

(2)

where k is the temperature-dependent thermal conductivity [W/(m °C)], T is the temperature [°C], q is the internal heat generation rate [W/m³], ρ is the density [kg/m³], c is the specific heat [J/(kg °C)], t is the time, x, y, and z are the coordinates [m] in the reference system, and ∇ is the spatial gradient operator.

The general solution of temperature distribution is obtained by applying the following initial and boundary conditions:

$$ T\left(x,y,z,0\right)={T}_0\left(x,y,z\right) $$

(3)

where T₀ is the initial temperature and assumed to be 25 °C.

$$ k\left(\frac{\partial T}{\partial x}{N}_x+\frac{\partial T}{\partial y}{N}_y+\frac{\partial T}{\partial z}{N}_z\right)+{q}_s+{h}_c\left(T-{T}_a\right)+{h}_r\left(T-{T}_a\right)=0 $$

(4)

where N_x, N_y, and N_z are the direction cosines of the outward drawn normal to the boundary, h_c and h_r are the convection radiation heat transfer coefficient [W/(m² °C)], respectively. T_a is the ambient temperature and assumed to be 25 °C. q_s is the boundary heat flux, here q_s = 0. The radiation heat transfer coefficient is expressed as:

$$ {h}_r=\varepsilon \sigma \left({T_s}^2+{T_a}^2\right)\left({T}_s+{T}_a\right) $$

(5)

where σ is the Stefan-Boltzmann constant, ε is the effective emissivity.

Radiation losses are dominating for higher temperatures in the weld zones, while convection losses for lower temperatures away from the weld [20]. Therefore, a comprehensive heat transfer coefficient h was used to take into account both of convection and radiation:

$$ h={h}_c+{h}_r $$

(6)

Substituting Eq. (6) and q_s = 0 to Eq. (4), the boundary condition can be rewritten as follows:

$$ k\left(\frac{\partial T}{\partial x}{N}_x+\frac{\partial T}{\partial y}{N}_y+\frac{\partial T}{\partial z}{N}_z\right)+h\left(T-{T}_a\right)=0 $$

(7)

where h is temperature dependent and is given by Eq. (8) [21].

$$ h=\Big\{{\displaystyle \begin{array}{c}0.0668{T}_s\;\left(\mathrm{W}/{\mathrm{m}}^{2{}^{\circ}}\mathrm{C}\right)\kern1.92em 0\le {T}_s\le {500}^{{}^{\circ}}\mathrm{C}\\ {}0.231{T}_s-82.1\;\left(\mathrm{W}/{\mathrm{m}}^{2{}^{\circ}}\mathrm{C}\right)\kern1.68em {T}_s>{500}^{{}^{\circ}}\mathrm{C}\end{array}} $$

(8)

The comprehensive heat transfer coefficient h and other temperature-dependent material properties used in the simulation of welding temperature are illustrated in Fig. 3. In addition, the heat transfer due to fluid flow in the weld pool was taken into account by an artificial increase in thermal conductivity above the melting temperature. The latent heat of fusion was assumed to be 270 J/g between the solidus temperature of (1440 °C) and the liquidus temperature (1500 °C).

Fig. 3

Temperature-dependent material properties

3 Determining the DEHSM parameters based on ANSYS optimizer tool

3.1 General description of ANSYS optimizer tool

ANSYS optimizer tool has been widely used to deal with the optimization problems in engineering, such as the topological optimization [22], optimum cross section of cantilever beams [23], and optimum initial configuration of grid structures [24]. As long as the optimization problems are modeled mathematically with appropriate variables and constraint conditions, the majority of optimization problems in engineering can be usually solved by the ANSYS optimizer tool. Therefore, the ANSYS optimizer tool was employed in this study to determine the DEHSM parameters. Therefore, the ANSYS optimizer tool was employed in this study to determine the DEHSM parameters.

The optimization variables and constraint conditions required by the ANSYS optimizer tool are defined with the design variables, state variables, and the objective function. The design variables are independent variables, which vary between their upper and lower bounds. The state variables are dependent variables, which change with the design variables to constrain the design requirements. The objective function is also a dependent variable that needs to be minimized. In summary, during the optimization process, the design variables will be adjusted automatically using optimization algorithms to minimize the objective function, under the constraints that the state variables are not greater than their limits. The designs variables, state variables, and objective function used to determinate the DEHSM parameters are detailed as follows:

• 1. Design variables. For a given welding process, there are three parameters of the DEHSM that are known: the welding voltage U, current I, and efficiency η. However, there are six parameters needed to be solved: four geometric parameters (a_r, a_f, b, c) and two fractions parameters (f₁, f₂). Of these six parameters, a_r and a_f have little influence on weld widths and penetrations, while the influences of b, c, f₁, and f₂ are great [11]. Considering that there is only one independent parameter in f₁ and f₂ owing to f₁ + f₂ = 2, thus three parameters, i.e., b, c, and f₁, were defined to be the design variables. Simultaneously, the other two parameters, a_r and a_f, were assumed to be a half and double of the measured weld width (W_m), respectively: a_r = 1/2W_m, a_f = 2W_m [1]. The initial values of b and c (described as b₀ and c₀, respectively) were assigned to be the measured weld width (W_m) and penetration (D_m), that is b₀ = W_m and c₀ = D_m. Because b and c are separately and closely related to the weld width and penetration (see Fig. 1), the intervals of b and c were assumed to be [0.8W_m, 1.2W_m] and [0.8D_m, 1.2D_m], respectively. The initial value of f₁ was assumed as 0.6, and it can take values in the interval of [0.4, 0.7].

• 2. State variable. The peak value of welding temperature T_p has a significant influence on the welding simulation results. A previous study [11] also took T_p as a criterion to verify the WHSM parameters. Therefore, in this study, T_p was chosen to be the state variable, and it must not exceed its upper bound. However, until now very few reports on the peak temperature in a weld pool have been published, except for a reference value of about 3000 °C provided by Radaj [25]. Therefore, the upper bound of T_p was assumed to be 3000 °C in the optimization process.

• 3. Objective function. In optimization analyses, the objective function is the variable that needs to be minimized. Therefore, the deviation between the measured and calculated weld pool shapes was defined as the objective function, as expressed in Eq. (9). In this case, the smaller the objective function is, the more similar the simulated weld pool is to the measured one.

$$ OBJ=\max \left\{{W}_{\mathrm{c}}-{W}_{\mathrm{m}}||,{D}_{\mathrm{c}}-{D}_{\mathrm{m}}\right\} $$

(9)

where OBJ represents the objective function; W_c and W_m are the calculated and measured weld widths, respectively, and D_c and D_m represent the calculated and measured penetrations, respectively.

The W_c and D_c used to calculate OBJ and the state variable T_p are all extracted from the welding simulation results. However, it is necessary for the ANSYS optimizer tool to update the related parameters automatically, without interrupting its solution processes. In this case, the relevant parameters (W_c, D_c, and T_p) must be extracted automatically through a certain routine. Thus, the DEHSM parameters can be solved programmatically.

Of these three variables W_c, D_c, and T_p, the extraction of T_p from the simulation results is relatively simple and easy because it can be directly obtained from the nodal temperatures. However, the extractions of W_c and D_c are more complex and difficult, because their extracting procedure generally involves knowledge of the finite element method and computer graphics. For this issue, this paper presents a technique for extracting W_c and D_c by using a subroutine written in the ANSYS parametric design language. This technique will be described in the next section.

When all the steps mentioned above are completed, the optimization analysis can be executed using the command “OPEXE.” In this case, the design variables (b, c, and f₁) will be adjusted automatically under the condition that the state variable (T_p) does not exceed its upper bound, and the objective function (OBJ) will be minimized until it is less than a given allowable tolerance (e). Here, e was assumed to be 1 mm. When OBJ < e, it indicates that the optimization process has converged. At this point, the b, c, and f₁ obtained will be the most accurate parameters of the DEHSM. The whole solution processes of b, c, and f₁ are implemented by optimization algorithms embedded in the ANSYS optimizer tool. The first-order optimization algorithm was used in this study, which has been elaborated by Beck [26]; the reader who wishes learn more could consult this report.

3.2 Extraction of the weld pool shape from simulation results

The extraction of the weld pool shape from the simulation results was indispensable for these approaches that determine WHSM parameters according to weld pool shapes. For this issue, Li [27] extracted W_c and D_c by using linear interpolation between two adjacent nodal temperatures. However, the interpolation function used was not linear, even if the finite element model was created with first-order hexahedral elements because the second- and third-order items exist in the interpolation function. As a result, the finite element model has to be meshed sufficiently fine, so that an accurate result can be achieved. Consequently, it will lead to a large finite element model and lengthy computation time.

For this problem mentioned above to be solved and for the parameters of weld shapes to be extracted automatically, a technique was developed in this study based on the knowledge of isoparametric transformation and computer graphics, which will be described in the paragraphs that follow.

Linear hexahedral elements with eight nodes, as shown in Fig. 4, were commonly used in the simulation of welding temperature, and their shape functions can be defined by Eqs. (10) and (11).

$$ {N}_i=\frac{1}{8}\left(1+{\xi}_0\right)\left(1+{\eta}_0\right)\left(1+{\varsigma}_0\right)\kern0.48em \left(i=1,2,\cdots, 8\right) $$

(10)

$$ {\xi}_0={\xi}_i\xi \kern0.48em {\eta}_0={\eta}_i\eta \kern0.48em {\varsigma}_0={\varsigma}_i\varsigma $$

(11)

where ξ_i, η_i, and ζ_i denote the coordinates of node i in a natural coordinate system.

Fig. 4

Linear hexahedral element

Supposing that the temperature of each node in the element shown in Fig. 4 is known, and for a node i, its temperature is denoted by T_i (i = 1, 2, …, 8), then the temperature at any point within the element can be obtained by using the shape function, as expressed as follows:

$$ T\left(\xi, \eta, \varsigma \right)=\sum \limits_{i=1}^8{T}_i{N}_i $$

(12)

Considering that D_c and W_c have to be extracted on a cross section of a weld bead, then a layer of elements around the bead was isolated for further investigation, as shown in Fig. 5, where the shaded area represents the section to extract D_c and W_c. It is noteworthy that the shaded area should contain the node that has the peak value of temperature; otherwise, D_c and W_c will be inclined to the small side.

Fig. 5

Layer of elements used to extract W_c and D_c

On the shaded area shown in Fig. 5, the ζ equals unity (ζ = 1). Thus, substituting ζ = 1 into Eq. (10) yields Eq. (13).

$$ {N}_i=\Big\{{\displaystyle \begin{array}{c}\frac{1}{4}\left(1+{\xi}_0\right)\left(1+{\eta}_0\right)\kern0.6em i=1,2,3,4\\ {}0\kern7.519999em i=5,6,7,8\end{array}} $$

(13)

Subsequently, substituting Eq. (13) into Eq. (12) gives Eq. (14).

$$ T\left(\xi, \eta \right)=\sum \limits_{i=1}^4{T}_i{N}_i $$

(14)

There is not any ζ-related item on the left side of the equal sign in Eq. (9), because ς ≡ 1 in the shaded area. Simultaneously, all ζ-related items on the right side of the equal sign are equal to zero. This is analogous to the situation in which a three-dimensional hexahedron element was simplified into a two-dimensional quadrilateral element.

Let T(ξ, η) in Eq. (14) be the material melting point T_m; then, the expression of the boundary curve of a weld pool can be obtained, as described in Eq. (15).

$$ {T}_m=\sum \limits_{i=1}^4{T}_i{N}_i $$

(15)

Upon expanding and rewriting Eq. (15), the expression of the boundary curve of a weld pool can be simplified as follows:

$$ {T}_m=A+ B\xi + C\eta + D\xi \eta $$

(16)

where

$$ A=\frac{1}{4}\sum \limits_1^4{T}_i\kern0.48em B=\frac{1}{4}\sum \limits_1^4{\xi}_i{T}_i\kern0.48em C=\frac{1}{4}\sum \limits_1^4{\eta}_i{T}_i\kern0.48em D=\frac{1}{4}\sum \limits_1^4{\xi}_i{\eta}_i{T}_i $$

(17)

It is worth noting that the boundary of the weld pool described in Eq. (16) was established in a normalized coordinate system based on a regularly shaped element. However, D_c and W_c should be extracted in a global coordinate system for any arbitrarily shaped element. Therefore, the boundary of a weld pool expressed by Eq. (16) should be converted to a form that is applicable for arbitrarily shaped elements in the global coordinate system. This will be achieved using an isoparametric transformation which is elaborated as follows.

Figure 6 shows a diagram of the isoparametric transformation for a quadrilateral element, where the x-axis is perpendicular to the direction of welding, towards the weld toe, and in accordance with the Y-axis shown in Fig. 5. The y-axis is in accordance with the Z-axis shown in Fig. 5 and towards the weld root.

Fig. 6

Diagrammatic sketch of isoparametric transformation for quadrilateral element: a in normalized coordinate system, for regularly shaped element; b in global coordinate system, for arbitrarily shaped element

The normalized coordinates can be transformed into global coordinates using the following equations.

$$ x=\sum \limits_1^4{N}_i{x}_i\kern1em y=\sum \limits_1^4{N}_i{y}_i $$

(18)

where x_i and y_i are the node coordinates in the global coordinate system.

On rearranging and expanding Eq. (18), it can be simplified as follows.

$$ x=\frac{1}{4} MNX\kern1em y=\frac{1}{4} MNY $$

(19)

where

$$ M=\left[1\kern0.5em \xi \kern0.5em \eta \kern0.5em \xi \eta \right] $$

(20a)

$$ N=\left[\begin{array}{cccc}1& 1& 1& 1\\ {}{\xi}_1& {\xi}_2& {\xi}_3& {\xi}_4\\ {}{\eta}_1& {\eta}_2& {\eta}_3& {\eta}_4\\ {}{\xi}_1{\eta}_1& {\xi}_2{\eta}_2& {\xi}_3{\eta}_3& {\xi}_4{\eta}_4\end{array}\right] $$

(20b)

$$ X={\left[{x}_1\kern0.5em {x}_2\kern0.5em {x}_3\kern0.5em {x}_4\right]}^T $$

(20c)

$$ Y={\left[{y}_1\kern0.5em {y}_2\kern0.5em {y}_3\kern0.5em {y}_4\right]}^T $$

(20d)

From Eqs. (19) and (20), it can be observed that both two expressions have the second-order item ξη. Thus, an explicit expression of the boundary of a weld pool as Eq. (16) cannot be obtained after the isoparametric transformation. Consequently, in the global coordinate system, it is not possible to calculate the D_c and W_c by the approach of solving extreme values with a partial derivative. For this issue, a series of characteristic points $\left({\xi}_i^{\prime },{\eta}_i^{\prime}\right)$ were selected from the boundary described by Eq. (16) to represent the weld pool shape. After obtaining the coordinates of these characteristic points, Eqs. (19) and (20) were used to transform them into the global coordinate system. In this case, $\left({\xi}_i^{\prime },{\eta}_i^{\prime}\right)$ will be transformed into $\left({x}_i^{\prime },{y}_i^{\prime}\right)$. Finally, D_c and W_c can be obtained through the ranges of $\left\{{x}_i^{\prime}\right\}$ and $\left\{{y}_i^{\prime}\right\}$, respectively.

Based on the relevant theories mentioned above, the procedure for extracting D_c and W_c is summarized as follows.

• 1. Extract information of elements.

A layer of elements in and adjacent to the weld bead was isolated and defined as a set of elements, which was denoted by E. Subsequently, for a given element in E, its element number and the first to the fourth node numbers were stored in the first to the fifth rows of ED, respectively. ED is an array parameter, which is N rows long and five columns wide; being N the total number of elements in E. For a given element i in E, its element number is stored in ED(i, 1) and its four node numbers are stored in ED(i, 2) to ED(i, 5), respectively.

• 2. Extract node temperature.

For each element in E, the data stored in ED is used to extract its four node temperatures and assign them to T_N × 4(i, 1) to T_N × 4(i, 4). Here, T is an array parameter with a dimension of N times four.

• 3. Judge whether the isotherm of T = T_m exists within an element in E.

For each element in E, the knowledge of computer graphics is used to judge whether there is an isotherm of T = T_m in a quadrilateral composed by its four nodes. The judging procedure commonly has two steps are as follows.

Assign a value to C(i, j) according to T(i, j). Here, C is a sign function, which is valued by Eq. (21).

$$ C\left(i,j\right)=\Big\{{\displaystyle \begin{array}{c}+1\kern0.96em T\left(i,j\right)>{T}_{\mathrm{m}}\\ {}-1\kern0.96em T\left(i,j\right)<{T}_{\mathrm{m}}\\ {}0\kern1.08em T\left(i,j\right)={T}_{\mathrm{m}}\end{array}} $$

(21)

where T represents the node temperature, T_m is the material melting point, i is the element number, and j denotes the j-th node in the element i.

For the element i, the sum of these four items of C(i, j) was denoted by Sum, as expressed in Eq. (22). When the temperature of each node in element j is greater than or less than T_m, the absolute value of Sum equals four, that is ∣Sum ∣  = 4. In this case, there is no isotherm of T = T_m in the element i, as shown in Fig. 7a. Otherwise, ∣Sum ∣  ≠ 4, in this case, there is an isotherm in the element i, as shown in Fig. 7b.

$$ Sum=\sum \limits_{j=1}^4C\left(i,j\right) $$

(22)

Fig. 7

Diagram for determining whether the isotherm of T = T_m exists in an element: a there is no the isotherm of T = T_m; b there exists the isotherm of T = T_m

For each element in E, determine whether an isotherm of T = T_m exists according to these steps listed above. After this procedure is completed, define these elements with the isotherm of T = T_m as a new set of elements, which is denoted as E′.

• 4. Extract the coordinates of characteristic points on the isotherm of T = T_m.

For each element in E′, a series of characteristic points in the isotherm of T = T_m were chosen to represent the weld pool shape. Assuming that the coordinates of characteristic points were described by $\left({\xi}_{ik}^{\prime },{\eta}_{ik}^{\prime}\right)$ where the subscript i and k respectively denote the element number and characteristic point number, then $\left({\xi}_{ik}^{\prime },{\eta}_{ik}^{\prime}\right)$ can be extracted by the following two steps.

The first step is to determine the intersection points (P₁ and P₂, see Fig. 8) of the isotherm and element boundary. For a given element i, substitute ξ = 1, ξ = − 1, η = 1, and η = − 1 into Eq. (16), then four points will be obtained, which are (1, η_i1), (− 1, η_i2), (ξ_i1, 1), and (ξ_i1, − 1). However, only two of them are located at the boundary of the element. The two points can be determined by a judgment criterion, based on whether ∣η_i1∣, ∣η_i2∣, ∣ξ_i1∣, and ∣ξ_i2∣ is less than one. If it is, the associated point is located at the element boundary; otherwise, it is outside of the boundary. Here, the intersection points were assumed to be P₁ (ξ_i1, 1) and P₂ (ξ_i1, − 1), as shown in Fig. 8b.

Fig. 8

Coordinate transformation: a normalized coordinate system; b global coordinate system

The second step is to calculate the coordinates of the characteristic points. Supposing that the characteristic points were located at an equal interval along the ξ- or η-axis, the coordinates of these characteristic points can be calculated according to Eq. (16). Specifically, first calculate the ξ-coordinates of these characteristic points based on Eq. (23), which are denoted by ${\xi}_{ik}^{\prime }$. After obtaining ${\xi}_{ik}^{\prime }$, substitute it into Eq. (16), the related η-coordinate will be obtained. Here, assume that the coordinate of the point k of the element i is $\left({\xi}_{ik}^{\prime },{\eta}_{ik}^{\prime}\right)$.

$$ {\xi}_{ik}^{\prime }={\xi}_{i1}+\frac{\left({\xi}_{i2}-{\xi}_{i1}\right)}{\left(K-1\right)}\left(k-1\right)\kern0.48em \left(k=1,2,\cdots K\right) $$

(23)

where i represent the element number; K is the total number of characteristic points.

For each element in E′, calculate its coordinates of characteristic points using the above steps.

• 5. Coordinate transformation. Substituting $\left({\xi}_{ik}^{\prime },{\eta}_{ik}^{\prime}\right)$ into Eq. (19), the corresponding coordinates in the global coordinate system, denoted by $\left({x}_{ik}^{\prime },{y}_{ik}^{\prime}\right)$, will be obtained.

• 6. Calculated W_c and D_c. After obtaining $\left({x}_{ik}^{\prime },{y}_{ik}^{\prime}\right)$ for all elements in E′, D_c and W_c can be obtained from the following equations.

$$ {W}_c=\underset{k=1\to K}{\max }{\left\{{x}_{ik}^{\prime}\right\}}_{i\in {E}^{\prime }}-\underset{k=1\to K}{\min }{\left\{{x}_{ik}^{\prime}\right\}}_{i\in {E}^{\prime }} $$

(24)

$$ {D}_c=\underset{k=1\to K}{\max }{\left\{{y}_{ik}^{\prime}\right\}}_{i\in {E}^{\prime }}-\underset{k=1\to K}{\min }{\left\{{y}_{ik}^{\prime}\right\}}_{i\in {E}^{\prime }} $$

(25)

A flow chart was designed to help understand the procedure for extracting W_c and D_c from the simulation results, as shown in Fig. 9.

Fig. 9

Flow diagram for extracting W_c and D_c from simulation results

To verify the approach described above for automatically extracting the weld pool from simulation results, the welding temperature of a butt weld was first simulated. Then, the weld pool shape was extracted using the proposed approach and compared with that displayed by the ANSYS postprocessor, as shown in Fig. 10. The curve on the right side in Fig. 10a is the weld pool boundary that was extracted and sketched based on 180 characteristic points.

Fig. 10

Verification of the proposed method for extracting the weld pool shape from simulated results: a symmetrical Comparison; b superposition comparison

From Fig. 10a, it can be observed that the extracted boundary of the weld pool is consistent with that displayed by the ANSYS postprocessor. For further comparison, the right part of Fig. 10a was mirrored along the center line and then moved slightly to the right side, as shown in Fig. 10b. From Fig. 10b, it is can be observed that the inflections and configurations of the two boundary curves are highly consistent.

In summary, from the comparisons shown in Fig. 10, it can be determined that the proposed approach can precisely extract the shape of weld pools from the simulation results without interrupting or stopping the solution process of the DEHSM parameters.

3.3 Verification of the proposed method for determining the DEHSM parameters

To verify the proposed method for determining the DEHSM parameters, four sets of D_m and W_m, measured by Li [27], were used to determine the DEHSM parameters using the proposed method, and the calculated results are summarized in Table 1. The D_m and W_m in Table 1 were measured from four butt joints with a dimension of 600 mm × 300 mm × 16 mm, and the butt joints were deposited by submerged-arc welding with a welding speed of 16.67 mm/s and a power coefficient of 0.9 [23].

Table 1 DEHSM parameters determined by the proposed method

From Table 1, it can be determined that the deviations between the measured and calculated D_m and W_m are all less than 1 mm, and the relative errors are not greater than 6%. This indicates that the proposed method can be efficiently used to determine the DEHSM parameters.

Figure 11 shows a visual comparison between the simulated and experimental weld pools. From Fig. 11, it can be observed that: (i) The simulated weld widths and penetrations are in good agreement with experimented ones; (ii) The experimental weld widths shrink rapidly at a small depth from the weld surface, while the simulated weld pools are generally in the shape of an ellipse. Consequently, the experimental weld pools appear more slender than the simulated ones. This suggests that the ellipsoid-shaped DEHSM probably cannot capture the characteristics of rapid shrinkage of the weld width in the case of submerged-arc welding.

Fig. 11

Comparison between the simulated and experimental weld pools: aI = 900 A, U = 32 V; bI = 1000 A, U = 30 V; cI = 1000 A, U = 32 V; dI = 1100 A, U = 32 V

3.4 Causes and countermeasures for the failures of the proposed method

It is worth noting that some failure may occur in the applications of the proposed method, such as problems when the object function OBJ exceeds a given tolerance, or that the state variable T_p exceeds its upper bound. For this issue, two possible causes and corresponding countermeasures will be discussed:

• 1. The lower and upper bounds of the design variables were inappropriately defined. In the optimization analysis, the design variables (b, c, and f₁) must vary in their domains to minimize the object function OBJ. However, it could happen that after traversing all the combinations of b, c, and f₁ between their lower and upper bounds, there is still no combination of them that can make the OBJ be less than the given tolerance e. In this case, it will be judged by the ANSYS to be a situation of non-convergence. To overcome this issue, the bounds of b, c, and f shall be expanded, but c should not be larger than the thickness of the weldment.

• 2. The constraint conditions used in the optimization process are too strict. If the tolerance of OBJ is so small that the optimization result can hardly be obtained. For example, if OBJ ≤ 0.1 mm, which means that the deviation of the measured and calculated D and W cannot be greater than 0.1 mm, then smaller element sizes (less than 0.2 mm) and additional computational time will be required. If the element sizes around the weld bead are less than 2 mm, it is advised that OBJ ≤ 1 mm, and a satisfying result will be obtained.

4 Conclusions

• (1) In this study, a method for determining the DEHSM parameters was proposed based on the ANSYS optimizer tool. A comparison of the simulated and experimental weld pool shapes demonstrates that the proposed method can efficiently determine the DEHSM parameters with a high accuracy. However, the effects of fluid flow on the weld pool shapes were not considered in the present study, therefore, the proposed method may be only valid for simulations that do not take the fluid flow into account.

• (2) In the optimization process of DEHSM parameters, too small range of design variables or too strict constraint conditions will result in the failure of the proposed method. In this case, expanding the limits of design variables or relaxing the constraint conditions may help to achieve an optimization results.

• (3) In the case of submerged-arc welding, although the weld width and penetration can be precisely simulated using the DEHSM, the ellipsoid-shaped DEHSM still cannot capture the characteristics of rapid shrinkage of the weld width. Therefore, it is necessary to develop a new heat source model that suitable for submerged-arc welding in future research.