1 Introduction

Plate structures can be loaded in compression, tension, shear or torsion. If the limit load is reached, plastic collapse can occur [1, 2]. In addition, the heat-affected-zone as well as over- or undermatching filler affects the local yield strength [3]. Especially, the differences in static strength are important if ultra-high-strength steels (UHSS) are used [4]. It is widely recognized that an axially loaded plate under plane stress can fail in a number of different ways [5]. A key aspect of such failure is the critical plane, which in this investigation means the plane where first global yielding and then final rupture occur. The critical plane-approach is used also in multiaxial fatigue analyses to describe the plane, where the fatigue failure occurs [6]. In statically loaded plate structures, the location of critical plane depends on the ductility of the material and the approach used. In Fig. 1 are illustrated potential critical planes for axially loaded plate, available either from literature [5] or practice.

Fig. 1
figure 1

Critical planes of axially loaded plates based on the following approaches: a principal stress, b maximum shear stress, c octahedral shear stress, d strain-ratio and e practice

Full size image

In Fig. 1a, the failure occurs perpendicular to the first principal stress. This mode is typical for brittle material but also for ultra-high strength steel with transverse welds. The failure mode happens especially in butt welds with thin plates, where softening is wide relative to plate thickness. The second mode (Fig. 1b) with α = 45° is based on maximum shear stress, e.g., the Tresca criterion. The third mode (Fig. 1c) with α = 54.7° is based on octahedral shear stress and is justified as a practical solution by offering many potential slip lines in the grains [5]. The fourth mode with α = 35.3° is based on the critical principal strain ratio. However, the conventional approaches seem not to match the results from experimental tests, where an approximately 30° failure angle is found, as illustrated in Fig. 1e.

This rupture path can be non-dependent on the material (metal alloy) or cross-section shape, as illustrated in Fig. 2.

Fig. 2
figure 2

Failure paths with α = 30°: a starting failure in S960 plate, b in aluminium alloy plate [7] and c in a tubular structure made of stainless steel

Full size image

Unlike conventional welded joints made of mild or low strength steels, the softening effect in the HAZ of ultra-high strength steel welds affects the load capacity [8]. In order to avoid this capacity reduction, it is sometimes recommended that the weld be designed such that it is inclined relative to the direction of loading. Because such welds incur extra costs in fabrication, the benefit from such inclined welds must be confirmed beforehand. In addition, designers must be aware of the worst-case scenario of designing the welds at an angle that matches the natural failure path. Consequently, it is clear that the failure path must be known precisely. The angle of the failure path and the weld and their effects on capacity of the joint are the focus of this investigation.

2 Goal

This research has two main goals regarding the load carrying capacity of axially loaded plate structures:

  1. (a)

    To create a theoretical model for predicting the critical plane of yielding and failure.

  2. (b)

    To assess the effect of the angle of inclined welds on the capacity of the joint.

3 Material

The investigated joints were fabricated of S960 QC steel using a GMAW-process. S960 QC steel is direct quenched UHSS with a nomina-l yield strength of 960 MPa. The filler material was a slightly under-matching filler metal, Böhler Union X96. The nominal chemical compositions and mechanical properties of the base and filler material are presented in Tables 1 and 2.

Table 1 Chemical composition of the parent and filler materials (nominal values, weight %)
Full size table
Table 2 Mechanical properties of the parent and filler materials (nominal values)
Full size table

4 Critical plane

4.1 General yield criterion

The general yield criterion can be written as a function of the stress invariants [9]:

$$ f\left({I}_1,{I}_2,{I}_3,{k}_1,{k}_2,\dots \right)=0 $$
(1)

Where:

I 1 :

first invariant of the stress tensor

I 2 :

second invariant of the stress deviator tensor

I 3 :

third invariant of the stress deviator

k 1, k 2 ,…:

experimentally defined material constants such as yield stress etc.

The first invariant of the stress tensor representing the hydrostatic pressure is assumed in many applications to have no effect on the yielding and is thus neglected. Based on the fixing the function f, the general yield criterion still offers several special hypotheses for failure in terms of capacity and critical plane. In this study, the plate is subjected to tension load F, causing uniform stress (σ x) over the plate cross section (bt) in the direction of the x-axis, and the other directions are free, as illustrated in Fig. 3.

Fig. 3
figure 3

Inclined failure path model for an axially loaded plate

Full size image

Under plane stress conditions the stress at the angle α to the loading direction can be defined:

$$ {\sigma}_{\alpha }={\left\{n\right\}}^T\left[S\right]\left\{n\right\} $$
(2)

where the direction vector of the plane is n:

$$ \left[n\right]=\left\{\begin{array}{l} \cos \alpha \\ {} \sin \alpha \end{array}\right\} $$
(3)

and the stress matrix [S]:

$$ \left[S\right]=\left[\begin{array}{l}{\sigma}_x\kern1.75em {\tau}_{xy}\\ {}{\tau}_{xy}\kern1.75em {\sigma}_{\mathrm{y}}\end{array}\right] $$
(4)

This gives for the normal stress on the plane:

$$ {\sigma}_{\alpha }={\sigma}_x{ \cos}^2\alpha +{\sigma}_y{ \sin}^2\alpha +2{\tau}_{xy} \sin \alpha \cos \alpha $$
(5)

and for the shear stress on the plane:

$$ {\tau}_{\alpha }=-\left({\sigma}_x-{\sigma}_y\right) \sin \alpha \cos \alpha -{\tau}_{xy}\left({ \sin}^2\alpha - \cos {}^2\alpha \right) $$
(6)

where σ x is the stress in the main loading direction and σ y the stress in the transverse direction, and τ xy is the shear stress in the plate. With a simple ideal elastic-plastic material model with yield strength f y without strain hardening effect, the capacity can be estimated based on the yield strength of the material.

4.2 Principal stress criterion

In the case presented in Fig. 1a, the principal stress σ 1 = σ x , and with the idealized material model, the axial load carrying capacity F of the plate is simply:

$$ F=bt{\sigma}_1=bt{f}_y $$
(7)

4.3 Maximum shear stress criterion

According to this yield criterion, proposed originally by Tresca, the yielding occurs in the plane of the maximum shear stress, as illustrated in Fig. 4.

Fig. 4
figure 4

Stresses on the inclined plane

Full size image

The critical angle α for failure can be derived from the shear stress Eq. (6) by considering simple axial loading with σ y  = τ xy  = 0:

$$ {\tau}_{\alpha }=-{\sigma}_x \sin \alpha \cos \alpha $$
(8)

The maximum shear stress can be defined by differentiating the Eq. (6):

$$ \frac{d{\tau}_{\alpha }}{d\alpha }=-{\sigma}_x\left({ \cos}^2\alpha -{ \sin}^2\alpha \right)=0 $$
(9)

This gives:

$$ \alpha =\frac{\pi }{4}=45 \deg $$
(10)

and

$$ {\tau}_{\alpha }={\sigma}_{\alpha }=\frac{\sigma_x}{2} $$
(11)

The loading capacity F based on the maximum shear stress criteria when σ x  = f y is:

$$ F=\frac{bt}{ \cos \alpha}\left[{\tau}_{\alpha } \sin \alpha +{\sigma}_{\alpha } \cos \alpha \right]=\frac{bt{f}_y}{2}\left( \tan \alpha +1\right)=bt{f}_y $$
(12)

As is widely known, in this case, the maximum shear stress criterion gives, for isotropic material, the same capacity as the maximum principal stress criteria, see Eq. (7).

4.4 Octahedral shear stress criterion

A plane whose normal vectors have equal angles with each of the principal axes (i.e., having direction cosines equal to 1/√3) is called an octahedral plane as illustrated in Fig. 5a [5]. In a relatively thin plate loaded by axial loading, the situation can be analysed as a 2D-case, as shown in Fig. 5b.

Fig. 5
figure 5

a Octahedral plane [5] and b stresses on an inclined plane

Full size image

The octahedral shear stresses τ oct acting on the plane can be defined for axial plane stress loading:

$$ {\tau}_{oct}=\frac{1}{3}\sqrt{2\left({I}_1^2-3{I}_2\right)}=\frac{1}{3}\sqrt{{\left({\sigma}_1-{\sigma}_2\right)}^2+{\left({\sigma}_2-{\sigma}_3\right)}^2+{\left({\sigma}_3-{\sigma}_1\right)}^2}=\frac{\sqrt{2}}{3}{\sigma}_1 $$
(13)

The hydrostatic stress σ h perpendicular to the octahedral plane is:

$$ {\sigma}_h=\frac{I_1}{3}=\frac{\sigma_1+{\sigma}_2+{\sigma}_3}{3}=\frac{\sigma_1}{3} $$
(14)

The angle α of the critical plane can now be defined:

$$ a=\frac{\pi }{2}-\frac{1}{2} \arctan \left(\frac{\tau_{oct}}{\frac{\sigma_1}{2}-{\sigma}_h}\right)=\frac{\pi }{2}-\frac{1}{2} \arctan \left(\frac{\sqrt{2}}{\frac{3}{2}-1}\right)=0.954\ \mathrm{rad}=54.7 \deg $$
(15)

The capacity based on the octahedral stresses is:

$$ F=\frac{bt}{ \cos \alpha}\left[{\tau}_{och} \sin \alpha +{\sigma}_h \cos \alpha \right]=\frac{bt{f}_y}{3}\left(\sqrt{2} \tan \alpha +1\right)=bt{f}_y $$
(16)

4.5 Strain increment method

The generalized Hooke’s law for plane stress is:

$$ {\varepsilon}_1=\frac{1}{E}\left[{\sigma}_1-\nu \left({\sigma}_2+{\sigma}_3\right)\right] $$
(17)

It can be assumed to be valid also for plastic strain increments dε [10]. Consequently, by considering the Poisson’s ratio ν = 0.5, the ratio of principal plastic strain increments can be defined:

$$ \frac{d{\varepsilon}_2}{d{\varepsilon}_1}=\frac{\sigma_2-\nu {\sigma}_1}{\sigma_1-\nu {\sigma}_2}=\frac{2{\sigma}_2-{\sigma}_1}{2{\sigma}_1-{\sigma}_2}=-\frac{1}{2} $$
(18)

The critical plane where the failure takes place, illustrated in Fig. 6, can now be defined:

$$ \alpha =\frac{\pi }{4}-\frac{1}{2} \arcsin \left[\frac{1+\frac{d{\varepsilon}_2}{d{\varepsilon}_1}}{1-\frac{d{\varepsilon}_2}{d{\varepsilon}_1}}\right]=\frac{\pi }{4}-\frac{1}{2} \arcsin \left[\frac{1-\frac{1}{2}}{1+\frac{1}{2}}\right]=0.615\ \mathrm{rad}=35.3 \deg $$
(19)
Fig. 6
figure 6

a Plastic strain and b Mohr circle for strain rates

Full size image

Similar results can be derived by means of the Mohr strain rate circle, shown in Fig. 6b [11]. By assuming the strain rate ratio is equal to the plastic increment rate, the critical plane can be defined:

$$ \alpha =\frac{\pi }{4}-\frac{1}{2} \arcsin \left[\frac{\sigma_1+{\sigma}_2}{3\left({\sigma}_1-{\sigma}_2\right)}\right]=\frac{\pi }{4}-\frac{1}{2} \arcsin \left[\frac{1}{3}\right]=0.615\ \mathrm{rad}=35.3 \deg $$
(20)

This is the complement angle for the octahedral angle of 54.7 deg. The critical plane defined by means of void coalescence is also close to this angle (0 < α < π/4) [11, 12], but the exact value is based on micro level material parameters such as micro-void volume fraction.

The load capacity based on the strain ratio criterion is:

$$ F=\frac{bt}{ \cos \alpha}\left[{\tau}_{\alpha } \sin \alpha +{\sigma}_{\alpha } \cos \alpha \right]=bt{f}_y\left[{ \sin}^2\alpha +{ \cos}^2\alpha \right]=bt{f}_y $$
(21)

4.6 Vanishing strain plane approach

By using a simple plane stress assumption, the strain in angle α can be defined by the following formula:

$$ {\varepsilon}_{\alpha }={\varepsilon}_x{ \sin}^2\alpha +{\varepsilon}_y{ \cos}^2\alpha +{\gamma}_{xy} \sin \alpha \cos \alpha $$
(22)

If the plate is under axial tensile loading only, the strain ε α varies from -νε x to ε x in accordance with α = 0 … 90, as illustrated in Fig. 7.

Fig. 7
figure 7

Strain value dependence on the angle α

Full size image

On the critical plane, the strain ε α is vanishing

$$ {\varepsilon}_{\alpha }={\varepsilon}_x{ \sin}^2\alpha -\nu {\varepsilon}_x\left(1-{ \sin}^2\alpha \right)={\varepsilon}_x\left[\left(1+\nu \right){ \sin}^2\alpha -\nu \right] $$
(23)

For steel in the elastic regime, ν = 0.3 gives:

$$ \alpha = \arcsin \sqrt{\frac{\nu }{1+\nu }}= \arcsin \sqrt{\frac{0.3}{1.3}}=0.5\ \mathrm{rad}=28.7 \deg $$
(24)

However, in the fully plastic regime, the Poisson’s ratio becomes ν = 0.5, which gives:

$$ \alpha = \arcsin \sqrt{\frac{\nu }{1+\nu }}= \arcsin \sqrt{\frac{0.5}{1.5}}=0.615\ \mathrm{rad}=35.3 \deg $$
(25)

Consequently, this yields the same critical angle and load carrying capacity as the previously investigated strain-increment method.

4.7 Critical plane based on simple force balance and von Mises yield criterion

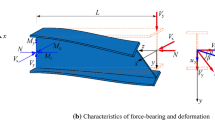
The force balance can be established by assuming there is only shear and normal stress acting on the critical plane and the load parallel to the critical plane vanishes in a yielding condition, as presented in Fig. 8. This idea is very similar to the definition of fillet weld capacity presented in Eurocode 3, part 1–8 [13].

Fig. 8
figure 8

a Stress components on the inclined plane due to the external force and b the capacity of the critical plane dependent on angle α

Full size image

The equilibrium stress components are:

$$ {\sigma}_{\alpha }=\frac{F{ \cos}^2\alpha }{bt} $$
(26)
$$ {\tau}_{\alpha }=\frac{F \sin \alpha \cos \alpha }{bt} $$
(27)

The equivalent stress can be defined by applying the von Mises criterion. In the yielding state:

$$ {\sigma}_{eqv}=\sqrt{\sigma_{\alpha}^2+3{\tau}_{\alpha}^2}=\frac{F \cos \alpha }{bt}\sqrt{{ \cos}^2\alpha +3{ \sin}^2\alpha }=\frac{F \cos \alpha }{bt}\sqrt{3-2{ \cos}^2\alpha }={f}_y $$
(28)

The capacity of the joint is:

$$ F=\frac{bt{f}_y}{ \cos \alpha \sqrt{3-2{ \cos}^2\alpha }} $$
(29)

The function is illustrated in Fig. 8b, and the minimum capacity of the joint can be defined:

$$ \frac{dF}{d\alpha }=bt{f}_y\left[\frac{ \sin \alpha }{\left(3-2{ \cos}^2\alpha \right)}\left(\frac{1}{{ \cos}^2\alpha }-\frac{2}{3-2{ \cos}^2\alpha}\right)\right]=0 $$
(30)

which can be simplified to the form (in addition to sin α = 0)

$$ 4{ \cos}^2\alpha =3 $$
(31)

which gives an angle for the critical plane:

$$ \alpha = \arccos \frac{\sqrt{3}}{2}=\frac{\pi }{6}\ \mathrm{rad}=30 \deg $$
(32)

By substituting this result in Eq. (29), the capacity can be defined:

$$ F=\frac{bt{f}_y}{ \cos \alpha \sqrt{3-2{ \cos}^2\alpha }}=\frac{2\sqrt{2}bt{f}_y}{3}=0.943bt{f}_y $$
(33)

If we apply the same idea for pure shear loading, the approach gives the critical plane at an angle of 45°, which agrees with experimental results. Thus, this model seems to be applicable for other loading conditions as well. This new minimum load carrying capacity (MLCC) approach bases on the assumption that the stress parallel to the critical plane vanishes and the distortion energy hypothesis is applicable for ductile material.

5 Experimental tests

5.1 Test specimens

Five butt-joints were fabricated for investigation of the effect of the inclination angle of the joint (α w ) on the capacity of the joint in terms of load and deformation performance. The test specimen is illustrated in Fig. 9, and the dimensions are given in Table 3. More detailed information about the preparation and testing of the joint is available in reference [14].

Fig. 9
figure 9

Test specimen with 45° inclination angle: a drawing and b welding preparation of the joint

Full size image
Table 3 Dimensions (minimum values of a and b parts) of test specimens
Full size table

Because HAZ softening in the weld has an effect on the capacity of the joint, the heat input was controlled carefully. The joint was fabricated by three passes using a GMAW-process and a slightly undermatching filler metal (Union X96) with 1-mm solid core wire. The welding parameters are given in Fig. 10, where I = current, U = voltage and v = welding speed.

Fig. 10
figure 10

Welding of butt joints: a run sequence, b result and c) parameters

Full size image

The prepared specimens and the hardness distribution in the joint are illustrated in Fig. 11. Because all the joints were prepared using the same welding parameters, and the joint geometry is the same, the cooling rates should be the same for all specimens, except the area close to the edges of the specimen, where the incline of the joint may cause asymmetric heat conduction.

Fig. 11
figure 11

a Set of test specimens and b hardness distribution in the joint

Full size image

5.2 Test set-up

The test arrangement is shown in Fig. 12. The tensile load was applied to the specimen by pin end connections, which ensures centric loading. The strains were measured by ARAMIS-system.

Fig. 12
figure 12

Test set up: a loading rig with ARAMIS-system and b loading of the specimen

Full size image

5.3 Test results

5.3.1 Joints without inclined welds

The failure angles were measured also from some previous tests seen in Fig. 14 and the results are presented in Table 4. Further tests covering base plates as shown in Fig. 13a (referring “no welds” in Table 4), load- or non-load carrying transverse joints as shown in Fig. 13b (“transverse welds” in Table 4) and longitudinal claddings (“longitudinal” in Table 4).

Table 4 Failure angles
Full size table
Fig. 13
figure 13

Failure path in an axially loaded plates: a no weld, b joints with transverse weld and c longitudinal cladding weld

Full size image

5.3.2 Joints with inclined welds

Figure 14a presents the load displacement curves for joints with different inclined welds. The adjacent table gives numerical values for ultimate load capacity F u, ultimate relative displacement δ u /δ u, BM and ultimate elongation ε u over the weld (from toe to toe, obtained from ARAMIS)

Fig. 14
figure 14

a Load-displacement behaviour of joints with inclined welds and b maximum values

Full size image

The failure modes from the experimental tests together with ARAMIS-results are presented in Fig. 15. ARAMIS is a non-contact and material-independent measuring system based on digital image correlation. The results here are strain values presented as colours. The comparison between failure modes and ARAMIS-results proves that the method enables to predict the location of the failure path precisely.

Fig. 15
figure 15

Failure paths and strains from ARAMIS

Full size image

In Fig. 16, the calculated strain values are compared with results from strain gauges and ARAMIS. It can be seen that the true strain stress value from ARAMIS diverges from the calculated and gauge-measured strain values after 550 MPa nominal stress level is reached (the true stress value is a little bit higher). At lower levels, the difference follows the logarithm rule. Strain gauges are located in the middle of the specimen and it measures true strains, but the gauges are not located in the softening area, which explains the difference with the ARAMIS results.

Fig. 16
figure 16

Strain gauge values

Full size image

6 FEA

FEA calculations were carried out to compare the critical planes with numerical methods. Figure 17 illustrates the results from LS DYNA- and ABAQUS-programs using the von Mises yield criterion and shell or solid elements. No damage criterion was introduced to the model using ABAQUS but LS DYNA uses the effective plastic damage criterion, which is included in material number 81/82. Due to this model, the damage is defined based on the changes of the cross-section of the material with the respect to the softening and rupture strains.

Fig. 17
figure 17

Rupture by LS DYNA a just starting and b at final state c critical zones by ABAQUS

Full size image

The analyses used the material parameters of the base material obtained from Table 1. Inelastic response is introduced as pair tabular values of true stresses and true plastic strains along with isotropic hardening rule. FS Dyna gave the critical plane as being at an angle of 30.5° when shell elements were used and a 32.0° angle when solid elements were used. ABAQUS with solid elements gave an angle of 28.3° for the critical plane. All the models estimated the same ultimate capacity, which was close to the capacity based on the nominal ultimate tensile strength and the original cross section area of the plate.

7 Discussion

The minimum load carrying capacity (MLCC) approach based on the von Mises criterion indicates that failure will occur at a 30° angle, Eq. (32), which differs from the critical planes of 35.3°, 45° and 54.7° of the other approaches considered. Based on the assumption on the role of the hydrostatic pressure on the failure, two geometrical solutions for definition of the critical planes can be defined as illustrated in Fig. 18.

Fig. 18
figure 18

Geometrical definition of critical planes (a and b) based on hydrostatic pressure

Full size image

Based on the hydrostatic stress state, the following equations can be created

$$ \sigma \sin {\alpha}_a=\sigma \cos {\alpha}_a \sin \beta =\sigma \cos {\alpha}_a \cos \beta $$
(34)

or

$$ \sigma \cos {\alpha}_b=\sigma \sin {\alpha}_b \sin \beta =\sigma \sin {\alpha}_b \cos \beta $$
(35)

The balance provides β = 45° and the critical planes α a  = 35.3° and α b  = 54.7°, which are the two potential octahedral planes. However, none of the experimental results matched with these results and especially the later model, although theoretically correct, seems not be realistic based on experimental result from joint with a w  = 60°.

The average failure angle in the 26 experimental tests (see Table 4) was 29.4° and FEA predicted angles quite close to this figure. Thus, the failure angle of 30° seems to be reasonably accurate, both theoretically and in practice. Although FEA obtained the same critical failure mode as MLCC-approach, the reduction of capacity was less than 5.7 % found in theoretical approach.

Theoretical results based on MLCC give a slightly lower load carrying capacity, Eq. (33), compared to the other approaches, which all give the same capacity as the principal stress approach. The experimental results can be compared to the results of the MLCC-approach and FEA by fixing the calculated and experimental results as equating the case of a transverse weld (αw = 0). Consequently, the softening will be considered equally in the both results. The results of this comparison are given in Table 5. Agreement with the different inclined angles is good except for αw = 60°. The logical reason for this discrepancy is that the failure mode no longer follows the inclined weld angle.

Table 5 Comparison of experimental and theoretical results
Full size table

The softening effect plays an important role in the capacity of welded joints made of high strength steels [15–17]. In this work, it is seen that the softening controls the critical failure plane in plates with inclined welds in a weld angle regime from αw = 0 to 45° (see Fig. 15). Based on the hardness distribution, the softening effect seems to decrease the strength by about 20 %. However, the width of the continuous softening zone in the HAZ is quite narrow. The narrow softening zone has minor effect on the transverse loading capacity of the joint due to the triaxial stress state. In shear loading, however, the width is not such a critical parameter and thus the narrow softening zone has a more significant decreasing effect on to the load carrying capacity.

The angle of the failure path has little effect on the load carrying capacity in the regime of α = 0…45°. It is important to understand this point when designing joints with inclined angles. When high strength steel is used, the inclined angle αw must be about 60° in order to avoid the weakening effect due to softening. This finding is in conflict with some older design recommendations advocating use of inclined joining for high-strength steel plates. The recommendation for an approximately 60° joint angle concerns not only for butt welds but also fillet welds. Although the softening effect is partly compensated by a larger constraint effect due to the greater triaxiality of the fillet weld, the same critical angle limit (60°) should be considered for joints with fillet welds. However, the recommendations for fillet welds require still more investigations. This increase considerably the importance of this phenomenon because of the several practical applications, some of which are illustrated in Fig. 19.

Fig. 19
figure 19

Some applications where the critical failure plane due to weld softening should be considered

Full size image

8 Conclusions

Based on experimental tests and theoretical calculations, the following conclusions can be drawn:

  • The minimum load carrying capacity (MLCC) approach giving a failure plane of 30° seems to be the dominating mechanism also in practice

  • The capacity is not very sensitive from the angle of failure plane in regime of α = 0…45 degrees

  • The MLCC approach is valid for plates without welds also for welded plates, if the weld has no weakening effect on the capacity of the joint (this is the case generally with conventional low strength steels but with joints, where the constrain effect due to joint and weld will compensate the softening effect)

  • The joints made of HSS with softening effect the critical failure plane follow the inclining angle of weld in regime of αw = 0… 45 degrees

  • The critical angle should be considered in design of all type of joint with inclined welds.