Introduction

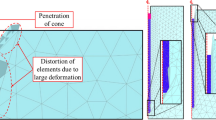
In the last few decades, significant advancement has happened and robust algorithms are developed in different numerical procedures, e.g. finite element method, mesh free methods, boundary element method. These numerical methods have been successfully applied in solving challenging boundary values problems in geotechnical engineering—pile penetration analysis (Qiu et al. [21]; Dijkstra et al. [10]), spudcan penetration analysis [13] are some examples. Although researchers have attempted to analyze advanced boundary value problems using numerical techniques, very few work has been done in simulating common laboratory and field tests which are universally used for determining soil properties before construction of an infrastructure, e.g. vane shear test, standard penetration test, cone penetration test etc. [25]. In the present work, the most commonly used field test has been considered for simulation, viz. static cone penetration test (SCPT).

The SCPT is an in situ test widely used for determining relative density, friction angle and stiffness modulus for sand [3, 18, 24]. The resistance to penetration of cone in soil consists of two terms viz. cone resistance and sleeve resistance. Let F t be the total force experienced during penetration of cone, F c be the cone tip resistance given in terms of force and F s is sleeve friction resistance encountered during penetration. The cone resistance, more commonly used in geotechnical practices, is expressed in the form of stress given by

$$ q_{\text{c}} = {{4F_{\text{c}} }/{\uppi d_{\text{c}}^{ 2} }} $$
(1)

where q c is the cone tip resistance, d c is the diameter of cone.

In the literature, there are various analytical methods available to study cone penetration resistance in dense sand which includes bearing capacity theory by limit plasticity assuming Mohr–Coulomb failure criterion of soil [12, 16, 20], cavity expansion theory by application of kinematic field in soil domain [4, 23, 27] and strain path method where cone is assumed to be surrounded by an incompressible, inviscid fluid [5]. However, these methods have limited applicability because the deformation patterns assumed in bearing capacity theory and cavity expansion theory are not justified by the experimental observations. Also, in the approach proposed by Baligh [5], the resistance to distortion of soil was ignored in the calculation of the kinematic field, while it was later assumed to exist in the calculation of stresses, thus creating certain incompatibilities. Laboratory chamber studies have also been carried out to study penetration of cone in soil media [2, 6, 14, 30].

Finite element method has been used by many researchers to simulate cone penetration test [15, 17, 26]. Kiousis et al. [17] analyzed the cone penetration problem for soil deposits found in Louisiana sites by incorporating the large strain formulation along with changing boundary conditions near the cone tip after each penetration step and considering material and geometric nonlinearities. Their analysis does not take the natural flow of soil into account and uses a predefined displacement field of soil around the cone tip. They also neglected the interface friction between cone and soil. Van Den Berg et al. [26] used arbitrary Lagrangian–Eulerian (ALE) approach for cone penetration in layered soil deposit. They assumed the cone to have rigid boundary conditions and the soil to move around the cone tip in a specified displacement field. They started their analysis by placing the cone in a pre-bored hole which may result in underestimation of horizontal stresses on cone. They concluded that a penetration of at least four times the diameter of cone is needed for the full development of cone resistance in sand layer. Huang et al. [15] simulated cone penetration test in cohesionless soil using finite element method. In order to account for the contribution of interface friction in cone resistance, they multiplied the cone resistance at zero friction \( \left( {\bar{q}_{{\text{c}}} } \right) \) with a cone tip factor η given by

$$ q_{\text{c}} = \eta \bar{q}_{\text{c}} $$
(2)

where q s is the actual cone tip resistance as shown in Fig. 1. They introduced a factor υ in this Equation to account for effect of dilation angle given by

$$ \eta = 1 + \upupsilon \cot \left( \alpha/2 \right)\tan \upphi_{\text{sc}} \quad 0.7 < \upupsilon < 1.1 $$
(3)

where υ is a fitting parameter determined through least-square fit method. A value of 0.86 is chosen in this study for υ which is used in Eq. (3) based on numerical CPT data and least square fit method as discussed by Huang et al. [15].

Fig. 1
figure 1

Illustration of contact interface friction angle and cone resistance

Full size image

The objective of the present study is to simulate SCPT using large deformation, three dimensional finite element method and compare the simulation results with the experimental data obtained from the literature. The coupled Eulerian–Lagrangian (CEL) tool in finite element software Abaqus/Explicit (Abaqus manual version 6.11 [1]) has been used for the simulations [21]. The soil stress–strain response has been simulated using the Mohr–Coulomb constitutive model. The cone has been modeled as rigid body. In the CEL simulations, the soil flows through the finite element mesh surrounding the cone and thus the CEL method successfully overcomes the excessive mesh distortion issues encountered in conventional finite element simulation. Herein, the elastoplastic deformation of soil is presented and output in the form of cone tip resistance is used for establishing a relationship between cone tip resistance and the mean effective stress.

Numerical Modeling

The Abaqus/Explicit procedure uses an explicit central-difference integration rule for integrating the Equations of motion for a body. The explicit time integration technique must be stable while calculating different parameters for the next time increment. The limit for the conditional stability of central difference operator is governed by the highest frequency of system given by

$$ \Delta t \le \frac{2}{{\upomega_{\hbox{max} } }} $$
(4)

where ωmax denotes the highest eigenvalue in the system. The explicit algorithm integrates through time using several time increments. The stability of these small time increments is governed by the size of smallest element (L min ) of the mesh and the dilatational wave speed (c d) across that element given by

$$ \Delta t \approx \frac{{L_{\hbox{min} } }}{{c_{\text{d}} }} $$
(5)

The estimation of Δt given by Eq. (5) is an approximate value which is not conservative in most of the cases. The actual time increment adopted in Abaqus/Explicit depends on stiffness behavior in a model accompanied with penalty contact. The dilatational wave speed used in Eq. (5) is calculated using hypoelastic material moduli defined in material’s constitutive response. In case of an isotropic, elastic material the value of dilatational wave speed is calculated by using Lamé’s constants (λ0, μ0) and density of material (ρ) which is given by

$$ c_{\text{d}} = \sqrt {\frac{{\uplambda_{0} + 2\upmu_{0} }}{\uprho }} $$
(6)

Coupled Eulerian–Lagrangian Technique

The Eulerian formulation in Abaqus provides stresses and strains in a convected co-ordinate system as opposed to Lagrangian formulation which provides stresses and strains with respect to a fixed co-ordinate system. In Eulerian analysis, material flows through the elements which are fixed in space and some material may flow out of Eulerian part thus making it excluded from analysis. Thus there is no distortion of mesh in Eulerian part. The material may completely fill the element or may fill a part of it. The part of the Eulerian element which do not have any material assignments are considered as void in the analysis. The Eulerian volume fraction (EVF) tool is used to assign material in an element. If an element is completely filled with material then its EVF is equal to unity and if there is no material in an element then its EVF is equal to zero. Eulerian part can only be meshed with three dimensional EC3D8R elements from Abaqus library.

The time incrementation in CEL technique is based on operator split of governing equation, which results in traditional Lagrangian phase followed by an Eulerian phase. There is also a check of element deformation after the end of Lagrangian time increment phase in which a tolerance limit is used to determine elements having significant deformation. This check allows elements having very little or no deformation to remain inactive during Eulerian phase.

Problems involving penetration or rotation of Lagrangian part in Eulerian part needs to be dealt with special care as heavy flow of material takes place through the mesh. Hence, a void space needs to be created at Eulerian mesh boundary to account for the flow of material replaced by penetration or rotation. This void space is necessary to track the heave of soil during penetration in CPT and also to track the material flow.

Numerical Modelling of SCPT

Numerical simulation of SCPT in different relative densities of sand has been carried out using the CEL method. Herein, soil domain has been modelled using the Eulerian elements and the cone has been modelled using the Lagrangian elements. The stress–strain response of soil is simulated using the Mohr–Coulomb constitutive model and the cone is modelled as steel with rigid body properties. The geometry of cone presented in this study is prepared by taking advantage of symmetry of the problem. The soil domain is modelled as a quarter cylindrical domain of height 3.5 m. The cone is modelled with dimensions presented in Table 1. Height of Eulerian part is taken as 3.5 m and radius as 0.50 m for recording the penetration values up to 1 m. Cone is modelled as a rigid body which will not undergo any deformation during analysis. A reference point is generated in space to control the motion of the cone which is needed to assign a constant velocity of penetration to cone. The soil domain has a void section of 50 cm in the upper part as shown in Fig. 2 to model the flow of material displaced by the insertion of the cone.

Table 1 Material and geometrical properties of cone
Full size table
Fig. 2
figure 2

Mesh diagram of CPT model with reference point having velocity of 0.4 m/s in negative z-direction

Full size image

In SCPT, soil is modelled using Mohr–Coulomb plasticity criterion with parameters specified in Table 2 based on the relative densities of sand. The following simplified relationship is used to calculate the dilation angle (ψ) for different types of sands having different friction angles [7] given by

$$\uppsi = \upphi^{\prime} - \upphi_{\text{cv}} $$
(7)

where \( \upphi^{\prime} \) denotes the friction angle for sand and ϕcv denotes critical state friction angle equal to 30°.

Table 2 Soil parameters for various types of sands used in this study
Full size table

In the present study, cone diameter d c is equal to 0.0358 m. To separate F c from F t, the interface friction angle is set to zero and total force is determined during penetration. Thus the obtained force with interface friction angle equal to zero is equivalent to cone resistance without any frictional resistance, i.e. F c|ϕsc=0 = F t|ϕsc=0. It is to be noted that when the interface friction is not zero, then there will be a component of interface friction in addition to F c|ϕsc=0.

Among the boundary conditions in the soil domain, the velocity of nodes at the bottom of the soil domain is kept zero in all active degree of freedoms. The outer surface of cylindrical domain is kept constrained from horizontal motion of nodes, i.e. x- and y-directions of velocity is zero. Symmetric boundary conditions are applied on the plane of symmetry in the model. The x-plane of symmetry in the model restricts the velocity of nodes in x-direction but allow the nodes to move in y- and z-directions. Similarly the velocity of nodes in y-direction is kept zero for y-plane of symmetry while keeping the velocity in x- and z-directions to be free. The general contact algorithm in Abaqus and penalty contact with interface friction angle equal to two-third of sand friction angle is used between cone and soil to define the contact between cone and the surrounding soil.

Initial stresses are defined in the model based on the density of soil and surcharge applied at the soil void interface. The earth pressure coefficient at rest \( (K_{0} = 1 - { \sin }\upphi^{\prime}) \) is used to calculate the horizontal stresses at any given depth. The reference point defined in this analysis to control the motion of rigid body cone as shown in Fig. 2 has six active degrees of freedom. This reference point has been assigned a constant velocity of penetration in z-direction as initial condition to control the motion of the cone and all other five degrees of freedom have been assigned zero velocity throughout the analysis.

There are two types of loading applied in this study—one is to account for the effect of gravity and the other is the surcharge loading. All these loadings are defined in the first step of the analysis which is a Dynamic/Explicit procedure. The effect of gravity is introduced by specifying an acceleration of 10 m/s2 in negative z-direction for the material assigned section in the Eulerian part. It is to be noted that no gravity loading was applied to the cone in order to restrict gravity induced penetration of the rigid cone in the soil domain. The second type of loading used is the application of surcharge at the soil void interface. This surcharge is applied to study the effect of higher depth of soil penetration without modelling the complete depth of soil medium. For example, a surcharge of 80 kPa represents that the soil void interface is located at a depth of 4 m in soil domain of unit weight 20 kN/m3. Different values of surcharge are used herein to study the dependence of cone tip resistance on the surcharge applied.

Numerical Simulation of SCPT

Calibration

The calibration of SCPT model is presented herein to prove that the analysis is independent on the size of mesh elements and velocity of penetration. Table 3 shows description of three different types of mesh used in this study to calibrate the numerical model. Figure 3a shows the output from three different numerical models with different size of mesh in the form of total force required to penetrate the cone in soil domain. These analyses are performed for contact interface friction angle equal to two-third of the friction angle for dense sand. Based on these results, the medium mesh is chosen in this study to simulate the cone penetration problem. The second step of calibration in this study is performed to ensure that the results are independent of the velocity of cone penetration. Figure 3b shows the result in the form of total force required for penetration of the cone in soil domain for different penetration velocities of cone. A velocity of 0.4 m/s is chosen for further analysis of cone penetration. This velocity is preferred because it will also decrease the CPU time and increase the economy of analysis. The use of such high velocity is justified by the decrease in analysis run time and increase in efficiency of numerical model without sacrificing the accuracy of the results. Velocity higher than 0.4 m/s is not used so that results are not influenced by inertial and momentum properties of soil media which will provide much larger and fluctuation values of cone resistance.

Table 3 Description of mesh size for (CPT)
Full size table
Fig. 3
figure 3

Calibration of numerical model a mesh independency (with frictional interface) and b velocity independency (with smooth interface)

Full size image

It is to be noted that two types of analysis are carried out for one simulation of cone penetration. One analysis is carried out with frictionless interface and the other with frictional interface with interface friction angle equal to two-third of soil friction angle. Then the Eq. (3) (with υ = 0.86) is used to calculate the cone resistance from frictionless analysis and sleeve resistance is calculated by subtracting cone resistance from the total resistance as obtained by frictional analysis.

Results and Discussions

The main emphasis in the study of SCPT is given to the tip resistance encountered by cone tip during penetration of cone in cohesionless soil. Tip resistance is calculated by using Eq. (3) with results obtained from frictionless interface between soil and cone. However, distribution of total global sleeve friction is also presented in this study. The sleeve friction is calculated for the complete shaft which is penetrated in soil domain. Thus the contact area between cone tip and soil remains constant after the full penetration of cone tip but the contact area between sleeve and soil keeps on increasing with increasing penetration depth. Figure 4 shows the distribution of cone tip resistance and global sleeve friction for dense sand \( (\upphi^{\prime} = 37.5^\circ ) \). This figure shows that at the penetration depth of 1 m, magnitude of cone resistance is equal to 6876 kPa as compared to only 12 kPa sleeve resistance. The average value of friction ratio for 1 m penetration is recorded as 0.72 %. Based on Robertson and Campanella [22], soil with friction ratio 0.72 % and cone resistance as 6876 kPa will be classified as sandy soil. According to Douglas and Olsen [11], for the above stated values of cone and sleeve resistance, the soil will be classified as non-cohesive coarse grained soil. This value of friction ratio and cone resistance justifies the material modelling of soil as dense sand.

Fig. 4
figure 4

Distribution of a cone resistance and b sleeve friction for dense sand with zero surchage

Full size image

The variation of sleeve friction along the sleeve length is also considered in this analysis. Figure 5 shows the stress distribution on the sleeve at penetration depth of 0.35 m. The values on y axis represent the distance of points from conical part of the cone. The distribution shows a constant value of 2 kPa for penetration depth of 0.35 m with zero surcharge and dense sand (ϕ = 37.5°). Figures 6, 7 and 8 show the radial and vertical stress contours surrounding the cone tip at a depth of 0.5 m. The vertical stress below the cone tip is observed to be higher than the radial stress which is reasonable.

Fig. 5
figure 5

Sleeve stress distribution along shaft

Full size image
Fig. 6
figure 6

Radial stress distribution contours in x-direction at a penetration depth of 0.5 m

Full size image
Fig. 7
figure 7

Radial stress distribution contours in y-direction at a penetration depth of 0.5 m

Full size image
Fig. 8
figure 8

Axial stress distribution contours in z-direction at a penetration depth of 0.5 m

Full size image

Figure 9 shows the variation of horizontal stresses at fixed points in soil domain. These points are chosen at depths of 0.25, 0.50 and 0.75 m. The values of stresses are plotted on logarithmic scale because of very high value of stress corresponding to an individual point when the cone passes through that point. This distribution shows that there is very high increase in horizontal stresses (around 200 kPa for soil node at a depth of 0.25 m corresponding to dense sand with zero surcharge) when the cone passes through a particular point. However, as the cone goes down in soil, the sleeve resistance come into play and the horizontal stresses become constant (around 5 kPa for soil node at depth of 0.25 m corresponding to dense sand with zero surcharge) which remains unaffected by further penetration of cone.

Fig. 9
figure 9

Distribution of horizontal stresses for three fixed nodes in numerical model (dense sand with zero surcharge)

Full size image

The analyses are performed herein for different values of surcharge like 40, 80, 160 and 240 kPa. The Eq. (8) given below by Clausen et al. [8] is used to present the results of obtained cone resistance q c in terms of relative density of sand because the Mohr–Coulomb model does not take into consideration of soil relative density. The relative density of sand depends on the stress conditions and compressibility of soil given by

$$ D_{\text{R}} = 0.4\ln \left[ {\frac{{q_{\text{c}} }}{{22.\sqrt {\sigma^{\prime}_{\text{v0}} .p_{\text{a}} } }}} \right]\quad p_{\rm a} = \, 100{\text{ kPa}}. $$
(8)

Table 4 shows the values of average relative densities as obtained using Eq. (8). The average of these relative densities for a particular soil type is taken to symbolize the soil. The results of finite element analyses are then compared with that reported in Baldi et al. [3] in terms of averaged relative densities as calculated from Eq. (8). Figure 10 shows the comparison between current study and Baldi et al. [3]. The comparison shows a good agreement between the results obtained from Baldi et al. [3] and current study. It may be noted that in the numerical model presented in this study, the Young’s modulus is constant in the soil domain. But in reality, the Young’s modulus of soil is dependent on the stress condition of soil. The difference between experimental data and the simulation results can thus be attributed to the constant Young’s modulus value considered herein.

Table 4 Relative densities of sands under study as calculated according to Clausen et al. [8]
Full size table
Fig. 10
figure 10

Comparison between present study and Baldi et al. [3] with D R calulated from Clausen et al. [8]

Full size image

The next comparison is made between results from current study and various results using bearing capacity theory, calibration chamber testing and cavity expansion solutions as obtained from the literature. Results from bearing capacity solution reported by Durgunoglu and Mitchell [12, DM], cavity expansion solutions reported by Collins et al. [9] combined with correlation given by Yasafuku and Hyde [28, YH&C], cavity expansion solution reported by Collins et al. [9] combined with bearing capacity factor correlation given by Ladanyi and Johnston [19, LJ&C], chamber correlation test results reported by Houlsby and Hitchman [14], and experimental results reported by Yu and Mitchell [29] are compared with current solution by CEL analysis in this section as shown in Fig. 11. The comparison between normalized stresses \( \left( {q_{\rm c} /\sigma_{{\rm v}0}^{{\prime }} } \right) \) for surcharge value 240 kPa shows good agreement between the results.

Fig. 11
figure 11

Comparison between experimental data and predicted cone factor solution for several studies with current study for 240 kPa surcharge pressure

Full size image

Conclusions

A numerical model is developed in order to understand the response of cohesionless soil for different relative densities subjected to SCPT. The material is modelled using the Mohr–Coulomb failure criterion and the response of soil is studied till a constant value of tip resistance is achieved. The dependence of soil Young’s modulus on stress is not considered in this study which causes variation in results at higher penetration depths. From the comparison with existing numerical results and experimental data, it is concluded that the response of numerical model presented in this study is reasonable for intermediate depths of cone penetration and thus, CEL can successfully simulate the large deformation response of soil at the time of cone penetration.

As observed in the numerical analyses, the CEL procedure is very well suited for problems involving large deformation. The successful representation of VST and SCPT using CEL proves that CEL is a potential tool for large deformation in Geotechnical Engineering.