S-parameter measurement-based asymmetric surface acoustic wave interdigital transducer characterization

Abstract

SAW (surface acoustic wave) resonators using asymmetrical interdigital transducers (IDTs) are experimentally characterized and its physical characteristics are modeled in terms of layout dimensions. It is shown that since the acoustic waves within a piezoelectrical material can be modulated by exploiting asymmetrical IDT layout variations, the physical characteristics of a SAW resonator (e.g., energy loss and out-of-band rejection characteristics) can be considerably improved. Test patterns for experimental characterizations are designed and fabricated with a LiTaO₃ piezoelectric substrate. Then S-parameters are measured in a broad frequency band (50 MHz–6.05 GHz). The physical characteristics of an asymmetrical SAW IDT structure are represented with a metallization factor ($\xi_{i}$) that indicates how much area the metal occupies within IDTs. Thereby, SAW-based microwave components can be designed efficiently with the asymmetrical IDT structures.

1 Introduction

Piezo-based electromechanical devices have wide practical applications. With the advent of 5G/6G mobile communication technology, not only do frequency spectrum up to 6 GHz have to be utilized but also high-frequency and broadband RF components for various mobile handsets need be developed [1,2,3]. In general, SAW devices are more advantageous below 3 GHz in cost and performance than those using BAW (Bulk Acoustic Wave) technology, whereas above 3.5 GHz, BAW devices such as FBAR (thin-film Bulk Acoustic Resonator) are unique and provide good performance. However, BAW technology also has fundamental limitations such as very difficult thickness control for higher frequency operation and the dramatic increase of loss as the operating frequency increases. Recently, although its fabrication cost is much higher than the conventional SAW, advanced SAW technology such as IHP (incredible high-performance) SAW.

HAL (hetero-acoustic layer) SAW that operates on more than 3 ~ 5 GHz [4, 5] are developed. Now, there is a gray frequency area between 1.5 GHz and 3.5 GHz for both SAW and BAW technology. Thus, neither technology can fully displace the other. Thus, in the future, it is expected that both SAW and BAW technologies play a complementary role each other.

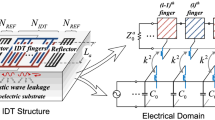
Typically, a SAW device in the radio frequency (RF) range can convert electric waves to acoustic waves using an interdigital transducer (IDT) to a piezoelectric material (e.g. LiNbO₃ or LiTaO₃), and vice versa (see Fig. 1). Furthermore, since the resonance frequency of the IDT can be well controlled with IDT layout configurations and manufacturing process, the piezoelectric devices are employed for many wireless circuits or filters [6]. Recently, as data processing speed and switching edge rates exceed several tens of GHz (gigahertz), design requirements for high-frequency circuit components become much more stringent [7]. In today’s miniaturized microwave integrated systems, SAW filters are extensively employed mainly due to low manufacturing costs and convenient design flexibility [8].

Fig. 1

SAW resonator

Acoustic waves generated at the surface of a piezoelectric material with an input signal source are scattered in all directions of the material body since the elastic stiffness constants of the piezoelectric material are of an inherently tensor quantity. Thus, if we select one of the surface wave propagation directions as the input signal propagation direction (i.e., longitudinal direction), all the other directional waves should be regarded as lost signals. In practice, since the large portion of the acoustic waves of SAW IDT are scattered into many other directions. Thus, a considerable part of the input energy leaks within the piezoelectric substrate [9, 10]. The input energy loss results in signal deterioration and substantially relaxes the filter skirt characteristics due to the reduction of a quality factor (Q) of RF components such as resonators or filters. To date, although various manufacturing process technologies that reduce leakage [11,12,13,14,15,16,17,18,19] have been developed, these increase the manufacturing cost excessively. To improve the SAW IDT characteristics, although asymmetrical IDT design methods are exploited, their physical understanding is not sufficient enough to accurately design RF components.

In this paper, a high-frequency measurement-based physical characterization method for an asymmetrical SAW IDT is presented. In asymmetrical SAW IDT the resonance frequency and quality factor considerably are modulated. We represented the resonance frequency variation of the asymmetrical IDT structure is in terms of the metallization factor ($\xi_{i}$) of IDT. Thereby, the resonance frequency can be efficiently determined even in asymmetrical IDT structures. We will show that the physical model concerned with asymmetrical IDT structure can be usefully exploited for RF component designs.

2 Physical modeling of SAW IDT

2.1 Mathematical formulation of SAW IDT

Applied time-varying electrical signals to a solid elastic material, particles within the material vibrate. Atomic vibration within the materials is again converted into electrical energy, and vice versa. Thus, the physical phenomena concerned with SAW IDT should be understood in a holistic way (but not piece-meal), combining the electromagnetic waves with the mechanical motional vibrations. Otherwise, their interactions may not be clearly interpreted. At high frequency, in general, electrical signal propagation can be considered electromagnetic wave propagation.

In contrast, the particle vibrations can be characterized with particle displacement $u\left( {r,t} \right)$ and restoring force (i.e., stress $T\left( {r,t} \right)$), where $r$ indicates a space vector. The particle displacement due to deformation from an equilibrium position can be represented with stain,

$$ S\left( {r,\,t} \right) = \frac{1}{2}\left( {\nabla u\left( {r,\,t} \right) + \, {{\nabla \widetilde{u\left( {r,t} \right)}}}} \right) \equiv \nabla_{s} u\left( {r,\,t} \right)\,, $$

(1)

where the tilde ( ~) designates a transpose of a matrix. Taking the time derivative at both sides, the particle velocity can be yielded

$$ \frac{{\partial S\left( {r,\,t} \right)}}{\partial t} = \nabla_{s} \frac{{\partial u\left( {r,\,t} \right)}}{\partial t} = \nabla_{s} v\left( {r,\,t} \right). $$

(2)

On the other hand, elastic restoring force (i.e., stress) with no body source force can be represented by

$$ \nabla \cdot T\left( {r,\,t} \right) = \rho \frac{{\partial^{2} u\left( {r,\,t} \right)}}{{\partial t^{2} }} = \rho \frac{{\partial v\left( {r,\,t} \right)}}{\partial t}, $$

(3)

where $\rho$ and $v$ (= ${{\partial u} \mathord{\left/ {\vphantom {{\partial u} {\partial t}}} \right. \kern-\nulldelimiterspace} {\partial t}}$) are the mass density and the particle velocity, respectively. The stress and strain are related with the below tensor equation

$$ T\left( {r,\,t} \right) = c:S\left( {r,\,t} \right) + \eta :\frac{{\partial S\left( {r,\,t} \right)}}{\partial t}, $$

(4)

where $c$ is stiffness tensor and $\eta$ is viscosity tensor. Assuming a lossless medium and no body force sources, the stress and velocity can be represented as below:

$$ \frac{{\partial T\left( {r,\,t} \right)}}{\partial t} = c:\frac{{\partial S\left( {r,\,t} \right)}}{\partial t}. $$

(5)

Combining (2) with (5), the acoustic velocity and stress can be represented as below:

$$ \nabla_{s} v\left( {r,\,t} \right) = s:\frac{{\partial T\left( {r,\,t} \right)}}{\partial t}, $$

(6)

where $s$ is compliance tensor that is the inverse of the stiffness tensor, $c$. The acoustic energy variations of (3) and (6) can be considered a pair of acoustic wave equations for stress and particle velocity.

2.2 Asymmetrical SAW IDT

Since resonance frequencies for a resonator are directly correlated with IDT finger layouts and material characteristics, they need careful investigation. A quality factor (Q) which is defined as an energy ratio of “a maximum stored energy within a system to a dissipated energy per one cycle” is often used to express a figure of merit for a SAW resonator. The Q can be approximately determined using the measured S-parameters [20, 21]

$$ Q_{measure} \left( \omega \right) = \frac{{\omega \tau_{gd} \left| {S_{11} } \right|}}{{1 - \left| {S_{11} } \right|^{2} }}, $$

(7)

where $\tau_{gd} = \arctan \left( {{{{\text{Im}} \left( {S_{11} } \right)} \mathord{\left/ {\vphantom {{{\text{Im}} \left( {S_{11} } \right)} {{\text{Re}} \left( {S_{11} } \right)}}} \right. \kern-\nulldelimiterspace} {{\text{Re}} \left( {S_{11} } \right)}}} \right)$. However, from the theoretical point of view, the Q for a resonator is an implicit function of the IDT configurations and the phase velocity of acoustic waves. In practice, although the quality factor (Q) can be substantially improved with asymmetrical IDT structures, they make component designs far more complicated due to acoustic wave velocity modulation. To relax the design complexity, we represent the SAW IDT characteristics with a metallization factor that can obviously express a deviation from a symmetrical IDT.

A typical IDT resonator is configured with n-metal fingers and two reflectors. Note that half of IDT fingers have positive potential, while the remaining half fingers have a negative potential. If the metal width of the $i$-th finger is $w_{i}$ and the spacing between the $i$-th finger and the ($i + 1$)-th one is $s_{i}$, the pitch width per a finger (K) of an IDT can be defined as

$$ \,\,K \equiv \frac{1}{n} \cdot \sum\limits_{i = 1}^{n} {\left( {w_{i} + s_{i} } \right)} . $$

(8)

The ratio of the metal width occupied by the $i$-th finger to the K (i.e., the $i$-th finger metallization) is defined as a spatial ratio per a finger

$$ \,\,\xi_{i} \equiv \frac{{w_{i} }}{K}\,. $$

(9)

Then, the total metallization of an IDT can be defined as below:

$$ \,\,\zeta_{total} \equiv \frac{{\,\,\,\,\,w_{total\,\,metal\,\,width} }}{{\,\,\,\,\,w_{total\,\,IDT\,\,width} }} = \frac{{\sum\nolimits_{i = 1}^{n} {K \cdot \xi_{i} } }}{n \cdot K} = \frac{{\sum\nolimits_{i = 1}^{n} {w_{i} } }}{n \cdot K}\,\,. $$

(10)

Note the resonance frequency of an IDT plays a pivotal role in many practical applications. The resonance frequency is strongly correlated with $\xi_{i}$ of an IDT. Since the metal width is equal to the spacing between metals in a symmetrical IDT, the $i$-th finger metallization ($\xi_{i}$) is represented as

$$ \left( {\zeta_{i} } \right)_{sym} \equiv \zeta_{o} = \frac{1}{2}\,\,\,\forall \,\left( {symmetrical\,\,IDT} \right). $$

(11)

In general, the energy loss which is mainly due to the leakage concerned with the tensor effects of elastic constants of the piezoelectric substrate substantially deteriorates its resonance performance [22]. We determine $\xi_{i}$ ($i = 1,2, \cdots ,n$) to maximize the quality factor (Q) in a given IDT space (i.e., for a given K) iteratively. Although the acoustic energy loss can be considerably reduced with asymmetrical IDT structures; however, its resonance frequency deviates from that of the symmetrical structure as shown Fig. 2 (a). This is becoming asymmetrical IDT modulates metal loading effect (i.e., elastic constant variation due to additional metal stress), followed by effective acoustic wave phase velocity. Therefore, unlike the symmetrical IDT structure, for accurate RF resonator designs, the resonance frequency variations due to asymmetrical IDTs should be carefully determined in the early stage of design. The resonance frequency variation for an asymmetrical IDT can be represented with a function of $\left( {K,\xi_{i} } \right)$

$$ f_{r} \left( {K,\xi_{i} } \right) = f_{r} \left( {K,\xi_{0} } \right) + \delta_{r} \left( {K,\xi_{i} } \right), $$

(12)

where the frequency deviation factor ($\delta_{r}$) can be represented as

$$ \delta_{r} \left( {K,\xi_{i} } \right) \approx \left[ {f_{r} \left( {K + \Delta K,\xi_{o} } \right) - f_{r} \left( {K,\xi_{o} } \right)} \right] \cdot \left( {{{\xi_{i} } \mathord{\left/ {\vphantom {{\xi_{i} } {\xi_{o} }}} \right. \kern-\nulldelimiterspace} {\xi_{o} }} - 1} \right). $$

(13)

Fig. 2

Resonance frequency variations of series-connected resonators. (a) For symmetrical resonators ($\xi_{i} = 0.5$) with K variations. (b) For asymmetrical resonators with $\xi_{i}$ variations (for $K = 1.2um$)

Note that since $f_{r} \left( {K,\xi_{0} } \right)$ and $f_{r} \left( {K + \Delta K,\xi_{0} } \right)$ are the resonance frequencies for the given $K$ and $K + \Delta K$ for the symmetrical IDTs, the $f_{r} \left( {K,\xi_{0} } \right)$ can be readily determined with a few symmetrical test patterns. Resonance frequency is concerned with K and $\xi_{i}$ as shown in Fig. 2(b). As the K and $\xi_{i}$ increase, the resonance frequency decreases linearly. Note that the anti-resonance frequency of a series resonator is the resonance frequency of the parallel resonator, and vice versa as shown in Fig. 3. In addition, for an accurate resonance frequency determination the capacitance variation due to $\xi_{i}$ should be accurately determined. The electric field patterns of the outermost fingers differ from those of the internal ones due to fringing effects. Thus, the total IDT capacitance for symmetrical IDT can be approximately represented with

$$ C_{{_{IDT} }}^{symmetry} \approx \left( {n - 2} \right)C_{internal} + 2C{}_{outer}\,\,\forall \,\left( {\xi_{i} = \xi_{o} } \right)\,, $$

(14)

where $C_{internal}$ and $C_{outer}$ indicate the internal capacitance per a finger of an IDT and the two outermost finger capacitances of an IDT, respectively. The $C_{internal}$ and $C_{outer}$ can be readily determined using two IDT test patterns with different number of fingers. Since the capacitance is approximately proportional to the metal width, the capacitance per finger for the internal fingers capacitance in an asymmetrical IDT can be approximately determined with

$$ C_{j}^{asymmetry} \approx C_{j}^{symmetry} \cdot \left( {\frac{{2w_{j} }}{K}} \right) = C_{j}^{symmetry} \cdot \left( {\frac{{\xi_{i} }}{{\xi_{0} }}} \right)\,, $$

(15)

where the $C^{sym}$ is the $j$th finger capacitance for the symmetrical structure. Note that for a given $K$ (i.e., for a given resonance frequency), $w_{j}$ is the $j$-th metal width in the asymmetrical structure. Thus, the total capacitance for an asymmetrical IDT can be approximately determined with capacitances of the symmetrical IDTs,

$$ C_{IDT}^{asymmetry} \approx \sum\limits_{i = 2}^{n - 1} {C_{i}^{symmetry} \cdot \left( {\frac{{\xi_{i} }}{{\xi_{0} }}} \right) + C_{1} + C_{n} } \,. $$

(16)

Fig. 3

Response frequency variations of parallel-connected resonators. (a) for symmetrical resonators ($\xi_{i} = 0.5$) with K variations. (b) for asymmetrical resonators with $\xi_{i}$ variations (for $K = 1.2um$)

As shown in Fig. 4, the IDT capacitance using (16) has an excellent agreement with experiment data.

Fig. 4

Capacitance variations due to $\xi_{i}$ variations

3 Experiments

The test structures (SAW resonators and filters) for experimental characterizations were designed and fabricated on a 42° YX-LiTaO₃ (42° rotated Y-cut X-propagation LiTaO₃) piezoelectric substrate. IDT electrodes composed of AlCu 1400 Å and Ti 200 Å are passivated with SiN (silicon nitride). The experimental set-up is shown in Fig. 5. S-parameters for test patterns are measured in the frequency range of 50 MHz to 6.05 GHz. For S-parameter measurements, each port of VNA (vector network analyzer: Anritsu MS46122A) [23] was connected to the microwave probe tip (Cascade ACP40-GSG-150). An impedance standard substrate (Cascade 101- 190 for 2-port measurements) was employed to calibrate the VNA using the SOLT (short, open, load, and thru) standards. The pad parasitics, due to the DUT (device under test) probing during measurements, were de-embedded using the conventional Y-parameter de-embedding technique [24]. Then we determined the resonance frequencies from the measured S-parameters for both impedances and admittances of the resonators.

Fig. 5

Experiment set-up. (a) measurement equipment set-up. (b) schematic representation of measurement system. Note that symmetric IDT structure and asymmetric IDT structure have the same pitch but different ratio of metal width and space width

4 Results and discussion

The physical characteristics of a resonator can be well understood in terms of its resonance frequency and Q that are strongly correlated with piezoelectric material characteristics (e.g., acoustic wave phase velocity and electroacoustic conversion efficiency) and IDT layout dimensions (i.e., $\xi_{i}$ variations, see Fig. 6). Note that although $K$ is constant, the quality factor has substantial variations with $\xi_{i}$ as shown in Fig. 7. The resonance frequencies for a given $K$ are also dependent upon the $\xi_{i}$ variations as shown in Fig. 2(b). Thus, the $\xi_{i}$ is a crucial physical design parameter for a resonator. As an example, the filter bandwidth using a high-frequency SAW resonator filter can be accurately determined with the resonator frequencies, whereas its rejection characteristics are strongly correlated with the Q. That indicates a resonator design should be optimized in terms of $\xi_{i}$. The optimal $\xi_{i}$ that provides the largest Q near an intended resonance frequency can be readily determined by representing the longitudinal acoustic waves with an acoustic transmission line [25, 26]. In a frequency band, the maximum Q can be determined with a set of suitable ($K$, $\xi_{i}$) as shown in Fig. 7.

Fig. 6

Maximum quality factor variations with the K and $\xi_{i}$ variations

Fig. 7

Quality factor variations due to $\xi_{i}$ variations

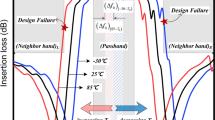
To show that the proposed technique can be usefully exploited for an RF filter design, we designed a test filter (a bandpass filter of which the center frequency is 2.55 GHz with pass bandwidth 110 MHz) as shown in Fig. 8. A radio frequency (RF) bandpass filter must satisfy not only the passband, but also the rejection bands (i.e., both left and right rejection band). Using the asymmetrical SAW resonators, the filter skirt characteristics can be considerably improved as shown in Fig. 8. To show the validity of the proposed technique, the other test filter (band 3 duplexer) in which the band gap between Tx (passband: 1710-1785 MHz) and Rx (passband: 1805-1880 MHz) is so tight to be 20 MHz and the bandgap between band 3 Rx and neighbor band (i.e., band 1 Rx) is just only 40 MHz is illustrated. Such a complicated multiplexed filter design with tight bandgaps, is may not be possible to meet the design specification with a simple design using symmetrical IDT structure. As shown in Fig. 9, a design based on symmetrical structure may result in the design failure since the rejection between the bands cannot be achieved. In contrast, designing the asymmetrical IDT design, the filter skirt can be improved in 25% which is equal to the 4 MHz reduction. Note that such a reduction of the filter skirt slope may result in a large amount of the rejection level (from about -25 dB to about -50 dB) in such narrow band gap. A radio frequency (RF) bandpass filter must satisfy not only the passband, but also the rejection bands (i.e., both left and right rejection band). Using the asymmetrical SAW resonators, the filter skirt characteristics can be considerably improved as shown in Fig. 9. Thereby, the design failure based on symmetrical resonators can be overcome with the proposed asymmetrical SAW IDTs.

Fig. 8

A bandpass filter design improvement using asymmetrical SAW IDTs, (a) S₂₁ (b) circuit representation for the filter

Fig. 9

Design improvement for band 3 duplexer (simulation data) using the proposed technique

In general, the crucial design variable for a resonator design is a periodic length of IDT finger which is strongly correlated with the center frequency. Thus, given a filter design specification, above all, the pass band based on symmetrical resonator structures should be specified with various design topologies. Then rejection specification should be satisfied. The asymmetrical design technique can be conveniently exploited to improve the rejection specification design. We summarized the systematic design procedure (see Fig. 10) that is proposed in this work.

Fig. 10

Algorithm to optimize the filter design using asymmetrical resonators

5 Conclusion

SAW IDT structures are widely utilized in RF circuits or system designs. However, they have fundamental limitations due to inherent leakage and loss of piezoelectric materials. The quality factor of the symmetrical resonator is inferior to that of the asymmetrical structure. In this work, we proposed a new physical characteristic method based on broadband S-parameter measurements. Representing a resonator with a function of the metallization factor (K $\xi_{i}$) which can be determined with IDT layouts, we physically modeled the IDT capacitance and resonance frequency in terms of $\xi_{i}$. Then, the optimal $\xi_{i}$ is determined in an iterative way by representing the longitudinal acoustic waves within a piezoelectrical substrate with a transmission line. We showed that physical characteristics for a bandpass filter, as an example, can be considerably improved with test filters designed using the proposed technique.