Introduction

During braking, the friction liner rigorously slides over brake disc and produces large heat, which is to be dissipated into surroundings. The ease, with which brake disc releases the generated heat, makes the brake more effective and reliable, due to which brake disc is made to be ventilated with the help of vanes between the two surfaces of the disc and holes on the surfaces. Finding the best braking performance using different configurations of the brake disc is an appealing problem for researchers. Afzal et al. [1] reviewed different experimental and numerical studies made on brake disc with regards to thermal and structural performance. Duzgun [2] investigated different possible ventilation configurations for the structural design of brake disc for integrated thermal and structural activities. Yan et al. [3] proposed X-type lattice structured brake disc, whereas Yan et al. [4] modified their earlier design of ventilated brake disc for enhancement of performance.

Finite element analysis (FEA) is one of the simulation tools which can be used to solve complex boundary value problems. Due to the high cost associated with the experimentation of brake disc considering different structural designs, scientists have focused on using FEA. FEA was used by Balhocine et al. [5] to understand the frictional contact and design aspects of the brake disc, whereas Riva et al. [6] used FEA to simulate the brake disc with airborne particles. Pevec et al. [7] utilized FEA to predict the cooling factors of the brake disc, while Shahzamanian et al. [8] used it to analyse the combine thermal-elastic performance considering the symmetry of brake disc. Zhang et al. [9] used FEA to study a blend between the thermal and mechanical properties of a ventilated brake disc.

MCDM is an operational research tool used to decide on the selection of an alternative based on different criteria. Rajamanickam et al. [10] applied TOPSIS to optimize the EDM process parameters of titanium alloys. Srirangan et al. [11] used TOPSIS to optimize the TIG welding process parameters of super-alloys. They also examined relation between process parameters and response variables. Memari et al. [12] utilized the method to select sustainable suppliers for different case studies. They reported that the TOPSIS approach accurately ranked the alternatives. Vivekananda et al. [13] used FEA and TOPSIS to optimized process parameters of the vibration-assisted turning process. EDAS or evaluation based on distance from average solution is an MCDM that calculates the distance of each alternative from the average solution and uses this information to select the best alternative. Researchers employed EDAS in a broad range of technological solutions to engineering problems. Ghorabaee et al. [14] applied EDAS to evaluate the construction equipment with emphasis on sustainability. Madhu et al. [15] selected suitable biomass material maximizing the yield using EDAS. Boral et al. [16] presented failure mode effect analysis using EDAS approach, whereas Emovon et al. [17] reviewed application of MCDM techniques including EDAS in the field of material selection. Similarly, COPRAS (Complex Proportional Assessment) is an advanced MCDM methodology which is based on the evaluation of alternatives to the solution of the problem proportionately [18, 19]. The additive ratio assessment (ARAS) method was introduced by Zavadskas and Turskis in 2010. ARAS is the advanced method of MCDM, used by investigators to different fields of applications and reported with improved solutions [20, 21].

The literature review reveals that there is no study reported on the selection of optimal brake design parameters by using MCDM on FEA simulation data. Thus, in this study, an attempt has been made to address this lacuna. Four different MCDM methods—EDAS, COPRAS, TOPSIS and ARAS—are used to conduct a comparison study to determine the optimal design variables. The rest of the article is arranged in the following form—the subsequent section introduces the problem considered in the study. The multi-criteria decision-making methodology used in the study is also described in this section. The next section contains the discussion of the results obtained from the finite element and the MCDM study. Finally, conclusions based on the study are presented in the final section.

Materials and Methods

Problem Statement

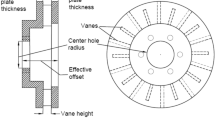
In case of disc brake, the friction liner slides over the rotating disc to provide the braking action rigorously, which generates large stresses due to heat and impact load. To release the heat generated effectively, the brake disc is ventilated in terms of vanes and holes on the surface, with different configurations. Figure 1 shows the design parameters of a ventilated brake disc. The decision regarding the optimal selection of the combination of the design parameters for high performance and life of brake disc without failure is a critical task.

Fig. 1
figure 1

Ventilated brake disc model and parameters

Full size image

In this work, considering five different design parameters (inboard plate thickness, outboard plate thickness, vane height, effective offset and centre hole radius) and a two-level full factorial design, different design configuration of the brake disc is modelled and analysed in ANSYS for maximum fatigue life using finite element analysis. Figure 2 shows the boundary conditions and loadings considered in FEA to simulate the exact braking conditions. Respective to full factorial design, thirty-two simulation runs were carried out on the brake disc listed in Table 1.

Fig. 2
figure 2

Boundary conditions and loading imposed

Full size image
Table 1 Design variables and performance parameters (full factorial design)
Full size table

Multi-criteria Decision-Making

Criteria Weight Determination by SDV Method

The derived ranking and performance score obtained in any MCDM study depends on the weight allocated to the criteria to a large extent. Often the assignment of weights in MCDM-based decision-making situations are done by the decision-makers. However, due to the uncertainties associated with human-based decision-making process, the end result may be influence by the decision-maker’s biases. To avoid this, in this study, an objective weight allocation methodology called the standard deviation method (SDV) is used.

Standard deviation method unbiasedly allocates weights to each criterion and significantly improves the MCDM approach by minimizing the personal bias involved in decision-making. Normalization is performed before the calculation of weights by using the SDV method.

$$ B_{ij} = \frac{{x_{ij} - \hbox{min} \left( x \right)_{ij} }}{{\hbox{max} \left( { x} \right)_{ij} - \hbox{min} \left( x \right)_{ij} }} $$
(1)
$$ {\text{SDV}}_{J} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{m} \left( {B_{ij} - B_{j} } \right)^{2} }}{m}} $$
(2)

where Bj is the average of the values for the ith measure, where j = 1, 2, 3.

$$ W_{j} = \frac{{{\text{SDV}}_{j} }}{{\mathop \sum \nolimits_{j = 1}^{n} {\text{SDV}}_{j} }} $$
(3)

Using the aforementioned relations, the weight vector for the current material selection problem was calculated as follows:

$$ W = \left[ {\begin{array}{*{20}c} {0.34} & {0.66} \\ \end{array} } \right] $$
(4)

EDAS Method

The evaluation based on distance from average solution (EDAS) method was proposed by Ghorabaee et al. [22] in 2015. In this method, initially the MCDM problem and the weights for the criteria are expressed as Eqs. (4) and (5), respectively.

Let D = xij be a decision matrix, where \( x_{ij} \in {\mathbb{R}} \).

$$ D = \left[ {\begin{array}{*{20}c} {x_{11} } & {x_{12} } & \cdots & {x_{1n} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{m1} } & {x_{m2} } & \cdots & {x_{mn} } \\ \end{array} } \right] $$
(5)

Next, criteria-wise average solutions are calculated.

$$ {\text{AV}}_{j} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} x_{ij} }}{n} $$
(6)

The positive distances from average (PDA) are calculated as

$$ {\text{PDA}}_{ij} = \left\{ {\begin{array}{*{20}c} {\frac{{\hbox{max} \cdot \left( {0,\left( {x_{ij} - {\text{AV}}_{j} } \right)} \right)}}{{{\text{AV}}_{\text{j}} }} | j \in B} \\ {\frac{{\hbox{max} \cdot \left( {0,\left( {{\text{AV}}_{j} - x_{ij} } \right)} \right)}}{{{\text{AV}}_{j} }} | j \in C} \\ \end{array} } \right. $$
(7)

The negative distances from average (NDA) are calculated as

$$ {\text{NDA}}_{ij} = \left\{ {\begin{array}{*{20}c} {\frac{{\hbox{max} \cdot \left( {0,\left( {{\text{AV}}_{j} - x_{ij} } \right)} \right)}}{{{\text{AV}}_{j} }} | j \in B} \\ {\frac{{\hbox{max} \cdot \left( {0,\left( {x_{ij} - {\text{AV}}_{j} } \right)} \right)}}{{{\text{AV}}_{j} }} | j \in C} \\ \end{array} } \right. $$
(8)

The PDA and NDA matrices are formed based on Eqs. (7) and (8) and has an order of n × m. Next by using the weight vector in Eq. (4), the weighted sum of PDA and NDA is calculated.

$$ {\text{SP}}_{i} = \mathop \sum \limits_{j = 1}^{m} w_{j} {\text{PDA}}_{ij} $$
(9)
$$ {\text{SN}}_{i} = \mathop \sum \limits_{j = 1}^{m} w_{j} {\text{NDA}}_{ij} $$
(10)

Next, the normalized values of SP and SN are calculated.

$$ {\text{NSP}}_{i} = \frac{{{\text{SP}}_{i} }}{{\max_{i} \left( {{\text{SP}}_{i} } \right)}} $$
(11)
$$ {\text{NSN}}_{i} = 1 - \frac{{{\text{SN}}_{i} }}{{\hbox{max} ._{i} \left( {{\text{SN}}_{i} } \right)}} $$
(12)

The appraisal score is then calculated as

$$ {\text{AS}}_{i} = \frac{{\left( {{\text{NSP}}_{i} + {\text{NSN}}_{i} } \right)}}{2}\,{\text{such}}\,{\text{that}}\,0 \le {\text{AS}}_{i} \le 1 $$
(13)

Based on decreasing appraisal score, the alternatives are ranked from the best alternative to the worst alternative.

COPRAS Method

COmplex PRoportional Assessment or COPRAS method was introduced by Zavadskas and Kaklauskas [23]. The COPRAS methods initiates by expressing the MCDM problem and the weights for the criteria in terms of Eqs. (4) and (5), respectively. Next, the decision matrix is normalized by using Eq. (14), and the weighted normalized matrix is calculated as per Eq. (15).

$$ n_{ij} = \frac{{x_{ij} }}{{\mathop \sum \nolimits_{j = 1}^{n} x_{ij} }} $$
(14)
$$ N_{ij} = w_{j} *n_{ij} $$
(15)

where i ∈ [1, m] and j ∈ [1, n].

Next, calculate the sum Bi of the benefit criteria values,

$$ B_{i} = \mathop \sum \limits_{j = 1}^{k} N_{ij} $$
(16)

Next, calculate the sum Ci of the cost criteria values,

$$ C_{i} = \mathop \sum \limits_{j = k + 1}^{m} N_{ij} $$
(17)

where k are the benefit criteria and (m − k) are the cost criteria.

Calculating the relative significance Qi of each alternative

$$ Q_{i} = B_{i} + \frac{{\hbox{min} \left( {C_{i} } \right) \cdot \mathop \sum \nolimits_{i = 1}^{n} C_{i} }}{{C_{i} \cdot \mathop \sum \nolimits_{i = 1}^{n} \left( {\frac{{\hbox{min} \left( {C_{i} } \right)}}{{C_{i} }}} \right)}} $$
(18)

Next, determine the utility degree for each alternative as

$$ {\text{UD}}_{i} = \frac{{Q_{i} }}{{\hbox{max} \left( {Q_{i} } \right)}} \times 100\% $$
(19)

TOPSIS Method

Technique for Order of Preference by Similarity to Ideal Solution or TOPSIS is a robust and widely accepted MCDM technique in operation research and production engineering, which was originally introduced in 1981 by Hwang and Yoon [24]. TOPSIS begins by expressing the MCDM problem and the weights in form of Eqs. (4) and (5), respectively. Next, the normalized decision matrix (nij) of each criterion is computed by using Eq. (20),

$$ n_{ij} = \frac{{x_{ij} }}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{m} x_{ij}^{2} } }} $$
(20)

Then, the weighted normalized matrix is determined by using Eq. (21),

$$ N_{ij} = w_{j} *n_{ij} \quad {\text{for}}\quad i \in \left[ {1,m} \right]\quad {\text{and}}\quad j \in \left[ {1,n} \right] $$
(21)

Next, the ideal positive (best) and ideal negative (worst) solutions are estimated by using Eqs. (22) and (23), respectively.

$$ A_{j}^{ + } = \left\{ {\begin{array}{*{20}c} {\hbox{max} \cdot N_{ij} | j \in {\text{B}}} \\ {\hbox{min} \cdot N_{ij} | j \in {\text{C}}} \\ \end{array} } \right. $$
(22)
$$ A_{j}^{ + } = \left\{ {\begin{array}{*{20}c} {\hbox{min} \cdot N_{ij} | j \in {\text{B}}} \\ {\hbox{max} \cdot N_{ij} | j \in {\text{C}}} \\ \end{array} } \right. $$
(23)

where B is a vector of benefit function and C is the vector of the cost function, for i ∈ 1, m and j ∈ 1, n.

The separation measurement and the relative closeness coefficient are then determined. In TOPSIS, the difference between each response from the ideal positive (best) solution is given by Eq. (24).

$$ S_{i}^{ + } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {N_{ij} - A_{j}^{ + } } \right)^{2} \quad } {\text{for}}\quad i \in \left[ {1,m} \right]\quad {\text{and}}\quad j \in \left[ {1,n} \right] $$
(24)

Similarly, the difference between each response from the ideal negative (worst) solution is given by Eq. (25).

$$ S_{i}^{ - } = \sqrt {\mathop \sum \limits_{j = 1}^{n} \left( {N_{ij} - A_{j}^{ - } } \right)^{2} \quad } {\text{for}}\quad i \in \left[ {1,m} \right]\quad {\text{and}}\quad j \in \left[ {1,n} \right] $$
(25)

The corresponding closeness coefficient (CCi) of the ith alternative is calculated using Eq. (26).

$$ {\text{CC}}_{i} = \frac{{S_{i}^{ - } }}{{ S_{i}^{ + } + S_{i}^{ - } }}\quad {\text{where}}\quad 0 \le {\text{CC}}_{i} \le 1,\quad i \in \left[ {1,m} \right] $$
(26)

Finally, the rank of the alternatives in the decreasing order of the CCi value is calculated.

ARAS Method

ARAS or additive ratio assessment method was introduced in 2010 by Zavadskas and Turskisis [25]. It starts by assuming the MCDM problem and the weights for the criteria in terms of Eqs. (4) and (5), respectively. For a MCDM problem consisting of m alternatives and n criteria, let D = xij be a decision matrix, where \( x_{ij} \in {\mathbb{R}} \).

$$ D = \left[ {\begin{array}{*{20}c} {x_{01} } & {x_{02} } & \cdots & {x_{0n} } \\ {x_{11} } & {x_{12} } & \cdots & {x_{1n} } \\ {x_{21} } & {x_{22} } & \cdots & {x_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {x_{m1} } & {x_{m2} } & \cdots & {x_{mn} } \\ \end{array} } \right] $$
(27)

where \( x_{01} , x_{02} , \ldots x_{0n} \) indicates the optimal of the 1st, 2nd and nth attribute, respectively. If the value of xoj is unknown, the following two equations can be used.

$$ x_{0j} = \left\{ {\begin{array}{*{20}c} {\hbox{max} \cdot x_{ij} | j \in B} \\ {\hbox{min} \cdot x_{ij} | j \in C} \\ \end{array} } \right. $$
(28)

Next, the decision matrix is normalized as,

$$ n_{ij} = \frac{{x_{ij} }}{{\mathop \sum \nolimits_{j = 0}^{m} x_{ij} }} $$
(29)

The weighted normalized matrix is calculated as per Eq. (30).

$$ N_{ij} = w_{j} *n_{ij} $$
(30)

The optimality function Si is the value which is regarded as the larger the better, which is specified through Eq. (31) for ith alternative

$$ S_{i} = \mathop \sum \limits_{j = 1}^{n} N_{ij} $$
(31)

The utility degree is used for the final ranking of alternatives. The utility degree is in the interval (0, 1). The utility degree Ki for ith alternative is obtained by

$$ K_{i} = \frac{{S_{i} }}{{S_{0} }} $$
(32)

where S0 is the optimality value of Si.

Results and Discussion

Finite Element Modelling and Analysis

The finite element model is simulated according to the run orders shown in Table 1. The FE analysis is carried out considering boundary conditions simulating the actual conditions of braking. Brake pressure of 2 MPa is applied on both the brake pads from outside. Frictional contact between brake shoe and the disc is incorporated. In static structural analysis using ANSYS, the brake disc are given angular velocity [5]. Based on a pilot study, the hexahedral type of element is chosen for the finite element analysis. Since, a low mesh discretization would lead to errors in the computed solutions while a high mesh discretization would lead to high computational time and thus, lead to wastage of computation resources. Thus, a mesh sensitivity test is carried out to ascertain that the chosen mesh discretization is appropriate. Figure 3 shows the fatigue life at various number of nodes. It is seen that the FE model converges as the number of nodes are increased to around 50000 nodes. Thus, this mesh discretization is used in the rest of the study. Further to evaluate the accuracy of the present FE model, it is compared with published results. As shown in Table 2, the maximum, average and minimum von Mises stress of the present model are compared with literature and was found to have around 15% deviation when compared to Belhocine et al. [5]. For FE models, this error is reasonable and thus, this model is used for further study. Figures 4 and 5 show the resulting fatigue life and axial deflection for run order 32; due to space limitation all the simulations are not included. The current model of the brake disc is safe and attains maximum fatigue life as shown in Fig. 4. Maximum fatigue life for the current loading application is 1700000 cycles of operation of brake. Figure 5 shows that the axial deflection of the disc is maximum at the outer ring of the inboard plate of the brake disc, which emphasize that it should be focused during design.

Fig. 3
figure 3

Convergence of the FEA model

Full size image
Table 2 Comparison of results from current model with the literature
Full size table
Fig. 4
figure 4

Resulting fatigue life of the brake disc for run order 32

Full size image
Fig. 5
figure 5

Resulting axial deformation of the brake disc for run order 32

Full size image

Ranking of Alternatives by MCDM

In this work, fatigue life (cycles) and axial deflection (mm) are considered as the performance parameters. While for an effective brake design, the fatigue life is considered to be maximized, the axial deflection needs to be as low as possible. Considering a full factorial design-based FEA simulated dataset shown in Table 1, the normalized decision matrix for EDAS is calculated and reported in Table 3. Figure 6 shows the normalized values of SP and SN for each alternative. In this approach, it is desired that the sum of normalized SP and normalized SN is high. From Fig. 6, it is clear that normalized SN values of the alternatives are much less sensitive as compared to the normalized SP values. Trial number 26, 31 and 32 show the most promising performance in terms of the sum of SP and SN values. The appraisal score obtained for the different trial designs of the brake disc is shown in Fig. 7. It is seen that trial number 31 has the highest appraisal score. Correspondingly in Fig. 6, trial number 31 is seen to have the largest sum of normalized SP and normalized SN. The trial wise ranking by EDAS is shown in Table 4. Similarly, the variation of the COPRAS utility degree with respect to the trial numbers is shown in Fig. 8. The highest utility degree is seen for trial number 26 and second highest for trial number 31.

Table 3 Normalized decision matrix for the MCDMs
Full size table
Fig. 6
figure 6

Normalized values of SP and SN for each alternative calculated by EDAS

Full size image
Fig. 7
figure 7

Appraisal score by EDAS for each alternative

Full size image
Table 4 Ranking obtained by the four MCDMs
Full size table
Fig. 8
figure 8

Utility degree by COPRAS for each alternative

Full size image

Figure 9 reports the Euclidean distances of each alternative from the positive ideal solution and negative ideal solution as calculated using TOPSIS. In Fig. 9, the Euclidean distance from the positive ideal solution should be as low as possible. However, on the contrary, the Euclidean distance from the negative ideal solution should be high. This would indicate that the alternative is near the positive ideal solution but far away from the negative ideal solution. It is seen that both trial number 26 and 31 are the farthest away from the negative ideal solution but trial number 31 is nearest to the positive ideal solution. The variation of the closeness coefficient as shown in Fig. 10 shows that it is the highest for trial number 31. The utility degree calculated for each trial by ARAS as shown in Fig. 11 shows a similar trend.

Fig. 9
figure 9

Euclidean distances of each alternative

Full size image
Fig. 10
figure 10

Closeness coefficients by TOPSIS for each alternative

Full size image
Fig. 11
figure 11

Utility degree by ARAS for each alternative

Full size image

Comparison of the MCDMs

The rankings obtained by the four different MCDMs are reported in Fig. 12 and Table 4. It is seen that in all the three other MCDMs except COPRAS, trial number 31 is found to the most optimal value. In COPRAS, however trial 26 is found to be the optimal performer. The similarity in ranking as obtained by the four MCDMs is evaluated using correlation analysis in Fig. 13. It is seen that in general, all the MCDMs produce similar ranking on the problem and thus have a high correlation among themselves. Among the different pairs of the four MCDMs, the correlation is seen to be the weakest between COPRAS and TOPSIS.

Fig. 12
figure 12

Rank of each alternative by four different MCDMs

Full size image
Fig. 13
figure 13

Correlation matrix of the four MCDMs

Full size image

Optimal Design Parameter Selection

By using level aggregation of the MCDM performance measures, the optimal settings for each of the design variables are determined. Figure 14 shows that a high inboard plate thickness is desirable. Further, it is seen that the optimal performance of the brake is most sensitive to inboard plate thickness but has low sensitivity to outboard plate thickness, vane height, effective offset and centre hole radius.

Fig. 14
figure 14

Optimal level of design parameter selection by using level aggregation method for a Inboard plate thickness b vane height c effective offset d Outboard plate thickness e centre hole radius

Full size image

Conclusions

In this research, optimal design variables in the design of a disc brake are studied and analysed using a finite element analysis and a multi-criteria decision-making approach. The fatigue life (cycles) and axial deflection (mm) are considered as the performance parameters for the disc brake design. For an appropriate design, the fatigue life of the brake is sought to be more but the axial deflection must be minimized. This ensures a longer brae life and reliable performance throughout its life. Using a full factorial design, the five design variable [inboard plate thickness (mm), outboard plate thickness (mm), vane height (mm), effective offset (mm) and centre hole radius (mm)] considered in this study are analysed at two different levels. It is found that the multi-criteria brake performance is most sensitive to the inboard plate thickness but is affected very little by the other four design variables. Further, the comparison of the four different MCDM methods shows that the methods have a high correlation and thus, any one of them can be used to select the optimal design performance of the brake.