Introduction

In recent years, with rapid population growth and the need for industrial, agricultural, and urbanization development, a huge quantity of pollutants is generated and discharged into rivers, which leads to deterioration of the ecosystem quality and damage to river system functions. In many cases, the assimilative capacities of rivers have also been exploited to discharge into them. The water quality of rivers is degraded and drinking water operation, ecosystem health, and agricultural production are adversely affected and damaged when the wastewater discharged exceeds the assimilative capacity of the receiving water (Zolfagharipoor and Ahmadi, 2016). To improve river environments and achieve the water quality standards (WQS), governments are seeking to develop pollutant load control programs for the determination of the pollutant load removal levels between various sources (Jia and Culver, 2006).

An important program of river water quality is the waste-load allocation (WLA) which plays a significant role in the management and improvement of water quality ecosystems and standards in rivers (Zhang et al., 2018; Afshar and Masoumi, 2016). In the WLA model, a rational and cost-based allocation plan is primarily required for all river stakeholders. Therefore, it is obligatory to consider trade-offs between the cost of controlling the pollution at loading points and the loss at the withdrawal points of the river system at each level of WQS.

WLA model usually incorporates a simulation–optimization (S–O) approach that exploits the combined use of water quality simulation and optimization models. Optimization models maximize the total allocated load, whereas water quality models ensure that WQS are satisfied (Saadatpour and Afshar, 2007). Mathematical modeling has been used as an effective water quality management technique to resolve WLA problems, for which many different mathematical programming methods have been developed to simulate river system water quality management problems and minimize pollution costs (Zhang et al., 2018).

A brief literature survey reveals that toward the end of the 1960s, (Liebman and Lynn, 1966) developed a dynamic programming model to deal with river system WLA based on the results of Streeter and Phelps equations; (Loucks et al., 1967) and (Revelle et al., 1968) built a linear programming model for water pollution control. In the 1990s, researchers began to focus on addressing uncertainties in WLA models, using stochastic programming and Fuzzy concepts. Stochastic programming started with random chance-constrained programming and it has also been extended by dynamic programming models (Fujiwara et al., 1986; Tung and Hathhorn, 1990; Cardwell and Ellis, 1993; Revelli and Ridolfi, 2004; Mujumdar and Saxena, 2004; Qin et al., 2009; Dong et al., 2015). Subsequently, WLA fuzzy and interval programming models were developed (Mujumdar and Sasikumar, 2002; Mujumdar and Saxena, 2004; Karmakar and Mujumdar, 2006; Qin et al., 2007; Li and Huang, 2010; Nikoo et al., 2013; Guo et al., 2014; Meysami and Niksokhan, 2020).

Along with the development of modeling methods, different objectives are incorporated in solving the WLA problem, such as maximizing waste discharge within the assimilative capacity of the river (Zhang et al., 2009; Afshar and Masoumi, 2016), minimizing total costs of the treatment (Yandamuri et al., 2006; Saremi et al., 2010; Zolfagharipoor and Ahmadi, 2016; Saadatpour et al., 2019), minimization of inequity index for attaining proper equity among all the waste dischargers (Nikoo et al., 2012; Feizi Ashtiani et al., 2015), minimum violation of the value of the standards (Burn and Yulianti, 2001; Yandamuri et al., 2006; Zolfagharipoor and Ahmadi, 2016). Among these objectives, minimizing the total costs of the treatment and penalty of loading pollution is the most important from the viewpoint of the decision-making authority (Burn and Yulianti, 2001). (Feizi Ashtiani et al., 2015) Developed an S–O model for solving the waste-load allocation problem for Haraz River by minimizing total treatment costs and violation of the water quality standards. (Zhang et al., 2018), A Pigovian tax-based waste-load allocation (PT-WLA) strategy was proposed in the Tuojiang River provide an optimization method for water quality management and minimizing the total costs of the treatment. (Saadatpour et al., 2019) Developed a multi-objective model to minimize total costs and penalties of loading pollution. The results showed that the proposed method can optimize the management of costs and river quality system.

Survey researches show that most of the cited works about economic objectives in WLA are included minimizing wastewater treatment costs addressed by infrastructure and establishing wastewater treatment systems and cost of penalty for loading pollution in the steady-state condition of river flow (base-flow or critical flow). On the other hand, natural systems are subjected to a violation of quality standards and concentration in checkpoints exceeds the standard limit from diverse sources, different dischargers with various loading patterns make the decision-making process a real challenge. River system damages (RSD) in WLA models have not received as much attention as deserved when the concentration of pollution exceeds the WQS limit. RSD seems to be important from both of Pollutant Control Agency and the management of river system quality. The referred to investigations have not considered optimal standard limit and its RSD. The high cost of wastewater treatment makes it possible to a trade-off between the cost of treatment and the river system damage (RSD) at different WQS levels. Therefore, each discharger needs to achieve reasonable pollutant removal to a trade-off between the cost of treatment and the pollution loading loss at the optimal threshold limit.

The objective of this study is to present an effective methodology to determine both the optimal WLA and the optimal threshold limit of river water quality which is based on the evaluation of wastewater treatment costs and river system losses. A cost-based waste-load allocation (C-WLA) model was developed to achieve these goals for specified quality standard levels in a river system more realistically. The new aspects of this research are the presentation of a C-WLA model based on modeling the combination of control cost and ecosystem pollution damage, which provides flexibility in the trade-off between costs and losses. It is focused on evaluating and allocating pollution loads with river system damages (RSD) by simulation–optimization (S–O) approaches in unsteady flow conditions and time-variable patterns of loading pollution in a river system. The S–O model employs MIKE11 to simulate the fate and transport of Total Dissolved Solids) TDS (in Karoon River system. PSO algorithm was used for the optimization of the total cost of treatment and RSD. This research was developed in 2020 in the Karoon River system at Tarbiat Modares University.

Materials and methods

In this section, the methodology of the development of the C-WLA model to solve the problem of the optimal pollution loading and the optimal threshold limit of water quality of the river system is presented.

Problem description

In a river system with unsteady flow Qr with S1, S2, S3 …, Si point sources of pollutant and P1, P2, P3 …, Pm withdrawal points are located along the domain Ω. Also, pollutant concentration levels at checkpoints R1, R2, R3 …, Rj of the river system are monitored. Any increase beyond the pollution quality standard level creates damages at withdrawal points. As a result, to manage the water quality of the river system, the sum of water treatment cost at point sources and pollution loss at withdrawal points have to be minimized in the entire river system domain. The percentage of treatment x1, x2, x3 …, xi at each point source, the loading pattern (w*), and the optimal threshold concentration limit at checkpoints (y) are the decision variables to be determined in the optimization problem.

To facilitate the problem description, the fundamental assumptions and the mathematical definitions are given as follows:

  1. 1.

    A one-dimensional advection–dispersion equation is used to simulate the TDS concentration in the river system.

  2. 2.

    All pollution dischargers are assumed as point sources along the river.

  3. 3.

    Parameters and variables in the C-WLA model are assumed to be deterministic and obtained from historical data analysis.

  4. 4.

    In the simulation of the pollution loading damages, only salinity stress is considered with no water quantity lacking in the river system.

The objective function introduced below consists of the costs of wastewater treatment of each discharger and pollution losses at withdrawal points (Eq. 1):

$$\mathop {\min }\limits_{x\;y} \;Z = \sum\limits_{i = 1}^{N} {\sum\limits_{t = 1}^{T} {c_{{s_{it} }} } } + \sum\limits_{m = 1}^{M} {\sum\limits_{t = 1}^{T} {d_{mt} } } \;\;\;\;\;\;\;i = 1,2, \ldots N;\;\;\;\;m = 1,2, \ldots T$$
(1)

where Z is the objective function, cs is the treatment costs of the pollutant source at the location i in month t, dm is the loss of loading at the withdrawal point m. N is the number of pollutant point sources, T is the number of time steps in months, and M is the number of withdrawal points. More details regarding the cost and damage functions will be introduced in section ‘Economic model’. Notations and units are given in appendix A.

The objective function is subjected to the constraints given in Eqs. 2, 3, and 4. Equation 2 describes the river quality standard constraints in which all checkpoints must ensure that the pollutant concentrations in the river will not exceed the specified TDS threshold concentration limit (y).

$$C_{jt} \le y$$
(2)
$$C_{j\,\,t} = f(Q_{r} ,\,\,C_{0} ,\,\,U,\,\,A,\,\,Q_{w} ,\,\,w_{s} ,\,\,C_{s} ,\,\,Q_{s} ,x,\,\,D,\,\,K)\,\,\,\,j = 1,\,\,2,\,\ldots\,\,J;\,\,\,\,t = 1,\,\,2,\,\ldots\,\,T$$

where Cjt is the simulated concentration at checkpoint j in the river system, f is a function of the parameters shown inside the above parenthesis and can be determined by the pollution mass transfer differential equation. Qr and C0 are the flow discharge and initial concentration of the river system upstream, respectively; U and A are average flow velocity and cross-sectional area. ws = Qs.Cs is the waste load of dischargers; Qs and Cs are the discharge and the concentration of the point sources, respectively. Qw is the discharge of the withdrawal flow. K is the reaction coefficient of the pollutant, and D is the dispersion coefficient of the pollutant. J is the number of checkpoints.

Equation 3 states that the optimal treatment percentage (x) on monthly basis should not exceed the maximum allowable removal rates (xmax) and cannot be negative.

$$0 \le x_{i\,t} \le x_{\max }^{{}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,i = 1,\,\,2,\,\ldots\,\,N;\,\,\,\,\,\,\,\,t = 1,\,\,2,\,\ldots\,\,T$$
(3)

Equation 4 describes the threshold concentration limit in the river system (y), which should lie in between observed minimum concentration, Cmin and maximum concentration, Cmax. The concentration increment for y calculation is considered as 50 mg/l during the simulation period.

$$C_{\min } \le y \le C_{\max } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$
(4)

The flowchart of the C-WLA model to obtain the optimal management strategies in water quality management programs is illustrated in Fig. 1. The proposed methodology consists of a water quality simulation model, economic model calculation, and optimization algorithm coupled within the MATLAB (Ver. R2018b) program.

Fig. 1
figure 1

C-WLA model framework combining various modeling tools and data

Full size image

As presented in Fig. 1, values of the random vector of pollutant removal percents, x(x1, x2, x3 … xn) and the threshold concentration limit, y are initially selected. Then the simulation model is run using the pollutant point sources resulting after applying the pollutant removal percentages. The output of the simulator model is employed to estimate the system loss and the pollution concentration at each checkpoint. The results of the simulator are used in the optimization algorithm. If the required convergence criterium for the optimization is established, the modeling process will be ended and the x values are displayed as the optimal removal percentages and y value as the optimal threshold limit. Otherwise, new values of the vector x and y are selected and the procedure is repeated until the minimized objective function is achieved.

Economic model

The economic model comprises two main parts, the cost of wastewater treatment at the point sources and the river system damages (RSD) estimation at the withdrawal points. The RSD was estimated by the loss functions. The treatment cost of discharger’s wastewater involves construction, operation, and maintenance costs for the wastewater treatment plants (Saadatpour et al., 2019; Zhang et al., 2018). To estimate the treatment cost of the dischargers along with the river system, reverse osmosis (RO) and mechanical distillation (MED) desalination methods are defined with 85% treatment efficiency (KWPA, 2015). The wastewater treatment cost function (cs) can be calculated from the relationship between the waste load of dischargers (ws) and the removal percentage (xs) of a point source s that is generated based on historical data. A power function was estimated to fit the cost curve for discharger s given below using the Table Curve program tool (http://www.sigmaplot.co.uk/) with R2 equals to 0.93:

$$c_{s} { = }\alpha \,\,w_{s}^{\beta } x_{s}^{\gamma }$$
(5)

where the coefficients \(\alpha\),\(\beta\) and \(\gamma\) were estimated as 1.58, 1.13, and 1.08, respectively, based on historical data of the case study (KWPA, 2015).

River system damage (RSD) calculation is based on the violation of the water quality standard concentration at the withdrawal points as loss functions for drinking water application (dD), agricultural production (dA), and environmental degradation (dE). The loss function (dm) at the withdrawal point m can be written as given in Eq. 6:

$$d_{m} = d_{D} + d_{A} + d_{E}$$
(6)

Estimation of drinking water damage

The damages and losses related to drinking water may be defined as the costs of an alternative drinking water supply. It is calculated by combining alternative methods in the river system as follows (Eq. 7):

$$d_{D} = \left\{ {\begin{array}{*{20}c} {a\,\,T_{1} + b\,\,T_{2} + c\,T_{3} + d\,T_{4} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{m} > C_{{{{\text{std}}}}} } \\ {0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,C_{m} \le C_{{{{\text{std}}}}} } \\ \end{array} } \right.$$
(7)

where Cstd is the maximum admissibility of drinking water standard concentration that is 1500 mg/l (WHO, 2008). T1 is the increased cost in water treatment plant (WTP), T2 is the cost of household water purifier (HWP), T3 is the cost of mineral water packaging (MWP), T4 is the cost of mobile water tankers (MWT) when the pollutant concentration exceeds Cstd. a, b, c, and d are weighted coefficients determined based on regional circumstances.

Estimation of agricultural production damage

When the concentration of the pollutant in irrigation water exceeds the crop tolerance threshold, the crop is stressed, and consequently the crop yield decreases linearly as pollutant concentration increases (McNeal and Coleman, 1966; Munns and Termaat, 1986). To estimate the agricultural crop yield under the effect of salinity stress, Eqs. 8 and 9 are used (Maas and Hoffman, 1977).

$$d_{A} = \sum\limits_{k = 1}^{NC} {Ar_{k} Be_{k} (Y - Y^{\prime}\,)_{k} } \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,k = 1,\,\,2,\,\ldots\,\,,NC$$
(8)
$$Y^{\prime}{ = }Y.\,\left\{ {\begin{array}{*{20}c} {1 - A(\overline{S} - B)\,\,\,\,\,\,\,\,\,\,\,\,\,\overline{S} > B} \\ {1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\overline{S} \le B} \\ \end{array} } \right.$$
(9)

where dA, the loss of agricultural production; Ar, the agricultural crop area; Be, crop benefit; NC is the number of crops. Y—Ys is the crop yield reduction in which Y refers to the maximum crop yield and Y′ is crop yield under salinity stress condition which is calculated according to Eq. 9. In this equation, A is the crop yield reduction coefficient at a unit of salinity, B is the crop bearing salinity threshold, and \(\overline{S}\), average soil salinity which is a function of the salinity of irrigation water as given in Eq. 10 (Feinerman and Yaron, 1983; Delavar et al., 2015):

$$\overline{S} = \frac{{IR \times S_{w} - R(SM_{f} \times S_{f} - SM_{o} \times S_{o} )}}{DP}$$
(10)

where IR represents the irrigation depth; Sw is the irrigation water salinity; R is the depth of crop root; SMo and SMf are the initial soil moisture at the initial and final of the crop growth period, respectively; Si and Sf are soil salinity at the initial and final of the crop growth period and DP is deep water percolation.

Estimation of environmental degradation damage

Pollution loading into the receiving waters will lead to environmental degradation. Loss of environmental degradation for point source i was calculated according to the regulations of the Environmental Agency of Iran to Eq. 11 (IRANDOE, 2015).

$$d_{E} = \left\{ {\begin{array}{*{20}l} {\sum\limits_{{i = 1}}^{N} {\sum\limits_{{t = 1}}^{T} {Q_{S}{{_{{it}} }} \frac{{C_{S} {{_{{it}} }} - C_{{{\text{std}}}} }}{{C_{{{\text{std}}}} }}} } x_{{it}} PAE} \hfill & {C_{S}{{_{{it}} }} > C_{{{\text{std}}}} } \hfill \\ 0 \hfill & {C_{S}{{_{{it}} }} \le C_{{{\text{std}}}} } \hfill \\ \end{array} } \right.\quad \quad \quad i = 1,2,\ldots N;\; t = 1,2,\ldots T$$
(11)

where dE is the loss of environmental degradation that is determined by the getting penalty at the loading points due to violation of Cstd which represents the environmental water standard concentration that is 500 mg/l (IRANDOE, 2015). QS and CS are the discharge and the concentration of the point sources at the location i in month t. P, A, and E are, respectively, an economic conversion coefficient, a regional coefficient, and the environmental sensitivity coefficient that are determined based on regional circumstances.

Simulation model

The equations for simulating river systems are the Saint–Venant and advection–dispersion equations which can simulate flow and pollution transport in a one-dimensional unsteady state (Jamshidi et al., 2020). Saint–Venant equations consist of the continuity and momentum equations (Eqs. 12 and 13). These equations are used to determine the flow and water level as a function of space and time.

$$\frac{\partial Q}{{\partial x}} + \frac{\partial A}{{\partial t}} = q$$
(12)
$$\frac{\partial Q}{{\partial t}} + \frac{{\partial (\alpha \frac{{Q^{2} }}{A})}}{\partial x} + gA\frac{\partial H}{{\partial x}} + \frac{g}{{{c}^{2} }}\frac{Q\left| Q \right|}{{AR}} = 0$$
(13)

where Q is the river discharge, A is the flow area, q is lateral inflow, H denotes flow depth, c is Chezi roughness coefficient, R is the hydraulic radius, g is the gravity acceleration and \(\alpha\) is the momentum distribution coefficient.

Advection–dispersion equation (ADE) is the mass transfer of a dissolved or suspended material such as TDS concentration, under one-dimensional conditions in rivers. This equation is extracted by combining the equation of continuity and the first Fick's law, assuming a complete mixing of the pollutant at the cross-sectional level. The equation reflects two mechanisms: (1) advective transport with the flow and (2) dispersive transport due to concentration gradients. The equation is defined as Eq. 14.

$$\frac{\partial (AC)}{{\partial t}} + \frac{\partial (QC)}{{\partial x}} = \frac{\partial }{\partial x}\left( {AD\frac{\partial (C)}{{\partial x}}} \right) - AKC + C_{S} q$$
(14)

in which C is the pollutant concentration, D is the dispersion coefficient, K is the linear decay coefficient and CS represents source/sink concentration.

In this study, the MIKE11 numerical model was used to simulate and solve equations of flow and pollution mass transfer in the river system. MIKE11 model has been developed by the Danish Hydraulic Institute (DHI). This model is based on a hydrodynamic module (HD) coupled with an advection–dispersion module (AD). The HD, which is based on the fully dynamic wave description, solves the Saint–Venant Equations 12 and 13 by an implicit finite difference scheme with Six-Point Pattern of Abbott and the AD solves ADE Eq. 14 by an implicit finite difference scheme (Abbott and Ionescu, 1967). The model can simulate point and distributed source pollution and water abstraction along the water body. Hydraulic, geometry, hydrological, and water quality data are considered as the main input data of this model.

Optimization algorithm

In this study, Particle Swarm Optimization (PSO (algorithm is used to minimize the objective function (Eq. 1) with constraint (Eq. 2) and boundaries (Eqs. 3 and 4). The PSO algorithm was first proposed by (Eberhart and Kennedy, 1995). The PSO like all other evolutionary algorithms begins by creating a random population of particles. It imitates the social behavior of flying particles in a multidimensional search space, where each particle’s position forms a potential solution to the problem. The algorithm's essence is to search the solution space based on the movement of the particle group toward the best position faced in the past (Afshar and Masoumi, 2016).

In the PSO algorithm, the state of the ith particle in search space is addressed by its position xi and velocity vi in a multidimensional way. In a D-dimensional search space, the next position of each particle is addressed by its personal best experience (p-besti) and the global best experience of the swarm (g-besti) (Al-hotmani et al., 2022). Therefore, the new position and its velocity for each particle are defined as introduced in Eqs. 15 and 16:

$$x_{i} {(}t{) \,= \,}x_{i} {(}t - 1{) + }v_{i} {(}t{)}$$
(15)
$$v_{i} {(}t{)\, =\, }\omega \,.\,v_{i} {(}t - 1{) + }c_{{1}} .r_{{1}} {(}x_{{p\,best{(i,t)}}} - x_{i} {(}t{)) + }c_{{2}} .r_{{2}} {(}x_{{g\,best{(t)}}} - x_{i} {(}t{))}$$
(16)

where \(x_{i} {(}t{)}\) is the position of particle i in the new iteration, \(x_{i} {(}t - 1{)}\) is the particle position at the current iteration, \(v_{i} {(}t{)}\) is the velocity of particle i in the new iteration, \(v_{i} {(}t - 1{)}\) is the particle velocity at the current iteration. The \(x_{{g\,best{(t)}}}\) and \(x_{{p\,best{(i,t)}}}\) represent global best and personal best for particle i in the tth iteration. r1 and r2 are uniformly distributed random numbers [0, 1], c1 and c2 are tuning parameters that determine the relative weight of the cognitive and social components, respectively, and they are non-negative and less than 2. The inertia weight \(\omega\) is the particle's tendency to maintain its current state of motion. Its appropriate value is between 0.4 and 0.9 (Afshar and Masoumi, 2016; Eberhart and Shi, 1998).

Management scenarios

To evaluate and investigate the trade-off between pollution management and the damage costs within the C-WLA model, different strategies for river water quality levels are applied as shown in Table 1. Each of the strategies is investigated as a management scenario. Scenario I shows the Current situation loads in which no treatment takes place and scenario II represents the case of treatment of all dischargers of the river system. These two scenarios are the limit load conditions of the river system that are analyzed with no need to be included within the optimization process. Scenario III is the principal one of the C-WLA model investigation where its performance in determining the optimal pollution pattern (w*) and also the optimal threshold concentration limit (y) are evaluated. Besides, three other scenarios for drinking water (IV), agricultural (V), and river environmental (VI) applications at the checkpoints for water standard concentration limit with 1500, 3000, and 5000 mg/lit, respectively, are introduced. In Table 1, all the characters of the scenarios are presented.

Table 1 Different strategies for management of river quality system
Full size table

Case study

In this section, a reach of Karoon River is presented as a practical application example to demonstrate the efficiency of the C-WLA model.

Overview of the case study system

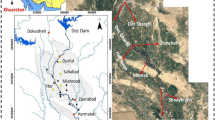
In this study, the intended reach is a 62 km long between Mollasani station (Chainage 0 km, which is located at 48° 52´ E and 31° 35´ N) to Ahvaz station (Chainage 62 km, which is located at 48° 41´ E and 31° 20´ N) (Fig. 2). Karoon River is located in the southwestern of Iran and is the main river of the Persian Guelph basin. It supplies water for several cities and villages. In addition, it includes several withdrawal locations for hundreds of hectares of agricultural lands and industrial areas. On the other hand, its environmental impact in the region is undeniable.

Fig. 2
figure 2

Location of Karoon river system and Schematic diagram of the reach under study

Full size image

In recent years, the Karoon river system due to the excessive pollution discharges from industrial, municipal, and agricultural sewage has become a serious environmental problem. Discharging of wastewaters has led to increased river salinity and it is a great risk of severe water pollution.

The reach of the river system under study is critical and vital due to the high population density which receives significant sewages of dischargers. The average river discharge at Ahvaz station in the year 2016 was 237 m3/s. All of the wastewater dischargers along the river reach consists of six major groups as point sources. There are eight withdrawal points along the reach. Accordingly, the river was divided into five reaches with five checkpoints at 9.5, 33, 45, 58, and 62 km (Fig. 2). The general properties of each discharger and withdrawal point are reported in Table 2. More details about the Karoon river system and input parameters and detail of simulation can be found in (Fakouri et al., 2018).

Table 2 Parameters for the dischargers and withdrawal points in the C-WLA model
Full size table

Loss of drinking water of Karoon River system was calculated at withdrawal points, P7, P8 for Ahvaz city. Calculations were conducted with loss of alternative drinking water supply according to Eq. 7, for 1,302,591 populations and 362,480 families (www.amar.org.ir). The weighting coefficients a, b, c, and d of Eq. 7 were determined as 0.35, 0.5, 0.1, and 0.05, respectively, in consultation with the experts of the Ahvaz water and wastewater office.

Loss of agricultural crop yield under the influence of salinity stress is calculated according to Eqs. 8–10. Based on the dominant crop pattern in the Karoon basin, 5 crop products including wheat, Corn, Onion, Potato, and Sugar beet were calculated on monthly basis for agricultural production damage at withdrawal points, P1, P3, P4 and P6. Characteristics of the crop pattern are given in Tables 3 and 4.

Table 3 Dominant crop pattern of the reach under study
Full size table
Table 4 Crop characteristics for agricultural damage estimation
Full size table

Loss of environmental degradation is calculated according to Eq. 11 and the coefficients P, A, and E, were determined as 2, 1.8, and 2, respectively, from the reports of the regulation of the Environmental Agency of Iran (IRANDOE, 2015).

Calibration and validation

Simulation models were applied for the unsteady flow for one year starting from 23 of Sept 2015 and ending on 23 of Sept 2016. The daily-measured river discharge hydrograph and monthly-measured TDS concentration were used as the upstream boundary conditions at the entrance of the river system. A rating curve for the hydraulics and zero gradients for the TDS concentration were used as boundary conditions downstream of the river reach. Also, dischargers were applied in the form of point sources and monthly averages. The steady-state initial results were used as initial conditions. 80 cross sections along the river reach with intervals of 800 m were employed. The grid interval and time steps were chosen as 500 m and 60 s, respectively, to satisfy the stability of the numerical simulation conditions in which the Courant number should be less than unity.

The river Manning’s roughness coefficient, n was selected as 0.035 (Fakouri et al., 2018). The value of the dispersion coefficient was calculated based on an empirical equation (Kashefipour and Falconer, 2002) (Eq. 17) equal to 103 m2/s. TDS is a conservative pollutant and the decay coefficient was considered as zero (Kanda et al., 2015).

$$D = 10.612\,\,H\,U\left( {\frac{U}{{u^{*} }}} \right)$$
(17)

where, H is flow depth, U is flow velocity, \(u^{ * } = \sqrt {gHS}\) is shear velocity, S is energy slope.

The model performance was verified for Manning’s n and D coefficient using river discharge, water level, and TDS terms from Feb to Sep 2015. Figure 3 indicates that the model accurately determines the flow and concentration parameters in the river system within the reach under study.

Fig. 3
figure 3

Comparison of the simulated and observed a Discharge, b water level, and c TDS concentration within the Ahvaz station

Full size image

Results and discussion

The C-WLA model was set up as presented in section ‘Problem description’ and then solved using the PSO algorithm. The population size was selected as 50 with 200 iterations, the coefficients c1 and c2 were considered 0.6 and 0.4 and the inertia weight w was set as 0.9. The C-WLA model was run on an Intel(R) Core i7-4820 k, CPU 3.70 GHz processor with 16 GB RAM and Windows 7, 64-bit operating system. In this study, six scenarios were considered. Results of each scenario including optimal treatment percentage (x), optimal load pattern (w*) of dischargers, optimal threshold concentration limit y, (only for scenario III), and its objective function (Z) in the Karoon river system were calculated and compared with each other. Also, the performance of the proposed model was evaluated.

Scenario I: current situation

Results of Scenario I show the current situation of cost and losses per year for the Karoon river system. In this scenario, no optimization has been applied. The treatment cost is zero except at point source of S5, 7.93 million US$s, where a simple RO system for wastewater treatment was employed. Table 5 illustrates the loss and cost of pollutant TDS in the Karoon river system. The result of the calculation shows that the river system in the current situation creates a loss of more than 80 million US$s. The loss includes Loss of Drinking water (52.26 million), Loss of Agricultural water (23.91 million US$s), and Loss of Environmental (4.16 million US$s). The high losses in the drinking sector show the importance of the river system in supplying the drinking water of Ahvaz city, which requires more attention to be paid (Afkhami et al., 2007). Also, the low environmental losses, compared to drinking and agriculture, are due to the low-quality standards proposed and employed for the penalty threshold in river systems. Therefore, it is necessary to consider these environmental regulations and standards in river basin development consideration.

Table 5 Cost and damage of pollutant sources in current situation scenario
Full size table

Scenario II: treatment of all dischargers

In scenario II, it is assumed that all sources of pollution are treated and the standard concentration level in the river system within the study reach is considered. Therefore, the damage is equal to zero. The cost of treatment is estimated as 204.08 million US$s. Table 6 illustrates the 95% treatment levels and their costs.

Table 6 Cost of treatment of pollutant sources in scenario II
Full size table

The results of scenarios I and II show that the cost of treatment of pollutant sources is about 2.5 times the losses. The reason for this result belongs to 1. The study reach is critical because it receives dischargers of agricultural, industrial, and domestic wastewaters. As studies have shown, in the reach understudy, about a 40% increase in salinity occurs for the Karoon River (Fakouri et al., 2018). 2. The dispersion effect on reducing the pollution concentrations in the river is negligible as well (Yu et al., 2014; Fakouri et al., 2018). 3. According to other researchers’ results, TDS as a conservative contaminant requires a high cost in terms of treatment and desalination (Kerachian and Karamouz, 2005).

Scenario III: C-WLA model

This scenario is considered as a principal one in this study. The final result of optimization introduces an optimal threshold concentration limit (y) of 2450 mg/l. Table 7 demonstrates the optimal treatment percentage (x). Figure 4 shows the optimal load pattern (w*) against the current load pattern (red symbol). The results of the C-WLA model demonstrate that with the optimal concentration limit of 2450 mg/l at water withdrawal points and the optimal load pattern, the sum of costs and losses are minimum.

Table 7 Optimal treatment percentage (x) of scenario III
Full size table
Fig. 4
figure 4

Optimal load pattern discharges (w*) for scenario III

Full size image

Table 8 shows the optimal results of point source treatment cost and the river system loss at withdrawal points for scenario III. As it is seen in Table 8, the sum of costs and losses equals 48.99 million US$s in which 30,31 million belongs to the treatment and pollution management costs whereas the drinking water, agricultural, and environmental losses reached 8.61, 7.74, and 2.23 million US$s, respectively, and the sum of them reached 18.68 million US$s.

Table 8 Results analysis of scenario III at point sourses and withdrawal points
Full size table

To investigate the efficiency of the proposed model, the C-WLA model was compared to WLA model using Qin and Huang’s method (Qin et al. 2007) under the deterministic condition at the standard level of 1000 mg/l. The results were compared in August month when the flow and pollution transfer are the most critical month in the Karoon river system. The results of the optimal load pattern (w*) for all dischargers are shown in Fig. 5. The error for w* between the C-WLA and the Qin and Huang’s model is negligible with R2 and RMSE and MAE as 0.99, 0.22 kg/s, and 0.21 kg/s, respectively. Then it is concluded that the C-WLA model has a good efficiency in managing the water quality of the river system.

Fig. 5
figure 5

Optimal loading pattern for the dischargers in the C-WLA and Qin and Huang’s model

Full size image

Scenario IV, V and VI: operational scenarios

The C-WLA model was conducted for operational scenarios in the river system Table 1. Figure 6 shows the w* of dischargers of the drinking water, agricultural operation, and environmental protection in months (2015–2016). The results indicate that w* for environmental operation is very close to the current loading conditions (red symbol). The current loading pattern satisfies the environmental standard in the river, except in a few cases. But, in other operational processes for drinking and agricultural purposes, the river is influenced by pollutant damages. Therefore, the selection of any management scenario has to be based on the results of optimization and trade-off between treatment cost and damages in the river system (Zhang et al., 2018).

Fig. 6
figure 6

Optimal loading discharges pattern (w*) for the operational scenarios

Full size image

Scenarios’ comparison

In this section, the previous scenarios which reflect different management strategies are compared to each other. Based on the objective function (Z), the best strategy is scenario III with a minimum sum of costs and losses. Table 9 introduces the results of various scenarios. The C-WLA model, scenario III, illustrates the best management strategy for pollution allocation within the river system. It produces 30.31 million US$s costs and 18.68 million US$s load losses. The result analysis of the scenarios shows that the trade-off between treatment cost and loss improves water quality and also reduces the economic costs within the river water quality management system which is confirmed by (Zhang et al., 2018; Kerachian and Karamouz, 2005).

Table 9 Economic performance of different management strategies
Full size table

Conclusion

The main purpose of this paper is to develop a mathematical model to solve a WLA problem under a cost minimization policy, i.e., calculation of the cost and loss of pollution loading, which was applied to the Karoon River system. The application of the proposed model to the Karoon River system demonstrated its practicality and efficiency, with the associated analyses indicating the influence of a cost-based policy on the management decisions to achieve water quality standards at a low-cost level for the C-WLA problem.

The model framework presented in this study combines the PSO algorithm with the flow and pollution transfer modules of MIKE11 software and economic modeling under different waste-load allocation management strategies scenarios. Using the proposed model, the optimal point sources and the total cost were obtained monthly for one year in each of the scenarios. Optimal treatment percentages were presented under various quality control scenarios of the river. The application of the proposed model to the Karoon River system case demonstrated the following:

There is a trade-off between cost and loss in the C-WLA modeling process, and the cost can significantly affect the discharger’s decisions. When the pollution damage is too low, there is no significant effect; however, overly high damage could result in heavy costs to the dischargers and excessive pollution costs.

The results of C-WLA scenario, III, compared to the other scenarios indicated more flexibility in improving water quality and reducing the cost and damages at different quality standard levels, thereby providing indirect evidence for the superiority of the proposed method in solving C-WLA problems. The presented model shows good performance.

It is suggested that in similar research, decision objectives be developed and the utility of each strategy in different criteria be further examined by using multi-criteria and multi-objective decisions to select other scenarios to address other aspects of the WLA issue.