Introduction

Modeling the mechanical properties of polymer blends and nanocomposites is an interesting area in polymer science and exciting method for the design of high performance materials. There are many models for predicting the modulus of polymer blends as a function of the composition. The simplest models are rule of mixtures and inverse rule of mixtures [1–3]. These models can be used to estimate the upper and lower extremes of tensile modulus, respectively. Other important models are Halpin–Tsai, Kerner and Takayanagi [4–6]. Takayanagi model is based on a combination of parallel and series sections and can be used for predicting the mechanical and viscoelastic properties of polymer blends. Kerner’s equation, underestimates the mechanical properties and is more appropriate for predicting the bulk or shear modulus of binary systems. The Halpin–Tsai equation can be considered as a generalized form of the Takayanagi model with some modifications [6]. Lee et al. [7] showed that Halpin–Tsai model could not predict the modulus of ternary blends accurately. In addition, different equations for predicting the tensile modulus have proposed for polymeric blends with co-continuous morphology [8–10]. Kolarik [11] has proposed an equivalent box model (EBM) for the moduli of blends beyond the percolation threshold of the minor component. Veenstra et al. [12] introduced the cross orthogonal skeleton (COS) model for predicting the mechanical properties of polymer blends without any adjustable parameters. The most recent model is a knotted interconnected skeleton structure (KISS) model, which is able to calculate the Young’s modulus of polymer blends with various morphologies [13].

On the other hand, many models for predicting the Young’s modulus of nanocomposites were proposed [14–16]. Ji et al. [17] modified the Takayanagi’s two-phase model by considering the interface phase and were able to predict mechanical properties of nanocomposites containing spherical or plate-like nanoparticles. Brune et al. [18] performed several modifications on the Halpin–Tsai model and derived an equation by considering the aspect ratio of nanoclays stacks. Dayma et al. [19, 20] showed that Takayanagi model is more accurate for predicting the mechanical properties of ternary nanocomposites compared to Halpin–Tsai model. Mooney’s model (originating from rheological models) was used for predicting of nanocomposites moduli and the results showed that this model overestimates the modulus at high nanoparticles loading [21, 22]. All the above models have been formulated for binary components while, they need to be modified for ternary systems.

The present study is motivated by the current interest on modeling of ternary systems. The novelty of this study is to combine various models for polymer blends and polymer nanocomposites and to offer a simple model for predicting the modulus of nanocomposites based on polymeric blends. This model is more applicable for those blends with high degree of continuity. In addition, the model results were compared with obtaining experimental data from low-density polyethylene/thermoplastic starch/nanoclay (LDPE/TPS/nanoclay) ternary nanocomposite. This blend was chosen because of highly continuous thermoplastic starch phase in the blend [23, 24]. In addition, the model results were compared with the other experimental data, which were obtained from literature.

Experimental

Materials

Commercial LDPE resin, LDPE0200 (MFI = 2 g/10 min, density = 0.92 g/cm3), was obtained from Bandar Imam Petrochemical Company, Iran. Wheat starch was obtained from Glocozal Company, Iran, which consisted of 25 wt% amylose and 75 wt% amylopectin. The moisture content was less than 10 wt% (as measured by thermogravimetric analysis). Analytical-grade glycerol was supplied from Dr. Mujalli Co., Iran. Commercial nanoclay, Cloisite 30B was provided from Southern Clay Company, USA. Cloisite® 30B is a natural montmorillonite modified by methyl, tallow, bis-2-hydroxyethyl, quaternary ammonium.

Preparation of thermoplastic starch (TPS)

First a suspension of starch/glycerol/water (50/30/20 wt%) was prepared. The starch suspension was fed into the first zone of the counter rotating twin-screw extruder (TSE) with six heating zones. Starch was gelatinized and plasticized in the first zones of the TSE. Water and other volatiles were emitted in the third zone at 110 °C and the extrudated TPS was pelletized after exiting the die. The screw speed was 110 rpm and the temperature profile was 90/110/110/130/135/130 °C. Under these conditions, the glycerol content of the TPS was estimated about 37.5 wt%.

In the next step LDPE granules, Cloisite 30B and TPS were dried in an oven at 65 °C overnight and then fed into the TSE. The screw speed was 120 rpm and the temperature profile was 125/135/140/140/145/135 °C. The extrudate was granulated and injection molded (Imen Machine, Iran). The compositions of the samples are shown in Table 1.

Table 1 Formulation of the samples
Full size table

Tensile test

Tensile tests were carried out according to ASTM D638 by an Instron universal testing machine (model 6025, UK) equipped with a 5-kN load cell. The crosshead speed was 10 mm/min and the relative humidity was 50 %. The mean values of the Young’s modulus were calculated from at least five measurements.

Model consideration

Binary blends

The components of the polymeric binary blends can be divided into two sections: parallel and series. One can assume that some of the minor phase is continuous (Φ 2p ) and the remaining is in series (Φ 2s ). Figure 1 shows this idea schematically. The volume fractions of the components are denoted with Φ and the indices 1, 2, p and s are related to matrix, minor phase, parallel and series sections, respectively.

Fig. 1
figure 1

Parallel and series sections in polymer blends: a box model of two-phase model containing series and parallel sections and b dimensions of continuous and series parts of each phase

Full size image

Figure 1b shows the system as a 1 × 1 square. The parallel parts are assumed to be rectangular and the series parts are considered as triangular and the force lines cross through their interface. Therefore:

$$ \Phi_{1} = \, \Phi_{1p} + \Phi_{1s} $$
(1)
$$ \Phi_{2} = \, \Phi_{2p} + \Phi_{2s} $$
(2)

The dimensions of these parts are:

$$ L_{2p} = \, \Phi_{2p} $$
(3)
$$ L_{s} = \, 2 \, \Phi_{2s} $$
(4)
$$ L_{1p} = \, \Phi_{1p} $$
(5)

From Fig. 1 it is clear that Φ 1s and Φ 2s are equal. Therefore, if the volume fraction of each part is known, the other ones can be calculated using Eqs. 1, 2, 3, 4, and 5. In the next step, percolation theory was used to estimate the volume fraction of continuous (Φ 2p ) and series (Φ 2s ) parts of minor phase [11, 25]:

$$ \Phi_{2p} = \, \Phi_{0} \left[ {\left( {\Phi_{2} - \, \Phi_{{2{\text{cr}}}} } \right)} \right]^{T}, \quad \Phi_{{2{\text{cr}}}} < \Phi_{2} < 0.5 $$
(6)
$$ \Phi_{2p} = \, 0, \quad \Phi_{2} < \, \Phi_{{2{\text{cr}}}} $$
(7)
$$ \Phi_{1S} = \, \Phi_{1} - \, \Phi_{1p} $$
(8)
$$ \Phi_{2S} = \, \Phi_{2} - \, \Phi_{2p} $$
(9)

where Φ 0 is the prefactor and Φ 2cr is the percolation threshold which is around 0.156 for spheres according to literature. Most experimental value of T is found to be in the range of 1.7 to 2. Similar to Jianfeng’s work, the T value is chosen to be equal to in this study [13].

The continuous fraction of the minor phase (Φ 2p ) is zero when the volume fraction of dispersed phase is lower than the percolation threshold. Although the prefactor is defined previously [11], but in this work a new approach is offered for calculation of this parameter by considering the continuity degree in the polymer blends. In many studies, it is shown that when the volume fraction of minor phase approaches 0.5 the continuity degree (Φ 2p /Φ 2) has a tendency towards one [24, 26–29]. Therefore:

$$ \Phi_{2p} = \Phi_{2} {\text{ at }}\Phi_{2} = 0.5 $$
(10)

By consideration of this condition the value of prefactor,Φ 0, is obtained and the final equation is:

$$ \Phi_{2p} = \, 4.22 \, \left( {\Phi_{2}-0.156} \right)^{2} , \, 0.156 \, < \Phi_{2} < 0.5 $$
(11)

It should be considered that this equation is valid only for minor phase (Φ 2 < 0.5).

Model for nanocomposites based on polymer blends

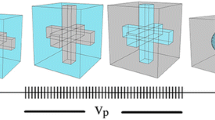
In this work, it was tried to present a model which is able to predict the modulus properties of polymer blend including nanoclay. It is supposed that when nanoclays are added to polymeric blends, the nanoparticles are located only in one phase (matrix, interface or dispersed phase). If nanoclay is located in just one phase, the binary blend system changes to binary nanocomposite and Eqs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 are used to estimate the volume fraction of each part. If nanoparticles find location at the interface, an interfacial phase would be formed. Therefore, three phases are distinguishable: matrix, dispersed phase and another phase containing nanoclay particles. The latter phase is divided into series and parallel sections as well. Figure 2 illustrates the new shape of these phases in series and parallel formats. Ip and Is are the thicknesses of parallel and series parts of the third phase.

Fig. 2
figure 2

Schematic representation of a three-phase model when nanoclay is localized at the interface. The third phase contains nanoclay. I p and I s are thicknesses of parallel and series parts of the third phase

Full size image

The third phase volume fraction is an unknown parameter (Φ 3) and can be obtained through curve fitting. It is assumed that the component composition of the third phase is the same as a neat binary blend. Thus, their volume fractions can be simply given by the following equations:

$$ \Phi_{3} = \, \Phi_{3p} + \, \Phi_{3s} $$
(12)
$$ \Phi_{3s} = \Phi_{s} \Phi_{3} $$
(13)
$$ \Phi_{3p} = \Phi_{p} \Phi_{3} $$
(14)

where Φ p and Φ s are the total volume fraction of parallel and series phases, respectively:

$$ \Phi_{p} = \, \Phi_{1p} + \Phi_{2p} $$
(15)
$$ \Phi {\text{s }} = \Phi_{{ 1 {\text{s}}}} + \Phi_{{ 2 {\text{s}}}} $$
(16)

The third phase consists of nanoclay and also some parts of each polymeric phases. Therefore, the volume fraction of phases 1 and 2 are reduced to the following values:

$$ v_{1p} = \, \Phi_{1p} - \Phi_{1} \Phi_{3p} $$
(17)
$$ v_{2p} = \Phi_{2p} - \Phi_{2} \Phi_{3p} $$
(18)
$$ v_{1s} = \, \Phi_{1s} - \Phi_{1} \Phi_{3s} $$
(19)
$$ v_{2s} = \, \Phi_{2s} - \Phi_{2} \Phi_{3s} $$
(20)

where v ip and v is are the corrected volume fractions of parallel and series parts of phases 1 or 2, respectively.

When nanoparticles are added into the blend, the volume fraction of nanoparticles (Φ n ) should be added to that phase containing nanoclay. For example, when nanoclay is located in the interface, then the third phase volume fraction (v 3) would be:

$$ v_{3} = \Phi_{3} + \Phi_{n} $$
(21)

When the volume fraction of each phase is attained, the modulus of binary blend or the nanocomposite can be calculated. In parallel region, all phases are continuous in the direction of the acting force and the lines of stress do not cross any interfaces. Based on the rule of mixtures, the modulus of the parallel section is given as follows:

$$ E_{p} = E_{1} v_{1p} + E_{2} v_{2p} + E_{3p} v_{3p} $$
(22)

where E 1, E 2, and E 3p are the moduli of the matrix, dispersed, and the parallel section of the third phase and their corresponding volume fractions in the parallel section are v 1p , v 2p , and v 3p , respectively.

In the series section, all components are discontinuous relative to the applied force and their continuity can be assumed to be zero. The modulus of this part is expressed by the inversed rule of mixtures:

$$ E_{s} = \frac{{v_{s} }}{{(v_{1s} /E_{1} + v_{2s} /E_{2} + v_{3s} /E_{3s} )}} $$
(23)

where

$$ v_{s} = \, v_{1s} + \, v_{2s} + v_{3s} $$
(24)

It is clear that:

$$ v_{1} = \, v_{1s} + v_{1p} $$
(25)
$$ v_{2} = \, v_{2s} + \, v_{2p} $$
(26)
$$ v_{1} + \, v_{2} + \, v_{3} = \, 1 $$
(27)

When the nanoclay is only located in one phase, v 3p and v 3s are zero. The final modulus (E t ) is given as the sum of parallel and series sections moduli:

$$ E_{t} = E_{1} v_{1p} + E_{2} v_{2p} + E_{3p} v_{3p} + \frac{{vs ^{2} }}{{\left( {\frac{{v_{1s} }}{{E_{1} }} + \frac{{v_{2s} }}{{E_{2} }} + \frac{{v_{3s} }}{{E_{3s} }}} \right)}} $$
(28)

In the present model, the main problem is the modulus of the interphase. Like Xing’s model, it is supposed that the modulus at each point has a linear relation with the distance from one surface [17]. For each edge, the modulus is the same as its neighboring zone. Therefore, the modulus at each point is:

$$ E_{3} \left( r \right) \, = \, E_{1} - \frac{[E1 - E2]}{I} r $$
(29)

where r is the distance along the normal direction of the surface and I is the third phase thickness in parallel (I p ) or series (I s ) section as shown in Fig. 2.

The average modulus of parallel part of the third phase (E 3p ) is calculated by integration along the layer length (according to the rule of mixtures) as follows:

$$ E_{3p} = \frac{1}{{I_{p} }}\mathop \int \limits_{0}^{Ip} \left(E_{1} - \frac{{[E_{1} - E_{2} ]}}{{I_{p} }}\right){\text{d}}r \, = \frac{{(E_{1} + E_{2} )}}{2} $$
(30)

The average modulus for series section of the interface phase (E3s), based on inversed rule of mixtures, is:

$$ E_{3s} = \frac{1}{Is}\mathop \int \limits_{0}^{Is} \frac{1}{{\left(E1 - \frac{{[E_{1} - E_{2} ]}}{{I_{p} }}\right)}}{\text{d}}r = \frac{{Ln(\frac{{E_{1} }}{{E_{2} }})}}{{E_{1} - E_{2} }} $$
(31)

The final equation for predicting the modulus of ternary blend (E t ) is:

$$ E_{t} = v_{1p} E_{1} + v_{3p} \frac{{(E_{1} + E_{2} )}}{2} + v_{2p} E_{2} + \frac{{v_{s}^{2} }}{{\frac{{v_{1s} }}{{E_{1} }} + \frac{{v_{2s} }}{{E_{2} }} + v_{3s} \frac{{(E_{2} - E_{1} )}}{{Ln\frac{{E_{1} }}{{E_{2} }}}}}} $$
(32)

It is clear that if E 2 << E 1, only the first two terms on the right hand of the equation are important and the other sections are negligible.

The modulus of the phase containing nanoclay

In this work to calculate the modulus of the phase containing nanoclay, the Xing model was used [17]. As it was mentioned earlier, this model is based on Takayanagi’s two-phase model and it is modified for a binary nanocomposite by considering the interface of nanoclay and polymeric matrix:

$$ \frac{1}{{E_{c} }} = \frac{{1 - \sqrt {\left[ {2\left( {\frac{\tau }{t}} \right) + 1} \right]V_{f} ]} }}{{E_{i} }} $$
$$ \begin{gathered} + \frac{{\sqrt {\left[ {2\left( {\frac{\tau }{t}} \right) + 1} \right]V_{f} ]} - \sqrt {V_{f} } }}{{[1 - \sqrt {\left[ {2\left( {\frac{\tau }{t}} \right) + 1} \right]V_{f} ]]} E_{i} \quad + \sqrt {\left[ {2\left( {\frac{\tau }{t}} \right) + 1} \right]V_{f} ]} \left( {k - 1} \right)E_{i} /Ln(k)}} \hfill \\ \quad + \frac{{\sqrt {V_{f} } }}{{[1 - \sqrt {\left[ {2\left( {\frac{\tau }{t}} \right) + 1} \right]V_{f} ]]} Ei + \frac{{\left\{ {\sqrt {\left[ {2\left( {\frac{\tau }{t}} \right) + 1} \right]V_{f} ]} - \sqrt {V_{f} } } \right\}\left( {k + 1} \right)E_{i} }}{2} + \sqrt {V_{f} } E_{f} }} \hfill \\ \end{gathered} $$
(33)

where τ and t are the interface and plate thickness of nanoclay, respectively; E i , E f , and E c are the moduli of neat phase, nanoclay and reinforced phase, respectively; k is one of the model parameters which should be obtained with curve fitting, and v f is the nanoclay volume fraction. Since the nanoclay is only located in one phase, its local concentration is greater than before and should be changed to larger values. Therefore, the corrected volume fraction of nanoclay (v f ) is:

$$ v_{f} = \frac{{\Phi_{n} }}{{v_{3} }} $$
(34)

where Φ n is the volume fraction of nanoclay and v 3 is the volume fraction of the phase containing nanoclay. It should be noted that this model could not consider the orientation of the nanoclays. Therefore, it is assumed that the nanoclay orientation is random in the third phase.

Comparison with experimental results

Figure 3 demonstrates the experimental data for modulus of binary blend based on LDPE/TPS and the model prediction at different TPS contents. It is seen that there is good agreement between the theoretical and experimental data. The inflection point around 40 wt% can be attributed to the highly continuous volume fraction of the minor phase which occurs sooner than phase inversion as it was stated before.

Fig. 3
figure 3

Comparison of experimental and theoretical data for the modulus of LDPE/TPS with different contents of TPS. The component properties are listed in Table 4

Full size image

To assess the model in the case of nanocomposites, the resulting experimental data for LDPE/TPS/Cloisite 30B were checked and compared with the model results (Fig. 4). It is seen again, that there is a good agreement between the experimental and theoretical data. In this case, it is assumed that nanoclay is located at the interface. In a study on PP/TPS/Cloisite 30B system (which is very similar to LDPE/TPS/Cloisite 30B), the TEM images showed that the nanoclay is located in the interface [30]. To prove this assumption, the wettability parameter may be estimated using this equation [31]:

Fig. 4
figure 4

Comparison of experimental and theoretical data for the modulus of LDPE/TPS (65/35 wt%) and different contents of Cloisite 30B. The component properties and model parameters are listed in Tables 4 and 5, respectively

Full size image
$$ \omega_{12} = \frac{{(\gamma_{\text{LD - nano}} - \gamma_{\text{TPS - nano}} )}}{{\gamma_{\text{LD - TPS}} }} $$
(35)

where ω 12 is the wettability parameter, γ ij is the interfacial tension between i and j phases. It is well known that when −1 < ω 12 < 1, the nanoclay is localized at the interface. With a coefficient higher than 1, the nanoclay would be located in TPS phase and by being lower than −1, it would be distributed at LDPE phase. Therefore, this equation can be used to predict the location of nanoclay. It is clear that when nanoclays are located at the interface, there is a third phase that should be considered with Eq. 32 and when nanoclays are located at one of the main phases (matrix or dispersed phase), the third phase volume fraction is set to zero.

The interfacial tensions can be estimated by different equations like harmonic-mean equation [32], Girifalco and Good [33] or geometric mean approach [34]. In this study, the geometric mean equation is used:

$$ \gamma_{12} = \gamma_{1} + \gamma_{2} - 2\sqrt {\gamma_{1}^{d} \gamma_{2}^{d} } - 2\sqrt {\gamma_{1}^{p}\gamma_{2}^{p} } $$
(36)

where γ i , γ d i and γ p i denote surface tension, dispersed component and polar component of phase i, respectively.

Tables 2 and 3 show the above parameters which are gathered from literature sources [35–37] and the calculated interfacial tensions. The resulting value for wettability parameter is 0.89 and it shows the above assumption is true. Although γ TPS/nano is very low, the nanoclay migrates and covers the interface and lowers the interfacial energy, because of high interfacial tension between LDPE and TPS phases.

Table 2 Surface tension of each phase. The surface tension of TPS with 30 wt% glycerol is used here as an approximation
Full size table
Table 3 Interfacial tensions between phases according to Harmonic equation
Full size table

For more investigation, other possible places for location of the nanoclay (that is nanoclay located in TPS or LDPE phase) are considered and shown schematically in Fig. 5. In these cases, there is no third phase and the model is reduced to the binary phases. It should be considered that the modulus of neat phase is substituted by the modulus of the phase including nanoclay, which is higher than that of origin phase.

Fig. 5
figure 5

Distribution of nanoclay at different phases: a in LDPE phase and b in TPS phase

Full size image

Figure 6 shows the modulus of the nanocomposites with the above assumptions with different nanoclay contents. In the case which nanoclay is located at TPS phase, due to much lower modulus of TPS (about 2.5 MPa) than LDPE (133 MPa) phase, the reinforcing effect of nanoclay on TPS is negligible compared to LDPE modulus. Therefore, the modulus of nanocomposite in this case is not changed significantly.

Fig. 6
figure 6

Comparison of experimental and theoretical data for the modulus of LDPE/TPS (65/35 wt%) and different contents of Cloisite 30B when the nanoclay is distributed in TPS or LDPE phase. The component properties and model parameters are listed in Tables 4 and 5, respectively

Full size image

In contrast, a high value was determined for modulus of the nanocomposite, where nanoclay was located at the LDPE phase. These values are larger than the experimental data and overestimate the composite modulus on a wide range of nanoclay concentration, even with the lowest adjustable parameters. This implies that this assumption lacks validity.

The published data in other literature sources were also used to check the model. For this purpose, the polylactic acid grafted maleic anhydride/thermoplastic starch/montmorillonite (PLA-g-MA/TPS/MMT) nanocomposite was considered [38]. The experimental data and the model results are compared in Fig. 7 for different nanoclay contents. The material properties are presented in Table 4. The authors present a TEM micrograph which shows that nanoclay is located at the interface. Eq. 32 is currently used to predict the modulus of the nanocomposite. The modulus predictions are relatively close to the experimental data. To check the model with a matrix phase containing nanoclay, the PP/EOR/nanoclay with various formulations is considered [39]. In this system, the modified nanoclay is located in PP phase (matrix). The components’ properties and adjustable parameters are used for modeling the three cases listed in Tables 4 and 5, respectively. The model and experimental results are shown in Fig. 8. The model results are moderately close to the experimental data, especially in the case of PP/EOR (60/40) nanocomposites. However, the experimental data for PP/EOR (70/30) display some deviations from model prediction. This can be ascribed to the agglomeration of nanoclay at high nanoclay content. Therefore, the related parameters should be changed with changes in concentration of the nanoclays, because the dispersion state at low and high nanoclay concentrations are changed significantly and the mechanical properties show two different trends. For more investigation, the other possible location of nanoclay in these two systems was assessed (Fig. 9a, b). It is clear that the results show large errors. Therefore, the model can be used to determine the nanoclay location

Fig. 7
figure 7

Comparison of experimental and theoretical data for the modulus of PLA-g-MA/TPS blends (60/40 and 73/27 wt%) with different contents of MMT (experimental data are from ref. [38]). The component properties and model parameters are listed in Tables 4 and 5, respectively

Full size image
Table 4 Material properties used for modeling
Full size table
Table 5 Curve fitting parameters which are used for modeling
Full size table
Fig. 8
figure 8

Comparison of experimental and theoretical data for the modulus of PP/EOR blends (60/40 and 70/30 wt%) with different contents of modified nanoclay (experimental data are from ref. [39]). The component properties and model parameters are listed in Tables 4 and 5, respectively

Full size image
Fig. 9
figure 9

Distribution of nanoclay a in PLA-g-MA or in TPS phase for PLA-g-MA/TPS (60/40) nanocomposites (experimental data are obtained from ref. 38) and b distribution of nanoclay at the interface or in EOR phase for PP/EOR (60/40) nanocomposites (experimental data are obtained from ref. [39])

Full size image

In addition, the presented model can be used to investigate the structure of the nanoclays in the blend, without using other expensive tests. Also, the adjustable parameters can provide some useful information about the internal structure of nanocomposites after fitting the experimental data with the model. For example, the parameters τ can be used to evaluate the interaction between the nanoclay and matrix. One can find the dispersion state and the interaction between matrix and nanoclay layers improve as τ increases.

Conclusion

A simple model was developed to predict the modulus of nanocomposites based on polymeric-based blends. First, a simple model was derived for binary polymer blends. Then, this model combined with Xing’s model to apply for the ternary nanocomposites. In addition, this model was modified to predict the modulus of the nanocomposites, when nanoclay was located at the interface. The experimental tests were performed on LDPE/TPS binary blend and LDPE/TPS/nanoclay nanocomposite. The moduli of these nanocomposites were compared with the model results. The experimental data of other ternary nanocomposites from literature were also compared with the model results. A good agreement was found between the presented model and the experimental data which implies that the model can be used to assess the nanoclay dispersion states and predict their location in the blend.