1 Introduction

An evacuation is part of an emergency process in which residents of a certain area, the so-called danger zone, have to flee due to a latent or imminent threat. Thus, an evacuation can be considered as the task of moving evacuees from the danger zone to safety in the best possible way. In doing so, the notion of goodness has a situational meaning, e. g. in the sense of speed or safety of the evacuation process. For instance, in case of a tsunami, the purpose of evacuation might be different compared to situations where the danger results from hazardous clouds. However, independent of the reason to evacuate, the process of evacuation and the time needed for evacuation is usually divided into three parts in the literature (see e. g. Graat et al. 1999; Hamacher and Tjandra 2002):

  • Time to recognize the dangerous situation: this is the time the residents of the danger zone need to realize that they are evacuees indeed. It strongly depends on the alarm system and the familiarity of the evacuees with those systems. It could be reduced by regular training with false alarms but it remains too hard to measure.

  • Time the evacuees need to decide to take action and to decide on the type of action: here, the knowledge about the evacuation system of the evacuees has the most influence. As before, this time can be reduced by appropriate emergency trainings and is hard to measure.

  • Time to move to safety, i. e. egress time: this time is certainly also influenced by human behavior in emergencies but it also depends on measurable factors such as the layout of the building, road networks or local conditions, respectively. This implies evacuation plans as well as their quality.

As pointed out, human behavior and organizational factors are the main contributors to the first two issues. As one might imagine, it is impossible to come up with an analytical description of those components. Furthermore, in contrast to human behavior measurable factors such as evacuation routes and the layout of the evacuation surroundings may be enhanced as a result of an analysis of the evacuation process. Therefore, we concentrate on the computation of the egress time, where we use the terms egress time and evacuation time as synonyms from now on.

In the literature, there exist various approaches to compute the egress time originating from different research perspectives. Literature on this topic is comprehensive and widely spread across different scientific communities and cannot be completely (but nevertheless exemplary) discussed here. It is classically subdivided into macroscopic and microscopic (see e. g. the seminal articles of Coclite et al. 2005; Hamacher and Tjandra 2002; Helbing and Schreckenberg 1999; Nagel and Schreckenberg 1992; Schadschneider et al. 2009; Seyfried et al. 2006) approaches.

Microscopic approaches focus on a detailed egress model capturing individuals and their (individual and group) behavior with typically high spatial and temporal resolution. They describe single evacuees with individual parameters such as e. g. speed and reaction time. The interaction between evacuees is also an important point in the microscopic modeling. Microscopic approaches allow the observation of local phenomena such as lane formation of pedestrians or the identification of bottlenecks. They are often based on simulation approaches and most of them can be classified either as models using cellular automata (Köster et al. 2011; Pandey et al. 2015; Tian et al. 2014), as social-force models (Johansson et al. 2014; Zanlungo et al. 2011) or as agent-based models (Bazzan and Klügl 2014; Nagel and Flötteröd 2012). Especially the latter stream of research has recently gained considerable attention in the scientific community.

In contrast to microscopic considerations, macroscopic models treat evacuees as a homogeneous group. The focus is more on common characteristics such as an average speed rather than individual properties. For the macroscopic modeling of an evacuation process, flow models are widely used, where the flow corresponds to the moving evacuees per unit time. The key advantage of macroscopic models is that it enables fast numerical simulation and optimization runs, respectively. In fact, these models allow for an optimization of the evacuation process leading to system optima as for instance the minimal evacuation time or the fastest evacuation routes. These optima result in provable lower bounds on the true evacuation time (Hamacher et al. 2010; Hamacher and Tjandra 2002).

Linear dynamic network flows provide fast and well-investigated algorithms for macroscopic models with discrete time steps (Chalmet et al. 1982; Choi et al. 1988). An overview of discrete time network models for evacuation planning can be found in Hamacher and Tjandra (2002) and the references therein.

In contrast, continuous time models are based on differential equations. Usually, the models are inspired by the underlying physics, see Helbing (1991), Hoogendoorn and Bovy (2000), Hughes (2002) for an overview. As most of these models are formulated on one- or two-dimensional corridors instead of networks, we apply a traffic flow model originally proposed in Coclite et al. (2005) to describe the evacuation process.

While the lines between these classical streams become more and more blurred, new fields of activities emerged such as unifying approaches connecting different methodologies (see, e. g. Hamacher et al. 2010; Kneidl et al. 2010), “nanoscopic” approaches aiming at modeling psychological and sociological aspects of egress movement (see, e. g. Chattaraj et al. 2009; Sivers et al. 2014), or, for instance, methods for combining egress models with others mathematical models influencing the egress indirectly (see, e. g. Dietrich et al. 2014; Göttlich et al. 2011) .

Since evacuation planning has been intensively investigated during the last decades (Chalmet et al. 1982; Choi et al. 1988; Graat et al. 1999; Gwynne et al. 1999; Hamacher et al. 2010; Hamacher and Tjandra 2002; Helbing 1991; Klüpfel et al. 2005; Schadschneider et al. 2009; Southworth 1991), our focus lies on the influence of a spreading hazardous material on the evacuation process. For the hazardous material, we assume a gaseous medium, which we model following our approach in Göttlich et al. (2011).

In this work, we introduce a more elaborate traffic flow model, which is the basis of the computation of an evacuation plan. We extend the linear continuous model presented in Göttlich et al. (2011) in the sense that congestions are allowed on the evacuation routes. This immediately leads to a nonlinear model that is able to capture the observed queuing. In a numerical example, we point out that this extension leads to longer evacuation times as anticipated.

This paper is organized as follows. In Sect. 2, we present the continuous time traffic flow model based on partial differential equations as well as the dynamic network flow model, which we use as the reference model throughout this work. Then, we explain how the information of gaseous hazard is coupled to the traffic flow model. We also propose different objective functions to solve the coupled optimization problem and close with a numerical study on different evacuation scenarios.

2 Network flow models

For all traffic flow models, we assume that the geometry of the roads is represented as a finite graph \({\mathcal {G}}=(V,E)\), where E is the set of edges (or paths) and V is the set of vertices (or intersections). By \(\delta ^-(v)\subset E\) and \(\delta ^+(v)\subset E\), we denote the in- and outgoing edges from a fixed vertex \(v\in V\), respectively. A vertex with no ingoing edges, i.e. \(\delta ^-(v)=\emptyset \), is called a source and the set of all sources is denoted by \(S\subset V\). By \(D\subset V\) we denote the set of destinations, i. e. all vertices \(v\in V\) without outgoing edges, i. e. \(\delta ^+(v)=\emptyset \). All other vertices \(V^{\mathrm{in}}=V{\setminus }\left( S \cup D \right) \) are called inner vertices.

We first introduce a nonlinear continuous model, which has been studied before, e.g. in Coclite et al. (2005), Garavello and Goatin (2012), Herty et al. (2009) proving the existence of solutions as well as in Göttlich et al. (2014), Herty and Klar (2003), Kühn (2015) considering numerical solution methods. Then, we furthermore introduce the linear dynamic network model. This is a widely used model in discrete optimization (cf. e. g. Ahuja et al. 1993) and has been also applied in the context of evacuation planning, e.g. in Fleischer and Tardos (1998), Hamacher and Tjandra (2002). We will use the latter as a benchmark solution for the nonlinear model.

2.1 A nonlinear network flow model

We first introduce a nonlinear time-continuous model, where evacuees on each edge \(e\in E\) are described by their density \(\rho _e(x,t)\), i. e. evacuees per unit length. The variable \(x\in \left[ a_e, b_e \right] \) denotes the position on the edge that has a spatial extension of length \(L_e = b_e - a_e\) and \(t\in {\mathbb {R}}_{>0}\) is a positive point in time.

The flow of evacuees \(f_e(\rho _e(x,t))\) on each edge \(e\in E\) is a function depending on the density of evacuees at point x and time t. To describe the evacuation process as realistically as possible we need to include congestions on the paths, i. e. edges. Thus, as flow functions, we consider the so-called hat function

$$\begin{aligned} f_e(\rho _e) = {\left\{ \begin{array}{ll} v_{e}^{\mathrm{max}} \cdot \rho _e &{} 0\le \rho _e \le \sigma _e \\ \mu _e - v_e^{\mathrm{max}} (\rho _e - \sigma _e) &{} \sigma _e \le \rho _e \le \rho _e^{\mathrm{max}} \end{array}\right. } \end{aligned}$$
(1)

as well as the Lighthill–Whitham–Richards relation

$$\begin{aligned} f_e(\rho _e) = v_e^{\mathrm{max}} \cdot \rho _e \left( 1-\frac{\rho _e}{\rho _e^{\mathrm{max}}} \right) , \end{aligned}$$
(2)

where \(v_e^{\mathrm{max}}\) denotes the maximal velocity, \(\rho _e^{\mathrm{max}}\) the maximal density, \(\sigma _e=\rho _e^{\mathrm{max}}/2\) the maximal density allowed for free flow and \(\mu _e\) the capacity of edge e.

At the beginning of each edge \(e\in E\), we introduce a queue \(q_e(t)\) measuring the evacuees waiting within the intersection in front of edge e to enter the edge.

Thus, the following traffic flow model is set up (see also Coclite et al. 2005; Garavello and Goatin 2012; Kühn 2015):

$$\begin{aligned}&\partial _t \rho _e(x,t) + \partial _x f_e\left( \rho _e(x,t) \right) = 0 \forall e\in E,\quad \, t\ge 0,\quad x\in \left( a_e, b_e \right) \end{aligned}$$
(3a)
$$\begin{aligned}&\partial _t q_{\tilde{e}}(t) = \sum _{e\in \delta ^-(v)} \alpha _{e\tilde{e}} f_e\left( \rho _e(b_e,t) \right) - f_{\tilde{e}}\left( \rho _{\tilde{e}}(a_{\tilde{e}},t) \right)&\begin{aligned} \forall v\in V^{\mathrm{in}}\,&\forall \tilde{e}\in \delta ^+(v), \\&\, \forall t\ge 0 \end{aligned} \end{aligned}$$
(3b)
$$\begin{aligned}&\left. \begin{aligned} \max \limits _{\alpha }&\sum _{e\in \delta ^-(v)} f_e\left( \rho _e(b_e,t) \right)&\\ {\text {s.t. }}\,&\begin{aligned} \partial _t q_{\tilde{e}}(t) =&\sum _{e\in \delta ^-(v)} \alpha _{e\tilde{e}} f_e\left( \rho _e(b_e,t) \right) \\&- f_{\tilde{e}}\left( \rho _{\tilde{e}}(a_{\tilde{e}},t) \right) \end{aligned}&\forall \tilde{e}\in \delta ^+(v) \\&0\le f_e\left( \rho _e(b_e,t) \right) \le \mathrm{su}_e^q\left( \rho _e(b_e,t) \right)&\forall e\in \delta ^-(v) \\&0\le f_{\tilde{e}}\left( \rho _{\tilde{e}}(a_{\tilde{e}},t) \right) \le \mathrm{de}_{\tilde{e}}\left( \rho _{\tilde{e}}(a_{\tilde{e}},t) \right)&\forall \tilde{e}\in \delta ^+(v) \\&0\le q_{\tilde{e}}(t) \le M_{\tilde{e}}&\forall \tilde{e}\in \delta ^+(v) \end{aligned} \right\}&\forall v\in V^{\mathrm{in}},\, t\ge 0 \end{aligned}$$
(3c)
$$\begin{aligned}&\rho _e(x,0) = \tilde{\rho }_e(x)& \forall e\in E,\, x\in (a_e, b_e) \end{aligned}$$
(3d)
$$\begin{aligned}&q_e(0) = \tilde{q}_e&\quad \forall e\in E \end{aligned}$$
(3e)
$$\begin{aligned}&f_e\left( \rho _e(a_e,t) \right) = f_e^{\mathrm{in}}(t)&\quad \forall e\in \delta ^+(v)\quad \forall v\in S=\left\{ v\in V\left| \right. v \text { is a source} \right\} . \end{aligned}$$
(3f)

Here, Eq. (3a) describes transport along the edges and additionally ensures mass conservation as well. The next Eq. (3b) models the filling and emptying of the queue, where \(0\le \alpha _{e\tilde{e}}\le 1\) is the distribution rate from edge e to \(\tilde{e}\) with \(\sum _{\tilde{e}} \alpha _{e\tilde{e}} = 1\). The maximal throughput at each inner vertex \(v\in V^{\mathrm{in}}\) is guaranteed by (3c), where the maximal supply of edge \(e\in \delta ^-(v)\) to vertex v is denoted by

$$\begin{aligned} \mathrm{su}_e^q(\rho _e(b_e,t)) = {\left\{ \begin{array}{ll} 0 &{} \text {if } \exists \tilde{e}\in \delta ^+(v): q_{\tilde{e}}(t)=M_{\tilde{e}} \\ f_e(\rho _e(b_e,t)) &{} \text {if } \rho _e(b_e,t)\le \sigma _e \\ f_e(\sigma _e) &{} \text {if } \rho _e(b_e,t) \ge \sigma _e \end{array}\right. } \end{aligned}$$
(4)

and

$$\begin{aligned} \mathrm{de}_e(\rho _e(a_e,t)) = {\left\{ \begin{array}{ll} f_e(\sigma _e) &{} \text {if } \rho _e(a_e,t)\le \sigma _e \\ f_e(\rho _e(a_e,t)) &{} \text {if } \rho _e(a_e,t) \ge \sigma _e \end{array}\right. } \end{aligned}$$
(5)

indicates the corresponding demand of the ongoing edge e. The queue is limited by \(M_e\ge 0\). The initial conditions for the densities, the queues as well as the boundary conditions for the edges leaving a source are given in (3d)–(3f).

2.2 A linear network flow model

We intend to compare the evacuation model (3) to a benchmark model. As such a benchmark model we choose the time-discrete network flow model (see e. g. Hamacher and Tjandra 2002; Krumke and Noltemeier 2005), since it is well understood and yields provable lower bounds on the evacuation times. Furthermore, it is closely related to model (3). In fact, we have shown in Göttlich et al. (2011) that model (6) and model (3) with a linear flow function \(f(\rho )=v\rho \) (instead of (1) or (2)) lead to consistent solutions.

The dynamic network flow model is also based on a graph \({\mathcal {G}}=(V,E)\) with vertices V and edges E. In contrast to model (3), the variables are now evaluated at discrete time steps \(0=t_0 < t_1 < \dots < t_k < \dots < t_{k_{\mathrm{max}}}=T\).

In the dynamic network flow model the variable \({f^{\mathrm{d}}}_e(t_k)\) describes the flow entering the edge \(e\in E\) at time \(t_k\) and \({q^{\mathrm{d}}}_v(t_k)\) is the flow waiting in vertex \(v\in V\) at time \(t_k\). According to model (3) we also prescribe capacity constraints for the maximum flow on each edge \(e\in E\) by  \({\mu }_e\), and use \({M}_v\) for the maximum amount stored in the queue of vertex \(v\in V\). Different to the model (3), where the travel time depends on the density or the current load of the edge, in the dynamic network flow model the flow is linear, i.e. a constant travel time \({\tau ^{\mathrm{d}}}_e\) is assigned to all edges \(e\in E\). This is the time the flow needs to traverse edge e. We restrict all parameters of the dynamic network flow model to be positive, rational numbers, i. e. \({\tau ^{\mathrm{d}}}_e, {\mu }_e, {M}_v\in {\mathbb {Q}}_{\ge 0}\) for all \(e\in E\) and \(v\in V\), respectively, since this guarantees solvability in polynomial time (see e. g. Krumke and Noltemeier 2005).

Considering a network which is initially empty, i.e. \({f^{\mathrm{d}}}_e(t_k)=0\) for all \(t_k\le 0\), and initial mass \({q^{\mathrm{d}}}_v(0) = {q^{\mathrm{d}}}_{v,0}\ge 0\) in the vertices \(v\in V\) the dynamic network flow model reads

$$\begin{aligned}&\min \, J^{\mathrm{d}}\left( ({f^{\mathrm{d}}}_e)_{e\in E}, ({q^{\mathrm{d}}}_v)_{v\in V} \right)&\end{aligned}$$
(6a)
$$\begin{aligned}&{\text {s.t. }}\, {q^{\mathrm{d}}}_v(t_k) - {q^{\mathrm{d}}}_v(t_k - 1) = \sum _{e\in \delta ^-(v)} {f^{\mathrm{d}}}_e(t_k - {\tau ^{\mathrm{d}}}_e)&\nonumber \\&\qquad \qquad \qquad \qquad \qquad - \sum _{e\in \delta ^+(v)} {f^{\mathrm{d}}}_e(t_k)&\forall v\in V, \quad k=1,\dots ,k_{\mathrm{max}} \end{aligned}$$
(6b)
$$\begin{aligned}&{q^{\mathrm{d}}}_v(0) = {q^{\mathrm{d}}}_{v,0}& \forall v\in V \end{aligned}$$
(6c)
$$\begin{aligned}&0\le {q^{\mathrm{d}}}_v(t_k) \le {M}_v& \forall v\in V,\quad k=0,\dots , k_{\mathrm{max}} \end{aligned}$$
(6d)
$$\begin{aligned}&0\le {f^{\mathrm{d}}}_e(t_k) \le {\mu }_e& \forall e\in E,\quad k=0,\dots , k_{\mathrm{max}}-{\tau ^{\mathrm{d}}}_e \end{aligned}$$
(6e)
$$\begin{aligned}&{f^{\mathrm{d}}}_e(t_k) = f_e^{\mathrm{in}}(t_k)& \forall e\in \delta ^+(v), \quad v\in S,\, k,\dots , k_{\mathrm{max}}\, . \end{aligned}$$
(6f)

Here, even for simulation purposes, an objective function \(J^{\mathrm{d}}\) is needed to get the problem solved numerically. All other equations are similar to (3). For example, equation (6b) ensures flow conservation through vertices \(v\in V\). The left-hand side of (6b) resembles the change of the queue at vertex v, whereas the right-hand side computes the surplus at vertex v as the difference of the ingoing and the outgoing flow at vertex v. Due to the constant travel time on each edge the ingoing flow to vertex v from edge e at time \(t_k\) is given as the flow entering edge e at time \(t_k-{\tau ^{\mathrm{d}}}_e\), i. e. by the value \({f^{\mathrm{d}}}_e(t_k-{\tau ^{\mathrm{d}}}_e)\). The remaining constraints are the initial values (6c) and the capacity constraints for the vertices and edges (6d), (6e), respectively, as well as the inflow in the sources \(v\in S\) (6f). For the discussion of the objective (6a) we refer the reader to Sect. 4.

There are two main differences between the dynamic network flow model (6) and the nonlinear time-continuous model (3). First, the dynamic network flow model is only defined on discrete time steps, i. e. it is a time-discrete model in contrast to the time-continuous model (3). As we will see in Sect. 5, to compute numerical solutions the model (3) must be discretized and will also be computed on a discrete time grid. However, the points in time can be very close in the sense of a continuous limit.

More important is that both models differ in the description of congestion. The dynamic network flow model (6) allows for congestion in the queues (that are located in vertices) solely, whereas model (3) allows for congestion on the edges, too. This is due to the different modeling of travel times.

3 Coupling Hazard to network flow models

We are interested in the influence of a gaseous hazard on the evacuation process. Therefore, we need to couple the hazardous information to models presented in Sect. 2, especially to the nonlinear traffic flow model (3). To generally do so we stick to our approach in Göttlich et al. (2011) and map the hazard onto the network by defining a cost parameter. The coupling is then resolved within an optimization problem [cf. Sect. 4, (12)] in which the cost parameter is included in the objective function.

Following Göttlich et al. (2011), we describe the hazard or rather the concentration of the hazard \(\omega \) by the diffusion–advection equation in the \({\mathbb {R}}^2\)-plane

$$\begin{aligned} \partial _t \omega - \kappa \Delta \omega + u\cdot \nabla \omega = 0 \end{aligned}$$
(7)

with diffusion constant \(\kappa \) and wind field u.

We solve Eq. (7) numerically using the Crank–Nicolson method (see e.g. Crank and Nicolson 1947; Göttlich et al. 2011; Kühn 2015) while the solution \(\omega \) of (7) also needs to be mapped onto the graph \({\mathcal {G}}=(V,E)\). This mapping shall fulfill the following requirements:

Requirement 1::

For each point in time \(t\ge 0\) and each edge \(e\in E\), there is exactly one parameter describing the contamination of edge e.

This is due to the fact that the evacuees are not allowed to switch an edge after they have entered it. Thus, there is no need for a spatial resolution on a certain edge. Furthermore, in this way we are able to compare the nonlinear continuous model (3) directly to the discrete network flow model (6).

Requirement 2::

For a contamination that is constant in time, an edge \(e_1\) with length \(L_{e_1}\) being longer than edge \(e_2\) (i. e. \(L_{e_1}>L_{e_2}\)) also has a larger cost parameter, i. e. \(c_{e_1} > c_{e_2}\) (cf. Fig. 1).

This represents that evacuees on longer edges are more exposed to the contamination of the hazard than those on shorter ones. Thus, they suffer a higher penalty for moving along such an edge.

Requirement 3::

For a contamination that is constant in time, it does not matter if an edge is split up in two edges (cf. Fig. 2). (Due to modeling issues it may be necessary to do such a splitting but that must not influence the solution.)

Fig. 1
figure 1

Two edges \(e_1\) and \(e_2\) of different length. The gray background indicates the concentration of hazard, to which evacuees on these edges are exposed

Full size image
Fig. 2
figure 2

One long edge e (above) can be replaced by two shorter edges \(e_1\) and \(e_2\) and the introduction of an additional vertex v (below)

Full size image

We take care of the requirements by defining a time- and edge-dependent cost function

$$\begin{aligned} \begin{aligned}&c\, : \, E\times {\mathbb {R}}_{\ge 0} \longrightarrow {\mathbb {R}}_{\ge 0} \\&\quad (e,t) \longmapsto c_e(t) = \int \limits _{t}^{t+\tau _e} w(\tilde{t})\left| _e \right. \, {\text {d}}\tilde{t} , \end{aligned} \end{aligned}$$
(8)

where \(\tau _e=L_e/v_e^{\mathrm{max}}\) is the minimal travel time needed to cross an edge e of length \(L_e\) with maximum possible velocity \(v_e^{\mathrm{max}}\).

We also assume that the path which is associated with edge e has a width \(d_e\) such that it covers an area \({ \left|{A_e} \right|} = L_e d_e\). Thus, we define the restriction of the hazardous material to the area \(A_e\) as

$$\begin{aligned} w(\tilde{t})\left| _e \right. = \frac{1}{{ \left|{A_e} \right|} } \iint \limits _{A_e} w(x,y,\tilde{t}) \, \, {\text {d}}x\, {\text {d}}y \, . \end{aligned}$$
(9)

Thus, the integrand of (8) represents an averaging of the value of the hazard over the area of the road.

However, the integration over the travel time in (8) takes care of the weighting of edges of different length, where the length is measured by the time evacuees spend on the edge. In this way, we guarantee that Requirements 2 and 3 are fulfilled.

Note that by integrating over time we take the dynamics of the hazard into account. This prevents evacuees being sent on an edge which is covered by the hazard in the time interval \(\left( \right. t, t+\tau _e\left. \right] \), which is not possible by solely considering the hazard at time t.

Using the minimal travel time yields only a lower bound for the true contamination of hazard the evacuees are exposed to, but enables to compare our results to discrete network flow models.

We also define a time-dependent cost function for each vertex \(v\in V\)

$$\begin{aligned} \begin{aligned}&c\, : \, V\times {\mathbb {R}}_{\ge 0} \longrightarrow {\mathbb {R}}_{\ge 0} \\&\quad (v,t) \longmapsto c_v(t) = \int \limits _{t}^{t+\epsilon } w(\tilde{t})\left| _v \right. \, {\text {d}}\tilde{t}, \end{aligned} \end{aligned}$$
(10)

where \(A_v\) is the area covered by the intersection associated with vertex v. The difference between (8) and (10) is that the latter is defined on vertices instead of edges.

For the computation of the area \(A_v\), we assume a standard intersection (e.g. a T-junction). Thus, we model the area covered by the intersection as a rectangle, which depends on the width of the adjacent edges with \(\epsilon >0\) being an arbitrarily small constant. This constant is set to \(\Delta t\) in the numerical method so that the evacuees waiting in a vertex are treated analogously to the evacuees moving on an edge.

Consequently, the restriction of the concentration of the hazardous material to the area \(A_v\) is defined as

$$\begin{aligned} w(\tilde{t})\left| _v \right. = \frac{1}{{ \left|{A_v} \right|} } \iint \limits _{A_v} w(x,y,\tilde{t}) \quad {\text {d}}x\, \, {\text {d}}y \, . \end{aligned}$$
(11)

Summarizing, the integrand of (10) averages the value of the hazard over the area of the intersection.

Remark 1

The definition of the cost function for the edges (8) and the vertices (10) implies that full information—or at least information about the time interval \(\left[ t, t+\tau ^* \right] \) with \(\tau ^* = \max \left\{ \tau _e \left| \right. e\in E \right\} >\epsilon >0\)—on the dynamics of the hazard is available in advance. Thus, this seems to be a good approach to analyze different evacuation scenarios to improve standard evacuation schedules. Additionally, if good forecasts on the dynamics of the hazard are available, it also serves as an online tool.

4 The choice of objective functions

We need to measure the quality of the evacuation plans. Therefore, we define an optimization problem with an objective function J measuring different evacuation objectives. The constraints of this optimization problem are those from the corresponding different network flow models

$$\begin{aligned} \begin{aligned} \min \,&J \\ {\text {s.t. }}\,&\text { considered network flow model (e.g. (3) or (6))} \, . \end{aligned} \end{aligned}$$
(12)

A standard objective function, not only in evacuation dynamics, is

$$\begin{aligned} J_{\mathrm{MF}} = - \int \limits _{0}^{T} \sum \limits _{d\in D} \sum \limits _{e\in \delta ^-(d)} f_e\left( \rho _e(b_e,t) \right) \, {\text {d}}t \end{aligned}$$
(13)

maximizing the flow reaching the sinks \(d\in D={ \left\{ {v\in V\left| \right. v \text { is a sink}} \right\} } \) in the time interval \(\left[ 0, T \right] \). (Note that due to the objective function being negative, this indeed yields a maximization.) This objective function is an upper bound on the number of evacuees, which can be saved in a certain time interval \(\left[ 0, T \right] \).

Having these bounds at hand, we consider the best possible evacuation in a next step. For example in case of fire or an explosion it is convenient to perform an evacuation as quickly as possible. For such situations we consider the quickest flow objective function

$$\begin{aligned} J_{\mathrm{QF}} = \max { \left\{ {t\in {\mathbb {R}}_{\ge 0} \left| f_e\left( \rho _e(b_e,t) \right) \ne 0 \begin{aligned}&\quad \text { for some } e\in \delta ^-(d) \\&\quad \text { and some } d\in D \end{aligned} \right. } \right\} } \, . \end{aligned}$$
(14)

It minimizes the last point in time (namely \(J_{\mathrm{QF}}\)) when some flow reaches a sink and thus ensures an evacuation as fast as possible.

In case of the quickest flow objective (14) we need an additional constraint in the optimization problem, ensuring that all evacuees reach a sink, namely

$$\begin{aligned} \int \limits _{0}^{\infty } \sum \limits _{d\in D} \sum \limits _{e\in \delta ^-(d)} f_e\left( \rho _e(b_e,t) \right) \, {\text {d}}t = \sum \limits _{e\in E} \int \limits _{a_e}^{b_e} \rho _e(x,0)\, {\text {d}}x + \sum \limits _{e\in E} q_e(0) \, . \end{aligned}$$
(15)

The left-hand side of (15) measures the number of evacuees reaching the sinks and the right-hand side sums up the initial mass in the network, i. e. all the people which have to be evacuated. If this constraint is satisfied, all evacuees have reached the sink. We assume that all evacuees are initially located in the network and do not enter over time, i. e. \(f^{\mathrm{in}}=0\).

Algorithmically, we can solve the Quickest Flow Problem, i.e. (12) with objective function (14) and as constraints both (3) and (15), by solving the maximum flow problem [i.e. (12) with (13)] for increasing time horizons \( T_{1} < T_{2} < \dots < T^{*} \) until the objective value of (13) coincides or is larger than the right-hand side of (15) (see e.g. Burkard et al. 1993; Fleischer and Tardos 1998; Hamacher and Tjandra 2002).

The quickest flow objective leads to a fast evacuation, i. e. small evacuation times, but it does not take care of the gaseous hazard since the fastest evacuation route may lead through the hazard. To this end, we define a time-dependent objective function

$$\begin{aligned} J_{\mathrm{TD}} = \int \limits _{0}^{\infty } \sum \limits _{e\in E} c_e(t) \int \limits _{a_e}^{b_e} \rho _e(x,t)\, {\text {d}}x \, {\text {d}}t + \int \limits _{0}^{\infty } \sum \limits _{v\in V} c_v(t) q_v(t) \, {\text {d}}t, \end{aligned}$$
(16)

which seeks to minimize the concentration of hazard the evacuees are exposed to. The cost functions \(c_{e}(t)\) and \(c_{v}(t)\) are given by (8) and (10), respectively.

As we consider a quite large network for our numerical studies with 971 vertices and 2432 edges, the computational effort for the time-dependent objective function (16) is rather high.

To reduce this effort at least for the reference model, i. e. the dynamic network flow model, we define an accumulated cost function

$$\begin{aligned} J_{\mathrm{AC}} = \int \limits _{0}^{\infty } \sum \limits _{e\in E} c_e^{\mathrm{AC}} \int \limits _{a_e}^{b_e} \rho _e(x,t)\, {\text {d}}x \, {\text {d}}t + \int \limits _{0}^{\infty } \sum \limits _{v\in V} c_v^{\mathrm{AC}} q_v(t) \, {\text {d}}t . \end{aligned}$$
(17)

We consider accumulated costs \(c_e^{\mathrm{AC}}\) and \(c_v^{\mathrm{AC}}\) for each edge \(e\in E\) and each vertex \(v\in V\), respectively,

$$\begin{aligned} \begin{aligned} c_e^{\mathrm{AC}}&= \int \limits _{0}^{\infty } c_e(t) \, \, {\text {d}}t , \\ c_v^{\mathrm{AC}}&= \int \limits _{0}^{\infty } c_v(t) \, \, {\text {d}}t . \end{aligned} \end{aligned}$$
(18)

This yields just a single cost parameter which is constant in time, for each element of the graph. Thus, we are able to solve the resulting optimization problem using static methods such as Min-Cost-Flow algorithms (see e. g. Ahuja et al. 1993; Hamacher and Klamroth 2000; Krumke and Noltemeier 2005). A faster computation time makes up for the quality loss of the projection.

A straightforward discretization of equations (14)–(17) implies the analogous form of \(J^d\) [see Eq. (6a)] for the discrete model (6).

The evacuation plans resulting from the objective functions (14), (16) and (17) and their discrete analogs are presented in Sect. 5.3.

5 Numerical examples

In this section, we apply the models and objective functions to compare different evacuation plans. The main goal thereby is to derive an evacuation plan for a large production site, where the relevant subgraph is shown in Figs. 6 and 7.

Before presenting the numerical results, we summarize the numerical solution methods for both models introduced in Sect. 5.1. Then, we exemplify the influence of the different flow functions by comparing the evacuation times on a given path (see Sect. 5.2). We close with the comparison of objective functions.

5.1 Numerical solution methods

For the dynamic network flow model (6), several methods exist to determine an optimal solution. In case of an evacuation the quickest flow problem is reduced to a sequence of quickest path problems, i. e. to the problem of finding the path which leads from a source to an (arbitrary) destination (i. e. safe location) in the shortest time. This is due to the assumption that it is not convenient for the evacuees to be split up to different paths during an evacuation process when starting from the same source. Such a problem is solved by a multi-criteria approach proposed in Rosen et al. (1991) which optimizes the travel time as well as the bottleneck capacity. If we additionally assume that all edges in the example from Sect. 5.3 have the same capacity this approach reduces to a Min-Cost-Flow problem with travel times of the edges as cost functions. This is solved by a Successive-Shortest-Path Algorithm (see e. g. Ahuja et al. 1993).

Model (6) equipped with the accumulated cost function (17) can be also solved with a static method since there is no time dependence in the parameters anymore. Thus, we use a Successive-Shortest-Path algorithm for its solution.

In contrast, the time-dependent objective function (16) yields a problem with dynamic parameters as the costs are time dependent. Thus, we use the time expanded network to resolve this time dependence. The so-called time expanded network \({\mathcal {G}}^T = (V^T,E^T)\) is constructed from the original network \({\mathcal {G}}=(V,E)\) by copying each vertex \(v\in V\) once for each time step \(0\le t_k \le t_{k_{\mathrm{max}}}\), i. e. \(V^T=\left\{ v^{t_k}\left| \right. v\in V, \, 0\le k\le k_{\mathrm{max}} \right\} \). For each edge \(e=(u,v)\) from vertex \(u\in V\) to vertex \(v\in V\) with travel time \(\tau _e\), edges \(e^t\in E^T\) are introduced leading from \(u^t\) to \(v^{t+\tau _e}\) for \(0\le t\le t_{k_{\mathrm{max}}}-\tau _e\). In the time expanded network, the travel time is coded in the graph structure and static methods, i. e. the Successive-Shortest-Path algorithm, can be applied in the time expanded network \({\mathcal {G}}^T\). Note that the size of \({\mathcal {G}}^T\) is significantly larger than \({\mathcal {G}}\), hence an increased computation time is expected.

To solve the nonlinear continuous model (3) numerically, we need to introduce discretization schemes for the differential Eqs. (3a) and (3b). For the partial differential Eq. (3a), we choose a staggered Lax–Friedrichs scheme on the grid \(x_{e,j}=j\cdot \Delta x\), where \(\Delta x\) denotes the space discretization. Furthermore, we use time steps \(t_n=n\cdot \Delta t\) of equal length with the discretization \(\Delta t= t_k - t_{k-1}\) for all \(1\le k\le k_{\mathrm{max}}\) corresponding to the discretization of model (6). Thus, the spatial discretization must be chosen to fulfill the stability (CFL)-condition (LeVeque (1992))

$$\begin{aligned} \frac{\Delta x}{\Delta t} { \left|{\max _{e\in E}\left\{ f_e^\prime (\rho _e) \left| \right. 0\le \rho _e\le \rho _{e,\text {max}} \right\} } \right|} \le \frac{1}{2} \, . \end{aligned}$$
(19)

This guarantees stability and convergence of the scheme according to Jiang et al. (1998), Kolb (2011). We fix an edge (and neglect the index e for a better readability) and choose the indices \(j \in \{2,\dots ,{ Nx }-1\}\) for the space discretization points and \(n \in \{ 0,\dots ,{ Nt }-1\}\) for the time discretization. Additionally, using the notation \(\lambda = \Delta t/\Delta x\), the evolution of the density discretized according to the staggered Lax–Friedrichs scheme reads

$$\begin{aligned} \rho _{0.5}^{n+1}&= \tfrac{1}{4} \left( 3 \rho _{0.5}^n + \rho _{1.5}^n \right) - \tfrac{\lambda }{2} \left[ f(\rho _{1.5}^n) + f(\rho _{0.5}^n) - 2 f(\rho _0^n) \right] , \end{aligned}$$
(20a)
$$\begin{aligned} \rho _{j-0.5}^{n+1}&= \tfrac{1}{4} \left( \rho _{j-1.5}^n + 2\rho _{j-0.5}^n + \rho _{j+0.5}^n\right) - \tfrac{\lambda }{2} \left[ f(\rho _{j+0.5}^n) - f(\rho _{j-1.5}^n)\right] , \end{aligned}$$
(20b)
$$\begin{aligned} \rho _{{ Nx }-0.5}^{n+1}&= \tfrac{1}{4} \left( \rho _{{ Nx }-1.5}^n + 3 \rho _{{ Nx }-0.5}^n\right) - \tfrac{\lambda }{2} \left[ 2 f(\rho _{{ Nx }}^n) - f(\rho _{{ Nx }-0.5}^n) - f(\rho _{{ Nx }-1.5}^n)\right] . \end{aligned}$$
(20c)

For the ordinary differential Eq. (3b), we choose a straightforward Euler-discretization. The initial conditions \(\rho _{j-0.5}^0\) are computed using cell averages for all cells \(j\in \left\{ 1,\dots ,{ Nx }\right\} \) and the boundary conditions are given by a discretization of \(f^{\mathrm{in}}\).

Note that with these numerical methods at hand, only model (6) can be solved to optimality, whereas model (3) is only a simulation. As we will see in the first example of Sect. 5.2, this difference in the numerical methods does not matter as therein the evacuation paths are unique.

For the second example, we concentrate on the influence of the objective functions on the evacuation routes and only secondarily on the difference of the models. We ensure the comparability of the results by optimizing first model (6) and then simulating the more realistic model (3) using the optimal solution. Doing this, we are able to compare the evacuation plans.

5.2 Comparison of traffic flow models

As a first numerical example, we consider the graph presented in Fig. 3 which is a subgraph of Fig. 6.

Fig. 3
figure 3

The source is located in \(u=27\) and the sink is \(v=26\), the red edges mark the main roads with double the capacity of the remaining edges

Full size image

The red edges mark the main path which coincides with the evacuation route of vertex \(u=27\). These edges have a larger capacity (\(\mu _e=2\) for \(e\in R={ \left\{ {e_{14}, e_{15}, e_{24}, e_{29}, e_{34}} \right\} } \) and \(\mu _{e_1} = \mu _{e_{42}} = 10\)) than the black edges (\(\mu _e=1\)) which represent side roads. The edges \(e_1\) and \(e_{42}\) are representing inflow and outflow edges of the network. All edges \(e\in E\) have the same length \(L_e=1\) and maximal velocity \(v_e^{\mathrm{max}}=1\). The maximal queue size for model (3) is (independent of the flow function) \(M_e=0\) for all \(e\in E\) and \(M_v=\sum _{e\in \delta ^+(e)} \mu _e\) for the dynamic network flow model (6).

We use this network to exemplify the influence of the flow functions on the evacuation time. As the path from vertex \(u=27\) to \(v=26\) is unique (the red edges), for a given inflow there is nothing to be optimized and we consider the results of a forward simulation of the following test cases only:

Test case 1::

Initially empty network, i. e. \(\tilde{\rho }_e(x)=0\), \(\tilde{q}_e=0\) for all edges \(e\in E\) with inflow

$$\begin{aligned} f_{e_1}^{\mathrm{in}}(t) = {\left\{ \begin{array}{ll} 2 &{} \text { if } t\le 9 , \\ 0 &{} \text { else} . \end{array}\right. } \end{aligned}$$
(21)
Test case 2::

Inflow constantly zero, i. e. \(f_{e_1}^{\mathrm{in}}(t)=0\), zero initial queues (\(\tilde{q}_e=0\) for all \(e\in E\)) and non-zero initial values for the densities

$$\begin{aligned} \tilde{\rho }_e(x) = {\left\{ \begin{array}{ll} 0.25 &{} \forall e\in E{\setminus }\left( R \cup { \left\{ {e_1, e_{42}} \right\} } \right) , \\ 1.5 &{} \forall e\in R \cup { \left\{ {e_1, e_{42}} \right\} } . \end{array}\right. } \end{aligned}$$
(22)
Test case 3::

Initial values according to test case 2, i. e. (22) and \(\tilde{q}_e=0\) for all \(e\in E\), and inflow according to test case 1, i. e. (21).

The first test case represents the situation usually considered in evacuation planning. The network is empty when the evacuation starts and as many evacuees as possible enter the evacuation route. The second test case evaluates the amount of time needed to clear the network of the background traffic which we assume to be present in average. The third test case combines the first two by considering an evacuation in case of initial traffic on the network. In test case 3, we expect congestion to occur according to the capacity constraints of the edges.

The evacuation times, i. e. the time the last evacuee leaves the network, are shown in Table 1. For the test cases 1 and 3, we also give the inflow to edge \(e_{42}\) in Figs. 4 and 5, respectively.

Table 1 Evacuation time for different test cases and traffic flow models
Full size table
Fig. 4
figure 4

Inflow to edge \(e_{42}\) for test case 1. Black, x DNFM. Red hat function. Blue LWR function

Full size image
Fig. 5
figure 5

Inflow to edge \(e_{42}\) for test case 3. Black, x DNFM. Red hat function. Blue LWR function

Full size image

For the first test case, we observe from Fig. 4 that all models show the same behavior. The rather large difference shown in Table 1 is due to numerical errors introduced by the diffusivity of the staggered Lax–Friedrichs scheme, which causes the density to smear out. As pointed out in Sect. 2.2, for the dynamic network flow model and the hat function we expect the results to coincide since there is no congestion in the network. For the LWR function as a flow function we expect those small differences because of the other two models being first-order approximations of the LWR function.

As shown in Fig. 5, the egress time increases for all three models due to the initial traffic in the network. Furthermore, we see that the effect is largest for the LWR flow function and smallest for the dynamic network flow model. This is due to the different handling of congestion. Whereas the dynamic network flow model (6) cannot handle congestion on an edge and stores the surplus in the vertex, model (3) is able to consider congestion on an edge. Therefore, the speed of the evacuees decreases, which slows down the evacuation process.

From Table 1, we additionally see that the evacuation of the background traffic and the evacuation of the danger zone cannot be considered separately, because the sum of the egress times of the first two test cases is for all models larger than for test case 3.

We conclude that on the one hand the separate handling from initial traffic and evacuation within an empty network is not appropriate. On the other hand, we observe that it is desirable to consider traffic flow models which are capable of handling congestion on the edges to get realistic lower bounds on the egress time.

Remark 2

We note that the dynamic network flow model (6) has been compared to a (validated) cellular automaton model (see Borrmann et al. 2012; Hamacher et al. 2010). The results have been also compared with some real observations. The study shows that the model (6) provides useful lower bounds and may serve as a good reference for more complex (simulation and optimization) models. Although a thorough validation of model (3) is work in progress. It might be assumed that the nonlinear model (3) may provide even tighter bounds.

5.3 Comparison of objective functions

In the second comparison, we deal with the different objective functions defined in Sect. 4. Therefore, we consider the hazard being driven by the wind in the two directions West and North (i. e. positive x-direction as well as positive y-direction).

We compute the optimal solution of the dynamic network flow model for all three objective functions, i. e. the quickest flow (14), the time-dependent (16) and the accumulated cost objective function (17), and compare the resulting objective values to the according objective values using the hat function and the LWR function. As pointed out above, we only consider a single path from a source to a sink in the optimal solutions.

Remark 3

Considering different (capacity constrained) paths from one source to a sink, a global optimization yielding system optima with respect to the according objective function is also possible. But especially while considering the time-dependent cost function (16) in some rare scenarios it may occur that some evacuees “take it for the team”, i. e. they are assigned to use higher contaminated edges than others to free capacity on lower contaminated edges. This can be avoided or at least restricted applying a presolving step. In this step the edges with a fatal contamination are identified and marked as unusable (e. g. by deleting them from the graph). The solution is then computed on the remaining network.

The results for all three models and all three objective functions are presented in Tables 2 and 3 separately for each wind direction. To compare all objective functions, we compute the evacuation time, i.e. the time the last evacuee reaches a safe location, not only for the quickest flow (14) but also for both other objective functions. Consequently, we also compute a cost for the quickest flow evaluating the time-dependent objective function (16) for the solution of the quickest flow. Note that while the evacuation time of the quickest flow does not change according to the wind direction its costs will do so.

Table 2 Evacuation times and objective value for time-dependent objective function (16) for the optimal solution of all three objective functions defined in Sect. 4 and hazard moving in positive x-direction (into the East)
Full size table
Table 3 Evacuation times and objective value for time-dependent objective function (16) for the optimal solution of all three objective functions defined in Sect. 4 and hazard moving in positive y-direction (into the North)
Full size table
Fig. 6
figure 6

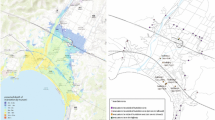
The red rectangle indicates the danger zone from where we assume the hazard to originate. The green vertices mark the safe locations nearest to the danger zone. The blue, magenta and dark green edges show the optimal paths corresponding to the objective functions (14), (17) and (16), respectively, leading from the red vertices in the danger zone to a safe location for wind in Eastern direction (i. e. positive x-direction)

Full size image
Fig. 7
figure 7

The red rectangle indicates the danger zone from where we assume the hazard to originate. The green vertices mark the safe locations nearest to the danger zone. The blue, magenta and dark green edges show the optimal paths corresponding to the objective functions (14), (17) and (16), respectively, leading from the red vertices in the danger zone to a safe location for wind in Northern direction (i. e. positive y-direction)

Full size image

Considering the wind from West to East (see Table 2; Fig. 6), we see that the three different objective functions yield different evacuation paths. While the quickest flow objective function (14) minimizes the evacuation time, it disregards the dynamics of the hazard. Thus, the contamination the evacuees are exposed to while following this path is very large compared to the time-dependent objective function (16). The latter objective takes the dynamics of the hazard into account and minimizes the exposure of the evacuees to the hazard. This results in paths with longer evacuation times. But by this the moving hazard is avoided in the best possible way. We see from Fig. 6 (green, dashed edges therein) that for the objective function (16) only the upper most vertex is evacuated to the upper safe location, while for the other vertices, it is more beneficial to be evacuated to the lower safe location.

Considering the objective function (17) we obtain from Fig. 6 (magenta, dashed edges therein) that the minimization in this case yields paths which are similar to the quickest paths (blue, dashed edges in Fig. 6) but are slightly more efficient in avoiding the hazard (cf. Table 2). Compared to the time-dependent objective function (16) it does not achieve comparably good results. Thus, we can say that the objective function (17) is an intermediate strategy. Concerning the hazard costs it performs better than the quickest paths as it takes the hazard into account. But it is outperformed by the time-dependent objective function as it neglects the dynamics of the hazard due to the time integration. The importance of the dynamics becomes obvious when comparing the safe locations reached by the different evacuation plans. An evacuation to the South is only executed when considering the time-dependent objective function (16). This is due to the fact that the hazard crosses the evacuation route (green path) (e.g. the one starting in the upper right vertex) after the evacuees have passed this part of the route. Thus, the route is safe. As the objective function (17) integrates the cost of each edge over time, it is unable to recognize such safe routes. Consequently, an evacuation to the South is omitted. This is due to the fact that the objection function (17) takes the hazard into account but neglects the dynamics of the hazard as it integrates over the time. Thus, it is not able to recognize that the hazard needs more time to reach the evacuation route of the upper right vertex according to (16) (green path) than the evacuees need to pass. Consequently, an evacuation to the South is omitted as there the direction of movement of the hazard needs to be crossed.

In Table 3 we compare the evacuation routes resulting from the optimization of the objective functions (14), (16) and (17) for a hazard being driven to the North by the wind. In this case, the hazardous cloud moves over the quickest evacuation routes (cf. Fig. 7 blue, dashed edges therein). Thus, the objective function (14) preforms worse concerning the amount of hazard taken by the evacuees. The objective function (16) again yields the evacuation routes, which have the highest evacuation time and are the most efficient in avoiding the hazard (cf. Fig. 7; Table 3). In contrast to the case with wind to the East, the objective function (17) now identifies for the lower left vertices in the danger zone the evacuation routes leading away from the moving hazard to be optimal. Consequently, the performance of (17) is better compared to (16) than in the case before.

Summarizing, we see that the safety of the evacuees can be improved by considering alternative objective functions such as (16) and (17). Furthermore, we deduce that detours, which enlarge the evacuation time, may also lead to a safer evacuation. Comparing the newly proposed objective functions (16) and (17) we conclude that the reduction of computation time when considering (17) is outweighed by the better quality of the evacuation route gained by the consideration of (16), when considering evacuation paths for vertices close to the danger zone.