Snapshots of mathematics teacher noticing during task design

Abstract

Designing a mathematically worthwhile task is critical for promoting students’ reasoning. To improve task design skills, teachers often engage in collaborative lesson planning activities such as lesson study. However, to learn from the process of lesson study, it is important for teachers to notice productively the concepts, students’ confusion and the design of the task. But what researchers mean by productive noticing varies. In this article, I present the FOCUS Framework which highlights two characteristics of productive noticing: having an explicit focus for noticing and focusing noticing through pedagogical reasoning. Using these two characteristics, I develop snapshots of noticing as a representation of practice to present a fine-grained analysis of teacher noticing. Through vignettes of teachers discussing the design of a task to teach fractions, I illustrate how two teachers’ noticing can be analysed and represented using snapshots of noticing. To conclude, I highlight what snapshots of noticing tell us about a teacher’s noticing and suggest ways to use these snapshots in future studies of noticing.

Snapshots of mathematics teacher noticing during task design

With the aim to promote students’ mathematical reasoning, recent reforms in mathematics education have positioned teaching as a deliberate practice (Ball and Forzani 2009; Lampert and Graziani 2009; Smith and Stein 2011). Enacting this type of teaching requires careful attention to lesson planning, in which teachers need to consider how the mathematics concepts are presented, the kind of tasks used in teaching, and how discussions are conducted during the lesson. As Smith et al. (2008) have asserted, orchestrating a mathematically productive discussion hinges on detailed lesson planning before the lesson is implemented. If lesson planning has a direct influence on what and how mathematics is taught, it is then critical for researchers to make teachers’ thinking visible so that they can support teachers in the process of lesson planning (Li et al. 2009; Pegg 1989).

An important aspect of lesson planning is to select, adapt, or design tasks to promote learning during teaching. A growing body of research suggests that it is critical that teachers engage students with appropriate tasks to develop mathematical reasoning (Anthony and Walshaw 2009; Brodie 2010; Sullivan et al. 2013). Thoughtful use of tasks provides ample opportunities for students to generalise, explain, and justify their mathematical ideas (Ball and Bass 2003; Breen and O’Shea 2010; Smith and Stein 2011; Sullivan et al. 2013). However, as Mason and Johnston-Wilder (2006) argue, there is often a gap between students working on the tasks and students learning from doing the task. Learning from doing the task is not trivial because students have to engage with the mathematical activities embedded in the task to become sensitised to the mathematical concepts. Therefore, teachers need to be aware of how mathematical concepts are presented through the design of the tasks to use them effectively (Mason and Johnston-Wilder 2006).

One way to support teachers to think more deeply about the design of a task is collaborative lesson planning (Alston et al. 2011; Lewis et al. 2009; Smith et al. 2008; Stigler and Hiebert 1999; Takahashi and McDougal 2016). Lesson study is a form of teacher professional development that involves collaborative lesson planning (Lewis et al. 2009). Even though the processes involved in lesson study may potentially enhance teachers’ thinking about content and pedagogy (Lewis et al. 2009), participation in the processes without an inquiry stance does not necessarily lead to teacher learning (Fernandez et al. 2003; Takahashi and McDougal 2016). Teachers often fail to see the content from a student’s perspective (Fernandez et al. 2003), or focus on superficial features of a task or lesson during planning (Choy 2013). Hence, it is important to understand what teachers notice about designing a task during collaborative lesson planning (Mason 2002; Sherin et al. 2011a).

This article extends previous research that focused on noticing in-the-moment of teaching and during post-lesson discussion by examining teachers’ noticing when they are planning a lesson. To bring task design into the realm of noticing, I built on Mason’s (2002) assumption that advanced preparation can help make noticing more productive, and developed the FOCUS Framework to characterise productive noticing. With regard to lesson planning, this framework pinpoints specific actions that teachers can take when designing a task to reveal students’ thinking. These specific actions are encapsulated in a theoretical model which draws attention to how teachers anticipate and analyse students’ reasoning during task design. By comparing teachers’ actions and decisions with the theoretical model, I develop snapshots of noticing to describe, analyse, and represent their noticing. In this article, I introduce the FOCUS Framework and snapshots of noticing, and illustrate how snapshots of noticing are used to compare what and how two teachers notice when designing a task to teach fractions of a set. The key research question was:

What and how do teachers notice when they design tasks that promote students’ mathematical reasoning during lesson planning?

Task design: a deliberate practice in teaching mathematics

This study presupposes that enacting productive mathematics teaching practices is “deliberate work” (Franke et al. 2007, p. 228), and some aspects of this teaching expertise can be planned (Stein et al. 2008). For example, orchestrating a classroom discussion involves teachers planning how students’ responses to tasks are used to initiate classroom discourses, and facilitating such interactions to shape their students’ reasoning (Stein et al. 2008). This work is challenging as teachers need to consider the use of discussion strategies. To support teachers in this work, Stein et al. (2008, p. 321) introduced five essential practices for teachers to master: anticipating, monitoring, selecting, sequencing and connecting. As Stein et al. (2008) highlight, each of these practices draws from and depends on the practices before it. Of particular interest in this article is the practice of anticipating students’ responses to the task, which emphasises planning as a means to reduce teachers’ reliance on improvisation during teaching (Smith and Stein 2011). More importantly, effective implementation of these five practices are predicated upon a well-designed task, which engages students in communicating their mathematical reasoning. It is critical, therefore, for teachers to attend carefully to how they design or use tasks to promote student reasoning.

Considerations for using mathematical tasks

There are three important considerations for designing or adapting a task. Firstly, the goal of a mathematical task is to develop students’ understanding of mathematical concepts by engaging them with mathematical processes. This calls for teachers to maintain a clear focus on the mathematics involved (Anthony and Walshaw 2009; Sullivan et al. 2013). Focusing on mathematics goes beyond asking students to work on a series of computations. Instead, teachers who focus on the mathematical aspects of a task, do so by identifying the key mathematical ideas to be weaved into the task, and provide opportunities for students to do mathematics (Anthony and Walshaw 2009; Smith and Stein 1998; Sullivan et al. 2013). A good starting point for teachers to think about task design is students’ misconceptions. By analysing students’ misconceptions, teachers can begin to conceive how tasks may be used to provide opportunities for students to learn from their mistakes (Anthony and Walshaw 2009).

In line with this, Yang and Ricks (2012) detail how Chinese teachers design a task using the “Three Points”: the “Key Point”, “Difficult Point”, and the “Critical Point” (p. 54). The Key Point is the main mathematical concept of the lesson, and the Difficult Point is the set of cognitive obstacles, persistent errors, or misconceptions that students may have when learning the concept. By anticipating students’ Difficult Point, teachers can include features in the tasks to support their learning. The Critical Point is the “heart of the lesson”, which highlights the approach teachers use to support students in overcoming their Difficult Points (Yang and Ricks 2012, p. 43). Collectively, the Three Points provide a useful frame, similar to the milieu of mathematics-student-teacher (Brousseau 1997; Mason and Johnston-Wilder 2006) for teachers to examine the design of a task before its implementation.

Secondly, it is crucial for teachers to deliberate on how mathematical thinking is embedded in the instructions of a task (Mason and Johnston-Wilder 2006). The intended mathematical activity of a task which consists of the actions and thoughts may not always correspond to what students do. For example, students may draw different triangles (action), measure the interior angles in a triangle (action), and calculate the total interior angle sum (action), without realising that their teacher’s intention was to get them to conjecture about the constant sum of the three angles (action and thought). Hence, a mathematical activity may not have occurred even though the task has been completed correctly (Mason and Johnston-Wilder 2006). Mathematics tasks should be carefully designed to direct students’ attention on the mathematical ideas and structures as they work on the tasks. Carefully designed mathematics tasks provide opportunities for students to decide on their problem solving approaches, and deliberate on the quality of their own responses (Stein et al. 1996) without always relying on teachers to provide directions (Anthony and Walshaw 2009). This type of tasks are not only characterised by their “higher-level cognitive demands” (Smith and Stein 1998, p. 348), but also incorporate students’ current mathematical background to maximise learning (Brodie 2010; Mason and Johnston-Wilder 2006).

Lastly, it is necessary for students to make their mathematical thinking as visible as possible (Lesh et al. 2000). Students engage successfully with tasks when they are able to express their thinking explicitly (Doerr 2006) using multiple representations (Anthony and Walshaw 2009; Sullivan et al. 2013). By considering the use of multiple representations, teachers can then have a better sense of what and how students are thinking about the mathematics (Doerr 2006). As Anthony and Walshaw (2009) argue, working with different representations may help students develop their mathematical proficiencies. This is consistent with what Thomas (2006, p. 233) called representational versatility or “the ability to work seamlessly within and between representations, and to engage in procedural and conceptual interactions with representations”. To develop representational versatility, the choice of representations or models should relate directly to the mathematical concepts embedded in the task (Sullivan et al. 2013). Given that representational versatility is a strong indicator of student understanding, teachers are encouraged to create tasks that engage students in using a wide variety of representations to develop their fluency in using and translating between representations (Anthony and Walshaw 2009; Sullivan et al. 2013).

Anticipating students’ responses to task

The design of the task, as Henningsen and Stein (1997) point out, is necessary but not sufficient for enhancing student reasoning. For example, Smith and Stein (1998) found that it is critical for teachers to support student reasoning by “pressing” them to “provide meaningful explanations or make meaningful connections”, without “reducing the complexity and cognitive demands of the tasks” (p. 546). This corresponds to what Mason and Johnston-Wilder (2006) termed as “scaffolding and fading” (p. 83). However, building on students’ thinking is often viewed by teachers as spontaneous rather than deliberate (Smith and Stein 2011). To reduce the improvisation aspect of supporting students’ reasoning, it is important for teachers to anticipate how students may perceive the task mathematically (Lampert 2001; Smith and Stein 2011; Stein et al. 2008) by interpreting the task from a student’s perspective (Fernandez et al. 2003).

Anticipating students’ responses requires teachers to focus on how students understand and approach a mathematics task by considering the strategies students may use and the possible confusion they may have (Smith and Stein 2011; Stein et al. 2008). This is similar to how Chinese teachers think about task design using the Three Points (Yang and Ricks 2012). This work is challenging because teachers have to draw on their mathematical knowledge for teaching (Ball et al. 2008), knowledge of what their students know about the topic (Stein et al. 2008), and their knowledge of students’ common misconceptions. As Mason (2002) argues, systematic reflection is an important practice for anticipating students’ thinking. Therefore, it is important for teachers to focus on what students have met before coming to the lesson.

The notion of a met-before (McGowen and Tall 2010) is useful for teachers when anticipating students’ responses. A met-before, according to McGowen and Tall (2010), is “a mental structure that we have now as a result of experiences we have met-before” (p. 171), and refers to the knowledge or beliefs one may hold based on previous experiences. However, unlike a misconception, a met-before may promote or hinder the learning of a concept. For example, a part-whole conception of fractions may support students in extending the idea of fractions to describe part of a set of discrete objects; but the concept image of a circle divided into four equal parts (See Fig. 4), which reflects a part-whole conception of fractions, may also hinder students in using fractions to describe part of a set of objects. Hence, teachers should be mindful of the met-befores associated with a concept (McGowen and Tall 2010) to better understand students’ confusion when they attempt a task.

Mathematics teacher noticing

Being mindful of students’ thinking and having a different act in mind lies at the heart of noticing (Mason 2002). This notion of noticing highlights the importance of enhancing perception and raising awareness. Mathematics teacher noticing is also conceptualised as a set of three inter-related processes: seeing, interpreting, and deciding to respond to students’ thinking (Jacobs et al. 2011a). This involves teachers attending and making sense of instructional details to make instructional decisions. Noticing can enhance mathematics teaching practices (Mason 2002) and has been conceived as an emerging construct to describe teaching expertise (Sherin et al. 2011b). Many researchers examined what teachers notice from video clips of lessons (Star et al. 2011; van Es 2011); whereas others, such as Sherin et al. (2011c), captured what teachers notice in-the-moment during lessons. In both approaches, teachers were shown clips of classroom teaching and were asked to highlight certain features of the instruction (Sherin et al. 2011c; Star et al. 2011; van Es 2011). However, these approaches focus mainly on noticing during or after the lesson. In this article, I focus on noticing before the lesson by examining what and how teachers notice when designing tasks.

Despite the apparent simplicity of the construct of teacher noticing, the ability to “notice productively” is both difficult to master, and complex to study (Jacobs et al. 2011, p. xxvii). Moreover, what constitutes productive noticing varies and remains uncertain. While teachers notice all the time, noticing is considered to be productive only if teachers make instructional decisions that promote students’ reasoning. For example, teachers often fail to notice the mathematical concepts or processes embedded in the tasks (Star et al. 2011; Vondrová and Žalská 2013). Or they may also be distracted by noticing features that have no direct impact on enhancing mathematical thinking (Ball 2011; Star and Strickland 2008). Furthermore, teachers may not relate students’ strategies to the key mathematical characteristics of the problem although they can describe the specific strategies used by students (Fernandez et al. 2012). This article offers the FOCUS Framework as a means to characterise productive noticing and study teachers’ noticing when they plan, teach and review lessons.

The FOCUS framework: characterising productive noticing

The main challenge to studying what teachers notice is that people attend to different things simultaneously with varying levels of details (Mason 2011). To deal with the complexity of describing and analysing teaching, Lampert (2001) proposed a photography metaphor to represent how a teacher can actively zoom in and zoom out, across time and relationships, to focus on different aspects of teaching. Adopting a similar metaphor, I view teacher noticing as taking mental snapshots of instructional episodes that focus on different aspects of teaching and learning. The FOCUS Framework highlights two critical characteristics of productive noticing: having an explicit focus for noticing (what to notice) and focusing noticing through pedagogical reasoning (how to notice). In this section, I briefly describe the development of the FOCUS Framework, before I elaborate on the two key characteristics of productive noticing, and present snapshots of noticing as an analytical representation to study noticing.

The development of the FOCUS framework

Using a design-based approach (Zawojewski et al. 2008), the FOCUS Framework was developed from data collected during a three-phase doctoral research on teacher noticing during lesson planning, teaching and post-lesson discussion. All three Singapore schools which participated in my study were familiar with lesson study, which provided a way to study how teachers plan, teach and reflect on lessons. The detailed research design has been described elsewhere (Choy 2015), and here, I focus on how the initial FOCUS Framework was conceived, tested, and refined.

Data from all three schools were collected and generated through voice recordings of the lesson study discussions and video recordings of the lessons. All the recordings were reviewed with the field notes taken, and noteworthy segments were marked for transcription to enable further analysis. These segments were characterised by discussions about the Three Points, which were the key areas for investigation in this study (Brousseau 1997; Cohen et al. 2003; Yang and Ricks 2012). Verbatim transcripts of the marked segments were produced, and these included pauses (…), and ungrammatical or colloquial language which were not edited. Words were added into the transcript to enhance clarity and these were indicated using angled parentheses [], and actions, if any, were indicated within curved parentheses ().

Consistent with the design-based research paradigm, data analysis occurred at two distinct levels: An ongoing data analysis, which informed the development of the FOCUS Framework, and a retrospective data analysis at the end of each data collection phase. Using a “thematic approach” proposed by Bryman (2012, p. 578), findings related to teachers’ noticing were developed by identifying codes and themes related to elements of productive mathematical noticing. The thematic approach was useful because it helped summarise the key features of a large body of data. I used the Three Point Framework (Yang and Ricks 2012) and the three processes of noticing, (Jacobs et al. 2010) to code and develop themes from the selected segments. The themes observed were then reviewed in relation to other selected episodes. The systematic thematic approach taken helped to ensure the coherence and consistency of the themes generated (Braun and Clarke 2006).

The initial FOCUS Framework was developed from the themes generated during data analysis. These themes together with the initial FOCUS Framework were then revised and tested concurrently as I worked with teacher participants to enact lesson designs in the other phases. To confirm or refute the themes, the selected transcripts and video clips were read and viewed repeatedly. Possible characteristics of productive noticing which either support or refute my analysis were highlighted. These characteristics were then compared with the tentative characteristics of productive noticing in the initial FOCUS Framework. Through these iterations of testing and refutation, the framework was revised and then used to analyse the episodes to check for interpretative consistency. My analytic approach drew on the method of Constant Comparison (Cobb and Whitenack 1996; Glaser 1965) which is also used by other researchers in design-based research (Cobb and Gravemeijer 2008; Zawojewski et al. 2008). Two key characteristics of productive noticing were formulated from the themes at the end of the third phase: having an explicit focus for noticing and focusing noticing through pedagogical reasoning.

Having an explicit focus for noticing

Research has generally focused on developing teachers’ ability to notice a wide range of classroom features without specifying what they should notice (Jacobs et al. 2010; Star et al. 2011). Some findings, such as Star et al. (2011), suggest that it is unclear whether an explicit focus is helpful for enhancing teacher noticing; while others, like Goldsmith and Seago (2011), highlight that teachers begin to notice specific aspects of students’ thinking when given an explicit focus. However, teachers may still find it challenging to sieve out and reflect on critical details amongst the ‘buzz’ in the classroom when asked to focus on a specific aspect of teaching. Nevertheless, the FOCUS Framework suggests that an explicit focus is useful for supporting teachers to notice relevant instructional details. Drawing and expanding on Yang and Ricks (2012) framework, I identify two key foci for noticing: The Three Points as well as the alignment between these three points. The alignment of the Three Points refers to whether the teacher’s course of action (Critical Point) targets students’ confusion (Difficult Point) when they are learning the concept (Key Point). The process of aligning the Three Points is often challenging as it requires teachers to ascertain the linkages between the Three Points (Choy 2014; Yang and Ricks 2012).

Focusing noticing through pedagogical reasoning

This alignment between the teaching approach and students’ confusion is not intuitive, and has to be mediated by the teacher’s pedagogical reasoning. By pedagogical reasoning, I refer to how teachers justify their instructional decisions or claims about students’ thinking based on what they attend to. This emphasis on pedagogical reasoning is consistent with the argument made by Goldsmith and Seago (2011) that it is the “artful” use (p. 184) of classroom artefacts which presents a way for teachers to justify their claims about students’ reasoning. Similarly, van Es (2011) highlights the need for teachers to analyse their observations and provide the evidence or justification for making an instructional response. Pedagogical reasoning has also been identified as the key mechanism in making sense of the observations to make instructional decisions (Barnhart and van Es 2015; Choy 2014; Stockero 2014). Therefore, when teachers focus their noticing by pedagogical reasoning and justify their claims or decisions using their observations, they are more likely to make instructional decisions that promote student reasoning.

Representing teacher noticing using snapshots of noticing

The FOCUS Framework provides the basis for a theoretical model of noticing that describes what and how a teacher can notice productively when learning from practice (See Fig. 1). It maps a teacher’s noticing processes (attending, making sense, and responding) through the three stages of a lesson cycle (planning, teaching, and reviewing) to the three key productive practices for mathematical reasoning (designing lesson to reveal thinking; listening and responding to student thinking; and analysing student thinking). Functioning as a representation of practice (Grossman and McDonald 2008), the model describes a theoretical process of productive noticing which highlights explicitly the three focal points and suggests how the alignment between them can be achieved through specific actions taken by a teacher.

Fig. 1

Theoretical model for productive noticing (Choy 2015, p178.)

For example, in Fig. 1 (left), a teacher who notices productively should work through the following steps when planning a lesson:

• 1. Identify specifics of the mathematical concept for the lesson;

• 2. Recognise what students find difficult or confusing about the concept;

• 3. Analyse why students find the concept difficult or confusing;

• 4. Analyse possible ways to address students’ confusion when learning the concept;

• 5. Develop and implement a high-level cognitive demand task (Smith and Stein 1998) to target students’ confusion about a concept.

Steps 1 and 2 can broadly be subsumed under the attending component of noticing; steps 3 and 4 under making sense; and step 5 under responding. By comparing a teacher’s noticing with the theoretical model, a snapshot of noticing is developed. This provides a picture of what and how the teacher notices when planning a task.

The main aim of this article is to offer snapshots of noticing as a means for describing and studying noticing. Snapshots of noticing provide a wide-angle view of a teachers’ noticing through the lesson cycle, as well as a close-up view of noticing at each stage of the lesson cycle. In the next section, I set the context for the two vignettes involving two teachers, Anthony and James, during task design. I then illustrate the use of snapshots of noticing to represent, describe and analyse their noticing when designing a task.

Two vignettes: Anthony and James

Context of the vignettes

Six teachers from Greenhill Primary School (a pseudonym) in Singapore participated in this study. Greenhill Primary School is a government, co-educational single session primary school situated in the eastern part of Singapore. The school enrolment was around 700, which was smaller than the average size of a regular primary school in Singapore. The mathematics lesson study group was recruited and six teachers volunteered for the study: Kirsty (facilitator); Cindy; Flora; Rani; Anthony; and James (research teacher). Table 1 presents the profiles of these teachers.

Table 1 Profile of teacher participants for this study

Here, I focus on a subset of recordings taken from five lesson study sessions which occurred during the second phase of my study. The sessions were of different durations ranging from an hour to two hours, but all the five sessions were used for collaborative planning of the lesson. In this article, I focus on discussing Anthony’s and James’s noticing as they collaborated with other teachers to design the main task for the lesson.

In the next section, I analyse Anthony’s and James’s noticing and present their snapshots of noticing for comparison.

Snapshots of Anthony’s non-productive mathematical noticing

In this vignette, Anthony identified a specific difficulty that students might have when they need to sum up fractions with different denominators:

• 1. Researcher: So, usually, how do you show 2/3 + 1/4?

• 2. Anthony: So, if we follow exactly the textbook, what we are using now. The textbook tries to draw a complete whole, and cut into parts. They didn’t explain, but just give the LCM [Lowest Common Multiple]. Students start to be confused, why give 12 parts and not 24 or 18 parts?

  • I (Researcher) asked Anthony to show the teachers how the textbook presents the explanation for 2/3 + 1/4. He drew the following diagrams on the board.

    

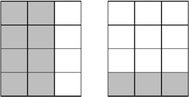
• 3. Anthony: So the children will ask, why do you give me 12 equal parts? Why didn’t you give me 6 or 18 equal parts? So, Ah… we look at the multiples of 3, 6, 9, and so on… at the end, we have 4, 8, 12… Coincidentally, we find just the lowest common multiple, so we have to use is 12. So, to me, this has to come back to 2/3 of a set of 12, and this is 1/4 of a set of 12. So, this goes back to the same problem [referring to the fraction of a set] and we are turning around the same problem.

• 4. Researcher: So how do you help them to bridge the gap?

• 5. Anthony: No choice… Because they are not in the same family, we want them to do some transaction, or you want to mix them together, we need to make them look alike. Like I told them, you come from Thailand, you come from China, you speak your own language, you cannot stay in Singapore. Then what to do? Follow our language lah. Speak English. English is our common language. In this case, 12 is our common language, so we use 12.

• 6. Researcher: So diagrammatically… the problem is that we start with the 12 units. If we don’t start off with the 12 units, how do we explain that it is 12?

• 7. Anthony: They will tell me this… My teacher tell me… this one, you multiply me and I multiply you. [Laughter] So, if the question is not that big, sometimes they are given 5/6 and then 4/9. They start to multiply 9 with 6 and 6 with 9 [yeah! That’s right?] and the numbers get bigger and bigger? Then they don’t know how to do.

• 8. Researcher: Did they know why they have to do it this way?

• 9. Kirsty: No.

• 10. James: [Imitates students] My teacher told me.

• 11. Anthony: They will say, because you told me, they are not in the same family, so I had to make them alike. So, if I have denominators of the same kind, it is easier for us to do. So, they forget about the lowest common multiple and then they just make the numbers bigger and bigger. There are cases like 12 and 9, they multiply the numbers together to make 108. In the end, they do not know how to reduce to smaller fractions.

• 12. Kirsty: Actually, I agree with him. This problem is very common.

• 13. Anthony: This problem is really very, common. Even the best children also end up with this problem.

• 14. Kirsty: Because they fail to understand the factors and multiples well. They don’t know the least common [multiple]…

By highlighting how the textbook presented the explanation for summing two fractions (Lines 2 and 3), Anthony focused on one of the three points, and described it in detail. He perceived that the lack of explanation when using the lowest common multiple (LCM) is a Difficult Point for students (Line 2). Anthony could describe the difficulty from his students’ perspective (e.g., “So the children will ask, why do you give me 12 equal parts? Why didn’t you give me 6 or 18 equal parts?”), and his attention to this confusion was further demonstrated by his elaborated students’ responses (Line 11).

However, Anthony’s noticing was considered non-productive according to the FOCUS Framework because he did not analyse the reasons for the difficulty, nor considered other possible explanations for the need to change denominators. Even though he suggested the use of area models to explain the operation, Anthony appeared to have only considered the seemingly arbitrary division of the whole into 12 equal parts, without connecting this to the original issue he raised—that students might add 2/3 and 1/4 to give 3/7. Similarly, while the other teachers resonated with him on the prevalence of students’ lack of understanding of the rule to change denominators (Lines 9 to 14; Kirsty—Line 12 and 14; James—Line 10), they also focused mainly on students’ lack of procedural knowledge, and did not consider how the area model could have led to students’ erroneous answer shown in Fig. 2.

Fig. 2

A possible student error on the use of area model

Anthony and the other teachers did not consider the possibility that students might still make the same mistake, even though they have changed the two fractions to the same denominator. Therefore, they missed an opportunity to gain new insights into models of fraction which could have helped them think more carefully about the use of representations. Furthermore, Anthony decided to use an analogy to explain the rule of changing denominators to the same number. Although the analogy is helpful in reminding students of the need to change the denominators, it lacks the mathematical connection to explain the procedure. So, Anthony’s explanation did not target students’ confusion about the concept. The alignment could have been enhanced if he had considered different explanations for the rule of common denominators (Mason 2002), and had analysed them to justify their effectiveness.

The above vignette highlights Anthony’s ability to identify and recognise specific details regarding the confusion associated with the concept. However, he did not analyse the reasons for the confusion, nor did he consider other possible ways to support students in overcoming the confusion. Anthony’s snapshot of noticing is represented in Fig. 3 (centre).

Fig. 3

Snapshots of noticing (left—theoretical; centre—Anthony’s; right—James’)

Snapshots of James’ productive mathematical noticing

In contrast, James explained how a met-before (McGowen and Tall 2010) of “fraction as part of a whole” may hinder students’ understanding of ‘fraction of a set’:

• 16. James: I think the objective for fraction of a set is for students to see, to interpret fraction as part of a set of objects. Previously, the fraction [concept] they learnt is more of part of a whole. They are very used to thinking about part out of a whole. Now that we give them a lot of whole things, they cannot link that actually these fractional parts can refer to a set of whole things also. So I think, to me I feel that the connection that is missing, is that, how this fraction concept—which is part of one whole which they have learnt so far—can be linked to whole things. For example, previously we used to teach fractions as parts of a cake or pizza. From that, how can it be that we have many pizzas, we don’t cut out the pizza, there is a fraction of the pizzas. I think they cannot make a link there…

• 17. Teachers: [Inaudible discussion.]

• 18. James: For me, the main difficulty is to relate part of a whole into items that are “whole” but you take a fraction out of it. So, I think that’s where the confusion comes. [After a while, James gave a more concrete example to illustrate what he meant.]

• 19. James: For example, if you say 3/4 of the cats are… [Imitating the students] Ah… you cut the cat into three quarters? (Laughter.) Cut each cat into four parts. So, yeah, but based on what they learnt so far, that may be the first thought they might have. To them, fraction could still be cutting up into parts. Whereas, fractions of a set, we leave the things as a whole entity but we look it as a collection of things. …, that would be the main difficulty.

Here, James not only described specific details about the concept (“… to interpret fraction as part of a set of objects.”) and the confusion (“They are very used to thinking about part out of a whole.”), but he could relate these aspects to his knowledge and experience. James suggested that students may only perceive fractions as “part of a whole” (See Fig. 4); and highlighted how the examples used by teachers to teach fractions (“…teach fractions as parts of a cake or pizza…”) may have been stuck in the students’ minds.

Fig. 4

Fractions as part of a whole

According to James, students’ perception of fraction as “part of a whole” was in conflict with the concept of fractions as part of a set of objects. The link between students’ image of fraction as “part of a whole” (Fig. 4) and their difficulty to grasp the idea of ‘fraction of a set’ was further elaborated by James using two examples—the pizza and the cat (Lines 16 and 19). He drew teachers’ attention to how students think about fractions with his vivid example of “cutting up the cat” and illustrated how students might conceive fractions as “cutting up into parts” (Line 19). James reiterated the same point when Kirsty asked whether students could identify what is 1/4 of a set of eight circles during another discussion.

• 20. Kirsty: What I was thinking is… let’s say, I have 8 circles right… I leave all of them blank, and I tell them to shade to show 1/4 of the circles is shaded red…

• 21. James: Oh… My first thought is…

• 22. Kirsty: Would they be able to know that actually 2 will be shaded out of the 8?

• 23. James: They will cut out every circle and circle 1/4…

  

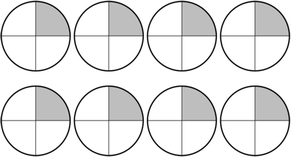
• 24. Kirsty: Oh… they will?

• 25. James: That’s my first thought that the students will do…

In this short exchange, James reiterated the confusion when he anticipated how students might respond to the question posed by Kirsty. This (Line 23) and the other examples (Lines 16 and 19) demonstrated James’s understanding of the confusion. James’s noticing of students’ possible confusion could potentially enhance students’ thinking because it helped other teachers to focus on the concept and confusion when designing the task. The link between the concept and confusion was further heightened when James highlighted another example from the textbook (Line 26), before suggesting a possible approach:

• 26. James: I think that the difficulty is putting the things into the sets. And imagining that each of this set is one part. The textbook makes it look like a very good way to teach this, they arrange the items very neatly into visible lines like this, for example, like this one, 2 fifths of the circles are yellow. It is very clear and you can see two sections. But without the pictures, the children cannot imagine neatly like that.

  

• 27. Flora: Pictorial to abstract.

• 28. James: So, when we are doing this, they can get it. Because it is very clear, because visually, yellow colour two sides, purple colour three sides, so, total you have five rows and all that. So, very clearly they can tell you, but once without pictorial, they get lost already. So I think it’s the transition from the pictorial to abstract.

• 29. Cindy: Actually, we usually use the colour cubes as manipulative…

• 30. James: Here, we start with concrete and then moved to pictorial. From concrete to pictorial, they are still okay. Once we move to a non-picture, they cannot imagine already.

• 31. Cindy: Yes…

• 32. James: Especially when some of the numbers, we are talking about something like 36 pupils in the class, 1/3 of them, too many for them to imagine in their mind, how to arrange into something like that. So, I think that’s the biggest difficulty. So, if we just talk about this part, they can understand, even if bigger numbers, they can still see and can tell… oh ¼ of the cups, how many are there? Oh… 4… With the colours everything there. Once, there are no more pictures, they cannot make it.

• 33. Flora So, when you give them concrete right? Did you tell them how to arrange it or they themselves will arrange it? And then, maybe we could ask them to articulate why they arrange it that way. You know like, they then probably say, if there are 22 cubes, then they know they can use their multiplication tables and they group it into groups of 2 or… you know. Maybe we find out what they are thinking… you know… and bring it to the abstract part. So, they have the items already, but they have the numbers, then they can visualise and link it later?

Unlike Anthony, James went beyond the surface features of the textbook’s representations and directed the teachers’ attention to how the diagrams might have made it obvious for students to see the partitioning. He hypothesised that students might find it difficult when the diagrams were removed (Lines 28 and 32). This prompted Flora to suggest getting students to “arrange” the items into the partitions and explain why they are arranged that way (Line 33). James went on to elaborate on Flora’s suggested approach:

• 34. James: I think the confusion part also comes when… for example… this example here… we tell that … 1/4 of the cups are yellow and then the answer is 4 cups. Huh…1/4 and then why got 4 in the 1/4? They cannot link between the… the 1/4 in their mind is still 1/4 of a whole… and then there is this four cups, four whole things… and so they cannot link.

• 35. Researcher: So, what is the key thing that can help them to link these two ideas?

• 36. James: I was thinking whether we can put it into… something more familiar because… eh… they have learnt models, how to represent questions in model also, so, I was just looking at this… instead of just doing this, could we box the whole thing up instead (Draws Fig. 5). And to them, they are familiar with the part-whole model… a whole box is a whole… so while keeping the items inside and we draw the box… and… and… yes… we tell them that this looks familiar, and it looks like the model as a whole, right? These lines can be the partitioning of the whole model. While doing that… they can still see that the 4 items are still inside the parts. I don’t know whether that can help them to make the connection that if this 1 box is 1/4 of the whole, inside that box, I have four things. And this is where the 4 came from?

  Fig. 5

  

  Use of the model method to show partition of a set of objects

• 37. Flora: Would they have… the experience of drawing the model for this? Because the whole and the fraction, they don’t get the connection, right?

• 38. James: If we tell them to draw us a model of 1/4, I think they can at least can draw the model and partition it 1/4 one part. Because there’s still that concept of whole. But it’s the… when you put in all the items, then they don’t know what to do with it already.

James not only suggested using the part-whole model method (familiar to all students in Singapore) to direct students’ attention to the idea that one partition of the whole (a fraction) can contain “whole objects” (Line 36), but also explained why this is possible (Lines 34, 36, and 38). His suggested approach built on student’s image of fraction as “part of a whole” by using a different representation of the part-whole concept (See Fig. 5). This provided a scaffold for students to extend their notion of fractions by emphasising fraction as a means to express the relationship between a part and its whole. As explained by James, the part-whole model was used to support students in overcoming their confusion. What James noticed informed the design of the task, and his noticing is characterised as productive. This is because he not only identified and analysed the specifics of the Three Points, but more importantly, he considered the reasons behind students’ confusion, and examined different instructional alternatives to clear up the confusion. A snapshot of James’ noticing is shown in Fig. 3 (right).

Snapshots of teacher noticing: what they tell us about a teacher’s noticing

In summary, I introduce the FOCUS Framework to reflect two critical characteristics of productive teacher noticing: the focus for noticing and the focusing of noticing. In this article, I extend extant research on teacher noticing to examine what teachers notice when designing a task. The two characteristics of productive noticing are used to develop snapshots of noticing for researchers to analyse teacher noticing at two levels.

First, the snapshots provide a fine-grained analysis of the key competencies of teaching, which includes listening and responding to students’ thinking and reflecting about students’ thinking (See Fig. 1). Each snapshot of noticing represents a teacher’s noticing in terms of what was noticed, and how the noticing occurred. Second, these snapshots can be combined to give a portrait of teachers’ noticing when interacting with students and mathematics across the three stages of a lesson cycle. Refer to Fig. 1 for a simplified theoretical portrait of noticing, or refer to Choy (2015, p. 236) for a more elaborate example of a portrait of noticing.

Portraits of noticing are representations of practice (Grossman and McDonald 2008) which can be used to analyse teaching by documenting the processes of noticing through the lesson cycle. They present a new perspective on teacher noticing that is different from the levels of noticing expertise developed by van Es (2011), and do not assess teachers’ ability to notice through scoring using a rubrics (Jacobs et al. 2011a). Instead, these multiple snapshots show teachers’ processes of noticing as they go through the lesson cycle. Collectively, the snapshots can pinpoint specific actions for teachers to take when developing their noticing expertise. By examining different portraits of noticing, researchers have access to a more dynamic and comprehensive way of characterising teacher noticing.

As a research tool, snapshots of noticing can be used by mathematics educators to analyse and model a teacher’s noticing processes during lesson planning, teaching, and post-lesson discussion. These snapshots document a teacher’s focus in noticing and the processes involved in noticing. Patterns in terms of what and how a teacher noticed can be seen from the snapshots. These patterns provide researchers a way to infer a teacher’s knowledge, beliefs and goals for teaching which can be used to account for why the teacher noticed the way he or she did. The snapshots provide researchers useful insights into the construct and mechanism of productive noticing.

In addition, the snapshots of noticing can be used by teachers for self-reflection. By examining their own snapshots, teachers can identify the gaps in their noticing and consider ways to improve their teaching practices. The use of the snapshots thus provides a way for teachers to be “methodical without being mechanical” (Mason 2002, p. 61) when reflecting on their teaching practices. Although the theoretical model may be too simplistic for modelling actual classroom interactions, its simplicity offers a starting point for teachers to examine their own teaching practices and consider alternative teaching strategies.

The FOCUS Framework was developed in the context of lesson study groups, and it remains to be seen whether the framework can be applied to other instructional contexts. Future studies could also explore the use of these snapshots to support teachers in honing important teaching competencies, such as designing a task or orchestrating a discussion. Notwithstanding the limitations of a small-scale design-based research study, the FOCUS Framework offers a reasonable model of productive noticing which can be used to develop snapshots of noticing for describing teachers’ noticing through the lesson cycle.