A Novel Area Coverage Technique for Maximizing the Wireless Sensor Network Lifetime

Abstract

This paper presents a mathematical model to geometrically optimize the density of active sensor nodes in a wireless sensor network (WSN) using concentric hexagonal tessellations and the concept of coverage contribution area for randomly deployed nodes in the field of interest (FOI). Some of the WSN applications, such as environmental monitoring, security, surveillance and health care require the target area to be covered a number of times. This number is denoted by a variable $k$ and is known as the ‘degree of coverage.’ The problem of achieving required degree of coverage is formulated as $k$-coverage problem. An algorithm has been proposed to generate maximum number of disjoint-independent subsets of sensor nodes as an optimized solution to the $k$-coverage problem, along with maximizing the WSN lifetime. Superiority and efficacy of the technique have been verified by mathematical analysis as well as simulations carried out using MATLAB.

1 Introduction

Wireless sensor networks (WSNs) consist of low cost, indispensable, low powered pint-sized sensing devices called sensor nodes [1]. Sensor nodes can be either static or mobile. A sensor network can have three scenarios viz. network with only static sensor nodes, network with only mobile sensor nodes and a network with a combination of both static and mobile sensor nodes. In the present research work, only the static aspect of sensor nodes is explored. The small size, low cost and indispensable nature of sensor nodes allows the WSN to be scalable and flexible. This makes them well suited for harsh and remote regions. However, being battery operated limits their capabilities and puts a constraint on energy usage. This leaves the WSN with two options in order to be able to serve the application for the required period of time viz. (i) periodic replacement or recharging of batteries and (ii) implementation of energy-conserving algorithms. Periodic replacement and recharging of batteries are often not feasible as because the sensor nodes are usually deployed in a large number at unreachable and hostile locations. Therefore, it is very crucial that the WSN must utilize the available energy judiciously, through power saving algorithms to avoid the untimely failure of sensor nodes.

Present paper targets the coverage problem in WSNs. Coverage provided by the sensor nodes is regarded as a prime performance metrics of quality of service (QoS) delivered by a WSN [2]. Although sometimes, coverage is often traded for network lifetime. However, this trade-off may not be beneficial for applications where prolonged lifetime with compromised coverage shall not serve the required purpose [3]. Therefore, an optimized, energy-efficient coverage of the FOI, meeting the constraints on the lifetime of a WSN is the focus of the present study.

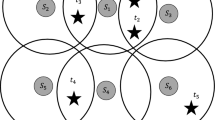
Figure 1a shows that a triangular area $A$ is completely covered by a node $n_1$ of sensing radius $r$. However, as seen in Fig. 1b the same area is completely covered by two nodes, namely $n_1$ and $n_2$ each of sensing radius $r$. The circular region around a node signifies its sensing region as per the Boolean sensing model [4]. In Fig. 1b, every point in $A$ is covered twice using two nodes. This is referred to as redundant coverage with degree of coverage $k$ = 2. Many applications specifically require redundant or $k$-coverage. This is due to the reasons like providing fault tolerance to the network, achieving intrusion detection, increasing the reliability of sensed data, etc. Coverage can be achieved in two ways, i.e., deterministically and non-deterministically. The former process involves the deployment of nodes at pre-determined locations in the FOI in a controlled manner. Pre-planned deployment strategies do reduce the deployment cost. The latter involves random scattering or random deployment of sensor nodes which has a much wider scope of applications. This is particularly useful for the unreachable and harsh locations where deterministic deployment is not feasible. In the present study, randomly deployed sensor nodes are considered for obtaining $k$-coverage. To achieve $k$-coverage through random deployment in an energy-efficient way, all the nodes can’t be kept active all the time. Doing so shall incur huge number of transmission and reception operations. This results in redundant data accumulation at the destination nodes. Such a situation is bound to happen due to spatial and temporal correlation among the nodes [5]. Hence, only a subset of nodes is kept active. This subset is referred to as a cover-set and it is capable of providing the required coverage and connectivity in the network with minimal nodes. Prolonging the network lifetime with energy-efficient coverage requires a minimal sensor spatial density of active set of nodes and maximal disjoint cover-sets. In this paper, a solution for the $k$-coverage problem has been proposed using the concept of CCA and maximal cover-sets generation with minimal size. Further, the sensor spatial density has been optimized for a value of $k \ge 1$. This study targets the applications of WSN which require continuous monitoring of the FOI for a long span of time. Such applications include security surveillance, habitat monitoring and fire detection systems.

Fig. 1

a Single coverage provided to the triangular area using single node with sensing radius r; b redundant (double) coverage provided using two nodes with sensing radius r

1.1 Significance of this Research and Contributions

In the present research work, the concept of coverage contribution area is used in a unique way with the help of concentric hexagonal tessellations. Concentric hexagonal tessellations provide a clear and easy way of choosing multiple nodes from the inner hexagon to cover the outer hexagon. This process leads to a minimal sensor spatial density and minimal area of overlap of sensing area due to two main reasons viz., (i) nodes are chosen from smaller area to cover a larger area, (ii) shape of a hexagon resembles the most with the disk shapes sensing region as compared to a triangle and a square.

The prime focus of the present study is the ‘energy-efficient coverage’ aspect in randomly deployed WSN. Random deployment results in more number of deployed nodes as compared to the actual requirement which not only increases the cost of deployment but also increases the power consumption in the network. These disadvantages can be very well turned into an advantage by using it to prolong the lifetime of the network. To achieve this, instead of activating all the nodes at once, only a subset of nodes is activated. Proposed algorithm activates minimal nodes at any point during the network lifetime. This minimizes the rate of energy consumption in each subset and results in prolonged network lifetime. Present work provides flexible degree of coverage provided to each and every point in the FOI. Another major benefit is the degrees of coverage for $k > 1$ which provides fault tolerance for node failure to a good extent by preventing immediate disconnection and coverage loss by allowing the activation of two or more nodes to cover each point in the FOI. Activation of minimal nodes in the network also reduces the circulation of redundant data in the network, minimizes the transmissions and therefore decreases the chances of collisions. The main contributions of the present research work include:

• Sensor spatial density of the nodes is minimized using the hexagonal tessellation-based field partitioning.

• Concept of coverage contribution area (CCA) is used to activate minimal nodes in the FOI with required degree of coverage and connectivity.

• Proposed algorithm DCH-PCA results in maximal number of cover-sets with minimal size.

• Rate of energy consumption is considerably low as compared to other recent research works. Comparative analysis also shows a significant increase in WSN lifetime.

The superiority of present work has been proved with the help of valid comparisons with other existing energy-efficient coverage approaches. These approaches include DCRT-PCA (2017) [6], three local search algorithms viz. local search, fixed depth and variable depth (2018) [7], multi-dominating subtree algorithm (2019) [8], $\alpha MOC-\rho CDS-C$, $\rho CDS-BD-C$ and $\rho CDS-BFS$ (2019) [9] and CCM-RL (2020) [10]. The rest of the paper is organized as follows. Section 2 covers a brief literature review. The network model, concept of CCA, target field partitioning and energy consumption model are elucidated in Sect. 3. Sections 4 and 5 present the sensor spatial density analysis and coverage algorithms. Detailed discussion of the simulation results is presented in Sect. 6. Finally the work is concluded in Sect. 7 with an insight for future research directions.

2 Literature Review

The energy constraint in WSNs has been receiving attention. Over the years, various energy-efficient protocols for WSN have been reported [3,4,5]. In random deployment, a huge number of sensor nodes need to be scattered in the target area to ensure that all the points are covered. These nodes are far more than the actual required number of nodes. Even after deploying such huge number of nodes, the deployment can’t guarantee the coverage and connectivity especially when the application requires coverage degree greater than unity for every point in the target area. Hence, coverage and connectivity become important issues for not only ensuring the quality of network but also for maximizing the lifetime of the network. Coverage and lifetime maximization of WSNs are reported in the literature [11,12,13]. Good network connectivity ensures reliable data delivery in a WSN. Huang et al. [14] have investigated covering schemes for continuous partial coverage in WSNs. A multi-working sets alternate covering method has been given to satisfy the coverage requirement. Katti [15] has provided target coverage using coversets. Proposed algorithm uses the number of targets monitored by a node and its remaining energy to find an energy-efficient path to sink node. Huang et al. [16] have formulated the problem of coverage in WSNs as a decision problem. Their results help in determining the uncovered areas in a sensor network for random deployment. In order to do so, the sensing area of each sensor is checked rather than checking the coverage at every point in the target area. Li et al. [17] have provided an optimization algorithm for area coverage based on the mathematical model for sensing nodes in WSN. Ammari et al. [18] have proposed a percolation theory-based coverage and connectivity solution. Nazhad et al. [19] have used harmony search to solve the $k$-coverage problem in WSNs. Ashouri et al. [20] have optimally generated disjoint sets for $k$-coverage. The reported method is based on the transformation of the problem into the well-known Boolean satisfiability (SAT) problem. Ammari et al. [21] have highlighted the importance of sensing coverage for WSNs. Different subsets of total nodes have been scheduled in such a way that in each scheduling round, every location in the target area is covered by at least $k$ active sensors. Ma et al. [22] have considered two 802.15.4 WSNs to analyze the partial coverage overlapping problem. A Markov chain-based analytical model is used to identify the performance degradation due to coverage overlap. Abbas et al. [23] have investigated the coverage of sensor network with heterogeneous sensing nodes. It is analyzed that when sensing nodes of two different radii are used for complete coverage, then coverage density increases and sensing cost decreases. Sakai et al. [24] have explored the issue of node deployment to achieve connectivity and coverage. Identical and symmetric deployment patterns are considered. Zhang et al. [25] have used sleep wake scheduling with polynomial approximation independent of the value of the degree of coverage while improving the energy efficiency. Yu et al. [6] have presented both centralized and distributed protocols to solve $k$-coverage problem in WSNs. These protocols are based on the concept of coverage contribution area (CCA). Minimal sensor spatial density is aimed while providing redundant coverage in target area. Furthermore, methods for target area coverage and to extend WSN lifetime have been reported by researchers [26, 27]. Pino et al. [7] have introduced three multiple search algorithms viz. local search, fixed depth search, variable depth search for generating dominating sets and enhancing the network lifetime. Yang et al. [8] have proposed a multi-dominating subtree-based algorithm to produce connected dominating sets. Several dominating subtrees are constructed which are then merged to form the final tree by eliminating the redundant nodes. Song et al. [9] have formulated dominating sets problem as minimum $\alpha MOC-\rho CDS$ problem which aims at constructing $\rho$-range connected dominating sets with $\alpha$ times minimum routing cost where $\rho = \frac{maximum\, transmission \, radius}{minimum\, transmission\, radius}$ and $\alpha \ge 5$. Sharma et al. [10] have presented a Nash Q learning-based algorithm where each node self-learns its optimal action out of four actions viz. sleep, hibernate, activate, sensing range customization to achieve the desired coverage and maintain connectivity. However, along with efficient coverage and connectivity, energy efficiency and network lifetime are very prominent performance requirements of a randomly deployed WSN. In the present research work, the same has been attempted.

The present study targets the challenge of providing energy-efficient coverage to the WSN. It deals with the concept of CCA. CCA of an area $A$ is the area in which a node deployed at any point covers $A$ completely. Basic idea is to divide the target area into a number of non-overlapping tessellations of the same kind. The concept of CCA was introduced by Yu et al. [6]. But unlike [6], the proposed model selects nodes from each tessella to cover its CCA. The objective of the work is to decrease the sensor spatial density $(SSD)$ of the active nodes and minimize the energy consumption by activating minimal nodes at any point during the network lifetime.

Fig. 2

a Triangular tessellation; b square tessellation; c hexagonal tessellation for target field partitioning

3 Network Model

In the present paper, a randomly deployed WSN is considered. Each node has a unique identifier. Every node is assumed to have the same sensing and the same communication capabilities, thereby forming a homogeneous WSN. The proposed algorithm for maximal disjoint subsets generation is centralized, which is executed at the sink node. Therefore, the sink is assumed to have all the knowledge regarding the locations, identifiers, residual energies, sensing radii and communication radii of the sensor nodes. Boolean sensing and communication models are used to define the sensing and communication regions of the sensor nodes. This assumes them to be in the form of circular disks centred at the node itself. The radius of the disk being equal to the sensing and communication radii, respectively. A point $p$ at location $(x_p , y_p)$ is said to be covered by a sensor node $n$, located at $(x_n , y_n)$ if the following condition holds,

$$\begin{aligned} dist(p , n) \le r \end{aligned}$$

(1)

where $r$ is the sensing radius of $n$ and function $dist$ gives the Euclidean distance between $p$ and $n$. It is defined as the straight line distance between $p$ and $n$ in two-dimensional Euclidean plane. Similarly, two nodes $n_i$ and $n_j$ located at $(\ x_i , y_i)\$ and $(\ x_j , y_j)\$, respectively, can communicate with each other if Eq. (2) holds,

$$\begin{aligned} dist(n_i , n_j) \le R \end{aligned}$$

(2)

where $R$ is the communication radius of $n_i$ and $n_j$.

3.1 Target Field Partitioning

The first step involved in the present approach is to find the right tessellation for field partitioning. A tessellation is generated in a two-dimensional plane using the repetition of a geometric shape with no overlaps and no gaps. A regular tessellation is a tessellation that covers a two-dimensional plane with regular polygons of the same size. There are three regular tessellations composed of triangles, squares and hexagons, respectively [28]. Figure 2a-c illustrates the three different ways of partitioning a two-dimensional plane. All the three tessellations have been explored, to identify the best tessellation.

3.2 Estimation of Coverage Contribution Area

The concept of CCA has been introduced by Yu et al. [6]. CCA of an enclosed region $A$ is defined as another region $CCA(A)$, such that if a node is deployed anywhere in $CCA (A)$, it completely covers $A$ and vice versa. $CCA(A)$ can be a point or an enclosed area whose shape and size depend on the shape and size of $A$. Mathematically, a region $C$ shall be considered as the CCA of a region $A$, denoted as $CCA(A)$, if and only if the following two conditions hold:

• Cond-1: $\forall p \in C, \forall q \in A, such \, that, \Vert p-q \Vert < r$ ;

• Cond-2: $\exists t \notin C, \exists v \in A, such \, that, \Vert v-t \Vert > r$.

Here the first condition mandates that for $C = CCA(A)$, a node placed at any point in $C$ covers all the points in $A$ through its sensing range. $p$ refers to any point inside $C$ and $q$ refers to any point inside $A$. $\Vert p-q \Vert$ is the Euclidean distance between $p$ and $q$. Second condition instructs that a node placed at any point lying outside $C$ must not cover at least one point in $A$. $v$ refers to any point inside $A$ and $t$ refers to any point outside $C$. $\Vert v-t \Vert$ is the Euclidean distance between $v$ and $t$.

Figure 3 shows CCA of a circle. Three circles of different radii are taken and CCA of each circle is defined. Radii of the circles are defined in terms of the sensing radius ($r$). Figure 3a shows a circular area with radius equal to r. Hence, the CCA is the centre of this circle. It means that this area will be covered completely only if the node is deployed at the centre. Figure 3b considers a circular region with radius equal to half the sensing radius. The CCA for such a region is the region itself. Any node deployed outside of the circle will not be able to cover the area completely. Figure 3c takes a circular region of radius equal to one third of the sensing radius. In this situation, CCA is a circle concentric to the given circle with a radius twice larger.

Fig. 3

a CCA estimation of circle with radius $r$; b circle with radius $r$/2; c circle with radius $r$/3

Fig. 4

a CCA estimation of triangular tessellation with side equal to $r$; b square tessellation with diagonal equal to $r$/2; c hexagonal tessellation with side equal to $r$/2

Figure 4 illustrates CCA estimation for three tessellations. Triangular tessellation is considered in Fig. 4a. The side of the triangle is taken equal to the sensing range $r$ of the sensor node. CCA comprises of the triangle itself plus the area bounded by three arcs with three sides of the triangle. Shape of this CCA is also referred to as Reuleaux triangle (illustrated in Fig. 5). In Fig. 5, it can be seen that the three points $p_1$, $p_2$ and $p_3$ are equidistant from each other. Reuleaux triangle is denoted as $rt(h)$. $h$ denotes the width of the Reuleaux triangle. Mathematically,

$$\begin{aligned} rt(h) = {p \in R^2 \mid p \in S(p_1 , h) \cap S(p_2 , h) \cap S(p_3 , h)} \end{aligned}$$

(3)

where $S(x, y)$ denotes the circular disk centred at $x$ with a radius of $y$ [6]. CCA of a triangle yields a Reuleaux triangle only when the side of the triangle is taken equal to the sensing radius, otherwise the CCA often yields an irregular polygon bounded by arcs. The shape and size of the CCA depend on the relationship between the side of the triangle and the sensing radius. It is very important to note that the side of the triangle can’t be greater than the sensing radius as in this case a single node shall not be able to cover the tessellation completely. Therefore, the CCA does not exist for a single node.

In Fig. 4b, diagonal of the square is taken equal to the sensing radius $r$. In this case, the CCA comprises of the area formed by the circle in which the square is shown inscribed. In Fig. 4c, side of the hexagon is taken as half of the sensing radius and its CCA comprises of the area of the circle, centred at the centre of the hexagon. As the size of the tessellation decreases with respect to the sensing radius, while the sensing radius is kept the same, the size of the CCA increases.

Fig. 5

Reuleaux triangle of width $h$ [6]

Table 1 Area of CCA and $SSD$ obtained for three tessellations

3.3 Energy Consumption Estimation

The energy consumption model with respect to each node is presented here [6, 19, 29]. It is assumed that the initial energy of all the deployed nodes is the same. This is typically the case in most of the randomly deployed wireless sensor networks. Transmission and reception are two of the high-cost operations. Unnecessary transmissions and retransmissions result in an equal or lower number of reception operations, denoted as $\mid T_{tx} \mid \ge \mid T_{rx} \mid$, $T_{tx}$ and $T_{rx}$ denote a transmission and reception operation, respectively. This leads to unnecessary energy consumption or energy wastage. Hence, it must be avoided at all costs. Keeping all the nodes active at all times leads to communication overhead and retransmissions. This situation needs to be avoided by keeping only the required number of nodes active at a particular time. Energy cost of transmission is given as [29]:

$$\begin{aligned} E_{tx} (b, d) = E_{elec} \times b + e_{amp} \times b \times d^2 \end{aligned}$$

(4)

where $E_{tx}$ is the total energy required to transmit a packet of $b$ bits through a distance $d$. $E_{elec}$ is the amount of energy consumed by the circuit when data are transmitted or received. $e_{amp}$ denotes the energy consumed by the transmitter amplifier and is a function of $b$ and $d$. From (4), it is evident that $e_{amp}$ is energy consumed by the transmitter amplifier per bit per square distance between the sender and the receiver. Energy cost of receiving a packet is given as follows [29]:

$$\begin{aligned} E_{rx} (b) = E_{elec} \times b \end{aligned}$$

(5)

where $E_{rx}$ denotes the total energy consumed to receive a packet of $b$ bits. Energy is consumed even when a node is in an idle state. Hence, idle nodes must be put to a sleep mode where the transmitting and receiving circuitry is turned off and only a low power consuming radio is kept on [19].

4 Sensor Spatial Density Analysis

Sensor spatial density $(SSD)$ of a region $A$ is defined as the ratio of total active nodes in $A$ to its area. This study aims to minimize its value, provided the total nodes active in target field $F$ provide coverage to every point in $F$, where

$$\begin{aligned} F = \int _{l}^{u} f(A) dA \end{aligned}$$

(6)

In order to optimize the value of $SSD$, efforts have been made to cover as much area as possible with $k$ sensor nodes and for that, it is very crucial to decide the region from where $k$ nodes are to be chosen. The present work deals with the novel concept of choosing nodes from the smallest possible area to cover as much large area as possible. $SSD$ is determined in accordance with (7)

$$\begin{aligned} SSD = \frac{k}{Area \, of \, the \, region \, A} \end{aligned}$$

(7)

Further, if the covered area could be converted to one of the three popular tessellations as mentioned in Section 3.1, then the area of overlap can also be minimized. This is illustrated in the present section.

Triangular Tessellation This tessellation has been initially explored in [23], side of the triangle is taken equal to the sensing radius and $SSD$ of 0.8141k/$r^2$ is reported (shown in Table 1 in column 3 for $\lambda =1$). In [6], a triangle of side equal to half of the sensing radius is considered and $SSD$ is 0.62069$k/r^2$ (shown in Table 1, column 3 for $\lambda =2$). Figure 4a shows the CCA of the triangle for $\lambda = 1$, i.e., side of triangle = $r$. It comprises of a triangle and the area bounded by three arcs with the sides of triangle. In the present study, side of the triangle is further decreased as a variable of sensing radius $(i.e.,\,s=r/\lambda$, where $\lambda = \{{1,2,3\ldots }\} )$, to see its effect on the $SSD$. It is observed from Table 1, that although the $SSD$ decreases when the side is decreased with respect to the sensing radius, the number of triangles required to partition the field increases. This increases the time complexity $(\{{mlog(m)}\}$, where $m$ signifies the number of tessellas to partition the FOI of sorting the tessellas according to their weights. The analysis is stopped at $\lambda = 5$ because the area, from where the nodes for providing $k$ coverage are to be chosen, becomes very small.

Square Tessellation Although this tessellation has been explored by the researchers, the concept of CCA has not been applied for it. The same has been attempted in the present work, and the results are presented. The case of a square for covering it completely with the sensing range of a single sensor node, diagonal ($l$) is varied in terms of the sensing radius (i.e., $l = r/ \lambda$). The effect on the $SSD$ due to such a variation is shown in Table 1. Figure 4b is used to compute $SSD$ for $\lambda = 1$. Circular region in which the square is inscribed forms the CCA. It is analyzed that the number of square tessellas required to cover the FOI will increase as $\lambda$ increases. Therefore, the time complexity of sorting them increases.

Hexagonal Tessellation Side ($s$) for the hexagonal tessellation is taken as $r/\lambda$. Figure 6a shows the CCA of a hexagonal tessellation with $side = r/4$. The area bounded by the circle of radius $\frac{3r}{4}$ represents the CCA. Figure 6b shows the condensed CCA to form the concentric hexagonal tessellations. Area is calculated in terms of the sensing radius of the deployed nodes. $A_1$ denotes the area of each triangle in Fig. 6a, and $A_2$ denotes the area bounded by each arc of circular CCA and the side of outer hexagon. For example, the area of CCA for $\lambda =4$ is given by (8).

Fig. 6

a Uncondensed CCA of hexagonal tessellation; b redundant coverage using concentric hexagonal tessellations

$$\begin{aligned} Area\Bigg (CCA\Bigg (\frac{r}{4}\Bigg ) \Bigg ) = 54A_1 + 6A_2 \end{aligned}$$

(8)

where

$$\begin{aligned} A_1= & {} \frac{\sqrt{3}}{4} \Bigg ( \frac{r}{4} \Bigg ) ^2 \end{aligned}$$

(9)

$$\begin{aligned} A_2= & {} \frac{w}{2} \Bigg (\frac{3r}{4}\Bigg )^2 - \frac{\sqrt{3}}{4} \Bigg (\frac{3r}{4}\Bigg )^2 \end{aligned}$$

(10)

where $w$ denotes the angle subtended by each arc at the center of circular CCA. For $w=1.0472$ radians, $A_2 = 0.051$ $r^2$.

Hence,

$$\begin{aligned} Area\Bigg (CCA\Bigg (\frac{r}{4}\Bigg ) \Bigg ) = (\ 1.7694)\ r^2 \end{aligned}$$

(11)

and

$$\begin{aligned} SSD\Bigg (\frac{r}{4}\Bigg ) = (\ 0.5651)\ \frac{k}{r^2} \end{aligned}$$

(12)

The investigation of variation in the $SSD$ with respect to the decrease in the area of hexagonal tessellation has been carried out for $\lambda$ varying from 1 to 5 as shown in Table 1. However, the $SSD$ value for $\lambda$ =5 is quite low. It is further explored whether this $SSD$ is enough to provide $k$-coverage to the target area or not. Hence, the dominating sets generated for this case are checked. It is analyzed that for such a low value of $SSD$, the highest degree of coverage that could be achieved for 1000 number of deployed nodes is just 2. This is because the size of the inner tessella becomes too small and the probability of finding $k$ number of nodes for $k \ge 3$ becomes close to zero. Hence, the best case considered for implementation of proposed cover-set/ dominating set generating algorithm is for $\lambda =4$ using hexagonal tessellation.

In the present work, the idea of choosing nodes from a smaller region to cover a larger region to optimize the $SSD$ is implemented. In order to guarantee the coverage of the larger region by choosing nodes from the smaller region, firstly, the former must form the CCA of the latter, and secondly, the former must be able to partition the FOI in a non-overlapping fashion. Hence, the area from where the nodes are to be chosen and the area to be covered must be considered in one of the three tessellations. It has been observed through the CCA estimation of the three tessellations that only the CCA of a hexagon can be condensed to form a hexagon. In case of the triangular one, the CCA can’t be condensed to form a triangle but is an irregular shape. For the square tessellation, although the CCA can be condensed to form a square, but the area of overlap formed by the sensing ranges of the adjacent squares is four times larger as compared to that of the hexagon. Therefore, hexagonal tessellation has been considered in the subsequent work of the present study.

5 $k$-coverage Algorithms

A $k$-covered target area also guarantees connectivity if $R$ $\ge$ 2$r$, where $R$ denotes the communication radius [21, 29]. In the present study $R = 2r$, which guarantees connectivity when $k$-coverage is ensured. A centralized algorithm has been proposed and presented in this section to achieve $k$-coverage using the concentric hexagonal tessellations for a target area randomly deployed with sensor nodes.Each outer hexagon has a side of $\frac{3r}{4}$. Here, $r$ is the sensing radius of the sensor nodes deployed in the target field. Inner hexagons of side $\frac{r}{4}$ each are taken, concentric to each outer hexagon of side $\frac{3r}{4}$, as shown in Fig. 6b. Nodes inside the inner hexagons are used to cover the outer hexagons. This study uses the concept of CCA. Property-1 given below is an important characteristic of a CCA [6]:

• Property-1: Any node in the CCA of an area $A$ shall completely cover the area $A$. Further it is analyzed and leads to another property,

• Property-2: Any node in area $A$ shall completely cover its CCA.

Inner hexagons are used to cover the outer hexagons, carved out of their CCAs, and concentric to them. Therefore, smaller area is used to choose the nodes to cover a larger area. Each small hexagon of side $\frac{r}{4}$ is attributed a weight which is equal to the number of nodes which have their selected variable set to 0. All the small hexagons are then sorted according to the descending order of their weights. Bigger hexagons containing the small hexagons are placed in a non-overlapping fashion and their collection is shown in Fig. 7 and is referred to as a “pattern.” Each such pattern is constructed using a “base hexagon.” Centre coordinates of this base hexagon are used to estimate the centre coordinates of the other hexagons adjacent to it. However, a single pattern can’t be used to achieve $k$-coverage. It will not only leave the nodes outside small hexagons unused but will also lead to at the most one cover-set only. Hence, the pattern is shifted by varying centre coordinates of the base hexagon. More patterns are generated using pattern shifting, and their number depends on the size of the field as well as on the value by which $x$ or $y$ coordinates of the centre of base hexagon are varied. For a square of a side 100m and shifting value of 10m, 121 patterns are generated and for a side of 250m and for the same shifting value, 676 patterns are generated. Although the FOI is considered to be a square, proposed algorithm becomes independent of the shape of the FOI, once, target field partitioning is done using the non-overlapping concentric hexagonal tessellations. Coverage is estimated by ensuring that, for each outer hexagon partitioning the FOI, its inner hexagon has sufficient nodes to provide the required degree of coverage.

Fig. 7

Random deployment of sensor nodes in a field partitioned using hexagonal tessellations

Dynamic Centralized Hexagon-based Partition Coverage Algorithm (DCH-PCA) Hexagon-tessellations are used to partition the target field. In order to provide $k$-coverage to the target field, every hexagon tessella must be $k$-covered. Nodes are chosen from inner concentric hexagon to $k$-cover the outer concentric hexagon. The proposed algorithm makes use of centralized approach for providing the coverage. After the nodes have been deployed randomly in the target field, Algorithm 1 is executed to initialize the network. First of all, target field $T$ is divided into non-overlapping regular hexagons of side $\frac{3r}{4}$ each, with the help of the set $P$, which denotes the set of patterns. $H^{\frac{3r}{4}}(T)$ denotes the set containing hexagons used to partition the target field. Each pattern $p_i \in P$ contains the centre coordinates of base hexagon $H_b$. Another set of hexagons $H^{\frac{r}{4}}(T)$ is generated such that each hexagon $h^c_i \in H^{\frac{r}{4}}(T)$ has a side of $\frac{r}{4}$ and is concentric to a hexagon $h_i \in H^{\frac{3r}{4}}(T)$. For $i^{th}$ pattern $p_i$, sink node estimates the set of sensors $n_i$ for each hexagon $h^c_i$ such that every node in this set lies inside or on the boundary of hexagon $h_i$. Set $n_i$ is updated as $nNew_i$ by filtering out the nodes from the original set $n_i$ which have $node_j.selected$ variable active with a value equal to 1. Each hexagon $h^c_i \in H^{\frac{r}{4}}(T)$ is assigned a weight $w^{hex}_i$ which is equal to $\mid nNew_i \mid$. Each sensor node $node_j$ is also assigned a weight $w^n_j$. It is computed as follows [6]

$$\begin{aligned} w^n_j = \alpha \Bigg ( \frac{count_j}{24} \Bigg ) + \beta \Bigg ( \frac{e_j}{e_{initial}} \Bigg ) \end{aligned}$$

(13)

where $\alpha + \beta = 1$. $count_j$ is defined as number of uncovered Reuleaux triangles which completely reside in the sensing range of $node_j$. $e_j$ is the residual energy of $node_j$, and $e_{inital}$ is the initial energy [6]. In the present work, $\alpha$ is taken as 0, because each $h_i \in H^{\frac{3r}{4}}(T)$ is completely covered by any node inside $h^c_i \in H^{\frac{r}{4}}(T)$. Therefore, $count_j$ does not contribute to the weight $w_j^n$. Yu et al. [6] have set $\beta = 0$, thereby ignoring the residual energy. Doing so, the low powered nodes may get drained off their energies early. Therefore, the present work sets $\beta = 1$ for Algorithm 2. Each $p_i \in P$, refers to the centre coordinates of base hexagon $H_b$. Such a pattern $p_i$ is considered a valid cover-set only if every hexagon in this pattern is $k$-covered. For each hexagon $h^c_i$, a set of useful nodes (useful nodes for a cover-set are the ones for which the “selected” variable is set to 0) is maintained and updated every time a new pattern is considered in Algorithm 2. This updated set of nodes for each $h^c_i$ is denoted by $nNew_i$. Weight $w^{hex}_i$ assigned to each hexagon $h^c_i$ is used to sort the set $H^{\frac{r}{4}}(T)$ according to ascending order of their weights. This sorted set is denoted by $H_s^{\frac{r}{4}}$. It is used to select $k$ nodes from each $h_i^c \in H^{\frac{r}{4}}(T)$. To reject or accept a pattern $p_i$, every $h_i^c \in H^{\frac{r}{4}}(T)$ is checked for the presence of $k$ nodes. If at least $k$ nodes are present in every $h_i^c \in H^{\frac{r}{4}}(T)$, then all the hexagons in $H^{\frac{3r}{4}}(T)$ will be $k$ covered. Such a pattern $p_i$ is added to the set of valid cover-sets $CS$, and all the selected nodes are added to the set $CN$. Invalid patterns are added to a separate set $CS'$. Nodes are arranged in the descending order of their weights with respect to each hexagon $h_i^c$. This sorted set of nodes for each hexagon $h_i^c$ is saved in $nNew_i$.

5.1 Time Complexity Analysis

Time complexity analyzed for DCH-PCA refers to its computational complexity. It is basically the computation time required to execute an algorithm. In case of DCH-PCA, time complexity depends on two variables viz. $P$, i.e., the number of patterns and $H_s^{\frac{r}{4}}$ which denotes the number of inner hexagonal tessellations. Time complexity is estimated as O($P$ ($\vert H_s^{\frac{r}{4}} \vert$) + ( $\vert H_s^{\frac{r}{4}} \vert$) $\log$ ($\vert H_s^{\frac{r}{4}} \vert$)). This complexity is significantly low as compared to the complexity of O($n^{3}$) as reported in [9] and O($n^{3}$) and O($n^{2}$) as reported in [10] where $n$ denotes the number of nodes deployed in the FOI.

6 Results and Discussion

Table 2 Simulation parameters and their corresponding values

Fig. 8

Number of cover-sets verses the number of deployed sensors while varying $k$ for a sensing radius of 15 m. b sensing radius of 20 m. c sensing radius of 25 m

The simulation results have been generated using MATLAB. A network environment is constructed using the network model described in Sect. 3, and simulation parameters are initialized as shown in Table 2. Based on the mathematical analysis of sensor spatial density (SSD), hexagonal tessellations are used to partition the randomly deployed target area. Field partitioning is discussed in Sect. 5. Network is initialized using Algorithm 1. Algorithm 2 is used to generate maximal number of disjoint coversets with minimal nodes to minimize the energy consumption. First coverset is activated by the sink node from the set $CS$. The sink node discards an active coverset and activates the next coverset when the active coverset can no longer provide the required $k$-coverage.

In this section, simulation results for the proposed centralized algorithm are presented. The performance has been compared with dynamic centralized Reuleaux triangle-based partition algorithm (DCRT-PCA) [6], three local search algorithms viz. local search, fixed depth and variable depth [7], multi-dominating subtree algorithm [8], $\alpha MOC-\rho CDS-C$, $\rho CDS-BD-C$ and $\rho CDS-BFS$ [9] and CCM-RL [10]. Five parameters are considered for comparison analysis of the simulation results, viz. number of cover-sets, average size of cover-sets, average number of rounds of service, average lifetime of the network and average rate of energy consumption. Sub-sections 6.1 and 6.2 contain the analysis for various degrees of coverage and sensing radii. In Sect. 6.3, number of rounds were averaged out for various degrees of coverage. For comparative analysis in Sects. 6.4, 6.5 and 6.6, single degree of coverage and a sensing radius of 20 m is taken. Two field sizes are considered with their values specifically mentioned in the respective sub-sections. Table 2 provides the list of simulation parameters with their corresponding values used in the simulation.

6.1 Effect of Degree of Coverage ($k$) on the Number of Cover-sets

Target area is considered in the form of a square with each side equal to 100 m. Value of $k$ is varied from 1 to 4 while that of sensing radius is taken as 15 m, 20 m and 25 m. Figure 8a–c shows the number of cover-sets generated for various sensing radii with respect to different values of $k$. All three figures show an increase in the number of cover-sets with an increase in the number of deployed nodes. It can be seen from the figures that as the value of $k$ increases, number of cover-sets decrease. This is because as $k$ increases, the probability of finding $k$ nodes in a hexagon $h_i^c \in H_s^{\frac{r}{4}}(T)$ decreases.

Fig. 9

Variation in the average size of cover-sets with respect to increase in the number of deployed sensors for different values of $k$ and a sensing radius of 15 m. b sensing radius of 20 m. c sensing radius of 25 m

6.2 Effect of Degree of Coverage ($k$) on the Average Size of Cover-Sets

Figure 9 shows the variation in average size of the cover-sets when number of deployed nodes is varied for a particular value of sensing radius and the degree of coverage. It can be seen from Fig. 9a that for $k$ = 1 and 2, the average size of the cover-sets varies nominally with increase in deployed sensor nodes. However, for $k$ = 3 and 4, the value of average cover-set size increases. This increase is particularly significant when the number of sensor nodes is varied from 1500 to 1750. This anomaly is a result of the element of randomization introduced due to random deployment of nodes which affects the number of cover-sets and therefore the average size. The same can be observed for $k$ = 3, 4 in Fig. 9b. In Fig. 9a and (b), average size of the cover-sets for 250 nodes at $k=4$ can’t be plotted as the number of cover-sets generated for such a small number of nodes is 0. On the other hand, such is not a case for Fig. 9c where the sensing radius is higher (25 m). This is because with a larger sensing radius ($r$), the number of hexagons whose side is taken in terms of $r$, decrease. Therefore, the number of nodes required to provide $k$-coverage shall decrease. Figure 10 shows the variation in the average size of cover-sets with the number of deployed sensor nodes for $k \in {\ 1, 2, 3, 4}\$. It is pertinent to mention that for the case when number of nodes for $k=4$, the average size of the cover-sets is not defined and hence not plotted. This is because the number of cover-sets in this case is 0. Nodes are too less in number to provide a coverage degree of 4 at a time at every point. It is analyzed that the proposed approach generates higher number of cover-sets as compared to approach in [6].

Fig. 10

Average size of cover-sets verses the number of deployed sensors while varying the value of $k$

Fig. 11

Average number of rounds of service delivered by the network during its lifetime

6.3 Average Number of Rounds Completed by the Network Versus the Percentage of Dead Nodes in the Network

Figure 11 illustrates the effect on the average number of rounds completed by the network as the residual energy of the nodes starts to deplete and the percentage of dead nodes increases. The observations discussed for Fig. 11 are based on the results obtained for a total of 1000 nodes deployed in $250\,\hbox {m} \times 250\,\hbox {m}$ of target area. The number of rounds are averaged out as per Eq. (14).

$$\begin{aligned}&Avg(Rnds) \nonumber \\&\quad = \frac{Rnds(CS_{1})+Rnds(CS_{2})+Rnds(CS_{3}) + \cdots + Rnds(CS_{T})}{T}\nonumber \\ \end{aligned}$$

(14)

where $Rnds(CS_{i})$ denotes the number of rounds completed by the network when a $CS{i}$ is active. $CS_{i}$ denotes the ith coverset and $T$ denotes the total coversets generated for total deployed nodes. The average is generated each time when the number of active nodes declines 20% for each coverset. As it is evident from the graph, a total of 1650 rounds are completed by the network for a fixed rate of increase of 20% in the dead nodes. Average increment in the number of rounds is equal to 29.5%. Constrained shortest path energy aware routing algorithm is used to transmit the data packets to the sink [30]. However, the results obtained are independent of the routing algorithm used.

Fig. 12

Variation in the number of cover-sets with the number of deployed sensors for a $k = 1$; b $k = 2$; c $k = 3$; d $k = 4$

6.4 Comparison Between DCH-PCA and DCRT-PCA with Respect to the Number of Coversets

A square region of area $250m \times 250m$ has been considered. The number of randomly deployed sensors is varied from 1000 to 4000. Proposed DCH-PCA has been compared with DCRT-PCA [6]. Figure 12 provides a comparison of both the algorithms with respect to the number of cover-sets. It can be seen from Fig. 12a–d that the proposed DCH-PCA algorithm generates higher number of cover-sets as compared to DCRT-PCA [6] for degree of coverage $k={1,2,3,4}$. It is inferred that the proposed algorithm is particularly more efficient than [6] for larger number of randomly deployed nodes.

6.5 Comparison of DCH-PCA with Multi-dominating Sub-tree Algorithm, $\alpha MOC-\rho CDS-C$, $\rho CDS-BD-C$ and $\rho CDS-BFS$ with respect to the Average Size of the Cover-Sets

Fig. 13

Average size of the cover-sets versus the total number of deployed sensors in the target area

Fig. 14

a Effect of the degree of coverage ($k$) on the average lifetime of the network; b comparison of DCH-PCA with LS, FD and VD with respect to the average network lifetime

The number of nodes active in a particular coverset directly impacts the energy consumed by that coverset during the time it is active. This directly contributes to the power consumed by the network during its lifetime. In order to minimize the energy expenditure, it is important to ensure that minimal nodes are active in each coverset. Figure 13 shows a comparison between the average size of a coverset generated by DCH-PCA, sub-tree algorithm, $\alpha MOC-\rho CDS-C$, $\rho CDS-BD-C$ and $\rho CDS-BFS$. In order to be able to compare, single degree of coverage is considered with 20m of sensing radius and $100m \times 100m$ target area. It can be observed that proposed approach generates significantly smaller coversets when the average size of the cover-sets is plotted against the total number of deployed nodes. Multi-dominating subtree algorithm generates coversets with average size lesser than the size achieved with three algorithms viz. $\alpha MOC-\rho CDS-C$, $\rho CDS-BD-C$ and $\rho CDS-BFS$. The difference in the sizes of coversets produced by multi-dominating subtree $\rho CDS-BD-C$ and $\rho CDS-BFS$ is nominal. But $\alpha MOC-\rho CDS-C$ generates very large coversets as compared to other algorithms under consideration. Comparing with the best (multi-dominating tree) amongst the other four, DCH-PCA generates smaller coversets with an average difference of 26.9%.

6.6 The Comparative Analysis of DCH-PCA with Local Search, Fixed Depth, Variable Depth, CCM-RL and DCRT-PCA with respect to the Average Network Lifetime and Average Rate of Energy Consumption

In general, lifetime of a WSN is defined as the period starting from its initialization to point when it can no longer provide the required coverage and connectivity to the target area. In the present paper, lifetime of WSN is the sum of the lifetimes of individual coversets for a particular number of deployed nodes.

The lifetime of the WSN can therefore also be defined as the period beginning with the activation of the first cover-set to the point where no cover-set in the collection of cover-sets can provide the necessary coverage and connectivity to the target area. Since a cover-set is a subset of the total nodes with minimal nodes, hence, it is rendered useless when at least one node gets depleted of its energy. Therefore,

$$\begin{aligned}&Lifetime \, of\, a\, CS \nonumber \\&\quad = Lifetime \,of\, a\, node\, with\, minimum\, intial\, energy\nonumber \\ \end{aligned}$$

(15)

In the present paper, all the nodes have the same initial energy. Hence,

$$\begin{aligned} Lifetime\, of\, a\, CS = \frac{initial\, energy}{rate\, of\, energy\, depletion} \end{aligned}$$

(16)

The effect of the degree of coverage on the average lifetime is illustrated in Fig. 14a. Highest lifetime is achieved for single degree of coverage. This is implicit from the fact that each coverset providing single degree of coverage consumes lower energy as compared to higher degrees. When the nodes are incremented by 50, the average lifetime increases with an average percentage of 5.8%, 6.4%, 6.7% and 6.3% for $k=1$, 2, 3,4 respectively. In Fig. 14b, the average lifetime achieved in DCH-PCA is compared with the algorithms proposed in LS, FD and VD [7]. It is observed that DCH-PCA achieves an average of 15.2%, 9.1% and 5.84% higher lifetime as compared to LS, FD and VD, respectively. The longest average lifetime of 43.8 h is recorded for 250 nodes with 20 m of sensing radius.

Fig. 15

Average rate of energy consumption in each cover-set versus the total number of delayed sensors in the target area

Figure 15 shows a comparison of DCH-PCA with DCRT-PCA [6] and CCM-RL [10] with respect to the average rate of energy consumption, i.e., power in each cover-set. Target area of $250\,\hbox {m} \times 250\,\hbox {m}$ is considered. The rate of energy consumption is estimated by Eq. (17).

$$\begin{aligned}&Rate\, of\, energy\, consumption\, in\, a\, CS \nonumber \\&\quad = \frac{E_{CS}}{Average\, lifetime\, of\, the\, CS} \end{aligned}$$

(17)

where $E_{CS}$ denotes the average energy consumed by the $CS$ during its lifetime and is estimated using Eqs. (4) and (5). From Fig. 15, it can be seen that DCH-PCA shows significantly lower amount of power consumption as compared to the other two. DCRT-PCA shows highest power consumption amongst the three. This validates the superiority of proposed approach over the other algorithms.

7 Conclusion

In the present work, the coverage problem of a randomly deployed WSN has been dealt-with. A solution is proposed that is based on target area hexagonal partitioning. Other symmetrical and non-overlapping tessellations were also explored to determine the best tessellation to minimize the sensor spatial density. A dynamic centralized hexagon-based partition coverage algorithm (DCH-PCA) has been proposed to generate cover-sets to achieve energy-efficient coverage and extended network life. Results for simulation were recorded and compared with DCRT-PCA [6], three local search algorithms [7], multi-dominating subtree algorithm [8], $\alpha MOC-\rho CDS-C$, $\rho CDS-BD-C$ and $\rho CDS-BFS$ [9] and CCM-RL [10]. A thorough comparative analysis has been carried out to prove the effectiveness of the proposed approach in terms of the number of cover-sets, average size of the cover-sets, number of rounds of service, longevity of the network and energy consumption rate.

DCH-PCA, the proposed algorithm, is centralized where control is provided solely to the sink node. Sink node is responsible for generating the cover-sets and activating them. This was done to relieve the low-powered individual sensor nodes from any such responsibility. Such a case, however, needs a much powerful sink node and also increases the chances of sink becoming a bottle neck. It is important to examine the mobility, fading and shadowing aspects of the sensor nodes too. Hence, a hybrid cover-sets generation algorithm for a sensor network with both mobile and static nodes shall be taken up as future scope of this work.