1 Introduction

To exploit the existing infrastructure of AC power systems, most of microgrids are predominantly AC, and so AC microgrids are widely addressed in the literature [1,2,3]. With the advancements of power electronic industry, the integration of renewable energy resources is rapidly growing [4]. As most of the generated renewable energy is DC, e.g., photovoltaic systems, the integration of DC microgrids has been attracting considerable attention in recent years [5,6,7]. To combine the benefits of AC and DC systems, the concept of hybrid AC–DC microgrids is currently emerging [8,9,10,11]. In hybrid AC–DC microgrids, bidirectional voltage source converters (VSCs), referred to as interlinking converters (ICs), interface the DC microgrids with the AC subsystem. Due to the absence of utility-grid support in the isolated mode of operation, hybrid microgrids generally need both voltage support in terms of reactive power, and frequency support in terms of active power at the AC side, as well as a DC voltage support at the DC side. In addition, bidirectional power flow is processed through ICs to increase the overall system efficiency and reliability [11]. However, the lack of mechanical inertia poses a threat to the dynamic stability of the hybrid system, and hence a thorough analysis under wide variation range of operating conditions is necessary.

Due to the bidirectional power flow through ICs, conventional droop characteristics cannot be used; hence, a centralized control was proposed for multiple ICs in [12]. However, concerns have been raised against the reliability of using centralized control as a fast communication link. Distributed controllers, on the other side, are more reliable [13, 14]. The authors in [13] proposed a modified decentralized dual-based droop control for only one bidirectional IC power flow using current controller loops. To achieve smooth energy exchange between AC and DC subgrids, energy storage units have been used at the DC side of ICs in [15, 16].

Dynamic characteristics of synchronous machines have been emulated and implemented in the control structure of ICs. The application of the virtual synchronous machine (VSM) controller introduces a virtual inertia to the hybrid microgrid, which improves the dynamic performance and stability [10, 17]. It is reported that the appropriate VSM control algorithm is based on a second-order model to enhance the response following fault conditions [18]. Generally, most of the work in the literature employs VSM controllers in the unidirectional power flow applications, i.e., standalone AC microgrids. It is only the work in [19] that focuses on the integration of DC microgrids to the AC side using VSM controllers. However, the work is considered in the grid-connected mode where the system inertia is inherently maximized.

Motivated by the potential features and flexibility of hybrid AC–DC microgrids, this paper presents more insights and investigations on the parallel-operation of ICs. The considered challenges are; (1) circulating currents between parallel-connected ICs, (2) nonlinearity of ICs as seen by the AC subgrid, and (3) the synchronization of ICs following fault conditions or scheduled maintenance.

  1. (1)

    With respect to circulating currents, they appear in parallel-operated converters because of several reasons such as the switching frequency, dead-time, and drifting hardware components [20]. According to [20], circulating currents between ICs consist of two types; which are zero-sequence and cross-currents. The cross-circulating currents flow from the AC side to the DC capacitor. In contrast, the zero-sequence circulating currents flow from the AC to DC side. In addition, exchanging active power from the AC into the DC subsystem raises circulating current issues due to the nonlinear behavior of IC. In spite of these challenges, the trend in hybrid microgrids is to implement parallel-connected ICs to increase the system reliability, utilize converters with lower power ratings, and hence ease the modular maintenance and reduce costs [21, 22].

  2. (2)

    Nonlinear loads infrequently draw current or change their impedance during the cycle of the AC voltage. As ICs are usually VSCs, they are equipped with antiparallel diode rectifiers (Fig. 1). Subsequently, diode rectifiers draw discontinuous and non-sinusoidal AC currents with a high content of the total harmonic distortion (THD). In this case, the AC current waveforms have double pulses per half cycle and so ICs become harmonic voltage sources [23, 24]. As a result, the AC voltage at the point of common coupling (PCC) becomes more distorted [25]. This nonlinear behavior is also linked to circulating currents between ICs.

    Fig. 1
    figure 1

    Hybrid AC–DC system with parallel interlinking converters

    Full size image

    In the literature, the integration of nonlinear rectifiers to AC microgrids has been investigated, and several solutions are reported [26,27,28,29]. However, there are not enough studies on nonlinear ICs in hybrid AC–DC microgrids under rectification and inversion operation. This is a more challenging condition due to the additional functionalities that are needed from ICs to allow bidirectional power flow and frequency support.

  3. (3)

    Microgrid synchronization is a bit different in comparison with synchronizing a traditional synchronous machine with classical electrical systems. This is due to the fact that many distributed generation (DG) units form the microgrid voltage and frequency based on decentralized droop control [30, 31]. The synchronization of AC microgrids using the phase-locked loop (PLL) has been achieved in [30]. However, this method has significant adverse effects on the overall system stability [32]. The inclusion of a resynchronization algorithm as a part of IC controllers is necessary in hybrid microgrids. None of the reports in the literature have discussed this issue.

The contribution of this paper is to address and mitigate the preceding challenges in hybrid microgrids. The primary contribution of this research is to solve the operation issues, including: (1) nonlinear load behavior of the IC, (2) re-synchronization issue of the IC after disturbance, and (3) circulating current issue between parallel ICs. The solution for these issues is based on the implementation of VSM with dual-droop (DD) to achieve a bidirectional power flow capability. Applying the concept of the VSM with power reference modification, based on considering the AC and DC electrical quantities variation for the ICs, solves these issues. The proposed VSM-DD controller enables multiple parallel ICs to behave as a synchronous machine (SM) for supporting both subgrids, with consideration of the variations of the DC voltage and the AC frequency during the isolated operation of a hybrid AC/DC microgrid. This paper presents a comprehensive stability analysis of the hybrid microgrid with the proposed VSM-DD controller. A comparative study with existing solutions in the literature is also presented. Further, the application of the proposed VSM-DD controller prevents the issue of circulating current that occurs in the parallel ICs during the rectification operation mode.

The remainder of the paper is organized as follows: Sect. 2 describes the architecture of hybrid AC–DC microgrids; Sect. 3 introduces the control of interlinking converters; Sect. 4 describes autonomous operation of hybrid AC–DC microgrids. The state-space model of hybrid AC–DC microgrid is presented in Sect. 5. The system small-signal stability analysis is evaluated in Sect. 6. The simulation results and analysis are presented in Sect. 7, and the final section offers conclusions.

2 Architecture of Hybrid AC–DC Microgrids

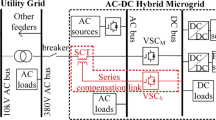
As shown in Fig. 1, an adapted version of a medium-voltage hybrid AC–DC microgrid based on IEEE Standard 399 is considered in this paper [28]. The system is divided into three different components which are named as the AC and DC subgrid, and the ICs. The hybrid system consists of two dispatchable distributed generation (DG) units at the AC and DC sides.

The controller loop structure of the AC subgrid converters and the ICs are implemented based on a cascaded synchronous reference frame (SRF). On the other hand, the control loop structure for the DC subgrid converters is based on cascaded voltage and current control [28].

According to the secondary distribution system configuration, a spot network configuration provides the highest reliability compare to other configurations such as radial or secondary-bank systems. The spot network configuration consists of more than one transformer connected in parallel, which increases the system reliability [24]. It is noted that a similar configuration is proposed for ICs in Fig. 1.

Figure 2 shows a more detailed representation for the parallel-operated ICs. The values of circulating currents between ICs can be represented by the cross- and zero-sequence currents using (1) and (2), respectively [20].

$$I_{\text{cir}}^{\text{cross}} = \frac{1}{2}\left( {\frac{{{\text{vo}^{\prime}}}}{{R_{{{\text{f}^{\prime}}}} + sL_{{{\text{f}^{\prime}}}} }} - \frac{{{\text{vo}^{\prime\prime}}}}{{R_{{{\text{f}^{\prime\prime}}}} + sL_{{{\text{f}^{\prime\prime}}}} }}} \right)$$
(1)
$$I_{\text{cir}}^{\text{zero}} = \frac{1}{3}\left[ {\left( {I_{a1} + I_{b1} + I_{c1} } \right) - \left( {I_{a2} + I_{b2} + I_{c2} } \right)} \right]$$
(2)

where \({\text{vo}^{\prime}}\), \({\text{vo}^{\prime\prime}}\) are the output voltages of each converter; \(R_{{{\text{f}^{\prime}}}}\), \(R_{{{\text{f}^{\prime\prime}}}}\), \(L_{{{\text{f}^{\prime}}}}\), and \(L_{{{\text{f}^{\prime\prime}}}}\) are the AC filter components of the converters; \(I_{a}\), \(I_{b}\) and \(I_{c}\) are phase currents for each converter; and \(s\) is the Laplace operator.

Fig. 2
figure 2

Circulating currents between parallel ICs

Full size image

3 Control of Interlinking Converters

In this section, a brief description of existing controllers of ICs in hybrid systems is presented. The proposed VSM-DD controller is then investigated.

3.1 Current Control of ICs

Figure 3 shows the traditional current control loops for ICs [33,34,35]. The \(d\)-component of the current reference is defined from the active power reference (\(P_{\text{ref}}\)), whereas the \(q\)-component is set to zero. Therefore, the IC in Fig. 3 is not responsible for the PCC voltage control or reactive power compensation [33, 36]. The advantage of including a voltage controller loop includes the provision of the IC to support the regulation of the AC voltage. It is shown in this paper that the tight regulation of PCC voltage contributes to the minimization of circulating currents. In other words, the control structure of ICs in Fig. 3 is not recommended.

Fig. 3
figure 3

Current control of ICs in hybrid systems

Full size image

3.2 VSM Control of ICs

Many VSM controllers are developed to enable the VSC to mimic the behavior of synchronous machines. As shown in Fig. 4, a VSM controller with a second-order dynamics is adopted in this paper due to the improved performance following fault conditions [18]. In order to implement the second-order VSM controller, it is necessary to replace the power controller loop with the swing equation to generate the orientation angle θ.

Fig. 4
figure 4

VSM control of ICs in hybrid microgrids

Full size image

The general form of the swing equation is based on Newton’s second law of motion as given in (3) [37]. Equation (3) can be multiplied by the rotor synchronous speed (\(\omega_{SM}\)) to get the representation in term of active power (4) [38].

$$\frac{{{\text{d}}^{2} \delta }}{{{\text{d}}t^{2} }} + D_{\text{d}} \frac{{{\text{d}}\delta }}{{{\text{d}}t}} = \tau_{\text{m}} - \tau_{\text{ele}}$$
(3)
$$\omega_{\text{VSM}} \frac{{{\text{d}}^{2} \delta }}{{{\text{d}}t^{2} }} + D\omega_{\text{VSM}} \frac{{{\text{d}}\delta }}{{{\text{d}}t}} = P_{\text{m}} - P_{\text{ele}}$$
(4)

The derivative term of the rotor angle, \(\frac{{{\text{d}}\delta }}{{{\text{d}}t}} = \Delta \omega = \omega_{\text{VSM}} - \omega_{g}\), is the rotor speed deviation in electrical radians per second [1]. Thus, it is more convenient to replace the second-order differential equation term in (4) by two first-order equations, as follows:

$$J\omega_{\text{VSM}} \frac{{{\text{d}}\Delta \omega }}{{{\text{d}}t}} = P_{\text{mech}} - P_{\text{ele}} - \left( {\omega_{\text{vsm}} {-} \omega_{\text{con}} } \right) D_{\text{d}}$$
(5)
$$\frac{{{\text{d}}\delta }}{{{\text{d}}t}} = \Delta \omega$$
(6)

where \(J\), \(P_{\text{mech}}\), \(P_{\text{ele}}\) denote the virtual inertia, the mechanical input power, and the reference power command; \(D_{\text{d}}\) is the damping coefficient; \(\omega_{\text{vsm}}\) represents the synchronous speed that is generated by the swing equation whereas \(\omega_{\text{con}}\) is the estimated angular frequency of ICs. In fact, there are several methods to estimate the converter frequency such as frequency measurement based on zero crossings, and frequency measurement based on phasor rate of rotation [39]. In this paper, a PLL is used as a frequency meter to determine. However, the self-synchronization controller does not depend on the PLL.

4 Autonomous Operation of Hybrid AC–DC Microgrids

The autonomous operation of AC and DC microgrids depends on autonomous droop controllers. In the AC side, the generated active and reactive power are correlated to the frequency and the PCC voltage, respectively [1]. In the DC side, the load power is correlated to the DC bus voltage. To allow accurate bidirectional power flow through ICs, a continuous monitoring of the DC voltage and system frequency is required. This is clearly can be seen from where the combined droop curves for active and DC power are depicted in Fig. 5. More details are presented in the following subsections.

Fig. 5
figure 5

Combined AC–DC droop characteristics for ICs in hybrid microgrids

Full size image

4.1 Interlinking Converters

The mathematical representation of the dual-droop characteristics in Fig. 5 is as given in (7)–(9).

$$P_{\text{IC}}^{\text{ref}} = \left\{ {\begin{array}{*{20}c} 0 & { {\text{if}}\;\omega < \omega_{\hbox{min} } \& V_{\text{dc}} < V_{\text{dc}}^{\hbox{min} } } \\ {P_{\text{IC}}^{\text{ac}} - P_{\text{IC}}^{\text{dc}} } & {\text{otherwise}} \\ \end{array} } \right.$$
(7)
$$P_{\text{IC}}^{\text{dc}} = \left\{ {\begin{array}{*{20}c} {\frac{{v_{\hbox{min} }^{\text{dc}} - v^{\text{dc}} }}{{m_{p}^{\text{dc}} }}} & {{\text{if}}\;V_{\text{dc}} < V_{\text{dc}}^{\hbox{min} } } \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$$
(8)
$$P_{\text{IC}}^{\text{ac}} = \left\{ {\begin{array}{*{20}c} {\frac{{\omega_{\hbox{min} } - \omega }}{{m_{p}^{\text{ac}} }}} & {{\text{if}}\;\omega < \omega_{\hbox{min} } } \\ 0 & {\text{otherwise}} \\ \end{array} } \right.$$
(9)

where \(P_{\text{IC}}^{\text{ref}}\) is the reference power command of ICs; \(P_{\text{IC}}^{\text{dc}}\) and \(P_{\text{IC}}^{\text{ac}}\) are the calculated DC and AC power; \(V_{\text{dc}}^{\hbox{min} }\) and \(\omega_{\hbox{min} }\) are the minimum DC bus voltage and system frequency, respectively; whereas \(m_{p}^{\text{dc}}\) and \(m_{p}^{\text{ac}}\) are the equivalent droop coefficients for the DC and AC subgrids, respectively.

In the case of conventional droop control for ICs, the current reference is determined by dividing the power reference in (7) by the voltage magnitude [40]. However, in the applied VSM control strategy, the power reference is fed directly to the swing equation model (Eq. (5)), and the desired amount of power is then established based on the phase angle \(\theta\), as indicated in Fig. 4.

4.2 AC Subgrid

The DG units in the AC subgrid consist of three-phase VSCs energized from renewable energy DC sources [33]. Each DG unit feeds the load based on the predefined droop gains. As a result, in order to have equal power sharing for all DG units when the system parameters are symmetrical, the droop gains should also be identical [41]. The sum of the total injected active power by all DG units must be equal to the common AC load, as can be seen in (10).

$$P_{{{\text{AC}}\;{\text{load}}}} = \mathop \sum \limits_{i = 1}^{n} P_{\text{AC}} \left( i \right) \cdot m_{\text{AC}} \left( i \right)$$
(10)

where \(P_{{{\text{AC}}\;{\text{load}}}}\) denotes the total AC load; \(P_{\text{AC}} \left( i \right)\) represents the injected power from each DG unit whereas \(m_{\text{AC}} \left( i \right)\) represents the droop gain of the DG unit. The variable (\(n\)) represents the number of DG units in the AC microgrid.

4.3 DC Subgrid

Each DG unit within the DC subgrid consists of a half-bridge DC–DC converter energized by a DC source. The DC bus voltage is controlled by the DG units based on droop control. The sum of the total power injected by each DG unit must be equal to the common DC load, as can be seen in (11).

$$P_{{{\text{DC}}\;{\text{load}}}} = \mathop \sum \limits_{i = 1}^{n} P_{\text{DC}} \left( i \right) \cdot m_{\text{DC}} \left( i \right)$$
(11)

where \(P_{\text{DC}} \left( i \right)\) represents the injected power from the DG, and \(m_{\text{DC}} \left( i \right)\) represents the droop gain of the DG unit.

5 State-Space Model of Hybrid AC–DC Microgrid

In this section, the derivation of the state-space modeling is presented to evaluate the overall dynamic performance. For simplicity, the switches S1 and S2 in Fig. 1 are open. The general representation of VSCs in the AC subgrid is shown in Fig. 6 whereas the converter topology in the DC subgrid is shown in Fig. 7. The readers are referred to [1, 39, 42] for further details.

Fig. 6
figure 6

General Control Structure of VSCs interfacing a DG Unit in the ac subgrid

Full size image
Fig. 7
figure 7

Half-bridge DC–DC Converter in the dc subgrid

Full size image

5.1 Small-Signal Model of VSCs in the AC Subgrid

5.1.1 Power Circuit Model

Applying Kirchhoff’s current and voltage laws on the power circuit in Fig. 6, the dynamic equations of the voltages and current flowing through the VSC are listed in (12)–(14).

$$\frac{{{\text{dic}}v_{dq} }}{{{\text{d}}t}} = \frac{{Vcv_{dq} }}{{L_{\text{f}} }} - \frac{{Vo_{dq} }}{{L_{\text{f}} }} - \frac{{R_{\text{f}} \cdot {\text{ic}}v_{dq} }}{{L_{\text{f}} }} \pm \omega \cdot {\text{ic}}v_{qd}$$
(12)
$$\frac{{{\text{dvo}}_{d} }}{{{\text{d}}t}} = \pm \;\omega \cdot {\text{vo}}_{qd} + \frac{{{\text{ic}}v_{dq} }}{{C_{\text{f}} }} - \frac{{io_{dq} }}{{C_{\text{f}} }}$$
(13)
$$\frac{{{\text{d}}io_{dq} }}{{{\text{d}}t}} = \frac{{Vo_{dq} }}{{L_{o} }} - \frac{{ Vg_{dq} }}{{L_{o} }} - \frac{{R_{o} \cdot io_{dq} }}{{L_{o} }} \pm \omega \cdot io_{qd}$$
(14)

where \(w\) is the angular speed of the rotation of the d–q frame; \(R_{\text{f}} ,\;L_{\text{f}}\) and \(C_{\text{f}}\) are the AC filter components whereas the coupling components for the AC microgrid are represented by \(R_{o}\) and \(L_{o}\). The state-space representation in the linearized small-signal sense is shown in (15) [1].

$$\begin{aligned} \left[ {\mathop {\Delta x_{p} }\limits^{ \cdot } } \right] & = {\mathbb{A}}_{\text{LCL}} \left[ {\Delta x_{p} } \right] + {\mathbb{B}}_{{{\text{LCL}}1}} \left[ {\begin{array}{*{20}c} {\Delta vcv_{d} } \\ {\Delta vcv_{q} } \\ \end{array} } \right] \\ & \quad + {\mathbb{B}}_{{{\text{LCL}}2}} \left[ {\begin{array}{*{20}c} {\Delta vg_{d} } \\ {\Delta vg_{q} } \\ \end{array} } \right] + {\mathbb{B}}_{{{\text{LCL}}3}} \left[ {\begin{array}{*{20}c} {\Delta \omega } \\ \end{array} } \right] \\ \end{aligned}$$
(15)

where

$$\begin{aligned} \left[ {\Delta x_{p} } \right] & = \left[ {\begin{array}{*{20}c} {\Delta {\text{ic}}v_{d} } & {\Delta {\text{ic}}v_{q} } & {\Delta io_{d} } & {\Delta io_{q} } & {\Delta vo_{d} } & {\Delta vo_{q} } \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{LCL}}1}} & = \left[ {\begin{array}{*{20}c} {1 /L_{\text{f}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & {1 /L_{\text{f}} } & 0 & 0 & 0 & 0 \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{LCL}}2}} & = \left[ {\begin{array}{*{20}c} 0 & 0 & { - 1/L_{o} } & 0 & 0 & 0 \\ 0 & 0 & 0 & { - 1 /L_{o} } & 0 & 0 \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{LCL}}3}} & = \left[ {\begin{array}{*{20}c} {{\text{ic}}v_{q} } & { - {\text{ic}}v_{d} } & {io_{q} } & { - io_{d} } & {vo_{q} } & { - vo_{d} } \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{A}}_{\text{LCL}} & = \left[ {\begin{array}{*{20}c} { - R_{\text{f}} /L_{\text{f}} } & \omega & 0 & 0 & { - 1 /L_{\text{f}} } & 0 \\ { - \omega } & { - R_{\text{f}} /L_{\text{f}} } & 0 & 0 & 0 & { - 1 /L_{\text{f}} } \\ 0 & 0 & { - R_{o} /L_{o} } & \omega & { - 1 /L_{o} } & 0 \\ 0 & 0 & { - \omega } & { - R_{o} /L_{o} } & 0 & { - 1 /L_{o} } \\ {1 /C_{f} } & 0 & { - 1 /C_{\text{f}} } & 0 & 0 & \omega \\ 0 & {1 /C_{\text{f}} } & 0 & { - 1 /C_{\text{f}} } & { - \omega } & 0 \\ \end{array} } \right] \\ \end{aligned}$$

5.1.2 Current Controller

The current control loops are shown in (16), (17) whereas the linearized small-signal state-space model is derived in (18), (19).

$$L_{\text{f}} \frac{{{\text{dic}}v_{d} }}{{{\text{d}}t}} = \left( {K_{\text{pc}} + \frac{{K_{\text{ic}} }}{s}} \right) \times \left( {i^{\text{ref}}_{d} - {\text{ic}}v_{d} } \right)$$
(16)
$$L_{\text{f}} \frac{{{\text{dic}}v_{q} }}{{{\text{d}}t}} = \left( {K_{\text{pc}} + \frac{{K_{\text{ic}} }}{s}} \right) \times \left( {i^{\text{ref}}_{q} - {\text{ic}}v_{q} } \right)$$
(17)
$$\left[ {\begin{array}{*{20}c} {\mathop {\Delta \gamma_{d} }\limits^{ \cdot } } \\ {\mathop {\Delta \gamma_{q} }\limits^{ \cdot } } \\ \end{array} } \right] = \left[ 0 \right]\left[ {\begin{array}{*{20}c} {\Delta \gamma_{d} } \\ {\Delta \gamma_{q} } \\ \end{array} } \right] + {\mathbb{B}}_{c1} \left[ {\begin{array}{*{20}c} {\Delta vcv_{d} } \\ {\Delta vcv_{q} } \\ \end{array} } \right] + {\mathbb{B}}_{c2} \left[ {\Delta x_{p} } \right]$$
(18)
$$\left[ {\begin{array}{*{20}c} {\mathop {\Delta vcv_{d} }\limits^{ \cdot } } \\ {\mathop {\Delta vcv_{q} }\limits^{ \cdot } } \\ \end{array} } \right] = {\mathbb{C}}_{c} \left[ {\begin{array}{*{20}c} {\Delta \gamma_{d} } \\ {\Delta \gamma_{q} } \\ \end{array} } \right] + {\mathbb{D}}_{c1} \left[ {\begin{array}{*{20}c} {\Delta vcv_{d} } \\ {\Delta vcv_{q} } \\ \end{array} } \right] + {\mathbb{D}}_{c2} \left[ {\Delta x_{p} } \right]$$
(19)

where

$$\begin{aligned} {\mathbb{B}}_{c1} & = \left[ {\begin{array}{*{20}c} {K_{\text{ic}} } & 0 \\ 0 & {K_{\text{ic}} } \\ \end{array} } \right]; \quad {\mathbb{B}}_{c2} = \left[ {\begin{array}{*{20}c} { - K_{\text{ic}} } & 0 & 0 & 0 & 0 & 0 \\ 0 & { - K_{\text{ic}} } & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ {\mathbb{C}}_{c} & = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]; \quad {\mathbb{D}}_{c1} \left[ {\begin{array}{*{20}c} {K_{\text{pc}} } & 0 \\ 0 & {K_{\text{pc}} } \\ \end{array} } \right]; \\ {\mathbb{D}}_{c2} & = \left[ {\begin{array}{*{20}c} { - K_{\text{pc}} } & { - \omega L_{\text{f}} } & 0 & 0 & 1 & 0 \\ {\omega L_{\text{f}} } & { - K_{\text{pc}} } & 0 & 0 & 0 & 1 \\ \end{array} } \right] \\ \end{aligned}$$

and \(\Delta \gamma_{d}\) and \(\Delta \gamma_{q}\) are the state variables for the integral gains.

5.1.3 Power Controller

The linearized differential equations of the power measurement are modeled as following:

$$\begin{aligned} & \mathop {\Delta P}\limits^{ \cdot } \\ & \quad = \left( {\frac{3}{2}} \right)\left( {\omega_{\text{f}} \left( {\left( {\Delta {\text{vo}}_{\text{d}} \cdot io_{d} } \right) + \left( {\Delta {\text{vo}}_{q} \cdot io_{q} } \right) + \left( {{\text{vo}}_{d} \Delta io_{d} } \right) + \left( {{\text{vo}}_{q} \cdot \Delta io_{q} } \right) - \Delta P} \right)} \right) \\ \end{aligned}$$
(20)
$$\begin{aligned} & \mathop {\Delta Q}\limits^{ \cdot } \\ & \quad = \left( {\frac{3}{2}} \right)\left( {\omega_{\text{f}} \left( {\left( {\Delta {\text{vo}}_{d} \cdot io_{q} } \right) - \left( {\Delta {\text{vo}}_{q} \cdot io_{d} } \right) + \left( {{\text{vo}}_{d} \Delta io_{q} } \right) - \left( {{\text{vo}}_{q} \cdot \Delta io_{d} } \right) - \Delta Q} \right)} \right) \\ \end{aligned}$$
(21)

The linearized state-space model is then derived in (22) whereas the output equation is obtained in (23).

$$\left[ {\begin{array}{*{20}c} {\mathop {\Delta P}\limits^{ \cdot } } \\ {\mathop {\Delta Q}\limits^{ \cdot } } \\ {\mathop {\Delta \theta }\limits^{ \cdot } } \\ \end{array} } \right] = {\mathbb{A}}_{p} \left[ {\begin{array}{*{20}c} {\Delta P} \\ {\Delta Q} \\ {\Delta \theta } \\ \end{array} } \right] + {\mathbb{B}}_{p1} \left[ {\Delta x_{p} } \right]$$
(22)
$$\left[ {\begin{array}{*{20}c} {\Delta {\text{vo}}_{d} } \\ {\Delta {\text{vo}}_{q} } \\ \end{array} } \right] = {\mathbb{C}}_{d} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\Delta P} \\ {\Delta Q} \\ \end{array} } \\ {\Delta \theta } \\ \end{array} } \right]$$
(23)

where

$$\begin{aligned} {\mathbb{A}}_{d} & = \left[ {\begin{array}{*{20}c} { - \omega_{\text{f}} } & 0 & 0 \\ 0 & { - \omega_{\text{f}} } & 0 \\ { - m_{p} } & 0 & 0 \\ \end{array} } \right] \\ {\mathbb{B}}_{d1} & = \frac{3}{2}\left[ {\begin{array}{*{20}c} 0 & 0 & {\omega \cdot {\text{vo}}_{d} } & {\omega \cdot {\text{vo}}_{q} } & {\omega \cdot io_{d} } & {\omega \cdot io_{q} } \\ 0 & 0 & { - \omega \cdot {\text{vo}}_{q} } & {\omega \cdot {\text{vo}}_{d} } & {\omega \cdot io_{q} } & { - \omega \cdot io_{d} } \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right] \\ {\mathbb{C}}_{d} & = \left[ {\begin{array}{*{20}c} 0 & { - n_{p} } & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right] \\ \end{aligned}$$

5.1.4 Voltage Controller

Similar to the current controller, the auxiliary state variables of the voltage controller loops are denoted as \(\Delta \varphi_{d}\) and \(\Delta \varphi_{q}\), and the linearized state-space model is given in (24). Generally, the feedforward gain in the voltage controller loops is taken around 0.8 in order to expand the operation bandwidth [43].

$$\left[ {\begin{array}{*{20}c} {\mathop {\Delta \varphi_{d} }\limits^{ \cdot } } \\ {\mathop {\Delta \varphi_{q} }\limits^{ \cdot } } \\ \end{array} } \right] = \left[ 0 \right]\left[ {\begin{array}{*{20}c} {\Delta \varphi_{d} } \\ {\Delta \varphi_{q} } \\ \end{array} } \right] + {\mathbb{B}}_{v1} \left[ {\begin{array}{*{20}c} {\Delta {\text{vo}}_{d} } \\ {\Delta {\text{vo}}_{q} } \\ \end{array} } \right] + {\mathbb{B}}_{v2} \left[ {\Delta x_{p} } \right]$$
(24)
$$\left[ {\begin{array}{*{20}c} {\mathop {\Delta io_{d} }\limits^{ \cdot } } \\ {\mathop {\Delta io_{d} }\limits^{ \cdot } } \\ \end{array} } \right] = {\mathbb{C}}_{v} \left[ {\begin{array}{*{20}c} {\Delta \gamma_{d} } \\ {\Delta \gamma_{q} } \\ \end{array} } \right] + {\mathbb{D}}_{v1} \left[ {\begin{array}{*{20}c} {\Delta vcv_{d} } \\ {\Delta vcv_{q} } \\ \end{array} } \right] + {\mathbb{D}}_{v2} \left[ {\Delta x_{p} } \right]$$
(25)

where

$$\begin{aligned} & {\mathbb{B}}_{v1} = \left[ {\begin{array}{*{20}c} {K_{\text{iv}} } & 0 \\ 0 & {K_{\text{iv}} } \\ \end{array} } \right];\quad {\mathbb{B}}_{v2} = \left[ {\begin{array}{*{20}c} { - 1} & 0 \\ 0 & { - 1} \\ \end{array} } \right] ;\quad {\mathbb{C}}_{v} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right] \\ & {\mathbb{D}}_{v1} \left[ {\begin{array}{*{20}c} {K_{\text{pv}} } & 0 \\ 0 & {K_{\text{pv}} } \\ \end{array} } \right]; \quad {\mathbb{D}}_{v2} = \left[ {\begin{array}{*{20}c} 0 & 0 & H & 0 & { - K_{\text{pc}} } & { - \omega C_{\text{f}} } \\ 0 & 0 & 0 & H & {\omega C_{\text{f}} } & { - K_{\text{pc}} } \\ \end{array} } \right] \\ \end{aligned}$$

5.1.5 Final State-Space Model of VSCs in AC Subgrid

Using the previous sub-models, and with mathematical manipulations, the final state-space model of the VSC in the AC subgrid is given in (26).

$$\left[ {\mathop {\Delta x_{\text{inv}} }\limits^{ \cdot } } \right] = {\mathbb{A}}_{\text{inv}} \left[ {\Delta x_{\text{inv}} } \right] + {\mathbb{B}}_{\text{inv}} \left[ {\Delta vg_{dq} } \right]$$
(26)

where

$$\begin{aligned} \Delta x_{\text{inv}} & = \left[ {\Delta icv_{d} \quad \Delta icv_{q} \quad \Delta io_{d} \quad \Delta io_{q} \quad \Delta vo_{d} \quad \Delta vo_{q} \quad \Delta \gamma_{d} } \right. \\ & \quad \left. {\Delta \gamma_{q} \quad \Delta \varphi_{d} \quad \Delta \varphi_{q} \quad \Delta \theta \quad \Delta P\quad \Delta Q} \right]^{\text{T}} \\ \Delta vg_{dq} & = [ \Delta vg_{d} \quad \Delta vg_{q} ]^{\text{T}} ; \quad {\mathbb{B}}_{\text{inv}} = \left[ {\left( { - {\mathbb{B}}_{{{\text{LCL}}2}} *R_{l} } \right)\quad 0} \right]^{\text{T}} \\ \end{aligned}$$

The matrix \(\left( {{\mathbb{A}}_{\text{inv}} } \right)\) is detailed in “Appendix” (43)

5.2 Small-Signal Model of VSCs in the DC Subgrid

The general representation of the DC–DC converter interfacing in the DC subgrid is shown in Fig. 7. In fact, it is similar to the AC subgrid from the LC filter’s point of view, but the main difference is the converter circuit structure, which is a half-bridge DC–DC converter.

5.2.1 Power Circuit Model

The dynamic equations of the voltages and currents through the DC–DC converters are written as following:

$$L_{{{\text{f}^{\prime}}}} \frac{{{\text{d}}il}}{{{\text{d}}t}} = V_{\text{in}} - V_{{{\text{o}^{\prime}}}} - R_{{{\text{f}^{\prime}}}} \cdot il$$
(27)
$$L_{{{\text{o}^{\prime}}}} \frac{{{\text{d}}io}}{{{\text{d}}t}} = V_{{{\text{o}^{\prime}}}} - V^{\prime}_{\text{dc}} - R_{{{\text{o}^{\prime}}}} \cdot io$$
(28)
$$C_{{{\text{f}^{\prime}}}} \frac{\text{dvo}}{{{\text{d}}t}} = il - io^{\prime}$$
(29)

where the DC filter components are represented by \(R_{{{\text{f}^{\prime}}}} ,\;L_{{{\text{f}^{\prime}}}}\) and \(C_{{{\text{f}^{\prime}}}}\) whereas the coupling components are represented by \(R_{{{\text{o}^{\prime}}}}\) and \(L_{{{\text{o}^{\prime}}}}\).

The system controllers are a similar to the VSC in the AC subgrid and consist of current, voltage, and power controllers. However, there is no need to use the d–q orientation due to the fact that the control quantities are already DC. The state-space representation form of the power circuit that includes three states is derived in (30).

$$\left[ {\begin{array}{*{20}c} {\Delta il} \\ {\mathop {\Delta io}\limits^{ \cdot } } \\ {\mathop {\Delta {\text{vo}}}\limits^{ \cdot } } \\ \end{array} } \right] = {\mathbb{A}}_{\text{pdc}} \left[ {\begin{array}{*{20}c} {\Delta il} \\ {\mathop {\Delta io}\limits^{ \cdot } } \\ {\Delta {\text{vo}}} \\ \end{array} } \right] + {\mathbb{B}}_{{{\text{pdc}}1}} \left[ {\Delta v_{\text{in}} } \right] + {\mathbb{B}}_{{{\text{pdc}}2}} \left[ {\Delta v_{\text{dc}} } \right]$$
(30)

where

$$\begin{aligned} {\mathbb{A}}_{\text{pdc}} & = \left[ {\begin{array}{*{20}c} {\frac{{R_{{{\text{f}^{\prime}}}} }}{{L_{{{\text{f}^{\prime}}}} }}} & 0 & {\frac{1}{{L_{{{\text{f}^{\prime}}}} }}} \\ 0 & { - \frac{{R_{{{\text{o}^{\prime}}}} }}{{L_{{{\text{o}^{\prime}}}} }}} & {\frac{1}{{L_{{{\text{o}^{\prime}}}} }}} \\ {\frac{1}{{C_{{{\text{f}^{\prime}}}} }}} & {\frac{1}{{C_{{{\text{f}^{\prime}}}} }}} & 0 \\ \end{array} } \right]; \\ {\mathbb{B}}_{{{\text{pdc}}1}} & = \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{{{\text{f}^{\prime}}}} }}} \\ 0 \\ 0 \\ \end{array} } \right]; \quad {\mathbb{B}}_{{{\text{pdc}}1}} = \left[ {\begin{array}{*{20}c} 0 \\ {\frac{ - 1}{{L_{{{\text{o}^{\prime}}}} }}} \\ 0 \\ \end{array} } \right] \\ \end{aligned}$$

5.2.2 Current, Voltage, and Power Controllers

The current and voltage controller consist of one state variable in each due to the use of the PI controller;

$$V_{\text{in}}^{*} = \left( {i_{l}^{*} - i_{l} } \right) \left( {K_{\text{pcdc}} + \frac{{K_{\text{icdc}} }}{s}} \right)$$
(31)
$$i_{l}^{*} = \left( {V_{\text{o}}^{{*{\prime }}} - V^{\prime}_{\text{o}} } \right)\left( {K_{\text{pvdc}} + \frac{{K_{\text{ivdc}} }}{s}} \right) + FI_{\text{o}}$$
(32)

Measuring the DC power requires an LPF to suppress the switching harmonics; thus, using the LPF introduces a state variable for the power controller. Equation (33) shows the linearized DC power.

$$\mathop {\Delta P_{\text{dc}} }\limits^{ \cdot } = \left( {\omega_{\text{f}} \left( {\left( {\Delta V^{\prime}_{\text{o}} \;*\;io^{\prime}} \right) + \left( {V^{\prime}_{\text{o}} \;*\;\Delta io^{\prime}} \right)- \Delta P_{\text{dc}} } \right)} \right)$$
(33)

5.2.3 Final State-Space Model of DC–DC Converters in DC Subgrid

Following mathematical manipulations, the final state-space model of the DC–DC converter is derived in (34).

$$\left[ {\mathop {\Delta x_{{{\text{inv}}_{\text{dc}} }} }\limits^{ \cdot } } \right] = {\mathbb{A}}_{{{\text{inv}}_{\text{dc}} }} \left[ {\Delta x_{{{\text{inv}}_{\text{dc}} }} } \right] + {\mathbb{B}}_{{{\text{inv}}_{\text{dc}} }} \left[ {\Delta v_{\text{dc}} } \right]$$
(34)

where \(\Delta x_{{{\text{inv}}_{\text{dc}} }} = \left[ {\begin{array}{*{20}c} {\Delta il} & {\Delta io} & {\Delta {\text{vo}}} & {\Delta P_{\text{dc}} } & {\Delta \varphi v_{\text{dc}} } & {\Delta \gamma i_{\text{dc}} } \\ \end{array} } \right]^{\text{T}}\)

$${\mathbb{B}}_{{{\text{inv}}_{\text{dc}} }} = \left[ {\begin{array}{*{20}c} { - \frac{{K_{\text{pcdc}} *K_{\text{pvdc}} }}{{L_{{{\text{f}^{\prime}}}} }}} \\ { - \frac{1}{{L_{{{\text{o}^{\prime}}}} }}} \\ 0 \\ 0 \\ { - K_{\text{ivdc}} } \\ { - K_{\text{icdc}} *K_{\text{pvdc}} } \\ \end{array} } \right]$$

The matrix \(\left( {{\mathbb{A}}_{{{\text{inv}}_{\text{dc}} }} } \right)\) is presented in “Appendix” (44)

5.3 Small-Signal Model of the Interlinking Converter

The model of ICs is similar to the VSC in the AC subgrid except for the power controller. The circuit diagram of ICs is depicted in Fig. 8. The power control of ICs is based on the swing equation, as shown earlier in Fig. 4. The swing equation consists of two state variables, which are shown in (35), (36).

$$\frac{{{\text{d}}\omega }}{{{\text{d}}t}} = \frac{{P_{\text{ref}} }}{2J} - \frac{{P_{\text{IC}} }}{2J} - \frac{{K_{\text{d}} *\omega_{\text{VSM}} }}{2J} + \frac{{K_{\text{d}} *\omega_{g}^{*} }}{2J}$$
(35)
$$\frac{{{\text{d}}\delta }}{{{\text{d}}t}} = \omega_{\text{VSM}}$$
(36)

where Pref and PIC are denoted for reference power command and instantaneous power of IC, respectively, while Kd is denoted for virtual damping coefficient.

Fig. 8
figure 8

Systematic of IC in the hybrid microgrid system

Full size image

5.3.1 Power Circuit Model

Similar to the VSC in the AC subgrid, the power circuit model of ICs is given in (37)–(39) whereas the state-space representation is given in (40).

$$\frac{{{\text{d}}iic_{dq} }}{{{\text{d}}t}} = \frac{{V_{dq} }}{{L_{\text{f}} }} - \frac{{m_{dq} V_{\text{dc}} }}{{L_{\text{f}} }} - \frac{{R_{\text{f}} \cdot iic_{dq} }}{{L_{\text{f}} }} \pm \omega \cdot iic_{qd}$$
(37)
$$\frac{{{\text{d}}v{\text{ic}}_{dq} }}{{{\text{d}}t}} = \pm \omega \cdot V_{qd} + \frac{{iic_{dq} }}{{C_{\text{f}} }} - \frac{{io_{dq} }}{{C_{\text{f}} }}$$
(38)
$$C_{\text{dc}} \frac{{{\text{d}}v_{\text{dc}} }}{{{\text{d}}t}} = 1.5\;m_{d} \;iic_{d} - 1.5\;m_{q} \;iic_{q} - io_{\text{dc}}$$
(39)

The state-space representation form of the power circuit that consists of five states; which is derived in (40).

$$\begin{aligned} \left[ {\mathop {\Delta x_{\text{pIC}} }\limits^{ \cdot } } \right] & = {\mathbb{A}}_{\text{PIC}} \left[ {\Delta x_{\text{pIC}} } \right] + {\mathbb{B}}_{{{\text{PIC}}1}} \left[ {\begin{array}{*{20}c} {\Delta m_{d} } \\ {\Delta m_{q} } \\ \end{array} } \right] \\ & \quad + {\mathbb{B}}_{{{\text{PIC}}2}} \left[ {\begin{array}{*{20}c} {\Delta io_{d} } \\ {\Delta io_{q} } \\ \end{array} } \right] + {\mathbb{B}}_{\text{PIC3}} \left[ {\begin{array}{*{20}c} {\Delta \omega } \\ \end{array} } \right] + {\mathbb{B}}_{\text{PIC4}} \left[ {\begin{array}{*{20}c} {\Delta io_{\text{dc}} } \\ \end{array} } \right] \\ \end{aligned}$$
(40)

where

$$\begin{aligned} \left[ {\Delta x_{\text{pIC}} } \right] & = \left[ {\begin{array}{*{20}c} {\Delta iic_{d} } & {\Delta iic_{q} } & {\Delta vic_{d} } & {\Delta vic_{q} } & {\Delta v_{dc} } \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{PIC}}1}} & = \left[ {\begin{array}{*{20}c} {V_{\text{dc}} /L_{\text{f}} } & 0 & 0 & 0 & { - 1.5io_{d} /C_{\text{dc}} } \\ 0 & {V_{\text{dc}} /L_{\text{f}} } & 0 & 0 & { - 1.5io_{q} /C_{\text{dc}} } \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{A}}_{\text{PIC}} & = \left[ {\begin{array}{*{20}c} { - R_{\text{f}} /L_{\text{f}} } & \omega & { - 1 /L_{\text{f}} } & 0 & {m_{d} /L_{\text{f}} } \\ { - \omega } & { - R_{\text{f}} /L_{\text{f}} } & 0 & { - 1 /L_{\text{f}} } & {m_{q} /L_{\text{f}} } \\ {1 /C_{\text{f}} } & 0 & 0 & \omega & 0 \\ 0 & {1 /C_{\text{f}} } & { - \omega } & 0 & 0 \\ { - 1.5m_{d} /C_{\text{dc}} } & { - 1.5m_{q} /C_{\text{dc}} } & 0 & 0 & 0 \\ \end{array} } \right] \\ {\mathbb{B}}_{{{\text{PIC}}2}} & = \left[ {\begin{array}{*{20}c} 0 & 0 & { - 1 /C_{\text{f}} } & 0 & 0 \\ 0 & 0 & 0 & { - 1 /C_{\text{f}} } & 0 \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{PIC}}3}} & = \left[ {\begin{array}{*{20}c} {iic_{q} } & { - iic_{d} } & {V_{q} } & { - V_{d} } & 0 \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{PIC}}4}} & = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {1 /C_{\text{dc}} } \\ \end{array} } \right]^{\text{T}} \\ \end{aligned}$$

5.3.2 Current and Voltage Controller

The state-space models of the current and voltage controllers are similar to the VSCs within the AC subgrid, and so the models are not repeated here.

5.3.3 Final State-Space Model of ICs

The final model of the IC including the power circuit and controllers is derived in (41).

$$\left[ {\mathop {\Delta x_{{{\text{inv}}_{\text{IC}} }} }\limits^{ \cdot } } \right] = {\mathbb{A}}_{{{\text{inv}}_{\text{IC}} }} \left[ {\Delta x_{{{\text{inv}}_{\text{IC}} }} } \right] + {\mathbb{B}}_{{{\text{inv}}_{\text{IC}} }} \left[ {\begin{array}{*{20}c} {\Delta io_{d} } \\ {\Delta io_{q} } \\ {\Delta io_{\text{dc}} } \\ \end{array} } \right]$$
(41)

The matrix \(\left( {{\mathbb{A}}_{{{\text{inv}}_{\text{IC}} }} } \right)\) is presented in “Appendix” (45), while \(\left( {\Delta x_{\text{inv}} } \right)\) and \(\left( {{\mathbb{B}}_{{{\text{inv}}_{\text{IC1}} }} } \right)\) are written as follow:

$$\begin{aligned} \Delta x_{\text{inv}} & = \left[ {\begin{array}{*{20}c} {\Delta icv_{d} } & {\Delta icv_{q} } & {\Delta io_{d} } & {\Delta io_{q} } & {\Delta {\text{vo}}_{d} } & {\Delta {\text{vo}}_{q} } \\ \end{array} } \right. \\ & \quad \left. {\begin{array}{*{20}c} {\Delta \gamma_{d} } & {\Delta \gamma_{q} } & {\Delta \varphi_{d} } & {\Delta \varphi_{q} } & {\Delta \omega } & {\Delta \delta } \\ \end{array} } \right]^{\text{T}} \\ {\mathbb{B}}_{{{\text{inv}}_{\text{IC1}} }} & & = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {\begin{array}{*{20}c} {\left( {Bp1Di1Dv1Cvr} \right)} \\ { + \left( {Bp1Di1Dv3} \right)} \\ { + Bp2} \\ \end{array} } \right)} \\ {\left( {\begin{array}{*{20}c} {\left( {Bi1Dv1Cvr} \right)} \\ { + \left( {Bi1Dv3} \right)} \\ \end{array} } \right)} \\ {Bv1*Cvr} \\ \end{array} } \\ {Bs2} \\ \end{array} } \right] \\ \end{aligned}$$

5.4 Complete Small-Signal State-Space Model of the Hybrid AC–DC Microgrid

The complete state-space model of the entire hybrid AC/DC system is written in Eq. (42), and it is detailed in “Appendix” (46) [42]. Therefore, the evaluation of the eigenvalue concept can be done based on Eq. (42) to analyze the stability of a hybrid AC/DC microgrid. The eigenvalues expose the frequency components of the overall system’s states.

$$\left[ {\mathop {\Delta x_{\text{Hybrid}} }\limits^{ \cdot } } \right] = {\mathbb{A}}_{\text{Hybrid}} \left[ {\Delta x_{\text{Hybrid}} } \right]$$
(42)

6 Small-Signal Stability Analysis

In this section, the performance of ICs with the proposed VSM-DD controller is compared to the reported dual-droop current controllers in the literature [9, 15, 33].

The overall eigenvalues of the entire hybrid AC/DC microgrid were evaluated, as shown in Fig. 9, based on the initial operation values that were determined from the time-domain simulation in PSCAD/EMTDC. Figure 9a presents the evolution of the hybrid microgrid eigenvalues using a VSM controller for the IC, while Fig. 9b presents the eigenvalues of the hybrid microgrid using just a current controller for the IC, as reported in the literature. Based on the stability analysis, it is therefore to be noted that the existence of the voltage controller loop in the IC moves the high frequency modes of the eigenvalues close to the origin which are associated to the converter AC filter and lines current, as shown in Fig. 9. The rational for this difference is that the voltage controller loop should have less bandwidth compared to the current controller loop in order to achieve a better attenuation of high frequency distortion.

Fig. 9
figure 9

Eigenvalue spectrum for the hybrid AC/DC microgrid a based on VSM; b based on only current controller

Full size image

It is clear that the hybrid AC/DC microgrid’s stability is most sensitive to the AC droop coefficient when the IC is in inversion operation mode as shown in Fig. 10. Both hybrid AC/DC microgrid systems are more sensitive to the active power dynamics as shown in Fig. 10 for varying AC power gain of ICs and in Fig. 11 for varying DC power gain. Clearly, varying the AC droop coefficients for both systems with identical ranges causes the hybrid microgrid based on current controller for the ICs to be unstable. The reason for the instability issue is the absence of disturbance rejection that can be provided via voltage controller as shown in Figs. 3 and 4, respectively. The system where its ICs based on only current controller has wider bandwidth due to the absence of voltage controller loop as depicted in Figs. 10b and 11b, respectively. Nevertheless, including the voltage controller loop provides a valuable disturbance rejection function and prevents AC voltage degradation. However, it is shown in the time-domain simulations that the proposed controller provides enhanced disturbance rejection. It is therefore recommended that the droop coefficients for VSM-DD controllers are redesigned to provide a better stability margin.

Fig. 10
figure 10

Trace of the eigenvalues as a function of the AC active power droop coefficient, a based on VSM-DD, b based on only current controller

Full size image
Fig. 11
figure 11

Trace of the eigenvalues as a function of the DC power droop coefficient: a based on VSM-DD; b based on only current controller

Full size image

Figure 11 shows the effect of the DC droop coefficients on the system stability. The stability margin of the hybrid AC/DC microgrid is less sensitive to the DC droop coefficient compared to the AC droop coefficient. When the IC is in inversion operation mode based on the VSM control concept, as shown in Fig. 11a, varying the DC droop coefficient moves the complex dominant eigenvalues to the origin point. On the other hand, the dominant eigenvalue of the system based on just the current controller loop is in real form with the same condition, as shown in Fig. 11b.

Figure 12 shows the performance of the proposed VSM-DD controller as the virtual inertia and damping coefficient are varied. The impact of varying the virtual inertia on the system eigenvalues is less than the effect of varying the virtual damping gain as shown in Fig. 12a and b, respectively. Clearly, an added degree of freedom is created which can be utilized to tune the system dynamics and maintain the overall stability.

Fig. 12
figure 12

Trace of hybrid microgrid based on VSM-DD controller: a as a function of virtual damping; b as a function of virtual inertia

Full size image

7 Scheme Evaluation Results

A nonlinear time-domain model for the hybrid microgrid system in Fig. 1 has been simulated in PSCAD/EMTDC software to verify the analytical results and show the effectiveness of the proposed VSM-DD controller. The work presented in this paper covers the examination and comparison of two hybrid AC/DC systems: one based on the proposed VSM-DD controller for the IC, and the other on dual-droop with only current control as reported in the literature [9, 19, 25]. The cases that were simulated in order to evaluate the effectiveness of the modified VSM-DD control strategy are explained below. The investigation presented here was concentrated on four important cases including the small-signal analysis and assessment.

Four simulation scenarios are considered in this section; (1) investigation of circulating currents between ICs, (2) IC performance as AC DG unit, (3) IC performance as nonlinear load as seen by the AC subgrid, 4) synchronization of ICs following faults or scheduled maintenance.

7.1 Circulation Currents Between ICs

The main issue examined in this case is the circulating current between the parallel ICs, which has been the subject of numerous published studies, whose goal was to minimize and mitigate this current [44,45,46,47]. This case comprises the evaluation of two identical hybrid AC/DC systems consisting of parallel ICs. The IC controller of one of the hybrid systems was based on using just the inner current loop, as proposed in [9, 19, 25]. The ICs of the second hybrid system are relied on the proposed VSM-DD control concept introduced in this paper.

In this case study, the operating conditions that were explained in case 1 were applied at t = 2 s. Figure 13 shows the existence of the circulating current during power exchange from the AC to the DC subgrid. As mentioned earlier, the components of the circulating current are namely cross- and zero-sequence circulating currents. The cross-circulating current is defined as the current circulated between the AC side and the DC capacitor. On the other hand, the zero-sequence circulating current is the current flow from the AC PCC voltage to DC side PCC. Based on the outcome results, the cross-circulating current is higher in comparison with the zero-sequence circulating current. Figure 13a shows that the total cross-circulating current based on the use of a current controller is about 0.125 A, but it is equal to zero when VSM-DD controller is applied. The zero-sequence circulating current is depicted in Fig. 13b for both systems with different IC controller. Using just current controller for the IC produces almost 0.12 A, compared to the VSM that equals to zero. It can be seen that with the current controller loop, the total power transfer fluctuates due to the sensitivity of the droop controller and the absence of the voltage controller, while the VSM-DD control concept suppresses this effect.

Fig. 13
figure 13

The ICs circulating current types, a cross-circulating current type between parallel ICs, b zero-sequence circulating current type between parallel ICs

Full size image

It is thus clear that using only traditional inner current control of parallel ICs introduces more operational difficulties, such as voltage and current harmonics, as well as unbalanced AC voltage at the PCC due to the lack of inertia. The introduced IC controller based on a VSM-DD control concept smooths out fluctuations and improves overall system performance. The benefits associated with the ability of a VSM-DD control algorithm to emulate the properties of traditional SMs in a hybrid AC/DC system mean that this algorithm offers greater efficiency, rather than just using current controller loop. As is evident from Fig. 13, compared to the traditional current control methods reported in the literature, the introduced concept for controlling ICs uses virtual inertia and damping to prevent the development of a circulating current between the parallel ICs. Therefore, circulating currents are yielded during the rectification mode of ICs with the current controllers only, whereas almost no circulating currents exist with the proposed VSM-DD controller.

7.2 Performance of ICs as AC DG Unit

The rational for this case is that the performance of the ICs when suppling the overloaded AC subgrid is similar to the conventional DGs in AC subgrid. Indeed, the issue of nonlinear load behavior does not occur in this case of operation. The results of this case are illustrated in Fig. 14. As can be seen in Fig. 14a, the AC subgrid becomes overloaded at t = 4 s where the AC load is increased from 1 to 2.22 MW. Figure 14b shows that the ICs for both systems compensated the shortage 0.225 MW in the active power from the DC subgrid; which includes lines losses. The behavior of ICs based on the proposed VSM-DD control has a well damped response compared to ICs based on conventional current controller. Figure 14c and d illustrate that the AC subgrid based on the proposed VSM-DD has less voltage dip compared to the system in which the ICs controller is based on conventional current controller due to the inertia existence. In fact, it can be clearly observed that the proposed controller for ICs improves the power quality of the entire hybrid AC–DC microgrid.

Fig. 14
figure 14

Performance of ICs as a DG unit seen by the ac subgrid. a The active power during AC subgrid overloading conditions; b active power injected to the AC subgrid from the DC subgrid through ICs; c AC voltage at the PCC

Full size image

7.3 Performance of ICs as Nonlinear Loads

In this case, the focus is on the issue of the IC behavior as nonlinear load. In Fig. 15, both subgrids operate under low-load conditions: the AC subgrid load is equal to 1 MW while the load in the DC subgrid is equal to 1.5 MW. At t = 3 s, the DC load increases from 1.5 to 2.3 MW, which represents an overloaded condition for the DC DG units. In response, the IC compensates for the shortage of power from the dispatchable DG unit in the AC subgrid to maintain the DC subgrid in a healthier operating condition, as shown in Fig. 15a, which indicates the power exchange from the AC to the DC subgrid via the IC.

Fig. 15
figure 15

Performance of ICs as nonlinear loads as seen by the AC subgrid. a IC power exchange during DC subgrid overloading conditions; b AC voltage during the exchange of power from the AC to the DC subgrid; c AC voltage at the PCC with current control; d AC voltage at the PCC with the proposed VSM-DD controller

Full size image

In the case of using just current control technique, the AC voltage in the AC subgrid is degraded due to the power exchange from AC to DC subgrid, as illustrated in Fig. 15b. The AC voltage fluctuations issue leads to violations of the standard requirements. The AC subgrid voltage becomes unbalanced during this situation as presented in Fig. 15c. Applying the proposed VSM-DD controller on IC utilizes this effect to support the AC voltage and helps to enhance the performance of the hybrid microgrid, as shown in Fig. 15b. Also, the applied IC controller based on the proposed VSM-DD controller smooths out these fluctuations by introducing inertia into the IC controller loop. In the systems reported in the literature, the DC subgrid affects the AC subgrid power quality, and causes fluctuations in the PCC voltage due to the lack of inertia. The introduced VSM-DD control for IC offers a remedy for this problem, which occurs during the exchange of power from the AC to the DC subgrid, as shown in Fig. 15d. In addition, integrating the VSM-DD controller into the IC also improves power quality in the entire hybrid AC/DC system.

Figure 15 shows the effect of the exchange of power from the AC subgrid to the DC subgrid through parallel ICs. At t = 3 s, the DC subgrid imports about 0.55 MW, including power losses attributable to converters and line resistance as shown in Fig. 15a. Using multiple ICs based on a conventional current controller clearly produces more voltage fluctuations, along with their associated power quality issues as illustrated in Fig. 15c. In contrast, the virtual inertia, and damping that accompanies the use of the proposed VSM-DD IC controller, eliminates these difficulties, as shown with blue curve in Fig. 15a, b, and d.

The proposed VSM-DD controlled contributes to the damping of the PCC voltage whereas the pure current controller lacks any AC voltage regulation. More importantly, the introduced virtual inertia contributes to the system damping.

7.4 Synchronization of ICs Following Outage

This case highlights the benefits of the proposed VSM-DD on IC controller over current control methods that employ just inner loop. Multiple ICs offer advantages similar to those provided by parallel transformers in a distribution system, including: increased availability of the electrical system during maintenance activities, increased power system reliability in the case of fault-initiated tripping, and easier load transportation.

At t = 6 s as shown in Fig. 16, one of the ICs is disconnected because of a short circuit situation in both hybrid AC/DC systems. Overall system performance is still reliable, with respect to supplying the required load, and using a conventional current controller for just one IC decreased the AC voltage fluctuations. Nevertheless, for one or for multiple ICs, the proposed modified VSM-DD controller is unaffected by this issue, as shown in Fig. 16b. At t = 9 s, the IC is reconnected to the system when it is assumed that the fault has been cleared. In this case, the IC based on a conventional current controller loses its synchronization and causes unstable operation for the entire hybrid AC/DC system, as illustrated in Fig. 16c. However, the proposed VSM-DD controller has a unique self-synchronization feature, such that reconnecting the IC based on the VSM controller results in a stable operation even in abnormal conditions. Fig. 16b indicates that the virtual inertia and damping creates a smooth transient response to the reconnection of the parallel ICs. It is apparent that the concept of parallel ICs increases overall system reliability and availability.

Fig. 16
figure 16

Synchronization of ICs following outages. a Effect of power exchange on the AC subgrid load in the case of multiple ICs; b power supplied to the DC subgrid via parallel ICs based on VSM-DD; c power supplied to the DC subgrid via parallel ICs based on CC

Full size image

Figure 16 reflects a major advantage of the proposed VSM-DD controller over the conventional current control; seamless synchronization and black startup performance. This case indicates that the virtual inertia and damping creates a smooth transient response to the reconnection of the parallel ICs. On the contrary, the conventional current controller loses its synchronization and causes unstable operation for the entire hybrid system as illustrated in Fig. 16c.

8 Conclusions

This paper has revealed the operational issues associated with parallel ICs, as well as a novel control strategy application for multiple ICs in a hybrid AC–DC system. The usage of VSM control also provides self-synchronization feature when an IC is reconnected following a short circuit or required scheduled maintenance. The work reported in this paper has involved the examination and comparison of two hybrid AC–DC microgrids with different controllers for ICs, VSM-DD and the conventional current controller. The impact of the VSM-DD controller on the stability of the hybrid system has been validated using time-domain simulation under PSCAD/EMTDC environment. The results demonstrate that the VSM-DD controller is more efficient than the current control methods described in the literature. Further, when the IC is reconnected following abnormal operating conditions or scheduled maintenance, the performance offered by the VSM-DD controller is superior. It should be noted that a remapping of the droop coefficients within both subgrids is recommended before implementing the proposed controller in order to maintain a similar stability margin to the conventional controllers.

The future work will be focused on the effect of short circuit issue in isolated hybrid AC/DC microgrid performance. The rational is that the system controllers are based on droop control concept which will be very sensitive to the variation of system’s voltages and frequency.