1 Introduction

Supplier selection is considered as an important part of supply chain management (SCM). One of the most important actions for creating and protecting a strong relationship between customers and organization is the process of evaluation, selection and continuous improvement to the suppliers. Selection of suppliers as a complex multi-criteria decision-making (MCDM) problem addresses both qualitative and quantitative criteria [1,2,3,4,5]. It is worth noting that one of the challenges in this area is uncertainty and limitations of information and data. In recent years in the SCM, the performance of potential suppliers has been evaluated against multiple criteria rather than considering a single factor cost [6]. Despite the importance of decision-making techniques for the construction of effective decision models for supplier selection, there are very few developments in the selection of suppliers by considering resilient criteria in the SCM. However, in previous studies there have been multiple attempts on using MCDM techniques for supplier selection. Resilience, which is the ability of the system to return to its original state or a better one after being disturbed, assumes great significance in this context [7]. Resilience has become an important concept in organizational management due to the importance of investigating effects of a disaster on an organization and its reversal to the normal state [8]. In summary, resilience strategies must be developed since it is a solution to overcome disruptions.

There are limited studies on the resilient supplier selection problem. Tang [9] regarded flexible supply base as one of the primal enablers of supply chain resilience. Hamel and Valikangas [10] viewed resilience as a distinct source of sustainable competitive advantage for suppliers. Haldar et al. [11] developed a quantitative approach for strategic supplier selection under a fuzzy environment in a disaster scenario. Using this method, organizations could design resiliency plans to mitigate the vulnerability of a supply chain system.    Sahu et al. [12] adapted an efficient decision support system (DSS) to facilitate evaluation and selection of resilient suppliers in fuzzy context with VIKOR approach. Haldar et al. [13] incorporated an analytic framework with technique for order of preference by similarity to ideal solution (TOPSIS) and analytic hierarchy process (AHP) for supply chain design to help decision makers (DMs) in selecting the most ideal resilient supplier under a disruption scenario.

It can be concluded from the above that resilient supplier selection has been addressed by several scholars in recent years. However, several issues are not properly considered in it. One aspect is using the right tools to address uncertainty. Classic fuzzy sets are able to address the judgments of experts in the process, but they cannot address aspects, such as disagreements and hesitancy. Moreover, addressing the membership degrees by intervals rather than crisp values is more practical under uncertain environments [14, 15]. Also, determining the weights of DMs for increasing the performance of the methodology has not been well addressed.

Given the existing gaps in resilient suppler selection, the purpose of this paper is to provide a method that effectively addresses uncertainty in supplier selection. For this reason, interval-valued intuitionistic fuzzy (IVIF) numbers have been used. Due to the difference in DMs in terms of expertise and knowledge, the importance of them based on objective and subjective weights is considered by introducing a new approach. Weights of criteria are addressed by using a mathematical approach based on the concept of entropy. Also, to use information in a more effective way, the method applies a last aggregation approach.

The rest of this paper is organized as follows. In Sect. 2, IVIFSs concepts are briefly reviewed. In Sect. 3, the proposed decision-making approach is presented and Sect. 4 presents the application of the proposed approach. To conclude the paper, Sect. 5 depicts the concluding remarks of this paper.

2 Preliminaries

Atanassov and Gargov [16] introduced the implication of IVIFSs, which are an extension of intuitionistic fuzzy sets introduced by Atanassov [17]. IVIF numbers express membership degree, non-membership degree and hesitation degree by using intervals rather than crisp values. These numbers have received increased attention in real-world applications [18]. This is due to the enhancement in management of uncertainty over some other methods that prefers definite numbers to confidence intervals. In this section, some definitions and concepts of IVIF numbers are described.

Definition 1

Let \(\tilde{\alpha }=\left( \left[ a_{1},b_{1} \right] ,\left[ c_{1},d_{1} \right] \right) , \tilde{\beta }=\left( \left[ a_{2},b_{2} \right] ,\left[ c_{2},d_{2} \right] \right) \) where \(\left[ a_{\mathrm {i}},b_{\mathrm {i}} \right] \subseteq \left[ 0,1 \right] , \left[ c_{\mathrm {i}},d_{\mathrm {i}} \right] \subseteq \left[ 0,1 \right] \) and \(0\le b_{i}+d_{i}\le 1\; \forall i\) be two IVIF numbers. Therefore, the followings are defined [16]:

$$\begin{aligned}&\tilde{\alpha }\oplus \tilde{\beta }=\left( \left[ a_{1}+a_{2}-a_{1}a_{2},b_{1}+b_{2}-b_{1}b_{2} \right] ,\left[ c_{1}c_{2},d_{1}d_{2} \right] \right) .\end{aligned}$$
(1)
$$\begin{aligned}&\tilde{\alpha }\otimes \tilde{\beta }=\left( \left[ a_{1}a_{2},b_{1}b_{2} \right] ,\left[ c_{1}+c_{2}-c_{1}c_{2},d_{1}+d_{2}-d_{1}d_{2} \right] \right) .\end{aligned}$$
(2)
$$\begin{aligned}&\omega \tilde{\alpha }=\left( \left[ 1-\left( 1-a_{1} \right) ^{\omega },1-\left( 1-b_{1} \right) ^{\omega } \right] ,\left[ c_{1}^{\omega },d_{1}^{\omega } \right] \right) ,\quad \omega >0 .\end{aligned}$$
(3)
$$\begin{aligned}&\tilde{\alpha }^{\omega }=\left( \left[ a_{1}^{\omega },b_{1}^{\omega } \right] ,\left[ 1-\left( 1-c_{1} \right) ^{\omega },1-\left( 1-d_{1} \right) ^{\omega } \right] \right) , \quad \omega >0. \end{aligned}$$
(4)

The extension division operator can be defined as follows [19]:

$$\begin{aligned} \frac{\tilde{\alpha }}{\tilde{\beta }}= & {} \left( \left[ \min \left( a_{1},a_{2} \right) ,\min \left( b_{1},b_{2} \right) \right] ,\left[ \max \left( c_{1},c_{2} \right) ,\right. \right. \nonumber \\&\left. \left. \max \left( d_{1},d_{2} \right) \right] \right) . \end{aligned}$$
(5)

Also, subtraction operator is defined as follows [20]:

$$\begin{aligned} \tilde{\alpha }\ominus \tilde{\beta }=\left( \left[ \frac{a_{1}-a_{2}}{1-a_{2}},\frac{b_{1}-b_{2}}{1-b_{2}} \right] ,\left[ \frac{c_{1}}{c_{2}},\frac{d_{1}}{d_{2}} \right] \right) . \end{aligned}$$
(6)

Definition 2

Let \(\tilde{\alpha }=\left( \left[ a_{1},b_{1} \right] ,\left[ c_{1},d_{1} \right] \right) , \tilde{\beta }=\left( \left[ a_{2},b_{2} \right] ,\left[ c_{2},d_{2} \right] \right) \) be two IVIF numbers. To compare these numbers, a generalized improved score (GIS) function based on unknown degree is defined as follows [21]:

$$\begin{aligned} \hbox {GIS}(\tilde{\alpha })= & {} \frac{a_{1}\mathrm {+}b_{1}}{2}+\kappa _{1}a_{1}\left( 1-a_{1}-c_{1} \right) \nonumber \\&+\kappa _{2}b_{1}\left( 1-b_{1}-d_{1} \right) , \hbox {GIS}\left( \tilde{\alpha } \right) \in \left[ 0,1 \right] , \end{aligned}$$
(7)

where \(\kappa _{1}+\kappa _{2}=1\) and \(\kappa _{1},\kappa _{2}\mathrm {\ge 0}\) show attitudinal characters of the GIS function. Finally, the comparison between IVIF numbers is obtained based on the following logic:

$$\begin{aligned} \tilde{\alpha }> & {} \tilde{\beta }\quad {\hbox {if}} \;\mathrm {GIS}\left( \tilde{\alpha } \right) >\mathrm {GIS}\left( \tilde{\beta } \right) .\nonumber \\ \tilde{\alpha }< & {} \tilde{\beta }\quad {\hbox {if}}\; \mathrm {GIS}\left( \tilde{\alpha } \right) <\mathrm {GIS}\left( \tilde{\beta } \right) .\nonumber \\ \tilde{\alpha }= & {} \tilde{\beta }\quad {\hbox {if}}\; \mathrm {GIS}\left( \tilde{\alpha } \right) =\mathrm {GIS}\left( \tilde{\beta } \right) . \end{aligned}$$
(8)

Definition 3

Let \(\tilde{A} \left\langle \left( x,\left[ {\mu _{{\tilde{A} l}} \left( x \right) ,\mu _{{\tilde{A} u}} \left( x \right) } \right] ,\left[ {\vartheta _{{\tilde{A} l}} \left( x \right) ,} { \left( x \right) } \right] ,\left[ {\pi _{{\tilde{A} l}} \left( x \right) ,\pi _{{\tilde{A} u}} \left( x \right) } \right] \right) :xX \right\rangle \) and \( \tilde{B} \left\langle \left( x,\left[ {\mu _{{\tilde{B} l}} \left( x \right) ,\mu _{{\tilde{B} u}} \left( x \right) } \right] ,\right. \right. \left. \left. \left[ {\vartheta _{{\tilde{B} l}} \left( x \right) ,\vartheta _{{\tilde{B} u}} \left( x \right) } \right] ,\left[ {\pi _{{\tilde{B} l}} \left( x \right) ,\pi _{{\tilde{B} u}} \left( x \right) } \right] \right) :xX \right\rangle \) be two IVIF numbers, while \( X\in \left\{ x_{1},x_{2},\ldots ,x_{n} \right\} ; \) then, the normalized Hamming distance operator can be defined as [22]:

$$\begin{aligned} d_{h}(\tilde{A},\tilde{B} )= & {} \frac{1}{4n}\sum \limits _{i=1}^n ( | \mu _{\tilde{A}l} ( x_{i})-\mu _{\tilde{B}l} ( x_{i}) |+ | \mu _{\tilde{A}u} ( x_{i})\nonumber \\&-\,\mu _{\tilde{B}u} ( x_{i})|+ | \vartheta _{\tilde{A}l} ( x_{i})\nonumber \\&-\,\vartheta _{\tilde{B}l} ( x_{i})|+ | \vartheta _{\tilde{A}u} ( x_{i})-\vartheta _{\tilde{B}u} ( x_{i} )|+ | \pi _{\tilde{A}l} ( x_{i})\nonumber \\&-\,\pi _{\tilde{B}l} ( x_{i})|+ | \pi _{\tilde{A}u} (x_{i})-\pi _{\tilde{B}u} ( x_{i})|). \end{aligned}$$
(9)

Definition 4

Let \(\tilde{x_{j}}=\left( \left[ a_{j},b_{j} \right] ,\left[ c_{j},d_{j} \right] \right) (j\in N)\) be a collection of IVIFNs and \(w_{j}={(w_{1},w_{2},\ldots ,w_{n})}^{T}\) be the weight vector that \(\lambda _{j}\) implying importance degree of \(\tilde{x_{j}}\), with limitations \(w_{j}\ge 0~(j\in N)\) and \(\sum _{j=1}^n {w_{j}=1}\), and let interval-valued intuitionistic fuzzy weighted averaging (IVIFWA): \(\Phi ^{{\varvec{n}}}\rightarrow \Phi \) if [22]:

$$\begin{aligned}&\left( \tilde{x}_{1},\tilde{x}_{2},\ldots ,\tilde{x}_{n} \right) =w_{1}\tilde{x}_{1}\oplus w_{2}\tilde{x}_{2}\oplus \ldots \oplus w_{n}\tilde{x}_{n}\nonumber \\&\quad =\left( \left[ 1-\mathop {\prod }\limits _{j=1}^n \left( 1-a_{j} \right) ^{w_{j}} ,1 -\mathop {\prod }\limits _{j=1}^n {(1-b_{j})}^{w_{j}} \right] ,\right. \nonumber \\&\qquad \left. \left[ \mathop {\prod }\limits _{j=1}^n {{(c_{j})}^{w_{j}},\mathop {\prod }\limits _{j=1}^n {(d_{j})}^{w_{j}} } \right] \right) . \end{aligned}$$
(10)

3 Proposed Method of Resilient Supplier Selection

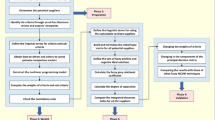
In this section, the introduced method of resilient supplier selection is presented. The method has the following main steps. First, the required data and judgments are gathered. Then, weights of criteria are computed by introducing a novel method. IVIF-COPRAS is presented to rank the suppliers based on [14]. Then, the subjective and the objective weights of DMs are computed. Finally, the scores and weights are used in an aggregation process to reach a final ranking of suppliers based on the resilience concept.

3.1 Description of Making IVIF Decision Matrices

The first step of the method consists of creating decision matrices based on experts opinions, while all matrix components are IVIF numbers. The procedure begins by forming a decision matrix that consists of criteria and alternatives for each DM. Let \(X=\left\{ x_{1},x_{2},\ldots ,x_{s} \right\} \) be a set of suppliers and \(C=\left\{ c_{1},c_{2},\ldots ,c_{n} \right\} \) be a set of criteria. Let \(D=\left\{ d_{1},d_{2},\ldots ,d_{g} \right\} \) be a set of DMs. Suppose that \(\tilde{M}^{(k)}{=\left( \tilde{m}_{ij}^{(k)} \right) }_{s\mathrm {\times }n}\)is an IVIF decision matrix, where \(\tilde{m}_{ij}^{(k)}\) is score of supplier \(x_{i}\) with respect to criterion \(c_{j}\) that is expressed by the \(d_{k}\mathrm {. }\tilde{m}_{ij}^{(k)}\) is displayed as follows:

$$\begin{aligned} \tilde{M}^{(k)}= & {} \left[ {\begin{array}{*{20}c} \tilde{m}_{11}^{(k)} &{}\quad {\begin{array}{*{20}c} \tilde{m}_{12}^{(k)} &{}\quad \cdots \\ \end{array} } &{}\quad \tilde{m}_{1n}^{(k)}\\ {\begin{array}{*{20}c} \tilde{m}_{21}^{(k)}\\ \vdots \\ \end{array} } &{}\quad {\begin{array}{*{20}c} {\begin{array}{*{20}c} \tilde{m}_{22}^{(k)}\\ \vdots \\ \end{array} } &{}\quad {\begin{array}{*{20}c} \cdots \\ \ddots \\ \end{array} }\\ \end{array} } &{}\quad {\begin{array}{*{20}c} \tilde{m}_{2n}^{(k)}\\ \vdots \\ \end{array} }\\ \tilde{m}_{s1}^{(k)} &{}\quad {\begin{array}{*{20}c} \tilde{m}_{s2}^{(k)} &{} \quad \cdots \\ \end{array} } &{} \quad \tilde{m}_{sn}^{(k)}\\ \end{array} } \right] ,\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} , \end{aligned}$$
(11)
$$\begin{aligned} \tilde{m}_{ij}^{(k)}= & {} \left( \tilde{\mu }_{ij}^{\left( k \right) },\tilde{\vartheta }_{ij}^{\left( k \right) },\tilde{\pi }_{ij}^{\left( k \right) } \right) =\left( \left[ \mu _{ij}^{-(k)},\mu _{ij}^{+(k)} \right] ,\left[ \vartheta _{ij}^{-(k)},\vartheta _{ij}^{+(k)} \right] ,\right. \nonumber \\&\left. \left[ \pi _{ij}^{-(k)},\pi _{ij}^{+(k)} \right] \right) . \end{aligned}$$
(12)

In Eq. (12), \(\tilde{\mu }_{ij}^{\left( k \right) },\tilde{\vartheta }_{ij}^{\left( k \right) }\;\text {and}\;\tilde{\pi }_{ij}^{\left( k \right) }\) are closed intervals and represent membership degree, non-membership degree and hesitation degree, respectively. For each element \(\tilde{m}_{ij}^{(k)}\), the hesitation degree is obtained as follows:

$$\begin{aligned} \tilde{\pi }_{ij}^{\left( k \right) }= & {} \left[ \pi _{ij}^{-(k)},\pi _{ij}^{+(k)} \right] \nonumber \\= & {} \left[ 1-\mu _{ij}^{+\left( k \right) }-\vartheta _{ij}^{+\left( k \right) },1-\mu _{ij}^{-\left( k \right) }-\vartheta _{ij}^{-(k)} \right] . \end{aligned}$$
(13)

3.2 Description of Computing Criteria Weights

Step 1: Normalize the decision matrix

The first step is to normalize the \( \tilde{M}^{(k)}{=\left( \tilde{m}_{ij}^{(k)} \right) }_{s\times n}\) matrix with a linear method. The criteria are categorized into two sections of profit criteria (subset B) and cost criteria (subset C). Normalized matrix \(\tilde{N}^{(k)}{=\left( \tilde{n}_{ij}^{(k)} \right) }_{s\times n}\)can be determined as follows:

$$\begin{aligned} \tilde{N}^{(k)}=\left[ {\begin{array}{*{20}c} \tilde{n}_{11}^{(k)} &{}\quad {\begin{array}{*{20}c} \tilde{n}_{12}^{(k)} &{}\quad \cdots \\ \end{array} } &{}\quad \tilde{n}_{1n}^{(k)}\\ {\begin{array}{*{20}c} \tilde{n}_{21}^{(k)}\\ \vdots \\ \end{array} } &{}\quad {\begin{array}{*{20}c} {\begin{array}{*{20}c} \tilde{n}_{22}^{(k)}\\ \vdots \\ \end{array} } &{}\quad {\begin{array}{*{20}c} \cdots \\ \ddots \\ \end{array} }\\ \end{array} } &{}\quad {\begin{array}{*{20}c} \tilde{n}_{2n}^{(k)}\\ \vdots \\ \end{array} }\\ \tilde{n}_{s1}^{(k)} &{}\quad {\begin{array}{*{20}c} \tilde{n}_{s2}^{(k)} &{}\quad \cdots \\ \end{array} } &{}\quad \tilde{n}_{sn}^{(k)}\\ \end{array} } \right] , \quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} , \end{aligned}$$
(14)

where \(\tilde{n}_{ij}^{(k)}\) is obtained based on Eqs. (15)–(19).

$$\begin{aligned} \tilde{n}_{ij}^{(k)}= & {} \left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) },\tilde{\dot{\vartheta }}_{ij}^{\left( k \right) },\tilde{\dot{\pi }}_{ij}^{\left( k \right) } \right) =\left( \left[ \dot{\mu }_{ij}^{-(k)},\dot{\mu }_{ij}^{+(k)} \right] ,\right. \nonumber \\&\left. \left[ \dot{\vartheta }_{ij}^{-(k)},\dot{\vartheta }_{ij}^{+(k)} \right] ,\left[ \dot{\pi }_{ij}^{-(k)},\dot{\pi }_{ij}^{+(k)} \right] \right) . \end{aligned}$$
(15)

The lower bound of membership degree for \(\tilde{n}_{ij}^{(k)}\) is denoted by \(\dot{\mu }_{ij}^{-(k)}\) and calculated based on Eq. (16).

$$\begin{aligned} \dot{\mu }_{ij}^{-(k)}=\frac{\mu _{ij}^{-(k)}}{\sqrt{\left( {\sum }_{i=1}^s \left( \left( \mu _{ij}^{-(k)} \right) ^{2}+\left( \mu _{ij}^{+(k)} \right) ^{2} \right) \right) }}. \end{aligned}$$
(16)

The upper bound of membership degree for \(\tilde{n}_{ij}^{(k)}\) is denoted by \(\dot{\mu }_{ij}^{+(k)}\) and calculated based on Eq. (17).

$$\begin{aligned} \dot{\mu }_{ij}^{+(k)}=\frac{\mu _{ij}^{+(k)}}{\sqrt{\left( {\sum }_{i=1}^s \left( \left( \mu _{ij}^{-(k)} \right) ^{2}+\left( \mu _{ij}^{+(k)} \right) ^{2} \right) \right) } }. \end{aligned}$$
(17)

The lower bound of membership degree for \(\tilde{n}_{ij}^{(k)}\) is denoted by \(\dot{\vartheta }_{ij}^{\mathrm {-(}k)}\) and calculated based on Eq. (18).

$$\begin{aligned} \dot{\vartheta }_{ij}^{-(k)}=\frac{\vartheta _{ij}^{-(k)}}{\sqrt{\left( {\sum }_{i=1}^s \left( \left( \vartheta _{ij}^{-(k)} \right) ^{2}+\left( \vartheta _{ij}^{+(k)} \right) ^{2} \right) \right) }}. \end{aligned}$$
(18)

The upper bound of membership degree for \(\tilde{n}_{ij}^{(k)}\) is denoted by \(\dot{\vartheta }_{ij}^{\mathrm {+(}k)}\) and calculated based on Eq. (19).

$$\begin{aligned} \dot{\vartheta }_{ij}^{+(k)}=\frac{\vartheta _{ij}^{+(k)}}{\sqrt{\left( {\sum }_{i=1}^s \left( \left( \vartheta _{ij}^{-(k)} \right) ^{2}+\left( \vartheta _{ij}^{+(k)} \right) ^{2} \right) \right) }}. \end{aligned}$$
(19)

Step 2: Calculate the entropy matrix.

Entropy is used to measure uncertainty in the system. This concept, as an objective approach, can be used instead of subjective approaches (e.g., AHP) for determining weights. However, its output includes more realistic results. In many studies, entropy method has been used to determine the weights [23, 24]. This method is used to compute uncertainty in information in terms of probability theory.

\(E\left( \tilde{m}_{ij}^{\left( k \right) } \right) \) is the entropy of \(\tilde{m}_{ij}^{\left( k \right) }\) and is defined based on Eq. (20) [25].

$$\begin{aligned} E\left( \tilde{n}_{ij}^{\left( k \right) } \right)= & {} \frac{\min \left\{ F_{Q}\left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) } \right) ,F_{Q}\left( \tilde{\dot{\vartheta }}_{ij}^{\left( k \right) } \right) \right\} +\pi _{F_{Q}\left( \tilde{n}_{ij}^{(k)} \right) }}{\max \left\{ F_{Q}\left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) } \right) ,F_{Q}\left( \tilde{\dot{\vartheta }}_{ij}^{\left( k \right) } \right) \right\} +\pi _{F_{Q}\left( \tilde{n}_{ij}^{(k)} \right) }},\nonumber \\&\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} , \end{aligned}$$
(20)

where \(\pi _{F_{Q}\left( \tilde{n}_{ij}^{(k)} \right) }=1-F_{Q}\left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) } \right) -F_{Q}\left( \tilde{\dot{\vartheta }}_{ij}^{\left( k \right) } \right) \); \(F_{Q}\left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) } \right) =F_{Q}\left( \left[ \dot{\mu }_{ij}^{-(k)},\dot{\mu }_{ij}^{+(k)} \right] \right) =\lambda \dot{\mu }_{ij}^{-(k)}+(1-\lambda )\dot{\mu }_{ij}^{+(k)}\); \(\lambda \) is the attitudinal character of Q [26].

Equation (20) can also be calculated as follows:

$$\begin{aligned} E\left( \tilde{n}_{ij}^{\left( k \right) } \right)= & {} \frac{1-\left| F_{Q}\left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) } \right) -F_{Q}\left( \tilde{\dot{\vartheta }}_{ij}^{\left( k \right) } \right) \right| +\pi _{F_{Q}\left( \tilde{n}_{ij}^{(k)} \right) }}{1+\left| F_{Q}\left( \tilde{\dot{\mu }}_{ij}^{\left( k \right) } \right) -F_{Q}\left( \tilde{\dot{\vartheta }}_{ij}^{\left( k \right) } \right) \right| +\pi _{F_{Q}\left( \tilde{n}_{ij}^{(k)} \right) }}, \nonumber \\&\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(21)

Step 3: Calculate the divergence index.

According to the entropy theory, if the entropy value for a criterion is smaller across alternatives, the criterion should be assigned a bigger weight; thereupon, the higher value of divergence index shows more importance of relevant criterion [25, 27].

Divergence index is computed in Eq. (22).

$$\begin{aligned} d_{j}^{(k)}= & {} 1-\sum \limits _{i=1}^s {E\left( \tilde{n}_{ij}^{\left( k \right) } \right) , } \quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} ;\nonumber \\&\quad j\in \left\{ 1,2,\ldots ,n \right\} . \end{aligned}$$
(22)

Step 4: Calculate the normalized weights.

In cases where DMs have incomplete information about weights, the following linear programming model is used.

$$\begin{aligned}&\hbox {Max}\sum \limits _{j=1}^n \sum \limits _{i=1}^s d_{j}^{(k)} w_{j}^{(k)},\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} .\end{aligned}$$
(23)
$$\begin{aligned}&{\hbox {Subject to:}}\nonumber \\&W\in S^{\left( k \right) }, \quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} .\end{aligned}$$
(24)
$$\begin{aligned}&{\sum }_{j=1}^n {w_{j}^{(k)}=1,\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} .}\end{aligned}$$
(25)
$$\begin{aligned}&w_{j}^{(k)}\ge 0,\quad \forall j\in \left\{ 1,2,\ldots ,n \right\} . \end{aligned}$$
(26)

Otherwise, if no information is available, weights of the criteria are obtained by Eq. (27).

$$\begin{aligned} w_{j}^{(k)}=\frac{d_{j}^{(k)}}{\sum \nolimits _{j=1}^n d_{j}^{(k)} }, \quad \forall j\in \left\{ 1,2,\ldots ,n \right\} . \end{aligned}$$
(27)

3.3 Description of Ranking Based on IVIF-COPRAS Method

Since the method is last aggregation, the following is applied for each DM separately. This approach avoids information loss caused by early aggregations.

Step 1: Calculate the weighted normalized IVIF assessment matrix \(\tilde{\hat{N}}^{(K)}\).

$$\begin{aligned} \tilde{\hat{N}}^{(K)}=\left[ {\begin{array}{*{20}c} \tilde{\hat{n}}_{11}^{(k)} &{} {\begin{array}{*{20}c} \tilde{\hat{n}}_{12}^{(k)} &{} \cdots \\ \end{array} } &{} \tilde{\hat{n}}_{1n}^{(k)}\\ {\begin{array}{*{20}c} \tilde{\hat{n}}_{21}^{(k)}\\ \vdots \\ \end{array} } &{} {\begin{array}{*{20}c} {\begin{array}{*{20}c} \tilde{\hat{n}}_{22}^{(k)}\\ \vdots \\ \end{array} } &{} {\begin{array}{*{20}c} \cdots \\ \ddots \\ \end{array} }\\ \end{array} } &{} {\begin{array}{*{20}c} \tilde{\hat{n}}_{2n}^{(k)}\\ \vdots \\ \end{array} }\\ \tilde{\hat{n}}_{s1}^{(k)} &{} {\begin{array}{*{20}c} \tilde{\hat{n}}_{s2}^{(k)} &{} \cdots \\ \end{array} } &{} \tilde{\hat{n}}_{sn}^{(k)}\\ \end{array} } \right] ,\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} , \end{aligned}$$
(28)

where

$$\begin{aligned} \tilde{\hat{n}}_{ij}^{(k)}= & {} w_{j}^{(k)}\tilde{n}_{ij}^{(k)}=\left( \left[ 1-\left( 1-\dot{\mu }_{ij}^{-\left( k \right) } \right) ^{w_{j}^{\left( k \right) }},1-\left( 1-\dot{\mu }_{ij}^{+\left( k \right) } \right) ^{w_{j}^{\left( k \right) }} \right] ,\right. \\&\left. \left[ \left( \dot{\vartheta }_{ij}^{-(k)} \right) ^{w_{j}^{(k)}},\left( \dot{\vartheta }_{ij}^{+(k)} \right) ^{w_{j}^{(k)}} \right] \right) . \end{aligned}$$

Step 2: Calculate the \(B_{i}^{(k)}\) index for each supplier and DM, while incorporating criteria are benefit ones.

$$\begin{aligned} \tilde{B}_{i}^{(k)}=\sum \limits _{j=1}^p \tilde{\hat{n}}_{ij}^{(k)} ,\quad \forall i\in \left\{ 1,2,\ldots ,s \right\} , \end{aligned}$$
(29)

where p represents the number of profit criteria.

Step 3: Calculate \(C_{i}^{(k)}\) index for each supplier and DM, while incorporating criteria are cost ones.

$$\begin{aligned} \tilde{C}_{i}^{(k)}=\sum \limits _{j=p+1}^n \tilde{\hat{n}}_{ij}^{(k)} ,\quad \forall i\in \left\{ 1,2,\ldots ,s \right\} , \end{aligned}$$
(30)

where \(n-p\) represents the number of cost criteria.

Step 4: Calculate the relative weight of each alternative based on the following formula.

$$\begin{aligned} Q_{i}^{(k)}= & {} {\hbox {GIS}(\tilde{B}}_{i}^{(k)})+\frac{{\sum }_{i=1}^s {\hbox {GIS}\left( \tilde{C}_{i}^{(k)} \right) } }{\hbox {GIS}\left( \tilde{C}_{i}^{(k)} \right) {\sum }_{i=1}^s \left( \hbox {GIS}\left( \tilde{C}_{i}^{(k)} \right) \right) ^{-1} }, \nonumber \\&\quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} ;i\in \left\{ 1,2,\ldots ,s \right\} , \end{aligned}$$
(31)

where \(\hbox {GIS}\left( \tilde{C}_{i}^{(k)} \right) \) and \( \hbox {GIS}\left( \tilde{B}_{i}^{(k)} \right) \) are scores of \(\tilde{C}_{i}^{(k)}\) and \(\tilde{B}_{i}^{(k)}\), respectively. The formula for calculating the GIS function is shown in Eq. (7).

Step 5: Choose a supplier with the highest priority over others; in other words, determine the maximum \(Q_{i}\) for each DM (\(Q_{max}^{(k)}=\mathop {\max }\limits _{i}Q_{i}^{(k)})\). As a result, the above alternative may vary for each DM.

Comparison of IVIF numbers is performed by the method of Garg [21] presented in Eq. (7).

Step 6: Calculating the utility degree of each alternative.

$$\begin{aligned} D_{i}^{(k)}= & {} \frac{Q_{i}^{(k)}}{Q_{max}^{(k)}}\times 100\% , \quad \forall k\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} ;\nonumber \\&\quad i\in \left\{ 1,2,\ldots ,s \right\} . \end{aligned}$$
(32)

It is worth noting that an alternative that has a higher \(D_{i}^{(k)}\) has a higher priority than others.

As a result, the following matrix is obtained

$$\begin{aligned} D=\left[ {\begin{array}{*{20}c} D_{1}^{(1)} &{}\quad {\begin{array}{*{20}c} D_{1}^{(2)} &{}\quad \cdots \\ \end{array} } &{}\quad D_{1}^{(g)}\\ {\begin{array}{*{20}c} D_{2}^{(1)}\\ \vdots \\ \end{array} } &{}\quad {\begin{array}{*{20}c} {\begin{array}{*{20}c} D_{2}^{(2)}\\ \vdots \\ \end{array} } &{}\quad {\begin{array}{*{20}c} \cdots \\ \ddots \\ \end{array} }\\ \end{array} } &{}\quad {\begin{array}{*{20}c} D_{2}^{(g)}\\ \vdots \\ \end{array} }\\ D_{s}^{(1)} &{}\quad {\begin{array}{*{20}c} D_{s}^{(2)} &{}\quad \cdots \\ \end{array} } &{}\quad D_{s}^{(g)}\\ \end{array} } \right] . \end{aligned}$$
(33)

3.4 Calculate Weights of the DMs

In the presented approach, the DMs’ weight computations proposed by Liu and Li [28] are extended under an interval-valued intuitionistic fuzzy environment.

3.4.1 Calculate Subjective Weights of the DMs

Weights of DMs can be divided into subjective and objective weights. Subjective weights are related to known information, like the level of familiarity with the issue at hand. The subjective weights are obtained by comparing the scores of each alternative by each DM against the criteria.

\(T_{fr}\) is defined as relative importance index of \(d_{f}\) from the point of view of \(d_{r}\) and its calculation is expressed in Eq. (34).

$$\begin{aligned} T_{fr}= & {} 1-\frac{{\sum }_{i=1}^s {\sum }_{j=1}^n {d_{h}\left( \tilde{n}_{ij}^{\left( f \right) },\tilde{n}_{ij}^{\left( r \right) } \right) } }{{\sum }_{f=1}^g {\sum }_{i=1}^s {\sum }_{j=1}^n {d_{h}\left( \tilde{n}_{ij}^{\left( f \right) },\tilde{n}_{ij}^{\left( r \right) } \right) } },\nonumber \\&\quad r,f\epsilon \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} ;\quad r\ne f. \end{aligned}$$
(34)

The overall importance index is obtained from the sum of relative importance indicators. The overall importance index for fth DM is represented by \(T_{f}\) and is calculated based on Eq. (35).

$$\begin{aligned} T_{f}=\frac{{\sum }_{r=1}^g \left( T_{fr} \right) }{g-1}, \quad \forall f\epsilon \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(35)

The larger the index \(T_{fr}\), the closer the two DMs (f and r) to each other and hence the larger the index \(\mathrm {T}_{f},\) implying a higher subjective weight. Eventually, the normalized subjective weights for fth DM are calculated based on Eq. (36).

$$\begin{aligned} {sw}_{f}=\frac{T_{f}}{{\sum }_{f=1}^g T_{f} } , \quad \forall f\epsilon \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(36)

3.4.2 Calculate Objective Weights of the DMs

The quality of each DM’s judgment is related to objective weight. In other words, the intensity of the DMs agreement with the group determines its objective weight. The weighted average matrix is defined as the ideal matrix, and the judgment information of each DM is compared with it [29]. The weighted average matrix is defined as \(\tilde{A}=\left( \tilde{a}_{ij} \right) _{s\mathrm {\times }n}\) and is calculated in Eq. (37):

$$\begin{aligned} \tilde{a}_{ij}= & {} \frac{{\sum }_{k=1}^g \left( \tilde{n}_{ij}^{\left( k \right) }\times w_{j}^{\left( k \right) } \right) }{g}\nonumber \\= & {} \frac{\left( \left[ 1-{\prod }_{k=1}^g \left( 1-\dot{\mu }_{ij}^{-(k)} \right) ^{w_{j}^{\left( k \right) }} ,1-{\prod }_{k=1}^g \left( 1-\dot{\mu }_{ij}^{+(k)} \right) ^{w_{j}^{\left( k \right) }} \right] ,\left[ {\prod }_{k=1}^g \left( \dot{\vartheta }_{ij}^{-(k)} \right) ^{w_{j}^{\left( k \right) }} ,{\prod }_{k=1}^g \left( \dot{\vartheta }_{ij}^{+(k)} \right) ^{w_{j}^{\left( k \right) }} \right] \right) }{g}\nonumber \\= & {} \left( \left[ 1-\root g \of {{\prod }_{k=1}^g \left( 1-\dot{\mu }_{ij}^{-(k)} \right) ^{w_{j}^{\left( k \right) }} },1-\root g \of {{\prod }_{k=1}^g \left( 1-\dot{\mu }_{ij}^{+(k)} \right) ^{w_{j}^{\left( k \right) }} } \right] ,\right. \nonumber \\&\qquad \left. \left[ \root g \of {{\prod }_{k=1}^g \left( \dot{\vartheta }_{ij}^{-(k)} \right) ^{w_{j}^{\left( k \right) }} },\root g \of {{\prod }_{k=1}^g \left( \dot{\vartheta }_{ij}^{+(k)} \right) ^{w_{j}^{\left( k \right) }} } \right] \right) ,\nonumber \\&\quad \forall i\in \left\{ 1,2,\ldots ,s \right\} ,j\in \left\{ 1,2,\ldots ,n \right\} . \end{aligned}$$
(37)

Based on the above matrix, \(\gamma _{f}\) is defined as the degree of similarity index of fth DM to the group of DMs.

$$\begin{aligned}&\gamma _{f}=1-\frac{{\sum }_{i=1}^s {\sum }_{j=1}^n {d_{h}\left( \tilde{n}_{ij}^{\left( f \right) },\tilde{A}_{ij} \right) } }{{\sum }_{f=1}^g {\sum }_{i=1}^s {\sum }_{j=1}^n {d_{h}\left( \tilde{n}_{ij}^{\left( f \right) },\tilde{A}_{ij} \right) } },\nonumber \\&\quad \forall f\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(38)

The normalized objective weight for fth DM is calculated in Eq. (39).

$$\begin{aligned} {ow}_{f}=\frac{\gamma _{f}}{{\sum }_{f=1}^g \gamma _{f} } ,\quad \forall f\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(39)

Let \(\rho _{f}\) be the fth DM’s integrated weight, while \(\alpha ,\beta >0\) and \(\alpha \mathrm {+}\beta \mathrm {=1}\). These values can be varied according to the type of each problems. The integrated weight of fth DM is computed in Eq. (40).

$$\begin{aligned} \rho _{f}={sw}_{f}^{\alpha }\times {ow}_{f}^{\beta } , \quad \forall f\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(40)

Finally, normalized integrated weight is obtained according to Eq. (41).

$$\begin{aligned} \rho _{f}^{*}=\frac{\rho _{f}}{\sum \nolimits _{f=1}^g \rho _{f} } ,\quad \forall f\in \left\{ d_{1},d_{2},\ldots ,d_{g} \right\} . \end{aligned}$$
(41)

3.5 Description of Aggregation Based on WASPAS Method

The aim of this step is to rank suppliers based on the computed values of D utility degrees and weights of DMs, using WASPAS method [30]. Aggregated rankings are obtained in Eq. (42).

$$\begin{aligned} \zeta _{i}= & {} \varGamma \sum \limits _{j=1}^g \left( D_{i}^{(j)}\times \rho _{j}^{*} \right) +\left( 1-\varGamma \right) \prod \limits _{j=1}^g \left( D_{i}^{(j)} \right) ^{\rho _{j}^{*}} ,\nonumber \\&\quad \forall i\epsilon \left\{ 1,2,\ldots ,s \right\} , \end{aligned}$$
(42)

where \(\varGamma \in \left[ 0,1 \right] \)

The higher \(\zeta _{i}\) for each supplier expresses the higher priority of the supplier in the assessment process.

4 Applying the Introduced Resilient Supplier Selection

In this section, the effectiveness of the proposed method in the field of selection of resilient suppliers is shown, and the results of the proposed method are compared with the results of the study by Haldar et al. [11] and Sahu et al. [12] in two case studies, respectively. Table 1 is used to convert the linguistic variables to IVIF numbers for creating decision matrix. It should be noted that these values are also applied by Zavadskas et al. [30].

Table 1 Definition of linguistic variables for the rating
Full size table
Table 2 Ratings of the suppliers under general criteria
Full size table
Table 3 Results related to determining weights of DMs based on C1-C5
Full size table

4.1 The First Case Study

An automobile giant wishes to develop a proactive resiliency strategy to rank suppliers as its commitment to the global market. As a result based on study of Haldar et al. [11], four DMs have assessed candidate suppliers according to five criteria, and the results are shown in Table 2.

Existing criteria include: product quality (C1), reliability of the product (C2), functionality of the product (C3), customer satisfaction (C4) and cost of the product (C5). C5 is a cost criterion, and C1, C2, C3 and C4 are profit criteria.

The results of the implementation of the algorithm for the general criteria are shown in Tables 3, 4 and 5, while the values of the parameters are: \( \kappa _{1}=\kappa _{2}=0.5,\alpha =\beta =0.5,\lambda =0.6,\varGamma =0.4.\)

Table 3 shows the information related to determining the weight of each DM according to general criteria. In Table 4, weights of general criteria are shown.

Table 4 Weights of general criteria
Full size table
Table 5 Utility degree and WASPAS index of suppliers according to general criteria
Full size table

Also, the choice of suppliers according to three strategic planning criteria under flexible strategy is the next step. Three strategic planning criteria are considered in developing resiliency in the supply chain systems. These resiliency criteria include:

  • Investment in capacity buffers (R1)

  • Responsiveness (R2)

  • Capacity for holding strategic inventory stocks for crises (R3)

The judgments of DMs in order to rank suppliers based on the resiliency criteria are shown in Table 6.

Table 6 Ratings of the suppliers under resiliency criteria (first case study)
Full size table
Table 7 Results related to determining the weights of DMs based on R1-R3
Full size table

The final output of the proposed method for the resiliency criteria is shown in Tables 7, 8 and 9. The ranking of suppliers under the resiliency strategy is shown in Table 9. Table 7 shows the information related to determining the weight of each DM according to resiliency criteria. In Table 8, weights of resiliency criteria are presented.

Comparing the results of Table 10 shows that \( A_{2}\) is a the best supplier. Haldar et al. [11] have used the linear combination of normalized rates for ranking suppliers. Sensitivity analysis shows that \({ A}_{2}\) is the best supplier which has a greater closeness coefficient for both strategies. The proposed method presents similar results without the matrix of the importance of criteria from DMs. The parameters of the problem do not have an excessive impact on the results which indicates that this method is more efficient.

4.2 The Second Case Study

In this subsection, the case study presented by Sahu et al. [12] is used. This section includes five DMs, three criteria and five suppliers. The suppliers’ assessment matrix is shown in Table 11.

Table 8 Weights of resiliency criteria
Full size table
Table 9 Utility degree and WASPAS index of suppliers according to resiliency criteria
Full size table
Table 10 Comparison of selection priorities for suppliers with method of Haldar et al. [11]
Full size table
Table 11 Ratings of the suppliers under resiliency criteria (second case study)
Full size table

The results of the suppliers’ ranking with two methods of Sahu et al. [12], and the proposed method are shown in Table 12.

Table 12 Comparison of selection priorities for suppliers with method of Sahu et al. [12]
Full size table

The results of both methods are exactly the same. In addition, based on the \({{\hbox {OSI}}}_{{\hbox {NRi}}}\) index, \(S_{2}\) and \(S_{5}\) are close together, and their difference is less than 0.05. The similarity of these two suppliers is confirmed based on \(\zeta _{i}\) index as their difference is 0.04. In other words, both methods indicate that \(S_{2}\) and \(S_{5}\) are in the same group as \(S_{{2}}\) has little precedence over \(S_{5}\).

5 Conclusion

Supplier selection is an important task in supply chain management. Numerous individual and integrated approaches were proposed to solve the supplier selection problem. Disruptions and delays are big threats for the success of supply chains. One approach to address disruptions in supply chains is considering resilience. Resilient supplier selection is a new research and application direction. In this paper, a new method of resilient supplier selection was introduced. The presented method applied IVIFSs to address uncertainty in supply chain environments. Moreover, the suggested method applied entropy measure and a new mathematical model to address weights of criteria. Moreover, IVIF-COPRAS was used to rank the suppliers for each expert. Weight of each expert was computed by considering the subjective and the objective approach. In order to display the applicability of this approach, two case studies from the literature were adopted and solved. For future studies, applying this method in other real-world applications, such as project selection and strategy selection, could be interesting.