1 Introduction

Cable-stayed bridges are part of transportation networks that are vulnerable to seismic loads when different supports are subjected to different seismic loads.

In earthquake response analyses of cable-stayed bridges, application of the same ground motions at different piers are quite unrealistic. In these bridges, spatial variations of ground motion are important, particularly for large distances between the support points of long structural systems. In structural applications, spatially varying earthquake motion is generally modeled with the coherency function that consists of incoherence, wave-passage and site-response effects. The wave passage effect is the time delay in the arrival of the excitation at each support, and the incoherence and local site effects caused by the heterogeneity in the ground medium. For multi-support structures, the spatially varying excitation is called the Multi-Support Excitation (MSE). Incorporating MSE can yield results that are significantly different from those based on spatially uniform free-field ground motions which have been widely used in analysis and design of conventional structures. Furthermore, the interaction of the bridge with the surrounding soil may also affect the dynamic bridge responses that is, when the external forces (e.g., due to earthquakes) act on these bridges, structural and ground displacements are not independent of each other. Response of the soil and the motion of the structure are affected by each other, and this process is called the Soil–Structure Interaction (SSI). Therefore, it is important to consider the effects of SSI and MSE in determining the dynamic bridge responses.

The literature simultaneously considers that the spatially varying ground motion and SSI effects on the dynamic responses of the cable-stayed bridges is limited. Berrah and Kausel (1992) suggested a modified response spectrum method to account for the spatial variability effect by adjusting the spectrum at each support and the existing modal cross-correlation coefficients through two correction factors. Monti et al. (1996) conducted nonlinear seismic analyses of bridges subjected to multiple support excitations. Der Kiureghian et al. (1997) performed a comprehensive investigation of the multiple support response spectrums (MSRS) method for seismic analysis of three to five-span bridge structures. They paid attention to the effect of site response arising from variation in the soil conditions at different supports of the structure. Allam and Datta (1999) presented a frequency domain spectral analysis for the seismic analysis of cable-stayed bridges for the multi-component stationary random ground motion. Zanardo et al. (2002) studied the seismic response of multi-span simply supported bridges with base isolation devices. Their analyses focused on the causal relationship between pounding and the properties of a spatially varying earthquake ground motion. Soyluk (2004) investigated the spatial variability effects of ground motions on the dynamic behavior of long-span bridges by a random vibration based spectral analysis approach and two response spectrum methods. Quan et al. (2008) determined the seismic responses of a large-span cable-stayed bridge under multi-component multi-support earthquake excitations to highlight the influence of the coherency between different components of supports on bridge responses. Bhagwat et al. (2011) studied dynamic analysis of cable-stayed bridges with a single pylon and two equal side spans, with variations in geometry and span ranging from 120 to 240 m using ANSYS program. In the study, three different seismic loading histories are chosen with various characteristics to find the structural response of different geometries under seismic loading. Kuyumcu and Ates (2012) investigated the stochastic responses of a cable-stayed bridge subjected to spatially varying earthquake ground motion using the finite element method while considering SSI effects. Maravas et al. (2014) developed a simplified discrete system to simulate the dynamic behavior of a structure founded through footings or piles under harmonic excitation. Zhou et al. (2014) studied the seismic responses of a three-tower cable-stayed bridge scale model under MSE and determined the failure modes for two strong earthquake actions by using two different nonlinear finite element models. Atmaca et al. (2014) investigated the earthquake effects on a cable-stayed bridge isolated by single concave friction pendulum bearings. The finite element model of the base isolated and non-isolated bridge is modeled using SAP2000 (2016). Three different earthquakes were applied to the bridges in the longitudinal and transverse directions. Kim (2015) investigated wave passage effect on the response spectrum of a building structure built on a soft soil layer using a finite element program. Wang et al. (2015) studied effects of support structures on vertical dynamic responses of girder bridges under different vertical strong earthquake motions. It is observed that support structures may remarkably increase or decrease vertical seismic responses of girder bridges. Liu et al. (2016) developed a new response spectrum method considering the spatially varying ground motions by incorporating the ductility factor and strain rate into the conventional response spectrum method. Adanur et al. (2016a, b, c, 2017a, b) determined the stochastic response of a suspension bridge subjected to spatially varying ground motions considering the geometric nonlinearity. The spatial variability of the ground motion is considered with the incoherence, wave-passage and site-response effects. It is observed that each component of the spatially varying ground motion model has important effects on the dynamic behavior of the bridge.

The effect of spatially varying earthquake ground motions on the Fatih Sultan Mehmet Suspension Bridge was investigated by Apaydin et al. (2016). The multi-point earthquake analysis of the bridge was carried out to understand the importance of this type of earthquake action for such long span structures. The results obtained from current analysis were compared to the simple-point analysis performed in the previous studies to indicate the differences between the two analyses. The study shows that spatially varying ground motion at multi-point supports increases in tensile stress in the main cable clearly. The increase in tensile stress in the main cable at suspension bridges may cause the changing the accounts of all the structural elements. Hence, long span suspension bridges should be subjected to spatially varying multi-point earthquake excitations for reliably determining the realistic response of bridges.

The researchers (Liang et al. 2017) investigated seismic responses of pile foundations supporting long-span cable-stayed bridge considering the seismic soil–pile–structure interaction. Shaking table tests of an integral 1:70 scaled model for a long-span cable-stayed bridge were studied. The bridge model includes synthetic soil, pile group foundation and long span cable-stayed bridge structure. Three different bridge model systems of different stiffness, namely the floating system, the elastically constrained system and the supporting pier system were tested. The wave passage effect on pile foundation supporting long-span cable-stayed bridge were studied by tests for the first time.

Although most of the published literature has focused on the effects of spatial variability of earthquake ground motion and SSI independently, a comprehensive analysis with respect to the relative importance of these effects is still lacking. There is a small number of experimental studies focusing overall structural dynamic behavior of multi-span cable-stayed bridges under MSE including SSI. In this study, it is considered the simultaneous effects of the MSE and SSI on the structural responses of cable-stayed bridges.

2 Theoretical Formulation

2.1 MDOF System with Soil–Structure Interaction Effects

The substructure method idealizes the structure as a system of finite elements, and the soil either as a continuum or as a system of finite elements. This method is computationally efficient, because the two substructures, the structure and the soil, can be analyzed separately. It takes advantage of the important fact that the response due to earthquake ground motion is essentially contained in the lower few natural modes of vibration of the structure when the base is fixed. The equilibrium equations are formed separately for each substructure. The equations for the upper structure are solved with the SSI effects being considered by the interaction forces, which are represented by a foundation impedance matrix. In more detail, considering differential ground motions at the structural support points, the equations of motion for the upper structure can be written as

$$\left[ {\begin{array}{*{20}c} {\text{M}_{{\text{ss}}} } & {\text{M}_{{\text{sb}}} } \\ {\text{M}_{{\text{bs}}} \,} & {\text{M}_{{\text{bb}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\ddot{\text{u}}}_{\text{s}}^{\text{t}} } \\ {{\ddot{\text{u}}}_{\text{b}}^{\text{t}} } \\ \end{array} } \right\}\left[ {\begin{array}{*{20}c} {\text{C}_{{\text{ss}}} } & {\text{C}_{{\text{sb}}} } \\ {\text{C}_{{\text{bs}}} } & {\text{C}_{{\text{bb}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\text{u}}}_{\text{s}}^{\text{t}} } \\ {{\dot{\text{u}}}_{\text{b}}^{\text{t}} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\text{K}_{{\text{ss}}} } & {\text{K}_{{\text{sb}}} } \\ {\text{K}_{{\text{bs}}} } & {\text{K}_{{\text{bb}}} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\text{u}_{\text{s}}^{\text{t}} } \\ {\text{u}_{\text{b}}^{\text{t}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} \text{0} \\ {\text{p}_{\text{b}} } \\ \end{array} } \right\}$$
(1)

where [M], [C] and [K] are the mass, damping, and stiffness matrices, respectively; \(\left\{ {{\ddot{\text{u}}}} \right\},\left\{ {{{\dot{\rm u}}}} \right\},\) and {u} are the acceleration, velocity, and displacement vectors, respectively; and {pb} is the integration force vector; the subscripts “ss, bb and sb” denote the structural, support, and coupled degrees of freedom, respectively; the subscripts s and b refer to structure and base, respectively (Hao et al. 1989). Following the component modes synthesis formulation, the nodal displacement vector can be decomposed into dynamic and quasi-static displacement vectors as

$${\text{u}}^{\text{t}} = \left\{ {\begin{array}{*{20}l} {\text{u}_{\text{s}}^{\text{t}} } \hfill \\ {\text{u}_{\text{b}}^{\text{t}} } \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\text{u}_{\text{s}}^{\text{d}} } \hfill \\ {\text{u}_{\text{b}}^{\text{d}} } \hfill \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}l} {\text{u}_{\text{s}}^{{\text{qs}}} } \hfill \\ {\text{u}_{\text{g}} } \hfill \\ \end{array} } \right\},$$
(2)

where \(\left\{ {\text{u}_{\text{s}}^{\text{d}} } \right\}\) and \(\left\{ {\text{u}_{\text{b}}^{\text{d}} } \right\}\) is the interaction dynamic displacement of the structure and the structure–foundation contact points, respectively; {ug} is the corresponding spatially correlated free-field ground motion vector; \(\left\{ {\text{u}_{\text{s}}^{{\text{qs}}} } \right\}\) is the quasi-static displacement of the structure. The quasi-static displacements can be obtained by substituting Eqs. (2) into (1) and setting all dynamic terms to zero, so that

$$\left\{ {{\text{u}}_{\text{s}}^{\text{qs}} } \right\} = - \left[ {{\text{K}}_{\text{ss}}^{ - 1} } \right]\left[ {{\text{K}}_{\text{sb}} } \right]\left\{ {{\text{u}}_{\text{g}} } \right\}$$
(3)

After transforming into the frequency domain, the Eq. (1) can be re-written in terms of the dynamic response displacements as

$$\left\{ {{ - \upomega }^{2} } \right\}\left[ {\begin{array}{*{20}l} {{\text{M}}_{\text{ss}} } \hfill & 0 \hfill \\ 0 \hfill & {{\text{M}}_{\text{bb}} } \hfill \\ \end{array} } \right] + {\text{i}}\upomega\left[ {\begin{array}{*{20}l} {{\text{C}}_{\text{ss}} } \hfill & {{\text{C}}_{\text{sb}} } \hfill \\ {{\text{C}}_{\text{bs}} } \hfill & {{\text{C}}_{\text{bb}} } \hfill \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {{\text{K}}_{\text{ss}} } \hfill & {{\text{K}}_{\text{sb}} } \hfill \\ {{\text{K}}_{\text{bs}} } \hfill & {{\text{K}}_{\text{bb}} + {\text{S}}_{\text{I}} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\text{u}}_{\text{s}}^{\text{d}} ({\text{i}}\upomega)} \hfill \\ {{\text{u}}_{\text{b}}^{\text{d}} ({\text{i}}\upomega)} \hfill \\ \end{array} } \right\}=\left\{ {\begin{array}{*{20}l} {\left[ {{\text{M}}_{\text{ss}} } \right]\left[ {{\text{K}}_{\text{ss}}^{ - 1} } \right]\left[ {{\text{K}}_{\text{sb}} } \right]\left\{ {{\ddot{\text{u}}}_{\text{g}} ({\text{i}}\upomega)} \right\}} \hfill \\ { - \left[ {{\text{M}}_{\text{bb}} } \right]\left\{ {{\ddot{\text{u}}}_{\text{g}} ({\text{i}}\upomega)} \right\}} \hfill \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}l} 0 \hfill \\ {{\text{P}}_{\text{b}} ({\text{i}}\upomega)} \hfill \\ \end{array} } \right\}$$
(4)

where SI is the foundation impedance matrix. By summing the matrices on the left hand-side of Eq. (4), the equation of motion for the frequency domain in the substructure method can be written as

$$\left[ {\begin{array}{*{20}l} {{\text{I}}_{\text{ss}} ({\text{i}}\upomega)} \hfill & {{\text{I}}_{\text{sb}} ({\text{i}}\upomega)} \hfill \\ {{\text{I}}_{\text{bs}} ({\text{i}}\upomega)} \hfill & {{\text{I}}_{\text{bb}} ({\text{i}}\upomega) + {\text{S}}_{\text{I}} ({\text{i}}\upomega)} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {{\text{u}}_{\text{s}}^{\text{d}} ({\text{i}}\upomega)} \hfill \\ {{\text{u}}_{\text{b}}^{\text{d}} ({\text{i}}\upomega)} \hfill \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}l} {\left[ {{\text{M}}_{\text{ss}} } \right]\left[ {{\text{K}}_{\text{ss}}^{ - 1} } \right]\left[ {{\text{K}}_{\text{sb}} } \right]\left\{ {{\ddot{\text{u}}}_{\text{g}} ({\text{i}}\upomega)} \right\}} \hfill \\ {\mathcal{ - }\left[ {{\text{M}}_{\text{bb}} } \right]\left\{ {{\ddot{\text{u}}}_{\text{g}} ({\text{i}}\upomega)} \right\}} \hfill \\ \end{array} } \right\}$$
(5)

where \({\text{I}}_{\text{ij}} \left( {{\text{i}}\upomega} \right)\) is the corresponding sub-matrix obtained by summing up the mass, damping and stiffness matrices, and

$$\left\{ {\begin{array}{*{20}l} {{\text{u}}_{\text{s}}^{\text{d}} } \hfill \\ {{\text{u}}_{\text{b}}^{\text{d}} } \hfill \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {\left[\upphi \right]} \hfill & {\left[\upgamma \right]} \hfill \\ {\left[ 0 \right]} \hfill & {\left[ {\text{I}} \right]} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {\upupsilon_{\text{s}} } \hfill \\ {\upupsilon_{\text{b}} } \hfill \\ \end{array} } \right\} = \left[ {\text{Q}} \right]\left\{ {\text{Y}} \right\}$$
(6)

where I is a nb × nb identity matrix, [ϕ] is the mode shape matrix, and \(\left[\upgamma \right] = - \left[ {{\text{K}}_{\text{ss}}^{ - 1} } \right]\left[ {{\text{K}}_{\text{sb}}^{{}} } \right]\) is the influence matrix. Substituting Eqs. (6) into (4) leads to computing the structural responses in the frequency domain. Taking the inverse Fourier transform of the frequency responses leads to the time-histories of the structural responses and hence maximum structural responses.

2.2 Method for Simulating Spatially Varying Ground Motions

Ground motion simulation considered in this study is based on the simulation method developed by Hao et al. (1989). Spatially correlated multiple ground motion time-histories are simulated using a multiple random process theory. We ensure that every simulated time-history is compatible with the prescribed power spectral density function, and each pair has coherency values compatible with the prescribed cross coherency function. Assuming that earthquake ground motions are stationary random processes having zero mean values and known power spectral density and coherency functions, it can be simulating a series of spatially correlated ground motions as to be explained in the following:

Spatial variability of the ground motion is characterized with a dimensionless and complex valued coherency function in frequency domain. The coherency function for the accelerations at the support points i and j is

$$\upgamma_{\text{ij}} (\upomega) = \frac{{{\text{S}}_{\text{ij}} (\upomega)}}{{\sqrt {{\text{S}}_{\text{ii}} (\upomega)*{\text{S}}_{\text{jj}} (\upomega)} }}$$
(7)

where Sii(ω), Sjj(ω), and Sij(ω) indicate the auto-power spectral densities of the accelerations at the support points i and j, and their cross-power spectral density, respectively. We use an alternative coherency function proposed by Der Kiureghian (1996) in the following form:

$$\upgamma_{\text{ij}} (\upomega) =\upgamma_{\text{ij}} (\upomega)^{\text{i}} \exp \left| {{\text{i}}\left( {\uptheta_{\text{ij}} (\upomega)^{\upomega} +\uptheta_{\text{ij}} (\upomega)^{\text{s}} } \right)} \right|$$
(8)

where \(\upgamma_{\text{ij}} (\upomega)^{\text{i}}\), \(\upgamma_{\text{ij}} (\upomega)^{\upomega} ,\) and \(\upgamma_{\text{ij}} (\upomega)^{\text{s}}\) characterize the incoherence, wave-passage, and site-response effects, respectively. For the incoherence effect, we use the extensively used model proposed by Harichandran and Vanmarcke (1986), which is based on the analysis of recordings made by the SMART-1 seismography array in Lotung, Taiwan and is defined as

$$\left| {\upgamma_{\text{ij}} (\upomega)} \right|^{\text{i}} = {\text{Ae}}^{{ - \frac{{2{\text{d}}_{\text{ij}} }}{{\upalpha \uptheta \left(\upomega \right)}}\left( {1 - {\text{A}} +\upalpha{\text{A}}} \right)}} + \left( {1 - {\text{A}}} \right){\text{e}}^{{ - \frac{{2{\text{d}}_{\text{ij}} }}{{\upalpha \uptheta \left(\upomega \right)}}\left( {1 - {\text{A}} +\upalpha{\text{A}}} \right)}} ,$$
(9)
$$\uptheta(\upomega) = {\text{i}}\left[ {1 + \left( {\frac{\upomega}{{2\uppi{\text{f}}_{0} }}} \right)^{\text{b}} } \right]^{ - 0.5} ,$$
(10)

where dij is the distance between support points i and j. We use the values obtained by Harichandran et al. (1996) for the model parameters \({\text{A}},\upalpha,{\text{k}},{\text{f}}_{0} ,\) and b (A = 0.636; α = 0.0186; k = 31,200; f0 = 1.51 Hz, and b = 2.95). The wave-passage effect in Eq. (8) is given by

$$\uptheta_{\text{ij}} \left(\upomega \right)^{\upomega} = - \frac{{\upomega{\text{d}}_{\text{ij}}^{\text{L}} }}{{\text{v}_{\text{app}} }},$$
(11)

where vapp is the apparent wave velocity and \({\text{d}}_{\text{ij}}^{\text{L}}\) is the projection of dij on the ground surface along the direction of propagation of seismic wave. We use the shear wave velocities of 200, 600, and 1000 m/s for soft, medium, and firm sites, respectively. The site response effect due to the differences in local soil conditions is given by

$$\uptheta_{\text{ij}} (\upomega)^{\text{s}} = { \tan }^{ - 1} \frac{{{\text{Im}}\left[ {{\text{H}}_{\text{i}} (\upomega){\text{H}}_{\text{j}} ( -\upomega)} \right]}}{{\text{Re} \left[ {{\text{H}}_{\text{i}} (\upomega){\text{H}}_{\text{j}} ( -\upomega)} \right]}},$$
(12)

where \({\text{H}}_{\text{i}} (\upomega)\) and \({\text{H}}_{\text{j}} ( -\upomega)\) are the local soil frequency functions representing the filtration through soil layers. For the soil frequency response function, a model which idealizes the soil layer as a single degree of freedom oscillator of frequency ω i and damping ratio ξ i is used as shown below;

$${\text{H}}_{\text{i}} (\upomega) = \tfrac{{\upomega_{\text{i}}^{2} + 2{\text{i}}\upxi_{\text{i}}\upomega_{\text{i}}\upomega}}{{\upomega_{\text{i}}^{2} -\upomega^{2} + 2{\text{i}}\upxi_{\text{i}}\upomega_{\text{i}}\upomega}}.$$
(13)

The power spectral density function of the ground acceleration is modeled as a filtered white noise ground motion (Clough and Penzien 1993):

$${\text{S}}_{\text{ii}} (\upomega) = {\text{S}}_{0} \frac{{\upomega_{\text{g}}^{4} + 4\upxi_{\text{g}}^{2}\upomega_{\text{g}}^{2}\upomega^{2} }}{{\left( {\upomega\,_{\text{g}}^{2} { - \upomega }^{2} } \right)^{2} + 4\upxi_{\text{g}}^{2}\upomega_{\text{g}}^{2}\upomega^{2} }}\frac{{\upomega^{4} }}{{\left( {\upomega_{\text{f}}^{2} -\upomega^{2} } \right)^{2} + 4\upxi_{\text{f}}^{2}\upomega_{\text{f}}^{2}\upomega^{2} }},$$
(14)

where S0 is the intensity parameter, ωg and ξg are the resonant frequency and damping ratio of the first filter, and ωf and ξf are those of the second filter, respectively. We consider firm, medium, and soft soil sites at the support points of the bridge model. For the filter parameters of these soil sites, we use the numerical values from Der Kiureghian and Neuenhofer (1991) as given in Table 1.

Table 1 Power spectral density parameters for model soil types
Full size table

The power spectral density function is written in matrix form as

$${\text{S}}\left(\upomega \right) = \left[ {\begin{array}{*{20}c} {{\text{S}}_{11} } & {{\text{S}}_{12} } & \cdots & {{\text{S}}_{{1{\text{j}}}} } \\ {{\text{S}}_{21} } & {{\text{S}}_{22} } & \cdots & {{\text{S}}_{{2{\text{j}}}} } \\ \vdots & \vdots & \ddots & \vdots \\ {{\text{S}}_{{{\text{i}}1}} } & {{\text{S}}_{{{\text{i}}2}} } & \cdots & {{\text{S}}_{\text{ij}} } \\ \end{array} } \right]$$
(15)

in which Sii(ω) and Sij(ω) \(\left( {{\text{i}},{\text{j}} = 1,2, \ldots ,{\text{n}}} \right)\) are defined in Eq. (7) and n is the total number of inputs to the structure. Since the matrix S(ω) is positive definite and Hermitian, it can be decomposed into the multiplication of a complex lower triangular matrix L(ω) and its Hermitian matrix \({\text{L}}^{\text{H}} \left(\upomega \right)\) by the Cholesky’s method as

$${\text{S}}\left(\upomega \right) = {\text{L}}\left(\upomega \right){\text{L}}^{\text{H}} \left(\upomega \right).$$
(16)

The matrix L(ω) is defined as

$${\text{L}}(\upomega) = \left[ {\begin{array}{*{20}l} {{\text{L}}_{11} } \hfill & 0 \hfill & \cdots \hfill & 0 \hfill \\ {{\text{L}}_{21} } \hfill & {{\text{L}}_{22} } \hfill & \cdots \hfill & 0 \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {{\text{L}}_{{{\text{i}}1}} } \hfill & {{\text{L}}_{{{\text{i}}2}} } \hfill & \cdots \hfill & {{\text{L}}_{\text{ij}} } \hfill \\ \end{array} } \right],$$
(17)

in which

$${\text{L}}_{\text{ii}} (\upomega) = \left[ {{\text{S}}_{\text{ii}} (\upomega) - \sum\limits_{{{\text{k}} = 1}}^{{{\text{i}} - 1}} {{\text{S}}_{\text{ik}} ({\text{i}}\upomega){\text{S}}_{\text{ik}}^{*} ({\text{i}}\upomega)} } \right]^{1/2}\,\,{\text{i}} = 1,2, \ldots ,{\text{n}}$$
(18a)
$${\text{L}}_{\text{ij}} ({\text{i}}\upomega) = \frac{{{\text{S}}_{\text{ij}} ({\text{i}}\upomega) - \sum\limits_{{{\text{k}} = 1}}^{{{\text{j}} - 1}} {{\text{S}}_{\text{ik}} ({\text{i}}\upomega){\text{S}}_{\text{jk}}^{*} ({\text{i}}\upomega)} }}{{{\text{S}}_{\text{jj}} (\upomega)}}\,\,{\text{j}} = 1,2, \ldots ,{\text{i}}$$
(18b)

To simulate uniform ground motions, samples of stationary random processes \({\text{u}}_{1} \left( {\text{t}} \right),{\text{u}}_{2} \left( {\text{t}} \right), \ldots ,{\text{u}}_{\text{n}} \left( {\text{t}} \right)\) are generated (Hao et al. 1989). To do this,

$${\text{u}}_{\text{k}} \left( {\text{t}} \right) = \sum\limits_{{{\text{m}} = 1}}^{\text{k}} {\sum\limits_{{{\text{l}} = 1}}^{\text{N}} {{\text{A}}_{\text{km}} } } \left( {\upomega_{\ell } } \right)\cos \left[ {\upomega_{\ell } {\text{t}} + \theta_{\text{km}} \left( {\upomega_{\ell } } \right) + \varphi_{{{\text{m}}\ell }} \left( {\upomega_{\ell } } \right)} \right]$$
(19)

where \(\upomega_{\text{l}} = \ell \Delta\upomega\), \(\Delta\upomega =\upomega_{\text{N}} / {\text{N}}\), in which ωN represents an upper cut-off frequency, \({\varphi }_{{{\text{m}}\ell }} \left( {\upomega_{\ell } } \right)\) is a random phase angle uniformly distributed over the range 0–2π. φml and φrs should be statistically independent unless m = r and n = s; k represents the support points; \({\text{A}}_{\text{km}} \left( {\upomega_{\ell } } \right)\) and \(\uptheta_{\text{km}} \left( {\upomega_{\ell } } \right)\) denote the amplitudes and phase angles of the generated time histories, respectively, which ensure the spectrum of time histories compatible with those given in Eq. (15), and can be estimated by

$${\text{A}}_{\text{km}} \left( {\upomega_{\ell } } \right) = \sqrt {4\Delta\upomega} \left| {{\text{L}}_{\text{km}} \left( {\upomega_{\ell } } \right)} \right|\quad \quad 0 \le\upomega_{\text{k}} \le\upomega_{\text{N}} \,$$
(20a)
$$\uptheta_{\text{km}} \left( {\upomega_{\ell } } \right) = \tan^{ - 1} \left\{ {\frac{{\text{Im} \left[ {{\text{L}}{}_{\text{km}}\left( {\upomega_{\ell } } \right)} \right]}}{{\text{Re} \left[ {{\text{L}}{}_{\text{km}}\left( {\upomega_{\ell } } \right)} \right]}}} \right\}\quad 0 \le\upomega_{\text{k}} \le\upomega_{\text{N}}$$
(20b)

Because earthquake motions are non-stationary processes, the non-stationary ground motion time-histories at different locations can be obtained by multiplying each corresponding stationary time histories with an appropriate shape function \(\upxi\left( {\text{t}} \right)\):

$${\text{a}}_{\text{k}} \left( {\text{t}} \right) =\upxi\left( {\text{t}} \right){\text{ u}}_{\text{k}} \left( {\text{t}} \right),$$
(21)

where

$$\upxi\left( {\text{t}} \right) = \left\{ {\begin{array}{*{20}l} {\left( {{\text{t/t}}_{0} } \right)^{2} } \hfill & {0 \le {\text{t}} \le {\text{t}}_{0} } \hfill \\ 1 \hfill & {{\text{t}}_{0} < {\text{t}} \le {\text{t}}_{\text{n}} } \hfill \\ {\exp \left( { - 0.394\left( {{\text{t}} - {\text{t}}_{\text{n}} } \right)} \right)} \hfill & {{\text{t}}_{\text{n}} < {\text{t}}} \hfill \\ \end{array} } \right\},$$
(22)

in which t0 and tn, respectively, denote the initial and the ending time of the stationary segment in dominant earthquake vibration. Once a response spectrum has been specified for a given site, ground motion time-histories can be adjusted to be compatible with the specified spectrum. In this study, each simulated time-history is generated to be compatible with the EC 8 (2004) response spectra with damping ratio 0.02 normalized to 0.5 g PSA. EC 8 defines the reference elastic spectra Se in terms of the pseudo-acceleration as a function of the building natural period, T, by means of the following expressions:

$$\begin{array}{*{20}l} {0 \le {\text{T}} \le {\text{T}}_{\text{B}} ,} & {{\text{S}}_{\text{e}} = {\text{a}}_{\text{g}}\,{\text{S}}\left[ {1 + \frac{\text{T}}{{{\hbox{T}}_{\text{B}} }}\left( {2,5\upeta - 1} \right)} \right],} \\ {{\text{T}}_{\text{B}} \le {\text{T}} \le {\text{T}}_{\text{C}} ,} & {{\text{S}}_{\text{e}} = 2,5{\text{a}}_{\text{g}}\, {\text{S}}_{\upeta} ,} \\ {{\text{T}}_{\text{C}} \le {\text{T}} \le {\text{T}}_{\text{D}} ,} & {{\text{S}}_{\text{e}} = 2,5{\text{a}}_{\text{g}}\, {\text{S}}_{\upeta} \frac{{{\text{T}}_{\text{C}} }}\,{\text{T}},} \\ {{\text{T}}_{\text{D}} \le {\text{T}} \le 0,4{\text{s}},} & {{\text{S}}_{\text{e}} = 2,5{\text{a}}_{\text{g}}\, {\text{S}}_{\upeta} \frac{{{\text{T}}_{\text{C}}\, {\text{T}}_{\text{D}} }}{{{\text{T}}^{2} }},} \\ {{\text{a}}_{\text{g}} =\upgamma_{\text{I}} {\text{ a}}_{\text{g,R}} ,} \end{array}$$
(23)

where \({\text{a}}_{\text{g,R}}\) is the reference peak ground acceleration for ground type A; \(\upgamma_{\text{I}}\) is the importance factor; \(\upeta\) is the damping correction factor; S is the soil amplification factor; and TB, TC, and TD are characteristic periods of the response spectrum depending on the soil type. Table 2 shows the values of S, TB, TC and TD for different soil types. While generating response spectrum compatible ground motions, soil types classified according to the EC 8 are used for soft, medium and firm soil sites.

Table 2 Power spectral density parameters for model soil types
Full size table

We assume the ground motion duration to be 20 s. To improve the computational efficiency, the ground motions are generated in the frequency domain by using the fast Fourier transform technique, with the total number of points N = 512 for each simulated time history.

2.3 Adjustment of the Simulated Ground Motions

Bi and Hao (2011) investigated the effect of irregular topography and random soil properties on coherency loss of spatial ground motions on the surface of a layered site. The random soil properties considered in their analysis are shear modulus, soil density, and damping ratio of each layer, which are modeled by independent one-dimensional random fields in the vertical direction, and all are assumed to follow normal distributions. In our study, the coherency loss function of the surface ground motion is derived in two steps: first, the ground motion time histories are generated based on the power spectral density functions derived from one-dimensional wave propagation with random site properties, and then, the coherency loss function on the generated surface ground motions is statistically derived. Filtered Tajimi–Kanai power spectral density function parameters with duration T = 20 s and peak ground acceleration (PGA) 0.2 g based on the standard random vibration method are used (Der Kiureghian 1980).

In this study, ground motion time-histories are generated for MSE depending on the spatially varying ground motion components of incoherence, wave-passage and site response effects.

In addition, Fourier spectrums of ground acceleration time-histories that equal the velocity response spectrum for zero damping are used. A baseline correction method proposed by Chiu (1997) is also applied to each simulated acceleration time history. Displacement time histories are obtained from the double integration of the baseline corrected acceleration time histories. Figure 1 plots the baseline corrected displacements at support points along the bridge span. Each baseline corrected displacement is simultaneously applied to the model in the vertical and horizontal directions at support points.

Fig. 1
figure 1

Baseline corrected displacement at support points of the bridge

Full size image

3 Description of the Cable-Stayed Bridge

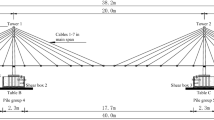
The bridge model used in this study is the Quincy Bay-view Bridge crossing the Mississippi River in the USA. The bridge has two H-shaped concrete towers, double plane semi-harp type cables and a composite concrete-steel girder bridge deck (Fig. 2).

Fig. 2
figure 2

a Quincy Bay-view bridge; b 3D model of the bridge

Full size image

The bridge has three spans and the cables are configured as double-plane fan type. As shown in Figs. 3, 4, the main span is 274 m, and the each of equal side spans are 134 m. The total length of the bridge is 542 m.

Fig. 3
figure 3

The dimensions and geometry of the bridge

Full size image
Fig. 4
figure 4

Cross section of the tower

Full size image

The height of towers from the waterline is about 70 m. There is a total of 56 cables, while 28 cables are supporting the main span, 14 cables are supporting each side span. The cable members are spaced 2.75 m at the upper part of the towers and equally spaced at the deck level on the sides as well as main span. The width of the deck from center to center of cables is 12 m. The left and right anchor supports are kept as pinned and roller supports, respectively. A detailed description of the bridge is given in Wilson and Gravelle (1991).

In this study, the generated structural model is analyzed to determine the dynamic performance of the bridge under MSE by considering SSI effects. All analyses are performed using SAP (2000) Version 18 software for each soil site. The soil–pile system is represented by three dynamic impedance coefficients corresponding to swaying, rocking, and cross-swaying-rocking terms.

The deck and tower members are modeled by frame elements. The cable element can be considered as truss element that weight is neglected. But under its own dead load and axial tensile force, a cable supported at its end will sag into a catenary shape. The axial stiffness of a cable may adjust with changes in the sag, and the stiffness characteristics of an inclined cable can exhibit a nonlinear behavior. For this nonlinear behavior, equivalent modulus of elasticity is used in the cables, which is known to well describe the catenary action of the cable (Wang et al. 2002). The properties of cables and soil sites are given in Tables 3 and 4, respectively.

Table 3 Properties of the cables
Full size table
Table 4 Properties of local soil conditions
Full size table

The bridge deck is considered as continuous beam as it does not transmit moment to the towers through the deck–tower connection. There are three sections on the elevation on the towers. The relevant properties of the bridge deck and towers are given in Table 5.

Table 5 Properties of the deck and the towers
Full size table

4 Modeling of the Bridge Pile Foundation

The model is composed of a super-structure and is founded on pile foundations. The system, shown in Fig. 5, founded on a single flexible circular solid pile of Young’s modulus Ep, diameter d, mass per unit length mp, and length L which is greater than effective pile length (Gazetas and Mylonakis 2002; Syngros 2004.). Accordingly, the pile can be modeled as an infinitely long beam. The soil around the pile is assumed to be a linearly elastic, homogeneous isotropic half space.

Fig. 5
figure 5

Model of a pile-supported structure using: a three impedance functions; and b two dynamic impedances below ground surface (reduced model)

Full size image

The soil–pile system can be represented by three dynamic impedance coefficients \({\text{K}}_{\text{xx}}^{*}\), \({\text{K}}_{\text{rr}}^{*}\), and \({\text{K}}_{\text{xr}}^{*}\) corresponding to swaying, rocking, and cross-swaying-rocking terms, respectively. In this study, the following dynamic impedance functions are used (for derivation, see, Novak 1974) based on the Winkler model of soil reaction

$$\begin{aligned} & {\text{K}}_{\text{xx}}^{*} = 4{\text{E}}_{\text{p}}\,{\text{I}}_{\text{p}}\uplambda^{3} , \\ & {\text{K}}_{\text{xr}}^{*} = 2{\text{E}}_{\text{p}}\, {\text{I}}_{\text{p}}\uplambda^{2} , \\ & {\text{K}}_{\text{rr}}^{*} = 2{\text{E}}_{\text{p}}\, {\text{I}}_{\text{p}}\uplambda, \\ \end{aligned}$$
(24)

where (\({\text{E}}_{\text{p}}\,{\text{I}}_{\text{p}}\)) is the bending stiffness of the pile cross-section, and λ is a wave number parameter controlling the attenuation of pile displacement with depth and is given by (Wolf and Von Arx 1978; Wolf et al. 1981)

$$\uplambda = \left( {\frac{{{\text{k}}_{\text{x}} - {\text{m}}_{\text{p}}\upomega^{2} + {\text{i}}\upomega{\text{c}}_{\text{x}} }}{{4{\text{E}}_{\text{p}}\,{\text{I}}_{\text{p}} }}} \right)^{1/4} ,$$
(25)

where kx and cx are the moduli of distributed springs and dashpots along the pile according to the Winkler assumption. These parameters are related to soil stiffness and frequency through the following (Wolf and Von Arx 1978; Wolf et al. 1981):

$${\text{k}}_{\text{x}} =\updelta{\text{E}}_{\text{s}} ,$$
(26)
$${\text{c}}_{\text{x}} = 6\left( {{\text{a}}_{0}^{\text{p}} } \right)^{ - 1/4}\uprho_{\text{s}}\,{\text{V}}_{\text{s}} {\text{d}} + 2\frac{{\upzeta{\text{k}}_{\text{x}} }}{\upomega},$$
(27)

in which \({\text{a}}_{0}^{\text{p}}\) is the dimensionless frequency parameter for a pile and given by

$${\text{a}}_{0}^{\text{p}} = \frac{{\upomega{\text{d}}_{\text{p}} }}{{{\text{V}}_{\text{s}} }},$$
(28)

where dp is the pile diameter, Vs is a value for the shear wave velocity in the soil, \(\updelta\) is the dimensionless Winkler factor and is given as a function of pile–soil stiffness ratio (Ep/Es) (Dobry et al. 1982)

$$\updelta = 1.67\left( {\frac{{{\text{E}}_{\text{p}} }}{{{\text{E}}_{\text{s}} }}} \right)^{ - 0.053} .$$
(29)

Under earthquake loading, the result of the distributed reactions is applied at depth e below the pile head (Fig. 5). Since the reference system is located at the pile head, a bending moment (\({\text{K}}_{\text{xx}}^{{}} \times {\text{e}}\)) corresponding to the cross-swaying-rocking impedance term \({\text{K}}_{\text{xr}}^{*}\) is necessary for assembling the foundation impedance matrix. This additional term is not compatible with the analysis of the spread footing, as the rocking and the swaying spring are coupled and, thereby, the corresponding displacements cannot be determined independently. To overcome this problem, the reference system is translated to a depth e, where the overall soil reaction is applied. Thus, the cross impedance \({\text{K}}_{\text{xr}}^{*}\) vanishes and the impedance matrix of the pile becomes diagonal, described solely by translational and rotational springs, as shown in Fig. 5b.

The transformed impedances \({\text{K}}_{\text{xxe}}^{*}\) and \({\text{K}}_{\text{rre}}^{*}\) can be easily determined from

$${\text{K}}_{\text{xxe}}^{*} = {\text{K}}_{\text{xx}}^{*} ,$$
(30)
$${\text{K}}_{\text{rre}}^{*} = {\text{K}}_{\text{rr}}^{*} - 2{\text{K}}_{\text{xr}}^{*} {\text{e}} + {\text{K}}_{\text{xx}}^{*} {\text{e}}^{2} ,$$
(31)

where e is the eccentricity and is defined as

$${\text{e}} = \frac{{{\text{K}}_{\text{xr}}^{*} }}{{{\text{K}}_{\text{xx}}^{*} }} = \frac{1}{{2\uplambda}}.$$
(32)

The soil–bridge interaction model used in this study under MSE is shown in Fig. 6. The bridge towers are supported on rigidly capped piles. The piles are spaced at two pile diameters. Pile foundations consist of (2 × 4) piles on both the left and right sides. As shown in Fig. 6, the transformed impedances \({\text{K}}_{\text{xxe}}^{*} {}^{\text{n}}\) and \({\text{K}}_{\text{rre}}^{*} {}^{\text{n}}\) are calculated for all soil cases and applied to the model under the pile head at depth e. In the figure, n is the number of pile. Under seismic loading, it will be assumed that the bridge supports are founded on different soil cases for dynamic analyses.

Fig. 6
figure 6

Soil–pile–bridge system subjected to longitudinal and vertical ground motions

Full size image

5 Modal Analysis

An adequate level of safety of large span bridges against dynamic loadings can be achieved if the dynamic properties of the bridge such as natural frequencies, mode shapes, and damping ratios are accurately determined. It is well known that the frequency of seismic motion and the variation of fundamental period affect the seismic response of the bridge.

We performed modal analysis to understand the effects of SSI on the fundamental period of bridge foundation-soil system, and determined the first 15 natural frequencies, fundamental periods and their corresponding mode shapes. The results for the first five modes are presented in Table 6.

Table 6 Natural frequencies, fundamental periods and corresponding mode shapes obtained from the modal analysis of the bridge
Full size table

In the Table 6, the first column is the mode numbers, the second column presents their corresponding mode shapes and the third column presents natural frequencies (f) and fundamental periods (T) for all soil types. Mode shapes are nearly the same for the bridge models on different sites. The first frequency of vibration in the transverse direction is about 0.20 Hz. The frequencies of vibration in all soil types are in the range of 0.20–0.60 Hz for the first five modes. The most significant modes of the bridge are below 1.5 Hz.

6 Dynamic Bridge Responses Under MSE

The behavior of two-dimensional finite element models of cable-stayed bridges have been widely studied. Studies that take into account the torsional effect are very few and some of these are given by ASCE (1992), Ermopoulos et al. 1993. The purpose of this study is to determine both SSI and MSE effects on the dynamic characteristics of three-dimensional cable-stayed bridge including pile foundation, in which the transformed impedances are calculated for three cases. The time histories of the ground motion are generated for different soil sites, and then simultaneously applied in horizontal and vertical directions to the selected bridge. The ground motions are assumed to travel across the bridge span supported at each point. A baseline correction method is also applied to each simulated acceleration and displacement time history plots. Seismic responses of the deck and tower obtained from the MSE analyses are compared, and are discussed for different soil cases.

The responses of the bridge in terms of vertical displacement for different soil sites along the deck are depicted in Fig. 7. This figure shows that, for each soil site, vertical displacements of the deck are significantly different each other’s. In addition, maximum vertical displacements occurred in the soft sites. In firm, medium, and soft sites, the maximum vertical displacements are 0.71, 0.57, and 0.87 m, respectively. In firm and medium sites, values of vertical displacements are nearly the same and so these curves overlap. Maximum vertical deck displacements that occurred in the soft site are approximately 0.5 times larger than those that occurred in the medium site. For all soil sites, vertical displacements are the largest between the middle of the supports and the deck/tower conjunction points.

Fig. 7
figure 7

Dynamic vertical displacement of the deck

Full size image

Internal member forces obtained on different sites are depicted in Figs. 8, 9 10, which also show the tower and deck lines. Internal member forces are larger in the soft site compared to the other sites. Dynamic axial forces along the deck are found to be highest in the middle of the left side span for all soil sites (see Fig. 8). These forces reduce near bridge supports, deck/tower conjunction points, and in the middle of the bridge span for all soil sites. The maximum axial forces are 58,668, 36,818, and 35,370 kN for soft, medium, and firm sites, respectively.

Fig. 8
figure 8

Dynamic axial forces along the deck

Full size image
Fig. 9
figure 9

Dynamic shear forces along the deck

Full size image
Fig. 10
figure 10

Dynamic bending moments along the deck

Full size image

Shear forces are found to be largest at points closer to supports and deck/tower conjunction points (see Fig. 9). The largest shear forces are generally obtained on the soft site. The maximum shear forces are 3858, 3344, and 2809 kN for soft, medium and firm sites, respectively.

Bending moments are lowest at points closer to supports and are highest in the middle of the bridge end span for all soil sites (Fig. 10). The largest bending moments are generally obtained on soft site.

The study was carried out on the bridge with symmetric geometry and dimensions. Due to multiple support excitation, the horizontal displacements of the left and right towers given in Figs. 11 are not the same. The largest horizontal displacements are observed for the soft site. For all soil sites, horizontal tower displacements are highest near the top of both towers (Fig. 11). Horizontal displacements on the soft site are up to twice as large as those on the firm site for the right tower. Horizontal displacements are in the range of 0.10–0.67 m.

Fig. 11
figure 11

Horizontal displacements on the towers

Full size image

The results in Figs. 13, 14 give that the left and right tower axial forces, shear forces, and bending moments are not the same for the different sites. Axial forces are largest for both towers on the soft site and the differences of these forces between towers are rather apparent (Fig. 12). While maximum axial forces on the left tower for firm, medium, and soft sites, are 5275, 6215, and 9646 kN, these on the right tower are 3343, 3200, and 4224 kN, respectively.

Fig. 12
figure 12

Dynamic axial forces along the tower height

Full size image

Tower shear forces are largest for the soft site on both towers (Fig. 13). The largest shear forces occur around the deck/tower conjunction points for each soil case. Shear forces are not the same on both towers, but they are close to each other on firm and medium sites. While maximum shear forces for firm, medium and soft sites, respectively, are 11457, 11301, and 15309 kN on the right tower, they are 12392, 11492, and 17991 kN on the left tower.

Fig. 13
figure 13

Dynamic shear forces along the tower height

Full size image

For each soil site, while tower bending moments are zero at the top and the bottom of each tower, the largest bending moments are found near the deck/tower conjunction region and the midpoints on each tower (Fig. 14). Minimum bending moments on the left tower are nearly the same for each soil site. Maximum bending moments on the left tower are 165253, 155897, and 228162 kNm for soft, medium and firm soil sites, respectively.

Fig. 14
figure 14

Dynamic bending moments along the tower height

Full size image

7 Conclusions

In the current study, the effectiveness of the soil–structure interaction and multiple support excitation was investigated. The soil surrounding the pile is linearly elastic and homogeneous isotropic half space. The system is represented by the dynamic impedance functions based on the Winkler model of soil reaction. The MSE is generated to be compatible with the spatially varying ground motion components such as incoherence, wave-passage, and site response for three soil cases. The baseline correction method is also used to each simulated acceleration and displacement time history plots. The time histories of simulated ground motions are applied to the bridge simultaneously for both longitudinal and vertical directions. The following conclusions can be drawn from the analysis of the considered bridge model:

It is apparent that when the bridge foundation rests on a soft site as opposed to other soil sites, the deck and tower responses are larger. In addition, the responses are significantly affected by the soil conditions. Neglecting the SSI effect may result in considerable damage to the bridge under severe earthquakes, and thus endanger overall structural safety.

Although the bridge has symmetric geometry and dimensions, due to multiple support excitation, the displacements of the deck and the left and right towers are not the same.

The results highlight the importance of deck vertical displacements and horizontal displacements of the hoop modeling of such bridges.

The results from the vertical displacement of the deck and the horizontal displacement of the tower suggest what the predicted values are for modeling such bridges.

Both MSE and SSI effects should be considered in the analysis of cable-stayed bridges, because these effects can significantly change the dynamic behavior of long span bridges.

The most important results obtained from the study; cable-stayed bridges are important structures and such long span bridges should be analyzed using spatially varying ground motion for their different supports to obtain reliable responses under earthquake load.