Introduction

Patients with percutaneous intervention of small coronary vessels seem to have a greater advantage from drug-eluting stents (DESs) compared to stenting of large native vessel. However, stent-based local drug delivery might be associated with delayed and incomplete endothelialization, and the potential risk of subacute and even late stent thrombosis.1,2,3,4,5,6,7,8,9 In light of these considerations, DESs are not typically the preferred choices for interventional treatment and endovascular therapies based on coated-balloon technologies were resurrected recently, and demonstrated greater assurance. Few model studies on drug-coated balloon (DCB) delivery have been carried out in recent past.10,11,12 The potential advantages of balloon-based local drug delivery over DES include homogeneous drug coating, rapid and uniform transfer of antiproliferative drugs during the angioplasty procedure, and also uniform longitudinal and circumferential delivery,13,14 which has been shown to be an effective substitute for sustained release.15 The balloon delivers high drug concentrations within the vessel wall over a short period of inflation time, and a significant portion of drug is in the undissolved state.10,16 First in-man trial with a paclitaxel-coated balloon catheter have shown beneficial effects in the treatment of coronary in-stent restenosis17 and in peripheral arteries.18 Several experimental and pre-clinical studies have evaluated long-term DCB efficacy for coronary and peripheral vascular beds by characterizing dose-dependent biologic and vascular bed-associated responses.13,19,20 None of these studies specifically focussed on quantifying the mechanistic underpinnings of drug release and tissue uptake, which leaves us with an incomplete understanding of how these devices work and what causes their failure. Different DCBs display distinct kinetic characteristics for a given drug due to differences in coating method, solubility, rate of release, binding capacity, tissue penetration and retention.21,22 However, these initial pre-clinical findings need to be corroborated by further investigation and longer follow-up data.

Kolachalama et al.10 showed that a large bolus of balloon-released Zotarolimus and its constituents transfer during inflation; some of the drug coating pervades the tissue while a fraction of the coating adheres to the mural interface. This animal study along with bench-top experiments and in silico modeling all disregarded the effect of interstitial fluid flow and the presence of plaque. As the arterial ultrastructure and the presence of atherosclerotic plaque in influencing vascular pharmacokinetics are likely to become critical considerations for the success of intravascular delivery device,9,19,23,24,25,26 Mandal et al.11 augmented plaque with non-uniform disease compositions as opposed to healthy arterial vessel in their model studies and opined that the presence of patient-specific atherosclerotic vessel with heterogeneous plaque compositions promotes non-uniform tissue uptake and retention of Zotarolimus, and drug distribution after balloon inflation within diseased arterial vessel tracks precisely with lesion-specific transport properties is an important consideration for DCB delivery technology. This study lacks the consideration of plasma convection and the internalization of drug in the process of endocytosis which seem to have a pivotal role in the success of this endovascular therapy.

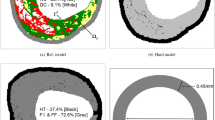
As a direct extension and application of the studies,10,11,12 a computational model is evolved by leveraging a finite difference scheme in staggered grids that provided with the flexibility to simulate the transport of a model drug and its retention together with its internalization in the process of endocytosis within a diseased porous vessel consisting of healthy tissue and regions of fibrous cap, fibro-fatty, calcified and necrotic core lesions.27 Mandal et al.11 simulated DCB delivery to arteries of heterogeneous plaque compositions obtained from intravascular ultrasound-derived virtual histology (IVUS-VH). The binding of drug was taken into consideration in their studies. In a bid to extend this latest model, the impact of interstitial fluid flow on the transport of free drug and its retention together with the internalization of bound drug and lysosomal degradation during endocytosis have been explored in the model considered. An advection–reaction–diffusion model that describes saturable reversible kinetics is considered to quantify arterial pharmacokinetics. The flow of interstitial fluid through diseased porous wall has been duly accounted for. An image segmentation technique based on an unsupervised clustering algorithm is leveraged to automatically get segmentations based on colors (Figs. 1a and 1b).28 Details of geometry reconstruction and image processing technique are reported in Mandal et al.11 The governing equations of motion along with the prescribed conditions are successfully solved by marker and cell (MAC) method primarily introduced by Harlow and Welch.29 The novelty of this study lies with the use of simple finite difference scheme in staggered grid setting in a highly heterogeneous region in order to quantify the therapeutic efficacy of drug.

Figure 1
figure 1

Virtual histology derived computational geometry. (a) Longitudinal image of the arterial vessel was obtained from König and Klauss.27 (b) An image processing technique based on k-means clustering was used to identify different sub-domains of the arterial vessel: fibrous (dark green), fibrofatty (light green), dense calcium (white), necrotic core (red) and gray (healthy tissue). c Outline of the final geometry derived for computational modeling.

Full size image

Computational Model

The computational domain is comprised of a longitudinal arterial segment derived via image processing (Fig. 1c). The governing equations representing the interstitial flow in the porous media are Brinkman equations and continuity equation for \(t > t_{0}\) whose manifestations in two-dimensional Cartesian coordinates system in conservative form are

$${\partial u_{x} \over \partial t} + {\partial u_{x}^{2} \over \partial x} + {\partial (u_{x}u_{y}) \over \partial y} = -{\frac{1}{\rho }}{\partial p \over \partial x} + {\mu \over \rho } \left[ {\partial ^2u_{x} \over \partial x^{2}} + {\partial ^{2}u_{x} \over \partial y^{2}}\right] - \frac{\mu }{\rho k}{u_{x}},$$
(1)
$${\partial u_{y} \over \partial t} + {\partial (u_{x}u_{y}) \over \partial x} + {\partial u_{y}^{2} \over \partial y} = -{\frac{1}{\rho }}{\partial p \over \partial y} + {\mu \over \rho } \left[ {\partial ^2u_{y} \over \partial x^{2}} + {\partial ^{2}u_{y} \over \partial y^{2}} \right] - \frac{\mu }{\rho k}{u_{y}},$$
(2)
$${\text {and}} \quad {\partial u_{x} \over \partial x} + {\partial u_{y} \over \partial y} = 0,$$
(3)

where x and y are the coordinates with the x-axis located along the centreline of the domain. The axial and the transverse components of velocity are \(u_{x}\) and \(u_{y},\) respectively, \(\rho\) is the density of plasma and \(\mu\) its viscosity. Here, k represents Darcy permeability. [It is assumed that during the period of inflation \((t_{0})\) of the balloon, all the pores along the lumen–tissue interfaces (in the sequel it is called ‘interfaces’ only) get blocked, so it is quite reasonable to assume that no interstitial fluid flow takes place during this period (\(0 \le t \le t_{0}\))].

The volume-averaged molar concentration of free drug eluted from coated balloon is denoted by \(c_{\text {f}}\) and that of bound drug, assuming completely immobilized in the tissue, is denoted by \(c_{\text {b}}.\) Now the bound drug is internalized by the cell in the tissue through the process of endocytosis. The internalization of bound drug can occur either by non-specific (fluid-phase) or receptor-mediated endocytosis or both. For simplicity, only receptor-mediated endocytosis has been considered here. From endosomes, internalized drugs have at least two possible fates: recycling to the cell surface (exocytosis) and degradation to lysosomes. In some cases, they are neither recycled nor degraded, rather they may move to an undetermined intracellular compartment for carrying out their signaling function, or routed to the Golgi. Particular routes, of course, depend on the outcome of separation or sorting events which occur within the endosome. In this model study, a portion of internalized drug particles, denoted by \(c_{\text {e}},\) experiences lysosomal degradation which ultimately recycles into the extracellular fluid. The governing equations representing the dynamics of the free, the bound and the internalized drug are given by

$${\partial c_{\text {f}} \over \partial t} + u_{x}{\partial c_{\text {f}} \over \partial x} + u_{y}{\partial c_{\text {f}} \over \partial y} = {D_{\text {T}}^{{l}}} \left[ {\partial ^{2}c_{\text {f}} \over \partial x^{2}}+ {\partial ^{2}c_{\text {f}} \over \partial y^{2}} \right] - \frac{\partial c_{\text {b}}}{\partial t},$$
(4)
$${\partial c_{\text {b}} \over \partial t} = {k_{\text {a}}^{{l}}}c_{\text {f}}\left( B_{\text {M}} - c_{\text {b}}\right) - {k_{\text {d}}^{{l}}}c_{\text {b}} - k_{\text {e}}c_{\text {b}} ,$$
(5)
$${\partial c_{\text {e}}\over \partial t} = {} k_{\text {e}}c_{\text {b}} - k_{\text {ld}}c_{\text {e}},$$
(6)

where \(k_{\text {a}}^{{l}}\) and \(k_{\text {d}}^{{l}} \; (l=1,\,2,\,3,\,4,\,5)\) are the association and dissociation rate constants, respectively, \(B_{\text {M}}\) is the net tissue binding capacity,10,11 \(k_{\text {e}}\) stands for internalization rate constant and \(k_{\text {ld}}\) denotes the rate of degradation in the lysosome.30 Here \(D_{\text {T}}^{l}\) are the coefficients of diffusivity defined by

$$D_{\text {T}}^{l} = \left( 1+\frac{B_{\text {M}}}{K_{\text {D}}}\right) D_{\text {eff}},$$
(7)

where \(K_{\text {D}}\) is the equilibrium dissociation constant and \(D_{\text {eff}}\) is the effective diffusivity of free drug.10,31,32

Boundary Conditions

Boundary Conditions for Interstitial Velocity

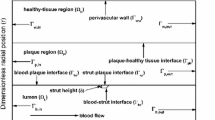
At the proximal (\(\Gamma _{\text {p}}^{\text {u}},\, \Gamma _{\text {p}}^{\text {l}}\)) and distal (\(\Gamma _{\text {d}}^{\text {u}},\, \Gamma _{\text {d}}^{\text {l}}\)) boundaries (Fig. 1c), the interstitial velocity boundary conditions are as follows33:

$$\begin{aligned}& u_{x} = 0 = \frac{\partial u_{y}}{\partial x}\quad {\text {on}} \; \Gamma _{\text {p}}^{\text {u}},\, \Gamma _{\text {p}}^{\text {l}}, \\&{\partial u_{x} \over \partial x} =0={\partial u_{y} \over \partial x} \quad {\text {on}}\; \Gamma _{\text {d}}^{\text {u}},\, \Gamma _{\text {d}}^{\text {l}}. \end{aligned}$$
(8)

At the perivascular end (\(\Gamma _{\text {u}},\, \Gamma _{\text {l}}\)), zero variations in normal direction for the velocity components are assumed34 which may be mathematically written as

$${\partial u_{x} \over \partial y} =0={\partial u_{y} \over \partial y} \quad {\text {on}}\; \Gamma _{\text {u}},\, \Gamma _{\text {l}}.$$
(9)

Since the interfaces (\(\Gamma _{\text {i}}^{\text {u}},\, \Gamma _{\text {i}}^{\text {l}}\)) for both the upper and lower regions are not regular, transmural filtration of interstitial fluid from lumen into tissue takes place along three directions (Fig. 1c), namely, the transverse as well as the forward and reverse stream directions. But due to nonavailability of data in the existing literature, an equal filtration velocity in absolute sense has been assumed for all the three directions. Therefore, the interface conditions for interstitial flow may be written mathematically as

$$u_{y}=V^{\text {filt}} \quad {\text {and}} \quad u_{x}=\pm V^{\text {filt}} \quad {\text {on}} \; \Gamma _{\text {i}}^{\text {u}},\, \Gamma _{\text {i}}^{\text {l}},$$
(10)

where \(V^{\text {filt}}\) is the prescribed filtration velocity.35 Note that in some portions of the interfaces, transmural filtration from lumen into tissue takes place in a direction opposite to that of stream implying negative filtration velocity.

Boundary Conditions for Drug

Symmetry boundary conditions for the free drug are applied at the proximal (\(\Gamma _{\text {p}}^{\text {u}},\, \Gamma _{\text {p}}^{\text {l}}\)) and distal (\(\Gamma _{\text {d}}^{\text {u}},\, \Gamma _{\text {d}}^{\text {l}}\)) boundaries. At the perivascular end (\(\Gamma _{\text {u}},\, \Gamma _{\text {l}}\)), a perfect sink condition is applied for the free drug. At the interfaces (\(\Gamma _{\text {i}}^{\text {u}},\, \Gamma _{\text {i}}^{\text {l}}\)), considering two extremes of zero flux and zero concentration for free drug, the following boundary condition, after the deflation of the balloon (\(t>t_{0}\)), may be used11:

$$\lambda J_{\text {f}}+(1-\lambda )V^{\text {filt}}c_{\text {f}}=0,$$
(11)

where \(J_{\text {f}}\) represents the interfacial flux for the free drug. Here \(\lambda\) is an adjustable parameter giving rise to zero concentration (\(\lambda =0\)), zero flux (\(\lambda =1\)), and combination of zero flux and zero concentration (\(0< \lambda < 1\)) interface conditions for the free drug.

At the interfaces, the flux from expanded DCB is estimated as10

$$J_{\text {b}}(t)=k_{1}a_{1}{\text {e}}^{-k_{1}t}/Z_{\text {MW}},\quad t \le t_{0},$$
(12)

where \(k_{1}\) and \(a_{1}\) are empirical constants, \(Z_{\text {MW}},\) the molecular weight of the drug and \(t_{0}\) is the balloon inflation time (Fig. 2).

Figure 2
figure 2

Drug release kinetics during balloon inflation for 180 s.

Full size image

Method of Solution

The above governing equations along with the boundary conditions are solved numerically by finite-difference method by imposing the release kinetics (12). The image-derived computational geometry is comprised of 26,111 pixels, encompassing the diseased arterial wall where each pixel is considered as a control volume. Control volume-based finite-difference discretization of those equations is carried out in staggered grids, usually known as MAC method. In this type of grid alignment, the interstitial velocity components, the pressure and the drug concentrations are calculated at different locations of the control volume, as indicated in Fig. 3. The discretization of the time derivative terms are based on the first order accurate two-level forward time differencing formula while the diffusive terms are discretized by second order accurate three-point central difference formula. The convective terms are, however, discretized with a hybrid formula consisting of central differencing and second order unwinding. In order to have second order spatial accuracy of the boundary conditions, some fictitious grid points outside the physical domain have been considered.

Figure 3
figure 3

A typical MAC cell.

Full size image

The equation for pressure derived from the discretised momentum and continuity equations is solved iteratively by successive-over-relaxation method with the chosen value of over-relaxation parameter as 1.2, in order to get the intermediate pressure field using the interstitial velocity field. Subsequently the maximum cell divergence of the velocity field is calculated and checked for its tolerance. If the tolerance limit is not satisfied, then the pressure at each cell of the domain is corrected and the interstitial velocities at each cell are adjusted accordingly by repeating the process. In the finite-difference formula, we assume \(x_{i}=i\delta x,\,y_{j}=j\delta y,\, t_{k}=k \delta t\) in which k refers to the time direction, \(\delta t,\) the time increment. Here, \(\delta x\) and \(\delta y\) denote the dimensions of the pixels. The computational code based on the following algorithm has been successfully programmed using FORTRAN language. Details of discretization and MAC methodology are presented in Mandal and Mandal36 and for the sake of brevity, these are not reported here.

Numerical Stability: Time-Stepping Procedure

Amsden and Harlow37 suggested that the number of calculation cycles and hence the running time could be reduced by the use of an adaptive time stepping routine which, at a given cycle, would automatically choose the time step most appropriate to the velocity-field at that cycle. Welch et al.38 discussed the stability and accuracy requirements for the MAC method. They suggested stability restriction involving the Reynolds number:

$$\delta t_{1} \le {\text {Min}} \left[ {Re \over 2}{{\delta x^{2} \delta y^{2}} \over {\delta x^{2} + \delta y^{2}}} \right] _{i,j}.$$

This stability condition is related to viscous effect which can be applied directly to select an appropriate time step.39

A more appropriate treatment is to require that no particles should cross more than one cell boundary in a given time interval,40 that is,

$$\delta t_{2} \le {\text {Min}} \left[ {{\delta x \over |u_{x}| } ,\, {\delta y \over |u_{y}|}} \right] _{i,j}.$$

For the two-dimensional advection–reaction–diffusion equations, the standard Courant–Friedrichs–Lewy stability criterion, depending on the diffusivity as well as dimensions of the control volume, gives rise to the time step \(\delta t_{3}\) as41

$$\delta t_{3} \left( {1 \over \delta x^{2}} + {1 \over \delta y^{2}} \right) {\text {Max}} \left( D_{\text {T}}^{\text {l}}\right) < {1 \over 2}.$$

The time step to be used at a given point in the calculation will be

$$\delta t = a\; {\text {Min}} \left[ {\delta t_{1}, \,\delta t_{2},\, \delta t_{3}}\right] ,$$

where \(0 < a \le 1;\) the reason for this extra added factor a led to a considerable computational savings.

Results and Discussion

In order to extend previous studies10,11,12 to allow for the exploration of the impact of (i) interstitial fluid flow in a porous diseased artery and (ii) internalization of bound drug together with lysosomal degradation during the process of endocytosis, we have leveraged finite difference scheme in staggered grids. For the purpose of numerical simulation of the quantities of significance, the plausible values of input parameters are given in Table 1. Steady states have been achieved when there was a \(10^{-6}\) reduction in the drug transport residual and the divergence of velocity field is less than \(10^{-16}\) at any cell in the absolute sense.

Table 1 Parameters used in the computational model.
Full size table

Figures 4a and 4b display the spatial patterns for the axial and the transverse velocity components of interstitial fluid streaming through the porous arterial wall. The velocity pattern, as appeared in Fig. 4a, has some interesting features to note that the axial velocity becomes positive and negative both, perhaps, owing to the irregular interfaces which led to bi-directional plasma filtration from the luminal side into the intima. However, the transverse velocity pattern is always positive due to filtration of plasma along the transverse direction only (Fig. 4b). These velocity components (convective velocity) are believed to greatly influence the distribution, retention and internalization of drug in case of endovascular balloon delivery.

Figure 4
figure 4

Velocity pattern at steady state. (a) Axial velocity; and (b) transverse velocity.

Full size image

Effect of Interstitial Flow (Convection) and Interface Conditions

The interstitial flow within the porous arterial wall is governed by Brinkman equations and continuity equations [Eqs. (1)–(3)]. For the purpose of demonstrating the influence of convection on the distribution of free drug and its retention together with the internalization of bound drug during endocytosis, a detailed quantitative analysis of the model considered has been carried out and the results are represented graphically. To the authors’ knowledge, no studies, till date, have considered the impact of internalization process in case of endovascular balloon delivery whose appreciable contribution can not be brushed aside. Moreover, in most of the earlier studies, of course, in stent-based delivery, a non-zero constant interstitial velocity was considered in the transverse direction only where the fluid momentum equations are not explicitly solved. Their consideration is an over-simplification on the fact that the interstitial velocity components may vary along the streamwise and transverse directions with varied signs (Figs. 4a and 4b). The predicted results indicate an initial first order decline phase followed by slower efflux of free drug in the absence of convection for both the upper and lower regions [Figs. 5a(i–ii)], however, convection turns out to have the concentration of free drug higher at all times considered herein. Moreover, when the interface is considered as a sink condition (\(\lambda =0\)), free drug taken up by the arterial wall from inflated balloon is cleared rapidly. Despite perivascular washout, clearance is usually delayed for hybrid condition (\(\lambda =0.5\)) and more delayed for zero flux (\(\lambda =1\)) interface condition. An interesting phenomena to be noted that in case of zero flux interface condition, the effect of convection is more pronounced with multiple peakings of averaged free drug as evident from the top curves of the Figs. 5a(i) and 5a(ii). Simulation predicts that non-uniform interstitial velocity components both in the axial and transverse directions of the regions led the averaged concentration of free drug long-lived, and eventually, the process retains for availability of more drug for binding [Figs. 5b(i–ii)]. Specifically, for the case of zero concentration interface condition, concentrations of free drug in the presence of convection at 25 h are reduced to \(\sim 0.37\) and \(\sim 0.26\%\) of its maximum value for both the upper and lower regions, respectively whose respective values in the absence of convection are \(\sim 0.22\) and \(\sim 0.14 \%.\) On the other hand, when the hybrid interface condition is used in the presence of convection, only \(\sim 3.22\) and \(\sim 2.68 \%\) of free drug are remained on the upper and lower regions, respectively while in the absence of convection, the respective values are \(\sim 1.23\), \(\sim 0.64\%,\) and \(\sim 49.8\), \(\sim 52.5\%\) of the concentrations of free drug are remained in the presence of convection for the case of zero flux interface condition for the upper and lower regions respectively as compared to \(\sim 1.93\) and \(\sim 1.01\%\) of their respective values in the absence of convection (see Table S1 for more details). Simulations show an initial build-up for bound drug followed by a decline in the event of the bound drug gets converted to internalized drug. As anticipated, the concentration of bound drug is higher for both regions in presence of convection and also the peak concentrations of averaged bound drug shift subsequently towards later times. It is worthwhile to note that convection promotes rapid saturation of binding sites in case of zero flux interface condition which confirms the non-negligible impact of the interstitial flow and interface conditions in endovascular therapies using DCB. Specifically, remains of \(\sim 15.4,\,\sim 38.7\) and \(\sim 98.3 \%\) of bound drug at 25 h on the upper region for zero concentration, hybrid and zero flux interface conditions respectively in the presence of convection turn out to smaller values in the absence of convection. The simulated results of bound drug for the lower region show analogous behavior with a distinction in their numerical values only (see Table S1 for more details). The drug internalization describes the cellular uptake of bound drug molecules after they got associated with the binding sites, and plays an important role for drug metabolism. Some portions of internalized drug experience lysosomal degradation in the process of endocytosis.30 Figures 5c(i–ii) exhibit the temporal variation of averaged concentration of internalized drug in the presence/absence of convection for different interface conditions. Here too, convection plays a significant role in the process of internalization during endocytosis. For a quantitative look at the simulated results of internalized drug, Table S1 shows again that only \(\sim 58.4,\,\sim 69.0\) and \(\sim 100 \%\) of internalized drug remained at 25 h in the presence of convection for zero concentration, hybrid and zero flux interface conditions respectively for upper region whose respective values are much lower in the absence of convection (see Table S1 for more details). Therefore, the arterial drug levels (free, bound and internalized) could have a sensitive response with respect to different interface conditions and presence of interstitial flow.

Figure 5
figure 5

Temporal variation of averaged drug concentration for zero concentration (\(\lambda =0\)), hybrid (\(\lambda =0.5\)) and zero flux (\(\lambda =1\)) interface conditions for balloon inflation time of 180 s. a(i) and a(ii) display free drug concentration for the upper and lower regions, respectively; b(i) and b(ii) be the same for bound drug; and c(i) and c(ii) be the same for internalized drug.

Full size image

Effect of Half-life and Transferable Drug Load Density

Simulations evaluated the effect of varying the half-life of release of coated drug from 180 s expansion of DCB on the temporal variation of tissue content and transmural variation of bound and internalized drugs at \(x=0.27\) cm. Here too, convection amplifies the distribution of free drug and its retention, and also the internalization of bound drug for upper region during the process endocytosis [Figs. 6a(i–iii), 8, 9 and 10]. Decreasing the half-life by half and one-fourth result in higher drug transfer at the end of 180 s balloon expansion and higher peak tissue content. The advantage of faster drug transfer saturates deeper binding sites in spite of perivascular clearance of excess free drug. In other words, faster drug transfer, though short-lived, promotes rapid saturation of binding sites [Fig. 6a(ii)]. The predicted results of internalized drug are analogous to those of bound drug [Fig. 6a(iii)]. Heterogeneity in drug distribution patterns can be better appreciated by looking at the transmural distribution profile [Figs. 6a(ii–iii), 6b(ii–iii)] and also at the spatial distributions (Figs. 8, 9 and 10). Here the non-uniform variations of all drug forms are due to the presence of necrotic core and calcified lesion in the atherosclerotic plaque as pockets of poor diffusivity lead to poor binding affinity which , in turn, give rise to less conversion of bound drug into its internalized form. Modeling using healthy tissue does predict less differential distribution10,11 which clearly establishes the impact of consideration of heterogeneous plaque compositions for the success of endovascular delivery using coated balloon. The predicted results for lower region are analogous to that of upper region with a distinction that the transmural profiles are less non-uniform due to almost absence of sites of poor diffusivity at \(x=0.27\) cm (Fig 6b(ii–iii)).

Figure 6
figure 6

Predicted influence of half-life (\(t_{1 \over 2}\)) for zero flux (\(\lambda =1\)) interface condition. a(i) Tissue content; a(ii) transmural distribution of bound drug; a(iii) transmural distribution of internalized drug, for upper region; and b(i) tissue content; b(ii) transmural distribution of bound drug; b(iii) transmural distribution of internalized drug, for lower region. Transmural data are recorded at 360 s. post balloon expansion time (balloon inflation time = 180 s).

Full size image

Figures 7a(i–iii) and 7b(i–iii) show how the load density \((a_{1})\) per unit area of the coated balloon affects the temporal as well as transmural variations of transferable drug in the upper and lower regions, respectively. Simulations that consider 2.3- and 3.9-fold load densities of coated drug show similar transiently elevated tissue content [Figs. 7a(i) and 7b(i)] and saturation of binding sites is extended with the increase of load density of transferable drug. Furthermore, the concentrations of bound and internalized drugs in both regions are modulated by the presence of interstitial flow [Figs. 7a(ii–iii) and 7b(ii–iii)]. One may note that the averaged concentration of free drug in the lower region is significantly higher as compared to that in the upper region owing to relatively smaller area covered by necrotic core and calcified lesion in the lower region.

Figure 7
figure 7

Predicted influence of transferable drug load density (\(a_{1}\)) for zero flux (\(\lambda =1\)) interface condition. a(i) Tissue content; a(ii) transmural distribution of bound drug; a(iii) transmural distribution of internalized drug, for upper region; and b(i) tissue content; b(ii) transmural distribution of bound drug; b(iii) transmural distribution of internalized drug, for lower region. Transmural data are recorded at 360 s. post balloon expansion time (balloon inflation time = 180 s).

Full size image

Spatiotemporal Patterns

Uniform uptake kinetics of transferable drug at the interfaces resulted in heterogeneous patterns that are dependent on plaque compositions and interface conditions (Figs. 8, 9 and 10). Arterial drug distribution and its retention together with the internalization as well are modulated by lesion-specific transport properties of the drug, exemplified by the diffusivity and the interface conditions. Drug mostly accumulated in and around the intimal region but within the pockets of necrotic core and calcified lesion, lower drug concentration is observed in comparison to the other regions (Figs. 8a–8f). Drug distribution patterns are more differential when the interface condition is treated as zero flux or hybrid (Figs. 8a–8d). Furthermore, in the presence of interstitial flow, drug is penetrated far away from the interfaces (Fig. 8) and so also its retention and internalization (Figs. 9 and 10). When the delivered drug is assumed to remain adherent at the interfaces and impede luminal wash out, modeled as zero flux interface condition, concentration of bound drug increases due to longer residence time of free drug (Figs. 9a and 9b). However, concentration of bound drug is lower for hybrid (Figs. 8c and 9d) and more lower for zero flux interface condition (Figs. 8e and 9f). The internalization of bound drug changes the arterial drug distribution and affects the drug availability in the tissue. Zhu and Braatz46 opined in their in silico modeling studies on stent-based delivery that the internalization process could aggravate the potential adverse effect of low drug levels at perivascular end in reducing in-stent restenosis and its impact varies with the internalization rate constant. The internalized drug distribution exhibits higher differential distribution in the transverse direction, however, has higher concentration close to the interfaces (Fig. 10). This attempt, first of its kind, to explore the impact of interstitial fluid flow and the internalization of bound drug during endocytosis would certainly help estimating the success of endovascular therapy using DCB and we want to revisit this issue when experimental data of rate constants become available.

Figure 8
figure 8

Spatial variation of free drug concentration at \(t=30\) min for balloon inflation time of 180 s for various interface conditions. The left panel shows the distribution patterns in the presence of convection while the right in the absence of convection. (a, b) Zero flux (\(\lambda =1\)); (c, d) hybrid (\(\lambda =0.5\)); (e, f) zero concentration (\(\lambda =0\)).

Full size image
Figure 9
figure 9

Spatial variation of bound drug concentration at \(t=30\) min for balloon inflation time of 180 s for various interface conditions. The left panel shows the distribution patterns in the presence of convection while the right in the absence of convection. ( a, b) Zero flux (\(\lambda =1\)); (c, d) hybrid (\(\lambda =0.5\)); (e, f) zero concentration (\(\lambda =0\)).

Full size image
Figure 10
figure 10

Spatial variation of internalized drug concentration at \(t=30\) min for balloon inflation time of 180 s for various interface conditions. The left panel shows the distribution patterns in the presence of convection while the right in the absence of convection. (a, b) Zero flux (\(\lambda =1\)); (c, d) hybrid (\(\lambda =0.5\)); (e, f) zero concentration (\(\lambda =0\)).

Full size image

Effectiveness of Delivery

In modeling endovascular delivery, one of the essential determinants is the effectiveness of drug delivery, denoted by \(\eta ,\) which is defined47 as \(\eta ={{\bar{c}} \over {c^{\max }_{\text {f}}}}\) where \(\bar{c}\) is the averaged concentration of free drug and \({c^{\max }_{\text {f}}}\) is the maximum concentration of free drug in the tissue. The delivery becomes effective for values of \(\eta\) near unity and ineffective for values of \(\eta\) near zero. Figures 11a(i–ii) show the effectiveness of drug delivery with \(k_{1}\) (reciprocal of half-life) for the upper and lower regions at \(t=10\) h, respectively. It is worth while to mention that as \(k_{1}\) increases (i.e., half-life decreases), the effectiveness of delivery does increase and also in the absense of convection, the delivery from coated balloon in case of zero concentration (\(\lambda =0\)) interface condition is more effective as compared to other two interface conditions. But the intriguing findings in presence of interstitial flow through a porous arterial wall show that the delivery is more effective for hybrid interface (\(\lambda =0.5\)) condition at \(t=10\) h. The role of convection is to enhance the effectiveness of delivery and also the plaque compositions contribute much to it (Fig. 11). Furthermore, the inferences drawn at \(t=10\) h may vary appreciably, both qualitatively and quantitatively, for larger times in the presence of convection [Figs. 11c(i–ii)]. It is anticipated that as the transferable drug load density (\(a_{1}\)) increases, the effective delivery increases and here too, delivery is more effective for zero concentration (\(\lambda =0\)) interface condition in the absense of convection [Figs. 11b(i–ii)]. Analyzing the results of the Fig. 11, one may conclude that the flow of interstitial fluid together with the interface conditions play significant roles which highlight the difficulty of interpreting the essential determinant like effectiveness of drug delivery by intuition alone. Figures 11a(i)–11c(ii) show that apparently ordered inferences drawn in the absense of convection for different interface conditions on the effectiveness of delivery are getting distorted in the presence of convection. To overcome this difficulty, animal studies under atherosclerotic state by taking into account the interstitial flow are warranted for.

Figure 11
figure 11

Predicted influence of \(k_{1}\) (reciprocal of half-life) on effectiveness of delivery for zero concentration (\(\lambda =0\)), hybrid (\(\lambda =0.5\)) and zero flux (\(\lambda =1\)) interface conditions for balloon inflation time of 180 s at \(t=10\) h. a(i) Upper region; a(ii) lower region; predicted influence of \(a_{1}\) (transferable drug load density) on effectiveness of delivery for zero concentration (\(\lambda =0\)), hybrid (\(\lambda =0.5\)) and zero flux (\(\lambda =1\)) interface conditions for balloon inflation time of 180 s at \(t=10\) h. b(i) Upper region; b(ii) lower region; temporal variation of effectiveness of delivery for both regions. c(i) Without convection; c(ii) with convection.

Full size image

Conclusions and Study Limitation

The model presented in this paper is thoroughly analyzed for the interplay amongst the interstitial flow, transport of free drug and its retention, and the internalization of drug in case of coated-balloon delivery through a patient-specific atherosclerotic plaque. Image processing using an unsupervised clustering technique is used to reconstruct the patient-specific geometry obtained from IVUS-VH. Quantifying pharmacokinetics in case of DCB delivery using computational model in a diseased patient-specific arterial segment consisting of non-uniform plaque compositions as opposed to modeling healthy arterial vessel is appealing and would certainly provide better understanding for the success of endovascular delivery using balloon catheter. Numerically solving the governing equations representing the flow of interstitial fluid and the transport of free drug and its bound phase together with its internalization during the process of endocytosis on an irregular domain of region-specific diffusivity values is particularly challenging. The in-house developed finite difference code in staggered grids allows one to quantify significant physiological factors. Simulated results predict the averaged concentration of free drug is long-lived and there is some availability of more drug for binding in the presence of interstitial flow. The results also indicate that faster drug transfer does promote rapid saturation of binding sites in spite of perivascular wash out and the arterial drug levels could have a sensitive response with respect to different interface conditions.

Many of the model parameters used in this study are either empirically derived or directly obtained from bench-top experiments. Derivation of all these parameters from human tissue is almost impossible and hence assignment of these parameters should be considered as an approximation towards quantifying arterial pharmacokinetics in humans. A thorough sensitivity analysis has been conducted in the absense of interstitial flow in our published paper.11 For the inferences derived in this paper to be generalizable, simulations of this nature need to be performed followed by experimental validation.