Dynamic Games of Social Distancing During an Epidemic: Analysis of Asymmetric Solutions

Abstract

Individual behaviors play an essential role in the dynamics of transmission of infectious diseases, including COVID-19. This paper studies a dynamic game model that describes the social distancing behaviors during an epidemic, assuming a continuum of players and individual infection dynamics. The evolution of the players’ infection states follows a variant of the well-known SIR dynamics. We assume that the players are not sure about their infection state, and thus, they choose their actions based on their individually perceived probabilities of being susceptible, infected, or removed. The cost of each player depends both on her infection state and on the contact with others. We prove the existence of a Nash equilibrium and characterize Nash equilibria using nonlinear complementarity problems. We then exploit some monotonicity properties of the optimal policies to obtain a reduced-order characterization for Nash equilibrium and reduce its computation to the solution of a low-dimensional optimization problem. It turns out that, even in the symmetric case, where all the players have the same parameters, players may have very different behaviors. We finally present some numerical studies that illustrate this interesting phenomenon and investigate the effects of several parameters, including the players’ vulnerability, the time horizon, and the maximum allowed actions, on the optimal policies and the players’ costs.

1 Introduction

COVID-19 pandemic is one of the most important events of this era. Until early April 2021, it has caused more than 2.8 million deaths, an unprecedented economic depression, and affected most aspects of people’s lives in the larger part of the world. During the first phases of the pandemic, non-pharmaceutical interventions (primarily social distancing) have been one of the most efficient tools to control its spread [13]. Due to the slow roll-out of the vaccines, their uneven distribution, the emergence of SARS-CoV-2 variants, age limitations, and people’s resistance to vaccination, social distancing is likely to remain significant in large part of the globe for the near future.

Mathematical modeling of epidemics dates back to early twentieth century with the seminal works of Ross  [33] and Kermack and McKendrick [24]. A widely used modeling approach separates people in several compartments according to their infection state (e.g., susceptible, exposed, infected, recovered, etc.) and derives differential equations describing the evolution of the population of each compartment (for a review, see [1]).

However, the description of individual behaviors (practice of social distancing, use of face masks, vaccination, etc.) is essential for the understanding of the spread of epidemics. Game theory is thus a particularly relevant tool. A dynamic game model describing voluntary implementation of non-pharmaceutical interventions (NPIs) was presented in [32]. Several extensions were published, including the case where infection severity depends on the epidemic burden [6], and different formulations of the cost functions (linear vs. nonlinear, and finite horizon vs. discounted infinite horizon or stochastic horizon) [11, 15, 37]. Aurell et al. [4] study the design of incentives to achieve optimal social distancing, in a Stackelberg game framework. The works [2, 10, 12, 17, 22, 30, 31, 39] study different aspects of the coupled dynamics between individual behaviors and the spread of an epidemic, in the context of evolutionary game theory. Network game models appear in [3, 18, 27, 29], and the effects of altruism on the spread of epidemics are studied in [8, 14, 23, 26]. Another closely related stream of research is the study of the adoption of decentralized protection strategies in engineered and social networks [19, 21, 36, 38]. A review of game theoretic models for epidemics (including also topics other than social distancing, e.g., vaccination) is presented in [9, 20].

This paper presents a dynamic game model to describe the social distancing choices of individuals during an epidemic, assuming that the players are not certain about their infection state (susceptible (S), infected (I), or removed (R)). The probability that a player is at each health state evolves dynamically depending on the player’s distancing behavior, the others’ behavior, and the prevalence of the epidemic. We assume that the players care both about their health state and about maintaining their social contacts. The players may have different characteristics, e.g., vulnerable versus less vulnerable, or care differently about maintaining their social contacts.

We assume that the players are not sure about their infection state, and thus, they choose their actions based on their individually perceived probabilities of being susceptible, infected, or removed. In contrast with most of the literature, in the current work, players—even players with the same characteristics—are allowed to behave differently. We first characterize the optimal action of a player, given the others’ behavior, and show some monotonicity properties of optimal actions. We then prove the existence of a Nash equilibrium and characterize it in terms of a nonlinear complementarity problem.

Using the monotonicity of the optimal solution, we provide a simple reduced-order characterization of the Nash equilibrium in terms of a nonlinear programming problem. This formulation simplifies the computation of the equilibria drastically. Based on that result, we performed numerical studies, which verify that players with the same parameters may follow different strategies. This phenomenon seems realistic since people facing the same risks or belonging to the same age group often have different social distancing behaviors.

The model presented in this paper differs from most of the dynamic game models presented in the literature in the following ways:

• (a) The players act without knowing their infection state. However, they know the probability of being susceptible, infected, or recovered, which depends on their previous actions and the prevalence of the epidemic.

• (b) The current model allows for asymmetric solutions, i.e., players with the same characteristics may behave differently.

The rest of the paper is organized as follows. Section 2 presents the game theoretic model. In Sect. 3, we analyze the optimization problem of each player and prove some monotonicity properties. In Sect. 4, we prove the existence of the equilibrium and provide Nash equilibrium characterizations. Section 5 presents some numerical results. Finally, ‘Appendix’ contains the proof of the results of the main text.

2 The Model

This section presents the dynamic model for the epidemic spread and the social distancing game among the members of the society.

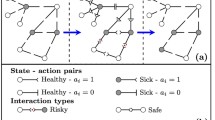
We assume that the infection state of each agent could be susceptible (S), infected (I), recovered (R), or dead (D). A susceptible person gets infected at a rate proportional to the number of infected people she meets with. An infected person either recovers or dies at constant rates, which depend on her vulnerability. An individual who has recovered from the infection is immune, i.e., she could not get infected again. The evolution of the infection state of an individual is shown in Fig. 1.

Fig. 1

The evolution of the infection state of each individual

We assume that there is a continuum of agents. This approximation is frequently used in game theoretic models dealing with a very large number of agents. The set of players is described by the measure space $([0,1),{\mathcal {B}}, \mu )$, where ${\mathcal {B}}$ is the Borel $\sigma$-algebra and $\mu$ the Lebesgue measure. That is, each player is indexed by an $i\in [0,1)$.

Denote by $S^i(t), I^i(t), R^i(t), D^i(t)$ the probability that player $i\in [0,1)$ is susceptible, infected, removed, or dead at time t. The dynamics is given by:

$$\begin{aligned} \begin{aligned} {\dot{S}}^i&= -ru^iS^iI^f\\ {\dot{I}}^i&=ru^iS^iI^f-\alpha ^i I^i\\ {\dot{R}}^i&=\bar{\alpha }^i I^i\\ {\dot{D}}^i&=(\alpha ^i-\bar{\alpha }^i) I^i \end{aligned}, \end{aligned}$$

(1)

where $r,\alpha ^i$ are positive constants, and $u^i(t)$ is the action of player i at time t. The quantity $u^i(t)$ describes player i’s socialization, which is proportional to the time she spends in public places. The quantity $I^f$, which denotes the density of infected people in public places, is given by:

$$\begin{aligned} I^f(t)=\int I^i(t)u^i(t)\mu (di). \end{aligned}$$

(2)

For the actions of the players, we assume that there are positive constants $u_m$, $u_M$, such that $u^i(t)\in [u_m,u_M]\subset [0,1]$. The constant $u_m$ describes the minimum social contacts needed for an agent to survive, and $u_M$ is an upper bound posed by the government.

The cost function for player i is given by:

$$\begin{aligned} J^i=G^i(1-S^i(T))-s^i\int _{0}^{T}u^i(t)\tilde{u}(t)\hbox {d}t-s^i\int _{0}^{T}\kappa u^i(t)\hbox {d}t, \end{aligned}$$

(3)

where T is the time horizon. The parameter $G^i>0$ depends on the vulnerability of the player and indicates the disutility a player experiences if she gets infected. The quantity $1-S^i(T)$ corresponds to the probability that player i gets infected before the end of the time horizon. (Note that in that case the infection state of the player at the end of the time horizon is I, R, or D.) The second term corresponds to the utility a player derives from the interaction with the other players, whose mean action is denoted by ${\tilde{u}}(t)$:

$$\begin{aligned} {\tilde{u}}(t) =\int u^i(t) \mu (di). \end{aligned}$$

(4)

The third term indicates the interest of a person to visit public places. The relative magnitude of this desire is modeled by a positive constant $\kappa$. Finally, constant $s^i$ indicates the importance player i gives on the last two terms that correspond to going out and interacting with other people.

Considering the auxiliary variable ${\bar{u}}(t)$:

$$\begin{aligned} {\bar{u}}(t) =\kappa +\tilde{u}, \end{aligned}$$

(5)

and computing S(T) by solving (1), the cost can be written equivalently as:

$$\begin{aligned} J^i =G^i\left( 1-S^i(0)e^{-r\int _{0}^{T}u^i(t)I^f(t)\mathrm{d}t}\right) -s^i\int _{0}^{T}u^i(t)\bar{u}(t)\hbox {d}t. \end{aligned}$$

(6)

Without loss of generality, assume that $R^i(0)=D^i(0)=0$ for all $i\in [0,1)$.

Assumption 1

(Finite number of types) There are M types of players. Particularly, there are $M+1$ values $0={\bar{i}}_0<\dots <{\bar{i}}_M=1$ such that the functions $S^i(0),I^i(0),G^i,s^i,\alpha ^i:[0,1)\rightarrow {\mathbb {R}}$ are constant for $i\in [{\bar{i}}_0,{\bar{i}}_1)$, $i\in [{\bar{i}}_1,\bar{i}_2),\dots$, $i\in [{\bar{i}}_{M-1},{\bar{i}}_{M})$. Denote by $m_j=\mu ([{\bar{i}}_{j-1},{\bar{i}}_{j}))$ the mass of the players of type j. Of course $m_1+\dots +m_M=1.$

Remark 1

The finite number of types assumption is very common in many applications dealing with a large number of agents. For example, in the current COVID-19 pandemic, people are grouped based on their age and/or underlying diseases to be prioritized for vaccination. Assumption 1, combined with some results of the following section, is convenient to describe the evolution of the states of a continuum of players using a finite number of differential equations.

Assumption 2

(Piecewise constant actions) The interval [0, T) can be divided in subintervals $[t_k,t_{k+1})$, with $t_0=0<t_1<\dots <t_N=T$, such that the actions of the players are constant in these intervals.

Remark 2

Assumption 2 indicates that people decide only a finite number of times ($t_k$) and follow their decisions for a time interval $[t_k,t_{k+1})$. A reasonable length for that time interval could be 1 week.

The action of player i in the interval $[t_k,t_{k+1})$ is denoted by $u^i_k$.

Assumption 3

(Measurability of the actions) The function $u^\cdot _k:[0,1)\rightarrow [u_m,u_M]$ is measurable.

Under Assumptions 1–3, there is a unique solution to differential equations (1), with initial conditions $S^\cdot (0),I^\cdot (0)$, and the integrals in (2), (4) are well defined (see Appendix A.1). We use the following notation:

$$\begin{aligned} {\bar{u}}_k=\int _{t_k}^{t_{k+1}} {\bar{u}} dt, \text { and } I^f_k = \int _{t_k}^{t_{k+1}} I^f(t) dt. \end{aligned}$$

For each player, we define an auxiliary cost, by dropping the fixed terms of (6) and dividing by $s^i$:

$$\begin{aligned} {\tilde{J}}^i(u^i,\bar{u},I^f)=-b^i\exp \left[ -r\sum _{k=0}^{N-1}u^i_kI^f_k\right] -\sum _{k=0}^{N-1}u^i_k\bar{u}_k, \end{aligned}$$

(7)

where $b^i=S^i(0)G^i/s^i$, and $u^i=[u^i_0,\dots ,u^i_{N-1}]^T$. Denote by $U=[u_m,u_M]^N$ the set of possible actions for each player. Observe that $u^i$ minimizes $J^i$ over the feasible set U if and only if it minimizes the auxiliary cost ${\tilde{J}}^i$. Thus, the optimization problem for player i is equivalent to:

$$\begin{aligned} \underset{u^i\in U}{\text {minimize}}~{\tilde{J}}^i(u^i,\bar{u},I^f). \end{aligned}$$

(8)

Note that the cost of player i depends on the actions of the other players through the terms $\bar{u}$ and $I^f$. Furthermore, the current actions of all the players affect the future values of $\bar{u}$ and $I^f$ through the SIR dynamics.

Assumption 4

For a player i of type j, denote $b_j=b^i$. Assume that the different types of players have different $b_j$’s. Without loss of generality, assume that $b_1<b_2<\dots <b_M.$

Assumption 5

Each player i has access only to the probabilities $S^i$ and $I^i$ and the aggregate quantities ${\bar{u}}$ and $I^f$, but not the actual infection states.

Remark 3

This assumption is reasonable in cases where the test availability is very sparse, so the agents are not able to have a reliable feedback for their estimated health states.

In the rest of the paper, we suppose that Assumptions 1–5 are satisfied.

3 Analysis of the Optimization Problem of Each Player

In this section, we analyze the optimization problem for a representative player i, given ${\bar{u}}_k$ and $I^f_k>0$, for $k=0,\dots ,N-1$.

Let us first define the following composite optimization problem:

$$\begin{aligned} \underset{A}{\text {minimize}}\left\{ -b^ie^{-A}+ f(A) \right\} , \end{aligned}$$

(9)

where:

$$\begin{aligned} f(A)=\inf _{u^i\in U}\left\{ -\sum _{k=0}^{N-1}u^i_k\bar{u}_k: \sum _{k=0}^{N-1}u^i_kI^f_k=A/r \right\} . \end{aligned}$$

(10)

The following proposition proves that (8) and (9) are equivalent and express their solution in a simple threshold form.

Proposition 1

• (i) If $u^i$ is optimal for (8), then $u^i\in {\tilde{U}}=\{u_m,u_M\}^N$.

• (ii) Problems (8) and (9) are equivalent, in the sense that they have the same optimal values, and $u^i$ minimizes (8) if and only if there is an optimal A for (9) such that $u^i$ attains the minimum in (10).

• (iii) Let $A_m=ru_m\sum _{k=0}^{N-1}I^f_k$ and $A_M=ru_M\sum _{k=0}^{N-1}I^f_k$. For $A\in [A_m,A_M]$, the function f is continuous, non-increasing, convex, and piecewise affine. Furthermore, it has at most N affine pieces and $f(A)=\infty$, for $A\not \in [A_m,A_M]$.

• (iv) There are at most $N+1$ vectors $u^i\in U$ that minimize (8).

• (v) If $u^i$ is optimal for (8), then there is a $\lambda '$ such that ${\bar{u}}_k/I^f_k\le \lambda '$ implies $u^i_k=u_m$, and ${\bar{u}}_k/I^f_k>\lambda '$ implies $u^i_k=u_M$.

Proof

The idea of the proof of Proposition 1 is to reduce the problem of minimizing (8) into the minimization of the sum of the concave function $-b^ie^{-A}$ with a piecewise affine function f(A). Then, the candidates for the minimum are only the corner points and of f(A) and the endpoints of the interval, where f is defined. The form of the optimal action $u^i$ comes from a Lagrange multiplier analysis of (10). For a detailed proof, see Appendix 2. $\square$

Remark 4

Part (v) of the proposition shows that if the density of infected people in public places $I^f$ is high, or the average socialization ${\bar{u}}$ is low, then it is optimal for a player to choose a small degree of socialization. The optimal action for each player depends on the ratio ${\bar{u}}_k/I^f_k$. Particularly, there is a threshold $\lambda '$ such that the action of player i is $u_m$ for values of the ratio below the threshold and $u_M$ for ratios above the threshold. Note that the threshold is different for each player.

Remark 5

The fact that the optimal value of a linear program is a convex function of the constraints constants is known in the literature (e.g., see [35] chapter 2). Thus, the convexity of the function f is already known from the literature.

Corollary 1

There is a simple way to solve the optimization problem (8) using the following steps:

• 1. Compute $\Lambda = \{{\bar{u}}_k/I^f_k: k=0,\dots ,N-1\}\cup \{0\}$.

• 2. For all $\lambda '\in \Lambda$ compute $u^{\lambda '}$ with:

  $$\begin{aligned} u^{\lambda '}_k = {\left\{ \begin{array}{ll} u_M ~~~\text {if ~} {\bar{u}}_k/I_k^f> \lambda '\\ u_m ~~~\text {if } {\bar{u}}_k/I_k^f\le \lambda ' \end{array}\right. }, \end{aligned}$$

  and $J^i(u^{\lambda '})$.

• 3. Compare the values of $J^i(u^{\lambda '})$, for all $\lambda '\in \Lambda$, and choose the minimum.

We then prove some monotonicity properties for the optimal control.

Proposition 2

Assume that for two players $i_1$ and $i_2$, with parameters $b^{i_1}$ and $b^{i_2}$, the minimizers of (9) are $A_1$ and $A_2$, respectively, and $u^{i_1}$ and $u^{i_2}$ are the corresponding optimal actions. Then:

• (i) If $b^{i_1}<b^{i_2}$, then $A_1\ge A_2$.

• (ii) If $b^{i_1}<b^{i_2}$, then $u_k^{i_2}\le u_k^{i_1}$, for $k=0,\dots ,N-1$.

• (iii) If $b^{i_1}=b^{i_2}$, then either $u_k^{i_2}\le u_k^{i_1}$ for all k, or $u_k^{i_1}\le u_k^{i_2}$ for all k.

Proof

See Appendix 3. $\square$

Remark 6

Recall that $b^i=S^i(0)G^i/s^i$. Thus, Proposition 2(ii) expresses of the fact that if (a) a person is more vulnerable, i.e., she has large $G^i$, or (b) she derives less utility from the interaction with the others, i.e., she has smaller $s^i$, or (c) it is more likely that she is not yet infected, i.e., she has larger $S^i(0)$, then she interacts less with the others.

Remark 7

The optimal control law can be expressed in feedback form (see Appendix A.4.1).

4 Nash Equilibrium Existence and Characterization

4.1 Existence and NCP Characterization

In this section, we prove the existence of a Nash equilibrium and characterize it in terms of a nonlinear complementarity problem (NCP).

We consider the set ${\tilde{U}}=\{u_m,u_M\}^N$, defined in Proposition 1. Let $v_1,\dots ,v_{2^N}$ be the members of the set ${\tilde{U}}$ and $p^j_l$ be the mass of players of type j following action $v_l \in {\tilde{U}}$. Let also $p^j=[p^j_1,\dots ,p^j_{2^N}]$ be the distribution of actions of the players of type j and $\pi =[p^1,\dots ,p^M]$ be the distribution of the actions of all the players.

Denote by:

$$\begin{aligned} \Delta _j = \left\{ p^j\in {\mathbb {R}}^{2^N}: p^j_l\ge 0, \sum _{l=1}^{2^N} p^j_l= m_j \right\} , \end{aligned}$$

(11)

the set of possible distributions of actions of the players of type j and by $\Pi =\Delta _1\times \dots \times \Delta _M$ the set of all possible distributions.

Finally, let $F:\Pi \rightarrow {\mathbb {R}}^{2^N\cdot M}$ be the vector function of auxiliary costs; that is, the component $F_{(j-1)2^N+l}(\pi )$ is the auxiliary cost of the players of type j playing a strategy $v^l$, as introduced in (7), when the distribution of actions is $\pi$. We denote $F^j(\pi )=[F_{(j-1)2^N+1}(\pi ),...,F_{j2^N}(\pi )]$ the vector of the auxiliary costs of the players of type j playing $v^l$, $l=1,\dots ,2^N$.

Let us recall the notion of a Nash equilibrium for games with a continuum of players (e.g., [28]).

Definition 1

A distribution of actions $\pi \in \Pi$ is a Nash equilibrium if for all $j=1,\dots ,M$ and $l=1,\dots ,2^N$:

$$\begin{aligned} \pi _{(j-1)2^N+l}>0 \implies l\in \underset{l'}{\arg \min }~F_{(j-1)2^N+l'}(\pi ) \end{aligned}$$

(12)

Let $\delta ^j(\pi )$ be the value of problem (8), i.e., the minimum value of the auxiliary cost of an agent of type j. This value depends on $\pi$, through the terms $I^f$ and $\bar{u}$. Define $\Phi ^j(\pi )=F^j(\pi )-\delta ^j(\pi )$ and $\Phi (\pi )=[\Phi ^1(\pi )...\Phi ^M(\pi )]$. We then characterize a Nash equilibrium in terms of a nonlinear complementarity problem (NCP):

$$\begin{aligned} 0\le \pi \perp \Phi (\pi )\ge 0, \end{aligned}$$

(13)

where $\pi \perp \Phi (\pi )$ means that $\pi ^T\Phi (\pi )=0$.

Proposition 3

• (i) A distribution $\pi \in \Pi$ corresponds to a Nash equilibrium if and only if it satisfies the NCP (13).

• (ii) A distribution $\pi \in \Pi$ corresponds to a Nash equilibrium if and only if it satisfies the variational inequality:

  $$\begin{aligned} (\pi '-\pi )^TF(\pi )\ge 0, \text {~~for all } \pi '\in \Pi \end{aligned}$$

  (14)

• (iii) There exists a Nash equilibrium.

Proof

See Appendix A.5. $\square$

Remark 8

In principle, we can use algorithms for NCPs to find Nash equilibria. The problem is that the number of decision variables grows exponentially with the number of decision steps. Thus, we expect that such methods would be applicable only for small values of N.

4.2 Structure and Reduced-Order Characterization

In this section, we use the monotonicity of the optimal strategies, shown in Proposition 2, to derive a reduced-order characterization of the Nash equilibrium.

The actions on a Nash equilibrium have an interesting structure. Assume that $\pi$ is a Nash equilibrium and:

$$\begin{aligned} {\mathcal {V}} = \{v^l\in {\tilde{U}}: \exists j: \pi _{(j-1)2^N+l}>0\}\subset {\tilde{U}}, \end{aligned}$$

(15)

is the set of actions used by a set of players with a positive mass. Let us define a partial ordering on ${\tilde{U}}$. For $v^1,v^2\in {\tilde{U}}$, we write $v^1\preceq v^2$ if $v^1_k\le v^2_k$ for all $k=1,\dots ,N$. Proposition 2(iii) implies that ${\mathcal {V}}$ is a totally ordered subset of ${\tilde{U}}$ (chain).

Lemma 1

There are at most N! maximal chains in ${\tilde{U}}$, each of which has length $N+1$. Thus, at a Nash equilibrium, there are at most $N+1$ different actions in ${\mathcal {V}}$.

Proof

See Appendix A.6. $\square$

For each time step k, denote by $\rho _k$ the fraction of players who play $u_M$, that is, $\rho _k=\mu (\{i:u^i_k=u_M\})$. Given any vector $\rho =[\rho _1\dots \rho _N]\in [0,1]^N$, we will show that there is a unique $\pi \in \Pi$, such that the corresponding actions satisfy the conclusion of Proposition 2(iii) and induce the fractions $\rho$. An example of the relationship between $\pi$ and $\rho$ is given in Fig. 2.

Fig. 2

In this example, $N=5$ and there are $M=3$ types of players, depicted with different colors. The mass of players below each solid line play $u_M$, and the mass of players above the line play $u_m$. Example 1 computes $\pi$ from $\rho$

Let us define the following sets:

$$\begin{aligned} \mathbb {I}_k = \{i\in [0,1): u^i_k=u_M\},~~\mathbb {K}_k = \{k': \rho _{k'}\ge \rho _k\}, ~~k=0,\dots ,N-1. \end{aligned}$$

Let $k_1,\dots ,k_N$ be a reordering of $0,\dots ,N-1$ such that $\rho _{k_1}\le \rho _{k_2}\le \dots \le \rho _{k_N}$. Consider also the set $\tilde{{\mathcal {V}}}=\{{\bar{v}}^1,\dots ,{\bar{v}}^{N+1}\}$ of $N+1$ actions ${\bar{v}}^n$ with:

$$\begin{aligned} {\bar{v}}^n_k ={\left\{ \begin{array}{ll}u_M \text {~~ if~~} k\in \mathbb {K}_{k_n} \\ u_m \text {~~ otherwise} \end{array}\right. }, ~~n=1,\dots ,N, \end{aligned}$$

(16)

and ${\bar{v}}^{N+1}_k=u_m$, for all k. Observe that $\bar{v}^{n+1}\preceq {\bar{v}}^{n}$. The following proposition shows that the set ${\mathcal {V}}$, defined in (15) is subset of the set $\tilde{{\mathcal {V}}}$.

Before stating the proposition, let us give an example.

Example 1

Consider the fractions described in Fig. 2. There are three types of players with total mass $m_1, m_2$, and $m_3$ with corresponding colors blue, pink, and yellow. In this example, we assume that the actions of each player $i\in [0,1)$ are given by:

$$\begin{aligned} u^i_k = {\left\{ \begin{array}{ll} 1, \text { ~~~ if ~~} i<\rho _k\\ 0, \text { ~~~ otherwise~~} \end{array}\right. } \end{aligned}$$

(17)

The sets $\mathbb {I}_k$ are given by:

$$\begin{aligned} \mathbb {I}_k = [0, \rho _k). \end{aligned}$$

The sets $\mathbb {K}_k$ are given by:

$$\begin{aligned} \mathbb {K}_0 = \{2\}, ~ \mathbb {K}_1 = \{2,3\}, ~\mathbb {K}_2 = \{2,3,1\},~ \mathbb {K}_3 = \{2,3,1,4\}, ~ \mathbb {K}_4 = \{2,3,1,4,0\}. \end{aligned}$$

The actions ${\bar{v}}^n$ are given by:

$$\begin{aligned} \begin{aligned}&{\bar{v}}^0 = [u_M,u_M,u_M,u_M,u_M], ~~{\bar{v}}^1 = [u_M,u_M,u_m,u_M,u_M],\\&{\bar{v}}^2 = [u_M,u_M,u_m,u_m,u_M],~~~{\bar{v}}^3 = [u_M,u_m,u_m,u_m,u_M], \\&{\bar{v}}^4 = [u_M,u_m,u_m,u_m,u_m],~~~~{\bar{v}}^5 = [u_m,u_m,u_m,u_m,u_m]. \end{aligned} \end{aligned}$$

(18)

The mass of the players of each type following each action is described in the following table:

Type	1	1	2	2	2	2	3	3
Mass	$\rho _2$	${\bar{i}}_1-\rho _2$	$\rho _3-m_1$	$\rho _1-\rho _3$	$\rho _4-\rho _1$	${\bar{i}}_2-\rho _4$	$\rho _0-{\bar{i}}_2$	$1-\rho _0$
Action	${\bar{v}}^0$	${\bar{v}}^1$	${\bar{v}}^1$	${\bar{v}}^2$	${\bar{v}}^3$	${\bar{v}}^4$	${\bar{v}}^4$	${\bar{v}}^5$

The following proposition and its corollary present a method to compute $\pi$ from $\rho$ in the general case (i.e., without assuming a set of actions in a form similar to (17)).

Proposition 4

Assume that $(u_k^i)_{i\in [0,1),k=0,\dots ,N-1}$, with $u^i\in \tilde{U}$, be a set of actions satisfying the conclusions of Proposition 2. Then:

• (i) For $k\ne k'$, either $\mathbb {I}_k\subset \mathbb {I}_{k'}$ or $\mathbb {I}_{k'}\subset \mathbb {I}_{k}$.

• (ii) If for some $k,k'$, it holds $\rho _k=\rho _{k'}$, then $\mu$-almost surely all the players have the same action on $k,k'$, i.e., $\mu (\{i:u^i_k=u^i_{k'}\})=1$.

• (iii) Up to subsets of measure zero, the following inclusions hold:

  

  where indicates that $\mu (\mathbb {I}_{k_{n}}\setminus \mathbb {I}_{k_{n+1}})=0$. Furthermore, $\mu (\mathbb {I}_{k })=\rho _{k}$.

• (iv) For $\mu$-almost all $i\in \mathbb {I}_{k_{n+1}}\setminus \mathbb {I}_{k_{n}}$, the action $u^i$ is given by ${\bar{v}}^{n+1}$, for $\mu$-almost all $i\in \mathbb {I}_{k_1}$, $u^i ={\bar{v}}^1$, and for $\mu$-almost all $i\in [0,1)\setminus \mathbb {I}_{k_N}$, $u^i_k ={\bar{v}}^{N+1}$.

Proof

See Appendix A.7. $\square$

Corollary 2

The mass of players of type j with action ${\bar{v}}^n$ is given by:

$$\begin{aligned} \mu (i: i \text { is of type } j, u^i={\bar{v}}^n) = \mu ([{\bar{i}}_{j-1},{\bar{i}}_j)\cap [ \rho _{k_{n-1}},\rho _{k_{n}})), \end{aligned}$$

(19)

where we use the convention that $\rho _{k_{0}}=0$, and $\rho _{k_{N+1}}=1$. Thus:

$$\begin{aligned} \pi _{{(j-1)2^N+l}}={\left\{ \begin{array}{ll} \mu ([{\bar{i}}_{j-1},{\bar{i}}_j)\cap [ \rho _{k_{n-1}},\rho _{k_{n}})) \text {~~if~~} v^l = {\bar{v}}^n\\ 0\quad \qquad \text {otherwise} \end{array}\right. } \end{aligned}$$

(20)

Proof

The proof follows directly from Propositions 4 and 2(ii). $\square$

Remark 9

There are at most $M+N+1$ combinations of j, l such that $\pi _{{(j-1)2^N+l}}>0.$

Let us denote by ${\tilde{\pi }} (\rho )$ the value of vector $\pi$ computed by (20).

Example 2

The situation is the same as in Example 1, but without assuming that the actions are given by (17). Then, Corollary 2 shows that ${\tilde{\pi }} (\rho )$ is given by the table in Example 1.

Proposition 5

The fractions $\rho _0,\dots ,\rho _{N-1}$ correspond to a Nash equilibrium if and only if:

$$\begin{aligned} H(\rho )=\sum _{j=1}^M\sum _{n=1}^{N+1} \mu ([{\bar{i}}_{j-1},\bar{i}_j)\cap [ \rho _{k_{n-1}},\rho _{k_{n}})) ({\bar{F}}_{j,\bar{v}^n}({\tilde{\pi }}(\rho ))-\delta ^j({\tilde{\pi }}(\rho )) )=0, \end{aligned}$$

(21)

where ${\bar{F}}_{j,{\bar{v}}^n}(\pi )$ is the cost of action ${\bar{v}}^n$, for a player of type j. Furthermore, $H(\pi )$ is continuous and nonnegative.

Proof

See Appendix A.8. $\square$

Remark 10

The computation of an equilibrium has been reduced to the calculation of the minimum of an $N-$dimensional function. We exploit this fact in the following section to proceed with the numerical studies.

5 Numerical Examples

In this section, we give some numerical examples of Nash equilibria computation. Section 5.1 presents an example with a single type of players and Sect. 5.2 an example with many types of players. Section 5.3 studies the effect of the maximum allowed action $u_M$ on the strategies and the costs of the players.¹

5.1 Single Type of Players

In this subsection, we study the symmetric case, i.e., all the players have the same parameter $b^i$. The parameters for the dynamics are $r=0.4$ and $a=1/6$ which correspond to an epidemic with basic reproduction number $R_0=2.4$, where an infected person remains infectious for an average of 6 days. (These parameters are similar to [22] which analyzes COVID-19 epidemic.) We assume that $u_m=0.4$ and that there is a maximum action $u_M=0.75,$ set by the government. The discretization time intervals are 1 week, and the time horizon T is approximately 3 months (13 weeks). The initially infected players are $I_0=0.01$. We chose this time horizon to model a wave of the epidemic, starting at a time point where $1\%$ of the population is infected. We assume that $\kappa =3$.

We then compute the Nash equilibrium using a multi-start local search method for (21). Figure 3 shows the fraction $\rho$ of players having action $u_M$ at each time step and the evolution of the total mass of infected players for the several values of b. We observe that, for small values of b, which correspond to less vulnerable or very sociable agents, the players do not engage in voluntary social distancing. For intermediate values of b, the players engage voluntary social distancing, especially when there is a large epidemic prevalence. For large values of b, there is an initial reaction of the players which reduces the number of infected people. Then, the actions of the players return to intermediate levels and keep the number of infected people moderate. In all the cases, voluntary social distancing ‘flattens the curve’ of infected people mass, in the sense that it reduces the pick number of infected people and leaves more susceptible persons in the end on the time horizon.

Fig. 3

a The fractions $\rho _k$, for $k=1,\dots ,13$, for different values of b. b The evolution of the number of infected people under the computed Nash equilibrium

We then present some results for the case where $b^i=200$. Figure 4 illustrates the evolution of $S^i(t)$ and $I^i(t)$, for the players having different strategies. We observe that the trajectories of $S^i$’s do not intersect. What is probably interesting is that the trajectories of $I^i$ may intersect. This indicates that, toward the end of the time horizon, it is probable for a person who was less cautious, i.e., she used higher values of $u^i$, to have a lower probability of being infectious.

Fig. 4

The evolution of the probabilities $S^i$ and $I^i$, for players following different strategies, for $b=200$. Different colors are used to illustrate the evolution of the probabilities for players using different strategies

5.2 Many Types of Players

We then compute the Nash equilibrium for the case of multiple types of players. We assume that there are six types of players with vulnerability parameters $G^1=100,~ G^2=200,~ G^3=400,~ G^4=800,~ G^5=1600,~ G^6=3200$. The sociability parameter $s^i$ is equal to 1, for all the players. The masses of these types are $m_1=0.5$ and $m_2=\dots =m_6=0.1$. The initial condition is for all the players $I_0=0.0001$, and the time horizon is 52 weeks (approximately a year). Here, we assume that the maximum action is $u_M=0.8$. The rest of the parameters are as in the previous subsection.

Figure 5 presents the fractions $\rho$ and the evolution of the probability of each category of players to be susceptible and infected. Let us note that the analysis of Sect. 4.2 simplifies a lot the analysis. Particularly, the set $\Pi$ has $(2^{52}-1)^6\simeq 8.3\cdot 10^{93}$ dimensions, while Problem (21) only 52.

Fig. 5

a The fractions $\rho _k$ of players having an action $u_M$. Note that the fractions correspond to players of all types. Since $s^i=1$, for all the types, it holds $b^1<\dots <b^6$, and thus, the more vulnerable players cannot have an action higher than the less vulnerable ones. b The probability of a class of people to be susceptible and infected. The colored lines correspond to the probabilities of being susceptible $S^i(t)$ and infected $I^i(t)$, for the several strategies of the players. The bold black line represents the mass of susceptible and infected persons (Color figure online)

5.3 Effect of $u_M$

We then analyze the case where the types of the players are as in Sect. 5.2, and the initial condition is $I_0=0.005$ for all the players, for various values of $u_M$. The time horizon is 13 weeks.

Figure 6a illustrates the equilibrium fractions $\rho _k$, for the various values of $u_M$. We observe that as $u_M$ increases, the fractions $\rho _k$ decrease. Figure 6b shows the evolution of the mass of infected players, for the different values of the maximum action $u_M$. We observe that as $u_M$ increases, the mass of infected players decreases. Figure 6c presents the cost of the several types of players, for the different value of the maximum action $u_M$. We observe that players with low vulnerability ($G=100$) prefer always a larger value of $u_M$, which corresponds to less stringent restrictions. For vulnerable players (e.g., $G=3200$), the cost is an increasing function of $u_M$; that is, they prefer more stringent restrictions. For intermediate values of G, the players prefer intermediate values of $u_M$. The mean cost in this example is minimized for $u_M=0.6$.

Fig. 6

a The fractions $\rho _k$, for the several values of the maximum action $u_M$. b The mass of infected people as a function of time, for the different values of the maximum action $u_M$. c The cost for the several classes of players, for the different values of the maximum action $u_M$. The bold black line represents the mean cost of all the players

6 Conclusion

This paper studied a dynamic game of social distancing during an epidemic, giving an emphasis on the analysis of asymmetric solutions. We proved the existence of a Nash equilibrium and derived some monotonicity properties of the agents’ strategies. The monotonicity result was then used to derive a reduced-order characterization of the Nash equilibrium, simplifying its computation significantly. Through numerical experiments, we show that both the agents’ strategies and the evolution of the epidemic depend strongly on the agents’ parameters (vulnerability, sociality) and the epidemic’s initial spread. Furthermore, we observed that agents with the same parameters could have different behaviors, leading to rich, high-dimensional dynamics. We also observe that more stringent constraints on the maximum action (set by the government) benefit the more vulnerable players at the expense of the less vulnerable. Furthermore, there is a certain value for the maximum action constant that minimizes the average cost of the players.

There are several directions for future work. First, we can study more general epidemics models than the SIR. Second, we can investigate different information patterns, including the cases where the agents receive regular or random information about their health state. Finally, we can compare the behaviors computed analytically with real-world data.

A Appendix: Proof of the Results of the Main Text

1.1 A.1 Existence of Solution to (1)

Note that the first two equations in (1) do not depend on $R^i$ and $D^i$. Thus, it suffices to show that the first two equations of (1) have a unique solution.

For any $i\in [0,1)$, if $[S^i(t),~I^i(t)]$ solve the differential equations (1), with initial condition $(S^i(0),I^i(0))\in [0,1]^2$, then $(S^i(t),I^i(t))$ remain in $[0,1]^2$. Thus, we consider the solution of the differential equations:

$$\begin{aligned} \begin{aligned} {\dot{S}}^i&= \text {sat}_B(-ru^iS^iI^f(t))\\ {\dot{I}}^i&=\text {sat}_B(ru^iS^iI^f(t)-\alpha ^i I^i) \end{aligned}, \end{aligned}$$

(22)

where $\text {sat}_B(z) = \max ( \min (z,B),-B)$, and $B=ru_M^2+\max _j\alpha _j$.

Consider the Banach space $X=L^1([0,1),{\mathbb {R}}^2)$, and let $x_0=(S^\cdot (0),I^\cdot (0)):[0,1)\rightarrow {\mathbb {R}}^2$. Then, under Assumptions 1,3, it holds $x_0\in X$. For each interval $[t_k,t_{k+1})$, the differential equations (22) with the corresponding initial conditions can be written as:

$$\begin{aligned} \dot{x}=f_k(x), x(t_k)=x^k_0, \end{aligned}$$

(23)

where for $x:i\mapsto [S^i,~I^i]^T$, the value of $f_k(x)\in X$ is given by:

$$\begin{aligned} f_k(x):i\mapsto [\text {sat}_B(-ru^i_k S^i{\mathcal {M}}_k x), ~\text {sat}_B(ru^i_k S^i{\mathcal {M}}_k x-\alpha ^i I^i)]^T, \end{aligned}$$

where ${\mathcal {M}}_k :X\rightarrow {\mathbb {R}}$ is a linear bounded operator with ${\mathcal {M}}_k x = \int I^i u_k^i \mu (di)$. For the initial condition, it holds $x_0^0=x_0$, and $x_0^k=x(t_k)$ is computed from the solution of (23) on the interval $[t_{k-1},t_k)$, for $k\ge 1$. For all k, $f_k$ is Lipschitz and thus there is a unique solution to (23) (e.g., Theorem 7.3 of [7]). Furthermore, both $I^\cdot (t)$ and $u^\cdot (t)$ are measurable and bounded. Thus, the integrals in (4), (2) are well defined.

Note that from Assumption 1, we only used the fact that $S^\cdot (0),I^\cdot (0):[0,1)\rightarrow {\mathbb {R}}$ are measurable and not the piecewise constant property.

1.2 Proof of Proposition 1

• (i) Since $rI^f_k>0$ and $b^i>0$, the cost (7) is strictly concave, with respect to $u_k^i$. Thus, the minimum with respect to $u_k^i$ is either $u_m$ or $u_M$.

• (ii) Since U is compact and ${\tilde{J}}$ is continuous, there is an optimal solution for (8). Denote by $u^{i,\star }$ this solution. Further, denote by $V_1=\tilde{J}^i(u^{i,\star })$ and $V_2 = \inf _A \{-b^ie^{-A}+f(A)\}$ the values of problems (8) and (9), respectively. Then, for $A^\star =\sum _{k=0}^{N-1}ru_k^{i,\star }I_k^f$, we have

  $$\begin{aligned} V_2\le -b^ie^{-A^\star }+f(A^\star )\le -b^i\exp \left[ -r\sum _{k=0}^{N-1}u^{i,\star }_kI^f_k\right] -\sum _{k=0}^{N-1}u^{i,\star }_k\bar{u}_k=\tilde{J}^i(u^{i,\star })=V_1, \end{aligned}$$

  where the first inequality is due to the definition of $V_2$ and the second inequality is due to the definition of $f(A^\star )$. To contradict, assume that $V_2<V_1$. Then, there is some A and an $\varepsilon >0$ such that:

  $$\begin{aligned} -b^ie^{-A}+f(A)<V_1-2\varepsilon . \end{aligned}$$

  (24)

  Thus, there is a ${\tilde{u}}^i$ such that $A=\sum _{k=0}^{N-1}r\tilde{u}_k^{i}I_k^f$ and $\sum _{k=0}^{N-1}\tilde{u}^{i}_k\bar{u}_k<f(A)+\varepsilon$. Combining with (24), we get ${\tilde{J}}^i({\tilde{u}})<V_1-\varepsilon$, which contradicts the definition of $V_1$. For $u^{i,\star }$ minimizing (8), the problem (9) is minimized for $A^\star =\sum _{k=0}^{N-1}ru_k^{i,\star }I_k^f$ and $u^{i,\star }$ attains the minimum in (10). To see this, observe that otherwise we would have $V_2<V_1$. On the other hand, assume that A minimizes (9) and $u^i$ attains the minimum in (10). Then, $V_2=-be^{-A}+f(A)=J^i(u^i)$. Furthermore, since $V_2=V_1$, it holds $J^i(u^i)=V_1$, and thus, $u^i$ minimizes $J^i$.

• (iii) The set $\left\{ u^i\in U: \sum _{k=0}^{N-1}u^i_kI^f_k=A/r \right\}$ is non-empty if and only if $A\in [A_m,A_M]$. Thus, the f(A) is finite if and only if $A\in [A_m,A_M]$.

  For $A\in [A_m,A_M]$, there exists an optimal solution $u^i$ that attains the minimum in (10). Since (10) is a feasible linear programming problem, there is a Lagrange multiplier $\lambda$ (e.g., Proposition 5.2.1 of [5]), and $u^i$ minimizes the Lagrangian:

  $$\begin{aligned} L(u^i,\lambda )=-\sum _{k=0}^{N-1}{\bar{u}}_k u_k^i +\lambda \sum _{k=0}^{N-1}I_k^fu_k^i-\lambda A/r. \end{aligned}$$

  (25)

  Thus, $u_k^i=u_m$, if ${\bar{u}}_k/I^f_k<\lambda$ and $u_k^i=u_M$, if ${\bar{u}}_k/I^f_k>\lambda$. To compute f(A), we reorder k, using a new index $k'$, such that ${\bar{u}}_{k'}/I^f_{k'}$ is non-increasing. Let:

  $$\begin{aligned} k'_A=\ max\left\{ {\bar{k}}_A': \sum _{k'=0}^{{\bar{k}}_A'-1} u_MI^f_{k'}+ \sum _{k'={\bar{k}}_A'}^{N-1} u_mI^f_{k'}\le A/r\right\} . \end{aligned}$$

  Then:

  $$\begin{aligned} \Sigma _{k_A'}+ u_{{\bar{k}}_A'}^iI^f_{{\bar{k}}_A'} = A/r. \end{aligned}$$

  where $\Sigma _{k_A'}=\sum _{k'=0}^{{\bar{k}}_A'-1} u_MI^f_{k'}+ \sum _{k'={\bar{k}}_A'+1}^{N-1} u_mI^f_{k'}$. Thus:

  $$\begin{aligned} f(A)=-\sum _{k'=0}^{k_A'-1} {\bar{u}}_{k'} u_M-\sum _{k'=k_A'+1}^{N-1} {\bar{u}}_{k'} u_m-\frac{{\bar{u}}_{k_A'}}{I^f_{k_A'}}(A/r -\Sigma _{k_A'}), \end{aligned}$$

  for $A/r\in [\Sigma _{k_A'}+ u_m I^f_{ k_A' } , \Sigma _{k_A'}+ u_M I^f_{ k_A' } ]$. It holds:

  $$\begin{aligned} \Sigma _{k_A'}+ u_M I^f_{ k_A' }=\Sigma _{k_A'+1}+ u_m I^f_{k_A' +1}. \end{aligned}$$

  Therefore, f is continuous and piecewise affine. Furthermore, since $\bar{u}_{k'}/I^f_{k'}$ is non-increasing with respect to $k'$, the slope of f is non-decreasing, i.e., it is convex. Thus, f is differentiable in all $(A_m,A_M)$ except of the points $A=\Sigma _{k'}+u_MI_{k'}^f$ with ${\bar{u}}_{k'}/I^f_{k'}>\bar{u}_{k'+1}/I^f_{k'+1}$. The linear parts of f are at most N.

• (iv) Since $-b^ie^{-A}$ is strictly concave in A, there are at most $N+1$ possible minima of $-b^ie^{-A}+f(A)$, which correspond to the points of non-differentiability of f in $(A_m,A_M)$ and the points $A_m$ and $A_M$. Observe that for $A=A_m$ or $A=A_M$, there is a unique $u^i$ minimizing (10). We then show that for all the non-differentiability points A of f, there is a unique $u^i$ minimizing (10). If A is a non-differentiability point, there is a $k'_0$ such that $A/r=\sum _{k'=0}^{k'_0}I_{k'}^fu_M+\sum _{k'=k'_0+1}^{N-1}I_{k'}^fu_m$ and ${\bar{u}}_{k'_0}/I^f_{k'_0}>{\bar{u}}_{k'_0+1}/I^f_{k'_0+1}$. We then show that the unique minimizer in (10) is given by $u^i_{k'}=u_M$ for $k'\le k'_0$ and $u^i_{k'}=u_m$ for $k'> k'_0$. Indeed, $u^i$ is feasible and if $u'\ne u^i$ is another feasible point, it holds:

  $$\begin{aligned} \sum _{k'=0}^{k'_0} (u_M-u'_{k'})I^f_{k'} +\sum _{k'=k'_0+1}^{N-1}(u_m-u'_{k'})I^f_{k'}=0. \end{aligned}$$

  Multiplying by ${\bar{u}}_{k'_0}/I^f_{k'_0}$, we get:

  $$\begin{aligned} \sum _{k'=0}^{k'_0} (u_M-u'_{k'})\frac{I^f_{k'}\bar{u}_{k'_0}}{I^f_{k'_0}} +\sum _{k'=k'_0+1}^{N-1}(u_m-u'_{k'})\frac{I^f_{k'}\bar{u}_{k'_0}}{I^f_{k'_0}}=0. \end{aligned}$$

  Then, using that $u_M-u'_{k'}\ge 0$, $u_m-u'_{k'}\le 0$, and that for $k'\le k'_0$, it holds ${\bar{u}}_{k'}/I^f_{k'}\ge \bar{u}_{k'_0}/I^f_{k'_0}$ and for $k'> k'_0$, it holds $\bar{u}_{k'}/I^f_{k'}<{\bar{u}}_{k'_0}/I^f_{k'_0}$, we have:

  $$\begin{aligned} -\sum _{k'=0}^{N-1}u'_{k'}{\bar{u}}_{k'} -\left[ -\sum _{k'=0}^{N-1}u^i_{k'}{\bar{u}}_{k'}\right] = \sum _{k'=0}^{k'_0} (u_M-u'_{k'})\frac{I^f_{k'}{\bar{u}}_{k'}}{I^f_{k'}} +\sum _{k'=k'_0+1}^{N-1}(u_m-u'_{k'})\frac{I^f_{k'}\bar{u}_{k'}}{I^f_{k'}}\ge 0, \end{aligned}$$

  and the inequality is strict if for some $k'>k'_0$, $u'_{k'}\ne u_m$. Therefore, $u^i$ is optimal and if $u'$ is also optimal, then it should satisfy $u'_{k'} = u_m$ for all $k'>k'_0$. Combining this with the fact that $\sum _{k'=0}^{N-1} u'_{k'} I^f_{k'}=A/r$ and $I^f_{k'}>0$, we get $u'=u^i$.

• (v) We have shown that if $u^i$ is optimal, then there is a $k'_0$ such that $u^i_{k'}=u_M$ for $k'\le k'_0$ and $u^i_{k'}=u_m$ for $k'>k'_0$. Then, using the original index k, the optimal control can be expressed as:

  $$\begin{aligned} u^i_k = {\left\{ \begin{array}{ll} u_M ~~~\text {if ~} {\bar{u}}_k/I_k^f\ge \lambda '\\ u_m ~~~\text {if ~} {\bar{u}}_k/I_k^f< \lambda ' \end{array}\right. }, \end{aligned}$$

  where $\lambda ' = {\bar{u}}_{k_0'}/I^f_{k_0'}$.

1.3 A.3 Proof of Proposition 2

• (i) Since $A_1$ is optimal for $b^{i_1}$ and $A_2$ is optimal for $b^{i_2}$, it holds:

  $$\begin{aligned} -b^{i_1}e^{-A_1}+f(A_1)\le -b^{i_1}e^{-A_2}+f(A_2),\\ -b^{i_2}e^{-A_2}+f(A_2)\le -b^{i_2}e^{-A_1}+f(A_1). \end{aligned}$$

  Adding these equations and reordering, we get:

  $$\begin{aligned} (b^{i_2}-b^{i_1})e^{-A_2}\ge (b^{i_2}-b^{i_1})e^{-A_1}. \end{aligned}$$

  And since $b^{i_2}>b^{i_1}$, we get $A_1\ge A_2$

• (ii) Using (v) of Proposition 1, and $A_1\ge A_2$, we get:

  $$\begin{aligned} A_1/r&= \sum _{k=0}^{N-1} u_k^{i_1}I^f_k = \sum _{k=0}^{N-1} \left( u_m+(u_M-u_m)h_{\lambda '_1}({\bar{u}}_k/I^f_k)\right) I^f_k \ge \\&\ge \sum _{k=0}^{N-1} \left( u_m+(u_M-u_m)h_{\lambda '_2}({\bar{u}}_k/I^f_k)\right) I^f_k = \sum _{k=0}^{N-1} u_k^{i_2}I^f_k= A_2/r \end{aligned}$$

  where $h_\lambda (\cdot )$ is the Heaviside function, i.e., $h_{\lambda '}(x)=1$ if $x\ge \lambda '$ and $h_{\lambda '}(x)=0$ otherwise. Therefore, $\lambda '_1\le \lambda '_2$.

• (iii) Assume that for $k_1\ne k_2$, $u^{i_1}_{k_1}=u^{i_2}_{k_2}=u_m$ and $u^{i_2}_{k_1}=u^{i_1}_{k_2}=u_M$. Then, using (v) of Proposition 1 we have:

  $$\begin{aligned} \lambda '_2< \frac{{\bar{u}}_{k_1}}{I^f_{k_1}}\le \lambda '_1,~~~ \lambda '_1\le \frac{{\bar{u}}_{k_2}}{I^f_{k_2}}< \lambda '_2, \end{aligned}$$

  which is a contradiction.

1.4 A.4 Optimal Control and Equilibria in Feedback Form

1.4.1 A.4.1 Optimal Control in Feedback Form

In this section, we express the optimal control law in feedback form using dynamic programming. Let $V_k(S^i_k,s^i,G^i)$ be the optimal cost-to-go from time k of a player with parameters $s^i,G^i$:

$$\begin{aligned} V_k(S^i_k,s^i,G^i)= \min _{u^i} \left\{ G^i -G^iS^i_k\exp \left[ -r\sum _{k'=k}^{N-1}u^i_{k'}I^f_{k'}\right] -s^i\sum _{k'=k}^{N-1}u^i_{k'}\bar{u}_{k'}\right\} , \end{aligned}$$

(26)

where $S^i_k=S^i(t_k) = S^i(0)\exp \left[ -r\sum _{k'=0}^{k-1}u^i_{k'}I^f_{k'}\right]$. The optimal cost-to-go can be expressed as:

$$\begin{aligned} V_k(S^i_k,s^i,G^i)= G_i +s^i {\tilde{V}}_k(S^i_k,G^i/s^i). \end{aligned}$$

We call ${\tilde{V}}_k$ the ‘auxiliary cost-to-go.’

Proposition 6

• (i) The auxiliary cost-to-go ${\tilde{V}}_k(S^i_k,G^i/s^i)$ is non-increasing and concave in $S^i_k$.

• (ii) The optimal cost-to-go $V_k(S^i_k,s^i,G^i)$ is non-decreasing in $G^i$, non-increasing in $s^i$, and non-increasing and concave in $S^i_k$.

• (iii) The optimal control law can be expressed in threshold form. That is, there are constants $l_0,\dots ,l_{N-1}$ such that the optimal control law for each player satisfies: $u^i_k = u_m$ if $S_k^iG^i/s_i>l_k$ and $u^i_k = u_M$ if $S_k^iG^i/s_i< l_k$. For $S_k^iG^i/s_i= l_k$, both $u^i_k = u_m$ and $u^i_k = u_M$ are optimal.

Proof

• (i) The auxiliary cost-to-go can be written as:

  $$\begin{aligned} {\tilde{V}}_k(S^i_k,s^i/G^i)= \min _{u^i} \left\{ -\frac{G^iS^i_k}{s^i}\exp \left[ -r\sum _{k'=k}^{N-1}u^i_{k'}I^f_{k'}\right] -\sum _{k'=k}^{N-1}u^i_{k'}\bar{u}_{k'}\right\} . \end{aligned}$$

  (27)

  Then, applying the principle of optimality we get:

  $$\begin{aligned} {\tilde{V}}_k(S^i_k,s^i/G^i)= \min _{u^i_k} \left\{ - u^i_{k}\bar{u}_{k}+ {\tilde{V}}_{k+1}(S^i_k\exp [ -r u^i_{k }I^f_{k }],s^i/G^i)\right\} . \end{aligned}$$

  (28)

  We use induction. For $k=N$, the auxiliary cost-to-go is given by ${\tilde{V}}_k(S^i_N,s^i/G^i) = -{G^iS^i_N/s^i}$. That is, $\tilde{V}_k(S^i_N,s^i/G^i)$ is non-increasing and concave in $S^i_N$. Assume that it holds for $k=k_0$. Then, for each fixed $u_{k_0}^i$, the quantity:

  $$\begin{aligned} - u^i_{k_0}\bar{u}_{k_0}+ \tilde{V}_{k_0}(S^i_k\exp [ -r u^i_{k_0 }I^f_{k_0 }],s^i/G^i), \end{aligned}$$

  is non-increasing and concave in $S^i_{k_0}$. Using (28), i.e., minimizing with respect to $u^i_{k_0}$, we conclude to the desired result.

• (ii) The monotonicity properties of $V_k$ are a direct consequence of its definition (26). The concavity of the optimal value follows easily from (i).

• (iii) From Proposition 1(i), we know that the optimal $u_k^i$ is in the set, $\{u_m,u_M\}$. Using Proposition 2 to the subproblem starting at time step k, and applying the principle of optimality, we get the desired result. The fact that if $S_k^iG^i/s_i= l_k$, then both $u^i_k = u_m$ and $u^i_k = u_M$ are optimal, is a consequence of the continuity of ${\tilde{V}}_k$.

$\square$

Remark 11

Propositions 6(iii) and 1(v) both express the optimal actions for a player i. The primary difference is that Proposition 1(v) uses dynamic programming, and thus, the policies obtained can better handle uncertainties in the individual dynamics of player i.

1.4.2 Equilibrium in Feedback Strategies

Consider a Nash equilibrium $\pi$ that induces the fractions $\rho _k$, the mean actions ${\bar{u}}_k$, and the mass of infected people in public places $I^f_k$, for $k=0,\dots ,N-1$. Consider also the auxiliary cost-to-go function ${\tilde{V}}_k$ defined in (27), and the corresponding thresholds $l_k$. Then, based on the strategies in Proposition 28(iii) we will describe a Nash equilibrium in feedback strategies. Consider the set of strategies:

$$\begin{aligned} u_k^i = {\left\{ \begin{array}{ll} u_m \text { if } S_k^iG^i/s_i>l_k \\ u_M \text { if } S_k^iG^i/s_i<l_k \\ u_M \text {~~~ if~~~} S_k^iG^i/s_i=l_k, \text {~and~}i< \rho _k\\ u_m \text {~~~ if~~~} S_k^iG^i/s_i=l_k, \text {~and~}i\ge \rho _k\end{array}\right. } \end{aligned}$$

(29)

.

Proposition 7

The set of strategies (29) is a Nash equilibrium.

Proof

Observe that the set of strategies (29) generates the same actions with the Nash equilibrium $\pi$. $\square$

1.5 A.5 Proof of Proposition 3

• (i) Assume that a $\pi \in \Pi$ satisfies (13) and fix a $j\in \{1,\dots ,M\}$. For any l such that $\pi _{(j-1)2^N+l}>0$, it holds $\Phi _{(j-1)2^N+l}(\pi )=0$, that is $F_{(j-1)2^N+l}(\pi )=\delta ^j(\pi )=\min _{ l'} F_{(j-1)2^N+l'}(\pi )$. Thus, $\pi \in \Pi$ is a Nash equilibrium.

  Conversely, assume that $\pi \in \Pi$ is a Nash equilibrium and fix a $j\in \{1,\dots ,M\}$. There is an l such that $\pi _{(j-1)2^N+l}>0$. Since $\pi$ is a Nash equilibrium, it holds $F_{(j-1)2^N+l}(\pi )=\delta ^j(\pi )$ and for all other $l'$, it holds $F_{(j-1)2^N+l'}(\pi )\ge F_{(j-1)2^N+l}(\pi )=\delta ^j(\pi )$, which implies (13).

• (ii) Assume that $\pi$ is a Nash equilibrium and $\pi '\in \Pi$. Then, $\sum _{l=1}^{2^N}\pi _{(j-1)2^N+l}=\sum _{l=1}^{2^N}\pi '_{(j-1)2^N+l}=m_j$. Since $\pi$ is a Nash equilibrium, it holds:

  $$\begin{aligned} \sum _{l=1}^{2^N} (\pi '_{(j-1)2^N+l}-\pi _{(j-1)2^N+l})^TF_{(j'-1)2^N+l}(\pi )\ge 0. \end{aligned}$$

  Thus, (14) holds.

  Conversely, assume that (14) holds, for some $\pi \in \Pi$. If $\pi$ is not a Nash equilibrium, then there is a j, l such that $\pi _{(j-1)2^N+l}>0$ and $F_{(j-1)2^N+l}>\delta ^j(\pi )$. Then, if $l'$ is such that $F_{(j-1)2^N+l'}=\delta ^j(\pi )$, taking $\pi '=\pi +\pi _{(j-1)2^N+l}e_{{(j-1)2^N+l'}}-\pi _{(j-1)2^N+l}e_{{(j-1)2^N+l}}$, we get $(\pi '-\pi )^TF(\pi )<0$, which is a contradiction.

• (iii) With a slight abuse of notation, we write $I^f_k(\pi ), {\bar{u}}_k(\pi )$ to describe the quantities $I^f_k, {\bar{u}}_k$ when the distribution of actions is $\pi$ and ${\tilde{J}}_j(v^l,\pi )$ to describe the auxiliary cost of a player of type j who plays action $v^j$ when the distribution of the actions is $\pi$.

Lemma 2

The quantities $I^f_k(\pi ), {\bar{u}}_k(\pi ), {\tilde{J}}_j({v^l},\pi )$, are continuous on $\pi$.

Proof

The state of the system evolves according to the set of $M2^{N+1}+1$ differential equations:

$$\begin{aligned} {\dot{S}}^{j,v^l}&= -r v^l_k S^{j,v^l}I^f,\\ {\dot{I}}^{j,v^l}&=r v^l_k S^{j,v^l}I^f-\alpha _j I^{j,v^l},\\ \dot{z}&= I^f, \end{aligned}$$

where $j=1,\dots ,M$, $l=1,\dots ,2^N$, $k: t\in [t_k,t_{k+1})$, and:

$$\begin{aligned} I^f = \sum _{j=1}^M\sum _{l=1}^{2^N} \pi _{(j-1)2^N+l }{I}^{j,v^l}v^l_k. \end{aligned}$$

The initial conditions are ${S}^{j,v^l}(0)={S}^{j}(0)$, ${I}^{j,v^l}(0)={I}^{j}(0)$, (Assumption 1) and $z(0)=0$.

The right-hand side of the differential equations depends continuously on $\pi$ through the term $I^f$. Furthermore, $S^{j,v^l}(t),I^{j,v^l}(t)$ remain in [0, 1] for all $j,v^l$. Thus, the state space of the system remains in $[0,1]^{M\cdot 2^N}\times {\mathbb {R}}$ and the right-hand side of the differential equation is Lipschitz. Thus, Theorem 3.4 of [25] applies and ${S}^{j,v^l}(t)$, ${I}^{j,v^j}(t)$ and z(t) depend continuously on $\pi$. Thus, $I^f_k = z({t_k+1}) -z({t_k})$ depends continuously on $\pi$. Furthermore, ${\bar{u}}_k$ is continuous (linear) on $\pi$. Finally, the auxiliary cost $J_j(v^l,\pi )$, due to its form (7), depends continuously $\pi$. $\square$

To complete the proof, observe that $F(\pi )$ is continuous and $\Pi$ is compact and convex. Thus, the existence is a consequence of Corollary 2.2.5 of [16].

Remark 12

An alternative would be to use Theorem 1 of [34] or Theorem 1 of [28], combined with Lemma 2 to prove the existence of a mixed Nash equilibrium and then use Assumption 1, to construct a pure strategy equilibrium. However, the reduction to an NCP is useful computationally.

1.6 A.6 Proof of Lemma 1

Every maximal chain begins with the least element $[u_m,\dots ,u_m]$ and ends at the greatest element $[u_M,\dots ,u_M]$. Every two consecutive elements of a maximal chain $v^l$, $v^{l+1}$ differ at exactly one point; otherwise, there exists a vector $v'$: $v^l\preceq v'\preceq v^{l+1}$ and thus the chain is not maximal.

Thus, beginning from $[u_m,\dots ,u_m]$ and changing at each step one point from $u_m$ to $u_M$, we get a sequence of $N+1$-ordered vectors. So, every maximal chain has length $N+1$.

Then, we prove that the number of such chains is N! using induction.

For $N=2$, it is easy to verify that we have two chains of 3 elements.

For $N=n$, we have n! maximal chains of $n+1$ elements. Then, for $N=n+1$ we consider one of the previous chains $v^1\preceq v^2\preceq \dots \preceq v^N$ and at each of its elements, we add an extra bit: $\tilde{v}^{i}=[v^i,\beta ^i]$. We observe that if $\beta ^i=u_M$, then for all $j>i$ it should hold $\beta ^j=u_M$, in order for the new vectors to remain ordered under $\preceq$.

Denote by $i_c$ the point that $\beta ^i$ change from $u_m$ to $u_M$. For each choice of $i_c: \quad \beta ^j=u_m, \quad j<i_c \quad \text {and} \quad \beta ^j=u_M, \quad j>i_c$, we take two ordered vectors $\tilde{v}^{i_c}_1=[v^{i_c},u_m]$ and $\tilde{v}^{i_c}_2=[v^{i_c},u_M]$ in the new chain, so we have two $\beta ^{i_c}$. Thus, we have $N+1$ possible choices for the $\beta =[\beta ^i]\in \{u_m,u_M\}^{N+1}$. This way we observe that from each chain in $(\{u_m,u_M\}^N,\preceq )$, we can construct $N+1$ chains in $(\{u_m,u_M\}^{N+1},\preceq )$.

Remark 13

The fact that ${\mathcal {V}}$ has at most $N+1$ elements is also a consequence of Corollary 1.

1.7 A.7 Proof of Proposition 4

• (i) To contradict, assume that $\mathbb {I}_k\not \subset \mathbb {I}_{k'}$ and $\mathbb {I}_{k'}\not \subset \mathbb {I}_{k}$. Then, there is a pair of players $i_1,i_2$ such that $u^{i_1}_k=u^{i_2}_{k'}=u_M$ and $u^{i_2}_k=u^{i_1}_{k'}=u_m$, which contradicts Proposition 2(iii).

• (ii) Without loss of generality, assume that $\mathbb {I}_k\subset \mathbb {I}_{k'}$. Then:

  $$\begin{aligned} \mu (\mathbb {I}_k)=\rho _k = \rho _{k'} = \mu (\mathbb {I}_k')=\mu (\mathbb {I}_k)+\mu (\mathbb {I}_{k'}\setminus \mathbb {I}_{k'}). \end{aligned}$$

  Thus, $\mu (\mathbb {I}_{k'}\setminus \mathbb {I}_{k})=0$. Combining with $\mathbb {I}_k\subset \mathbb {I}_{k'}$ and the definition of $\mathbb {I}_k, \mathbb {I}_{k'}$, we get $\mu (\{i:u^i_k=u^i_{k'}\})=1$.

• (iii) The equality $\mu (\mathbb {I}_{k })=\rho _{k}$ is immediate from the definition of $\rho _k$. Consider a pair $\mathbb {I}_{k_n}, \mathbb {I}_{k_{n+1}}$. There are two cases, $\rho _{k_n}<\rho _{k_{n+1}}$ and $\rho _{k_n}=\rho _{k_{n+1}}$. In the first case, we cannot have $\mathbb {I}_{k_{n+1}}\subset \mathbb {I}_{k_{n}}$. Thus, from (i) we have $\mathbb {I}_{k_{n}}\subset \mathbb {I}_{k_{n+1}}$. If $\rho _{k_n}=\rho _{k_{n+1}}$, then from part (ii).

  The inclusion $\mathbb {K}_{k_n}\supset \mathbb {K}_{k_{n+1}}$ is immediate from the definition.

• (iv) Let $i\in \mathbb {I}_{k_{n+1}}\setminus \mathbb {I}_{k_{n}}$. Then, since $i\not \in \mathbb {I}_{k_{n}}$ $u^i_{k_n'} =u_m$ for $n'\le n$. On the other hand, $\mu$-almost all $i\in I_{k_{n+1}}$ satisfy $i\in I_{k_{n'}}$, for $n'>n$. Thus, for $\mu$-almost all $i\in \mathbb {I}_{k_{n+1}}\setminus \mathbb {I}_{k_{n}}$, the action $u^i$ is given by (16). The proof is similar for $i\in \mathbb {I}_{k_1}$, and $i\in [0,1)\setminus \mathbb {I}_{k_N}$.

1.8 A.8 Proof of Proposition 5

If $\rho$ corresponds to a Nash equilibrium, then combining (13) and (20) we conclude that $H(\rho )=0$. Conversely, since all the terms of (21) are nonnegative, $H(\rho )=0$ implies that if $\mu ([{\bar{i}}_{j-1},\bar{i}_j)\cap [ \rho _{k_{n-1}},\rho _{k_{n}}))>0$, then $F_{(j-1)2^N+n}({\tilde{\pi }}(\rho ))=\delta ^j({\tilde{\pi }}(\rho ))$. Combining this with (20), we conclude that if for some j, l, $\pi _{(j-1)2^N+l}>0$, then $F_{(j-1)2^N+l}(\pi )=\delta ^j(\pi )$, where $\pi ={\tilde{\pi }}(\rho )$. That is, $\pi$ is a Nash equilibrium.

From (20), we observe that $\pi (\rho )$ is continuous with respect to $\rho$, since $\mu (\cdot )$ is the Lebesgue measure. Moreover, (21) can be expressed as:

$$\begin{aligned} H(\rho )=\pi (\rho )^T\Phi (\pi (\rho )). \end{aligned}$$

The fact that $H(\rho )$ is nonnegative is a result of (13). Furthermore, from Lemma 2, $F_{(j-1)2^N+n}(\pi )=\tilde{J}_j(v^n,\pi )$ is continuous with respect to $\pi$. Additionally, $\delta ^j(\pi )$, which is the minimum of $F_{(j-1)2^N+l}(\pi )=\tilde{J}_j(v^l,\pi )$ for all $v^l$, is continuous with respect to $\pi$ as the minimum of continuous functions. So, $\Phi (\pi )=F(\pi )-\delta (\pi )$ is continuous with respect to $\pi$ and $H(\rho )$ is continuous with respect to $\rho$ as composition of continuous functions.