Magnetohydrodynamic flow of Maxwell nanofluid with binary chemical reaction and Arrhenius activation energy

Abstract

The present paper addresses magnetohydrodynamics flow of Maxwell nanofluid due to stretching cylinder. To visualize the stimulus of Brownian movement and thermophoresis phenomena on Maxwell nanofluid, Buongiorno’s relation has been accounted. Moreover, heat source/sink, thermal radiation and convective condition are also attended. Mass transfer is studied by taking activation energy along with binary chemical reaction. Homotopic algorithm is adopted for the computational process of nonlinear differential systems. Five quantities, namely velocity, temperature, concentration and local Nusselt and Sherwood numbers are discussed. It is concluded that curvature parameter enhances for velocity, temperature and concentration fields. Temperature of fluid rises for radiation parameter and thermal Biot number. Clearly concentration of nanoparticles enhances with activation energy while it reduces with chemical reaction parameter. Heat transfer enhances while mass transfer rate reduces for Brownian movement and thermophoresis parameter.

Introduction

Convection heat transfer exists in many industrial or cooling equipment, where the heat transfer medium such as water, oil, ethylene/propylene glycol as the conventional fluids have been widely used. However, their limited thermal conductivity limits their convection heat transfer rate. In the recent past, nanofluids with amazing physical capabilities are utilized in many industrial and mechanical engineering processes such as optical grating, refrigeration, fuel cell optical modulator, medicine transportation, space exploration and thermal properties of engine oil. Additionally, the behavior of nanoparticles in diverse models is discussed extensively in the literature (see Choi and Eastman 1995; Sheikholeslami et al. 2017; Khan et al. 2017a; Hayat et al. 2018; Daniel et al. 2018; Ahmadi and Willing 2018 and some references therein). Many biological fluids such as foodstuff, detergents and egg white modify their flow characteristics subjected to shear stress. Liquids such as Maxwell, Oldroyd-B, Jeffrey and Sisko are characterized as non-Newtonian materials. Flow of Maxwell fluid on suddenly moved plate is discussed by Hayat et al. (2008). Sajid et al. (2017) computed flow of upper convected Maxwell fluid with joule heating effect. Flow of fractional Maxwell fluid flow by variable pressure gradient is studied by Zhang et al. (2018). Hayat et al. (2019a) elaborated mixed convective flow of Maxwell nanofluid.

Flows induced by stretching sheet are involved in metallurgical process, polyethylene oxide, polybutylene solution and chilling of microelectronics. The pioneering work on flow caused by stretching surfaces with constant speed is due to Sakiadis (1961). Wang and OnNg (2011) examined flow past a stretching cylinder with partial slip. Magnetohydrodynamics (MHD) flow of nanofluid by permeable cylinder is examined by Nourazar et al. (2017) Merkin et al. (2017) worked on stagnation point flow towards stretched cylinder. Kumar and Kumar (2017) studied radiation and porous medium effect in nanofluid flow by a stretching cylinder. Nagendramma et al. (2018) studied the thermal and solutal stratifications in flow of tangent hyperbolic nanofluid past a stretched cylinder.

Thermal radiation involvement is notable in power plants, safety of nuclear reactors and power technology. No doubt the recent researchers have already examined flows with radiation and some other aspects. For example, Pandey and Kumar (2017) worked on radiative nanofluid flow past a stretching cylinder with viscous dissipation. Nonlinear radiation in Casson nanofluid flow due to Ghadikolaei et al. (2018). Sithole et al. (2018) examined magnetohydrodynamic second-grade nanofluid flow in the presence of entropy generation. Maxwell nanofluid flow subject zero mass flux condition and heat sink/source is given by Khan et al. (2018a). Irfan et al. (2019a) studied the influence of non-uniform heat source/sink in flows of Oldroyd-B nanofluid.

The study of mass transfer phenomena with chemical reaction has a lot of applications in aerodynamics, extrusion of plastic, crystal growing, oil, water emulsions and rubber sheets. Activation energy is the minimum energy to start a chemical reaction. The term activation energy was initiated by Arrhenius (1889). The boundary layer fluid flow with binary chemical reaction is given by Bestman (1990). Kumar et al. (2018) discussed the flow of Carreau fluid with activation energy and binary chemical reaction. Activation energy and binary chemical reaction effects in flow of nanofluid are examined by Dhlamini et al. (2019). Khan et al. (2019) used the analysis of Prandtl–Eyring nanofluid flow with chemical reaction and activation energy. Impact of activation energy in chemically reactive radiative flow of Carreau nanofluid is proposed by Irfan et al. (2019b).

This attempt highlights the effects of thermal radiation, activation energy and chemical reaction in MHD flow of nanofluid by a stretching cylinder. The resulting nonlinear system is solved for the convergent solutions. The series solutions are derived using homotopic algorithm (Liao 2004; Turkyilmazoglu 2010; Hayat et al. 2017a, b, 2019b; Khan et al. 2017b) Discussion and final remarks are organized through plots.

Modeling

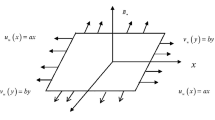
Here two-dimensional flow of Maxwell nanofluid past a stretching cylinder is modeled. Impacts of thermal radiation along with Joule heating and activation energy are studied. First-order chemical reaction is also considered. Convective boundary conditions are taken into account. Cylindrical coordinates $\left( {z,\,r} \right)$ are used to construct relevant equations. Let the cylinder with velocity $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w}_{w} = w_{0} \left( {\tfrac{z}{L}} \right)$ be stretched in the axial direction. Fluid is electrically conducting. Applied magnetic field of strength $B_{0}$ acts transversely to flow. Physical configuration is shown in Fig. 1.

Fig. 1

Flow geometry

Governing equations with boundary conditions for the given flow problems are (Khan et al. 2018b; Irfan et al. 2018):

$$\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} }}{\partial r} + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} }}{r} + \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{\partial z} = 0,\,$$

(1)

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{\partial r} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{\partial z} + \lambda \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w}^{2} \frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{{\partial z^{2} }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u}^{2} \frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{{\partial r^{2} }} + 2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{\partial r\partial z}} \right) = \nu \left( {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{\partial r}} \right) - \frac{{\sigma B_{0}^{2} }}{\rho }\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} + \lambda \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} }}{\partial r}} \right),$$

(2)

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial z}} \right) = \alpha \left( {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right) + \tau \left( {D_{\text{B}} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{\partial r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r} + D_{\text{T}} \left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right)^{2} } \right) - \frac{1}{{(\rho C_{p} )_{f} }}\frac{{\partial q_{r} }}{\partial r} + \frac{{\sigma B_{0}^{2} }}{{(\rho C_{p} )_{f} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w}^{2} ,$$

(3)

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{\partial r} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{\partial z}} \right) = D_{\text{B}} \left( {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{\partial r}} \right) + \frac{{D_{\text{T}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }}\left( {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right) - K_{\text{C}}^{2} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{\infty } } \right)\,\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }}} \right]^{n} \exp \left[ {\frac{{ - E_{\text{a}} }}{{k_{\text{a}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}} \right]^{n} ,$$

(4)

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} = 0,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{v} = 0,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w}_{f} ,\;k_{f} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r} = h(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } ),\,\;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{f} ,\quad {\text{at }}r = A, & \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \to 0,\, \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} \to \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } ,\, \, \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} \to \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{\infty } ,\,\quad {\text{as }}r \to \infty , & \\ \end{aligned}$$

(5)

where $\left( {u,\,w} \right)$ are the velocity components along with radial and transverse directions, $\rho$ the fluid density, $\sigma$ fluid electrical conductivity, $\lambda$ the relaxation time, $\tau = \tfrac{{(\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} )_{p} }}{{(\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} )_{f} }}$ the heat capacity ratio, $\alpha = \tfrac{{k_{f} }}{{(\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} )_{p} }}$ the thermal diffusivity, $g$ the gravitational acceleration, $K_{\text{C}}$ the reaction rate of solute, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}$ the temperature, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}$ the nanoparticles volume fraction, $D_{\text{T}}$ thermophoresis diffusion coefficient and $D_{\text{B}}$ the Brownian diffusion coefficient. By utilizing Rosseland’s concept, we have radiative heat flux $q$ as

$$q_{r} = - \frac{{4\sigma^{ * } \partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}^{4} }}{{3k^{ * } \partial r}},$$

(6)

in which $\sigma^{ * }$ and $k^{ * }$ represent Stefan–Boltzmann and Rosseland’s mean absorption coefficient. Temperature is expanded about $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty }$ into Taylor series:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}^{4} \approx 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty }^{3} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} - 3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty }^{4} .$$

(7)

Now Eq. (3) is reduced to

$$\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial z}} \right) = \alpha \left( {\frac{{\partial^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right) + \tau \left( {D_{\text{B}} \frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{\partial r}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r} + D_{\text{T}} \left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right)^{2} } \right) + \frac{1}{{\left( {\rho C_{p} } \right)_{f} }}\frac{{16\sigma^{ * } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty }^{3} }}{{3k^{ * } }}\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right).$$

(8)

The term

$$\left[ {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }}} \right]^{n} \exp \left[ {\frac{{ - E_{\text{a}} }}{{k_{\text{a}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}} \right]^{n}$$

(9)

is referred as the modified Arrhenius function. Here $k_{\text{a}} = 8.61 \times 10^{ - 5} \;{\text{eV/K}}$ represents the Boltzmann constant, $n$ the dimensional constant or rate constant having the range $- 1 < n < 1$ and $E_{\text{a}}$ the activation energy.

Considering

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{u} = & - \frac{A}{r}\sqrt {\frac{{\overset{\lower0.5em\hbox{$\smash{}$}}{w}_{0} }}{L}} \tilde{f}(\xi ),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} = \frac{{z\overset{\lower0.5em\hbox{$\smash{}$}}{w}_{0} }}{L}\tilde{f}^{\prime } \left( \xi \right),\quad \tilde{\theta }(\xi ) = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }},\, \, \\ \tilde{j }(\xi ) = & \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{\infty } }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{\infty } }},\quad \xi = \frac{{r^{2} - A^{2} }}{2A}\sqrt {\frac{{\overset{\lower0.5em\hbox{$\smash{}$}}{w}_{0} }}{L\nu }} , \\ \end{aligned}$$

(10)

we have

$$[(1 + 2\gamma \xi )\,\tilde{f}^{\prime \prime \prime } + 2\gamma \tilde{f}^{\prime \prime } ] + \beta \left[ {2\tilde{f}\tilde{f}^{\prime } \tilde{f}^{\prime \prime } - \tilde{f}^{2} \tilde{f}^{\prime \prime \prime } - \frac{\gamma }{(1 + 2\gamma \xi )}\tilde{f}^{2} \tilde{f}^{\prime \prime } } \right] - M(\tilde{f}^{\prime } - \beta \tilde{f}\tilde{f}^{\prime \prime } ) + \tilde{f}\tilde{f}^{\prime \prime } - \tilde{f}^{\prime 2} = 0,$$

(11)

$$\left( {\frac{1}{Pr}} \right)\,(1 + R_{\text{D}} )\,((1 + 2\gamma \xi )\,\tilde{\theta }^{\prime \prime } + 2\gamma \tilde{\theta }^{\prime } ) + N_{\text{B}} (1 + 2\gamma \xi )\,\tilde{\theta }^{\prime } \tilde{j}^{\prime } + N_{T} (1 + 2\gamma \xi )\,\tilde{\theta }^{\prime 2} + \tilde{f}\tilde{\theta }^{\prime } + Q\tilde{\theta } = 0,$$

(12)

$$\begin{aligned} ((1 + 2\gamma \xi )\,\tilde{j}^{\prime \prime } + 2\gamma \tilde{j}^{\prime } ) + \frac{{N_{\text{T}} }}{{N_{\text{B}} }}[(1 + 2\gamma \xi )\,\tilde{\theta }^{\prime \prime } + 2\gamma \tilde{\theta }^{\prime } ] - Sc\tilde{f}\tilde{j}^{\prime } & \\ - L_{\text{C}} Sc[1 + \alpha_{T} \tilde{\theta }]^{n} \exp \left( {\frac{ - E}{{1 + \alpha_{\text{T}} \tilde{\theta }}}} \right)\,\tilde{j} = & 0, \\ \end{aligned}$$

(13)

$$\tilde{f}(0) = 0,\, \, \tilde{f}^{\prime } (0) = 1,\, \, \tilde{f}^{\prime } (\infty ) = 1,\, \, \tilde{\theta }^{\prime } (0) = - B_{\text{T}} (1 - \tilde{\theta }(0)),\, \, \tilde{\theta }(\infty ) \to 0,\, \, \tilde{j}\left( 0 \right) \to 1,\, \, \tilde{j}\left( \infty \right) \to 0.$$

(14)

Here incompressibility condition (1) is trivially verified, where $M = \tfrac{{L\sigma B_{0}^{2} }}{{\rho w_{0} }}$ is the magnetic parameter, $\beta = \tfrac{{w_{0} \lambda }}{L}$ the Deborah number, $R_{\text{D}} = \tfrac{{16\sigma^{ * } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty }^{3} }}{{3k^{ * } k_{f} }}$ the radiation parameter, $Pr = \tfrac{{(\mu \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{p} )_{f} }}{{k_{f} }}$ the Prandtl number $,$ $N_{\text{B}} = \tfrac{{\tau (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{\infty } )\,D_{\text{B}} }}{\nu }$ the Brownian motion parameter, $N_{\text{T}} = \tfrac{{\tau (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } )\,D_{\text{T}} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } \nu }}$ the thermophoresis parameter, $Q = \tfrac{{Q_{0} L}}{{w_{0} (\rho C_{p} )_{f} }}$ the heat source/sink parameter, $L_{\text{C}} = \tfrac{{LK_{\text{C}}^{2} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w}_{0} }}$ the reaction-rate parameter, $Sc = \tfrac{\nu }{{D_{\text{B}} }}$ the Schmidt number, $\alpha_{\text{T}} = \tfrac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } }}$ the temperature difference parameter, $E = \tfrac{{ - E_{\text{a}} }}{{k_{\text{a}} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}$ the non-dimensional activation energy and $\gamma = \sqrt {\tfrac{L\nu }{{w_{0} A^{2} }}}$ the curvature parameter.

Local Nusselt number

Mathematically,

$$\, Nu_{z} = \frac{{zq_{w} }}{{k_{f} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty } } \right)}},$$

(15)

with

$$q_{w} = - \left[ {k_{f} \left( {1 + \frac{{16\sigma^{ * } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T}_{\infty }^{3} }}{{3k_{f} k^{ * } }}} \right)\,\left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{T} }}{\partial r}} \right)} \right]_{r = A} .$$

(16)

Now

$$\, Re^{ - 0.5} Nu_{z} = - \left( {1 + R_{\text{D}} } \right)\,\tilde{\theta }^{\prime } (0).$$

(17)

Sherwood number

$$\, Sh_{z} = \frac{{j_{w} }}{{D_{\text{B}} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C}_{\infty } )}},$$

(18)

$$j_{w} = - D_{\text{B}} \left( {\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{C} }}{\partial r}} \right)_{r = A} .$$

(19)

Dimensionless version of $Sh_{z}$ is

$$\, Re^{ - 0.5} Sh_{z} = - \tilde{j} ^{\prime } (0),$$

(20)

in which $Re = \tfrac{{z^{2} w_{o} }}{L\nu }$ denotes the local Reynolds number.

Homotopic solutions and convergence analysis

For local solutions, we choose

$$\tilde{f}_{0} (\xi ) = 1 - \exp ( - \xi ),\, \, \tilde{\theta }_{0} (\xi ) = \frac{{B_{\text{T}} }}{{1 + B_{\text{T}} }}\exp ( - \xi ),\, \, \tilde{j}_{0} (\xi ) = \exp ( - \xi ),$$

(21)

with

$${\mathbf{L}}_{1} (\tilde{f}) = \tilde{f}^{\prime \prime \prime } - \tilde{f}^{\prime } ,\, \, {\mathbf{L}}_{2} (\tilde{\theta }) = \tilde{\theta }^{\prime \prime } - \tilde{\theta },\, \, {\mathbf{L}}_{3} (\tilde{j}) = \tilde{j}^{\prime \prime } - \tilde{j},$$

(22)

and

$$\begin{aligned} {\mathbf{L}}_{1} \;[C_{1} + C_{2} \exp ( - \xi ) + C_{3} \exp (\xi )] = & 0,\, \\ {\mathbf{L}}_{2} \;[C_{5} \exp (\xi ) + C_{6} \exp ( - \xi )] = & 0,\, \\ {\mathbf{L}}_{3} \;[C_{7} \exp (\xi ) + C_{8} \exp ( - \xi )] = & 0. \\ \end{aligned}$$

(23)

Convergence

Auxiliary parameters $\hbar_{{\tilde{f}}} ,$ $\hbar_{{\tilde{\theta }}}$ and $\hbar_{{\tilde{j}}}$ gave us an opportunity to adjust convergence region for solutions of highly nonlinear system. The $\hbar$ curves are plotted for velocity, temperature and concentration (see Fig. 2). Permissible values of $\hbar_{{\tilde{f}}} ,$ $\hbar_{{\tilde{\theta }}}$ and $\hbar_{{\tilde{j}}}$ are adjusted in the ranges $- 1.05 \le \hbar_{{\tilde{f}}} \le - 0.2,$ $- 1.4 \le \hbar_{{\tilde{\theta }}} \le - 0.65$ and $1.6 \le \hbar_{{\tilde{j}}} \le - 0.2$ at 12th order of approximations. When $\hbar_{{\tilde{f}}} = - 0.4,$ $\hbar_{{\tilde{\theta }}} = - 1.1$ and $\hbar_{{\tilde{j}}} = - 0.7$ the series solutions converges in whole region of $\xi$$(0 < \xi < \infty ).$ Table 1 is also constructed for assurance of convergence.

Fig. 2

H curves

Table 1 Convergence of series solutions when $\gamma = Q = R_{\text{D}} = 0.1,$ $\beta = N_{\text{B}} = 0.2,$ $B_{\text{T}} = \alpha_{\text{T}} = 0.3,$ $M = Sc = 0.5,$ $E = 0.6,$ $N_{\text{T}} = 0.8,\, \, n = 0.9,$ $L_{\text{C}} = 1.1$ and $Pr = 1.5$

Discussions

The system of highly nonlinear ordinary differential equations with the respective boundary condition is solved analytically by means of homotopy analysis method. The computations are repeated until some convergence criterion is satisfied.

Velocity

Figure 3 displays the effect of curvature parameter on $\tilde{f}^{\prime } (\xi ).$ As expected velocity of fluid near the cylinder is increased. It is observed that the radius of cylinder will decrease with the increase of curvature parameter $\gamma .$ As a result, less surface of cylinder is in contact with fluid particles which produces a small resistance towards fluid particles. Hence, velocity enhances. Figure 4 is prepared to examine velocity of nanofluid for Deborah number $\beta .$ Velocity decreases for larger values of $\beta .$ Deborah number $\beta$ is a ratio of fluid relaxation time to its characteristic timescale. When shear stress is applied on fluid, then the time in which fluid attains its equilibrium position is called relaxation time. This time becomes larger for those fluids having higher viscosity. Thus, an increment in $\beta$ enhances the viscosity of fluid. As a result viscosity of fluid reduces. Note that if $\beta = 0$, fluid behaves like a Newtonian fluid. Contribution of magnetic parameter $M$ to velocity $f^{\prime}(\xi )$ is captured in Fig. 5. Through this figure it is noted that velocity reduces when $M$ is increased. Larger $M$ gives rise to more Lorentz force. As a result velocity is reduced. A resisting force is induced with the application of magnetic field which slows down the fluid flow.

Fig. 3

$\tilde{f}^{\prime } (\xi )$ for $\gamma$ variation

Fig. 4

$\tilde{f}^{\prime } (\xi )$ for $\beta$ variation

Fig. 5

$\tilde{f}^{\prime } (\xi )$ for $M$ variation

Temperature

Figure 6 displays the impact of Prandtl number on temperature profile. It is noted that the higher values of Pr causes the decline of temperature field. Temperature for curvature parameter is shown in Fig. 7. Clearly temperature is an increasing function of $\gamma$. Clearly temperature is an increasing function of $\gamma$. Physically, surface area of cylinder shrinks for higher values of curvature parameter which provides low heat transfer rate and thus temperature decays. Combined effect of Brownian movement $N_{B}$ and thermophoresis parameter $N_{\text{T}}$ on $\tilde{\theta }(\xi )$ is sketched in Fig. 8. There is an enhancement of temperature and related layer thickness for $N_{\text{B}}$ and $N_{\text{T}} .$ Actually the movement of nanoparticles in fluid is a cause of Brownian movement. Temperature of nanofluid is increased for thermophoresis parameter. It is because of the reason that with the support of thermophoresis phenomenon the temperature of the fluid increases in which heated particles are pulled away from high region to low. Figure 9 displayed the influence of thermal Biot number $B_{\text{T}}$ on temperature. Temperature of fluid enhances via higher $B_{\text{T}} .$ For larger $B_{\text{T}}$ there is an enhancement in internal thermal resistance of cylinder. Thus, temperature rises. Temperature for $R_{\text{D}}$ is also increased (see Fig. 10). Note that the mean absorption coefficient becomes less for $R_{\text{D}}$ and temperature is enhanced.

Fig. 6

$\tilde{f}^{\prime } (\xi )$ for $N_{1}$ variation

Fig. 7

$\tilde{\theta }(\xi )$ for $\gamma$ variation

Fig. 8

$\tilde{\theta }(\xi )$ for $N_{B}$ and $N_{T}$ variation

Fig. 9

$\tilde{\theta }(\xi )$ for $B_{T}$ variation

Fig. 10

$\tilde{\theta }(\xi )$ for $R_{D}$ variation

Concentration

Concentration $\tilde{j}(\xi )$ for curvature parameter $\gamma$ is shown in Fig. 11. Fluid concentration away from the cylinder is enhanced. Such response near the cylinder is reduced. The influence of temperature difference parameter $\alpha_{\text{T}}$ on concentration is noted in Fig. 12. It is observed that $\tilde{j}(\xi )$ is a decreasing function of $\alpha_{\text{T}} .$ Figure 13 clarifies the influence of non-dimensional chemical reaction parameter $L_{\text{C}}$ on concentration of nanoparticles. As predicted, the decline in nanoparticle concentration is noticed with an increase in $L_{\text{C}}$. The reason behind this argument is that the chemical reaction rate enhances the mass transport rate. Hence, nanoparticle’s concentration reduces. Exploration of dimensionless activation energy $E$ on nanoparticle concentration $\tilde{j}(\xi )$ is reflected in Fig. 14. Increasing behavior of concentration profile is investigated for larger $E$. It is noted that higher $E$ accelerates the solutal boundary layer thinness which enhances the species concentration. Weaker rate of reaction occurred due to higher energy activation and weaker temperature that resist the chemical reaction. Hence, species concentration increases.

Fig. 11

$\tilde{j}(\xi )$ for $\gamma$ variation

Fig. 12

$\tilde{j}(\xi )$ for $\alpha_{\text{T}}$ variation

Fig. 13

$\tilde{j}(\xi )$ for $L_{\text{C}}$ variation

Fig. 14

$\tilde{j}(\xi )$ for $E$ variation

Heat and mass transfer rates

Table 2 shows the variations of heat and mass transfer rates for different physical variables. Behavior of Brownian motion parameter $N_{\text{B}}$, thermophoresis parameter $N_{\text{T}}$ and activation energy parameter $E$ on $\left( {Re} \right)^{ - 0.5} Nu_{z}$ and $\left( {Re} \right)^{ - 0.5} Sh_{z}$ are tabulated in Table 2. Clearly heat transfer amount for $N_{\text{B}}$ and $N_{\text{T}}$ declined while reverse is true for $E$. Also the mass transport quantity decreased for $E$ and enhancement is noted for $N_{\text{B}}$ and $N_{\text{T}}$.

Table 2 Numerical values of $N_{\text{B}}$, $N_{\text{T}}$ and $E$ when $\gamma = Q = R_{\text{D}} = 0.1,$ $\beta = 0.2,$ $B_{\text{T}} = \alpha_{\text{T}} = 0.3,$ $M = Sc = 0.5,$ $n = 0.9,$ $L_{\text{C}} = 1.1$ and $Pr = 1.5$ are fixed

Comparison result

Table 3 presents the comparison of $- f''(0)$ for different values of Maxwell parameter in limiting case. This table ensures us the validity of our outcomes with former existing literature of Abel et al. (2012) and Megahed (2013).

Table 3 Comparison values of $\beta$ for Newtonian case, i.e., $M = 0$

Final remarks

Novel aspects of radiative Maxwell nanofluid flow with activation energy and binary chemical reaction are described. Velocity of fluid reduces for higher Deborah number. It is found that the curvature parameter has a tendency to increase fluid velocity, temperature and concentration. Brownian motion for temperature and concentration has a reverse response. Moreover, concentration is reduced for chemical reaction. For sufficiently large values of Biot number rises the temperature of fluid. Concentration profile reduces with higher temperature difference parameter while enhances with non-dimensional activation energy parameter.