1 Introduction

Traffic control has grown to be a key system problem as a result of the Internet’s extraordinary expansion in modern times. Streaming video, VoIP (Voice over IP), CoS (class of service), and other applications exhibit notable differences in session time and frame size. The researchers considered finding an efficient intention to manage congestion for TCP and IP protocols. The more significant component for control in IP networks is TCP flow.

The idea of quality of service was taken by IP networks. To comprehend their dynamic, modeling and analysis of networks Sharma et al. (2021) is imperative. A switch-based technique called active queue management, or AQM has been developed to address the TCP synchronization issue (Xiuchao et al. 2009) and the issue of congestion in the network. The source rate is opted by TCP as the base variable. Due to these dynamic properties, the combined TCP/AQM framework successfully resolves the synchronization issue and should result in fewer packets losing or being marked at every congestion point.

Active queue management (AQM)’s primary objective is to lower the average queue length in switches to reduce packet end-to-end delay. The other objective of AQM is to guarantee efficient utilization of system resources by minimizing packet loss that happens when queues overflow. It was advised that the random early detection method, also known as the RED algorithm, be used as the RFC2309 algorithm (Braden et al. 1998) since it can achieve the goals of the active queue management system. It can minimize packet loss ratios, also inhibit global synchronization and reduce the bias beside burst sources. Many researchers’ work has shown that tuning RED parameters (Sirisena et al. 2002; Yousefi’zadeh et al. 2008) is a very challenging task to improve the performance of networks under different traffic situations. Some modified RED schemes have been proposed to address this problem. Active queue management (AQM) techniques based on design and control-theoretic analysis have been presented. For networks using the transfer control protocol and active queue management, a fluid-flow model (Yousefi’zadeh et al. 2008) has been put forth. The evolution of the network’s unique variables, such as the normal TCP window length and queue size, is represented by this model. It appears that the transfer control protocol model accurately described how TCP traffic flow behaved. The construction of novel active queue management (AQM) control methods that take a control theory approach Alshehri et al. (2021) can therefore benefit greatly from it. It has been suggested (Misra et al. 2000) to utilize an active queue management strategy to predict changes and packet arrival rate to define the probability of packet drop. In (Xu and Sun 2014), three controllers were used in a modified Smith predictor that was released. In order to change the controller settings, a direct synthesis approach is employed. By changing a single design parameter, this method enables the user to determine a trade-off between performance and resilience. A modified Smith predictor with three controllers has been designed for integrating and unstable processes (Ajmeri and Ali 2017). The assigned capacity structure offers the tools for predictably allocating different service levels. The service allocation profiles, which provide a rational basis for cost allocation when they are in demand, indicate how resources are distributed (Kaya 2003). Understanding the dynamics of modeling and analyzing such networks is crucial. A twofold feedback loop structure is applied to the process in order to discover stability and improve performance (Clark and Fang 1998). An outer loop enables precise set-point tracking while an inner loop stabilizes the operation.

The internal mode controller and the controller in the outer loop are tuned using PID tuning. Use the Ziegler Nichols or autotuning based on relay feedback to modify the inner loop controller. When the queue is full, a drop tail is utilized, which drops packets. But it is not proper as a feedback control system for high-speeded networks since links are probably going to have huge queues in high-speed networks and this may expand the normal delay in the system. All the maximum critically, drop tail can regularly have low throughput and cause synchronization worldwide. To solve these problems, RED, which randomly removes packets proportional to the average queue length, has been proposed in Vijayan and Panda (2012). TCP can be used in a conventional wired communication system to transport trustworthy data between end hosts. To reduce the number of induced acknowledgments, a dynamic TCP-MAC (medium access control) interaction technique has been put forth (Menacer et al. 2021). When TCP is used with mobile ad hoc networks (MANETs) performance degradation is noticed in the system because MANET has various issues like transmission error and dynamic topologies. TCP variant for MANETs has been discussed in Szyguła et al. (2021). A hybrid controller design was proposed in Molia and Kothari (2018); Kanungo et al. (2020) which consists of a fuzzy Sharma and Saxena (2017) controller and a three-mode PID controller Mahmoud and Aziza (2020), Rajesh and Dash (2019).

To reduce the queue size of the TCP model and the effect of time delay, a modified Smith predictor design is recommended. This Smith predictor is constructed using three controllers from a second-order process model. With the use of three controllers in the proposed model settling time and oscillation can be controlled. The direct synthesis method is employed in controller design because it enables users to strike a balance between a single layout/tuning parameter’s durability and efficiency. A dynamic model of the Transfer Control Protocol is given in Section 2. Issues with active queue management control are discussed in Section 3. In Section 4, details of the Smith predictor are discussed. The Controller Design is shown there in Section 5. Section 6, which also contains a simulation study, wraps up the work.

2 Dynamic model of TCP

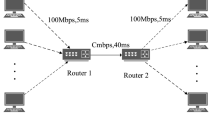
Stochastic differential equation analysis and fluid flow are used to suggest the performance of the TCP dynamic model (Floyd and Jacobson 1997). The simulation’s outcomes demonstrated that this model successfully captured TCP behavior. In order to ignore the TCP timeout procedure, a condensed form of that model is employed in this research work and is shown in Fig. 1. The following nonlinear differential equations represent the nonlinear model utilized for the simulations under various approximations.

$$\dot{\mathrm{W}}\left(\mathrm{t}\right)=\frac{1}{\mathrm{R}(\mathrm{t})}-\frac{\mathrm{W}\left(\mathrm{t}\right)}{2} \frac{\mathrm{W}\left(\mathrm{t}-\mathrm{R}\left(\mathrm{t}\right)\right)}{\mathrm{R}\left(\mathrm{t}-\mathrm{R}\left(\mathrm{t}\right)\right)}\mathrm{ p}(\mathrm{t}-\mathrm{R}\left(\mathrm{t}\right))$$
(1)
$$\dot{\mathrm{q}} \left(\mathrm{t}\right)=\mathrm{N}\left(\mathrm{t}\right)\frac{\mathrm{W}\left(\mathrm{t}\right)}{\mathrm{R}\left(\mathrm{t}\right)}-\mathrm{C}$$
(2)

where ẋ represents the time derivative.

Fig. 1
figure 1

TCP connection block diagram

Full size image

W = average TCP window size,

q = average queue length,

R = Round trip time, \(\mathrm{R}\left(\mathrm{t}\right)=\frac{\mathrm{q}}{\mathrm{C}}+{\mathrm{T}}_{\mathrm{p}}\)

C = queue capacity,

\({\mathrm{T}}_{\mathrm{p}}\) = Delay in propagation,

N = Number of TCP sessions.

p = Packet loss probability, p \(\in\)[0,1].

The TCP window control dynamic is defined by the first equation (Hollot et al. 2002). The term on its right side simulates both the window’s progressive drop along with the window’s additive extension in response to a packet marking. The bottleneck queue length is taken into account in the second equation as a further difference between connection capacity and packet arrival rate. The queue’s length and window size, q [o, q] and W [0, W], respectively, are both positive, limited metrics, that stand for the buffer’s maximum capacity and the window’s maximum size. The probability value also only ranges from [0,1]. The operational point (Wo, qo, po) is given by when (W,q) is taken into account as system state, also p is considered input.

\(\mathop {\text{W}}\limits^{.} = 0\) , \({\text{W}}_{o}^{2} {\text{p}}_{o} = 2\)

$$\dot{\mathrm{q}}=0,{\mathrm{W}}_{\mathrm{o}}=\frac{{\mathrm{R}}_{\mathrm{o }}\mathrm{C}}{\mathrm{N}}$$
(3)

The model’s small-signal linearization (1)

$$\updelta \dot{\mathrm{W}}\left(\mathrm{t}\right)=\frac{-2\mathrm{N}}{{\mathrm{R}}_{\mathrm{o}}^{2}\mathrm{C}}\mathrm{ \delta W}\left(\mathrm{t}\right)-\frac{{\mathrm{R}}_{\mathrm{o}}{\mathrm{C}}^{2}}{2{\mathrm{N}}^{2}}\mathrm{\delta p}\left(\mathrm{t}-{\mathrm{R}}_{\mathrm{O}}\right)$$
(4)
$$\updelta \dot{\mathrm{q }}\left(\mathrm{t}\right)=\frac{\mathrm{N}}{{\mathrm{R}}_{\mathrm{o}}}\mathrm{\delta W}\left(\mathrm{t}\right)-\frac{1}{{\mathrm{R}}_{\mathrm{o}}}\mathrm{\delta q}(\mathrm{t})$$
(5)

where \(\mathrm{\delta W}\left(\mathrm{t}\right)=\mathrm{W}\left(\mathrm{t}\right)-{\mathrm{W}}_{\mathrm{o}}\), \(\mathrm{\delta q}\left(\mathrm{t}\right)=\mathrm{q}\left(\mathrm{t}\right)-{\mathrm{q}}_{\mathrm{o}}\) and\(\mathrm{\delta p}\left(\mathrm{t}\right)=\mathrm{p}\left(\mathrm{t}\right)-{\mathrm{p}}_{\mathrm{o}}\), \({\mathrm{R}}_{\mathrm{o}}\)= Round trip time at operating time.

A further interpretation is possible when the TCP transmission window is much larger than 1. For many network scenarios, this condition holds true, and the time delay that impacts the window dynamic can then be disregarded.

The AQM action can be seen as a compensator that works together with the TCP dynamic in order to stabilize it.

$${\mathrm{P}}_{\mathrm{TCP}}\left(\mathrm{s}\right)=\frac{\frac{{\mathrm{R}}_{\mathrm{o}}{\mathrm{C}}^{2}}{2{\mathrm{N}}^{2}}}{\mathrm{s}+\frac{2\mathrm{N}}{{\mathrm{R}}_{\mathrm{o}}^{2}\mathrm{C}}}$$
(6)
$${\mathrm{P}}_{\mathrm{queue}}\left(\mathrm{s}\right)= \frac{\frac{\mathrm{N}}{{\mathrm{R}}_{\mathrm{o}}}}{\mathrm{s}+\frac{1}{{\mathrm{R}}_{\mathrm{o}}}}$$
(7)

3 AQM control problem

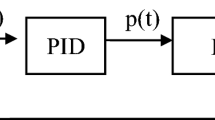
AQM feedback control structure is represented in Fig. 2. The purpose of the AQM controller (Xu et al. 2015; Khoshnevisan et al. 2020) is to monitor packets as an element of estimated queue length.

Fig. 2
figure 2

AQM feedback control structure

Full size image

From Fig. 2 a transfer function for plants P(s) could be

$$\mathrm{P }\left(\mathrm{s}\right)={\mathrm{P}}_{\mathrm{TCP}}\left(\mathrm{s}\right)*{\mathrm{P}}_{\mathrm{queue}}\left(\mathrm{s}\right)$$
$$\mathrm{P}\left(\mathrm{s}\right)=\frac{\frac{{\mathrm{C}}^{2}}{2\mathrm{N}}}{\left(\mathrm{s}+\frac{2\mathrm{N}}{{\mathrm{R}}_{\mathrm{o}}^{2}\mathrm{C}} \right)(\mathrm{s}+\frac{1}{{\mathrm{R}}_{\mathrm{o}}})}$$
(8)

The Block diagram similar to the feedback Control strategy is given in Fig. 3. The transfer function that results from Eq. (8) is P(s). In this design, the delay e sRo is taken into account, and C(s) is a controller or compensator used to regulate plant performance. C(s), an AQM transfer function indicates a control strategy which is defined as RED. This controller output is a loss probability which is an average queue length function. RED contains an LPF (low pass filter) and a nonlinear gain map.

Fig. 3
figure 3

A linearized AQM control system

Full size image

RED transfer-function (Unal et al. 2013) model is given by Eq. (9)

$$\mathrm{C}\left(\mathrm{s}\right)=\frac{{\mathrm{kL}}_{\mathrm{red}}}{\mathrm{s}+\mathrm{k}}$$
(9)

where

$${\mathrm{L}}_{\mathrm{red}}=\frac{{\mathrm{p}}_{\mathrm{max}}}{{\mathrm{max}}_{\mathrm{th}}-{\mathrm{min}}_{\mathrm{th}}}$$
(10)
$$\mathrm{k}=\frac{\mathrm{log}(1-\propto )}{\delta }$$

where the Mean Weight is \(\propto\) as well as the Sampling Frequency is \(\delta\).

\({min}_{th}\) is the minimum queue length beyond which packet marking is applied linearly.

The Loop’s Transfer Function is

$$\mathrm{L }\left(\mathrm{s}\right)=\mathrm{C}\left(\mathrm{s}\right) .\mathrm{P}(\mathrm{s}){\mathrm{e}}^{-{\mathrm{sR}}_{\mathrm{o}}}$$
$$\mathrm{L}\left(\mathrm{s}\right)=\frac{{\mathrm{kL}}_{\mathrm{red}}\frac{{\mathrm{C}}^{2}}{2\mathrm{N}}{\mathrm{e}}^{-{\mathrm{sR}}_{\mathrm{o}}}}{\left(\mathrm{s}+\frac{2\mathrm{N}}{{\mathrm{R}}_{\mathrm{o}}^{2}\mathrm{C}} \right)\left(\mathrm{s}+\frac{1}{{\mathrm{R}}_{\mathrm{o}}}\right)\left(\mathrm{s}+\mathrm{k}\right)}$$
(11)

Three poles along with a time delay exist in this L(s). The pole of the low-pass filter should be either placed outside the loop’s bandwidth or taken less than the P(s) corner frequencies to be able to get gain from this function while realizing the stability of the closed loop.

4 Smith predictor

Smith predictor is a delay compensation technique that is usually used in the control system. This method can be used for both small and large delays. The motive of the Smith predictor design is how to eliminate delay components from the system’s closed-loop (Bonald et al. 2000; Batista and Jota 2018). When time delay becomes significant then this delay produces instability in the system, so in the design method of the feedback control system, it is mandatory to take into consideration. There are numerous ways to enhance the system’s reaction. This section introduces a controller design to improve the functionality of the AQM conventional control structure.

Figure 4 represents a Smith predictor design. It is an idealistic one as the predictor’s transfer function \({G}_{p} \left(1-{e}^{-s{R}_{o}}\right)\) is assumed to cancel the delay effect in the loop perfectly. The delay compensation needs a perfect estimation of the process transfer function \({\mathrm{G}}_{\mathrm{p}}{\mathrm{e}}^{-{\mathrm{sR}}_{\mathrm{o}}}\) which is not possible. To implement the Smith predictor in a real-world scenario, estimate the value of \({\mathrm{G}}_{\mathrm{p}}\) and \({e }^{-s{R}_{o}}\). The modified Smith predictor structure presented in Fig. 5, in which unstable plant transfer function is represented by \({\mathrm{G}}_{\mathrm{p}}\), the plant time delay is represented by \({\mathrm{R}}_{o}\), plant model transfer function is represented by \({\mathrm{G}}_{\mathrm{m}}\) and the model time delay is represented by \({\mathrm{R}}_{m}.\) Gc2 is employed to stabilize the unstable process, and Gc1 serves as a set point tracking controller. A first-order filter has been employed in a feedback system to predict the disruption for the reduction of system uncertainty. For the model’s robustness in this structure, Gf (a first-order filter) is used.

Fig. 4
figure 4

The Smith predictor general structure for delay compensation

Full size image
Fig. 5
figure 5

Modified Smith predictor structure

Full size image

Given that the parameters of the process and the model are equal (Gp = Gm), the setpoint and disturbance responses can be expressed as

$$\mathrm{Y}\left(\mathrm{s}\right)={\mathrm{T}}_{\mathrm{r}}\left(\mathrm{s}\right)\mathrm{R}\left(\mathrm{s}\right)+{\mathrm{T}}_{\mathrm{d}}\mathrm{D}(\mathrm{s})$$

where

$${\mathrm{T}}_{\mathrm{r}}\left(\mathrm{s}\right)=\frac{\mathrm{Y}(\mathrm{s})}{\mathrm{R}(\mathrm{s})}=\frac{{\mathrm{G}}_{\mathrm{c}1}{\mathrm{G}}_{\mathrm{m}}{\mathrm{e}}^{-{\mathrm{R}}_{\mathrm{m}}\mathrm{s}}}{1+{(\mathrm{G}}_{\mathrm{c}1}+{\mathrm{G}}_{\mathrm{c}2}{)\mathrm{G}}_{\mathrm{m}}}$$
(12)
$${\mathrm{T}}_{\mathrm{d}}\left(\mathrm{s}\right)=\frac{\mathrm{D}(\mathrm{s})}{\mathrm{R}(\mathrm{s})}=\frac{{(1+\mathrm{G}}_{\mathrm{c}1}{\mathrm{G}}_{\mathrm{m}}+{\mathrm{G}}_{\mathrm{c}2}{\mathrm{G}}_{\mathrm{m}}-{{\mathrm{G}}_{\mathrm{c}1}{\mathrm{G}}_{\mathrm{m}}\mathrm{e}}^{-{\mathrm{R}}_{\mathrm{m}}\mathrm{s}}){\mathrm{G}}_{\mathrm{m}}{\mathrm{e}}^{-{\mathrm{R}}_{\mathrm{m}}\mathrm{s}}}{\left[1+\left({\mathrm{G}}_{\mathrm{c}1}+{\mathrm{G}}_{\mathrm{c}2}\right){\mathrm{G}}_{\mathrm{m}}\right][1+{{\mathrm{G}}_{\mathrm{f}}{\mathrm{G}}_{\mathrm{m}}\mathrm{e}}^{-{\mathrm{R}}_{\mathrm{m}}\mathrm{s}}]}$$
(13)

From Eqs. (11) and (12) It is possible to analyze that the load disturbance rejection controllers Gc1 and Gc2 (load disturbance elimination response) are distinct from one another (Kaya and Nalbantoğlu 2016; Tchamna et al 2019). Only the Gc1 controller is present for set-point tracking in the closed-loop transfer function. As a result, Gc1 can be tweaked to accomplish strong steps initially, But Gc1’s performance in load disturbance rejection is also impacted. Therefore, by modifying solely the disturbance rejection responses, Gc2 can be modified. The time delay is included within the design since it is an element of the characteristic equation for load disturbance rejection that arises from Eq. (12) Gc2. Equation (12) shows that if Gc1 is chosen with an integral action (either PI or PID), this integral action will lead the controller Gc1 to show a zero in the Y(s) R(s) and an undesired overshoot in the closed-loop performance (Armaghani et al. 2011). A set-point filter or set-point weighting is required to reduce overshoot.

The step response of a system is used as the performance metric for second-order systems.

The response’s rise time is the amount of time it takes to go from 0 to 100% of its final value.

$${t}_{r}=\frac{\pi -\theta }{{w}_{d}}$$

Here wd is the damped frequency.

Peak time is said to be the amount of time the answer takes to first reach the peak value.

$${t}_{p}=\frac{\pi }{{w}_{d}}$$

Peak overrun is the difference between the response’s peak value and its end value.

$${M}_{p}={e}^{-(\frac{\delta \pi }{\sqrt{1-{\delta }^{2}}})}$$

Here δ is the damping ratio.

The settling time is the length of time required for the response to stabilize.

5 Controller design

The Gc1 and Gc2 controller designs are included in the updated Smith predictor design. The design processes (Ajmeri and Ali 2017) for the controllers are discussed in this section. Gc1 plays a key role in integrating or stabilizing an unstable structure, whilst Gc2 is made to manage the removal of disturbances.

Equation (14) can be used to represent a second-order plus dead-time transfer function process model.

$${\mathrm{G}}_{\mathrm{m}}\left(\mathrm{s}\right)=\frac{{\mathrm{k}}_{\mathrm{m}}}{{\mathrm{s}}^{2}+\mathrm{as}+\mathrm{b}}{\mathrm{e}}^{-{\mathrm{R}}_{\mathrm{m}}\mathrm{s}}$$

A PI controller, Eq. (14), controls the forward closed loop Gc1.

$${\text{G}}_{{{\text{c}}1}} = {\text{k}}_{{\text{c}}} \left( {1 + \frac{1}{{{\text{T}}_{{\text{i}}} {\text{s}}}}} \right)$$
(14)

As a proportional-derivative controller (PD), Gc2 is represented by the

$${\mathrm{G}}_{\mathrm{c}2}={\mathrm{k}}_{\mathrm{d}}(1+{\mathrm{T}}_{\mathrm{d}}\mathrm{s})$$
(15)

Equation (12) can be used to obtain the resulting closed-loop transfer function, Tr(s). Delay free function is thus provided by

$${\mathrm{T}}_{\mathrm{r}}\left(\mathrm{s}\right)=\frac{{\mathrm{T}}_{\mathrm{i}}\mathrm{s}+1}{\frac{{\mathrm{T}}_{\mathrm{i}}}{{\mathrm{k}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{c}}}{\mathrm{s}}^{3}+\frac{{\mathrm{T}}_{\mathrm{i}}}{{\mathrm{k}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{c}}}\left(\mathrm{a}+{\mathrm{k}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{d}}{\mathrm{T}}_{\mathrm{d}}\right){\mathrm{s}}^{2}+\frac{{\mathrm{T}}_{\mathrm{i}}}{{\mathrm{k}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{c}}}\left(\mathrm{b}+{\mathrm{k}}_{\mathrm{d}}+{\mathrm{k}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{c}}\right)\mathrm{s}+1}$$
(16)

After normalization this equation

$${\mathrm{T}}_{\mathrm{r}}\left(\mathrm{s}\right)=\frac{{\mathrm{c}}_{\mathrm{i}}{\mathrm{s}}_{\mathrm{n}}+1}{{\mathrm{s}}_{\mathrm{n}}^{3}+{\mathrm{d}}_{2}{\mathrm{s}}_{\mathrm{n}}^{2}+{\mathrm{d}}_{1}{\mathrm{s}}_{\mathrm{n}}+1}$$
(17)

where the standardized Laplace complex variable \({\mathrm{s}}_{\mathrm{n}}=\frac{\mathrm{s}}{\propto }\), it implies that the framework response will be quicker than the standardized reaction by a factor of α.

Where \(\mathrm{\alpha }=({\frac{{\mathrm{k}}_{\mathrm{m}}{\mathrm{k}}_{\mathrm{c}}}{{\mathrm{T}}_{\mathrm{i}}})}^{1/3}\)

$${\mathrm{c}}_{\mathrm{i}}=\mathrm{\alpha }{\mathrm{T}}_{\mathrm{i}}$$
(18)
$${\mathrm{d}}_{2}=\frac{(\mathrm{a}+{\mathrm{k}}_{\mathrm{m}}{\mathrm{T}}_{\mathrm{d}})}{\mathrm{\alpha }}$$
(19)
$${\mathrm{d}}_{1}=\frac{\left(\mathrm{b}+({\mathrm{k}}_{\mathrm{d}}+{\mathrm{k}}_{\mathrm{c}}){\mathrm{k}}_{\mathrm{m}}\right)}{{\mathrm{\alpha }}^{2}}$$
(20)

It is obvious from the aforementioned equations that the time scale can be decided by the actions of kc, ci, and Ti, and kd through the choice of d1. d2 by the choice of Td. A trade-off between the chosen values of and ci may be made when choosing kc and Ti in practice because kc will likely be bound to bind the initial value of the control effort.

To achieve a decent load disturbance rejection, the controller Gf is necessary.

$${\mathrm{G}}_{\mathrm{f}}={\mathrm{k}}_{\mathrm{o}}$$
(21)

where

$${\mathrm{k}}_{\mathrm{o}}=\frac{\uppi -2{\mathrm{\varnothing }}_{\mathrm{pm}}}{{2\mathrm{k}}_{\mathrm{m}}{\uptheta }_{\mathrm{m}}}$$
(22)

For a known phase margin, use pm. You may find the best deal by using \({\varnothing }_{pm}=\) 60°.

6 Simulation and results

This research work is illustrated by MATLAB/Simulink simulator. All of the graphs show the instantaneous queue length’s interval variation, with seconds serving as the unit of time. Design parameters are listed in Table.1. Figures 6 and 7 display the step and frequency response of the TCP dynamic model.

Table 1 Parameters table
Full size table
Fig. 6
figure 6

Step response of TCP model

Full size image
Fig. 7
figure 7

Frequency response of TCP model

Full size image

Referring to the above table P(s) value can be found in Eq. (8)

$$\mathrm{P}\left(\mathrm{s}\right)=\frac{450{\mathrm{e}}^{-1.1\mathrm{s}}}{{\mathrm{s}}^{2}+1.46\mathrm{ s}+0.501}$$
(23)

An AQM control framework (Maihi and Atherton 1999) is used to improve output by modifiable variations in queue length to avoid either overflow (lost packets) or an empty buffer (interface underutilization). The AQM control system is intended to be stabilized by the RED controller. For α = 0.0001 and δ = 0.0008 find the value of k = 0.1250. So for this value of k, the calculated value of Lred = 0.000182 from Eq. (10).

From Eq. (9) RED transfer-function model is

$$\mathrm{C}\left(\mathrm{s}\right)=\frac{2.28\times {10}^{-5}}{\mathrm{s}+0.1250}$$

The loop transfer function from Eq. (11)

$$\mathrm{L}\left(\mathrm{s}\right)=\frac{0.1026\times {\mathrm{e}}^{-1.1\mathrm{s}}}{\left(\mathrm{s}+0.55\right)\left(\mathrm{s}+0.91\right)\left(\mathrm{s}+0.1250\right)}$$

The Step Response and frequency response of the RED controller are shown in Figs. 8 and 9. This response shows the improvement in gain margin. Figure 10 represents the step response of the proposed Smith predictor with dead time.

Fig. 8
figure 8

Step response of The RED controller

Full size image
Fig. 9
figure 9

Frequency response using The RED controller

Full size image
Fig. 10
figure 10

Smith predictor step response

Full size image

In the next simulation, a Smith predictor controller is proposed in place of the RED controller.

Case 1

Referring to the Table 1 P(s) can be found from Eq. (24)

$$\mathrm{P}\left(\mathrm{s}\right)=\frac{450{\mathrm{e}}^{-1.1\mathrm{s}}}{{\mathrm{s}}^{2}+1.46\mathrm{ s}+0.501}$$
(24)

A transfer function obtained with the Smith predictor is represented in Eq. (17). PI Controller \({\mathrm{G}}_{\mathrm{c}1}\) and PD controller \({\mathrm{G}}_{\mathrm{c}2}\) parameters are calculated by selecting the suitable value of α and \({\mathrm{c}}_{\mathrm{i}}\). For \({\mathrm{G}}_{\mathrm{c}1}\), Kc value is bounded to 1.25 and Ti is selected 1.56, α = 8.25 and \({\mathrm{c}}_{\mathrm{i}}\)= 0.63. From (Kumar et al 2020) 1.6, the ISTE optimal values of d2 and d1 are taken into consideration and 2.2, respectively. Equation (20) gives Kd = 0.274 and Eq. (19) gives Td = 0.026.

Selecting the value of Gf to give the phase margin of 60°. From Eq. (21) the value of Gf = 0.179. The step setpoint response of the projected technique is presented in Fig. 11. However, less oscillation is observed in the response with the proposed method.

Fig. 11
figure 11

System response with Smith predictor

Full size image

Case 2

The parameter of the TCP/AQM is shown in Table.2, and since 200 packets are expected in the queue, the better model is

Table 2 Parameters table
Full size table
$$\mathrm{P}\left(\mathrm{s}\right)=\frac{432 {\mathrm{e}}^{-1.76\mathrm{s}}}{{\mathrm{s}}^{2}+0.837\mathrm{ s}+0.153}$$

The developed Smith predictor may stabilize the Queue Length close to the reference queue size with fewer oscillations, as demonstrated in Fig. 12. Except for Gf = 0.0068, the Smith predictor controller’s parameters are identical to those in example 1. The RED is unable to maintain the length of the Queue close to the reference.

Fig. 12
figure 12

System response with a queue length of 200

Full size image

Table 3 lists the various time domain characteristics that are derived based on the system’s TCP session count. From the above table it can be concluded that if the number of sessions increases then peak time, the time for rising and settling will increase. So it was analyzed by the simulation that number of sessions can degrade the system performance. Figures 6 and 8 implied that the proposed controller can achieve a steady state faster than the RED controller. The modified controller design provides a faster response with the least oscillations. In every scenario, the suggested controller outperformed the competition and proved its capacity to run the network at high levels of utilization. According to this investigation, the developed controller is effective at controlling the queue length close to the destination and has a faster convergence rate and fewer fluctuations than others.

Table 3 Comparison of time-domain characteristics
Full size table

7 Conclusion

Smith predictor methodology was designed for the AQM control through robustness attributes. The outcomes demonstrated predominant transient reaction and stability. Although the designed AQM controller improves the response and effectiveness, it can resolve one of the principal shortcomings, the tuning of the controller. Peak, rising, and settling times for TCP sessions 100 and 150 were examined to determine system performance. Because the model’s parameters are accustomed to directly determining the Controller’s parameters, it doesn’t need controller tuning through the conventional tuning strategies, for example, phase margin or some other technique. Moreover, straightforwardness, low computational cost, and simple tuning are a few qualities that make it appropriate for edge or core routers. For future research, the self-tuning method of the designed controller will be reached out to an adaptive controller by evaluating the time-varying parameters of the network.