1 Introduction

In the current scenario, it is impossible to imagine work without a computer system. The embedded system plays a diverse role in a different field. For example, it is used in weather forecasting, controlling rockets etc. It also have a great importance in business, education and automated things. Therefore, a system should be error-free, more efficient and reliable. The tolerance of the system should be more to handle more and more work at a time.

If any system develops, then its software and hardware components are tested very carefully to make the system error-free. But, then also, there exist some probability of accident. There can be either degradation of the system or crash. Generally, the error occurs more in softwares than hardwares. In different fields, for various types of work, many software have to be installed in the system [Lyu (1996), Goyal and Ram (2016), Kumaresan and Ganeshkumar (2020)].

Reliability of the system is the probability of its adequate performance during a predefined period given that the system behavior is completely characterized in context of probability measures [Ram and Goyal (2016); Goyal et al. (2017), Cao et al. (2019)]. At most of the places, distributed system approach has been used which consists of multiple autonomous computer systems communicating through a network. A computer program running in a distributed system is called distributed program and the writing of such programs is called distributed programming [Goyal and Ram (2014), Rajaraman (2010), McCluskey and Mitra (2004)].

Many authors have worked on the reliability of various systems such as hardware systems, software systems but they did not study about the errors in embedded system. Soi and Aggarwal (1980) presented a model which described the future trends in the digital communication system and analyzed the availability behavior of next-generation digital communication system. Goel et al. (1993) designed a model for a satellite-based computer communication networks system in which a master station is connected with the remote micro earth stations in the country. Pham (1992) analyzed the reliability and mean time to failure of a high voltage system with two transmitters in addition to a power supply and addressed that the working of the system is affected by any failed component. The authors explained these analyses through numerical examples. In this study, they did not integrate human error and common-cause failure. Ram et al. (2013) developed a stochastic model of a complex repairable system by introducing the concept of the standby unit with the incorporation of distinct failures namely human error, minor failure, waiting time to repair, and unit failure, and obtained the various reliability measures by employing two types of the repair strategy.

Liu (1998) calculated the reliability of a load-sharing k-out-of-n system for arbitrary distribution by presenting a generalized model without considering human error and common-cause failure. Singh et al. (2013) modeled a series system with two units in which each unit is controlled by its controller and analyzed the cost–benefit of the system including the service cost but they did not consider the warranty period. Dhillon and Yang (1996) developed Markov models to perform reliability analysis of a repairable and non-repairable robot and its safety system and presented an expression for robot reliability, mean time between failure, and state probabilities but they did not obtain the expected profit. Pham and Wang (1996) developed the concept of imperfect maintenance and discussed several methods and optimal policies on imperfect maintenance for estimating the reliability measures. In this study, the authors did not analyze the effect of failure rates on reliability.

Billinton and Wang (1999) present a technique for system reliability distribution to evaluate the expected value of the system reliability measures. They also present a Monte Carlo simulation for system evaluation and compared the results found by both techniques. Qureshi (2008) provided a review of key traditional accident modeling approaches and their limitation and described new system theoretic approaches to the modeling and analysis of accidents in the safety–critical systems. Musa and Okumoto (1984) developed a software reliability model that predicts expected failure and better than existing software reliability models and is simpler than any of the models that approaches it in predictive validity. Goseva-popstojanova and Trivedi (2001) designed and detailed state of the architecture –based approaches to the reliability of component-based software and explained how it can be used to examine the software behavior.

Zhu and Pham (2019) proposed a model in which failures are categorized into three types such that hardware failure, software failure, hardware-software interaction failure. Hardware-software interaction failure is also divided into a software-induced hardware failure and hardware-induced software failure. They provide a Markov model and compared the result with and without hardware-software interaction failure. Teng et al. (2006) proposed a Markov model to analyze hardware-software interaction failure and apply the approach to a real telecommunication system. Zeng et al. (2019) proposed an approach to analyze the reliability of a non-repairable system based on path and integrals and explain the case studies with and without warm standby systems. Gertsbakh and Shpungin (2016) described various types of network reliability including static and dynamic reliability with Monte Carlo approach. Some importance measures for network reliability models has also been discussed in their book. While Zhang and Mahadevan (2017) evaluated the network reliability problem using game theory. In their study they design the problem of router and attacker as a two player game and optimized using Dijkstra and FW algorithm.

1.1 Research gaps

After the review of some papers related to embedded system, authors identify the following research gaps-

  1. (i)

    To develop the mathematical models for embedded systems.

  2. (ii)

    To analyse the reliability indices for the embedded system including human error and network failure.

  3. (iii)

    To investigate the mean time to failure and mean time to repair.

  4. (iv)

    To discussed the maintenance cost for the system.

  5. (v)

    To analyse the expected profit in the system.

  6. (vi)

    To study about the sensitivity of the system due to its component.

  7. (vii)

    To determine the effects of multi failures on it.

1.2 Objectives

The multiplicity of mathematical models developed so far considered reliability, cost analysis and MTTF of a complex system, with different types of failures and one type of repairs. But they did not consider one of the important aspects, role of human failure at the reliability of embedded system. In this paper, authors discussed the following points-

  • To design the mathematical model of embedded system with context of different types of errors such as human error, errors due to networking, due to intolerance of software, hardware errors, and errors due to the interaction of hardware and software.

  • To determine the system’s reliability by considering human error and network failure.

  • This paper details the effect of each failures on system’s working and provided that how these errors can be reduced or enhance the system reliability as MTTF and sensitivity study.

  • To analyse the expected profit in the system.

2 Mathematical model details

2.1 Assumptions

In the proposed model, the following assumptions have been made:

  1. (i)

    The system has probabilistic behaviour i.e. characterized by the constant hazard rate.

  2. (ii)

    Future states depend only on the current state not on the past state.

  3. (iii)

    In the initial state, the embedded system is in a good state.

  4. (iv)

    The system covers three types of states—good, degraded, and failed.

  5. (v)

    Only one change is allowed at a time in the transition states.

  6. (vi)

    The system has two types of failures- partial failure, complete failure.

  7. (vii)

    When the failed component is repaired, the system is consider as good as new.

  8. (viii)

    The failure and repair rates follow general distribution.

3 Notations

Notations associated with this work are described in Table 1.

Table 1 Notations
Full size table

3.1 System description

Authors have designed the mathematical model of embedded system (hardware and software combinatory system) under the consideration multi-failures such as such as human error, errors due to networking, due to intolerance of software, hardware errors, and errors due to the interaction of hardware and software. The system consists of hardware components and softwares to perform the task. System’s performance depends upon the working of its each component and software updation, and it also affected by the human interaction with the system. Unfortunately, many researchers avoided the human error in reliability analysis. Human error is a tag given to an achievement that has negative consequences or fails to achieve the desired task. Human error can be classified into two types non-critical (Type 1) and critical human error (Type 2) based on their action [Dhillon and Yang, 1993].

Human Error Type-1: Either an action that is not intended or desired by the human to perform a prescribed function within the specified limits of accuracy, sequence, or time that fails to produce the expected result and has led or has the potential to lead to an unwanted Consequence. For example, If pilot in command's improper decision to takeoff into deteriorating weather conditions (including turbulence, gusty winds, and an advancing thunderstorm and associated precipitation) when the airplane was overweight and when the density altitude was higher than he was accustomed to, resulting in an a stall caused by failure to maintain airspeed. (NTSB 1997, p. 53).

Human Error Type-2: A generic term to encompass all those actions in which a planned sequence of mental or physical activities fails to achieve its intended task, and when these failures cannot be attributed to some chance agency (Reason 1990). For example, Bhopal gas tragedy on 3 December, 1984.

Hardware Error Type-1: It can be corrected by the time limit. Due to this error, system achieves the degraded state and can be improved. Therefore, no data is lost or lost data can be retrieved.

Hardware Error Type-2: It cannot be corrected by the time limit. Due to this error, system failed completely and cannot be improved easily. Comprehensive data is lost by this error.

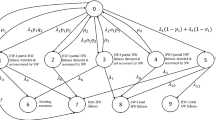
The proposed embedded system is divided into states, which are shown in the state transition diagram (Fig. 1). As per our assumption, initially, the system is in good working condition i.e. free from error. However, due to existence of several errors, system either goes to the degraded state or gets crash that means goes to a completely failed state. In the degraded state, system works with reduced efficiency but when it gets crashes or completely failed then system stop working. Mathematical model of the embedded system based on the states shown in Fig. 1 and described in Table 2, is derived with the help of Markov process. Markov process has a specific property of memoryless. So, failures allow the transition of the system memoryless. Markov process is completely characterized by its transition probability matrix. In a Markov model, authors associate with the state of the system of a probability Pij, indicating the probability of the system moving from state i to state j. This probability is called the transition probability. A matrix of transition state probabilities is called transition matrix.

Fig. 1
figure 1

State transition diagram

Full size image
Table 2 State description
Full size table

3.2 Formulation of the model

By the probability of consideration and continuity of arguments, one can obtain the following set of differential equations possesses the present mathematical model

$$\left[ {\frac{\partial }{\partial t} + \alpha_{1} + \lambda_{N} + \beta_{1} + \lambda_{S1} + \beta_{2} + \lambda_{SIT} + \alpha_{2} + \lambda_{C} } \right]P_{0} (t) = \mu \sum\limits_{i = 1}^{4} {P_{i} (t)} + \int\limits_{0}^{\infty } {\varphi (x)\left\{ {\sum\limits_{j = 5,6,8} {P_{j} (x,t)} } \right\}} dx$$
(1)
$$\left[ {\frac{\partial }{\partial t} + \lambda_{C} + \mu } \right]P_{1} (t) = \lambda_{N} P_{0} (t)$$
(2)
$$\left[ {\frac{\partial }{\partial t} + \lambda_{C} + \alpha_{2} + \mu } \right]P_{2} (t) = \alpha_{1} P_{0} (t)$$
(3)
$$\left[ {\frac{\partial }{\partial t} + \beta_{2} + \mu } \right]P_{3} (t) = \beta_{1} P_{0} (t)$$
(4)
$$\left[ {\frac{\partial }{\partial t} + \lambda_{S2} + \lambda_{SIT} + \mu } \right]P_{4} (t) = \lambda_{S1} P_{0} (t)$$
(5)
$$\left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \varphi } \right]P_{j} (x,t) = 0;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,j = 5,\,6,\,7,\,8,\,9$$
(6)

Boundary conditions

$$P_{5} (0,t) = \lambda_{S2} P_{4} (t)$$
(7)
$$P_{6} (0,t) = \beta_{2} \left[ {P_{3} (t) + P_{0} (t)} \right]$$
(8)
$$P_{7} (0,t) = \lambda_{SIT} \left[ {P_{0} (t) + P_{4} (t)} \right]$$
(9)
$$P_{8} (0,t) = \alpha \left[ {P_{2} (t) + P_{0} (t)} \right]$$
(10)
$$P_{9} (0,t) = \lambda_{C} \left[ {P_{0} (t) + P_{1} (t) + P_{2} (t)} \right]$$
(11)

Initial condition

$$P_{0} (0) = 1\;{\text{and}}\;{\text{other}}\;{\text{state}}\;{\text{probabilities}}\;{\text{are}}\;{\text{zero}}\;{\text{at}}\;t = \, 0.$$
(12)

Taking Laplace transformation of Eqs. (1) to (11) using Eq. (12)

$$\left[ {s + \alpha_{1} + \lambda_{N} + \beta_{1} + \lambda_{S1} + \beta_{2} + \lambda_{SIT} + \alpha_{2} + \lambda_{C} } \right]\overline{P}_{0} (s) = \mu \sum\limits_{i = 1}^{4} {\overline{P}_{i} (s)} + \int\limits_{0}^{\infty } {\varphi (x)\left\{ {\sum\limits_{j = 5,6,8} {\overline{P}_{j} (x,s)} } \right\}} dx$$
(13)
$$\left[ {s + \lambda_{C} + \alpha_{2} + \mu } \right]\overline{{P_{2} }} (s) = \alpha_{1} + \overline{{p_{0} }} (s)$$
(14)
$$\left[ {s + \lambda_{C} + \mu } \right]\overline{{P_{1} }} (s) = \lambda_{N} \overline{{P_{0} }} (s)$$
(15)
$$\left[ {s + \beta_{2} + \mu } \right]\overline{{P_{3} }} (s) = \beta_{1} \overline{{P_{0} }} (s)$$
(16)
$$\left[ {s + \lambda_{S2} + \lambda_{SIT} + \mu } \right]\overline{{P_{4} }} (s) = \lambda_{S1} \overline{{P_{0} }} (s)$$
(17)
$$\left[ {s + \frac{\partial }{\partial x} + \varphi (x)} \right]\overline{{P_{j} }} (x,s) = 0;\,\,\,\,\,\,\,\,\,\,\,j = 5,\,6,\,7,\,8,\,9$$
(18)

Boundary conditions

$$\overline{{P_{5} }} (0,s) = \lambda_{S2} \overline{{P_{4} }} (s)$$
(19)
$$\overline{{P_{6} }} (0,s) = \beta_{2} \left[ {\overline{{P_{0} }} (s) + \overline{{P_{3} }} (s)} \right]$$
(20)
$$\overline{{P_{7} }} (0,s) = \lambda_{SIT} \left[ {\overline{{P_{0} }} (s) + \overline{{P_{4} }} (s)} \right]$$
(21)
$$\overline{{P_{8} }} (0,s) = \alpha \left[ {\overline{{P_{2} }} (s) + \overline{{P_{0} }} (s)} \right]$$
(22)

3.3 Solution of the model

By solving Eqs. (13) to (18) using (19) to (22), we get

$$\overline{{P_{0} }} (s) = \frac{1}{D(s)}$$
$$\overline{{P_{1} }} (s) = \frac{{\lambda_{N} }}{{s + \lambda_{C} + \mu }}\overline{{P_{0} }} (s)$$
$$\overline{{P_{2} }} (s) = \frac{{\alpha_{1} }}{{S + \lambda_{C} + \alpha_{2} + \mu }}\overline{{P_{0} }} (s)$$
$$\overline{{P_{3} }} (s) = \frac{{\beta_{1} }}{{S + \beta_{2} + \mu }}\overline{{P_{0} }} (s)$$
$$\overline{{P_{4} }} (s) = \frac{{\lambda_{S1} }}{{S + \lambda_{S2} + \lambda_{SIT} + \mu }}\overline{{P_{0} }} (s)$$
$$\overline{{P_{5} }} (s) = \left( {\frac{{1 - \overline{{S_{\varphi } }} (s)}}{S}} \right)\lambda_{S2} A_{5} \overline{{P_{0} }} (s)$$
$$\overline{{P_{6} }} (s) = \left( {\frac{{1 - \overline{{S_{\varphi } }} (s)}}{S}} \right)\beta_{2} [1 + A_{4} ]\overline{{P_{0} }} (s)$$
$$\overline{{P_{7} }} (s) = \frac{1}{S}\lambda_{C} [1 + A_{5} ]\overline{{P_{0} }} (s)$$
$$\overline{{P_{9} }} (s) = \frac{1}{S}\lambda_{C} [1 + A_{2} + A_{3} ]\overline{{P_{0} }} (s)$$

where, \(A_{1} = \alpha_{1} + \lambda_{N} + \beta_{1} + \lambda_{S1} + \beta_{2} + \lambda_{SIT} + \alpha_{2} + \lambda_{C}\); \(A_{2} = \frac{{\lambda_{N} }}{{s + \lambda_{C} + \mu }}\); \(A_{3} = \frac{{\alpha_{1} }}{{S + \lambda_{C} + \alpha_{2} + \mu }}\); \(A_{4} = \frac{{\beta_{1} }}{{S + \beta_{2} + \mu }}\); \(A_{5} = \frac{{\lambda_{S1} }}{{S + \lambda_{S2} + \lambda_{SIT} + \mu }}\).

$$D(s) = s + A_{1} - \mu A_{2} - A_{3} \left( {\mu + \alpha_{2} \overline{{S_{\varphi } }} (s)} \right) - A_{4} \left( {\mu + \beta_{2} \overline{{S_{\varphi } }} (s)} \right) - A_{5} \left( {\mu + \lambda_{S2} \overline{{S_{\varphi } }} (s)} \right) - \overline{{S_{\varphi } }} (s)\left\{ {\lambda_{S2} + \beta_{2} + \alpha_{2} } \right\}$$

3.4 Probabilities of the upstate and downstate of the system

$$\overline{{P_{up} }} (s) = \sum\limits_{i = 0}^{4} {\overline{P}_{i} (s)}$$
$$= \left[ {1 + \sum\limits_{i = 2}^{5} {A_{i} } } \right]\overline{{P_{0} }} (s)$$
(23)
$$\overline{{P_{down} }} (s) = \sum\limits_{i = 5}^{9} {\overline{P}_{i} (s)}$$
$$= \left\{ {\left( {\frac{{1 - \overline{{S_{\varphi } }} (s)}}{s}} \right)\left\{ {\lambda_{S2} A_{5} + \beta_{2} (1 + A_{4} ) + \alpha_{2} (1 + A_{3} )} \right\} + \frac{1}{s}\left\{ {\lambda_{C} (1 + A_{2} + A_{3} ) + \lambda_{SIT} (1 + A_{5} )} \right\}} \right\}\overline{{P_{0} }} (s)$$
(24)

4 Particular cases and numerical computations

4.1 Availability analysis

Cogitate that the repair facility is available. Setting the value of various parameters as \(\lambda_{SIT} = 0.15\), \(\alpha_{1} = 0.5\), \(\alpha_{2} = 0.1\), \(\lambda_{N} = 0.4\), \(\beta_{1} = 0.2\), \(\beta_{2} = 0.1\), \(\lambda_{C} = 0.1\), \(\lambda_{S1} = 0.1\), \(\lambda_{S2} = 0.3\), \(\mu = 1\), \(\varphi (x) = 1\) [Zhang and Mahadevan (2017); Gertsbakh and Shpungin (2016); Ram and Goyal (2016)] and taking the inverse Laplace transformation of Eq. (23), one can obtain availability of the system in terms of time t as

$$P_{up} (t) = 0.1087594415e^{( - 2.845739222\,\,t)} + 0.03727835506e^{( - 1.433990048\,\,t)}$$
$$+ 0.02725880574e^{( - 1.3178559026\,t)} + 0.03648577384e^{( - 1.071699092\,\,t)} + 0.7902176241e^{( - 0.02001261288\,t)}$$
(25)

Now varying the time t from 0 to 50 unit in Eq. (25), one obtains the availability of the designed system as shown in Table 3 and corresponding Fig. 2 respectively.

Table 3 Availability of the System
Full size table
Fig. 2
figure 2

Availability vs Time

Full size image

4.2 Reliability Analysis

The system is how much reliable, can be calculated by taking the inverse Laplace transformation of Eq. (23) and setting the value of various parameters as \(\lambda_{SIT} = 0.15\), \(\alpha_{1} = 0.5\), \(\alpha_{2} = 0.1\), \(\lambda_{N} = 0.4\), \(\beta_{1} = 0.2\), \(\beta_{2} = 0.1\), \(\lambda_{C} = 0.1\), \(\lambda_{S1} = 0.1\), \(\lambda_{S2} = 0.3\), \(\mu = 0\), \(\varphi (x) = 0\)[Zhang and Mahadevan (2017); Gertsbakh and Shpungin (2016); Ram and Goyal (2016)], one can obtain the reliability of the system in terms of time t as

$$Rl(t) = 0.3529411765e^{( - 0.1\,\,t)} + 0.1851851852e^{( - 0.45\,\,t)} + 0.3125e^{( - 0.2\,\,t)} + 0.1493736383e^{( - 1.8\,t)}$$
(26)

Now, varying the time t from 0 to 15 in Eq. (26), one acquires the reliability of the designed system as shown in Table 4 and corresponding Fig. 3 respectively.

Table 4 Reliability of the system
Full size table
Fig. 3
figure 3

Reliability vs Time

Full size image

4.3 Mean time to failure (MTTF)

MTTF helps to analyse the effects of each failure on the system independently. One may get it by setting the repair rates equals to zero in Eq. (23) as:

$$MTTF = \mathop {\lim }\limits_{s \to 0} \overline{P}_{up} (s)$$
$$= \frac{{1 + \frac{{\lambda_{N} }}{{\lambda_{C} }} + \frac{{\lambda_{S1} }}{{\lambda_{S2} + \lambda_{SIT} }} + \frac{{\alpha_{1} }}{{\lambda_{c} + \alpha_{2} }} + \frac{{\beta_{1} }}{{\beta_{2} }}}}{{\alpha_{1} + \lambda_{N} + \beta_{1} + \lambda_{S1} + \beta_{2} + \lambda_{SIT} + \alpha_{2} + \lambda_{C} }}$$
(27)

Varying input parameters one by one at 0.1, 0.2,……………..,0.9 respectively and setting the other failure rates as \(\lambda_{SIT} = 0.15\), \(\alpha_{1} = 0.5\), \(\alpha_{2} = 0.1\), \(\lambda_{N} = 0.4\), \(\beta_{1} = 0.2\), \(\beta_{2} = 0.1\), \(\lambda_{C} = 0.1\), \(\lambda_{S1} = 0.1\), \(\lambda_{S2} = 0.3\) authors can get the MTTF concerning the variation of failure rates that signify in Table 5 and graphical representation shown in Fig. 4.

Table 5 MTTF of the system
Full size table
Fig. 4
figure 4

MTTF vs Variation in failure rates

Full size image

4.4 Expected profit

Expected profit has great importance to maintain system reliability. Let the service facility be always available, the expected profit during the interval [0, t) is given as:

$$E_{P} (t) = K_{1} \int\limits_{0}^{t} {P_{up} (t)dt} - tK_{2}$$
(28)

Let us cogitate the value of \(K_{1} = 1\), the value of K2 varies as 0.1, 0.3, and 0.5 respectively, one obtains Table 6 and Fig. 5, which epitomizes the graph of expected profit concerning time.

Table 6 Expected Profit as a function of time
Full size table
Fig. 5
figure 5

Expected Profit vs Time

Full size image

4.5 Sensitivity analysis

It is a very important analysis to predict the rate of change of parameters with respect to the particular variables [Henley and Kumamoto (1992), Andrews and Moss (1993)]. Sensitivity to a factor is defined as the partial derivative of the function concerning that factor [Goyal and Ram (2018)]. Here, these factors are the failure rates of the embedded system.

4.5.1 Sensitivity of reliability

The reliability of the embedded system is how much sensitive concerning each failure rate, can be analyzed by partial differentiation of inverse Laplace transform of Eq. (23), concerning the failure rates of each state. Reliability sensitivity can be calculated by putting the values of failure and repair rates as \(\lambda_{SIT} = 0.15\), \(\alpha_{1} = 0.5\), \(\alpha_{2} = 0.1\), \(\lambda_{N} = 0.4\), \(\beta_{1} = 0.2\), \(\beta_{2} = 0.1\), \(\lambda_{C} = 0.1\), \(\lambda_{S1} = 0.1\), \(\lambda_{S2} = 0.3\), \(\mu = 0\), \(\varphi (x) = 0\), in the partial derivatives of reliability function. Varying time t from 0 to 20 units and failure rates from 0.1 to 0.9, the sensitivity of reliability graphically revealed in Fig. 6. In Fig. 6, a1 stands for \(\alpha_{1}\), l1 stands for \(\lambda_{SIT}\), a2 stands for \(\alpha_{2}\), ln stands for \(\lambda_{N}\), b1 stands for \(\beta_{1}\), b2 stands for \(\beta_{2}\), lc stands for \(\lambda_{C}\), ls1 stands for \(\lambda_{S1}\), ls2 stands for for for \(\lambda_{S2}\).

Fig. 6
figure 6

Reliability sensitivity of the embedded system

Full size image

4.5.2 Sensitivity of MTTF:

The sensitivity in MTTF of the embedded system can be studied through the partial differentiation of Eq. (27) concerning the failure rates of the embedded system. By applying the set of parameters as \(\lambda_{SIT} = 0.15\), \(\alpha_{1} = 0.5\), \(\alpha_{2} = 0.1\), \(\lambda_{N} = 0.4\), \(\beta_{1} = 0.2\), \(\beta_{2} = 0.1\), \(\lambda_{C} = 0.1\), \(\lambda_{S1} = 0.1\), \(\lambda_{S2} = 0.3\), in partial differentiation of MTTF, one can calculate the MTTF sensitivity as shown in Table 7 and corresponding graphs shown in Fig. 7.

Table 7 MTTF sensitivity with variation in failure rates
Full size table
Fig. 7
figure 7

MTTF Sensitivity concerning failure rates

Full size image

5 Result discussions

In this research work, the authors have studied the numerous reliability characteristics such as availability, reliability, MTTF and profit concerning the service rate of the system. Through the overall study of the system, the following observations have been made:-

Figure 2 representing the graph of availability of system decreases with a high rate in the first five months reaches 70% and in the next five months its availability decreases to 70% to 65% but the rate is slow from the first five months. Availability continuously decreases with the same rate from 10 to 15 months and 15 to 20 months and till 50 months and after 50 months availability is only 30%.

Reliability of system decreases to 32% in first five months and it decreases to 12% in 10 months and 10% in 15 months and 8% in 20 months and it decreases uniformly and reaches 1% in 40 months and 0.21%in 45 months and reliability approach to almost 0% after 50 months (Fig. 3).

MTTF (Fig. 4) of software error due to intolerance, hardware error (type-2), and human error (type-2) decreases smoothly. MTTF of catastrophic failure decreases at a high rate.

MTTF of networking error increases because in starting possibilities of networking error is more and then it occurs very rarely.

MTTF of hardware error also increases because in starting if hardware error is removed then failure rate decreases after that hardware error occurs very rarely.

Figure 5 shows that the expected profit of the system increases with the increment in time but decreases as service cost increases. After a long time, profit decreases as time increase.

Reliability Sensitivity first increases concerning time and after some time it decreases in case of human error type-1, networking error, hardware error type-1 as shown in Fig. 6. It also decreases these errors. Reliability sensitivity decreases for a short period and after that increases in case of human error type 2, hardware type-2, catastrophic failure, error due to intolerance, software error type-1 and type-2. Reliability sensitivity increases in case of increment in these errors.

The sensitivity of MTTF (Fig. 7) is increasing rapidly for some time concerning the human error type 2, hardware type-2, catastrophic failure, and after a fixed period it increases slightly concerning time. MTTF sensitivity increases slightly and after some time it will be constantly concerning the error due to intolerance, software error type-1 and type-2, human error type-1. The sensitivity of MTTF decreases very slightly concerning time in case of networking error and hardware error type-2.

6 Conclusions

While the technical world existing, embedded system plays a pivotal role everywhere. This study focused on the mathematical model of embedded system under multiple failures using Markov process, to predict the effect of each failures on system’s working and provided some results that helps to get highly reliable system. As Dhillon and Yang (1993) have shown that the human error can affect the system working upto 70%, so, it must not be avoided in the evaluation of system reliability. Markov process provided the best result about the reliability evaluation of embedded system because multiple errors specially human error are depend only the current transition. Many researchers [Narayanan and Xie, 2006; Wattanapongsakorn and Levitan, 2004] have analysed the reliability of embedded system but they did not consider human error and networking error. Through the overall study, it is determined that the availability of the system decreases greatly in starting, and then it decreases uniformly. Similarly, in starting five months, the reliability of the system decreases straightly and after that, it decreases smoothly. After a fixed time the system’s reliability is constant. As months pass profit decreases and service rate increases. With the vital examination of the proposed system, the authors find that the system is more sensitive in concerning the networking error and human error type 2. Human error type 1 has the almost equivalent effect throughout the working but human error type 2 has big changes with time. These results are very beneficial for software engineers and system engineers. Embedded system is more appropriate then the externally software based system because it has less probability of human error as compare to externally software based system. As a direction for future work, we will try to study the designed model with the presence of common cause failure and find out the meantime to repair the system.