1 Introduction

Trade credit is a key concern for many enterprises with clear impact on inventory and finance. However, the impact of trade credit on the demand rate has been hardly explored by the researchers. The objective of this paper is to formulate an EOQ model to determine the retailer’s optimal replenishment as well as the credit policy under two levels of trade credit policy.

Inventory models with trade credit financing may have either one or two levels of available trade credit offered. Inventory models with one level of trade credit are those in which supplier offers a credit period to the retailer for making the payment and the retailer offers no credit period to its customers. In the past, many articles dealing with one-level trade credit inventory models have appeared in various research journals. (Goyal 1985) introduced the concept of permissible delay in payments in the EOQ model. Later, (Chung 1989) presented the discounted cash flows (DCF) approach for the analysis of the optimal inventory policy in the presence of trade credit. Aggarwal and Jaggi (1995) extended the (Goyal 1985)’s model to the case of deterioration. Jamal et al. (2000) further generalized the model to allow shortages. Hwang and Shinn (1997) considered the problem of determining the retailer’s optimal price and lot size simultaneously when the supplier permits delay in payments. (Teng 2002) provided an alternative conclusion from (Goyal 1985), and mathematically proved that it makes economic sense for a buyer to order less quantity and take benefits of the permissible delay more frequently. Chang et al. (2004) considered an inventory model for deteriorating items with instantaneous stock-dependent demand and time-value of money when credit period is provided. The review article by Chang et al. (2008) gives a complete and up-to-date survey of published inventory literature under trade credits.

In the two levels of trade credit policy, both the supplier and the retailer offer trade credit period to their respective customers. (Huang 2003) presented an inventory model assuming that the retailer also offers a credit period to his/her customer which is shorter than the credit period offered by the supplier, in order to stimulate the demand. Later, (Huang 2007) extended the same inventory model within the economic production quantity (EPQ) framework. Huang and Hsu (2008) have developed an inventory model under two-level trade credit policy by incorporating partial trade credit option at the customers of the retailer. (Liao 2008) developed an EOQ model with non-instantaneous receipt and exponentially deteriorating items under two-level trade credit financing. (Tsao 2009) developed an EOQ model under advance sales discount and two-echelon trade credits. (Jaggi et al. 2008) have developed an EOQ model in which the retailer’s demand is linked to credit period under two-level trade credit financing. Besides, credit linked demand, this paper also extended the (Huang, 2003)’s model by relaxing the assumption N < M. Teng and Chang (2009) also extended the (Huang 2007)’s model by relaxing the assumption N < M. In these papers, a retailer allows each customer with the same trade period N. The view point of (Jaggi et al. 2008) for two levels of trade credit policy have been widely explored by many researchers such as (Teng et al. 2009; Chen and Kang 2010; Chang et al. 2010; Ho 2011). Recently. (Thangam and Uthayakumar 2011) presented the two-echelon trade credit financing in a supply chain with perishable items and two different payment methods where supplier offers full trade credit to his retailer and the retailer in turn offers partial trade credit to market customers.

Further, trade credits also have impact on the demand of the item, which has been considered constant over the last 30 years of research work in this area. As far as the authors are aware of the published literature on inventory problems with trade credits, researchers have consistently ignored the impact of credit period on demand of the inventory item. By considering the trade credit’s impact on demand, retailer may have the higher demand and hence can improve their profit margins. Related to this context, recently, Jaggi et al. (2008) have developed an EOQ model in which the retailer’s demand is linked to credit period under two-level trade credit financing. Jaggi and Kausar (2009), Jaggi and Khanna (2009) and Thangam and Uthayakumar (2009) extended the Jaggi et al. (2008)’s model to the case of deterioration, inflation and price as well as credit period dependent demand respectively. In fact, the type of credit liked demand function which has been considered by these researchers assumed constant capturing rate, which may not be true in reality as it is observed that initially the credit period may not be effective in stimulating demand but over a period of time, it got a significant effect on demand and gradually reaches the saturation level. In order to incorporate this phenomenon, a dynamic credit-linked demand function has been considered which in fact takes care of both the instant as well as delayed impact of the credit period on demand in the proposed inventory model under two levels of trade credit policy. Here, the capturing rate is also a function of credit period. This type of demand function is very much prevalent in consumer durables, which eventually helps both supplier as well as the retailer to reframe their respective inventory policies.

2 Assumptions and notations

The following assumptions are made to develop the mathematical model:

  1. (1)

    The demand rate is a function of the credit-period offered by the retailer (N).

  2. (2)

    The supplier provides a fixed credit period M to settle the accounts to the retailer and the retailer, in turn, also offers a credit period N to each of its customers to settle the accounts.

  3. (3)

    Rate of replenishment is infinite.

  4. (4)

    Shortages are not allowed.

  5. (5)

    Lead-time is negligible.

In addition, following notations are used:

T :

Inventory cycle length

q(t):

The inventory level at time t

A :

Ordering cost per order

C :

Unit purchase price of the item

P :

Unit selling price of the item

I :

Inventory carrying charge per $ per unit time (excluding interest)

I e :

Interest rate that can be earned per $ per unit time

I p :

Interest rate payable per $ per unit time

M :

Retailer’s credit period offered by the supplier

N :

Customer’s credit period offered by the retailer

π(T, N) :

Retailer’s profit per unit time, function of cycle length (T) and customer’s credit period (N)

3 Mathematical formulation

As this paper assumes that the demand is influenced by customer’s credit period offered by the retailer (N), therefore, under the assumption that the marginal effect of credit period on sales is proportional to the unrealized potential of the market demand without any delay, the demand function is represented as a difference equation

$$ \lambda (N + 1 )- \lambda (N )= \alpha (N) [\lambda_{m} - \lambda (N ) ] { } $$
(1)

where λ(N) is the demand rate which is function of customer’s credit period (N), λ m is the maximum demand rate, α(N) is the rate of change of demand (capturing rate), is also function of customer’s credit period (N),

$$\alpha{(N)}= {\raise0.5ex\hbox{$\scriptstyle {r^{2} N}$}\kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {(1 + rN)}$}} \left( {\text{It can be estimated using the past data}}\right)$$
(2)

It is assumed here that α(N) is an increasing function in N and it reaches r as N tends to infinity. The solution of the above difference equation using probability generating function, under the condition that at N = 0, λ(0) = λ 0 (initial demand), keeping other attributes like price, quantity etc. at constant level, is given by

$$ \, D \equiv \lambda (N) = \lambda_{m} - \left( {\lambda_{m} - \lambda_{0} } \right)(1 + rN)\left( {1 - r} \right)^{N} $$
(3)

The above demand function is an S-shaped curve (Fig. 1) that shows initially credit period may not be effective in realizing the demand but as credit period increases it has a significant impact on demand and gradually reaches to its saturation level.

Fig. 1
figure 1

Credit linked demand function

Full size image

Using the above demand function, the various components of the retailer’s profit per unit time, π(T, N) are calculated which follows as:

$$ \left( {\text{a}} \right){\text{ Sales revenue }} = PD $$
(4)
$$ \left( {\text{b}} \right){\text{ Cost of placing an order }} = A/T $$
(5)
$$ \left( {\text{c}} \right){\text{ Cost of purchasing units }} = CD $$
(6)
$$ \left( {\text{d}} \right){\text{ Cost of carrying inventory }} = \frac{ICDT}{2} $$
(7)

Further, for computation of interest earned and payable, the following eight cases may arise:

$$ \begin{array}{*{20}c} {\left( i \right) \, N \le M \le T \, < \, T + N,} & {\left( {iv} \right) \, M \le N \le T \, < \, T + N} & {\left( {vii} \right) \, N \le T \, < \, T + N \le M} \\ {\left( {ii} \right) \, N \le T \le M \le T + N} & {\left( v \right) \, M \le T \le N \le T + N} & {\left( {viii} \right) \, T \le N \, < \, T + N \le M} \\ {\left( {iii} \right)T \le N \le M \le T + N} & {\left( {vi} \right) \, T \le M \le N \le T + N} & {} \\ \end{array} $$

Here the retailer sells his inventory from time 0 to T and offers each of his customers a credit period of N days from the time t to t + N and he starts getting the actual sales revenues from time N to T + N, therefore, for computation of interest earned and payable, we consider the cycle length from N to T + N instead of 0 to T. Further, during the process of calculating interest earned and payable for all the above mentioned eight cases, it was observed that the expressions of these three cases i.e. (i), (ii) and (iii) is exactly same as the expressions of the case N ≤ M ≤ T + N. Similarly, the expression of next three cases i.e. (iv), (v) and (vi) and two cases i.e. (vii) and (viii) is exactly same as the expression of the case M ≤ N ≤ T + N and N ≤ T + N ≤ M respectively.

Hence, the interest earned and payable for the following three cases namely (i) N ≤ M ≤ T + N (ii) N ≤ T + N ≤ M and (iii) M ≤ N ≤ T + N are as:

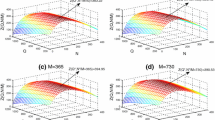
3.1 Case 1: N ≤ M ≤ T + N (Fig. 2)

In this case, the retailer starts getting actual sales revenues from time N to M and earns interest on average sales revenue for the time-period (M–N). At M accounts are settled, if all the credit sales are not realized, the finances are to be arranged to make the payment to the supplier.

Fig. 2
figure 2

When N ≤ M ≤ T + N

Full size image
$$ \left({\text{e}}\right)\;{\text{Consequently the interest earned per unit time is}}=\frac{{I_{e}PD\left({M-N}\right)^{2}}}{2T}$$
(8)

and

$$ \left( {\text{f}} \right){\text{ Interest payable per unit time is }} = \frac{{I_{p} CD\left( {T + N - M} \right)^{ 2} }}{2T} \, $$
(9)

Using the Eqs. (4)–(9), the retailer’s profit per unit time π 1(T, N) can be expressed as

$$ \pi_{1} (T,N) = \left( {P - C} \right)D - \frac{A}{T} + \frac{1}{2T}\left\{ {I_{e} P\left( {D(M - N)^{2} } \right) - ICDT^{2} - I_{p} CD\left( {T + N - M} \right)^{2} } \right\} $$
(10)

3.2 Case 2: N ≤ T + N ≤ M (Fig. 3)

In this case, the retailer earns interest on average sales revenues received during the period (N, T + N) and on full sales revenue for a period of (M – T – N) but no interest is payable by the retailer.

Fig. 3
figure 3

When N ≤ M + T ≤ N

Full size image
  1. (a)

    Consequently the interest earned per unit time is

$$ = \frac{{I_{e} P\left\{ {DT^{2} /2 + DT\left( {M - T - N} \right)} \right\}}}{T} = I_{e} PD\left( {M - N - T/2} \right) $$
(11)

As a result, using the Eqs. (4)–(7) and (11), the retailer’s profit per unit time,

π 2(T, N) in this case is

$$ \pi_{2} (T,N) = \left( {P - C} \right)D - \frac{A}{T} - \frac{ICDT}{2} + I_{e} PD\left(M - N - \frac{T}{2}\right) $$
(12)

3.3 Case 3: M ≤ N ≤ T + N (Fig. 4)

In this case, the retailer earns no interest but pays interest for a period of (N − M) and on average stock held during the cycle length (T).

Fig. 4
figure 4

When M ≤ N ≤ T + N

Full size image
  1. (b)

    Consequently the interest payable per unit time is

$$ = \frac{{I_{p} C\left\{ {DT\left( {N - M} \right) + DT^{2} /2} \right\}}}{T} = I_{p} CD\left( {N - M + T/2} \right) $$
(13)

As a result, using the Eqs. (4)–(7) and (13), the retailer’s profit per unit time,

π 3 (T, N) in this case is

$$ \pi_{3} (T,N) = \left( {P - C} \right)D - \frac{A}{T} - \frac{ICDT}{2} - I_{p} CD\left( {N - M + \frac{T}{2}} \right) $$
(14)

Therefore, the retailer’s profit per unit time π(T, N) is

$$ \pi (T,N) = \left\{ {\begin{array}{*{20}c} {\pi_{1} \left({T,N} \right)} & {if} & {N \le M \le T + N} \\ {\pi_{2}\left( {T,N} \right)} & {if} & {N \le T + N \le M} \\{\pi_{3} \left( {T,N} \right)} & {if} & {M \le N \le T + N}\\\end{array} } \right. $$
(15)

which is a function of two variable T and N where T is continuous and N is discrete.

4 Solution procedure

Our problem is to determine the optimum value of T and N which maximizes π(T,N). For a fixed value of N, taking the first and second order derivatives of π 1(T,N), π 2(T,N) and π 3(T,N) with respect to T, we get

$$ \pi^{\prime}_{1} (T,N) = \frac{A}{{T^{2} }} - \frac{ICD}{2} - \frac{{PI_{e} D\left( {M - N} \right)^{2} }}{{2T^{2} }} - \frac{{CI_{P} D}}{{2T^{2} }}\left\{ {T^{2} - \left( {N - M} \right)^{2} } \right\} $$
(16)
$$ \pi^{\prime\prime}_{1} (T,N) = \frac{{ - 2A - D(M - N)^{2} (CI_{p} - PI_{e} )}}{{T^{3} }} $$
(17)
$$ \pi^{\prime}_{2} (T,N) = \frac{A}{{T^{2} }} - \frac{ICD}{2} - \frac{{PI_{e} D}}{2} $$
(18)
$$ \pi^{\prime\prime}_{2} (T,N) = \frac{ - 2A}{{T^{3} }} $$
(19)
$$ \pi^{\prime}_{3} (T,N) = \frac{A}{{T^{2} }} - \frac{ICD}{2} - \frac{{CI_{P} D}}{2} $$
(20)
$$ \pi^{\prime\prime}_{3} (T,N) = \frac{ - 2A}{{T^{3} }} $$
(21)

For fixed N, Eqs. (19) and (21) imply that π 2(T,N) and π 3(T,N) are concave on T > 0. However, π 1(T, N) is concave on T > 0 if CI p  > PI e . Concavity of π(T, N) with respect to N is also examined (Appendix).

Thus, there exists a unique value of T (say T *1 ) which maximizes π 1(T) as

$$ T_{1}^{*} = \sqrt {\frac{{2A - D(M - N)^{2} (PI_{e} - CI_{p} )}}{{(I + I_{p} )C}}} $$
(22)

T *1 would satisfy the condition 0 ≤ (M − N) ≤ T provided

$$ 2A - D\left( {M - N} \right)^{2} \left[ {IC + I_{e} P} \right] \ge 0 $$
(23)

Similarly, there exists a unique value of T (say T *2 ) which maximizes π 2(T) as

$$ T_{2}^{*} = \sqrt {\frac{2A}{{(IC + I_{e} P)D}}} $$
(24)

T *2 would satisfy the condition 0 ≤ T ≤ (M − N) provided

$$ 2A - D\left( {M - N} \right)^{2} \left[ {IC + I_{e} P} \right] \le 0 $$
(25)

Likewise, we can obtain the optimal value of T (say T *3 ) which maximizes π 3 (T) as

$$ T_{3}^{*} = \sqrt {\frac{2A}{{(I + I_{p} )CD}}} $$
(26)

T *3 would satisfy the condition (M − N) ≤ 0 ≤ T provided

$$ 2A - CD\left( {M - N} \right)^{2} \left[ {I + I_{p} } \right] \ge 0 $$
(27)

Combining the three possible cases, we obtain the following theorem.

Theorem 1

For a fixed value of N,

  1. (a)

    If 2A − D(M − N)2[IC + I e P] ≥ 0 then T * = T *1

  2. (b)

    If \( 2A - D\left( {M - N} \right)^{2} \left[ {IC + I_{e} P} \right] \le 0 \) then \( T^{*} = T_{2}^{ * } \).

  3. (c)

    If \( 2A - CD\left( {M - N} \right)^{2} \left[ {I + I_{p} } \right] \ge 0 \) and (M–N) < 0 then \( T^{*} = T_{3}^{ * } \).

Proof

It immediately follows from (23), (25) and (27).

In order to jointly optimize T and N, we propose the following algorithm:

  • Step 1. Set N = 1.

  • Step 2. Determine the optimal values of T (i.e. T *1 or T *2 or T *3 ) using Theorem 1.

  • Step 3. If T ≥ M–N ≥ 0 then calculate π 1(T, N) else go to step 5.

  • Step 4. If π 1(T,N) > π 1(T, N − 1), increment the value of N by 1 and go to step 2 else current value of N is optimal and the corresponding value of T and π(T, N) can be calculated.

  • Step 5. If 0 ≤ T ≤ M − N then calculate π 2(T, N) else go to step 7.

  • Step 6. If π 2(T, N) > π 2(T, N − 1), increment the value of N by 1 and go to step 2 else current value of N is optimal and the corresponding value of T and π(T, N) can be calculated.

  • Step 7. If M − N ≤ 0 ≤ T then calculate π 3(T, N).

  • Step 8. If π 3(T,N) > π 3(T, N − 1), increment the value of N by 1 and go to step 2 else current value of N is optimal and the corresponding value of T and π(T, N) can be calculated.

4.1 Special case

If we take the capturing rate α(N) as a constant (say r) then the difference Eq. (1) will become as

$$ \lambda (N + 1) - \lambda (N) = r[\lambda_{m} - \lambda (N)] \, $$

and its solution will be

$$ D \equiv \lambda (N) = \lambda_{m} - \left( {\lambda_{m} - \lambda_{0} } \right)\left( {1 - r} \right)^{N} $$

which is identical to demand function as Eq. (1) in Jaggi et al. (2008). Hence, all the results of Jaggi et al. (2008) can be deduced.

5 Numerical example

Let λ m  = 300 units/day, λ 0  = 100 units/day, r = 0.1, A = $500/order, M = 60 days, C = $10/unit, P = $13/unit, I p  = 0.0411 % per day (or 15 % per year), I e  = 0.0274 % per day (or 10 % per year) and I = 0.0411 % per day (or 15 % per year).

Using the proposed algorithm, we obtained the optimal results as: Optimal cycle length (\( T^{*} \)) = 20.34 days, optimal credit period offered by retailer (N *) = 54 days, demand captured (D) = 296 units and profit per day (π *) = $845.

Using the above data, the results of Jaggi et al. (2008) are as: Optimal cycle length (T *) = 20.96 days, optimal credit period offered by retailer (N *) = 39 days, demand captured (D) = 297 units and profit per day (π *) = $865.

Now comparing the two results, one can easily observe that credit period offered by the retailer does not necessarily have its impact on demand instantaneously it has a lag which is being captured by the present model because here the retailer has to offer 54 days of credit period to their consumers to capture 296 units of demand whereas in the previous model 39 days of credit period was sufficient to capture the almost same demand. Hence, here the retailer has to offer more credit period to capture the same demand which also causes decreases in the retailer’s profit.

In order to gain more insight of the model, the sensitivity has been performed on r, M and I p and results are summarized in Tables 1, 2 and 3 respectively.

Table 1 Effects of changing r on the optimal solution
Full size table
Table 2 Effects of changing M on the optimal solution
Full size table
Table 3 Effects of changing Ip on the optimal solution
Full size table

  • Table 1 shows that as the r (i.e. capturing rate, (N)) increases, cycle length (T) increases marginally while retailer’s credit period (N) decreases significantly. Also, there is substantially increase in profit.

  • It is observed from the Table 2, as M increases both cycle length (T) and retailer’s credit period (N) increases marginally but retailer’s profit increases significantly. It is also seen that even if M = 0, N > 0, which is a single level credit due to retailer.

  • From Table 3 it is observed that increase in the interest payable rate (I p ) causes lower cycle length (T), retailer’s credit period (N) so as profit.

6 Conclusion

This paper investigates the impact of a dynamic credit-linked demand function on the retailer’s optimal credit and replenishment policy with two levels of trade credit. The retailer’s demand function is considered to be a discrete logistic function of the credit period offered by him to its customers. The main objective behind using this type of demand function is that it is capable of capturing the instant as well as delayed impact of credit period on the demand which has not yet been attracted the researcher’s attention. An easy to use algorithm is proposed which gives the optimal values of the cycle length as well as the credit period offered by the retailer. Numerical results show that for the credit linked demand functions having higher capturing rate, retailer should offer less credit period to their customers and vice versa. Hence, this model takes care of both the instant as well as delayed impact of the credit period on demand. If we assume the capturing rate of demand to be constant, then the observation in this paper is consistent with the observation in Jaggi et al. (2008). This model can be extended for deteriorating items, and under inflationary conditions which is being worked out.