Consensus model based on probability K-means clustering algorithm for large scale group decision making

Abstract

Nowadays, the increasing complexity of the social environment brings much difficulty in group decision making. The more uncertainty exists in a decision-making problem, the more collective wisdom is needed. Therefore, large scale group decision making has attracted a lot of researchers to investigate. Since the probabilistic linguistic terms have impressive performance in expressing DMs’ opinions, this paper proposes a novel method for large scale group decision making with probabilistic linguistic preference relations. More specifically, (1) a probability k-means clustering algorithm is introduced to segment DMs with similar features into different sub-groups; (2) an integration method is proposed to construct the collective probabilistic preference relation that retains initial information to the most extent; (3) taking the personality of each DM into account, a consensus model is constructed to improve the rationality and efficiency of consensus reaching process. Several simulation experiments are designed to analyze the influence factor in the feedback mechanism and make some comparative analysis with the existing method. Finally, an illustrative example of contractor selection is conducted to verify the validity of the proposed method.

1 Introduction

To guarantee the reliability of decision-making results, consensus reaching process (CRP) is an important topic in group decision making (GDM) which is to obtain the best solution agreed by all decision makers (DMs) [1, 2]. In practice, it is a challenge to get completely consistent decision results with all DMs owing to their different backgrounds, knowledge, and motivations. Then, a concept of “soft” consensus was introduced, which assesses the consensus level in a more flexible way and reflects the agreement of the majority in a group [3]. Many CRP methods in GDM based on “soft” consensus have been proposed in the past years. Alonso et al. [4] designed a consensus model including CRP with fuzzy linguistic preference relations and applied it to Web 2.0 communities which is a novel field. Parreiras et al. [5] presented a flexible consensus method for GDM under multi-granular linguistic environment. To avoid information loss, it allows DMs to express their opinions in individual domain during the CRP. Combining with a semi-supervised autonomy approach, Palomares et al. [6] introduced a consensus support system to conduct the CRP and model DMs’ behaviors through a software agent. The research of Morente-Molinera et al. [7] was devoted to developing the CRP to support multi-criteria GDM with heterogeneous and dynamic information. However, as the society continues to pursue the democratization and scientificity of decision-making, it requires the scale of participation in decision-making to gradually grow. In areas such as market selection for group shopping [8], e-democracy [9], social networks [10, 11], traditional group decision making in which few DMs are involved is gradually unable to meet the requirements of realistic problems. Therefore, large scale group decision making (LSGDM) [12,13,14,15] is attracting increasing attention. It is universally acknowledged that LSGDM problems involve the number of DMs varying from twenty to hundreds [16]. On the one hand, more DMs means that LSGDM problems contain interdisciplinary information from different fields. On the other hand, DMs with different backgrounds and experiences often have different ways of thinking about problem solving. The decision-making process with large number of DMs needs to provide a more comprehensive analysis towards the problem and improves the scientific and rationality of the outcome [12, 17, 18]. Therefore, how to make full use of the initial information and obtain reasonable results should be solved. Although a lot of consensus methods have been effective in solving GDM problems, they cannot be directly applied to LSGDM problems. The conflicts among these DMs from different professional fields are difficult to be handled accurately through consensus methods that refer to a small number of DMs. Therefore, it would be more ideal and desired to develop an adaptive consensus method within a large-scale context, which not only includes consideration of situations involving a large number of DMs, but also assists the group to reach an acceptable consensus by adjusting evaluation information from DMs.

The growing complexity in practical problems leads that DMs prefer to provide evaluation information by making pairwise comparison between any two objects. Preference relation [19, 20] is a commonly used type which is more in accordance with people’s thinking conventions. Different types of preference relations have been proposed, such as fuzzy preference relation [21, 22], hesitant fuzzy preference relation [23], triangular fuzzy preference relation [24,25,26], intuitionistic fuzzy preference relation [27], etc. Nevertheless, these preference relations, which are represented by numerical values, are insufficient for the DMs to express their opinions. In general, the expressions like “excellent”, “common”, “disappointing”, which are more appropriate and flexible to represent opinions of DMs [28, 29], are commonly used. Linguistic terms, as a convenient way for the DMs to model the subjective information, were introduced in the research carried out by Zadeh [30]. However, due to the fuzzy thoughts of people, a single linguistic term is not able to depict DMs’ opinions under uncertainty. For this reason, the concept of hesitant fuzzy linguistic term set (HFLTS), which allows DMs to provide their assessments with several continuous linguistic terms, has been proposed [31,32,33]. HFLTS can not only describe those imprecise expressions but also retain more original information. With such advantages, a few studies about LGSDM based on HFLTSs have been introduced [34, 35]. However, the HFLTS is insufficient in some cases. For example, a DM may think that the object is ‘good’ with the probability of 55%, and give ‘slightly good’ with the probability of 35%. HFLTS fails to describe this probabilistic information and cannot depict the difference in the importance of different evaluations. To increase the elasticity of linguistic terms to portray such more general situations, the probabilistic linguistic term set (PLTS) [36] which assigns each linguistic term a corresponding probability to denote its importance degree or weight was proposed. Then, the probabilistic linguistic preference relation (PLPR) was developed as a more general technique for GDM problems, which represents DMs’ preferences by several probabilistic linguistic terms [37, 38]. Scholars have made efforts to investigate problems concerning CPR based on PLPRs. With a cosine similarity measure based on PLTS, Luo et al. [39] presented the corresponding consensus degree of PLPRs and established an optimization model to obtain the ranking of constructed wetlands. Liu et al. [40] developed a two-stage consensus model with the feedback mechanism to achieve a high consensus degree based on PLRP in GDM. Gao et al. [41] designed a group consensus decision making framework to solve the selection of green supplier. Since the PLPR exhibits its superiority in representing the comparative judgments of alternatives, it possesses the application prospect to be applied in LSGDM. Nevertheless, most of the existing studies focus on how to manage GDM with PLPRs or provide the several consensus models with PLTSs. There is currently no systematic research on LSGDM with PLPRs, so it is necessary to conduct a detailed study on this.

The process of solving an LSGDM problem consists of three parts: (1) a clustering method to divide DMs with similar opinions into different clusters; (2) a consensus process to ensure the reliability and reasonability of decision-making results; (3) a selection process to obtain the final solution. We propose a probability k-means clustering algorithm to segment DMs into several sub-groups according to their preferences. It is obvious that breaking down the larger problem into smaller pieces is helpful for simplifying computations. Moreover, the clustering process provides the benefits of the more reliable analysis for supporting decisions. On the other hand, there exists non-cooperation behaviors during the consensus reaching process. For some uncontrollable factors in practice and different considerations of DMs, the group is scarcely possible to get a consistent decision-making result directly. Some DMs may be unwilling to change their original evaluations to achieve consensus with the group. To address this issue, we exclude DMs who are uncooperative and update the weights of the clusters to ensure CRP works properly. The main contributions of this paper are briefly summarized as follows:

• (1) This paper utilizes PLPRs as a convenient and impactful way for DMs to express evaluation information, which effectively portrays the complexity and uncertainty in large scale group decision making.

• (2) This paper proposes a probability k-means clustering algorithm to classify large number of DMs. Furthermore, several simulation experiments between the traditional k-means clustering algorithm and the proposed one are designed to verify the high efficiency and strong robustness of the probability k-means clustering algorithm.

• (3) This paper introduces a novel consensus model which proposes a more reasonable process to identify the objects that need to be revised in the feedback mechanism, which greatly improve the efficiency of the CRP. In addition, this paper explores how the parameter in CRP impacts the decision-making results.

• (4) Non-cooperation behaviors are effectively managed in the feedback mechanism. DMs are given sufficient freedom to decide whether to modify their evaluations or not. If they are willing to change their opinions, they can also decide how to modify their preference values.

The rest of this paper is organized as follows: Sect. 2 reviews some basic concepts related to PLTS and PLPR, and then introduces some distance measures for PLTSs. In Sect. 3, a novel consensus model for LSGDM is proposed to assist the group to reach a consensus, and the corresponding method for selecting the optimal alternative is developed. Several simulation experiments are conducted to demonstrate the superiority and availability of the proposed model in Sect. 4. Finally, a practical case for contractor selecting is given to verify the rationality of the proposed method in Sect. 5.

2 Preliminaries

2.1 Probabilistic linguistic information

Based on a subscript-symmetric linguistic scale $S = \left\{ {s_{\alpha } \left| \alpha \right. = - \tau , \ldots , - 1,0,1, \ldots ,\tau } \right\}$, the probabilistic linguistic term set (PLTS) [36] is defined as:

$$ L\left( p \right) = \left\{ {L^{n} \left( {p^{n} } \right)\left| {L^{n} \in S,p^{n} \ge 0,n = 1,2, \ldots ,\# } \right.L\left( p \right),\sum\limits_{n = 1}^{\# L\left( p \right)} {p^{n} \le 1} } \right\} $$

(1)

where $L^{n} \left( {p^{n} } \right)$ is called a probabilistic linguistic element (PLE) that contains the $n{\text{ - th}}$ linguistic term $L^{n}$ and its corresponding probability $p^{n}$, and $\# L\left( p \right)$ is the number of the linguistic terms in $L^{n}$. If the PLEs in PLTS satisfy $\sum\limits_{n = 1}^{\# L\left( p \right)} {p^{n} = 1}$, then they are normalized.

For example, suppose that a uniformly and symmetrically distributed linguistic term set $S$ is given as: $S = \left\{ \begin{gathered} s_{ - 3} = worst,{\kern 1pt} {\kern 1pt} {\kern 1pt} s_{ - 2} = worse,{\kern 1pt} {\kern 1pt} {\kern 1pt} \hfill \\ s_{ - 1} = bad,s_{0} = same,s_{1} = good, \hfill \\ s_{2} = better,s_{3} = best \hfill \\ \end{gathered} \right\}$. Then $L_{1} \left( p \right) = \left\{ {s_{1} \left( {0.5} \right),s_{2} \left( {0.4} \right)} \right\}$ denotes that the preference degree of the DM towards the object is $s_{1}$ with the probability of 50%, and is $s_{2}$ with the probability of 40%.

For a PLTS, the score function of $L\left( p \right)$ is defined as:

$$ E\left( {L\left( p \right)} \right) = s_{\sigma } $$

(2)

$$ \sigma = \frac{{\sum\limits_{n = 1}^{\# L\left( p \right)} {r^{n} p^{n} } }}{{\sum\limits_{n = 1}^{\# L\left( p \right)} {p^{n} } }} $$

(3)

where $r^{n}$ denotes the subscript of the linguistic term $L^{n}$. The deviation degree of $L\left( p \right)$ is defined as:

$$ \alpha = \frac{1}{{\sum\limits_{n = 1}^{\# L\left( p \right)} {p^{n} } }}\left( {\sum\limits_{n = 1}^{\# L(p)} {\left( {p^{n} \left( {r^{n} - \sigma } \right)} \right)^{2} } } \right)^{\frac{1}{2}} $$

(4)

For any two PLTSs, there are two basic operations: $L_{1} \left( p \right) \oplus L_{2} \left( p \right) = \cup_{{r_{1}^{n} \in L_{1} \left( p \right),r_{2}^{n} \in L_{2} \left( p \right)}} \left\{ {r_{1}^{n} p_{{^{1} }}^{n} \oplus r_{2}^{n} p_{2}^{n} } \right\}$, $\left( {L\left( p \right)} \right)^{\rho } = \cup_{{r_{1}^{n} \in L_{1} \left( p \right),r_{2}^{n} \in L_{2} \left( p \right)}} \left\{ {\left( {r_{1}^{n} } \right)^{{\rho p_{{^{1} }}^{n} }} } \right\}$, where $r_{j}^{n} \left( {j = 1,2} \right)$ denotes the subscript of the linguistic term $L_{j}^{n}$.

To realize the operations between PLTSs, for a PLTS $L\left( p \right)$, a normalized expression $p^{N\left( n \right)} = \frac{{p^{n} }}{{\sum\limits_{n = 1}^{\# L\left( p \right)} {p^{n} } }}$ $\left. {\left( {n = } \right.1,2, \ldots ,\# L\left( p \right)} \right)$ is given. Then the normalized PLTS can be obtained, which is denoted as $L^{N} \left( p \right) = \left\{ {} \right.$$\left. {L^{N\left( n \right)} \left( {p^{N\left( n \right)} } \right)\left| {n = 1,2, \ldots ,\# } \right.L\left( p \right),\sum\limits_{n = 1}^{\# L\left( p \right)} {p^{N\left( n \right)} = 1} } \right\}$. For the normalized PLTS, some operations are defined [36]:

$$ L_{1} \left( p \right) \oplus L_{2} \left( p \right) = \left\{ {r_{1}^{{n_{1} }} \oplus r_{2}^{{n_{2} }} \left( {p_{{^{1} }}^{{n_{1} }} p_{{^{2} }}^{{n_{2} }} } \right)\left| {n_{1} = 1, \ldots ,\# } \right.L_{1} \left( p \right);n_{2} = 1, \ldots ,\# L_{2} \left( p \right)} \right\};\xi L_{1} \left( p \right) = \left\{ {\xi r_{1}^{n} p_{{^{1} }}^{n} \left| {n_{1} = 1, \ldots ,\# } \right.L_{1} \left( p \right)} \right\} $$

However, the result calculated with the above formulas is out of the range $\left[ { - \tau ,\tau } \right]$, then the transformation function is introduced [42]: if $s_{\alpha } > s_{\tau }$, then $f\left( {s_{\alpha } } \right) = s_{\tau }$; if $s_{\alpha } < s_{\tau }$, then $f\left( {s_{\alpha } } \right) = s_{ - \tau }$; if $s_{ - \tau } \le s_{\alpha } \le s_{\tau }$, then $f\left( {s_{\alpha } } \right) = s_{\alpha }$.

To make sure that two different PLTSs have the same number of linguistic terms, linguistic terms with zero probability should be added to the shorter one. The added linguistic terms are the largest one in the shorter PLTS [37]. For example, if we have $L_{1} \left( p \right) = \left\{ {s_{ - 2} \left( {0.4} \right),s_{ - 1} \left( {0.6} \right)} \right\}$ and $L_{2} \left( p \right) = \left\{ {s_{ - 2} \left( {0.2} \right),s_{ - 1} \left( {0.4} \right),s_{1} \left( {0.4} \right)} \right\}$, then the normalized PLPTs are obtained as: $L_{1} \left( p \right) = \left\{ {s_{ - 2} \left( {0.4} \right),s_{ - 1} \left( {0.6} \right),s_{ - 1} \left( 0 \right)} \right\}$ and $L_{2} \left( p \right) = \left\{ {s_{ - 2} \left( {0.2} \right),} \right.$$\left. {s_{ - 1} \left( {0.4} \right),s_{1} \left( {0.4} \right)} \right\}$.

Considering that the preference relation is an efficient tool to depict the DMs’ opinions, the PLPR is provided to compare objects in pairs [38]. For a collection of objects $X = \left\{ {x_{i} \left| {i = 1,2, \ldots ,m} \right.} \right\}$, the PLPR can be denoted as $B = \left( {b\left( p \right)_{ij}^{k} } \right)_{m \times m} \subset X \times X$, where $b\left( p \right)_{ij}^{k}$ indicates the preference degree to which $x_{i}$ is preferred to $x_{j}$. For all $i,j = 1,2, \ldots ,m$, $b_{ij}^{k} \left( {i < j} \right)$ should satisfy:

• 1. $p_{ij}^{n} = p_{ji}^{n}$, $b_{ij}^{n} = neg\left( {b_{ji}^{n} } \right)$, $b\left( p \right)_{ii} = \left\{ {s_{0} \left( 1 \right)} \right\} = \left\{ {s_{0} } \right\}$, $\# b\left( p \right)_{ij} = \# b\left( p \right)_{ji}$;

• 2. $b_{ij}^{n} p_{ij}^{n} \le b_{ij}^{n + 1} p_{ij}^{n + 1}$ for $i \le j$, $b_{ij}^{n} p_{ij}^{n} \ge b_{ij}^{n + 1} p_{ij}^{n + 1}$ for $i \ge j$.

Moreover, to aggregate normalized PLPRs, the aggregation operator with PLTS is given as follows: Let $L_{k} \left( p \right) = \left\{ {L_{k}^{N\left( n \right)} \left( {p_{k}^{N\left( n \right)} } \right)\left| {n = 1,2, \ldots ,\# } \right.L\left( p \right),\sum\limits_{n = 1}^{\# L\left( p \right)} {p_{k}^{N\left( n \right)} = 1} } \right\}\left( {k = 1,2, \ldots ,m} \right)$ be $m$ PLTSs, $L_{k}^{N\left( n \right)}$ and $p_{k}^{N\left( n \right)}$ are the $n{\text{ - th}}$ linguistic term and its corresponding probability in $L_{k} \left( p \right)$ respectively. $w = \left( {w_{1} ,w_{2} , \ldots ,w_{m} } \right)^{T}$ is the weight vector of $L_{k} \left( p \right)\left( {k = 1,2, \ldots ,m} \right)$, $w_{k} \ge 0\left( {k = 1,2, \ldots ,m} \right)$ and $\sum\limits_{k = 1}^{m} {w_{k} = 1}$. Then, the probabilistic linguistic weighted averaging operator (PLWA) is defined as:

$$ \begin{gathered} PLWA\left( {L_{1} \left( p \right),L_{2} \left( p \right), \ldots ,L_{m} \left( p \right)} \right) = \mathop \oplus \limits_{k = 1}^{m} w_{k} L_{k} \left( p \right) = w_{1} L_{1} \left( p \right) \oplus w_{2} L_{2} \left( p \right) \oplus \cdots \oplus w_{m} L_{m} \left( p \right) \hfill \\ = \cup_{{r_{1}^{n} \in L_{1} \left( p \right)}} \left\{ {w_{1} r_{1}^{n} p_{{^{1} }}^{n} } \right\} \oplus \cup_{{r_{2}^{n} \in L_{2} \left( p \right)}} \left\{ {w_{2} r_{2}^{n} p_{2}^{n} } \right\} \oplus \cdots \oplus \cup_{{r_{m}^{n} \in L_{m} \left( p \right)}} \left\{ {w_{m} r_{m}^{n} p_{{^{m} }}^{n} } \right\} \hfill \\ \end{gathered} $$

(5)

2.2 Distance measures for probabilistic linguistic information

For any two normalized PLTSs $L_{1} \left( p \right)$ and $L_{2} \left( p \right)$ ($\# L_{1} \left( p \right)$ and $\# L_{2} \left( p \right)$ are the numbers of linguistic terms in $L_{1} \left( p \right)$ and $L_{2} \left( p \right)$ respectively, $\# L_{1} \left( p \right) = \# L_{2} \left( p \right) = \# L\left( p \right)$), the distance measure between $L_{1} \left( p \right)$ and $L_{2} \left( p \right)$ which is denoted as $d\left( {L_{1} \left( p \right),L_{2} \left( p \right)} \right)$ should satisfy three conditions below [37]:

• 1. $0 \le d\left( {L_{1} \left( p \right),L_{2} \left( p \right)} \right) \le 1$;

• 2. $d\left( {L_{1} \left( p \right),L_{2} \left( p \right)} \right) = 0$ if and only if $L_{1} \left( p \right) = L_{2} \left( p \right)$;

• 3. $d\left( {L_{1} \left( p \right),L_{2} \left( p \right)} \right) = d\left( {L_{2} \left( p \right),L_{1} \left( p \right)} \right)$.

Then, three distance measures have been proposed. The basic distance measure between two PLTEs is defined as:

$$ d\left( {L_{1}^{{n_{1} }} \left( {p_{{_{1} }}^{{n_{1} }} } \right),L_{2}^{{n_{2} }} \left( {p_{2}^{{n_{2} }} } \right)} \right) = \left| {\frac{{p_{1}^{{n_{1} }} r_{1}^{{n_{1} }} }}{\tau } - \frac{{p_{2}^{{n_{2} }} r_{2}^{{n_{2} }} }}{\tau }} \right| $$

(6)

where $r_{1}^{{n_{1} }}$ and $r_{2}^{{n_{2} }}$ denote the subscripts of the linguistic terms $L_{1}^{{n_{1} }} \left( {p_{{_{1} }}^{{n_{1} }} } \right)$ and $L_{2}^{{n_{2} }} \left( {p_{2}^{{n_{2} }} } \right)$ respectively.

The Hamming distance [37] between $L_{1} \left( p \right)$ and $L_{2} \left( p \right)$ is given as:

$$ d_{h} \left( {L_{1} \left( p \right),L_{2} \left( p \right)} \right) = \frac{1}{\# L\left( p \right)}\sum\limits_{n = 1}^{\# L\left( p \right)} {d\left( {L_{1}^{n} \left( {p_{1}^{n} } \right),L_{2}^{n} \left( {p_{2}^{n} } \right)} \right)} $$

(7)

The Euclidean distance [37] between $L_{1} \left( p \right)$ and $L_{2} \left( p \right)$ is given as:

$$ d_{e} \left( {L_{1} \left( p \right),L_{2} \left( p \right)} \right) = \sqrt {\frac{1}{\# L\left( p \right)}\sum\limits_{n = 1}^{\# L\left( p \right)} {\left( {d\left( {L_{1}^{n} \left( {p_{1}^{n} } \right),L_{2}^{n} \left( {p_{2}^{n} } \right)} \right)} \right)}^{2} } $$

(8)

For any two normalized PLPRs $B_{1} = \left( {L_{ij} \left( p \right)_{1} } \right)_{n \times n} {\kern 1pt} {\kern 1pt}$ and $B_{2} = \left( {L_{ij} \left( p \right)_{2} } \right)_{n \times n} {\kern 1pt} {\kern 1pt}$, the distance between $B_{1}$ and $B_{2}$ is defined as [37]:

$$ d\left( {B_{1} ,B_{2} } \right) = \sqrt {\frac{2}{{n\left( {n - 1} \right)}}\sum\limits_{j = i + 1}^{n} {\sum\limits_{i}^{n - 1} {\left[ {d_{h} \left( {L_{ij} \left( p \right)_{1} ,L_{ij} \left( p \right)_{2} } \right)} \right]^{2} } } } $$

(9)

3 Consensus model for LSGDM with PLPR

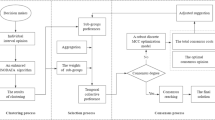
In this section, we first propose a probability k-means clustering algorithm to group DMs into different clusters, which is the foundation of the CRP for LSGDM. Later on, with clustering results, a consensus method is developed under a probabilistic linguistic environment. A complete framework of this procedure can be clearly illustrated by Fig. 1.

Fig. 1

The framework of the LSGDM consensus model

3.1 Probability k-means clustering process

In the existing studies, a lot of effective algorithms have been used to solve LSGDM problems, such as the PIS-based clustering method [43], the fuzzy c-means clustering (FCM) algorithm [8], the alternative ranking-based clustering (ARC) method [16], and the equivalence clustering method [44], etc. The k-means cluster algorithm, as an unsupervised machine learning algorithm, is the most commonly used clustering method. This algorithm simplifies the procedure of clustering with straightforward logic, which makes it easy to apply. However, there is an obvious disadvantage of this algorithm. The k-means algorithm is sensitive to the initially selected centroid points, which means that different random centroids lead to different clustering results. In this paper, a probability k-means clustering algorithm is introduced to overcome this weakness and detect the sub-groups from the preferences of all experts. The hierarchy clustering algorithm is adopted to determine initial clusters by using the Hamming distance function firstly. Here we give the entire steps of the centroids selection process:

3.1.1 Algorithm 1. Selecting the initial centroids

Input: $m$ normalized PLPRs $B = \left\{ {B^{t} \left| {t = 1, \ldots ,m} \right.} \right\}$ and the number of clusters $K\left( {K \ge 2} \right)$.

Output: $K\left( {K \ge 2} \right)$ initial clustering centroids.

Step 1. Regard each PLPR as an independent cluster. Based on Eq. (7), we calculate the Hamming distance between each pair of clusters $\left( {B^{u} ,B^{v} } \right)$, where $b_{ij}^{u} \left( p \right)$ and $b_{ij}^{v} \left( p \right)$ are PLTSs that belong to $B^{u} = \left( {b_{ij}^{u} } \right)_{n \times n} {\kern 1pt} ,i,j = {\kern 1pt} 1,2, \ldots ,n$ and $B^{v} = \left( {b_{ij}^{v} } \right)_{n \times n} {\kern 1pt} ,i,j = {\kern 1pt} 1,2, \ldots ,n$, $1 \le u,v \le m$.

$$ d_{h} \left( {b_{ij}^{u} \left( p \right),b_{ij}^{v} \left( p \right)} \right) = \frac{1}{\# b\left( p \right)}\sum\limits_{n = 1}^{\# b\left( p \right)} {d\left( {b_{ij}^{un} \left( {p_{ij}^{un} } \right),b_{ij}^{vn} \left( {p_{ij}^{vn} } \right)} \right)} $$

(10)

Then, we construct a PLPR distance matrix $D_{h} = \left( {d_{uv} } \right)_{m \times m}$. After finding the two closest clusters $B^{s}$ and $B^{q}$ where $d_{h} \left( {B^{s} ,B^{q} } \right) = \min \mathop {d_{h} }\limits_{{1 \le u,v\left( {u \ne v} \right) \le m}} \left( {B^{u} ,B^{v} } \right)$, We merge them into a new cluster $B^{sq}$. By utilizing the PLWA operator in Eq. (5), the centroid of the new cluster can be obtained.

Step 2. Calculate the Hamming distances between the new cluster $B^{sq}$ to other clusters and update the PLPR distance matrix.

Step 3. Repeat Step 1 and Step 2 until we get $K$ clustering centroids.

Then, the distances between samples and centroids are calculated by the Euclidean distance function, which constantly decreases until keeping stable during the iteration.

The procedure of the probability k-means clustering algorithm can be summarized as follows:

3.1.2 Algorithm 2. Probability k-means clustering algorithm

Input: $m$ normalized PLPRs $B = \left\{ {B^{t} \left| {t = 1, \ldots ,m} \right.} \right\}$, initial clustering centroids $C = \left\{ {C^{s} \left| {s = 1, \ldots ,} \right.} \right.\left. K \right\}$$\left( {K \ge 2} \right)$ and the number of clusters $K\left( {K \ge 2} \right)$.

Output: $K$ clustering centroids.

Step 1. Calculate the Euclidean distance between each $B^{t}$ to $C^{s}$, and assign $B^{t}$ to the nearest cluster. Based on Eq. (8), the distance between each $B^{t}$ to the centroids $C = \left\{ {C^{s} \left| {s = 1, \ldots ,} \right.} \right.\left. K \right\}$ can be obtained by:

$$ d_{e} \left( {b_{ij}^{t} \left( p \right),c_{ij}^{s} \left( p \right)} \right) = \sqrt {\frac{1}{\# b\left( p \right)}\sum\limits_{n = 1}^{\# b\left( p \right)} {\left( {d\left( {b_{ij}^{tn} \left( {p_{ij}^{tn} } \right),c_{ij}^{sn} \left( {p_{ij}^{sn} } \right)} \right)} \right)}^{2} } $$

(11)

Then, according to the Euclidean distance matrix $D_{e} = \left( d \right)_{m \times m}$, the PLPR is assigned to the nearest cluster whose centroid has the minimum distance with it, that is, if $d\left( {B^{t} ,C^{s} } \right) = \min \left\{ {d_{e} \left( {B^{t} ,C^{s} } \right)} \right\}$, then $B^{t}$ belongs to $C^{s}$.

Step 2. Recalculate and update the centroids of clusters by the PLWA operator.

Step 3. Repeat Step 1 and Step 2 until all centroids remain stable, which means that the distances between each PLPR and the centroids of clusters keep unchanged in the next round.

According to Algorithm 2, a large number of experts are divided into $K\left( {K \ge 2} \right)$ clusters. Then, we need to build a collective PLPR for each cluster by integrating PLPRs in this cluster. Most of the studies directly use the centroid of the cluster to represent experts’ preferences, which has a defect that the collected initial preference information cannot be fully reflected. Although the opinions of experts in the same cluster are similar, we consider the hesitation of experts to avoid information loss in the CRP.

Suppose that a group of experts give their evaluation values on an alternative set $X = \left\{ {x_{i} \left| {i = 1, \ldots ,n} \right.} \right\}$ by PLPRs. Then, these experts are classified into several clusters. For a cluster $C^{s} = \left\{ {e_{t}^{s} \left| {t = 1, \ldots ,\# e} \right.} \right\}$, a PLPR $B\left( {b_{ij}^{st} \left( p \right)} \right)_{n \times n}$ is provided by the $t{\text{ - th}}$ DM in the $s{\text{ - th}}$ cluster $C^{s}$, and $b_{ij}^{st} \left( p \right)$ indicates the preference degree of the alternative $x_{i}$ over $x_{j}$. Then, the collective PLPR of the cluster $C^{s}$ denoted as $CH^{s} = \left( {h_{ij}^{s} } \right)n \times n$ can be obtained, where

$$ h_{ij}^{s} = \frac{1}{t}\mathop \oplus \limits_{u = 1}^{t} b_{ij}^{su} \left( p \right) $$

(12)

Example 1.

Given two normalized PLTSs $b_{{1}} \left( p \right) = \left\{ {s_{ - 2} \left( {0.3} \right),s_{ - 1} \left( {0.7} \right)} \right\}$ and $b_{2} \left( p \right) = \left\{ {s_{ - 2} \left( {0.15} \right),s_{ - 1} \left( {0.3} \right),} \right.$ $\left. {s_{0} \left( {0.1} \right),s_{1} \left( {0.4} \right)s_{2} \left( {0.05} \right)} \right\}$, then, according to Eq. (12), the collective PLTSs can be obtained as follows:

$b_{{1}} \left( p \right) \oplus b_{2} \left( p \right) = \frac{1}{2}\left\{ {s_{ - 2} \left( {0.15 + 0.3} \right),s_{ - 1} \left( {0.3 + 0.7} \right),s_{0} \left( {0.1} \right),s_{1} \left( {0.4} \right)s_{2} \left( {0.05} \right)} \right\} = \left\{ {s_{ - 2} \left( {0.225} \right),s_{ - 1} \left( {0.5} \right),s_{0} \left( {0.05} \right),} \right.$$\left. {s_{1} \left( {0.2} \right)s_{2} \left( {0.025} \right)} \right\}$.

3.2 The consensus measures

The consensus measure, as an important foundation of LSGDM, is used to determine whether the group has reached a consensus. In this paper, we propose a consensus measure based on the similarity degree between each pair of clusters.

Let $C^{u}$ and $C^{v}$ be two clusters, $CH^{u} = \left( {h_{ij}^{u} } \right)_{n \times n}$ and $CH^{v} = \left( {h_{ij}^{v} } \right)_{n \times n}$ are the collective PLPRs of these clusters respectively. The similarity matrix denoted as $SM^{uv} = \left[ {\begin{array}{*{20}c} - & \cdots & {sm_{1n}^{uv} } \\ \vdots & \ddots & \vdots \\ {sm_{n1}^{uv} } & \cdots & - \\ \end{array} } \right]$ can be derived by Eq. (7) as:

$$ sm_{ij}^{uv} = 1 - d\left( {h_{ij}^{u} ,h_{ij}^{v} } \right) = 1 - \frac{1}{{\# h_{ij} }}\sum\limits_{n = 1}^{{\# h_{ij} }} {d\left( {h_{ij}^{u\left( n \right)} \left( {p_{ij}^{u\left( n \right)} } \right),h_{ij}^{v\left( n \right)} \left( {p_{ij}^{v\left( n \right)} } \right)} \right)} $$

(13)

where $sm_{1n}^{uv}$ indicates the similarity degree between the two clusters $C^{u}$ and $C^{v}$. It should be noted that this matrix can be regarded as an upper triangle matrix.

After obtaining the similarity matrix, the consensus degree of each pair of sub-groups can be derived by:

$$ SGSI^{uv} = \frac{{\sum\limits_{i = 1}^{n} {\sum\limits_{j = 1,i \ne j}^{n} {sm_{ij}^{uv} } } }}{{n \times \left( {n - 1} \right)}} $$

(14)

Subsequently, the group consensus index, $\overline{SGSI}$, is defined as:

$$ \overline{SGSI} = \frac{2}{{K\left( {K - 1} \right)}}\sum\limits_{u = 1}^{K - 1} {\sum\limits_{v = u + 1}^{K} {SGSI^{uv} } } $$

(15)

Obviously, $\overline{SGSI} \in \left[ {0,1} \right]$, the smaller value of $\overline{SGSI}$ indicates the lower consensus level of the whole group.

For the cluster $C^{u}$, the consensus degree towards the alternative $x_{i}$ (denoted as $sa_{i} \left( {i = 1,2,...,n} \right)$) is calculated by:

$$ sa_{i}^{u} = \frac{{\sum\limits_{j = 1,i \ne j}^{n} {sm_{ij}^{u} } }}{n - 1} $$

(16)

where $sm_{ij}^{u} = \frac{1}{K - 1}\sum\limits_{v = 1,u \ne v}^{K} {sm_{ij}^{uv} }$.

The classified sub-groups contain different numbers of experts, which means that the importance of each sub-group is different. In this paper, the weights of sub-groups are calculated based on their sizes. Suppose that there are $K$ sub-groups and $\# e^{u}$ represents the number of experts in the $u{\text{ - th}}$ sub-group. The weight of the $u{\text{ - th}}$ sub-group is derived by:

$$ w^{u} = \frac{{\# e^{u} }}{{\sum\limits_{u = 1}^{K} {\# e^{u} } }} $$

(17)

3.3 The feedback mechanism

As introduced in the Introduction, the CRP is a negotiation process, which requires a moderator to conduct the comparison between the actual consensus level $\overline{SGSI}$ and the threshold value of the acceptable consensus degree $\lambda$. If $\overline{SGSI} < \lambda$, the group needs to discuss how to adjust the PLPRs for achieving the required consensus level, otherwise, the moderator can end the consensus reaching process and start the selection process. In what follows, considering different behaviors of experts, we propose a novel feedback mechanism with supervision to improve the efficiency of consensus reaching. The whole feedback mechanism consists of four main stages: identify the preference values that need to be modified, determine the direction of adjusting, obtain the recommended values from the moderator and generate advice for experts.

3.3.1 The identification rules for adjusting

Based on the consensus degree, three identification rules are obtained:

• (1) Identify the sub-group that needs to revise preference values. We find pairs of clusters whose consensus degree fails to satisfy the threshold value $\lambda$, and choose the two clusters with the smallest value of $SGSI$. Then, we calculate the similarity degrees between these two clusters and other clusters respectively and select the one that has fewer similarity degrees to other clusters. It is noted that only one cluster is identified in each iteration.

• (2) Identify the alternatives of which evaluation values need to be revised. Based on Eq. (16), we identify the alternative set $\overline{X}$ that should be modified from the selected cluster by:

  $$ \overline{X} = \left\{ {x_{i} \left| {\mathop {\min }\limits_{i} \left\{ {sa_{i} \left| {sa_{i} < \lambda ,i = 1,2, \ldots ,n} \right.} \right\}} \right.} \right\} $$

  (18)

• (3) Identify the preference values that need to be revised by:

  $$ h_{ij} = \left\{ {\left( {i,j} \right)\left| {x_{i} \in \overline{X} \wedge sm_{ij} < \lambda ,i \ne j} \right.} \right\} $$

  (19)

To illustrate this process clearly, the following example is presented:

Example 2.

Consider that there are five clusters $\left\{ {C^{1} ,C^{2} ,C^{3} ,C^{4} ,C^{5} } \right\}$ and five alternatives $\left\{ {x_{1} ,x_{2} ,x_{3} ,} \right.x_{4} ,$ $\left. {x_{5} } \right\}$. The values of $SGSI$ among these clusters can be obtained. Suppose that the value of $SGSI_{23}$ is the smallest one, then we need to compare $\sum\limits_{j \ne 2,3}^{5} {SGSI_{2j} }$ and $\sum\limits_{j \ne 2,3}^{5} {SGSI_{3j} }$. If $\sum\limits_{j \ne 2,3}^{5} {SGSI_{2j} < \sum\limits_{j \ne 2,3}^{5} {SGSI_{3j} {\kern 1pt} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} }$, then the cluster $C^{2}$ is the cluster that needs to be modified, otherwise, the cluster $C^{3}$ is the selected one. Suppose that the alternative $x_{3}$ in the cluster $C^{2}$ is selected according to Eq. (18). Then, $sm_{31}$, $sm_{32}$, $sm_{34}$ and $sm_{35}$ should be compared with the preset threshold value $\lambda$. If only $sm_{34} < \lambda$, $h_{34}$ which indicates the preference values of the alternative $x_{3}$ over the alternative $x_{4}$ should be modified. As a result, the moderator should require experts in the cluster $C^{2}$ to change their preference values of $x_{3}$ over $x_{4}$.

3.3.2 The suggestion rules for adjusting

Later on, to improve the consensus degree of the group, the process of confirming how to modify PLPRs should be carried out. In this part, the moderator makes recommendations from two perspectives including the direction of adjustment and the recommended values. Before setting the suggestion rules, we first obtain the collective PLPR (denoted as $CH^{G} = \left( {h_{ij}^{G} } \right)_{n \times n}$) of all clusters except the selected cluster that needs to be modified by:

$$ h_{ij}^{G} = \mathop \oplus \limits_{u = 1,u \ne v}^{K} \left( {w^{u} h_{ij}^{u} } \right) = \cup_{{r_{ij}^{u} \in L_{ij}^{u} }} \sum\limits_{u = 1,u \ne v}^{K} {w^{u} r_{ij}^{u} } $$

(20)

where $w^{u}$ represents the weight of the cluster $C^{u}$ and $C^{v}$ denotes the selected cluster.

Then, combining the preference values in the collective PLPR $CH^{G}$ with the original values in the PLPR of the selected cluster $C^{v}$, the recommended values can be derived by:

$$ \tau_{ij} = \rho h_{ij}^{v} + \left( {1 - \rho } \right)h_{ij}^{G} $$

(21)

where $\rho \left( {0 < \rho < 1} \right)$ is a preset adjustment parameter, $h_{ij}^{v}$ and $h_{ij}^{G}$ are preference values of the alternative $x_{i}$ over the alternative $x_{j}$. This modified pattern not only provides a convenient way in adjusting PLPRs that do not meet the requirement, but also improves the efficiency of the consensus reaching process. It is worth noting that experts may be unwilling to adopt the recommended values provided by the moderator due to cognitive competence and some psychological factors. Under such a situation, taking the recommended value as a reference, the moderator can just provide the direction of adjustment for those experts.

The direction rules are also designed based on the scores of the collective PLPR $CH^{G}$ and the PLPR of the selected cluster $C^{v}$. Here are the details of the direction rules:

• (1) If $E\left( {C^{v} } \right) < E\left( {CH^{G} } \right)$, then all experts in the cluster $C^{v}$ need to increase their preference values that need to be modified.

• (2) If $E\left( {C^{v} } \right) > E\left( {CH^{G} } \right)$, then all experts in the cluster $C^{v}$ need to decrease their preference values that need to be modified.

$E\left( {C^{v} } \right)$ and $E\left( {CH^{G} } \right)$ are obtained by the score function in Eqs. (2) and (3). With the proposed feedback mechanism, the expert group can finally reach a consensus after rounds of modification.

Considering the individual needs of experts, the proposed feedback mechanism, which is guided by the moderator with interaction, is more reliable and reasonable than the automatic system. The experts are allowed to modify their preference values according to the recommended values or the direction of adjustment rather than update the PLPRs by the system automatically.

In some cases, experts in the sub-group may refuse to cooperate, which means that they would not modify their evaluations. Some feedback mechanisms [45, 46] exclude those stubborn experts from the decision-making process or remove evaluation values that have not reached a consensus. Consistent with these mechanisms, experts in the selected cluster are divided into two parts. Experts who refuse to modify their opinions are dropped out, and the rest of the experts should provide their reconsidered preference values.

Algorithm 3 is presented to manifest the whole process of the proposed consensus method.

3.4 Algorithm 3. The proposed consensus method

Input: $K$ clusters $\left\{ {C^{1} ,C^{2} , \ldots ,C^{K} } \right\}$, the threshold value $\lambda$, the maximum rounds $\delta$ and the adjustment parameter $\rho \left( {0 < \rho < 1} \right)$.

Output: the number of iterations $I$, the modified collective PLPRs $\left\{ {CH^{1 * } ,CH^{2 * } , \ldots ,CH^{K * } } \right\}$.

Step 1. Set $I = 1$, calculate the collective PLPRs of each cluster $\left\{ {CH^{1} ,CH^{2} , \ldots ,CH^{K} } \right\}$ based on Eq. (12).

Step 2. Compute the group consensus index. If $\overline{SGSI} \ge \lambda$, then the group has reached an acceptable consensus and the consensus reaching process ends, otherwise, go to the next step.

Step 3. Obtain the preference values that need to be modified as described in Subsection 3.3.1.

Step 4. Determine whether experts are willing to cooperate. If some of them are unwilling to modify their opinions, then exclude them from this selected sub-group.

Step 5. Update the weight vector of clusters based on Eq. (17), and then obtain the collective PLPR of the unselected sub-groups.

Step 6. According to the suggestion rules in Subsection 3.3.2, experts adjust their evaluation values under the guidance of the moderation. And let $I = I + 1$, then go to Step 2.

Remark 1.

Generally, the threshold value $\lambda$ is up to the evaluation values of experts and the required consensus degree of the actual LSGDM problems. If the group requires a strict consensus level in LSGDM problem, they should set a higher value for $\lambda$.

Once the group reaches an acceptable consensus, the selection process is subsequently presented. A lot of research explores the prioritization methods for probabilistic linguistic decision-making problems, but this part uses Pang’s rule to obtain the ranking result. The overall PLPR can be derived by integrating all PLPRs from experts. According to the PLWA operator, the comprehensive preference values of alternatives denoted as $PV_{i} ,i = 1,2, \ldots ,n$ are obtained. Then the score of $PV_{i}$ is obtained by Eqs. (2) and (3). Here are the ranking rules of $PV_{i}$ [36]: (1) if $E\left( {PV_{i} } \right) > E\left( {PV_{j} } \right)$, then the alternative $x_{i}$ is preferred to the alternative $x_{j}$; (2) if $E\left( {PV_{i} } \right) < E\left( {PV_{j} } \right)$, then the alternative $x_{j}$ is preferred to the alternative $x_{i}$; (3) if $E\left( {PV_{i} } \right) = E\left( {PV_{j} } \right)$, then we need to compare the deviation degree obtained by Eq. (4): (1) if $\alpha \left( {PV_{i} } \right) > \alpha \left( {PV_{j} } \right)$, then the alternative $x_{j}$ is preferred to the alternative $x_{i}$; (2) if $\alpha \left( {PV_{i} } \right) < \alpha \left( {PV_{j} } \right)$, then the alternative $x_{i}$ is preferred to the alternative $x_{j}$; (3) if $\alpha \left( {PV_{i} } \right) = \alpha \left( {PV_{j} } \right)$, then the alternative $x_{i}$ and the alternative $x_{j}$ are both the best solution.

The consensus reaching process is presented in Fig. 2.

Fig. 2

Consensus reaching process of LSGDM problems

4 Discussions

In this section, we design several simulation experiments to verify the effectiveness of the probability k-means clustering algorithm and analyze how the adjustment parameter impacts the CRP.

Firstly, we make a comparative analysis between the traditional k-means clustering algorithm and the proposed probability k-means clustering algorithm to demonstrate the superiority and rationality of the proposed one. In the traditional k-means algorithm, the initial cluster centroids are randomly selected from PLPRs provided by experts, then the distances between each PLPR and the initial centroids is obtained, and the final clustering centroids can be found based on these distances. Since different random centroids may result in completely different clustering results, this paper uses a hierarchical clustering method to determine the initial centroids from PLPRs of experts, so that the final clustering results cannot be affected by the uncertainty of the initial centroids.

Then, we use MATLAB to design experiments to simulate the two algorithms mentioned above. In these simulation experiments, 20 initial PLPRs are randomly generated rather than given by experts. The required number of clusters is set as: $K = 5$. Two algorithms are applied to handle these 20 PLPRs for four times, the final clustering results are shown in Table 8 (in Appendix).

As we can see from Table 8, the initial centroids determined by the traditional k-means algorithm are different, which leads to different clustering results. Whereas, the clustering results derived by the probability k-means algorithm remain unchanged with certain initial centroids. This is to say, the proposed clustering algorithm is more reliable and reasonable.

After that, to further ensure the efficiency and applicability of the proposed algorithm, we compare the number of iterations with the increase of the required number of clusters $K$. We change the value of $K$ from 5 to 10 and obtain the final number of iterations by two algorithms respectively. By running this simulation for 500 times, the average number of iterations can be presented in Fig. 3.

Fig. 3

The iterative times by two algorithms

As Fig. 3 described, the number of iterations of the traditional k-means clustering algorithm decreases with the increase of the required number of clusters, while the number of iterations of the probability k-means clustering algorithm generally keeps stable. Furthermore, for 20 PLPRs in this simulation experiment, the number of iterations of the k-means clustering algorithm is between 3 and 5. But the number of iterations of the proposed algorithm is between 1 and 2, which are obviously less than that of the traditional k-means clustering algorithm.

With the above analysis, the probability k-means clustering algorithm performs better than the traditional k-means clustering algorithm since the former not only can provide a more accurate clustering result but also can keep efficient and stable.

The adjustment parameter $\rho$, which reflects the degree to which experts are willing to accept the recommended values, can directly affect the efficiency of consensus reaching process. The larger the value of $\rho$ indicates that experts in the selected cluster are more reluctant to modify their opinions in each iteration, resulting in the increase of the number of iterations. For the purpose of exploring how the adjustment parameter impacts the number of iterations, we set the acceptable consensus threshold as: $\lambda = 0.9$, the required number of clusters as: $K = 5$, the maximum rounds as: $\delta = 100$. Then, we let the value of $\rho$ increase from 0.1 to 0.9. After randomly generating 20 PLPRs to represent the evaluations of experts, the proposed consensus method is applied to assist the group reach a consensus. By running this simulation for 500 times, the average number of iterations is presented in Fig. 4.

Fig. 4

The iterative times by various adjustment parameters

Figure 4 shows that the required number of iterations to reach a consensus increases with the increase of adjustment parameter. It can be seen from the curve that the first derivative is great than 0, which indicates that the growth rate is also increasing. In a conclusion, the adjustment parameter has a great influence on the CRP. When the value of $\rho$ decreases, the recommended value gradually gets closer to preference values in the collective PLPR of the group and the number of iterations significantly decreases. Thus, for urgent LSGDM problems, it is appropriate for experts to adopt a smaller value of $\rho$. For LSGDM problems that require full consideration of experts’ initial opinions, it needs to adopt a larger adjustment parameter.

5 Case study

In this section, we apply the proposed consensus model to solve a practical LSGDM case. Then, the comparative analysis is conducted to demonstrate the feasibility of the proposed method.

5.1 Contractor selection for the construction projects

As the scale and number of construction projects continue to expand and increase, the bidding mechanism is also constantly developing. In reality, the contractor selection plays an important role in project implementation, which determines the effectiveness of the project implementation. With the improvement of contractors’ competitive strength, it is necessary to develop scientific decision-making methods to assist the bidding mechanism, so that the optimal contractor can be selected to increase the profits of enterprises.

Suppose that there is a project underbidding. 20 experts (denoted as $\left\{ {e_{1} ,e_{2} , \ldots ,e_{20} } \right\}$) are invited to evaluate four candidate contractors (denoted as $\left\{ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right\}$) from several aspects, such as credibility, strength, management system and other factors. By using PLPRs (denoted as $\left\{ {B_{1} ,B_{2} , \ldots ,B_{20} } \right\}$), the experts are asked to provide the comparative results (see Table 9 in Appendix) between pairs of those contractors. In this case, the number of sub-groups, the threshold value, the adjustment parameter, and the maximum rounds of discussion are set as $K = 5$, $\lambda = 0.9$, $\rho = 0.5$, $\delta = 20$, respectively.

After that, the proposed consensus method can be applied to solve this LGSDM problem as follows:

Step 1. Classify 20 experts into 5 sub-groups based on the probability k-means clustering algorithm. At first, five initial centroids are derived by Algorithm 1 as: $C^{1} = \left\{ {e_{1} } \right\}$, $C^{2} = \left\{ {e_{9} } \right\}$, $C^{3} = \left\{ {e_{10} ,e_{20} } \right\}$, $C^{4} = \left\{ {e_{4} ,e_{7} ,e_{12} ,e_{15} } \right\}$, $\left. {C^{5} = \left\{ {e_{1} ,e_{3} ,e_{5} ,e_{6} ,e_{8} ,} \right.e_{11} ,e_{13} ,e_{14} ,e_{16} ,e_{17} ,e_{18} ,e_{19} } \right\}$. Then, with Algorithm 2, the final sub-groups are derived as follows: $C^{1} = \left\{ {e_{1} } \right\}$, $C^{2} = \left\{ {e_{9} } \right\}$, $C^{3} = \left\{ {e_{10} ,e_{20} } \right\}$, $C^{4} = \left\{ {e_{4} ,e_{7} ,e_{12} ,e_{15} } \right\}$, $C^{5} = \left\{ {e_{1} ,e_{3} ,} \right.$$\left. {e_{5} ,e_{6} ,e_{8} ,e_{11} ,e_{13} ,e_{14} ,e_{16} ,e_{17} ,e_{18} ,e_{19} } \right\}$.

Step 2. Obtain the collective PLPRs of five sub-groups by Eq. (12) which are shown in Table 10 (in Appendix).

Step 3. Construct the similarity matrixes (see Table 11 in Appendix) and the similarity degrees for pairs of sub-groups (see Table 1). Then, the consensus degree of the whole group is $\overline{SGSI} = 0.64$, which is less than the threshold value $\lambda = 0.9$. Therefore, the feedback mechanism in Subsection 3.3 ought to be activated to assist the group to reach a consensus.

Table 1 The similar degree $SGSI$ between pair of clusters

Step 4. According to the identification rules, the experts in the sub-group $C^{2}$ should modify their preference information in the first round of iteration. Then, the preference values in PLPRs in the sub-group $C^{2}$ that need to be adjusted are identified (as $h_{14} ,$$h_{24} ,$$h_{34}$), and the recommended values are derived by the suggestion rules (see Table 2).

Table 2 Initial and modified PLPRs

Step 5. Since the expert $e_{9}$ is willing to accept the recommended values given by the moderator, the consensus degree of the group after the first round of modification can be obtained: $\overline{SGSI} = 0.70$.

Obviously, the consensus degree still fails to satisfy the consensus requirement. Iterative calculations need to be repeated in the feedback mechanism until the consensus degree $\overline{SGSI}$ reaches the threshold value $\lambda$. During this process, each expert’s opinions should be fully respected. The experts finally reach a consensus through 11 rounds of modification in this case and the change of the whole CRP shown in Fig. 5. Due to the limited space, here we just present the detailed process of the first round and the final results. Ultimately, we have $\overline{SGSI} = 0.9005 > \lambda$, which indicates that the consensus reaching process ends.

Fig. 5

The group consensus index of CRP

Step 6. Subsequently, obtain the collective PLPR of the group by aggregating all PLPRs (see Table 3), and calculate the scores of alternatives (see Table 4).

Table 3 Finial PLPRs of group

Table 4 The scores of alternatives

The final ranking of alternatives is $x_{4} \succ x_{2} \succ x_{3} \succ x_{1}$, which indicates that the contractor $x_{4}$ performs best in the selection process.

5.2 Comparative analyses and discussions

5.2.1 Comparison with the other linguistic environment

With the impressive performance in depicting the fuzzy thoughts of DMs, HFLPR has been widely used in practical applications. For the sake of exhibiting the superiority of PLPR, we apply the proposed methods with HFLPRs to solve the problem in this subsection. As for the same problem concerning the contractor selection, the evaluation values are expressed in the form of PLPR. We extract the linguistic terms of probability linguistic elements in PLPRs to construct HFLPRs as the initial judgment matrices.

During the process of clustering, the hesitant fuzzy average operator is defined to obtain the centroids of clusters as follows:

$$ HFAW\left( {\gamma_{1} ,\gamma_{2} ,...,\gamma_{m} } \right) = \mathop \oplus \limits_{k = 1}^{m} w_{k} \gamma_{k} = \cup_{{r_{1}^{n} \in \gamma_{1} \left( p \right)}} \left\{ {r_{1}^{n} w_{1} } \right\} \oplus \cup_{{r_{2}^{n} \in \gamma_{2} \left( p \right)}} \left\{ {r_{2}^{n} w_{2} } \right\} \oplus ... \oplus \cup_{{r_{m}^{n} \in \gamma_{m} \left( p \right)}} \left\{ {r_{m}^{n} w_{m} } \right\} $$

(22)

where $\gamma_{k}$ is a hesitant fuzzy linguistic element (HFLE) of the HFLTS and $w = \left( {w_{1} ,w_{2} , \ldots ,w_{m} } \right)^{T}$ is the weight vector of those HFLEs. In this case, $w_{k} = \frac{1}{m}$. Then, we have the final clustering results through the Hamming distance and the Euclidean distance between HFLTSs:

$$ d\left( {\gamma_{1} ,\gamma_{2} } \right) = \left[ {\frac{1}{\# \gamma }\sum\limits_{k = 1}^{\# \gamma } {\left( {\left| {\frac{{r_{1}^{{n_{1} }} - r_{2}^{{n_{2} }} }}{\tau }} \right|} \right)}^{\varpi } } \right]^{\varpi } $$

(23)

if $\varpi = 1$, then this function indicates the Hamming distance between $\gamma_{1}$ and $\gamma_{2}$, otherwise, it indicates the Euclidean distance between $\gamma_{1}$ and $\gamma_{2}$.

After that, similarity matrices are constructed by:

$$ sm_{ij}^{uv} = 1 - d\left( {\gamma_{ij}^{u} ,\gamma_{ij}^{v} } \right) $$

(24)

where $d\left( {\gamma_{ij}^{u} ,\gamma_{ij}^{v} } \right) = \frac{1}{\# \gamma }\sum\limits_{k = 1}^{\# \gamma } {\left| {\frac{{r_{ij}^{u\left( n \right)} - r_{ij}^{v\left( n \right)} }}{\tau }} \right|}$.

The score of alternatives is calculated by the following formula:

$$ \frac{1}{m}\sum\limits_{k = 1}^{\# \gamma } {r^{n} } $$

(25)

Under the hesitant fuzzy linguistic environment, after 11 iterations of modification, we have $\overline{SGSI} = {0}{\text{.9106 > }}\lambda$, which indicates that the group has reached a consensus and the negotiation ends. The results are shown in Table 5.

Table 5 The final result of this case with HFLPR

Based on the two types of preference relations, the rankings of alternatives obtained by the proposed method are the same. However, it can be found that the scores of alternatives are completely different. Hesitant fuzzy linguistic information only considers that DMs may hesitate among different linguistic terms, but does not realize that they may also have different priorities for these possible linguistic terms. This will result in the loss of original information when experts express complex views. Moreover, the differences between the scores of alternatives based on PLPRs are more obvious than that based on HFLPRs, which indicates that utilizing PLPRs to describe decision information is more accurate. Consequently, for LSGDM, PLPRs are more reliable than HFLPRs.

5.2.2 Comparison with an existing consensus model

Yu et al. [47] proposed a hierarchical punishment-driven consensus model based on the PLTSs for LSGDM problems. Firstly, Yu et al. adopted the hierarchical clustering method to divide experts into several groups. Then, they detected the clusters which need to be advised by the minimum value of consensus index obtained by different consensus measures. Then, the feedback mechanism was proposed to select how to adjust the opinion in the cluster by comparing the attainment rate of the consensus index with its threshold. There were hard adjustment mode and soft adjustment mode. The hard adjustment mode means that the selected cluster need to adjust all evaluation elements in the matrix by the same adjustment parameter, while the soft adjustment mode can utilize different adjustment parameters for each element in the PLTS matrix.

However, the PLTSs depict the evaluation information of the alternative $x_{i}$ under the criterion $crt_{i}$. In order to make sure the comparability, this subsection uses the same case for comparative demonstration and supposes that there are four criteria with the same weight $\omega_{crt} = \left( {0.25,0.25,0.25,0.25} \right)$. Other parameters are set as same as Yu et al.’s research [47]: $\overline{ARoCI} = 0.95$, $\overline{IX} = 1$, $\sigma = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}$, $a = 2$, $b = 4$. Table 6 shows the CRP of the hierarchical punishment-driven consensus model and Table 7 demonstrates that the alternative $x_{4}$ is the best optimal.

Table 6 The CRP result of this case with Yu et al.’s research

Table 7 The final result of this case with Yu et al.’s research

By comparison, we can see that although the final solution of the two methods is the same, the method we present requires more iterations due to adjustment rules. The proposed method can precisely locate the position where the evaluation information needs to be modified. However, regardless of the hard adjustment mode or the soft adjustment mode, the hierarchical punishment-driven consensus model modifies all the opinions in a cluster, which can easily cause dissatisfaction among experts and lead to disagreements with the group. In addition, since this model requires more thresholds to be set in advance, the consensus efficiency will be more susceptible to impact.

6 Conclusion

With the increasing complexity of group decision making, this paper aims at developing an effective consensus method for LSGDM problems with probability linguistic preference information. In this paper, we have introduced a probability k-means clustering algorithm which improves the selection of initial centroids in the clustering process. The results of several simulation experiments have demonstrated the superiority and rationality of the proposed algorithm. The proposed feedback mechanism not only considers the evaluation information of all experts, but also enables a large number of experts to reach a consensus efficiently. In addition, a method to manage non-cooperative behaviors has been proposed to deal with the challenges in LSGDM. Due to different consensus level requirements of different LSGDM problems, we have analyzed the effect of the adjustment parameter during CRP. Last but not least, the process to select the optimum contractor for the construction projects is presented to illustrate the applicability of the novel consensus method.

For future research, we are dedicated to investigating the clustering algorithms based on PLPRs, which can improve the efficiency and quality of the clustering process for LSGDM problems. Moreover, in view of the feature of LSGDM, there are still some obstacles in CRP such as how to protect minority opinions with a better efficiency. Thus, different feedback mechanisms are worthy to be studied as well.

Appendix

See Tables

Table 8 The clustering result in two different methods

8,

Table 9 The PLPRs of 20 experts

9,

Table 10 The collective PLPRs of sub-group

10,

Table 11 Initial similarity matrixes

11.