Incremental enhanced α-expansion move for large data: a probability regularization perspective

Abstract

To deal with large data clustering tasks, an incremental version of exemplar-based clustering algorithm is proposed in this paper. The novel clustering algorithm, called Incremental Enhanced α-Expansion Move (IEEM), processes large data chunk by chunk. The work here includes two aspects. First, in terms of the maximum a posteriori principle, a unified target function is developed to unify two typical exemplar-based clustering algorithms, namely Affinity Propagation (AP) and Enhanced α-Expansion Move (EEM). Secondly, with the proposed target function, the probability based regularization term is proposed and accordingly the proposed target function is extended to make IEEM have the ability to improve clustering performance of the entire dataset by leveraging the clustering result of previous chunks. Another outstanding characteristic of IEEM is that only by modifying the definitions of several variables used in EEM, the minimization procedure of EEM and its theoretical spirit can be easily kept in IEEM, and hence no more efforts are needed to develop a new optimization algorithm for IEEM. In contrast to AP, EEM and the existing incremental clustering algorithm IMMFC, our experimental results of synthetic and real-world datasets indicate the effectiveness of IEEM.

1 Introduction

Clustering is to partition a data set into some similar groups, and these groups often are called as clusters. Data clustering is a fundamental tool for data analysis that aims to identify some inherent structure present in a set of objects. Based on this conclusion, clustering has been proved to be a key tool in machine learning and data mining [1–9].

Current clustering algorithms usually work in “batch” mode, which means they process all data points at the same time as shown in Fig. 1. In real world, sometimes we need to cluster an incoming data stream or a large dataset. In these cases, limited by memory, we cannot process all these enormous data at the same time. Thus, when clustering large data, scholars usually select those algorithms which would work in the “chunk” mode. By “chunk” mode we mean incremental or online clustering algorithms, which delete former chunk to free memory for latter chunk as shown in Fig. 1. That is to say, incremental clustering algorithms cluster large datasets chunk by chunk. Furthermore, incremental clustering algorithms are based on the assumption that data in different chunks are similar in both distributions and features. In this case, clustering results of each chunk will be beneficial for obtaining the final clustering result of the entire dataset. Therefore, clustering result of the last chunk is also efficient for the entire large dataset.

Fig. 1

Clustering in “batch” and “chunk” mode

Although there are many types of clustering algorithms, we focus on exemplar-based clustering algorithm in this paper due to its wide applications and outstanding advantages [10, 21–24]. By exemplars we mean those cluster centers are chosen from actual data. In [10], Frey proved that all exemplar-based clustering problems can be seen as minimizing an energy function defined by a Markov Random Field (MRF). The minimization methods for MRF, mainly include message-passing-based algorithms such as Loopy Belief Propagation (LBP) [11] and graph cuts [12] algorithms such as fast α-expansion move algorithm [13]. One typical exemplar-based clustering algorithm is called Affinity Propagation (AP) [10] which resorts to LBP. In 2003, researchers have proved that graph cuts based optimization algorithms perform better than LBP in minimizing the energy function of MRF [12, 15]. Accordingly, Yu Zheng in [16] proposed a novel exemplar-based clustering algorithm, called Enhanced α-Expansion Move (EEM), which resorts to graph cuts as the minimization method. What’s more, a significant advantage of the exemplar-based clustering algorithms is that it indeed requires no assumption of the number of clusters in advance. This advantage benefits exemplar-based clustering algorithms when dealing with large data in “chunk” mode.

Exemplar-based clustering algorithms have gained numerous achievements in recent years [17–24]. However, these algorithms need to store a similarity matrix of the entire dataset, which indeed limits the ability of exemplar-based algorithms for processing large data. AP clustering algorithm utilizes a sparse matrix to process large dataset, however, such a strategy results in information missing which would lower clustering performance and efficiency. In this paper, we work on extending the typical exemplar-based clustering algorithm EEM into an incremental version to process large datasets chunk by chunk. Although several incremental versions of AP have been proposed in [21–24], they aimed at dealing with dynamic datasets or semi-supervised clustering instead of large datasets.

In this paper, we develop a novel incremental exemplar-based clustering algorithm, called Incremental Enhanced α-Expansion Move (IEEM) clustering, for large datasets. The contributions of our work have the following three aspects:

• 1) With the help of the maximum a posteriori (MAP) principle, both AP and EEM can be explained with a unified probabilistic framework, which indeed results in the new unified target function of clustering. In this case, by defining probabilities of the exemplar set and similarities between data and their exemplars, both AP and EEM share exactly the same target function.

• 2) Algorithm IEEM is an exemplar-based clustering algorithm which processes large data by “chunk” mode. Typical exemplar-based clustering algorithms require computing the similarity matrix of the entire dataset, which is a time-consuming process for a large dataset. Since convincing clustering results of several chunks within a large dataset will be similar with each other, IEEM leverages clustering results of previous chunks to improve the clustering efficiency of the entire dataset. In the end, exemplars chosen by the last chunk will be viewed as the exemplars of the entire large dataset as well.

• 3) With the proposed target function of IEEM, the same minimization procedure of EEM and its theoretical spirit can be kept in IEEM through only modifying the definitions of several involved variables. Therefore, no additional efforts are required to design the optimization procedure of IEEM. Our experimental results verify the effectiveness of IEEM in clustering large datasets.

The rest of the paper is organized as follows. Section 2 briefly reviews other incremental clustering algorithms for large datasets. In Sect. 3, a unified explanation of exemplar-based clustering algorithms with the help of the maximum a posteriori principle is first given. Then on the basis of this explanation, algorithm IEEM and its theoretical analysis are stated in detail. Section 4 gives thorough experimental results and evaluations. Section 5 concludes the paper.

2 Related works

Clustering large datasets or data streams has been becoming an important issue due to the increasing availability of enormous information over time. For dynamic data clustering, the difficulty is that it’s hard to find a proper exemplar for both pre-existing data and new-coming data. Incremental clustering framework is adopted to handle this difficulty [21]. For large data clustering, one significant challenge is that the data is too large to be stored in memory or be handled within an acceptable running time. According to Huber’s description [25], a large dataset is defined as the size of 10⁸ bytes. In this sense, incremental clustering algorithms process data chunk by chunk. One chunk is a packet or a small portion of the entire dataset. The chunk size can be decided by the users. A significant advantage of incremental clustering algorithms is no need to scan the whole dataset in advance. In this section, we will briefly introduce some previous clustering algorithms for large data.

Bagirov et al. divided the existing incremental clustering algorithms into two classes: Single Pass Incremental Algorithms (SPIAs) and Cluster Center Adding Algorithms (CCAAs) [26]. Most of the existing incremental clustering algorithms are SPIAs, where new data are added at each iteration and cluster centers are revised accordingly. Namely, clustering result of the previous chunk is combined into the next chunk and the final clustering result for the entire dataset is generated after the last chunk is processed. In CCAAs, the number of clusters may increase as more and more data pouring in. Considering that chunks within large data will be similar with each other, we only focus on SPIAs in this paper.

It should be noted that many incremental clustering algorithms have been designed to process large datasets. For example, BIRCH [27] is proposed to handle large data in a hierarchical way. BIRCH performs compactly and efficiently in spherically clusters with no dependence on data presentation order. However, BIRCH suffers from being able to deal with only low dimensional data, and thus it may not terminate. On the other hand, several incremental fuzzy approaches were designed to process large data clustering in a chunk-by-chunk way. Typical examples include Single-pass Fuzzy C Means (SPFCM) [28], Online Fuzzy C Means (OFCM) [29] and Incremental Multiple Medoids-based Fuzzy Clustering (IMMFC) [37].

As for exemplar-based clustering algorithm, as mentioned above, several incremental versions have been proposed [21–24]. However, the existing incremental exemplar-based clustering algorithms aim at clustering dynamic data or semi-supervised clustering instead of clustering large data. In this study, by proposing a novel incremental clustering framework, we extend exemplar-based clustering algorithms with the ability of processing large data.

3 Incremental enhanced α-expansion move clustering algorithm

3.1 Unified target function for exemplar-based clustering

Assume ${\mathbf{X}} = \{ {\mathbf{x}}_{1} ,{\mathbf{x}}_{2} , \ldots {\mathbf{x}}_{N} \} \in {\mathbb{R}}^{N*D}$ is an input dataset for clustering in which Nis the total number of D-dimensional data points, and E = {E(x ₁), E(x ₂), …, E(x _N )}is the exemplar set where E(x _m ) is the exemplar chosen by data point x _m . For current exemplar set, its prior probability is assumed as.

$$p({\mathbf{E}}) = \frac{1}{{\sigma \sqrt {2\pi } }}e^{{ - \sum\limits_{m = 1}^{N} {\sum\limits_{n > m}^{N} {\theta_{m,n} ({\mathbf{E}}({\mathbf{x}}_{m} ),{\mathbf{E}}({\mathbf{x}}_{n} ))/2\sigma^{2} } } }}$$

(1)

where σ denotes the Gaussian kernel’s width, and

$$\begin{aligned}& \theta_{m,n} ({\mathbf{E}}({\mathbf{x}}_{m} ),{\mathbf{E}}({\mathbf{x}}_{n} )) \hfill \\&\quad = \left\{ \begin{array}{ll} {\text{I}}, &\hfill \\ {\mathbf{E}}({\mathbf{x}}_{m} ) = n,{\mathbf{E}}({\mathbf{x}}_{n} ) \ne n\;or\;{\mathbf{E}}({\mathbf{x}}_{n} ) = m,&\quad {\mathbf{E}}({\mathbf{x}}_{m} ) \ne m \hfill \\ 0,&\quad {\rm otherwise} \hfill \\ \end{array} \right. \hfill \\ \end{aligned}$$

(2)

in which I is a large constant. The definition is as same as that in [11]. For a single data point x _m , the probability for it to choose E(x _m ) as its exemplar is assumed to be.

$$p({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} ) = \frac{1}{{\sigma \sqrt {2\pi } }}e^{{ - d({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} )/2\sigma^{2} }}$$

(3)

where $d({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} )$ is the Euclidean distance between data point x _m and its exemplar E(x _m ). Once the exemplar set is fixed for each iteration of certain exemplar-based clustering algorithm, according to Eq. (1), p (E) will remain unchanged during each iteration.

According to exemplar-based clustering algorithms, a valid exemplar set must satisfy the following two requirements:

• 1) If a data point x _m is selected as an exemplar by any other data point, then x _m must choose itself as its exemplar. Namely, if there is a data point x _n with E(x _n ) = m, then E(x _m ) = m. Therefore, the restriction can be represented by $\forall m \in \{ 1,2, \ldots ,N\} ,{\mathbf{E}}({\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} ) = {\mathbf{E}}({\mathbf{x}}_{m} )$;

• 2) Among current exemplar set, all data points have selected the greatest possible one as their exemplars, that is to say, $\forall m \in \{ 1,2, \ldots N\} ,p({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} ) = \mathop {max}\limits_{{l \in {\mathbf{E}}}} p({\mathbf{x}}_{m} ,{\mathbf{x}}_{l} )$.

A clustering algorithm aims at making sure every data point choose the one with maximum probability in current exemplar set as its own exemplar. Thus in the end, all data points choose their exemplars in terms of $p({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} ) = \mathop {max}\limits_{{l \in {\mathbf{E}}}} p({\mathbf{x}}_{m} ,{\mathbf{x}}_{l} )$. In order to achieve this goal, according to the maximum a posteriori (MAP) principle and in terms of Eqs. (1), (2) and (3), we should have a unified target function for exemplar-based clustering algorithms as follows:

$$\begin{aligned} \mathop {\hbox{max} }\limits_{{\mathbf{E}}} Q({\mathbf{E}}) &= \mathop {\hbox{max} \;}\limits_{{\mathbf{E}}} ln\prod\limits_{m = 1}^{N} {p({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} )p({\mathbf{E}})} \hfill \\ & = \mathop {\hbox{max} }\limits_{{\mathbf{E}}} (\sum\limits_{m = 1}^{N} {\ln p({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} )} + lnp({\mathbf{E}})) \hfill \\ \end{aligned}$$

(4)

after discarding the constant term, Eq. (4) becomes:

$$\begin{aligned} \mathop {\hbox{max} }\limits_{{\mathbf{E}}} - \sum\limits_{m = 1}^{N} {d({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} )/\sigma^{2} } - \sum\limits_{m = 1}^{N} {\sum\limits_{n > 1}^{N} {\theta_{m,n} ({\mathbf{E}}({\mathbf{x}}_{m} ),{\mathbf{E}}({\mathbf{x}}_{n} ))} } \hfill \\ = \mathop {\hbox{min} }\limits_{{\mathbf{E}}} \sum\limits_{m = 1}^{N} {d({\mathbf{x}}_{m} ,{\mathbf{x}}_{{{\mathbf{E}}({\mathbf{x}}_{m} )}} )/\sigma^{2} } + \sum\limits_{m = 1}^{N} {\sum\limits_{n > 1}^{N} {\theta_{m,n} ({\mathbf{E}}({\mathbf{x}}_{m} ),{\mathbf{E}}({\mathbf{x}}_{n} ))} } \hfill \\ \end{aligned}$$

(5)

As mentioned above, although Eq. (5) is derived by using the MAP framework, it is actually an energy function defined by MRF. By observing Eq. (5), according to [10, 16], we can readily obtain the link between it and the target function of AP and EEM, i.e.,

• 1) When σ = 1, Eq. (5) can be optimized by α-expansion move. In this case, Eq. (5) is exactly the same as the target function of algorithm EEM;

• 2) When I = ∞ and σ = 1, Eq. (5) can be optimized by LBP. Therefore Eq. (5) is exactly the same as the target function of algorithm AP;

• 3) With the introduction of σ, Eq. (5) seemingly gives a generalized version of exemplar-based clustering algorithms. However, after observing the definition of the second term in Eq. (5), by enlarging I as Iσ², we can get the same formulation with σ being 1. Therefore, it is enough for us to study Eq. (5) with σ being 1 rather than an arbitrary value in this paper.

In other words, with Eqs. (1–3), the MAP principle indeed helps us derive out Eq. (5) which can give the unified explanation of the above exemplar-based clustering algorithms. On the other hand, the suitability of both AP and EEM in extensive experiments shows us that the assumptions in Eqs. (1–3) are reasonable as well. What is more important, this unified explanation provides us the solid foundation of developing the proposed incremental clustering algorithm in the next subsection.

3.2 Incremental enhanced α-expansion move clustering algorithm

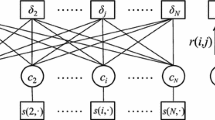
In this subsection, we focus on developing an incremental exemplar-based clustering algorithm which can process large datasets chunk by chunk. For each chunk, a set of exemplars is calculated to represent the chunk with one exemplar for each cluster. According to the conclusion of SPIAs [26], the exemplar set obtained from the last chunk will be appropriate for the entire data as well. We randomly divide the large dataset into K chunks where $K = \left\lceil {N/n} \right\rceil$. In this scenario, each former chunk contains the same number of data points, the number is denoted as n and is decided by users, while the last chunk contains less data if the entire data cannot be divided by n. Therefore each chunk can be represented as C _s  = {x _s1, x _s2, …, x _sn }, and the large dataset is defined as X = {x ₁, x ₂, …, x _N } = C ₀ ∪ C ₁… ∪ C _s … ∪ C _K . We also assume that N here is large enough such that clustering result of each chunk is similar and we can borrow the exemplar-set of previous chunk to guide the clustering for current chunk. In order to achieve this goal, by introducing a probability based regularization term into the generalized target function in Eq. (5), the probability based regularization and an incremental clustering algorithm IEEM is proposed in this subsection. We assume L _o  = {x _op |p ∊ E _o } denotes previous exemplar set obtained from previous chunk C _s-1 by an exemplar-based clustering algorithm. Besides, we define E _s as the exemplar set obtained by clustering chunk C _s , namely, E _s  = {E _s (x _s1), E _s (x _s2), …, E _s (x _sn )}where E _s (x _sp )is the exemplar chosen by x _sp , the corresponding exemplars are represented as L _s  = {x _sp |p ∊ E _s }. As shown in Fig. 2, we consider two main points. First, after clustering, for chunk C _s , each data point x _sp should choose the one with the greatest probability as its exemplar among current exemplar set L _s . More specifically, in Fig. 2, for a single current data point α _s at this moment, according to Eq. (3), exemplar c _s should be selected as its exemplar from the exemplar set L _s  = {a _s , b _s , c _s , d _s }. Second, new exemplars would be close enough to previous ones due to the similarity between previous chunk and current chunk, as illustrated in Fig. 2 where the closeness between previous exemplars {a _s−1, b _s−1, c _s−1, d _s−1}and new ones {a _s , b _s , c _s , d _s } would be maintained.

Fig. 2

Clustering process of current data chunk. The second part of Eq. (6) guarantees the value of $p({\varvec{\upalpha}}_{s} ,{\mathbf{c}}_{s} )$ being larger than $p({\varvec{\upalpha}}_{s} ,{\mathbf{a}}_{s} )$, $p({\varvec{\upalpha}}_{s} ,{\mathbf{b}}_{s} )$ and $p({\varvec{\upalpha}}_{s} ,{\mathbf{d}}_{s} )$; the third part, on the other hand, ensures the closeness between previous exemplars $\{ {\mathbf{a}}_{s - 1} ,{\mathbf{b}}_{s - 1} ,{\mathbf{c}}_{s - 1} ,{\mathbf{d}}_{s - 1} \}$ and new exemplars $\{ {\mathbf{a}}_{s} ,{\mathbf{b}}_{s} ,{\mathbf{c}}_{s} ,{\mathbf{d}}_{s} \}$

In the proposed clustering algorithm IEEM, the following target function is considered:

$$\begin{aligned} \mathop {\hbox{max} }\limits_{{{\mathbf{E}}_{s} }} Q({\mathbf{E}}_{s} )&= lnp({\mathbf{E}}_{s} ) + \sum\limits_{p = 1}^{n} {\ln p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )} \hfill \\ &\quad - \lambda \sum\limits_{p = 1}^{n} {[p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )} - p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} ))]^{2} \hfill \\ \end{aligned}$$

(6)

where the first two terms are exactly the same as that in Eq. (4), and the third term, as the proposed regularization one, denotes that with the similarity between adjacent chunks, the probability of current data point x _sp choosing E _s (x _sp ) as its exemplar should be close to that of x _sp choosing L _os (x _sp ). L _os (x _sp ) is defined as the most suitable exemplar for x _sp among the exemplar set obtained by clustering previous chunk C _s-1, namely

$${\mathbf{L}}_{os} ({\mathbf{x}}_{sp} ) = \mathop {argmax}\limits_{{{\mathbf{l}} \in {\mathbf{L}}_{s - 1} }} p({\mathbf{x}}_{sp} ,{\mathbf{l}})$$

(7)

Besides, λ denotes the regularization factor which makes the third term has the same magnitude with the first two terms. In this case, both terms will affect the procedure of clustering. This parameter is data dependent, and can be determined by grid search in experiments as stated in Sect. 4. As shown in Fig. 2, the first term in Eq. (6) guarantees the validation of current exemplar set {a _s , b _s , c _s , d _s }, the second term makes the value of p(α, c _s ) be larger than p(α, a _s ), p(α, c _s )and p(α, d _s ); the third part, on the other hand, ensures the closeness between previous exemplars {a _s-1, b _s-1, c _s-1, d _s-1} and new exemplars {a _s , b _s , c _s , d _s }.

Obviously, in terms of the MAP principle and from the probabilistic perspective, we can naturally introduce the probability based regularization term into the target function, which indeed results in a significant benefit from the above unified explanation of exemplar-based clustering algorithms. The distinctive advantage of the proposed target function in Eq. (6) is that we only leverage the clustering result, obtained from previous chunk instead of previous chunk itself, to guide the clustering for current chunk. Another merit, which will be seen below, is that we can minimize this target function by simply taking the same minimization framework in [16] through the generalized definitions of several variables and without requiring additional efforts in developing the optimization framework itself.

3.3 Optimization framework

As pointed out in [14], s–t graph cuts has been proved to perform better than LBP in minimizing this kind of energy functions defined by MRF. In other words, s–t graph cuts is only capable for pairwise or low-order energy functions [15], while the target function in Eq. (6) is apparently a high order one. We will prove that α-expansion move algorithm is capable in optimizing Eq. (6).

Theorem 1 The target function in Eq. ( 6 ) can be optimized by the α-expansion move algorithm.

Proof Firstly, we should note that Eq. (6) can equivalently become

$$\begin{aligned} \mathop {\hbox{min} \;}\limits_{{{\mathbf{E}}_{S} }} - lnp({\mathbf{E}}_{S} ) - \sum\limits_{p = 1}^{n} {\ln p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )} \hfill \\ + \lambda \sum\limits_{p = 1}^{n} {[p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )} - p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} ))]^{2} \hfill \\ = \mathop {\hbox{min} \;}\limits_{{{\mathbf{E}}_{S} }} \sum\limits_{p = 1}^{n} {\sum\limits_{q > 1}^{n} {\theta_{p,q} ({\mathbf{E}}_{s} ({\mathbf{x}}_{sp} ),{\mathbf{E}}_{s} ({\mathbf{x}}_{sq} ))} } + \sum\limits_{p = 1}^{n} {d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )} \hfill \\ - \lambda \sum\limits_{p = 1}^{n} {[p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )} - p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} ))]^{2} \hfill \\ \end{aligned}$$

(8)

Since $d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )$ in the second term of Eq. (8) only involves one exemplar variable so it is irrelevant to the proof. As to the third term (i.e., the proposed probability based regularization term) of Eq. (8), although it involves $p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{sp} )}} )$ and p(x _sp , L _os (x _sp )), it actually links to one variable in current exemplar set E _s , i.e., E _s (x _sp ). Therefore both terms are irrelevant to the proof, so we should only consider the first term.

Furthermore, along with the study in [16], in order to prove that Eq. (8) can be approximately optimized by the α-expansion move algorithm, we should focus on validating the correctness of the following inequality:

$$\begin{aligned} &\theta_{p,q} ({\mathbf{E}}_{s} ({\mathbf{x}}_{sp} ),{\mathbf{E}}_{s} ({\mathbf{x}}_{sq} )) + \theta_{p,q} (\alpha ,\alpha ) \hfill \\& \le \theta_{p,q} ({\mathbf{E}}_{s} ({\mathbf{x}}_{sp} ),\alpha ) + \theta_{p,q} (\alpha ,{\mathbf{E}}_{s} ({\mathbf{x}}_{sq} )) \hfill \\ \end{aligned}$$

(9)

in which α ∊ {1, 2, …, n} is an alternative exemplar in current exemplar set E _s . It can be seen that the proof of Eq. (9) is as same as the proof in [16], which has concluded that Eq. (9) holds true.

Finally, because Eq. (6) is equivalent to Eq. (8), so it can be minimized by the α-expansion move algorithm as well. □

In the standard α-expansion move algorithm, for a single data point it would either change its exemplar to x _α or do not change its exemplar at all. Accordingly the corresponding optimization is very time-consuming. To overcome this shortage, we can use an enhanced α-expansion move framework used in [16] to optimize Eq. (6), which will be discussed in detail in next subsection.

3.4 Algorithm IEEM

The process of expansion move involves a single data point. We define this data point as x _sα , thus we would consider the following two cases:

• I. x _sα is already selected as an exemplar by some data points in current chunk C _s , i.e., ∃x _sp  ∊ C _s , E _s (x _sp ) = α;

• II. x _sα is not an existing exemplar, namely ∀x _sp  ∊ C _s , E _s (x _sp ) ≠ α.

During the process of optimization, another exemplar is involved either. We define this exemplar as β and X _sβ as all data points in current chunk C _s with β as their exemplar, i.e., X _sβ  = {x _sp |E _s (x _sp ) = β}. Besides, ${\mathbf{X}}_{s\beta }^{\backslash \beta } = {\mathbf{X}}_{s\beta } - \{ {\mathbf{x}}_{s\beta } \}$ represents the set of data points in this cluster except x _sβ itself.

To improve the optimization efficiency, enhanced α-expansion move extends the expansion space from a single data point x _sα to the entire exemplar set L _s . Therefore, in this optimization strategy, when a data point needs to change its exemplar, instead of x _sα , it can choose the second best exemplar among all exemplars based on their similarities. Thus we assume the second best exemplar for a data point x _sp  ∊ X _sβ as:

$$S(p) = \mathop {argmin}\limits_{{l \in {\mathbf{E}}_{s} - \{ \beta \} }} d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{sl} )$$

(10)

Along with the study line in [16], below we will discuss how to realize the corresponding enhanced α-expansion move clustering by analyzing the above two cases with the proposed target function here.

3.5 Enhanced α-expansion move for case I

In this case, x _sα  ∊ L _s . In order to guarantee that the new exemplar is valid and optimal with respect to the α-expansion iteration, there exist two types of expansions.

Type i: The exemplar of current exemplar x _sβ is kept unchanged. Considering the assumption that every data point x _sp has chosen the most optimal exemplar ${\mathbf{E}}_{s} ({\mathbf{x}}_{sp} ) = \mathop {argmin}\limits_{{l \in {\mathbf{E}}_{s} }} d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{l} )$ during the process of iterations, all data points in current chunk C _s do not need to change their exemplars. As shown in Fig. 3a, in this type of expansion current exemplar set will make no change. Namely, the energy reduction of this type of expansion R _1.1 equals to zero, i.e., R _1.1 = 0.

Fig. 3

Case I: ${\mathbf{x}}_{s\beta }$ is an existing exemplar

Type ii: The exemplar of current exemplar x _sβ itself is changed as well. In this moment, all data points in cluster β must change their exemplars, otherwise the new exemplar set will become invalid. Let us keep in mind that this type of expansion will result in the deletion of the cluster β.

Note that the enhanced α-expansion move has expanded the expansion space to the entire exemplar set. Observing Fig. 3b, in this type of expansion, all data points x _sp  ∊ X _sβ will change their exemplars to S(p) as defined in Eq. (10) above. For this type of expansion, the energy reduction after expansion is:

$$\begin{aligned} R_{1.2} = \sum\limits_{{{\mathbf{x}}_{sp} \in {\mathbf{X}}_{s\beta } }} {\{ d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{S(p)} )} + \lambda [(p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ))^{2} - \hfill \\ 2(p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{S(p)} ))p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} )) - (p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{S(p)} ))^{2} ]\} \hfill \\ \end{aligned}$$

(11)

If 0 > R _1.2, the first type of expansion is applied, namely current exemplar set E _s is kept unchanged. Otherwise, the second type of expansion is applied, i.e., ∀x _sp  ∊ X _sβ , E _s (x _sp ) = S(p). In conclusion, the energy reduction of this case with cluster β is defined as:

$$R1 = \hbox{max} \{ R_{1.1} ,R_{1.2} \} .$$

(12)

3.6 Enhanced α-expansion move for case II

Now let us discuss the case in which x _sα is not used as an exemplar, i.e., x _sα  ∉ L _s . In this case, we can create a new exemplar set L _s ′ and E _s ′ by setting E _s ′(x _sα ) = α, and the remaining exemplars keeps unchanged. Then, we take L _s ′ as the initial exemplars. Just likewise in the previous analysis, two types of expansion in the above Case I can accordingly be applied to the new exemplar set E _s ′.

Type i: In this case, the exemplar of current exemplar x _sβ is kept unchanged, while some data points in cluster β need to change their exemplars to α, these data points are defined as:

$$\begin{aligned} &{\mathbf{X}}_{s\beta - > \alpha }^{\backslash \beta } = {\mathbf{X}}_{s\beta }^{\backslash \beta } \cap \hfill \\& \{ {\mathbf{x}}_{sp} |d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\alpha } ) + \lambda [p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\alpha } ) - p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} ))]^{2} \hfill \\& < d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) + \lambda [p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} ))]^{2} \} \hfill \\ \end{aligned}$$

(13)

Thus, the energy reduction of this type of expansion is computed by:

$$\begin{aligned} R_{2.1} = \sum\limits_{{{\mathbf{x}}_{sp} \in {\mathbf{X}}_{s\beta }^{\backslash \beta } }} {\{ d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\alpha } )} + \lambda [(p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ))^{2} - \hfill \\ 2(p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\alpha } ))p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} )) - (p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\alpha } ))^{2} ]\} \hfill \\ \end{aligned}$$

(14)

The expansion process has been shown in Fig. 4a.

Fig. 4

Case II: ${\mathbf{x}}_{s\beta }$ is not an existing exemplar

Type ii: The exemplar of current exemplar x _sβ itself is changed as well. Being similar to type ii of Case I, all data points in cluster β should change their exemplars. Figure 4b shows the expansion procedure, and the corresponding energy reduction is as follows:

$$\begin{aligned} R_{2.2} = \sum\limits_{{{\mathbf{x}}_{sp} \in {\mathbf{X}}_{s\beta } }} {\{ d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{S(p)} )} + \lambda [(p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ))^{2} - \hfill \\ 2(p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{s\beta } ) - p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{S(p)} ))p({\mathbf{x}}_{sp} ,{\mathbf{L}}_{os} ({\mathbf{x}}_{sp} )) - (p({\mathbf{x}}_{sp} ,{\mathbf{x}}_{S(p)} ))^{2} ]\} \hfill \\ \end{aligned}$$

(15)

We need to compare these two energy reductions. If R _2.1 > R _2.2 type i expansion is applied, i.e., $\forall {\mathbf{x}}_{sp} \in {\mathbf{X}}_{s\beta - > \alpha }^{\backslash \beta } ,{\mathbf{E}}_{s} '({\mathbf{x}}_{sp} ) = \alpha$. Otherwise type ii expansion is applied, i.e., ∀x _sp  ∊ X _sβ , E _s ′(x _sp ) = S(p). The procedure is repeated for all clusters in $\varvec{L}_{s}$. Only when R2 > 0, a new cluster will be added, where R2 is defined as:

$$\begin{aligned} &R2 = d({\mathbf{x}}_{s\alpha } ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{s\alpha } )}} ) - d({\mathbf{x}}_{s\alpha } ,{\mathbf{x}}_{s\alpha } ) \hfill \\& - \lambda [p({\mathbf{x}}_{s\alpha } ,{\mathbf{x}}_{s\alpha } ) - p({\mathbf{x}}_{s\alpha } ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{s\alpha } )}} )] \cdot \hfill \\& [p({\mathbf{x}}_{s\alpha } ,{\mathbf{x}}_{s\alpha } ) + p({\mathbf{x}}_{s\alpha } ,{\mathbf{x}}_{{s{\mathbf{E}}_{s} ({\mathbf{x}}_{s\alpha } )}} ) - 2p({\mathbf{x}}_{s\alpha } ,{\mathbf{L}}_{os} ({\mathbf{x}}_{s\alpha } ))] \hfill \\& + \sum\limits_{{\beta \in {\mathbf{L}}_{s} }} {\hbox{max} \{ R_{2.1} ,R_{2.2} \} } \hfill \\ \end{aligned}$$

(16)

That is to say, only if R2 > 0, E _s  = E _s ′, otherwise E _s is kept unchanged. In contrast to the algorithm derivations and analysis in [11], we readily find that for the proposed target function in Eq. (6) or (8), except for the changes of the definitions of some variables, we can directly take the same optimization framework of EEM to optimize the proposed target function of IEEM and hence no additional efforts are particularly needed to design a new algorithm framework for optimizing the proposed target function. The algorithm details of clustering a single chunk can be stated in Algorithm I below.

Observing the algorithm steps of the above algorithm for a single chunk, we can easily see that it actually simply takes the optimization framework of EEM in [16] to find optimal exemplar set for a single chunk. In the end, the clustering result of the last data chunk will be the most optimal for the entire large dataset, because every data chunk leverages the clustering result of previous data chunk. When the dataset is divided into K chunks, L _K will be the final exemplar set. For other chunk C _s , s ≠ K, their exemplar set can be computed by:

$${\mathbf{E}}_{s} ({\mathbf{x}}_{sp} ) = \mathop {\arg \hbox{min} }\limits_{{\beta \in {\mathbf{E}}_{K} }} d({\mathbf{x}}_{sp} ,{\mathbf{x}}_{K\beta } )$$

(17)

Each exemplar set E _s obtained by leveraging the clustering results of previous chunks. Thus, the final exemplar set for the large dataset will be E = E ₁ ∪ E ₂… ∪ E _K . Based on the above mathematical analysis, the proposed clustering algorithm IEEM for a large dataset can be summarized below.

Just likewise in EEM, each internal iteration within step 4 has a time complexity O(n ²) for each chunk C _s . Following EEM in [16], the proposed algorithm IEEM generally converges within 5 rounds of full expansion for each chunk C _s . Therefore, when dealing with a large dataset, if we directly apply algorithm EEM, the time complexity will be O(N ²). As to algorithm IEEM, assuming that the large dataset is divided into K chunks, the corresponding time complexity of IEEM for the entire dataset will be O(K * n ²). Remember that $K = \left\lceil {N/n} \right\rceil$, the time complexity of IEEM will approximately be O(N * n) which would be much smaller than O(N ²) as n may generally be set to be 500–1000 in terms of our experiments below, which is much less than N as we can see. On the other hand, EEM is less stable than AP because EEM first randomly generates the expansion order [16]. In IEEM, for every chunk, we need to randomly generate the expansion order in algorithm I, so algorithm IEEM should be more unstable than EEM. This unstability will be detail discussed in the next section.

4 Experimental results and evaluations

In this section, experimental results and evaluations are presented to verify the effectiveness and efficiency of our proposed clustering algorithm for large data. In order to do comparative study, we take three exemplar-based clustering algorithms, i.e., algorithm AP, algorithm EEM and the incremental multiple-medoid clustering algorithm IMMFC [37], as three comparison algorithms. As a recently-developed multiple-medoid fuzzy clustering algorithm, IMMFC can work well in an incremental manner only with the accurately preset number of clusters and good initialization of other parameters which are actually not a trivial work in practice. Therefore, when doing comparative study, we will observe its behavior under the same number of exemplars obtained by IEEM, and at the same time demonstrate its poor performance under inaccurately preset number of clusters. Also, we use the same strategy as in [37] to determine all parameters in IMMFC and obtain the average performance of IMMFC. Besides, because EEM works by randomly generating the expansion order, which obviously affects the clustering results, so in order to make our comparison fair, we take its average performance for 10 runs.

In order to observe the overall performances of the comparison algorithms, we adopt three performance indices, i.e., N ormalized M utual I nformation (NMI) [40], A djusted R and I ndex (ARI) [30] and Accuracy [31]. Our experiments about both synthetic and real datasets are carried out with MATLAB 2014a on a PC with 64 bit Microsoft Window 7, an Intel(R) Xeon(R) E5-2609 and 64 GB memory.

Without special specification, the parameters adopted in experiments are determined by grid-search. Since different values of d(x _sp , x _sp ) will produce different number of clusters, in accordance with the experiments in [10, 16–21], d(x _sp , x _sp ) is set to be the median value of all the similarities between data points, multiplied by the best value in {0.01,0.1,1,10, 50, 100,1000}. And we choose the value according to the number of true classes. As to regularization factor λ, in order to make all terms have the same magnitude, λ will be determined from {0.01, 0.05, 0.1, 0.5, 1, 3, 5, 10, 50}. Besides, we also preprocess all the involved datasets below through normalizing their attributes’ values to [0, 1].

4.1 Performance indices

Here we give the definitions of the three adopted performance indices NMI, ARI and Accuracy. In order to avoid confusion, here clusters represent the clustering result returned by a clustering algorithm on a dataset while classes are referred to as the exact labels of data in the dataset.

4.1.1 NMI

To estimate the quality of the obtained clustering result against the number of classes, we define NMI as follows:

$$NMI = \frac{{\sum\limits_{i = 1}^{\left| C \right|} {\sum\limits_{j = 1}^{\left| C \right|} {N_{i,j} \ln \frac{{NN_{i,j} }}{{N_{i} N_{j} }}} } }}{{\sqrt {\left( {\sum\limits_{i = 1}^{\left| C \right|} {N_{i} \ln \frac{{N_{i} }}{N}} } \right)\left( {\sum\limits_{j = 1}^{\left| C \right|} {N_{j} \ln \frac{{N_{j} }}{N}} } \right)} }}$$

(18)

where N _i,j is the number of common data points in the ith cluster and the jth class, N _i is the number of data points in ith cluster, N _j is the number of data in jth class, N is the total number of data points.

4.1.2 ARI [30]

The adjusted rand index ARI is the generalized version of Rand Index, and is defined as follows:

$$ARI = \frac{{\sum\limits_{i = 1}^{k} {\sum\limits_{j = 1}^{l} {\left( \begin{aligned} m_{ij} \hfill \\ 2 \hfill \\ \end{aligned} \right) - t_{3} } } }}{{\frac{1}{2}(t_{1} + t_{2} ) - t_{3} }}$$

(19)

where $t_{1} = \sum\limits_{i = 1}^{k} {\left( \begin{aligned} |C_{i} | \hfill \\ \;\;2 \hfill \\ \end{aligned} \right)}$, $t_{2} = \sum\limits_{j = 1}^{l} {\left( \begin{aligned} |C_{j} '| \hfill \\ \;\;2 \hfill \\ \end{aligned} \right)}$, $t_{3} = \frac{{2t_{1} t_{2} }}{N(N - 1)}$.

m _i,j is the number of common data points in the ith cluster and the jth class, C _i is the number of data points in ith cluster, C _j ’ is the number of data in jth class, N is the total number of data points.

4.1.3 Accuracy [31]

Accuracy is a more direct measure to reflect the effectiveness of clustering algorithms, which is defined as:

$$Accuracy = \frac{{\sum\limits_{i = 1}^{N} {\delta (c_{i} ,map(\hat{c}_{i} ))} }}{N}$$

(20)

where c _i is the real label of data points, and $\hat{c}_{i}$ is the obtained clustering label. δ(i, j) = 1, if i = j; δ(i, j) = 0, otherwise. Function $\text{map} ( \cdot )$ maps each obtained cluster to real class, and the optimized mapping function can be found in algorithm Hungarian [39].

The values of NMI, ARI and Accuracy range from 0 to 1, and the more it close to 1, the more effective the clustering algorithm is.

4.2 Synthetic example

We run IEEM on the 2D15(N = 5000, k = 15, d = 2) [32] dataset to observe its performance. 2D15 is a synthetic dataset composed of 5000 two-dimensional points with 15 classes. The dataset is considered as four chunks randomly, the distributions of the four chunks are shown in Fig. 5a–d. In this experiment, the regularization factor λ = 1, and the d(x _sp , x _sp ) is just the median value of all the similarities between data points. For the first chunk (i.e., chunk 1), we run the AP clustering algorithm, then Algorithm I adopted in algorithm IEEM is carried out on chunks 2–4. The clustering results for four chunks are shown in Fig. 5a–d respectively, the black pentagrams represent the exemplars for each cluster. In the end, Fig. 5e shows the similarity between clustering results of each chunk. It can be seen that the exemplars of every cluster in different chunks are located closely. When cluster current chunk, IEEM leverages the clustering results of previous chunks. Therefore, we can see that the exemplars of last chunk locate on the ideal positions for the entire dataset as well from Fig. 5e. The obtained clustering results are illustrated in Figs. 5, 6, 7, 8 and Table 1. Since both EEM and IEEM need to randomly generate the expansion order, their clustering results will be different in each trial [16]. So the corresponding values are averaged over 10 runs including standard deviation with randomly realization of chunks.

Fig. 5

Represent the clustering results on each chunk, among which a is obtained by AP, b–d are obtained by IEEM for a single chunk, and e represents the final clustering result for the entire dataset 2D15. We directly add clustering results of chunk 1–4 to obtain e. All exemplars above are marked with pentagrams

Fig. 6

NMI of AP, EEM, IMMFC and IEEM, and NMI of IEEM for each chunk

Fig. 7

ARI of AP, EEM, IMMFC and IEEM, and ARI of IEEM for each chunk

Fig. 8

ACCURACY of AP, EEM, IMMFC and IEEM, and ACCURACY of IEEM for each chunk

Table 1 Time consumption (seconds) of comparison algorithms on dataset 2D15

In particular, Fig. 6 shows the comparison results about NMI obtained by AP, EEM, IMMFC and IEEM. Figures 7 and 8 show the comparison results about ARI and Accuracy respectively, and k in IMMFC represent the pre-setting number of clusters. It can be seen that for every chunk, IEEM performs slightly worse than AP. It should be noted that since every chunk is not exactly the same and IEEM leverages the clustering results of previous chunks, the clustering performance of IEEM on only a single chunk does not assure that it may outperform AP. However, by processing data chunk by chunk and leveraging pervious clustering results to improve current clustering result, the final clustering result of the entire 2D15 dataset obtained by IEEM is effective.

As illustrated in Figs. 6, 7, 8, IEEM outperforms both EEM and AP in the average sense. On the other hand, IEEM has wider standard deviations than AP and EEM. The reason is that Algorithms I in IEEM first randomly generates the expansion order for each chunk as mentioned in Sect. 3 and thus the effect of this random process may perhaps be enlarged when IEEM works chunk by chunk. Therefore, how to reduce such standard deviations is an interesting topic in near future. Also, we can obtain the conclusion from Figs. 5, 6, 7, 8 and Table 1 that except for convincing clustering performances, AP seems to be better than IEEM in the sense of the running time. However, we should keep in mind that AP cannot directly work for large datasets (see the experiments below). IEEM indeed occupies much less running time than EEM. When the number of clusters is accurately preset, although IMMFC indeed outperforms IEEM in the sense of NMI, ARI and Accuracy, IEEM’s performance does not degrade a lot, in contrast to IMMFC. However, we should notice IMMFC’s poor performance in Figs. 6, 7, 8 when the number of clusters is inaccurately preset and at the same time we should also remember that how to accurately preset the number of clusters in advance is not a trivial work in practice.

4.3 Results on 2D15, KDD CUP 99

To select a proper value of the regularization factor λ, we first run IEEM on datasets 2D15 and KDD CUP 99. The characteristic of 2D15 has been shown in the previous subsection. On the other hand, KDD CUP 99 [33] is a real-world network intrusion detection dataset which totally includes 494,021 network connection records. The dataset is pre-processed as the same in [34], and has 34 continuous attributes out of the total 42 available attributes. Each connection is labelled among 23 classes, i.e., the normal class and the specific kinds of attacks. According to Huber-Wegman taxonomy of data sizes [25], in order to generate the large dataset, we randomly select 50,000 data points from KDD CUP 99 in this subsection. Limited by memory and time-consumption, neither AP nor EEM can directly be applied on this dataset, so we only show the clustering results of IEEM and IMMFC in this subsection.

In these experiments, each dataset is randomly divided into several equally sized chunks. The size of each chunk may be determined by users. Normally, it refers to a certain percentage of the entire dataset size. The size of the last chunk may be smaller than others if the entire dataset cannot be divided by the chunk size. For a large dataset, we conduct experiments with chunk sizes as 1, 2.5, 5 and 10 % of the entire dataset size. According to our experiments and the number of true classes of datasets, 2D15 require that d(x _sp , x _sp ) is set to be the median value of all the similarities between data points, while KDD CUP 99 requires the value to be multiplied by 10.

According to the above discussions, the regularization factor λ should be selected from [0.01, 0.05, 0.1, 0.5, 1, 3, 5, 10, 50]. We demonstrate the clustering performances with different λ and chunk sizes of both IEEM and IMMFC in Tables 2, 3 and Figs. 9, 10. For IEEM, we run AP algorithm on the first chunk for each dataset. All results below are averaged over 10 runs including standard deviation with randomly realization of chunks.

Table 2 Clustering results of IEEM and IMMFC on 2D15(N = 5000, k = 15, d = 2)

Table 3 Clustering results of IEEM and IMMFC on KDD CUP 99(N = 50 000,k = 23,d = 34)

Fig. 9

Clustering results of IEEM and IMMFC on 2D15 with different chunk sizes

Fig. 10

Clustering results of IEEM and IMMFC on KDD CUP 99 with different chunk sizes

In Tables 2, 3 and Figs. 9, 10, some convincing clustering performances on datasets 2D15 and KDD CUP 99 have been shown. By observing these tables and figures, and comparing with the clustering results of IMMFC, we can readily find that IEEM exhibits its capability of dealing with large data clustering tasks. We demonstrate the clustering results of these two datasets with different λ, and conclude that when λ = 0.01, 0.05, 0.1, 0.5, 1, 5, the clustering performances of IEEM on these two datasets are effective.

Besides, we show the time-consumption of both IEEM and IMMFC on 2D15 and KDD CUP 99 with different chunk sizes in Table 4. By observing these tables and figures, we can readily find that, compared with IMMFC, IEEM can cluster large data well when λ = 0.01, 0.05, 0.1, 0.5, 1, 5and chunk sizes = 1, 2.5, 5 and 10 %.

Table 4 Time consumption (seconds) of different chunk sizes

More specifically, we can observe the following conclusions from the above tables and figures:

• 1) From the mean and standard deviation perspective of NMI, ARI and Accuracy, with the proper regularization factor λ and the proper chunk size, IEEM can achieve considerably stable clustering results which are comparable to those obtained by IMMFC with the pre-setting number of clusters in advance. In other words, if the chunk size is so small that each chunk can not reflect the structure characteristic of the dataset, IEEM cannot assure the very acceptable clustering Accuracy, please see Fig. 9c.

• 2) As for the regularization factor λ, figures and tables above reveal that IEEM can achieve convincing clustering results in a comparatively large range of λ. More specifically, after normalizing all attributes’ values to [0, 1], the value of λ may be appropriately taken from {0.01, 0.05, 0.1, 0.5, 1, 5} in the above experiments on these two datasets. Thus, although IEEM is quite unstable as discussed above, we may reasonably postulate that the determination of λ is not very hard for users.

• 3) The chunk size has an effect on the clustering performances of both IEEM and IMMFC. Considering the size of the entire dataset, we believe that its value should not be so small that the structure characteristic of the dataset cannot be kept in each chunk. As depicted above, 1, 2.5,5 and 10 % are basically appropriate chunk sizes for IEEM and IMMFC if the entire dataset contains tens of thousands data points which either AP or EEM cannot directly work on at this moment.

• 4) By comparing the time-consumptions in Tables 1 4, we can figure out that a proper size of chunk will be very beneficial for reducing IEEM’s time-consumption. In terms of Tables 2, 3 and Figs. 9, 10, we can conclude that when each chunk owns 1000–2000 data points, both time-consumption and clustering performance of IEEM are satisfactory.

4.4 Results on MNIST, covertype forest

4.4.1 MNIST [35]

For MNIST dataset, it consists of ten classes, which are 0–9 handwritten digit images. There are 70,000 28 × 28 pixel images. We normalized the pixel value to [0, 1] by dividing 255 and each image is represented as a 784-dimensional feature vector.

4.4.2 Covertype forest [36]

Covertype forest comes from UCI Machine Learning Repository [36] and has 7 classes, 581,012 objects. Each object is represented as a 54-dimensional feature vector. As the same as KDD CUP 99, we randomly select 50,000 data points from this dataset to generate the large dataset required in this experiment.

MNIST and Covertype Forest are widely used as real-world datasets in large data clustering problems [30–33]. Referring to the above experiment, we consider λ = 0.01, 0.05, 0.1, 0.5, 1, 5and the chunk size = 1, 2.5, 5, 10 % and then run IEEM and IMMFC. The obtained Accuracy values of MNIST and covertype forest range from 0.30 to 0.40, which is also in line with the clustering results of IMMFC in [37]. The obtained NMI values are shown in Fig. 11. From the mean and standard deviation perspective, the clustering performances of IEEM with proper chunk sizes on MNIST and Covertype forest are comparable to those of IMMFC with the pre-setting number of clusters in advance.

Fig. 11

NMI of IEEM and IMMFC on MNIST and covertype forest with different chunk sizes

5 Conclusions

In order to solve the large data exemplar-based clustering tasks, we first utilize the maximum a posteriori (MAP) framework to measure the probabilistic relationships between data points and their exemplars, and also the prior probability of the exemplar set. This MAP framework can be used to unify algorithms AP and EEM. In addition, different from AP and just likewise EEM, we prefer graph cuts to optimize the proposed target functions due to this optimization algorithm performs better than that used in AP. So the unified explanation for exemplar-based clustering algorithms actually provides us the solid foundation for addressing large exemplar-based clustering tasks.

Furthermore, in this study, based on the proposed unified target function of AP and EEM, we propose a new algorithm IEEM by designing a new target function which can processes large data chunk by chunk. Because of the similarity between chunks, the clustering result of the last chunk is identified as the final clustering result for the entire large dataset. The clustering effectiveness of IEEM is verified by comparing the experimental results with AP, EEM and IMMFC on both synthetic and real-world large datasets.

Although IEEM shows encouraging clustering performances for large datasets, some issues still remain to be studied in near future. For example, IEEM has an implicit assumption that the data distributions of chunks are similar. If this assumption does not hold, the information of the previous chunks may produce a negative influence on current chunk clustering, and thus make IEEM obtain undesired clustering performance. Therefore, how to identify whether this assumption holds is an interesting topic. Besides, our experimental results also show that IEEM is quite unstable which has been detailed explained in Sect. 4. So we will focus on how to improve the stability of IEEM. On the other hand, since IMMFC only works worse on dataset MNIST, the relationship between the clustering performance of the algorithm IEEM and the dimensions of the datasets will be studied in the future as well. Another issue worthy to be studied is how to extend our work here for much larger scale and even massive data clustering.