Time Varying Stimulations in Simple Neural Networks and Convergence to Desired Outputs

Abstract

The influence of time varying inputs on a two layer neural network involving transmission delays is studied in this paper. The asymptotic behavior of solutions of the system is studied for a variety of input functions. Conditions for solutions of a system with time varying inputs to approach the solutions (including equilibrium solutions) of the corresponding system with constant inputs are derived. This explains how a system tolerates variations in external inputs. Most important contribution of the study is that conditions on the inputs of the system are derived so that solutions of the system converge to a pre-specified output. The usefulness of the results is highlighted through examples and simulations. This research provides a thorough mathematical support for an upcoming technology that enables one to build intelligent machines with more sophisticated learning capabilities.

Introduction

Replication of behavior of human brain by artificial neural network systems has long history. Right from McCulloch–Pitts perceptron models, Hopfield models (I generation) [4, 9, 11, 17–19], feed-back, recurrent neural networks (II generation) [12, 25] to spiking neural networks (III generation) [5–7], developments are going on in this exciting area to mimic the activities of human brain. Spiking neural networks exhibit the properties similar to those exhibited by biological neurons there by resemble our brain more closely than earlier generation networks and have widespread applications [8, 14–16, 21, 22, 24]. What ever be the network, external inputs are required to initiate a stimulation or bring the system into a state of activation. Inputs are required even after the system acquires activation dynamics. In the absence of such inputs, the system due to its resting potential may get back to its initial resting state. Further, inputs are necessary until the system yields a desired output.

When the systems are simple electric circuits and the inputs are electrical signals controlled by the designer, it may be reasonable to assume that the exogenous inputs to a neural network are mere constants as the variations in them are considered slow and little appreciable. However, for most of the applications, the purpose of study of the networks is to understand the functionality of human brain in a simplified form. The human brain is a very complex system performing multiple tasks. It is capable of generating its own inputs. As we may notice, the inputs to the brain are not simple constants but are invoked by thought processes that exhibit a dependence on time. Consider the basic example of recognizing a bench-mate of early school days after a long time. Is a simple constant input (hint) enough to recognize the person now? One starts with a simple hint and goes on stimulating the brain by increasing the intensity or number of such hints until the brain draws enough information (becomes enough active) to recall the face.

To be specific, our study in this paper is based on the observations that

• (1) the inputs to a system are not mere constants especially for networks that are designed to mimic the complex behavior of a human brain;

• (2) the inputs to a system are output-oriented.

That is, inputs to a system should produce a desired output. There are no specific rules that estimate the inputs required to generate a specific output. One should, at each stage, observe how the network responds to an input, check the corresponding output and compare with the desired output. In case the output is not the desired one, varying the inputs may help approach the desired output. This is a useful approach rather than modifying the network or training or changing the weights to suit our needs each time. Thus, same network may be used to carry out different tasks under different input conditions. This facilitates the network to perform multiple tasks rather than routinely converging to the stored memory states.

In neural networks, an equilibrium pattern corresponds to some memory state of the network and a recall of such a memory is viewed as stability of the network. A recall of the memory without any hints or guesses is usually regarded as a global activity while the recall with hints is local. The presence of external inputs influences the existence as well as the stability of equilibrium patterns of a system. Systems involving time dependent inputs have been inspiring researchers in recent years [1–4, 12, 13]. Mathematically, a variable input leads to non-autonomous system of differential equations. Researchers mainly concentrated on how to maintain the stability of the equilibrium solution of the original network when constant inputs are replaced by time varying inputs. The importance of inputs are usually undermined in literature. Their role is reduced to help find an equilibrium pattern subject to conditions on activation function and parameters of the network. Upon further restrictions on parameters, existence of a unique equilibrium pattern is established for any input, reducing its role further. But the study here is motivated by the observations mentioned above that systems with variable inputs are not just deviations from those with constant inputs but have definite role to play. In particular, the observation that ‘time varying inputs can drive quickly the state to a desired region of the activation space’ is crucial for the understanding of these systems. They may be viewed as external factors influencing the system. Mathematically, above discussion reduces to addressing the following questions.

• (i). If the equilibrium pattern for a system with constant inputs is stable(unstable), under what conditions the corresponding system with time dependent inputs approaches the same equilibrium pattern?

• (ii). How to understand the behavior of solutions of the corresponding system with time dependent inputs when the system with constant inputs has no equilibria?

• (iii). For an a priori specified output, under what conditions the solutions of a system with time dependent inputs approach that pre-specified output?

• (iv). How to choose output oriented inputs for the solutions of the system to approach that output?

Questions (i) and (ii) have already been attempted by researchers for various networks. Readers may, thus, feel acquainted with most of the results in Sect. 2 ahead for this reason. But we readdress these questions in the context explained above for a comprehensive presentation.

Before we provide appropriate answers to these questions for a general system, we begin our endeavor with a Hopfield neural network, namely,

$$\begin{aligned} \begin{aligned} x'_i (t)&= -a_i x_i (t) + \sum ^{n}_{j = 1} b_{i j} \; f_j (\lambda _j , y_j (t)) + I_i \\ y'_i (t)&= -c_i y_i (t) + \sum ^{n}_{j = 1} d_{i j} \; g_j (\mu _j , x_j(t)) + J_i \end{aligned} \end{aligned}$$

(1)

for $i = 1,2,\ldots , n$.

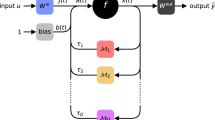
In (1), $a_i , c_i$ are positive constants known as decay rates, $I_i, J_i$ are exogenous inputs and $b_{i j}, d_{i j}$ are the synaptic connection weights for all $i,j = 1,2,\ldots , n$ and all these are assumed to be real or complex constants. The weight connections connect the ith neuron in one neuronal field to the jth neuron in another neuronal field. The functions $f_i$ and $g_i$ are the neuronal output response functions and are more commonly known as the signal functions. The constants $\lambda _i$ and $\mu _i$ represent the neuronal gains associated with the neuronal activations.

In practice, we need to handle images in our memory and our network should be capable of dealing with dynamically changing systems. Images are good test beds for artificial neural networks and richness of recognition capabilities of Hopfield networks are well established. Our selection of human brain analogy and selection of a Hopfield network model is mere symbolic which would enthuse the readers to understand the concept easily and adopt the technique for such real world problems. Further, the properties of (1) are well known and are studied in the literature extensively. It is known (c.f. [7]) that (1) is structurally stable, by which we mean that the existence of a unique equilibrium pattern (memory state) to (1) itself ensures its stability.

Since, time delays that arise in the propagation of information are very common and natural we consider the following modification of (1).

$$\begin{aligned} \begin{aligned} x'_i (t)&= -a_i x_i (t) + \sum ^{n}_{j = 1} b_{i j} \; f_j (\lambda _j , y_j (t-\tau )) + I_i \\ y'_i (t)&= -c_i y_i (t) + \sum ^{n}_{j = 1} d_{i j} \; g_j (\mu _j , x_j(t-\tau )) + J_i, \end{aligned} \end{aligned}$$

(2)

$i=1,2,\ldots ,n$. The the parameter $\tau >0$ signifies the time delay in propagation. The stability of (2) is conditional in the sense that we have to strain the parameters of (2) for the stability of the equilibrium patterns besides the conditions for its existence [9, 17–19].

In view of the recent developments with regard to (2), we study the influence of time dependent inputs on the system (2) which is already under the influence of time delays. Besides the variable inputs, we allow the parameters to be complex valued. Our results are applicable to a more general setup and wide range of networks in addition to networks such as (2). The readers would notice this as we move to the end of Sects. 2 and 3. Further, our study is going to provide a mathematical and logical platform for selecting inputs from a space defined by given values of desired output and sufficient conditions on parameters so that the system approaches the desired output.

The present paper is organized as follows. Section 2 deals with the properties of the solutions and their asymptotic behavior when time dependent inputs are introduced into (2). Further, sufficient conditions on parameters of the system with time dependent inputs under which its solutions approach the positive equilibrium pattern of (2). Several results are established in Sect. 3 on the estimation of inputs that lead to desired (preassigned) output. Further the simulated examples presented in this section illustrate the main results of this paper. A discussion follows in Sect. 4. In the final section, we make concluding remarks and present some open problems for enthusiastic researchers.

The Model and Asymptotic Behavior

We consider the following system which is a modification of system (2) by introducing $I_i =I_i(t)$ and $J_i =J_i(t),\; i=1,2,\ldots ,n$, both functions of time variable t, in place of the constant inputs, $I_i,\, J_i$.

$$\begin{aligned} \begin{aligned} x'_i (t)&= -a_i x_i (t) + \sum ^{n}_{j = 1} b_{i j} \; f_j (\lambda _j , y_j (t-\tau )) + I_i(t) \\ y'_i (t)&= -c_i y_i (t) + \sum ^{n}_{j = 1} d_{i j} \; g_j (\mu _j , x_j(t-\tau )) + J_i(t), \end{aligned} \end{aligned}$$

(3)

$i=1,2,\ldots ,n$.

The following initial functions are assumed for the system (3).

$$\begin{aligned} x_i (s) = \tilde{p_i} (s), \quad y_i (s) = \tilde{q_i} (s) \quad \text{ for } \; s \in (-\tau , 0 ], i=1,2,\ldots ,n, \end{aligned}$$

(4)

where $\tilde{p_i} , \tilde{q_i}$ are continuous, bounded functions on $(-\tau , 0]$.

We assume that the response functions $f_j$ and $g_j$ satisfy local Lipschitz conditions

$$\begin{aligned} \begin{aligned} |f_j(\lambda _j, y_j) - f_j(\lambda _j, \bar{y_j})|&\le \alpha _j | y_j - \bar{y_j} | \\ |g_j(\mu _j, x_j) - g_j(\mu _j, \bar{x_j})|&\le \beta _j | x_j - \bar{x_j}| \end{aligned} \end{aligned}$$

(5)

Here $\alpha _j(\lambda _j)$ and $\beta _j(\mu _j)$ are positive parameters.

A solution of (3) or (2) is denoted by (x(t), y(t)) where $x(t)=(x_1(t),x_2(t),\ldots ,x_n(t))$,

$y(t)=(y_1(t),y_2(t),\ldots ,y_n(t))$ throughout.

Since (3) is non-autonomous, it may not possess equilibrium patterns(constant solutions). Therefore, we study the asymptotic behavior of its solutions. In the following we present a variety of results on asymptotic nearness of its solutions.

Definition

Two solutions (x, y ) and $(\tilde{ x }, \tilde{ y })$ of the system (3) are asymptotically near if $\lim \limits _{t \rightarrow \infty } \; (x(t), y(t)) -(\tilde{x(t)}, \tilde{ y(t)})= 0.$

Our first result is

Theorem 2.1

For any pair of solutions (x, y) and $(\bar{x} ,\bar{y})$ of (3), we have

$$\begin{aligned} \lim _{t\rightarrow \infty } |(x,y)-(\bar{x} ,\bar{y})| =0 \end{aligned}$$

provided

$$\begin{aligned} A\equiv \min \left\{ a_i- \beta _i \sum _{j=i}^{n} |d_{ji}|,\;\; c_i-\alpha _i \sum _{j=i}^{n} |b_{ji}| \right\} >0 \end{aligned}$$

(6)

holds.

Proof

Consider the functional,

$$\begin{aligned} V(t)= & {} \sum ^{n}_{i = 1} \left[ \phantom {\sum ^{n}_{j = 1} |d_{i j}|} |x_i (t)- \bar{x_i}(t)| + |y_i (t)- \bar{y_i}(t)| \right. \\&+ \;\sum ^{n}_{j = 1} |b_{i j}| \int ^t_{t-\tau } |f_j(\lambda _j, y_j(s)) - f_j(\lambda _j, \bar{y_j}(s))| ds\\&\left. + \;\sum ^{n}_{j = 1} |d_{i j}| \int ^t_{t-\tau } |g_j(\mu _j, x_j(s)) - g_j(\mu _j, \bar{x_j}(s))|ds \right] . \end{aligned}$$

Then along the solutions of (3), the upper Dini derivative of V after a simplification is given by,

$$\begin{aligned} D^+ V\le & {} \sum ^{n}_{i = 1} \left[ \phantom {\sum ^{n}_{j = 1}} -a_i |x_i (t)- \bar{x_i}(t)| \right. \\&+ \; \sum ^{n}_{j = 1} |b_{i j}| |f_j(\lambda _j, y_j(t)) - f_j(\lambda _j, \bar{y_j}(t))| \\&\left. -\;c_i |y_i (t)- \bar{y_i}(t)| + \sum ^{n}_{j = 1} |d_{i j}| |g_j(\mu _j, x_j(t)) - g_j(\mu _j, \bar{x_j}(t))| \right] \\\le & {} -\sum ^{n}_{i = 1} \left[ \phantom {\sum _{j=i}^{n}}\Big (a_i-\sum _{j=i}^{n} |d_{ji}| \beta _i\Big ) |x_i (t)- \bar{x_i}(t)| \right. \\&\left. + \; \Big (c_i- \sum _{j=i}^{n} |b_{ji}| \alpha _i \Big )|y_i (t)- \bar{y_i}(t)| \right] ,\;\; \text{ using } \text{(6) } \\\le & {} -A \sum _{i=1}^n[|x_i (t)- \bar{x_i}(t)|+|y_i (t)- \bar{y_i}(t)|] \\< & {} 0, \;\; \text{ by } \text{ hypotheses }. \end{aligned}$$

Integrating both sides with respect to t,

$$\begin{aligned} V(t) + A \int _{0}^{t} \sum _{i=1}^n [|x_i (s)- \bar{x_i}(s)|+|y_i (s)- \bar{y_i}(s)|] ds \le V(0). \end{aligned}$$

Thus, V(t) is bounded on $[0,\infty )$ and $\int _{0}^{\infty } [|x_i (s)- \bar{x_i}(s)|+|y_i (s)- \bar{y_i}(s)|] ds <\infty$ for $i=1,2,\ldots ,n$. But $|x_i -\bar{x_i}|$ and $|y_i - \bar{y_i}|$ are also bounded on $[0,\infty )$. Hence, it follows that their derivatives are also bounded on $[0,\infty )$.

Therefore, $|x_i -\bar{x_i}|$ and $|y_i - \bar{y_i}|,\; i=1,2,\ldots ,n$ are uniformly continuous on $[0,\infty )$. Thus, we may conclude that $|x_i -\bar{x_i}|$ and $|y_i - \bar{y_i}| \rightarrow 0$ as $t\rightarrow \infty$ (see [20, Theorem B.4, p. 252]). This concludes the proof. $\square$

In fact the result may be proved in a more general setting. Consider

$$\begin{aligned} D^+ V \le -A \sum _{i=1}^n[|x_i (t)- \bar{x_i}(t)|+|y_i (t)- \bar{y_i}(t)|]. \end{aligned}$$

Multiplying both sides by $V^{p-1}$ for $2\le p <\infty$ we get

$$\begin{aligned} D^+ V \; V^{p-1}\le & {} -A V^{p-1} \sum _{i=1}^n[|x_i (t)- \bar{x_i}(t)|+|y_i (t)- \bar{y_i}(t)|] \\\le & {} -A \sum _{i=1}^n[{|x_i (t)- \bar{x_i}(t)|}^{p}+ {|y_i (t)- \bar{y_i}(t)|}^{p}], \\&\quad \text{ ignoring } \text{ other } \text{ product } \text{ terms }. \end{aligned}$$

Integrating from 0 to t we get

$$\begin{aligned} V^{p}(t) +p A \int _{0}^{t} \sum _{i=1}^n [|x_i (s)- \bar{x_i}(s)|^p +|y_i (s)- \bar{y_i}(s)|^p ] ds \le V^{p}(0). \end{aligned}$$

Thus, the functions are in $L^{p}$ space and the conclusions may be drawn as usual.

Remark 2.2

In [18, Theorem 3.1] conditions are established for the global stability of equilibrium pattern of (2). When inputs are disturbed, the existence as well as stability of equilibrium for (2) are lost, as a consequence. At the same time, Theorem 2.1 here establishes the asymptotic nearness of solutions. Surprisingly, conditions of Theorem 2.1 match with those of Theorem 3.1 [18]. We may notice that if the system (3) possesses bounded solutions then under the conditions of Theorem 2.1 all the solutions approach a bounded solution and hence, the behavior of the system is predictable. That may be the reason to search for an equilibrium pattern of the system.

The following result provides a set of conditions to guarantee boundedness of solutions of (3).

Theorem 2.3

Assume that the parameters satisfy the conditions (6). Further, let the response functions satisfy $f_j(0)=0,\; g_j(0)=0,\; j=1,2,\ldots ,n$ and the inputs satisfy $\int _0^{\infty } \sum _{i=1}^n |I_i(s)+ J_i(s)| ds <\infty$. Then all the solutions of (3) are bounded.

Proof

Consider the same functional as in Theorem 2.1, that is,

$$\begin{aligned} V(t)= & {} \sum ^{n}_{i = 1} \left[ \phantom {\sum ^{n}_{j = 1}} |x_i (t)| + |y_i (t)| \right. \\&+\;\sum ^{n}_{j = 1} |b_{i j}| \int ^t_{t-\tau } |f_j(\lambda _j, y_j(s))| ds \\&\left. +\;\sum ^{n}_{j = 1} |d_{i j}| \int ^t_{t-\tau } |g_j(\mu _j, x_j(s))|ds \right] . \end{aligned}$$

Then along the solutions of (3) we have the upper Dini derivative of V after some simplifications and rearrangement as in Theorem 2.1,

$$\begin{aligned} D^+ V\le & {} -A \sum _{i=1}^n [|x_i (t)|+|y_i (t)|] \\&+\;\sum _{i=1}^n |I_i(t)+ J_i(t)|. \end{aligned}$$

Integrating both sides from 0 to t and rearranging, we get

$$\begin{aligned} V(t)&+ A \int _0^{t} \sum _{i=1}^n \Big [|x_i (s)|+|y_i (s)|\Big ] \\&\quad \le \;V(0) +\int _0^{t} \sum _{i=1}^n |I_i(s)+ J_i(s)| ds. \end{aligned}$$

It is obvious from the assumptions on the inputs and parameters that V(t), $x_i(t)$ and $y_i(t)$ are bounded.

From Theorem 2.3 it follows that the solutions of (3) are bounded provided the inputs $I_i(t), \, J_i(t), \, i=1,2,\ldots ,n$ are integrally bounded or belong to $L^1$ on $[0,\infty )$. However, we notice that a simple application of Holder’s Inequality yields that if the variable inputs belong to $L^p$ space for some $p,\; 1\le p \le \infty$, the solutions of (3) belong to $L^q$ for some q satisfying $\frac{1}{p} + \frac{1}{q} =1$.

Now integral boundedness of inputs together with (6) is sufficient to ensure the boundedness of solutions of (3) that are asymptotically near. Henceforth, we assume tacitly that the solutions of (3) are bounded. This assumption is used in many of the results in subsequent parts of this work.

The following lemma [10] is used in our next result. $\square$

Lemma 2.4

If $\psi : [t_0,\infty ) \rightarrow [0,\infty )$ is continuous such that

$\psi ^{'} (t) \le -p \psi (t) + q \sup _{t-t_0\le s \le t} \{ \psi (s) \}$ for $t\ge t_0$ and if $p>q>0$ then there exist positive constants l, r such that $\psi (t) \le l e^{-rt}$ for $t\ge t_0$.

We shall now establish the conditions under which the solutions of (3) approach each other exponentially.

Theorem 2.5

For any set of input functions, any pair of solutions (x, y) and $(\bar{x} ,\bar{y})$ of (3) are asymptotically exponentially close provided the following inequality holds.

$$\begin{aligned} p \equiv \min \{a_1, a_2,\ldots ,a_n, c_1,c_2,\ldots ,c_n \}> \sum _{i=i}^{n}\sum _{j=i}^{n} \big ( \alpha _j |b_{ij}| + \beta _j |d_{ij}| \big ) >0. \end{aligned}$$

(7)

Proof

Consider the functional,

$$\begin{aligned} V(t) = \sum ^{n}_{i = 1} [ |x_i (t)- \bar{x_i}(t)| + |y_i (t)- \bar{y_i}(t)| ]. \end{aligned}$$

Then along the solutions of (3), the upper Dini derivative of V after a simplification is given by,

$$\begin{aligned} D^+ V\le & {} \sum ^{n}_{i = 1} \left[ \phantom {\sum ^{n}_{j = 1}}-a_i |x_i (t)- \bar{x_i}(t)|+\sum ^{n}_{j = 1} |b_{i j}| |f_j(\lambda _j, y_j(t-\tau )) - f_j(\lambda _j, \bar{y_j}(t-\tau ))| \right. \\&\left. -\;c_i |y_i (t)- \bar{y_i}(t)| + \sum ^{n}_{j = 1} |d_{i j}| |g_j(\mu _j, x_j(t-\tau )) - g_j(\mu _j, \bar{x_j}(t-\tau ))| \right] \\\le & {} \sum ^{n}_{i = 1} \left[ \phantom {\sum _{j=i}^{n}} -a_i|x_i (t)- \bar{x_i}(t)| +\sum _{j=i}^{n} \beta _j |d_{ij}| |x_i (t-\tau )- \bar{x_i}(t-\tau )| \right. \\&\left. -\;c_i |y_i (t)-\bar{y_i}(t)|+ \sum _{j=i}^{n} \alpha _j |b_{ij}| |y_i (t-\tau )-\bar{y_i}(t-\tau )| \right] \\\le & {} -p V(t) + \sum _{j=1}^n [ \alpha _j |b_{ij}| + \beta _j |d_{ij}|] V_j(t-\tau ) \\\le & {} -p V(t) + \sum _{j=1}^n [ \alpha _j |b_{ij}| + \beta _j |d_{ij}|] \sup _{-\tau \le \rho \le 0} \{V(\rho )\}.\\ \end{aligned}$$

Then by Lemma 2.4, we have $V(t) \le l e^{-rt}$ for $t\ge 0$ for some positive constants l, r. This completes the proof. $\square$

It may be observed that conditions on parameters in (7) are stronger than those in (6). However, for a faster rate of convergence of the network such as exponential convergence we may have to strain the parameters more.

Corollary 2.6

For given inputs I(t), J(t), any two solutions (x, y) and $(\bar{x}, \bar{y})$ of (3) are asymptotic to each other if the conditions of Theorem 2.5 are satisfied.

Proof

The proof follows from Theorem 2.5.

We shall now establish criteria using relevant matrix inequalities for asymptotic nearness of solutions of the system. The recent popularity of such techniques and the development of computational algorithms for easy verification of the conditions motivate us in this direction. We present our results in the following setup.

Let (x, y) and $(\bar{x}, \bar{y})$ be any two solutions of (3) where $x=(x_1,x_2,\ldots ,x_n)$, $y=(y_1,y_2,\ldots ,y_n)$, $\bar{x}=(\bar{x_1},\bar{x_2},\ldots ,\bar{x_n})$ and $\bar{y}=(\bar{y_1},\bar{y_2},\ldots ,\bar{y_n})$.

Define $u_i = x_i - \bar{x_i}$ and $v_i = y_i - \bar{y_i}$. Further, let $u=(u_1,u_2,\ldots ,u_n)$ and $v = (v_1,v_2,\ldots ,v_n)$.

Then using (3) for (x, y) and $(\bar{x}, \bar{y})$, we get

$$\begin{aligned} \begin{aligned} u'(t)&= - A u(t) + B^T \phi (v(t-\tau ))\\ v'(t)&= - C u(t) + D^T \psi (u(t-\tau )). \end{aligned} \end{aligned}$$

(8)

In (8), $A= (a_1,a_2,\ldots ,a_n)^T$, $C=(c_1,c_2,\ldots ,c_n)^T$ are column matrices, $B= (b_{ij})_{n\times n}$ and $D=(d_{ij})_{n\times n}$ are coefficient matrices.

Also $\phi = (\phi _1,\phi _2,\ldots ,\phi _n)$, $\psi = (\psi _1,\psi _2,\ldots ,\psi _n)$ where $\phi _i (v_i) = f_i(y_i) -f_i(\bar{y_i})$ and $\psi _i (u_i) = g_i(x_i) -g_i(\bar{x_i})$ are the modified response functions satisfying $\phi _i (0) = 0$ and $\psi _i (0) = 0$ for $i=1,2,\ldots ,n$. $\square$

The following result is a direct application of Theorem 1 of [13] and may be proved along those lines. Hence, details are omitted.

Theorem 2.7

For given parameters $\gamma _1,\; \gamma _2,\; \tau ,$ the solutions of (8) satisfy $(u,v) \rightarrow (0,0)$ as $t\rightarrow \infty$ provided there exist positive definite matrices $P,Q,S_1,S_2$ and positive diagonal matrices $Q_1,P_1$, a positive scalar $\epsilon$ and any matrices $Y_1$ and $Y_2$ satisfying the matrix inequalities:

$$\begin{aligned}&\left[ \begin{array}{c@{\quad }l@{\quad }c@{\quad }l@{\quad }c@{\quad }r} {\Pi _1} &{} {\gamma _1 \sqrt{\tau } {Y_1}^T} &{} {PB^T} &{} {-Y_1} &{} {-A^T P +{Y_1}^T} &{} 0 \\ * &{} -\gamma _1 P &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\epsilon P_1 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} -S_1 &{} {-Y_1}T &{} 0 \\ * &{} * &{} * &{} * &{} -\gamma _1 \tau ^{-1} P &{} PB^T \\ * &{} * &{} * &{} * &{} * &{} -\epsilon P_1 \end{array}\right]< 0\\&\left[ \begin{array}{c@{\quad }l@{\quad }c@{\quad }l@{\quad }c@{\quad }r} \Pi _2 &{} \gamma _2 \sqrt{\tau } {Y_2}^T &{} QD^T &{} -Y_2 &{} -C^T Q +{Y_2}^T &{} 0 \\ * &{} -\gamma _2 Q &{} 0 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} -\epsilon Q_1 &{} 0 &{} 0 &{} 0 \\ * &{} * &{} * &{} -S_2 &{} {-Y_2}T &{} 0 \\ * &{} * &{} * &{} * &{} -\gamma _2 \tau ^{-1} Q &{} Q D^T \\ * &{} * &{} * &{} * &{} * &{} -\epsilon Q_1 \end{array}\right]<0,\\&\left[ \begin{array}{l@{\quad }l} -P &{} \tau {Y_1}^T \\ * &{} -P \end{array} \right]<0, \,\,\, \text{ and } \;\;\; \left[ \begin{array}{l@{\quad }l} -Q &{} \tau {Y_2}^T \\ * &{} -Q \end{array}\right] <0, \end{aligned}$$

where $\Pi _1 = -PA - A^T P +Y_1 +{y_1}^T + S_1 + 2\epsilon \bar{M} Q_1 \bar{M}$, $\Pi _2 = -QB - B^T Q +Y_2 +{y_2}^T + S_2 + 2\epsilon M P_1 M$, and $M = diag(\alpha _1,\alpha _2,\ldots ,\alpha _n)$ and $\bar{M} = diag(\beta _1,\beta _2,\ldots ,\beta _n)$.

Notice that conditions on parameters in Theorem 2.7 include the time delay $\tau$. Thus, it provides a delay dependent result for asymptotic nearness of solutions.

Sensitivity to Stimulations

We have started with (3) as a modification of (2) but studied the behavior of its solutions independently. But our motto is to study the effect of time dependent inputs on a system running with constant inputs. For this, we regard (3) as a perturbation of (2) and observe the behavior of solutions of (3) with respect to those of (2) due to the perturbation of constant inputs.

The following result provides conditions under which all solutions of (3) are asymptotic to the solutions of (2), which shows that for a proper choice of input functions the stability of system (2) is not perturbed by the presence of time dependent inputs.

Theorem 2.8

Assume that the solutions of (3) are bounded. Further, let inputs satisfy $\int _0^{\infty } \sum _{i=1}^{n} |\tilde{I_i}(t)+ \tilde{J_i}(t)| dt <\infty$ where $\tilde{I_i}(t) =I_i(t)- I_i$, $\tilde{J_i}(t) = J_i(t) - J_i, \; i=1,2,\ldots ,n$ and also the parametric conditions (6) hold. Then for any solution (x, y) of (3) and $(\bar{x},\bar{y})$ of (2) we have

$$\begin{aligned} \lim _{t\rightarrow \infty } (x,y) =(\bar{x},\bar{y}). \end{aligned}$$

Proof

To establish this, we employ the same functional as in Theorem 2.1, that is,

$$\begin{aligned} V(t)= & {} \sum ^{n}_{i = 1} \Big [ |x_i (t)- \bar{x_i}(t)| + |y_i (t)- \bar{y_i}(t)|\\&+ \;\sum ^{n}_{j = 1} |b_{i j}| \int ^t_{t-\tau } |f_j(\lambda _j, y_j(s)) - f_j(\lambda _j, \bar{y_j}(s))| ds\\&+ \;\sum ^{n}_{j = 1} |d_{i j}| \int ^t_{t-\tau } |g_j(\mu _j, x_j(s)) - g_j(\mu _j, \bar{x_j}(s))|ds \Big ]. \end{aligned}$$

Proceeding as in Theorem 2.1 we get after a simplification and rearrangement,

$$\begin{aligned} D^+ V\le & {} -A \sum _{i=1}^n [|x_i (t)- \bar{x_i}(t)|+|y_i (t)- \bar{y_i}(t)|] \\&+ \;\sum _{i=1}^n |\tilde{I_i}(t)+ \tilde{J_i}(t)|. \end{aligned}$$

Rest of the argument is same as that of Theorem 2.1, and hence, omitted. Thus, the conclusion follows.$\square$

We notice that the integral conditions the inputs in Theorems 2.8 and 2.3 although look similar, they differ in spirit. The condition that $\int _0^{\infty } \tilde{I(t)} dt < \infty$ of Theorem 2.8 does not imply $\int _0^{\infty } I(t) dt <\infty$ of Theorem 2.3. Thus, boundedness of solutions is not realizable without suitable restrictions on inputs.

We now recall from [9, 18, 19] that the system (2) has a unique equilibrium pattern $(x^*,y^*)$ for any set of input vectors (I, J) provided the parameters satisfy,

$$\begin{aligned} a_i-\alpha _i \sum _{j=i}^{n} |b_{ji}|>0, \quad c_i- \beta _i \sum _{j=i}^{n} |d_{ji}| >0, \quad i=1,2,\ldots ,n. \end{aligned}$$

(9)

Then we have,

Corollary 2.9

Assume that all the hypotheses of Theorem 2.8 are satisfied. Further if (2) possesses equilibrium pattern $(x^*,y^*)$ then all solutions (x, y) of (3) approach $(x^*,y^*)$.

Proof

The result obviously follows form the observation that the equilibrium pattern $(x^*,y^*)$ is also a solution of (2) and the choice $(\bar{x},\bar{y})= (x^*,y^*)$ in Theorem 2.8.$\square$

The following example illustrates above results.

Example 2.10

Choose for (2), $a_1=5.6$, $a_2=5$, $c_1=5.5$, and $c_2=4.5$. Let

$$\begin{aligned}{}[b_{i j}] = \left[ \begin{array}{l@{\quad }l} 1+i &{} 1 \\ -1 &{} \frac{1}{\sqrt{2}}+ i \frac{1}{\sqrt{2}} \end{array}\right] , \quad [d_{i j}] = \left[ \begin{array}{l@{\quad }l} 1+i &{} 1+2i \\ 4i &{} 2+i \end{array}\right] . \end{aligned}$$

Choose the functions $f_i, g_i, i = 1,2$ as

$$\begin{aligned} f= & {} \left( \begin{array}{ll} f_1 \\ f_2 \end{array}\right) = \left( \begin{array}{ll} \tanh (\lambda _1y_1) \\ \tanh (\lambda _2 y_2) \end{array}\right) ,\\ g= & {} \left( \begin{array}{ll} g_1 \\ g_2 \end{array}\right) = \left( \begin{array}{ll} \tanh (\mu _1 x_1) \\ \tanh (\mu _2 x_2) \end{array}\right) . \end{aligned}$$

It is easy to see that $\alpha _j =\beta _j =1$ for $j=1,2$.

Further, for $i=1$, $\sum _{j=1}^2 |b_{ji}| =1+\sqrt{2} < \{c_1,a_1\}$, for $i=2$, $\sum _{j=1}^2 |b_{ji}| =2 < \{c_2,a_2 \}$, for $j=1$, $\sum _{j=1}^2 |d_{ji}| =4+\sqrt{2} < \{c_1,a_1\}$, and for $j=2$, $\sum _{j=1}^2 |d_{ji}| =2\sqrt{5} < \{c_2,a_2\}$.

Clearly conditions for both the existence of unique equilibrium and its stability are satisfied for any pair of constant inputs $I_i,\; J_i,\; i=1,2$.

Now choose

$$\begin{aligned} I_1(t) =I_1+e^{-t}, \quad J_1(t) =J_1+e^{-t} \sin \; t, \quad I_2(t) =I_2+t e^{-t} \end{aligned}$$

and $J_2(t) =J_2+e^{-t} \cos \; t$.

It is easy to see that since the condition $\int _0^{\infty } |\tilde{I_i}(t) +\tilde{J_i}(t)| dt <\infty$ holds, we have,

• (i). Conditions of Theorem 2.1 are satisfied and all solutions of (3) are asymptotic to each other.

• (ii). Conditions of Theorem 2.8 are satisfied and all solutions of (3) are asymptotic to each other under perturbations (variable inputs) and approach the equilibrium pattern of (2).

Remark 2.11

It is shown in [12] that for single layer compartmental system

$$\begin{aligned} x'_i (t) = -f_{10}(x_i(t)) + \sum ^{n}_{i = 1} f_{ji}(x_i(t)) + I_i(t), \quad j=1,2,\ldots ,n, \end{aligned}$$

the conditions for existence of an equilibrium solution and asymptotic stability are equivalent. But we notice for a two layer network such as (2) the conditions (9) for existence of an equilibrium solution and asymptotic stability of it (i.e.,(6)) vary. Thus, results presented in this part may be viewed as an extension or appropriate modification of the results of [12] for a Bidirectional Associative Memory network. Moreover, it is assumed in [12] that inputs to the system are monotone increasing, bounded , measurable functions while our requirements here are much less as may be noticed from the results established.

The study in [4, 25] deals with output convergence of recurrent neural networks. In all these papers it is assumed that (i) an equilibrium pattern always exists; (ii) inputs are continuous bounded functions and approach a constant input value. We notice that results in this section are comparable with those of above papers except for the networks chosen. More over, we present a variety of sufficient conditions widening the scope of application of our results.

The study in this section mainly concentrates on providing conditions for closeness of solutions of (3) which could not have constant equilibria and stability of equilibria of (2) even in the presence of variable inputs (that is, solutions of (3) approaching the equilibrium of (2)). This reviews the earlier studies for providing answers to first two questions posed in the introduction (Sect. 1).

We now present another result modifying the conditions on the response functions.

For this we rewrite system (2) as

$$\begin{aligned} X' (t) = F(X_{\tau }) \end{aligned}$$

(10)

letting

$$\begin{aligned} X(t)= & {} (x(t), y(t)),\; X_{\tau }(t) = (x(t-\tau ), y(t-\tau )) \quad \text{ and } \quad \\ F(X_{\tau })= & {} (F_1 (X_{\tau }), F_2 (X_{\tau })), \; \tau \ge 0 \end{aligned}$$

in which $x(t)= (x_1(t),x_2(t),\ldots ,x_n(t))$, $y(t)=(y_1(t),y_2(t),\ldots ,y_n(t))$ and $F_p =(F_{p1},F_{p2},\ldots , F_{pn}),\;\;p=1,2$, where

$$\begin{aligned} F_{1i} (t) =-a_i x_i (t) + \sum ^{n}_{j = 1} b_{i j} f_j (\lambda _j , y_j (t-\tau )) + I_i \end{aligned}$$

and

$$\begin{aligned} F_{2i}(t) = -c_i y_i (t) + \sum ^{n}_{j = 1} d_{i j} g_j (\mu _j , x_j(t-\tau )) + J_i \end{aligned}$$

and system (3) as

$$\begin{aligned} X' (t) = F(X_{\tau })+ G(t) \end{aligned}$$

(11)

in which $G(t) = (I(t)-I, J(t)-J)$ where $I(t) = (I_1(t),\ldots ,I_n(t))$, $J(t)= (J_1(t),\ldots ,J_n(t))$ are the variable inputs and $I=(I_1,\ldots ,I_n)$, $J=(J_1,\ldots ,J_n)$ are the constant inputs and the other terms are as in (10).

System (11) may be viewed as a perturbation of (10).

Let C denote the Banach space of all continuous functions defined on $[-\tau , \infty )$ with values in $R^{n}$ and with supremum norm. We identify (10) with (2) and similarly, (11) with (3). We have

Theorem 2.12

Assume that

$(A_1)$ for $X,Y \in R^n$, $X_{\tau }, Y_{\tau } \in C$ and for $h>0$, there exists an $\alpha >0$ such that

$$\begin{aligned} |X-Y+h(F(X_{\tau })-F(Y_{\tau }))| \le (1-\alpha h) |X-Y|. \end{aligned}$$

Assume further that $\int _0^{\infty } [|I(s)-I| + |J(s)-J)|] ds <\infty$. Then for any bounded solutions X and Y of (2) and (3) respectively

$$\begin{aligned} \lim _{t \rightarrow \infty } |X(t)-Y(t)| =0 \end{aligned}$$

holds.

Proof

Consider $V(t) = |X(t) - Y(t)|$. Then for sufficiently small $h>0$ we have

$$\begin{aligned} V'(t)= & {} \lim _{h\rightarrow 0^+} \frac{V(t+h) -V(t)}{h} \\= & {} \frac{|X(t+h)-Y(t+h)| - |X(t)-Y(t)|}{h} \\= & {} \frac{|X(t)-Y(t) + h(F(X_{\tau }) - F(Y_{\tau })) +h G(t)| - |X(t)-Y(t)|}{h} \\&\qquad \text{(from } \text{ definition } \text{ of } X',\; Y' \text{ for } \text{ sufficiently } \text{ small } h>0) \\\le & {} -\alpha |X(t)-Y(t)| +|G(t)|, \quad \text{ using } \text{ hypothesis } (A_1) \\\le & {} -\alpha V(t) + |I(t)-I| + |J(t)-J)|. \end{aligned}$$

Rest of the argument is similar to that of Theorem 2.8. Hence, the conclusion follows.

It is clear that when the variations in inputs are well within the neighborhood of the corresponding constant inputs as prescribed by the integral condition above then the solutions of the perturbed system are asymptotically near to the original system under the other hypothesis on signal functions.

The following result is an immediate consequence of Theorem 2.12 and needs no proof. $\square$

Corollary 2.13

Assume that the hypotheses of Theorem 2.12 hold. If (2) possesses an equilibrium pattern $X^*$ then for any solution Y of (3), we have

$$\begin{aligned} \lim _{t\rightarrow \infty } |Y(t)-X^*| =0. \end{aligned}$$

In the next section we address the question of attaining a desired output by restricting or selecting the inputs appropriately.

Convergence to an apriori Output: Estimation of Inputs

In this section, we try to answer the last two questions regarding the convergence to a pre-specified output raised in Sect. 1. First, we understand how to approach the given output by suitably selecting the inputs. Secondly, we estimate our inputs, depending on the output given, that help the solutions approach the given output.

Before we find the ways, we rearrange our system (3) suitably. We use the following notation. Let $(\bar{X},\bar{Y})\subseteq (\mathbf {R}^{n}, \mathbf{R}^{n})$ denote the set of all continuous, bounded real valued functions (x, y) defined on $[t_0,t_0+h)$. Define $T:(\bar{X},\bar{Y}) \rightarrow (\bar{X},\bar{Y})$ such that

$$\begin{aligned} (T(x,y))(t)= & {} \left( \eta -a \int _{t_0}^{t} x(s) ds +b \int _{t_0}^{t} f(y(s)) ds +\int _{t_0}^{t} I(s) ds, \right. \\&\left. \delta -c\int _{t_0}^{t} y(s) ds +d\int _{t_0}^{t} g(x(s)) ds +\int _{t_0}^{t} J(s) ds \right) . \end{aligned}$$

Define

$$\begin{aligned} \Vert (x,y)\Vert = \sup _{t_o \le t \le t_0+h} e^{-L(t-t_0)} \{ |x(t)|+|y(t)|\}, \end{aligned}$$

where $L >0$ is such that $K\equiv \max \{ a+\beta |d|, \; c+\alpha |b| \} <L$. Here $\alpha , \; \beta$ are the Lipschitz constants for the functions $f,\; g$ respectively. Further, since, x and y are bounded and f and g are continuous, we can find positive constants M and N such that

$$\begin{aligned} \int _0^t |e^{as} (f(y(s))|ds \le M e^{at}, \quad \int _0^t |e^{as} (g(x(s))| ds \le N e^{at}. \end{aligned}$$

For $\tau =0$, (3) may be represented as

$$\begin{aligned} \begin{aligned} x'(t)&= -ax(t) + b f(y(t)) +I(t) \\ y'(t)&= -cy(t) + d g(x(t)) +J(t), \end{aligned} \end{aligned}$$

(12)

in which $x(t)\!=\! (x_1(t),x_2(t), \ldots , x_n(t))$, $y(t)\!=\!(y_1(t),y_2(t),\ldots ,y_n(t))$, $a\!=\!(a_1,a_2,\ldots ,a_n)$, $c=(c_1,c_2,\ldots , c_n)$,

$$\begin{aligned} bf(y)= & {} \left( \sum _{j=1}^{n} b_{1j} f_j(y_j),\sum _{j=1}^{n} b_{2j} f_j(y_j),\ldots , \sum _{j=1}^{n} b_{nj} f_j(y_j) \right) , \\ dg(x)= & {} \left( \sum _{j=1}^{n} d_{1j} g_j(x_j),\sum _{j=1}^{n} d_{2j} g_j(x_j), \ldots , \sum _{j=1}^{n} d_{nj} g_j(x_j) \right) , \end{aligned}$$

$I(t) =(I_1(t),I_2(t),\ldots ,I_n(t))$ and $J(t) =(J_1(t),J_2(t),\ldots ,J_n(t))$.

We are now in a position to state and prove

Theorem 3.1

For an arbitrarily chosen output pattern $(\eta ,\,\delta )$, the system (12) has a solution that converges to this desired output provided the inputs satisfy the condition $\int _0^{\infty } e^{as}(|I(s)|+|J(s)|) ds < p e^{at},\; p>0$. Further more, the solution is unique.

Proof

For any pair of solutions (x, y) and (u, v) of (12), we have

$$\begin{aligned} \Vert T(x,y) - T(u,v)\Vert= & {} \sup _{t_o \le t \le t_0+h} e^{-L(t-t_0)} \Big \{|-a\int _{t_0}^{t} (x(s)-u(s)) ds \\&+\; b \int _{t_0}^{t} (f(y(s))-f(v(s))) ds | \\&+\; |-c\int _{t_0}^{t} (y(s)-v(s)) ds + d \int _{t_0}^{t} (g(x(s))-g(u(s))) ds| \Big \} \\\le & {} \sup _{t_o \le t \le t_0+h} e^{-L(t-t_0)} \Big \{(a+|d|\alpha ) \int _{t_0}^{t} |x(s)-u(s)| ds \\&+\; (c+|b|\beta ) \int _{t_0}^{t} |y(s)-v(s)| ds \Big \}\\\le & {} \sup _{t_o \le t \le t_0+h} e^{-L(t-t_0)} \Big \{ K \int _{t_0}^{t} (|x(s)-u(s)| +|y(s)-v(s)|) ds \Big \} \\\le & {} \sup _{t_o \le t \le t_0+h} e^{-L(t-t_0)} K \Vert (x,y) - (u,v) \Vert \int _{t_0}^{t} e^{L(s-t_0)} ds \\\le & {} \frac{K}{L} \Vert (x,y) - (u,v) \Vert < \Vert (x,y) - (u,v) \Vert . \end{aligned}$$

Thus, T is a contraction map and hence, has a unique fixed point (x, y) in $(\bar{X},\, \bar{Y})$ for all $t\ge t_0$ such that

$$\begin{aligned} \begin{aligned} x(t)&= \eta -a \int _{t_0}^{t} x(s) ds +b \int _{t_0}^{t} f(y(s)) ds +\int _{t_0}^{t} I(s) ds, \\ y(t)&= \delta -c\int _{t_0}^{t} y(s) ds +d\int _{t_0}^{t} g(x(s)) ds +\int _{t_0}^{t} J(s) ds, \end{aligned} \end{aligned}$$

(13)

which by continuity may be extended to $[0,\infty )$.

Now consider

$$\begin{aligned} x'(t) = -ax(t) + b f(y(t)) +I(t). \end{aligned}$$

A solution of this differential equation in the interval [0, t] may be given by

$$\begin{aligned} x(t) = x(0) e^{-at} + e^{-at} \int _0^t e^{as} \Big ( b f(y(s)) +I(s)\Big ) ds. \end{aligned}$$

Then

$$\begin{aligned} |x(t)| \le |x(0)| +|b|M + e^{-at} \int _0^t e^{as} |I(s)| ds. \end{aligned}$$

Thus, the boundedness of x(t) follows from the assumption on the inputs. Similar arguments are valid for y.

Now the convergence follows from (13) and the boundedness of (x, y).

Thus, $\lim _{t\rightarrow {\infty }} (x(t),y(t)) = (\eta ,\delta )$. The proof is complete. $\square$

See that uniqueness is assured in this result.

The condition on inputs in this result may be viewed as a requirement that if the input signals are random, the expected value of these signals be bounded by p.

Remark 3.2

Convergence to a desired output ($x\rightarrow \eta )$ presented here is totally different from output convergence (output function $g(x) \rightarrow g(x^*)$, value of the output function at $x=x^*$) as studied in [4, 25]. Further, one may have clearly noticed that (2) is only a medium for establishing our results and our results may very well be applied to other networks.

In the remaining part of the paper, we concentrate on selecting an appropriate input to make the network converge to a pre-specified output.

To begin with, we consider a single layer network given by

$$\begin{aligned} x'(t) = -ax(t) + b f(x(t)) +I(t). \end{aligned}$$

(14)

Let $\eta$ be the desired output and we need to give an estimate on the input I(t). Assume that $\eta$ is independent of t. Then above equation may be written as

$$\begin{aligned} x'= x'-{\eta }' = -a(x-\eta ) + b (f(x)-f(\eta )) +I(t)-a\eta + bf(\eta ). \end{aligned}$$

(15)

Assume that f satisfies the condition $|f(x)-f(y)| \le k |x-y|$ for some $k>0$.

We shall now establish our first result in this direction.

Theorem 3.3

Assume that the parameters and the response functions of the system (14) satisfy the condition $\tilde{\beta } \equiv a-|b|k>0$. For an arbitrarily chosen output $\eta$, the solutions of system (14) converge to this desired output provided the input satisfies either of the conditions

$$\begin{aligned} (i)\, \int _0^{\infty } |I(s) -(a\eta -bf(\eta ))| ds < \infty \quad \hbox { or } \; (ii) \, \lim _{t\rightarrow \infty } I(t) = a\eta -bf(\eta ). \end{aligned}$$

Proof

Let $V(x(t)) = |x(t)-\eta |$. Then differentiating V along the solutions of (14), and using (15), we have

$$\begin{aligned} D^+V\le & {} -a|x-\eta | + |b| |f(x)-f(\eta )|) \\&+ \; |I(t)-a\eta + bf(\eta )| \\\le & {} - [a- |b|k] |x-\eta | + |I(t)-a\eta + bf(\eta )|. \end{aligned}$$

This gives rise to

$$\begin{aligned} V'+ \tilde{\beta } V \le |I(t)-a\eta + bf(\eta )|. \end{aligned}$$

Rest of the argument is similar to that of Theorem 2.1 and invoking the condition (i) on I(t).

Again, it is easy to see from the last inequality above that

$$\begin{aligned} V(t) \le |I(t)-a\eta +b f(\eta )| [1-e^{-(a-|b|k)t}] +V(0)e^{-(a-|b|k)t} \rightarrow 0, \end{aligned}$$

for large t using condition (ii) on I(t). Hence, in either of the cases, $V= |x-\eta | \rightarrow 0$ follows. The proof is complete. $\square$

We shall extend this for a two layer network. Consider

$$\begin{aligned} \begin{aligned} x'(t)&= -ax(t) + b f(y(t)) +I(t)\\ y'(t)&= -cy(t) + d g(x(t)) + J(t). \end{aligned} \end{aligned}$$

(16)

Assuming that $(\eta ,\delta )$ is the desired output where both $\eta$ and $\delta$ are fixed with respect to t, we arrange (16) as

$$\begin{aligned} \begin{aligned} x'(t)&= -a(x(t)-\eta ) + b [f(y(t))-f(\delta )] \\&\quad + \; I(t)-a\eta +bf(\delta )\\ y'(t)&= -c(y(t)-\delta ) + d [g(x(t))-g(\eta )] \\&\quad + \; J(t)-c\delta + dg(\eta ). \end{aligned} \end{aligned}$$

(17)

Suppose that the response functions satisfy $|g(x)-g(\eta )| \le k|x-\eta |$ and $|f(y)-f(\delta )|\le l|y-\delta |$ for some positive k, l. We have

Theorem 3.4

Assume that the parameters of the system and the response functions satisfy the condition

$$\begin{aligned} 0< \tilde{\beta _1}\equiv \min \left\{ a-|d|k,\, c-|b|l \right\} <\infty . \end{aligned}$$

For an arbitrarily chosen output $(\eta ,\,\delta )$, the solutions of system (16) converge to $(\eta ,\delta )$ provided the inputs satisfy either of the conditions

$$\begin{aligned} (i) \, \int _0^{\infty } [|I(s) -a\eta +bf(\delta ))|+ |J(s)-c\delta +dg(\eta )|] ds < \infty ; \end{aligned}$$

or

$$\begin{aligned} (ii) \; \lim _{t\rightarrow \infty } (I(t),J(t)) = (a\eta -bf(\delta ),\; c\delta -dg(\eta )). \end{aligned}$$

Proof

Let $V(x(t) = |x(t)-\eta | + |y(t)-\delta |$.

Then the upper right derivative of V along the solutions of (16), using (17), we have

$$\begin{aligned} D^+V\le & {} -a|x-\eta | + |b| |f(y)-f(\delta )| + |I(t)-a\eta + bf(\delta )| \\&-c|y-\delta | + |d| |g(x)-g(\eta )| + |J(t)-c\delta + dg(\eta )| \\\le & {} -a|x-\eta | + |b|l |y-\delta | + |I(t)-a\eta + bf(\delta )| \\&-c|y-\delta | + |d|k |x-\eta | + |J(t)-c\delta + dg(\eta )| \\\le & {} - \tilde{\beta _1} V + |I(t)-a\eta + bf(\delta )|+|J(t)-c\delta +dg(\eta )|. \end{aligned}$$

We omit the details of the rest of the proof. The conclusion follows.$\square$

The following example illustrates the effectiveness of this result.

Example 3.5

$$\begin{aligned} x'(t)= & {} -3x(t) + 4 \tanh y(t) + I(t) \\ y'(t)= & {} -5y(t) + 2 \tanh x(t) + J(t). \end{aligned}$$

Now choose $I(t)= (3\eta - 4 \tanh \delta )(1+e^{-t})$ and $J(t) = (5\delta - 2\tanh \eta )(1+\frac{1}{t^2})$.

Fig. 1

Solutions approaching a priori output $(\eta ,\, \delta )= (1,20)$ in Example 3.5. x values range from 0 to 1 and y ranges from 0 to 40

Fig. 2

Solutions of system in Example 3.5 approaching desired output $(\eta ,\, \delta )=(10,11)$

Fig. 3

Real parts of solutions of system in Example 3.5 approaching corresponding real parts of desired values of $(\eta =2+3i,\ \delta =1+2i)$

Fig. 4

Imaginary parts of solutions of system in Example 3.5 approaching respective imaginary parts of desired output $(\eta =2+3i,\ \delta =1+2i)$

Clearly, for given $(\eta , \delta )$, we have all the conditions of Theorem 3.4 are satisfied, and hence, $(x,\, y) \rightarrow (\eta ,\, \delta )$, for sufficiently large t. These conclusions are confirmed by simulations for different sets of $(\eta ,\; \delta )$ that include complex values also. See Figs. 1, 2, 3, 4.

We shall now consider the time delay system,

$$\begin{aligned} \begin{aligned} x'(t)&= -ax(t) + b f(y(t-\tau )) +I(t) \\ y'(t)&= -cy(t) + d g(x(t-\tau )) + J(t). \end{aligned} \end{aligned}$$

(18)

As has been done earlier for a given $(\eta ,\delta )$, we write (18) as

$$\begin{aligned} x'(t)= & {} -a(x(t)-\eta ) + b [f(y(t-\tau ))-f(\delta )] \nonumber \\&+\;I(t)-a\eta +bf(\delta ) \nonumber \\ y'(t)= & {} -c(y(t)-\delta ) + d [g(x(t-\tau ))-g(\eta )] \nonumber \\&+\;J(t)-c\delta + dg(\eta ). \end{aligned}$$

(19)

We have

Theorem 3.6

Assume that the parameters of the system and the response functions satisfy the condition

$$\begin{aligned} 0< \min \left\{ a-|d|k,\, c-|b|l \right\} <\infty . \end{aligned}$$

For an arbitrarily chosen output $(\eta ,\,\delta )$, solutions of system (18) converge to $(\eta ,\delta )$ provided the inputs satisfy the condition $\int _0^{\infty } [|I(s)-a\eta +bf(\delta ))|+ |J(s)-c\delta +dg(\eta )|]ds< \infty$.

Proof

Employing the functional

$$\begin{aligned} V(x(t)= & {} |x(t)-\eta | + |y(t)-\delta | \\&+\;b \int _{t-\tau }^{t} |f(y(s))-f(\delta )| ds \\&+\;d \int _{t-\tau }^{t} |g(x(s))-g(\eta )| ds, \end{aligned}$$

using (19) and proceeding as in Theorem 2.1, the conclusion follows. $\square$

Since the conditions on parameters and input functions Theorems 3.4 and 3.6 are the same, it may imply that delays have no effect on convergence here.

Example 3.7

Consider

$$\begin{aligned} x'(t)= & {} -6x(t)+3 \tanh (y(t-\tau ))+ I(t) \\ y'(t)= & {} -4 y(t)+5 \tanh (x(t)-\tau )+ J(t) \end{aligned}$$

Here we have chosen $I(t)= (6 \eta -3 \tanh (\delta ))(1+e^{-t})$ and $J(t) = (4\delta - 5 \tanh (\eta ))(1+e^{-2t})$.

Fig. 5

Solutions converging to arbitrarily chosen output $(\eta , \; \delta )= (1,20)$ in Example 3.7. Figures taken for delay $\tau =5:$ x values range from 0.85 to 1.1 and y ranges from 0 to 25

Fig. 6

Convergence of solutions to a priori output $(\eta , \; \delta )= (80,-59)$ in Example 3.7, verified at delay length $\tau =20$

Clearly, for given $(\eta , \delta )$, all the conditions of Theorem 3.6 are satisfied, and hence, $(x,\, y) \rightarrow (\eta ,\, \delta )$, for sufficiently large t. As may be seen from Figs. 5 and 6, theoretical predictions are supported by simulations.

Let us extend this result to systems with time-dependent delays. We assume that $\tau =\tau (t)$ where $0\le \tau (t) <t$ is such that $p\le 1-\tau '(t) \le 1$ for some $p>0$. Obviously, $p=1$ for constant delays. We establish

Theorem 3.8

Assume that the parameters of the system and the response functions satisfy the condition

$$\begin{aligned} 0< a-\frac{|d|}{p} \, k<\infty , \quad 0< c-\frac{|b|}{p} \, l <\infty . \end{aligned}$$

For an arbitrarily chosen output $(\eta ,\,\delta )$, solutions of (18) converge to $(\eta ,\delta )$ provided the inputs satisfy the condition $\int _0^{\infty } [|I(s)-a\eta +bf(\delta ))|+ |J(s)-c\delta +dg(\eta )|]ds< \infty$.

Proof

Consider the functional

$$\begin{aligned} V(x(t))= & {} |x(t)-\eta | + |y(t)-\delta | \\&+ \;\frac{|b|}{p} \int _{t-\tau (t)}^{t} |f(y(s))-f(\delta )| ds + \;\frac{|d|}{p} \int _{t-\tau (t)}^{t} |g(x(s))-g(\eta )| ds. \end{aligned}$$

The upper right derivative of V along the solutions of (18) may be given as

$$\begin{aligned} D^+V\le & {} -a|x-\eta | + |b| |f(y(t-\tau (t))-f(\delta )| \\&+ \;|I(t)-a\eta + bf(\delta )| \\&-\;c|y-\delta | + |d| |g(x(t-\tau (t))-g(\eta )| \\&+\; |J(t)-c\delta + dg(\eta )| \\&+\;\frac{|b|}{p} |f(y)-f(\delta )| \\&-\;\frac{|b|}{p} |f(y(t-\tau (t))-f(\delta )| (1-\tau '(t)) \\&+\; \frac{|d|}{p} |g(x)-g(\eta )| \\&-\; \frac{|d|}{p} |g(x(t-\tau (t))-g(\eta )| (1-\tau '(t))\\\le & {} -\left( a-\frac{|d|}{p}\, k\right) |x-\eta | + |I(t)-a\eta + bf(\delta )| \\&-\;\left( c-\frac{|b|}{p}\, l\right) |y-\delta | + |J(t)-c\delta + dg(\eta )|. \end{aligned}$$

We omit the details of the rest of the proof. The conclusion follows as in earlier results. $\square$

Remark 3.9

Now consider the system

$$\begin{aligned} x'(t)= & {} -ax(t) + b f(y(t-\tau )) +I \nonumber \\ y'(t)= & {} -cy(t) + d g(x(t-\tau )) + J, \end{aligned}$$

(20)

where $I= a\eta -bf(\delta ),\; J=c\delta -dg(\eta )$ are constant inputs, given $\eta ,\; \delta$. It is easy to observe that $(\eta ,\; \delta )$ is an equilibrium pattern of (20). Then from Corollary 2.9, we have, solutions of (18) approach $(\eta ,\; \delta )$ when ever the variable inputs of (18) are well near those of (20) as specified in Corollary 2.9.

Thus, our technique is quite logical and clearly supports our contention that instead of following the inputs to find where they are taking the system to, we shall restrict or choose inputs to make the system cater to our requirements.

Simulations

To clearly see what is happening in Examples 3.5 and 3.7, we present some pictorial views. The figures are obtained by simulating equations using ODE23/DDE23 of MATLAB.

Example 3.5 is simulated for different sets of a priori outputs $(\eta ,\; \delta )$. We present here resultant figures for two different cases.

Firstly, we have chosen $(\eta ,\; \delta ) = (1,20)$. In this case solutions $(x,\; y)$ of system considered in Example 3.5 approached this output. Figure 1 depicts this.

We have simulated Example 3.5 again for output values $(\eta ,\; \delta ) = (10,\; 11)$. The convergence of solutions to this output may be observed from Fig. 2. We have chosen different scales for x and y axes to obtain a clear view of the behavior of x and y on the same graph.

Finally we have chosen complex values to outputs, namely, $(\eta ,\; \delta ) = (2+3i,\; 1+2i)$ and estimated corresponding inputs as given by the example. Interestingly, the system with all parameters set as real values produced desired output, of course, with a complex valued input. This signifies the correlation between input and output. Figures are drawn separately for real and imaginary parts here. Thus, simulations agree with the conclusions of Theorem 3.4 established for system (16).

To observe the behavior of solutions under the influence of time delay and to verify Theorem 3.6, we have simulated Example 3.7 for different values of $\eta$, $\delta$ and $\tau$. A couple of such simulation results are presented here. Figure 5 depicts how the solutions of the system in Example 3.7 approach the a priori chosen output $(\eta ,\; \delta ) = (1,\; 20)$ at time delay value $\tau = 5$. For another set of values of $(\eta ,\; \delta )= (80,\; -59)$, chosen for delay $\tau = 20$, Fig. 6 clearly show that the solutions approach the desired output as established by Theorem 3.6 for the time delay system (18). Though Theorem 3.6 says that delays have no influence on convergence, we have simulated for different lengths of delay for confirmation of theory. The present figures remained the same for any choice of delay though we specified delay $\tau$ in these.

Remark 3.10

Recent studies of dynamical systems are centered around existence, uniqueness of solutions including equilibrium states and their stability. One of the main aspects of present study - generation of inputs based on pre-specified output- is always backed by several real world phenomena, beginning with recognizing the face of a bench mate, discussed in Section 1, this focus is a welcoming new addition to the literature. The mathematical results presented are entirely new even for those who are working on qualitative theory of ordinary differential equations or delay differential equations.

Discussion

The study in this paper may be divided into two parts. In the first part, we started with a network which is obtained by introducing variable inputs in place of constant inputs in a Hopfield neural network. We studied the asymptotic behavior of the solutions, obtained conditions for their boundedness so that all the solutions of the system may approach a bounded solution and hence, the system is well behaved. The asymptotic nearness of the solutions is established by different ways namely, by employing the techniques of Lyapunov functionals, matrix inequalities, exponential convergence. Results include delay independent as well as delay dependent ones. We made no comparison of results but provided different paths for same conclusion. Global stability conditions automatically establish the uniqueness of equilibrium. Hence, they do not apply to systems offering multiple equilibria. For a complex, multi-processing system like a human brain global stability limits its thought process. Local asymptotic stability results do not require the equilibrium to be unique thus, allowing the parallel processing of multiple tasks. Our study here establishes conditions under which a system may tolerate external disturbances, fluctuations or variations in inputs. Since system with variable inputs evolves from system with constant inputs, we studied how the solutions of modified system are woven around the solutions of original system. Sufficient conditions are established in this direction.

In the second part, we concentrated on approaching a given output by (i) restricting the inputs suitably (Theorem 3.1) and (ii) by selecting the inputs basing on the output given appropriately (Theorem 3.3 etc.). Can we now recognize the face of our bench mate (x) basing on his features to day ($\eta$) by providing the inputs $I(\eta )$ ? Hopefully so, using any of the results Theorems 3.3–3.8.

We do not restrict the nature of the parameters whether real or complex and input functions may be chosen from $L^p$ spaces as we recorded at the end of Theorem 2.1. One surprising but interesting observation is the unifying condition $\int _0^{\infty } I(s) ds < \infty$ required by almost all the results in this paper. Right from asymptotic equivalence of Theorem 2.1–Theorem 3.6—for convergence to desired output, all the results essentially require this condition on inputs irrespective of the conditions on the parameters.

Concluding Remarks and Open Problems

Though we started and concluded with recognition of a bench-mate, there are questions that are haunting us for long years. As far as neural networks are concerned, we have to be content with what ever output we get for a given input. The transition from input to output in neural networks is like a black box. Whether the resultant output corresponding to a given input is the one we are actually looking for or it is the one generated by network on its own- is very difficult to find. At this stage, Theorem 3.1 says that the system offers a unique solution that approaches the given output, as long as our inputs are within the bounds prescribed. Further restrictions on the inputs (Theorem 3.3 etc.) force all the solutions of the system approach the desired output. This clearly ensures that the input and output are well correlated. A natural, instinctive selection of inputs is from a space related to the region of outputs indeed!

Best example for input-output correlated systems is a human brain. It receives information (input) regarding outputs such as faces, objects, incidents etc. from the environment (external source) which is then processed as thoughts. Memories or previous experiences are recorded as so called equilibrium states. A thought process may converge to an existing, stored equilibrium state or it may be recorded as a new memory or experience. How best the information is encoded in the input as received from sense organs about the output tells upon the convergence to such a memory state. Of course, this is within the scope of functional relations and parameters of the system as the inputs chosen depend on them also. Since, spiking neural networks behave as biological neurons, this concept of input-output relation will be interesting thing to study for these networks.

It would also be interesting to see how these results work for other networks such as recurrent neural networks, cellular neural networks, multi layer networks and similar structures. Also, the study of influence of inputs which are impulsive in nature (such as sudden sweeping thoughts in brain or sudden voltage fluctuations in a network) is another interesting area for researchers. This we leave for our future endeavor.

Since image processing, classification and regression are important applications of neural networks, we hope the present article would enthuse the researchers to try appropriate modifications of this technique for such discrete data cases. Further, we strongly feel that concept presented here is useful during training of networks. It could be of help in testing whether the weights chosen to train the network are appropriate or not once the input and output are pre-determined.

One may feel that the paper is full of mathematical content. But at the end, our approach establishes a clear relation between inputs and outputs and a technique to estimate inputs based on pre-defined values of output that makes the system approach this output. The efficiency of the technique is well supported by numerical examples and simulations. We strongly feel that this ready to use technique should reach working engineers, field experts and application oriented people for a case by case study of neural network systems for obtaining desired results, though mathematicians may be ready to enjoy these new additions to the literature.