1 Introduction

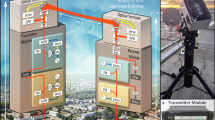
Free-space optical communication is an attractive technology for high performance data transfer applications such as ground-to-satellites (or satellite-to-ground) links. In comparison with conventionally used radio frequencies, optical links are of particular interest in terms of available bandwidth, data rate, power consumption, data transfer security, mass and volume [1]. Despite its great potential, some challenging aspects need to be addressed to exploit this promising technology. Indeed, optical communications suffer multiple distortions when crossing the atmosphere. One of the most noticeable impairments is caused by the fact that the atmosphere is continuously and randomly deviating the beam of light from its original direction, so called "beam wander” effect. These distortions not only impact the Bit Error Ratio (BER) but can even make the link unfeasible [2]. This phenomenon is even more critical for optical uplinks since the atmospheric turbulence happens close to the Earth\('\)s surface, where small angular deviations can lead to large pointing errors (beam displacement up to several hundred meters). To face this issue, the beam divergence can be increased by reducing the transmitter aperture. This approach, however, involves power losses. This is depicted on Fig. 1a.

Fig. 1
figure 1

a The uplink beam is deviated from its initial line of sight because of the atmospheric turbulence. A small beam diameter is used so as to increase the beam divergence (due to diffraction). This makes it possible to reach the satellite (at the expense of power losses). b A larger transmitter diameter is used and the orientation of the beam is controlled in such a way that the atmospheric turbulence is pre-compensated. This does not involve divergence power losses but requires a reference signal (in this case, the signal from the satellite)

Full size image

An alternative lies in controlling the orientation of the uplink signal in real time (i.e deviating the beam from its original direction), so as to (pre-)compensate the atmospheric turbulence. This is shown in Fig. 1b. In this case, the beam divergence does not need to be increased which reduces the power losses. This is challenging because (i) the turbulence has to be determined in the direction where the satellite will be at the time of the transmission (i.e the actual position angularly shifted by the point-ahead angle of the satellite) and (ii) the pre-compensation must be performed as fast as possible (typically at a frame rate of several hundreds Hertz). Two main approaches can be considered to determine the compensation to be applied to the uplink beam. The first one consists in using Laser Guide Star (LGS) based Adaptive Optics: a powerful laser is pointed in the direction one wants to estimate the turbulence, and is back reflected to Earth because of its interaction with the Sodium atoms in the mesosphere (at an altitude of \(\approx 90\) km). This produces a shining spot (artificial star) in the sky that can be used as a reference for the turbulence compensation [3]. This requires complex architecture and equipment but would make it possible to determine the turbulence in any direction, whatever the point ahead angle of the satellite. Conversely, in some cases, when the point-ahead angle of the satellite is small enough (this notion will be clarified in the next), the downlink signal of the satellite itself can be used as a reference for the pre-compensation. In this case, the efficacy of the pre-compensation will depend on the correlation between the downlink and the uplink signal. The later approach (i.e using the signal from the satellite) is that addressed in the present paper. In the aim of evaluating the degree of correlation between both line of sight (downlink and uplink), we propose to investigate the Tip/Tilt correlation between signals received from two independent stars featuring an angular separation similar to typical point-ahead angles of satellites (i.e about 4 arcsec for GEO satellites and 10 arcsec for LEO satellites). In other words, the differential Tip/Tilt motion between the double stars is used as an estimator of the typical decorrelation between the downlink and the uplink signals. This, in turn, makes it possible to evaluate the efficacy of the pre-compensation based on the downlink signal. In this framework, a test campaign was carried out in May 2018, at ESA\('\)s Optical Ground Station (located in Izaña, Tenerife) to perform measurements of double stars for different optical link scenarios (i.e for various angular separations and at several elevations as shown in Fig. 2). Note that we focus here on the compensation of the low-order modes (i.e Tip/Tilt modes) because their contribution account for \(\approx \) 85% of the total wavefront error. A similar study has been conducted in [4]; the authors estimated the correlation between the downlink path of a natural guide star (NGS) and a LGS, with respect to their angular separation. As opposed to them, in the present paper, the measurements were performed using natural stars only and compared to theoretical models. The paper also shows how the measurements were used to evaluate the jitter of the telescope and to help dimensioning a ground-based transmitter in case a pre-compensation is applied.

The paper is organized as follows: “Theoretical background” gives a brief theoretical introduction, “Measurement setup and acquisition parameters” describes the experimental setup, “Tilt error due to anisoplanatism” introduces the algorithm used to calculate the centroids of the double stars and compares the experimental results to the numerical models, “Jitter of the optical ground station” evaluates the jitter of the OGS and, finally, “Dimensioning of the ground-based transmitter aperture” assesses the impact of applying a tip-tilt pre-compensation to the uplink signal in case it is based on the received satellite signal.

Fig. 2
figure 2

Schematic drawing of the tests performed at ESA’s Optical Ground Station. Top: The Tip/Tilt correlations are measured for various elevations along the night, keeping the same targets. Bottom: Conversely, the elevation is kept constant and the target is changed, to evaluate the evolution of the correlation with respect to the angular separation

Full size image

2 Theoretical background

2.1 Atmospheric turbulence profiles

For a given site and at a particular time, the atmospheric turbulence is described by the so-called refractive-index structure, \(C_n^2 (h)\), which characterize the strength of the turbulence with respect to the altitude, h. Several models have been proposed to describe the behaviour of the atmosphere. Among them, the Hufnagel-Valley profile variations (HV) are commonly used [5]. Two profiles are considered in the next:

2.1.1 The Modified Hufnagel-Valley profile

The so-called Modified Hufnagel-Valley profile (MHV) is adapted to take into account the Optical Ground Station (OGS) altitude, \(H_{OGS}=2393\) m, and is given by [6]:

$$\begin{aligned}&C_n^2 (h)=0.00594 \ (\frac{v}{27})^2 \ (10^{-5} h)^{10} \ e^{-h/1000} + 2.7\times 10^{-16} \nonumber \\&\quad e^{-h/1500} A_0 e^{-H_{OGS}/700} e^{-(h-H_{OGS})/100} \end{aligned}$$
(1)

where v stands for the RMS cross wind velocity, and \(A_0\) is a reference sea-level turbulence value for scaling according to day- and night-time. In this paper, these parameters have been set to \(A_0=1.7 \times 10^{-14} m^{-2/3}\) and v = 21 m/s as suggested in [6] for the OGS. This model is defined for \(h < H_{OGS}\).

2.1.2 The Izaña Night-time Model

The results obtained with the MHV model will be compared to those obtained with the empirical Izaña Night-time Model (INM) [7]:

$$\begin{aligned} C_{n}^2(h)= {\left\{ \begin{array}{ll} C_{n0}^2 \left( \frac{h}{h_s}\right) ^{-2/3} \qquad \qquad h\le h_s\\ C_{n0}^2 \qquad \qquad h_i<h<h_s \\ C_n^2 exp\left( \frac{h_i}{h_r}\right) exp\left( \frac{-h}{h_r}\right) +C_{nl}^2 exp\left( \frac{-h}{h_l}\right) \\ +C_{nl}^2 3W^2\left( \frac{h}{h_t}\right) ^{10}exp\left( \frac{-10h}{h_t}\right) \qquad h \ge h_i \end{array}\right. } \end{aligned}$$
(2)

where h is the height above the terrain, \(h_s\) is the surface layer height (typically of a few meters), \(h_0\) is a reference height, greater or equal than \(h_s\), at which the value \(C_{n0}^2\), characterizing the structure constant in the zone with \(h^{-4/3}\) dependence, is found, \(h_r\) is the height marking the fall-off of the \(h^{-4/3}\) dependence (typically in the hundreds of meters); \(C_{nl}^2\) is the structure-constant characteristic value for free atmosphere; \(h_l\) is the height characterizing the exponential fall-off of the structure constant in the free-atmosphere region (typically a few thousands of meters); W is the root-mean-squared wind velocity averaged over the 5 to 20 km altitude interval, and \(h_t\) is the tropopause height. The values of these parameters are summarized in Table 1 as per [7].

Table 1 Values of the parameters for the Izaña Night-time Model
Full size table

It is worthwhile to point out that such empirical models can be useful to predict the order of magnitude of the expected turbulence or its trend when varying some parameters (e.g the elevations) but may be rather inaccurate because they do not account for instantaneous meteorological conditions, local topographic characteristics nor seasonal influences.

2.2 Isokinetic angle, tilt coherence time and beam wandering

With the foregoing definitions, the isoplanatic angle can be evaluated with [8, 9]:

$$\begin{aligned} \theta _0 = [2.91 \ (\frac{2\pi }{\lambda })^2 \ \sec (\gamma )^{8/3} \int C_n^2 (h) h^{5/3} dh]^{-3/5}, \end{aligned}$$
(3)

where \(\gamma \) is the zenith angle and \(\lambda \) is the operating wavelength.

The isoplanatic angle accounts for the whole distortion of the wavefront (low and high order modes). In order to decouple the contribution stemming from the tip-tilt modes (i.e those related to the beam wander effect), the tilt-isoplanatic angle or the isokinetic angle, is defined as the angle between two sources, at which one of them jitters with a magnitude of half of its diffraction-limited divergence, with respect to the other one. For \(\theta <D/40000\), the following approximation applies [10]:

$$\begin{aligned} \theta _{TA} = \frac{0.184 \ \lambda \ D^{1/6}}{[\sec (\gamma )^{3} \int C_n^2 (h) h^{2} dh]^{1/2}}, \end{aligned}$$
(4)

where D is the receiver diameter. As an example, the isokinetic angle is \(\approx 3.5 ''\) and \(\approx 4.5 ''\) for receiver diameters of respectively \(D=0.2\) m and \(D=1\) m (like the OGS and its guider telescope), at an elevation of \(36^{\circ }\) (typical elevation of EDRS or Alphasat satellites), at \(\lambda =1064\) nm. This value is close to the point-ahead angle of GEO satellites (\(\approx 4 ''\)). The relationship between the isokinetic angle and the point-ahead angle is of prime importance for optical communications: the larger the isokinetic angle, the higher the correlation between the downlink and the uplink signal and the more efficient the pre-compensation will be. Note that the low-order modes have effectively larger isoplanatic angle and correlation time than higher modes.

The tilt coherence time of the atmosphere is given by [11]:

$$\begin{aligned} \tau _{0} =12.33 \left( \frac{D}{r_0}\right) ^{1/6}\left( \frac{r_0}{v}\right) , \end{aligned}$$
(5)

where v is the wind speed transversal to the propagation of the laser beam and \(r_0\) is the Fried parameter given by [8, 9]:

$$\begin{aligned} r_0 = 0.185 \ \lambda ^{6/5} [\sec (\gamma ) \int C_n^2 (h) dh ]^{-3/5}, \end{aligned}$$
(6)

For the 1m-diameter OGS telescope and its 20cm-guider telescope, the tilt coherence time is respectively \(\approx 40\) ms and \(\approx 50\) ms for \(r_0=5\) cm and a wind speed of 21 m/s. To be efficient, the pre-compensation, must be applied as fast as possible, well below the tilt coherence time.

The RMS beam wander displacement experienced by an uplink beam is [12]:

$$\begin{aligned} \sigma _{BW}^2 \approx 0.54 \ (H-h_0)^2 \sec ^2(\gamma ) \left( \frac{\lambda }{2W_0}\right) ^2 \ \left( \frac{2W_0}{r_0}\right) ^{5/3}, \end{aligned}$$
(7)

where \(W_0\), H and \(h_0\) are respectively, the beam radius, the altitude of the satellite and of that of the transmitter. Since \(r_0\) is proportional to \(\lambda ^{6/5}\), \(\sigma _{BW}\) is constant regardless of the wavelength. Note, however, that because of the chromaticity dependency of the refraction law, the instantaneous beam wander does depend on the wavelength. One also notes, that large transmitters undergo a smaller beam wander than small aperture transmitters. However, since the divergence of the beam follows \(\propto \frac{1}{D}\), large beam transmitters are actually much more impacted by beam wander.

Finally, we remind here that the challenge lies in increasing the diameter of the beam (to avoid power losses) while actively pre-compensating the beam wander induced by the atmospheric turbulence.

2.3 One-axis RMS tilt anisoplanatism

As per the Taylor’s frozen-atmosphere model, commonly used to model atmospheric trubulences, the uncompensated atmosphere introduces a one-axis rms tilt error, given by the following equation [13]:

$$\begin{aligned} \sigma _{tilt}=0.427 \ \frac{\lambda }{D}\left( \frac{D}{r_0}\right) ^{5/6} \end{aligned}$$
(8)

Note the analogy with Eq. (7)

If the wavefront tilt measured in a given line of sight is used to estimate the tilt in another direction, then the one-axis rms tilt error that is due to anisoplanatism is given by [14, 15]:

$$\begin{aligned} {\left\{ \begin{array}{ll} \sigma _{TA;x} = \{2[1-C_x(\theta )]\}^{1/2}\sigma _{tilt} \\ \sigma _{TA;y} = \{2[1-C_y(\theta )]\}^{1/2}\sigma _{tilt} \end{array}\right. } \end{aligned}$$
(9)

where \(C_x(\theta )\) and \(C_y(\theta )\) are the correlations of the tilts at two points that are separated by an angular distance \(\theta \). The x axis is parallel to the line joining the two stars, whereas the y axis is perpendicular to this line and characterize the transverse relative motion. Squaring \(\sigma _{TA;x}\) and \(\sigma _{TA;y}\) and averaging gives a useful single measure of the one-axis rms tilt error that is due to tilt anisoplanatism:

$$\begin{aligned} \sigma _{TA}=[2-C_x(\theta )-C_y(\theta )]^{1/2}\sigma _{tilt} \end{aligned}$$
(10)

The correlation functions are given by:

$$\begin{aligned} C_{x,y}(\theta )=\frac{\int _{0}^{\infty }[A_0(s)\mp A_2(s)] C_n^2(h)dh}{\int _{0}^{\infty }C_n^2(h)dh}, \end{aligned}$$
(11)

with:

$$\begin{aligned} A_{0,2}(s)=\int _{0}^{\infty }[J_2(u)]^2 J_{0,2}(2su) u^{-14/3}du \end{aligned}$$
(12)

and

$$\begin{aligned} s=\frac{h\sec (\gamma ) \theta }{D} \end{aligned}$$
(13)

where the x and y indices in \(C_{x,y}(\theta )\) respectively refer to - and + sign in the integral. Numerical approximations of \(A_{0,2}(s)\), with less than 0.2% error, can be calculated by the following:

$$\begin{aligned} A_{0}(s)= & {} {\left\{ \begin{array}{ll} exp(-0.5866 \ s^{1.759}) &{} for \ 0\le s \le 0.55 \\ 0.6656\ s^{-1/3} \ [1+1/(6^3s^2)]&{} for \ s > 0.55 \end{array}\right. } \end{aligned}$$
(14)
$$\begin{aligned} A_{2}(s)= & {} {\left\{ \begin{array}{ll} exp(-1.941 \ s^{-0.4602}) &{} for \ 0\le s \le 0.625 \\ 0.1331\ s^{-1/3} \ [1-1/(6s^2)]&{} for \ s > 0.625 \end{array}\right. } \end{aligned}$$
(15)

Combining Eq. (1) or Eqs. (2, 6), and Eqs. (8–15) one can estimate the rms tilt error that is due to tilt anisoplanatism with respect to the elevation and the angular separation between two line of sight. A few points are worthy of comment. The foregoing equations are based on Kolmogorov’s theory which does not take into account the non-zero inner-scale and the finite outer scale of the atmosphere; a more general approach can be found in [16]. It is also worth mentioning the distinction between the Zernike tilt (i.e that applied to a mirror) and that measured by a centroid sensor, which is closely approximated by a gradient tilt. Strictly speaking, the present formalism applies to the Zernike tilt. However, because the two types of tilt have very similar standard deviations (\(\approx 3.5\%\) discrepancy), we choose to analyze the off-axis error in estimating the Zernike tilt as done in [17]. “Tilt error due to anisoplanatism” confronts the experimental results to the numerical predictions obtained with the model presented in this section. Before that, the following section describes the test campaign setup and the algorithm used to extract the relevant information.

3 Measurement setup and acquisition parameters

The test campaign was carried out in May 2018 at ESA’s Optical Ground Station located at the "Observatorio del teide” in Tenerife. Two telescopes were used: the 1m-diameter Ritchey-Chrétien telescope and its 20 cm-diameter guider telescope. An Andor Ixon EMCCD camera, fixed at the Cassegrain focus, was used for the measurements.

Table 2 Main parameters of the 1 m and 20cm-diameter telescopes used for the measurements
Full size table
Table 3 Main parameters of the camera used for the measurements
Full size table

In the framework of this test campaign, only double stars with the following characteristics were considered for measurements: (i) a magnitude smaller than 8 (ideally 6), (ii) a magnitude difference smaller than 3 (ideally 2) and (iii) an angular separation between 4 and 60 arcseconds. Two optical filters were used in front of the camera, one low-pass filter and one high pass-filter, to limit the optical spectrum to a range between 550nm and 650nm. Given the focal length of the main and the guider telescope, respectively 13.3 meters and 3 meters, and the pixel size of the Andor camera, 8 × 8 \(\mu m^2\), the plate scale corresponds to, 0.124 arcsec/pixel and 0.55 arcsec/pixel respectively. Each double star measurement consisted of a sequence of 10,000 short exposures frames. The integration time was set between 3 ms and 6 ms per frame depending on the star magnitude, which is well below typical tip-tilt coherence time defined in “Theoretical background” and long enough to reach an acceptable SNR. Therefore, the acquisition time of each 10 000-frames sequence lies between 30 and 60 s. Before post-processing the data, a visual inspection of each sequence was performed individually in order to discard the sequences that were not relevant or too noisy. Most of the measurements were performed several times within a short time interval (i.e several minutes). This allows to check the repeatability of the measurement as well as the accuracy of the centroiding algorithm. It also gives an indication of the atmosphere’s stability. The measurements were performed between 00h 00 and 6h am, from the 26th to 29th of May 2018. The main parameters of the telescopes and of the camera are summarized respectively in Tables 2 and 3. Details about the double stars analyzed in this paper are given in Appendix.

4 Tilt error due to anisoplanatism

This section first briefly describes the centroiding method that was used to process the data. Then, the experimental results are presented and compared to the numerical predictions.

4.1 Centroiding method

The stars were identified on each frame (and for each sequence) by applying an intensity threshold, so as to turn the gray-scale images into binary images (i.e a mask) and reject the sky background. The mask was then applied on the initial frame as shown on Fig. 3.

Fig. 3
figure 3

a The initial frame, b after thresholding, the gray-scale image is turned into a binary image, c result of the multiplication of (a) with (b)

Full size image

Particular care must be taken when choosing the threshold as an inadequate value may lead to a wrong result. Under-estimating the threshold will generally not reject most of the background of the frame, whereas over-estimating the threshold may lead to an unphysical segmentation of a star in a number of independent areas. These scenarios are illustrated hereafter. Figure 4a presents the initial frame; Fig. 4b shows the outcome of the algorithm when (too) low thresholds are applied to the initial frame. One observe that the algorithm cannot find the stars, and the result is strongly impacted by a very small change of the threshold value, which is not acceptable. Figure 4c shows a proper choice of the threshold value, the stars are well identified. Finally, Fig. 4d presents a case where, one of the star is truncated because of the too large threshold. Once the stars are identified, their relative distance (and motion) on the detector is estimated through an intensity-weighted centroid algorithm. Note that the double star relative motion is inherently insensitive to the jitter of the telescope due to the differential method used.

Fig. 4
figure 4

a Initial frame; b two different thresholds are applied: 970 and 975. The red crosses show the four centroids identified by the algorithm (one per star and per threshold). Note that two red crosses are superimposed which explains why one sees only three red crosses. For one star, the algorithm gives a very different result passing from a threshold of 970 to 975; for the second star, the algorithm output is constant but wrong: the threshold is too low. c the algorithm converges, it identifies correctly the stars; d the threshold is too high, one star is over-segmented

Full size image

From the foregoing discussion, follows that the estimation of the CoG depends on the applied threshold. However, In order to have reliable conclusions, the results should be independent of the threshold value. In fact, it has been observed that between those extreme "threshold-forbidden” regions, one can find a stable region where the standard deviation is constant, regardless the applied threshold. As an example, Fig. 5 shows the evolution of the standard deviation with respect to the threshold value, for a given sequence. One can clearly identify the region where the position of the centroid is impacted by the noise of the frame (the left part of the plot) as well as the region associated with the over-segmentation of the stars, which results in a divergence of the standard deviation. A stable region which does not depend on the threshold, is found between these two extremities. Note that in some cases (\(\approx 2\%\)), no convergence has been found, in which case the sequence has been discarded. The method has been found very robust with regard to the number of frames considered in the sample (keeping only 10% of them gives a very good approximation, i.e \(>90\%\) accuracy, of the standard deviation determined over the entire sequence). A curve similar to that presented on Fig. 5 was generated for each sequence, making it possible to determine the threshold that is required as an input for the centroiding algorithm.

Fig. 5
figure 5

Relative motion standard deviation as a function of the threshold. The algorithm converges once the threshold is higher than the background. A stable region is found between 1200 and 1900. If the threshold is too high, the algorithm may diverge

Full size image

4.2 Experimental results vs numerical predictions

Figure 6a and b present the results obtained with the 1m-diameter telescope, whereas Fig. 6c and d show the results acquired with the 20cm-guider telescope. The differential Tip/Tilt is shown with respect to the elevation (Fig. 6a and c), and for several double stars angular separations (Fig. 6b and d). Set of double stars featuring close characteristics (close angular separations or close elevations) were presented on the same plot. The results obtained with both atmospheric profiles (i.e the Modified Hufnagel-Valley model and the Izaña night-time model) are shown. Two curves per profile are used to indicate the angular separation (or elevation) range used for the simulation parameters. One observe that, despite the simplicity of the models, the experimental results are in rather good agreement with the numerical predictions for both telescopes, in terms of order of magnitude and trend. As predicted numerically, the 20 cm-diameter telescope is more sensitive to differential tilt than the 1 m-diameter telescope (the values range respectively from 0.05 to 0.15 arcsec with the 1m telescope and from 0.15 to 0.4 arcsec for the 20cm telescope). Note some (sudden) discrepancies between the model and the experimental results (e.g Fig. 6d at an angular separation of \(\approx 15''\)). This might be due to instantaneous degradation of the meteorological conditions (e.g gust of wind).

Fig. 6
figure 6

Comparison between the numerical simulations and the experimental results obtained with the 1 m OGS telescope and the 20 cm guider telescope. Both the MHV and the INM atmospheric profiles are presented (respectively in blue full lines and red dashed lines). Two curves per model are used to indicate the elevation or angular separation range of the simulations. The evolution of the rms error due to tilt anisoplanatism is shown as a function of the elevation and angular separation. a The angular separation between the double stars range between \(5.42''\) and \(6.848''\). b The elevations range between \(30^{\circ }\) and \(35^{\circ }\). c The angular separations ranges between \(4.69''\) and \(6.848''\). d The elevations range between \(30^{\circ }\) and \(40^{\circ }\). The measurements were performed between 00h 00 and 6 am. More details about the stars are given in Appendix

Full size image

5 Jitter of the optical ground station

Besides the turbulence-induced beam wander discussed in the previous section, another issue of concern arises from the jitter that may be experienced by the uplink beam, as a result of the vibrations of the ground station. These pointing errors can stem from the flexible motion (or rigid-body motion) of the telescope structure excited by the wind, from residual vibrations after the tracking of a target, from vibrations of machines fixed on the telescope, etc. This section shows how the jitter of the telescope can be estimated using two stars separated by an angle large enough to be considered as statistically independent. For the sake of simplicity, one consider only the jitter in one direction, x axis, but, obviously, the same reasoning holds for the y axis.

One first notes that the variance of the centre of gravity of the double stars system, \(Var(CoG_x)\), has two independent contributions: one arising from the jitter of the telescope, \(Var(CoG_x)\mid _{seeing=0}\), and one from the seeing, \(Var(CoG_x)\mid _{J_x=0}\) :

$$\begin{aligned} Var(CoG_x)=Var(CoG_x)\mid _{seeing=0} + Var(CoG_x)\mid _{J_x=0} \end{aligned}$$
(16)

JITTER= 0 AND SEEING \(\ne \) 0

$$\begin{aligned} Var(CoG_x)\mid _{J_x=0}= & {} Var(\frac{x_1+x_2}{2})\nonumber \\= & {} \frac{1}{4} [Var(x_1 )+Var(x_2)]\nonumber \\ {}= & {} \frac{1}{4} [Var(x_1-x_2)]\nonumber \\ {}= & {} \frac{1}{4} [Var(\Delta \ x)] \end{aligned}$$
(17)

where \(x_1\) and \(x_2\) stand for the absolute coordinate of star 1 and 2 with respect to a given coordinate system.

JITTER \(\ne \) 0 AND SEEING = 0

$$\begin{aligned} Var(CoG_x)\mid _{seeing=0} \equiv Var(J_x). \end{aligned}$$
(18)

One directly deduces the jitter of the telescope:

$$\begin{aligned} Var(J_x)=Var(CoG_x) - \frac{1}{4} [Var(\Delta \ x)], \end{aligned}$$
(19)

The measurements were performed a first time around 2h 00 am, and a second time around 4h 00 am on the 29th of May. The results are given in Table 4. One can see that the jitter is larger at 2h00 am. This can be due to a change of the wind velocity, or to a variation of the jitter with respect to the position of the telescope. In both cases, the results confirm the excellent pointing and tracking stability performances of the ESA’s OGS telescope, i.e., <0.5 arcsec.

Table 4 Estimation of the jitter of the OGS, based on measurements performed on the 29th of May 2018
Full size table

6 Dimensioning of the ground-based transmitter aperture

One now numerically estimates the maximum ground-based transmitter diameter that one can afford when a downlink signal based pre-compensation is applied. In the following, it is assumed that the effective transmitter aperture is not limited by the atmosphere (i.e., Fried parameter \(>>\) transmitter aperture diameter). However, in reality, the uplink beam divergence is constraint by the minimum of the ground-based transmitter aperture diameter and the Fried parameter. The pointing direction of the uplink beam is calculated based on the direction of the downlink signal and the point-ahead angle of the satellite. Note that the pointing loss due to the tilt anisoplanatism error, \(\sigma _{TA}\), is an inherent source of miss-pointing (i.e., it cannot be corrected by tip-tilt pre-compensation), and effectively introduces a loss, which depends on the divergence angle of the ground-based transmitter aperture as follows:

$$\begin{aligned} G=10 \ log_{10}{e^{-8\left( \frac{\sigma _{TA}}{\theta _{div}}\right) ^2}}=-80 \left( \frac{\sigma _{TA}}{\theta _{div}}\right) ^2 log_{10}{e}, \end{aligned}$$
(20)

where \(\theta _{div}=\frac{4\lambda }{\pi D}\) is the divergence of the beam. Note the sensitivity of the pointing loss with respect to the pointing error (\(\sigma _{TA}\) or \(\sigma _{BW}\)). Two scenarios are analysed: (i) GEO satellite case and (ii) LEO satellite case, both at 1064nm and 1550nm wavelengths. The point-ahead angle is typically \(\approx \) 4 arcsec (respectively \(\approx \)10 arcsec) for the GEO scenario (respectively LEO scenario). The rms tilt error due to anisoplanatism is estimated using both the MHV as well as INM atmospheric profiles, and considering three times the RMS error obtained with the numerical model (i.e \(3\ \sigma _{TA}\) in Eq. (20)). Figure 7 shows the pointing loss for various elevations (between \(30^{\circ }\) and \(60^{\circ }\)) for GEO and LEO satellites and a wavelength of \(\lambda =1064\)nm. The dashed line at − 3dB shows the maximal diameter that one can afford, accepting a pointing loss of 3dB. Note that substituing Eq. (8) and the definition of the divergence in Eq. (20), it follows that:

$$\begin{aligned} G \propto \left( \frac{1}{\lambda }\right) ^2. \end{aligned}$$
(21)

Therefore, from the curves shown at 1064 nm on Fig. 7, one can directly deduce the loss at any other wavelength. For the sake of simplicity the maximal diameter can also be deduced keeping the same curves and releasing the − 3dB constraint to − 6.4dB (for 1550 nm) as shown on the Figure. Similarly, other curves for \(1\sigma \), \(6\sigma \) can easily be deduced from Fig. 7 since \(G\propto \sigma _{TA}^2\). Finally, based on these results, Fig. 8 summarizes the largest diameter that one can afford accepting a loss of − 3dB, for LEO and GEO satellites, at 1064 nm as well as 1550 nm, with and without pre-compensation, as a function of the elevation. One sees that (i) the benefit of pre-compensating increases with the elevation, (ii) the curves without pre-compensation are flatter than those with pre-compensation, (iii) the efficacy of the pre-compensation is better for larger wavelengths because of the larger isokinetic angle (see Eq. (4)), and the sensitivity of the pointing loss as \(\frac{1}{\lambda ^2}\). Finally, note that for low elevations, or in case of strong turbulence, the pre-compensation can be of negative impact because of the lack of correlation between downlink and uplink signals.

Fig. 7
figure 7

Pointing loss due to tilt anisoplanatism as a function of the transmitter diameter, for GEO (full lines) and LEO satellites (dashed lines) and at elevations between \(30^{\circ }\) and \(60^{\circ }\). The curves are shown for 1064 nm and \(3\sigma _{TA}\). a and b were respectively obtained with the MHV and INM profiles. Note the discontinuity of some curves. This is due to the definition of Eqs. (14, 15)

Full size image
Fig. 8
figure 8

Maximal diameter that one can afford with and withour pre-compensation, as a function of the elevation, for GEO and LEO satellites, at 1064 and 1550 nm. a and b were respectively obtained with the MHV and INM profiles

Full size image

7 Conclusion

This paper reports on the results obtained further to a test campaign carried out at ESA’s Optical Ground Station (OGS) in May 2018. Double stars measurements were performed for different angular separations (ranging from \(4.5''\) to \(62''\)) and at various elevations (from \(10^{\circ }\) to \(80^{\circ }\)). The goal was to evaluate the impact of tilt-anisoplanatism error on an optical uplink pre-compensation when the downlink signal received from the satellite is used as a reference. First, a method aiming at extracting the double stars relative motion (differential tip-tilt) is described. Then, the experimental results are compared to the numerical simulations. Two atmospheric profiles were used, a Modified Hufnagel-Valley profile adapted for Tenerife as well as the Izaña Night-time profile. Measurements obtained with two telescopes were analyzed (the 1m-diameter OGS and the 20cm guider telescope). It turned out that the experimental results are in good agreement with the numerical predictions. More specifically, the order of magnitude of the experimental values is fully consistent with that obtained with the theoretical model and the trend is also rather well modelled as shown in Fig. 6 (specifically as a function of the elevation). It was then shown how to evaluate the jitter of the OGS, based on double stars far enough to be considered as independent (\(62''\)). The results confirm exceptional pointing and tracking stability performances of the OGS \(<0.5''\) rms. Finally, and based on the previous results, numerical predictions are presented to help dimensioning a ground based transmiter intended to be used for uplink pre-compensation based on the signal received from the satellite. The analysis were performed for LEO and GEO satellites at 1064 and 1550 nm. The results are presented on Fig. 8, considering an acceptable pointing loss of − 3dB and three times the typical RMS error due to tilt anisoplanatism. As an example, for typical elevations of EDRS or Alphasat GEO satellites (\(\approx 36^{\circ }\)), the numerical simulations indicate that tilt pre-compensation can be successfully applied to the uplink beam for transmitters diameters between 14cm to 18 cm at 1064 nm (and around 35 cm at 1550 nm). As for LEO satellites at the same elevations, diameters up to 11cm could be used at 1064 nm (and between 18 cm and 22 cm at 1550 nm). These values have to be compared to those without any pre-compensation: between 3 and 8 cm at 1064 nm (and between 5 and 13 cm at 1550 nm). Note that the simulations are based on averaged models that do not consider instantaneous meteorological conditions. Finally, the experimental results presented in this paper need to be confirmed by further test campaigns and extended to various operation conditions (e.g seasonal effects, daytime operation).