An Enhanced Interactive and Multi-criteria Decision-Making (TODIM) Method with Probabilistic Dual Hesitant Fuzzy Sets for Risk Evaluation of Arctic Geopolitics

Abstract

The psychological factors of experts play a special role in the process of decision-making, especially in some situations that experts are not completely rational. Traditional decision-making methods always just focus on the aggregation of positive preference information, which do not take the negative attribute information into account at the same time. The probabilistic dual hesitant fuzzy set (PDHFS) is one of the latest fuzzy sets, which can depict experts’ positive and negative preference information with the corresponding probability at the same time. Therefore, to manage the applications with incomplete rationality and two opposite kinds of uncertain preference information, this paper considers the influence of psychological behavior on decision-making results and introduces an interactive method based on the prospect theory. Taking the advantages of PDHFSs in group decision-making problems, we propose the distance measure of PDHFSs, based on which an improved TODIM (TOmada deDecisão Iterativa Multicritério) method under the probabilistic dual hesitant fuzzy environment is also developed. Meanwhile, we provide the specific implementation process of the proposed method. The proposed improved TODIM is applied to the risk evaluation of Arctic geopolitics. We also make a comparison with the traditional aggregation method of PDHFSs. The difference among alternatives obtained by the proposed TODIM method with prospect theory is much greater than the traditional aggregation methods without prospect theory. This paper highlights the benefits and advantages of the proposed TODIM method that is developed based on the prospect theory and probabilistic dual hesitant fuzzy distance measure.

Introduction

The rapid development of economy and society is accompanied by a large amount of uncertain information and knowledge, which also brings more opportunities and challenges [1]. Furthermore, the psychological behavior of experts also influences the decision-making process and results, especially in some situations that experts are not completely rational [2]. Therefore, it is necessary to develop some new methods to manage with the applications with incomplete rationality and different kinds of uncertain preference information.

How to make full use of uncertain information and measure it effectively and accurately is the key to manage uncertain decision-making problems. From the perspective of experts, it is not easy to understand every aspect and then provide accurate evaluation information due to the limitations of their knowledge [3]. Therefore, the research about how to manage with uncertainty and cognition has attracted lots of scholars. The theory of fuzzy set (FS) proposed by Zadeh [4] breaks through the limitations of classical set theory and provides an effective tool to depict the cognitive uncertainty of experts. On the basis of fuzzy set theory, scholars have expanded it to more types and broadened its application scope according to different scenarios. As one of the latest extended forms of fuzzy set, the hesitant fuzzy set (HFS) [5, 6] is a set consisting of several possible memberships. It can depict the situations in which experts cannot provide a certain consensus with sound reliability. That is to say, they are hesitant among several possible values. Later, Zhu and Xu [7] proposed the concept of probabilistic hesitant fuzzy set (PHFS), which associates the probability with HFS and remains more information than traditional HFS. The PHFS is a set consisting of several possible crisp values with the corresponding probabilistic distribution. Besides considering the negative impact of the alternatives, the dual hesitant fuzzy set (DHFS) [8, 9] was proposed to depict the membership and non-membership at the same time. It is a set of several possible and impossible crisp values. In the existing fuzzy set theory, the probability information of membership and non-membership is ignored. To solve the problem of dual hesitant fuzzy information loss in the group decision-making process, Hao et al. [10] proposed the concept of probabilistic dual hesitant fuzzy set (PDHFS), which makes up for the deficiency of the DHFS by combining the corresponding probabilistic information. As one of the latest fuzzy sets, the PDHFS can depict experts’ positive and negative preference information at the same time and remain the original information to the greatest extent. Hao et al. [10] also defined the basic operation laws and aggregation operators for PDHFSs.

The TODIM (TOmada deDecisão Iterativa Multicritério) [11] method is an effective tool to manage uncertain decision-making problems. Based on the prospect theory [12, 13], it can consider the psychological factors of experts, especially suitable for the situations where experts are not completely rational. Due to the unique advantages of the TODIM method, it has been developed to different fuzzy environments, such as intuitionistic fuzzy environment [14, 15], hesitant fuzzy environment [16, 17], and hesitant fuzzy linguistic information [18, 19]. The TODIM method has also been applied to green supplier selection [20, 21], water security evaluation [22], personnel evaluation [23], waste mobile phone recycling [24], and so on. However, since the research of PDHFS is still a relatively new direction, the study of the TODIM method under the probabilistic dual hesitant fuzzy environment is still blank [25]. Taking the prominent advantages of the PDHFS and the TODIM method, this paper tries to integrate the PDHFS into the TODIM method and propose a new interactive decision-making method, i.e., the improved TODIM method under the probabilistic dual hesitant fuzzy environment, named as PDHF-TODIM. We define the distance measure of probabilistic dual hesitant fuzzy information and other parameters in PDHF-TODIM. After that, the group decision-making method based on PDHF-TODIM is presented. We also provide a specific implementation process for the PDHF-TODIM method to manage actual evaluation problems. The main contributions of this paper are summarized as follows:

• (a) This paper defines the concept of probabilistic dual hesitant fuzzy distance measure to avoid the loss of information. It can make full use of the original preference information to the greatest extent by depicting the membership and non-membership with corresponding probabilistic information at the same time.

• (b) This paper proposes an improved TODIM method based on the probabilistic dual hesitant fuzzy distance measure and prospect theory. The improved TODIM method considers the situations in which experts are not completely rational and makes full use of both positive and negative preference information. The specific implementation process of the proposed method is also provided.

• (c) The proposed TODIM method under the probabilistic dual hesitant fuzzy environment is applied to the Arctic geopolitics risk evaluation. The comparison results demonstrate the advantages of the proposed improved TODIM method.

The outline of this paper is organized as follows: In the “Preliminaries” section, some basic knowledge about PDHFSs is presented in detail. After that, we define the concept of probabilistic dual hesitant fuzzy distance measure, based on which, an improved TODIM method under the probabilistic dual hesitant fuzzy environment is proposed. We also present the specific implementation process of the proposed method in the “The Novel TODIM Method Under the Probabilistic Dual Hesitant Fuzzy Environment” section. In the “Application to the Arctic Geopolitics Risk Evaluation” section, the proposed method is applied to the Arctic geopolitics risk evaluation. The results demonstrate the accuracy and advantages of improved TODIM method. Finally, some conclusions are presented in “Conclusions” section.

Preliminaries

In this section, we review some basic knowledge about the probabilistic dual hesitant fuzzy set (PDHFS).

Definition 2.1 [10]. For a reference set $X$, a probabilistic dual hesitant fuzzy set (PDHFS) $PD$ is depicted as:

$$PD\left( X \right) = \left\{ {\left\langle {x,h\left( x \right)\left| {p\left( x \right),g\left( x \right)\left| {q\left( x \right)} \right.} \right.} \right\rangle \left| {x \in X} \right.} \right\}$$

(1)

where $h\left( x \right)\left| {p\left( x \right)} \right.$ and $g\left( x \right)\left| {q\left( x \right)} \right.$ are two sets of several possible values where $h\left( x \right)$ and $g\left( x \right)$ denote the hesitant fuzzy membership and non-membership degrees to $X$, respectively, and $p\left( x \right)$ and $q\left( x \right)$ are the corresponding probability information of the two types of degrees. Furthermore, $0 \le \gamma ,\eta \le 1$,$0 \le \gamma^{ + } + \eta^{ + } \le 1$, $p_{i} \in \left[ {0,1} \right]$,$q_{j} \in \left[ {0,1} \right]$,$\sum\limits_{i = 1}^{\# h} {p_{i} } = 1$, and $\sum\limits_{j = 1}^{\# g} {q_{j} } = 1$, where $\gamma \in h\left( x \right)$, $\eta \in g\left( x \right)$, $\gamma^{ + } \in h^{ + } \left( x \right) = \cup_{\gamma \in h\left( x \right)} \max \left( \gamma \right)$, $\eta^{ + } \in g^{ + } \left( x \right) = \cup_{\eta \in g\left( x \right)} \max \left( \eta \right)$, $p_{i} \in p\left( x \right)$, and $q_{i} \in q\left( x \right)$. The symbols $\# h$ and $\# g$ denote the total numbers of elements in $h\left( x \right)\left| {p\left( x \right)} \right.$ and $g\left( x \right)\left| {q\left( x \right)} \right.$ respectively.

Remark 1. If the corresponding probability information $p\left( x \right)$ and $q\left( x \right)$ are the same, then the PDHFS reduces to the DHFS. Furthermore, if $g\left( x \right) = \emptyset$ and the probabilistic values of $p\left( x \right)$ are equal, then the PDHFS will reduce to the HFS.

For convenience, the pair $pd = \left\langle {h\left( x \right)\left| {p\left( x \right),g\left( x \right)\left| {q\left( x \right)} \right.} \right.} \right\rangle$ is named as the probabilistic dual hesitant fuzzy element (PDHFE), which is the basic element of the PDHFS $PD$.

Definition 2.2 [10]. Let $pd = \left\langle {h\left( x \right)\left| {p\left( x \right),g\left( x \right)\left| {q\left( x \right)} \right.} \right.} \right\rangle$ be a PDHFE; then, the complement of the PDHFE is defined as follows:

$$pd^{c} = \left\{ \begin{gathered} \begin{array}{*{20}c} {\bigcup\nolimits_{\gamma \in h,\eta \in g} {\left\{ {\left\{ {\eta |q_{\eta } } \right\},\left\{ {\gamma |p_{\gamma } } \right\}} \right\},} } & { \, g \ne \emptyset \, \, h \ne \emptyset } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\bigcup\nolimits_{\gamma \in h} {\left\{ {\left\{ {\left( {1 - \gamma } \right)|p_{\gamma } } \right\},\left\{ \emptyset \right\}} \right\},} } & {g = \emptyset \, h \ne \emptyset } \\ \end{array} \hfill \\ \begin{array}{*{20}c} {\bigcup\nolimits_{\eta \in g} {\left\{ {\left\{ \emptyset \right\},\left\{ {\left( {1 - \eta } \right)|q_{\eta } } \right\}} \right\},} } & {h = \emptyset \, g \ne \emptyset } \\ \end{array} \hfill \\ \end{gathered} \right.$$

(2)

Definition 2.3 [10]. Let $pd = \left\langle {h\left( x \right)\left| {p\left( x \right),g\left( x \right)\left| {q\left( x \right)} \right.} \right.} \right\rangle$ be a PDHFE; then, the score ($s$) and the deviation degree ($\sigma$) of the PDHFE $pd = \left\langle {h\left( x \right)\left| {p\left( x \right),g\left( x \right)\left| {q\left( x \right)} \right.} \right.} \right\rangle$ are defined, respectively, as follows:

$$s=\sum\limits_{i=1\gamma\epsilon h}^{\#h}\gamma_i\cdot p_i-\sum_{j=1_{\eta\epsilon g}}^{\#g}\eta_j\cdot q_j$$

(3)

$$\sigma=\sum\limits_{i=1}^{\#h}(\gamma_i-s\overset{}{\underset{}{)^2)\cdot Pi+\sum_{}^{\#g}{(\eta_i-s)}^2\cdot q_i)}}^{1/2}$$

(4)

where $\# h$ and $\# g$ denote the total numbers of elements in $h\left( x \right)\left| {p\left( x \right)} \right.$ and $g\left( x \right)\left| {q\left( x \right)} \right.$ respectively, $i = 1,2, \ldots ,n$.

Suppose that $pd_{1} = \left\langle {h\left( {x_{1} } \right)\left| {p\left( {x_{1} } \right),g\left( {x_{1} } \right)\left| {q\left( {x_{1} } \right)} \right.} \right.} \right\rangle$ and $pd_{2} = \left\langle {h\left( {x_{2} } \right)\left| {p\left( {x_{2} } \right),g\left( {x_{2} } \right)\left| {q\left( {x_{2} } \right)} \right.} \right.} \right\rangle$ are two PDHFEs, $s\left( {pd} \right)$ and $\sigma \left( {pd} \right)$ are the score and the deviation degree of the PDHFE $pd = \left\langle {h\left( x \right)\left| {p\left( x \right),g\left( x \right)\left| {q\left( x \right)} \right.} \right.} \right\rangle$. The comparison method for two PDHFEs based on the score and the deviation degrees is presented as follows:

• (1) If $s\left( {pd_{1} } \right) > s\left( {pd_{2} } \right)$, then $pd_{1} > pd_{2}$;

• (2) If $s\left( {pd_{1} } \right) < s\left( {pd_{2} } \right)$, then $pd_{1} < pd_{2}$;

• (3) If $s\left( {pd_{1} } \right) = s\left( {pd_{2} } \right)$ and $\sigma \left( {pd_{1} } \right) < \sigma \left( {pd_{2} } \right)$, then $pd_{1} > pd_{2}$;

• (4) If $s\left( {pd_{1} } \right) = s\left( {pd_{2} } \right)$ and $\sigma \left( {pd_{1} } \right) > \sigma \left( {pd_{2} } \right)$, then $pd_{1} < pd_{2}$;

• (5) If $s\left( {pd_{1} } \right) = s\left( {pd_{2} } \right)$ and $\sigma \left( {pd_{1} } \right) = \sigma \left( {pd_{2} } \right)$, then we define that $pd_{1}$ is equivalent to $pd_{2}$, denoted as $pd_{1} \sim pd_{2}$.

Definition 2.4 [10]. Let $pd$, $pd_{1}$ and $pd_{2}$ be three PDHFEs, and $pd = \left( {h|p,g|q} \right)$, $pd_{1} = \left( {h_{1} |p_{{h_{1} }} ,g_{1} |q_{{g_{1} }} } \right)$ and $pd_{2} = \left( {h_{2} |p_{{h_{2} }} ,g_{2} |q_{{g_{2} }} } \right)$, $\lambda >0$, then.

$$\begin{aligned}pd_{1} \oplus pd_{2} = & \bigcup\nolimits_{{\gamma_{1} \in h_{1} ,\eta_{1} \in g_{1} ,\gamma_{2} \in h_{2} ,\eta_{2} \in g_{2} }} \\ & {\left\{ {\left\{ {\left( {\gamma_{1} + \gamma_{2} - \gamma_{1} \gamma_{2} } \right)|p_{{\gamma_{1} }} p_{{\gamma_{2} }} } \right\},\left\{ {\left( {\eta_{1} \eta_{2} } \right)|q_{{\eta_{1} }} q_{{\eta_{2} }} } \right\}} \right\}}\end{aligned}$$

(5)

$$\begin{aligned}pd_{1} \otimes pd_{2} = & \bigcup\nolimits_{{\gamma_{1} \in h_{1} ,\eta_{1} \in g_{1} ,\gamma_{2} \in h_{2} ,\eta_{2} \in g_{2} }} \\ & {\left\{ {\left\{ {\left( {\gamma_{1} \gamma_{2} } \right)|p_{{\gamma_{1} }} p_{{\gamma_{2} }} } \right\},\left\{ {\left( {\eta_{1} + \eta_{2} - \eta_{1} \eta_{2} } \right)|q_{{\eta_{1} }} q_{{\eta_{2} }} } \right\}} \right\}}\end{aligned}$$

(6)

$$\lambda pd = \bigcup\nolimits_{\gamma \in h,\eta \in g} {\left\{ {\left\{ {\left( {1 - \left( {1 - \gamma } \right)^{\lambda } } \right)|p_{\gamma } } \right\},\left\{ {\eta^{\lambda } |q_{\eta } } \right\}} \right\}}$$

(7)

$$pd^{\lambda } = \bigcup\nolimits_{\gamma \in h,\eta \in g} {\left\{ {\left\{ {\gamma^{\lambda } |p_{\gamma } } \right\},\left\{ {\left( {1 - \left( {1 - \eta } \right)^{\lambda } } \right)|q_{\eta } } \right\}} \right\}}$$

(8)

Definition 2.5 [10]. Suppose that $pd_{i} \left( x \right)$ is a set of PDHFEs, then the probabilistic dual hesitant fuzzy weighted averaging (PDHFWA) aggregation operator is defined as follows:

$$\begin{gathered} PDHFWA\left( {pd_{1} ,pd_{2} ,...,pd_{n} } \right) = \mathop \oplus \limits_{i = 1}^{n} w_{i} pd_{i} \hfill \\ = \bigcup\limits_{\begin{subarray}{l} \gamma_{1} \in h_{1} ,\gamma_{2} \in h_{2} ,...\gamma_{n} \in h_{n} , \\ \eta_{1} \in g_{1} ,\eta_{2} \in g_{2} ,...\eta_{n} \in g_{n} \end{subarray} } {\left\{ {\left\{ {\left( {1 - \prod\limits_{i = 1}^{n} {\left( {1 - \gamma_{i} } \right)^{{w_{i} }} } } \right)\left| {\prod\limits_{i = 1}^{n} {p_{{\gamma_{i} }} } } \right.} \right\},\left\{ {\prod\limits_{j = 1}^{n} {\eta_{j}^{{w_{j} }} } \left| {\prod\limits_{j = 1}^{n} {q_{{\eta_{j} }} } } \right.} \right\}} \right\}} \hfill \\ \end{gathered}$$

(9)

where $w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T}$ is the corresponding weight of $pd_{i} \left( x \right)$, $w_{i} \in \left[ {0,1} \right]$ and $\sum\limits_{i = 1}^{n} {w_{i} } = 1$,$i = 1,2, \ldots ,n$.

The Novel TODIM Method Under the Probabilistic Dual Hesitant Fuzzy Environment

The TODIM is an interactive decision-making method and can better consider the psychological behavior of experts. However, in actual situations, it is not easy to depict the membership and non-membership of experts in group decision-making, and it is even harder to contain the several possible values and probabilistic information at the same time. Therefore, to avoid the information loss, this paper takes the advantages of PDHFSs in depicting the hesitant preference and uncertain knowledge. We first define the concept of distance measure of probabilistic dual hesitant fuzzy information, based on which, we further develop the TODIM method under the probabilistic dual hesitant fuzzy environment, named as PDHF-TODIM. Furthermore, the specific implementation process for the PDHF-TODIM method is also provided in detail.

The Distance Measure of Probabilistic Dual Hesitant Fuzzy Information

Definition 3.1 Let $PD_{M}$ and $PD_{N}$ be two PDHFSs; then, the distance measure between $PD_{M}$ and $PD_{N}$ is defined as $D\left( {PD_{M} ,PD_{N} } \right)$, which satisfies:

• (1) $0 \le D\left( {PD_{M} ,PD_{N} } \right) \le 1$;

• (2) $D\left( {PD_{M} ,PD_{N} } \right) = 0$, if $PD_{M} = PD_{N}$;

• (3) $D\left( {PD_{M} ,PD_{N} } \right) = D\left( {PD_{N} ,PD_{M} } \right)$;

Definition 3.2 Let $PD_{M} = \left\{ {\left\langle {x,h_{M} \left( x \right)\left| {p_{M} \left( x \right),g_{M} \left( x \right)\left| {q_{M} \left( x \right)} \right.} \right.} \right\rangle \left| {x \in X} \right.} \right\}$ and $PD_{N} =$ $\left\{ {\left\langle {x,h_{N} \left( x \right)\left| {p_{N} \left( x \right),g_{N} \left( x \right)\left| {q_{N} \left( x \right)} \right.} \right.} \right\rangle \left| {x \in X} \right.} \right\}$ be two PDHFSs; then, the generalized probabilistic dual hesitant fuzzy weighted distance between $PD_{M}$ and $PD_{N}$ is defined as:

$$D(PD_M,PD_N)=\left[\sum\limits_{i=1}^nw_i\left\{\left({\sum\limits_{j=1}^{{\#h}_M}}_{\gamma\in h}\gamma_{Mi}\cdot p_{Mi}-{\sum\limits_{j=1}^{{\#g}_M}}_{\eta\in g}\eta_{Mj}\cdot q_{Mj}\right)-\left({\sum\limits_{j=1}^{{\#h}_N}}_{\gamma\in h}\gamma_{Mj}\cdot q_{Mj}-{\sum\limits_{j=1}^{{\#g}_N}}_{\eta\in g}\eta_{Nj}\cdot q_{Nj}\right)\right\}^\lambda\right]^\frac1\lambda$$

(10)

where $w_{i}$ is the corresponding weight vector of $pd\left( {x_{i} } \right)$, $w_{i} \in \left[ {0,1} \right]$, and $\sum\limits_{i = 1}^{n} {w_{i} = 1}$, $\;i = 1,2, \ldots ,n$. The components $h\left( x \right)\left| {p\left( x \right)} \right.$ and $g\left( x \right)\left| {q\left( x \right)} \right.$ are two sets of several possible values where $h\left( x \right)$ and $g\left( x \right)$ denote the hesitant fuzzy membership and non-membership degrees to the set $X$ respectively. Furthermore, $0 \le \gamma ,\eta \le 1$,$0 \le \gamma^{ + } + \eta^{ + } \le 1$, $p_{i} \in \left[ {0,1} \right]$,$q_{j} \in \left[ {0,1} \right]$,$\sum\limits_{i = 1}^{\# h} {p_{i} } = 1$, and $\sum\limits_{j = 1}^{\# g} {q_{j} } = 1$, where $\gamma \in h\left( x \right)$, $\eta \in g\left( x \right)$, $\gamma^{ + } \in h^{ + } \left( x \right) = \cup_{\gamma \in h\left( x \right)} \max \left( \gamma \right)$, $\eta^{ + } \in g^{ + } \left( x \right) = \cup_{\eta \in g\left( x \right)} \max \left( \eta \right)$, $p_{i} \in p\left( x \right)$, and $q_{i} \in q\left( x \right)$. The symbols $\# h$ and $\# g$ denote the total numbers of elements in $h\left( x \right)\left| {p\left( x \right)} \right.$ and $g\left( x \right)\left| {q\left( x \right)} \right.$ respectively.

Remark 1. If $\lambda = 1$, then the generalized probabilistic dual hesitant fuzzy weighted distance is reduced to the probabilistic dual hesitant fuzzy weighted Hamming distance:

$$D_2(PD_M,PD_N)=\left[\sum_{i=1}^nw_i\left\{\left({\sum\limits_{j=1}^{{\#h}_M}}_{\gamma\in h}\gamma_{Mi}\cdot p_{Mi}-{\sum\limits_{j=1}^{{\#g}_M}}_{\eta\in g}\eta_{Mj}\cdot q_{Mj}\right)-\left({\sum\limits_{j=1}^{{\#h}_N}}_{\gamma\in h}\gamma_{Ni}\cdot q_{Ni}-{\sum\limits_{j=1}^{{\#g}_N}}_{\eta\in g}\eta_{Nj}\cdot q_{Nj}\right)\right\}\right]$$

(11)

If $\lambda = 2$, then the generalized probabilistic dual hesitant fuzzy weighted distance is reduced to the probabilistic dual hesitant fuzzy weighted Euclidean distance:

$$D_3(PD_M,PD_N)=\left[\sum_{i=1}^nw_i\left\{\left({\sum\limits_{j=1}^{{\#h}_M}}_{\gamma\in h}\gamma_{Mi}\cdot p_{Mi}-{\sum\limits_{j=1}^{{\#g}_M}}_{\eta\in g}\eta_{Mj}\cdot q_{Mj}\right)-\left({\sum\limits_{j=1}^{{\#h}_N}}_{\gamma\in h}\gamma_{Mj}\cdot q_{Mj}-{\sum\limits_{j=1}^{{\#g}_N}}_{\eta\in g}\eta_{Nj}\cdot q_{Nj}\right)\right\}^2\right]^\frac12$$

(12)

If $\omega = \left( {\frac{1}{n},\frac{1}{n}, \cdots ,\frac{1}{n}} \right)^{T}$, then $D_{2} (PD_{M} ,PD_{N} )$ is reduced to the normalized probabilistic dual hesitant fuzzy Hamming distance:

$$D_4(PD_M,PD_N)=\left[\frac1n\sum_{i=1}^nw_i\left\{\left({\sum_{j=1}^{{\#h}_M}}_{\gamma\in h}\gamma_{Mi}\cdot p_{Mi}-{\sum_{j=1}^{{\#g}_M}}_{\eta\in g}\eta_{Mj}\cdot q_{Mj}\right)-\left({\sum_{j=1}^{{\#h}_N}}_{\gamma\in h}\gamma_{Ni}\cdot p_{Ni}-{\sum_{j=1}^{{\#g}_N}}_{\eta\in g}\eta_{Nj}\cdot q_{Nj}\right)\right\}\right]$$

(13)

$D_{3} (PD_{M} ,PD_{N} )$ is reduced to the normalized probabilistic dual hesitant fuzzy Euclidean distance:

$$D_5(PD_M,PD_N)=\left[\frac1n\sum_{i=1}^n\left\{\left({\sum\limits_{j=1}^{{\#h}_M}}_{\gamma\in h}\gamma_{Mi}\cdot p_{Mi}-{\sum\limits_{j=1}^{{\#g}_M}}_{\eta\in g}\eta_{Mj}\cdot q_{Mj}\right)-\left({\sum\limits_{j=1}^{{\#h}_N}}_{\gamma\in h}\gamma_{Ni}\cdot p_{Ni}-{\sum\limits_{j=1}^{{\#g}_N}}_{\eta\in g}\eta_{Nj}\cdot q_{Nj}\right)\right\}^2\right]^\frac12$$

(14)

The Improved TODIM Under the Probabilistic Dual Hesitant Fuzzy Environment

Classical decision-making methods always suppose that experts are completely rational, which may lead to unreliable or wrong results due to the ignorance of experts’ psychological behavior in the decision-making process. For the decision-making problem that experts are not completely rational, it is necessary to consider the influence of psychological behavior on decision-making results. An effective tool is the TODIM method, which is an interactive method based on the prospect theory. Therefore, to solve the applications with incomplete rationality and different kinds of preference information under the probabilistic dual hesitant fuzzy environment, we develop a novel TODIM method based on the probabilistic dual hesitant fuzzy distance.

Suppose that there are $m$ alternatives to be evaluated, and each alternative has $n$ attributes, i.e., $x_{i}$ and $a_{j}$ respectively. $w = (w_{1} ,w_{2} , \ldots ,w_{n} )^{T}$ is the corresponding weight vector of the above $n$ attributes, and the alternatives are depicted by PDHFSs, i.e., $PD\left( {x_{i} } \right) = \left( {h_{j} \left( {x_{i} } \right)\left| {p\left( {x_{i} } \right),g_{j} \left( {x_{i} } \right)\left| {q_{j} \left( {x_{i} } \right)} \right.} \right.} \right)$, $i = 1,2, \ldots ,m$ and $j = 1,2, \ldots ,n$, and $\sum\nolimits_{j = 1}^{n} {w_{i} } = 1$. The evaluation information expressed by PDHFSs are all normalized, and the attributes are transformed into the same kind of type. Then, we introduce some related knowledge about the novel TODIM method under the probabilistic dual hesitant fuzzy environment as follows:

Definition 3.3 If $w_{j}$ ($j = 1,2, \ldots ,n$) are the weights of the corresponding attributes $a_{j}$($j = 1,2, \ldots ,n$), $w_{j*}$ has the largest value in the weight vector of the above $n$ attributes, i.e., $w_{j*} = \max \left\{ {w_{j} \left| {j = 1,2, \ldots ,n} \right.} \right\}$, and $j = 1,2, \ldots ,n$; then, the attribute $a_{j*}$ is selected as the reference attribute. The relative weight between the two attributes $a_{j}$ and $a_{j*}$ is defined as:

$$w_{j/j*} = w_{j} /w_{{j^{*} }}$$

(15)

Definition 3.4 Suppose that the probabilistic dual hesitant fuzzy distance between the alternatives $x_{i}$ and $x_{k}$ in terms of the attribute $a_{j}$ is $D(pd_j,(x_i),pd(x_k))$, and the relative weight between the attribute $a_{j}$ and the selected reference attribute $a_{j*}$ is $w_{j/j*}$, the attenuation factors of losses is $\theta$, $\theta > 0$; then, the dominance degree of the alternative $x_{i}$ over the alternative $x_{k}$ in terms of the attribute $a_{j}$ under the probabilistic dual hesitant fuzzy environment is $\phi_{j} \left( {x_{i} ,x_{k} } \right)$, which is defined as follows:

$$\phi_{j} \left( {x_{i} ,x_{k} } \right) = \left\{ \begin{gathered} \sqrt {{{\left( {w_{{j/j^{*} }} \cdot D\left( {pd_{j} \left( {x_{i} } \right)pd_{j} \left( {x_{k} } \right)} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {w_{{j/j^{*} }} \cdot D\left( {pd_{j} \left( {x_{i} } \right)pd_{j} \left( {x_{k} } \right)} \right)} \right)} {\sum\nolimits_{j}^{n} {w_{{j/j^{*} }} } }}} \right. \kern-0pt} {\sum\nolimits_{j}^{n} {w_{{j/j^{*} }} } }}} \begin{array}{*{20}c} {\begin{array}{*{20}c} {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} & {} \\ \end{array} pd_{j} \left( {x_{i} } \right) > pd_{j} \left( {x_{k} } \right)} \\ \end{array} \hfill \\ 0,\begin{array}{*{20}c} {} & {} & {} & {} & {} & {} & {} & {} & {} & {\begin{array}{*{20}c} {} & {} & {} & {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} pd_{j} \left( {x_{i} } \right)\sim pd_{j} \left( {x_{k} } \right)} \\ \end{array} } \\ \end{array} \hfill \\ - \frac{1}{\theta }\sqrt {{{\left( {\left( {\sum\nolimits_{j}^{n} {w_{{j/j^{*} }} } } \right) \cdot D\left( {pd_{j} \left( {x_{i} } \right)pd_{j} \left( {x_{k} } \right)} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {\sum\nolimits_{j}^{n} {w_{{j/j^{*} }} } } \right) \cdot D\left( {pd_{j} \left( {x_{i} } \right)pd_{j} \left( {x_{k} } \right)} \right)} \right)} {w_{{j/j^{*} }} }}} \right. \kern-0pt} {w_{{j/j^{*} }} }}} \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {} \\ \end{array} pd_{j} \left( {x_{i} } \right) < pd_{j} \left( {x_{k} } \right)} \\ \end{array} } \\ \end{array} \hfill \\ \end{gathered} \right.$$

(16)

Remark: If $pd_{j} \left( {x_{i} } \right) > pd_{j} \left( {x_{k} } \right)$, then the comparison $\phi_{j} \left( {x_{i} ,x_{k} } \right)$ between the alternative $x_{i}$ over the alternative $x_{k}$ in terms of the attribute $a_{j}$ indicates a gain; if $pd_{j} \left( {x_{i} } \right) < pd_{j} \left( {x_{k} } \right)$, then the $\phi_{j} \left( {x_{i} ,x_{k} } \right)$ indicates a loss; if $pd_{j} \left( {x_{i} } \right)\sim pd_{j} \left( {x_{k} } \right)$, then the $\phi_{j} \left( {x_{i} ,x_{k} } \right)$ indicates a nil.

Definition 3.5 To the dominance degree $\phi_{j} \left( {x_{i} ,x_{k} } \right)$ of the alternative $x_{i}$ over the alternative $x_{k}$ in terms of the attribute $a_{j}$, then the dominance of $x_{i}$ over $x_{k}$ under the probabilistic dual hesitant fuzzy environment is defined as:

$$\phi \left( {x_{i} ,x_{k} } \right) = \sum\limits_{j = 1}^{n} {\phi_{j} \left( {x_{i} ,x_{k} } \right)}$$

(17)

where $i,k = 1,2, \ldots ,m$, $j = 1,2, \ldots ,n$.

Definition 3.6 If the dominance of the alternative $x_{i}$ over the alternative $x_{k}$ under the probabilistic dual hesitant fuzzy environment is $\phi \left( {x_{i} ,x_{k} } \right)$, then the overall prospect value of the alternative $x_{i}$ under the probabilistic dual hesitant fuzzy environment is defined as:

$$\Phi \left( {x_{i} } \right) = \frac{{\sum\nolimits_{k = 1}^{m} {\phi \left( {x_{i} ,x_{k} } \right) - \mathop {\min }\limits_{i} \left\{ {\sum\nolimits_{k = 1}^{m} {\phi \left( {x_{i} ,x_{k} } \right)} } \right\}} }}{{\mathop {\max }\limits_{i} \left\{ {\sum\nolimits_{k = 1}^{m} {\phi \left( {x_{i} ,x_{k} } \right)} } \right\} - \mathop {\min }\limits_{i} \left\{ {\sum\nolimits_{k = 1}^{m} {\phi \left( {x_{i} ,x_{k} } \right)} } \right\}}}$$

(18)

where $i,k = 1,2, \ldots ,m$, $j = 1,2, \ldots ,n$.

Definition 3.7 Suppose that $\Phi \left( {x_{i} } \right)$ is the overall prospect value of the alternative $x_{i}$ under the probabilistic dual hesitant fuzzy environment, $\omega = (\omega_{1} ,\omega_{2} , \ldots ,\omega_{m} )^{T}$ is the corresponding weight vector of the $m$ experts; then, the integrated overall prospect value of experts is defined as follows:

$$\psi (x_{i} ) = \sum\limits_{k = 1}^{m} {\omega_{k} \Phi^{k} (x_{i}^{{}} )}$$

(19)

where $\omega_{k}$ is the $k$ th expert’s weight.

The best alternative has the largest integrated overall prospect value. By calculating the integrated overall prospect value $\psi (x_{i} )$, it is easy to obtain the priority orders and select the optimal alternative.

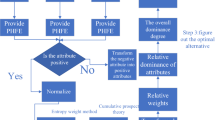
The detailed implementation steps of the novel TODIM under the probabilistic dual hesitant fuzzy environment is presented as follows:

• Step 1: Construct the normalized probabilistic dual hesitant fuzzy decision matrix $H = \left( {pd_{j} \left( {x_{i} } \right)} \right)_{m \times n}$ based on the collected original preference information of experts.

• Step 2: Determine the weight vector of attributes.

• Step 3: Select the reference attribute and then calculate the relative weight of every attribute.

• Step 4: Calculate the probabilistic dual hesitant fuzzy Euclidean distance between alternatives.

• Step 5: Figure out the dominance degree between alternatives based on the probabilistic dual hesitant fuzzy distance.

• Step 6: Calculate the overall prospect value based on the dominance degree.

• Step 7: Integrate the overall prospect value of every expert.

• Step 8: Select the optimal alternative by the calculated prospect values.

Group Decision-making Based on the Proposed TODIM Under the Probabilistic Dual Hesitant Fuzzy Environment

Due to the limitations of personal ability and knowledge, it is easy to lead subjective mistakes and cognitive bias in the decision-making process. With the continuous improvement of social specialization, group decision-making is an important method to overcome the limitations of single decision-making and attracts more and more attention. To deal with actual decision-making problems, experts in different fields are always invited to evaluate and provide preference information from various aspects. Therefore, we develop the novel group decision-making method based on the improved TODIM method under the probabilistic dual hesitant fuzzy environment, aiming to simulate and depict the evaluation information and psychological states of experts in the process of decision-making.

To better understand the detailed steps of the group decision-making method based on the novel TODIM method under the probabilistic dual hesitant fuzzy environment, a visual specific implementation process is also illustrated in Fig. 1 as follows:

Fig. 1

The visual specific implementation process of the improved TODIM method under the probabilistic dual hesitant fuzzy environment

With the increasing complexity of actual decision-making problems, it is unavoidable to face and manage different kinds of preference information and knowledge. To depict the preference information with a set of possible values and impossible values with the corresponding probabilities, this paper introduces the concept of PDHFS. In addition, the TODIM can make up for the deficiency of traditional decision-making methods in depicting the bounded rationality of decision-makers, and is more consistent with the actual situation and decision-making process. The proposed group decision-making method based on the improved TODIM under the probabilistic dual hesitant fuzzy environment combines the advantages of TODIM in considering the influence of psychological factors and the advantages of PDHFS in depicting complex uncertain information. It simulates the practical decision-making process better, which will provide a more reliable result.

Application to the Arctic Geopolitics Risk Evaluation

In this section, the proposed TODIM method under the probabilistic dual hesitant fuzzy environment is applied to the Arctic geopolitics risk evaluation (adapted from [10]) in detail. A comparison is further conducted to illustrate the advantages of the proposed method.

Example 4.1 [10]. The Arctic is the northward branch of the “21st Century Maritime Silk Road,” and its strategic position is becoming increasingly prominent. Affected by global warming, the trend of Arctic sea ice melting is more obvious. From the perspective of geopolitics, six of the eight countries around the Arctic, except Sweden and Finland, have declared that they have maritime territorial rights in the Arctic. The Arctic is also an area where the USA and Russia play a fierce game. In addition, China is a permanent observer state of the Arctic Council and holds a positive attitude towards Arctic affairs. The European Union, Japan, and even Brazil are also striving for the voice of the Arctic region. The complicated geopolitical situation has further raised the global strategic position of the whole Arctic region.

The geopolitical risk evaluation of Arctic area is essential for investors to understand the opportunities and risks [26, 27]. Taking the relevant countries adjacent to the Arctic, such as the USA, Russia, Canada, China, Denmark, and Norway as example, Hao et al. [10] determined four main attributes about the sources exploitation and utilization related to the Arctic: potential military conflicts (MCs), diplomatic disputes (DDs), dependence on emergency imports (EIs), and control over marine routes (MRs). Considering the advantages of PDHFS in depicting the uncertain information and preference, Hao et al. [10] also provided the evaluation information of alternatives by PDHFSs, which remained the original information of positive and negative values to the greatest extent. The detailed assessment information is provided as follows [10].

Consistent with Ref. [10], this paper also supposes that the corresponding weight vector of the above three experts and four main attributes are $\omega = (0.2,0.3,0.5)^{T}$ and $w = \left( {0.3,0.2,0.3,0.2} \right)^{T}$. Taking the decision matrix of the expert $P_{1}$ as an example (let $\lambda = 2$)_, then we can calculate the probabilistic dual hesitant fuzzy weighted Euclidean distance between different countries respectively. The calculation result is presented as follows.

After that, by comparing every two countries in terms of each attribute based on the above normalized decision matrix by the expert $P_{1}$, we can calculate the score and deviation degrees and then obtain the comparison results as follows.

Later, it is easy to determine the reference attribute $a_{j*}$ with the largest value of the weight $w_{j*} = \max \left\{ {w_{j} \left| {j = 1,2, \ldots ,n} \right.} \right\} = 0.3$. To avoid the loss of generality, this paper supposes that $\theta = 1$, then according to the calculation results of probabilistic dual hesitant fuzzy weighted Euclidean distances of different countries, it is easy to obtain the dominance degree $\phi_{j} \left( {x_{i} ,x_{k} } \right)$ of the country $x_{i}$ over the country $x_{k}$ under the attribute $a_{j}$ (see Tables 12, 3, 4, 5 and 6).

Table 1 The decision matrix of different countries by expert $P_{1}$

Table 2 The decision matrix of different countries by expert $P_{2}$

Table 3 The decision matrix of different countries by expert $P_{3}$

Table 4 The probabilistic dual hesitant fuzzy weighted Euclidean distances of different countries

Table 5 The pairwise comparison of corresponding countries under different attributes

Table 6 The dominance degree of different countries in terms of attribute $a_{1}$

Later, we can integrate the dominance degree $\phi_{j} \left( {x_{i} ,x_{k} } \right)$, and then calculate the overall dominance degree of the country $x_{i}$ over the country $x_{k}$, and the calculation results are presented as follows.

Based on the calculation results of overall dominance degree, it is easy to get the overall prospect value of alternative countries (See Table 7).

Table 7 The dominance degree of different countries in terms of attribute $a_{2}$

Similarly, we can also calculate the overall prospect values based on the decision matrix provided by the experts $P_{2}$ and $P_{3}$ (See Tables 8–9):

Table 8 The dominance degree of different countries in terms of attribute $a_{3}$

Table 9 The dominance degree of different countries in terms of attribute $a_{4}$

Based on the above calculation results, it is easy to obtain the integrated overall prospect value of three experts by Definition 3.5, which are presented as follows.

The larger integrated overall prospect value $\Phi \left( {x_{i} } \right)$ corresponds to the country which has the higher risk; i.e., the USA has the highest risk and Norway has the lowest risk. Thus, the potential risk order of the above related six countries is USA > Canada > Russia > China > Denmark > Norway.

Furthermore, it is also necessary to analyze the results thoroughly by comparing with the traditional aggregation method of PDHFSs. Since the detailed assessment information is provided by Hao et al. [10] in Tables 6, 8, 9, and 10, and the corresponding weight vector of the above three experts and four main attributes are also same to the proposed method in this paper; it is reasonable to adopt the probabilistic dual hesitant fuzzy weighted averaging (PDHFWA) aggregation operator to aggregate the detailed assessment information of different countries under every indicator. According to Definition 2.4, Hao et al. calculated the corresponding score functions values, which are presented in Tables 11, and 12.

Table 10 The overall dominance degree of different countries

Table 11 The overall prospect value of different countries based on the decision matrix provided by the expert $P_{1}$

Table 12 The overall prospect value of different countries based on the decision matrix provided by expert $P_{2}$

The score function values also indicate that the USA has the highest risk and Norway has the lowest risk, which are same with the results obtained by the proposed TODIM method. However, based on the score function values, the potential risk order of the six countries is USA > Denmark > China > Canada > Russia > Norway.

The risk order based on the above two methods are presented in Tables 13, 14, 15, and 16. Compared with our ranking results, it is obvious that the proposed TODIM method obtains the same results; i.e., the USA has the highest risk and Norway has the lowest risk. However, the difference of results by the proposed TODIM method with prospect theory is much greater than the traditional aggregation methods without prospect theory. The main reason is that the prospect theory considers the different risk attitudes of experts towards gain and loss. In addition, the conclusion obtained by the traditional aggregation method is that Denmark has the second highest risk, which is questionable. The main reason is that the evaluation information provided by some experts is not sufficient, and the differences on the evaluation information of Denmark are great. Furthermore, as an ally of the USA, Canada closely follows the USA in the attitudes and policies towards possible geopolitical disputes in the Arctic. It will certainly increase the investment risk. Besides, Russia is the largest country in the Arctic, and it regards the development of Arctic as one of the priority directions. Like other Arctic countries, Russia wants to make full use of its own geographical advantages to realize the national interests by developing the Arctic. Therefore, it is clear that the results derived by our approach are more reasonable, and the proposed TODIM method under the probabilistic dual hesitant fuzzy environment considers not only more probabilistic information but also the psychological behavior factors.

Table 13 The overall prospect value of different countries based on the decision matrix provided by expert $P_{3}$

Table 14 The integrated overall prospect value of three experts

Table 15 The score function values of the alternative six countries

Table 16 The risk order of the alternative six countries based on the two methods

The comparison results illustrate the accuracy and efficiency of the proposed TODIM method. If we integrate PDHFSs by traditional PDHFWA, there may be too many elements in the integrated PDHFSs, resulting in the dimension explosion and overload information. It will certainly increase the computational complexity of decision-making model and require more decision-making time. Hence, there are many limitations mentioned above in decision-making just by the integration and comparison of PDHFSs. To make full use of PDHFSs in the practical decision-making problems, it is necessary to develop an improved TODIM under the probabilistic dual hesitant fuzzy environment. The decision result by considering the hesitant fuzzy information with different preference degrees is more consistent with reality than that without considering hesitant fuzzy information with different preference degrees. One the one hand, considering the probabilistic dual hesitant fuzzy information with different preference degrees can better depict the experts’ evaluation information. On the other hand, from the perspective of group decision-making, the probabilistic dual hesitant fuzzy information can reflect more preference information of different experts. It illustrates the advantages of probabilistic dual hesitant fuzzy information in depicting the real perception and psychology. By combining the advantages of PDHFS in depicting uncertain information and the prospect theory in considering psychological factors of experts, the improved TODIM is a more reliable method. The application to the Arctic geopolitics risk evaluation validates the efficiency and advantages of the proposed TODIM method.

Conclusions

The traditional TODIM method is one of the earliest multi-attribute decision-making methods developed on the basis of prospect theory. It illustrates the risk preference and psychological factors in prospect theory by the dominance function. Besides, the value function is used to depict the different risk attitudes towards income or loss. However, it is always difficult for experts to provide accurate positive and negative preference information at the same time. In order to depict the uncertain information and fuzzy preference more accurately, this paper introduces the concept of PDHFS with the membership and non-membership consisting of several possible values with probability. Then, based on the proposed distance measure of probabilistic dual hesitant fuzzy information, this paper integrates the PDHFS into the TODIM and develops the improved TODIM method under the probabilistic dual hesitant fuzzy environment. Then, we also provide a visual specific implementation process of the improved TODIM method under the probabilistic dual hesitant fuzzy environment. The improved TODIM can not only depict the experts’ psychological factors, but also depict uncertain preference information more delicately. It makes full use of both positive and negative evaluation information at the same time. At last, the proposed method is applied to the Arctic geopolitics risk evaluation to demonstrate the advantages of our method in managing with actual problems. Besides, traditional aggregation method based on score function is introduced for comparisons to illustrate the rationality and accuracy of the proposed method.

However, there are also some shortcomings in the improved TODIM method. For example, it only considers the situations that the evaluation information is expressed by PDHFS. In the future, we will combine other kind of fuzzy information with the psychological factors of experts to manage with different kinds of actual problems.