Hot Deformation Behaviors of Ti-22Al-26Nb-2Ta Alloy Based on GA-LSSVM and 3D Processing Map

Abstract

The thermal compression tests of Ti-22Al-26Nb-2Ta alloy under T = 1173 ~ 1423 K and $\dot{\varepsilon }$ = 0.001 ~ 10 s⁻¹ were carried out on the Gleeble-3500 thermo-mechanical simulator. The flow stress curves were obtained, and the high-temperature rheological properties of the alloy were analyzed. The 3D activation energy maps were calculated and constructed. The least squares support vector machine (LSSVM) model of constitutive relation was established, and the penalty coefficient and kernel parameter of the LSSVM model were optimized by genetic algorithm (GA). The constitutive model of the alloy based on the GA-LSSVM algorithm was constructed. The predicted value of the model was also compared with the experimental data. The dynamic material model (DMM) and polar reciprocity model (PRM) were used to establish the 3D processing map of the alloy and appropriate thermal processing parameters. Our researches indicated that deformation temperature and strain rate have a great influence on the flow stress of Ti-22Al-26Nb-2Ta alloy. Ti-22Al-26Nb-2Ta alloy is a negative temperature-sensitive and a positive strain rate-sensitive material. The correlation coefficient of GA-LSSVM algorithm constitutive model is 0.9922, and the relative error of most samples is within 10%, accounting for 93.18%. The model has high prediction accuracy and strong generalization ability. The DMM processing map based on the Prasad instability criterion is more accurate in optimizing the processing parameters of the alloy than that of the PRM processing map through analyzing the 3D processing map and observing the microstructure. The instability modes in the instability region of the alloy mainly include adiabatic shear, crack, and local flow. The 1173 ~ 1273 K/0.001 ~ 0.003 s⁻¹ are the best parameters during the processing of the alloy.

Graphic Abstract

1 Introduction

Ti₂AlNb-based alloy belongs to the intermetallic compound of orthogonal ordered structure based on the O-phase, which has low-density, good high-temperature strength, high-temperature oxidation resistance, creep resistance, and other distinguished performances; the alloy is extensively used in the aerospace field [1,2,3,4]. In recent years, some scholars have developed new Ti₂AlNb-base alloy products by adding β phase-stable elements Ta, Y, Si, etc., which makes it a light and high-temperature structural material with great potential for aerospace. As the as-cast microstructure of Ti₂AlNb-based alloy is coarse, the resistance of hot deformation is high, and the requirements of deformation conditions are relatively strict; it is necessary to formulate or optimize the hot forming process parameters to avoid the formation of structural defects in the hot processing process to obtain the required products.

At present, there are many reports on the establishment of the Ti₂AlNb-based alloy constitutive model by using a phenomenological constitutive model (such as the Arrhenius model [5]), physical constitutive model (such as Zerilli-Armstrong model [6]), and artificial neural network (ANN) [7]. However, the construction process of a phenomenological constitutive model and physical constitutive model is complicated and requires work due to the many influencing factors of flow stress. Although ANN can simulate complex nonlinear mapping, problems, such as local optimization, long training time, and poor generalization, are easy to occur. With the development of big-data technology and intelligent algorithm in recent years, the data mining algorithm has been widely applied in material science research [8]. The least squares support vector machine (LSSVM) is a machine learning method based on statistical principles and has an important role in the big-data field. By using nonlinear mapping, the nonlinear regression of low-dimension space can be transformed into a linear regression of high-dimension space; that is the basic idea of LSSVM regression [9]. LSSVM can solve the problems of the small sample, overfitting, dimension disaster, and local minimum, and has strong generalization ability. However, LSSVM is seldom used in the metal-materials prediction of the hot deformation behavior. Therefore, it is necessary to establish a high-precision constitutive model by using LSSVM, which is an important basis for mastering the material rheological behavior and designing the hot forming process. In addition, the processing map is widely used to evaluate the hot workability of the material in the hot deformation processes. There is not only a dynamic material model (DMM) but also a polar reciprocity model (PRM) in the principles of hot processing maps. More attention has been paid to analyzing by the processing map and predicting the material instability in the hot working process or the determination of the stable zone of the hot working process parameters. Among processing maps, the 3D processing map can more intuitively reflect the variation law of parameters. The processing map has been applied to the formulation and optimization of the processing technology of high-temperature alloy, powder metallurgy, composite materials, and stainless steel, etc.; promising results have been achieved [10,11,12].

In this paper, the flow behaviors of Ti-22Al-26Nb-2Ta alloy at high temperature were analyzed through thermal compression tests, and the 3D activation energy maps were calculated and constructed. LSSVM was applied to the constitutive model construction of the alloy, and the genetic algorithm (GA) was used to optimize the parameters of the model; the GA-LSSVM algorithm constitutive model with high prediction accuracy was obtained. Besides, the DMM and PRM were used to establish the 3D processing map of the alloy, which was verified by combining with the observation of microstructure. Finally, the optimal processing parameter range of the alloy was obtained. It is helpful to understand and master the high-temperature deformation behavior of Ti₂AlNb-base alloy by establishing the high-precision constitutive relation model and drawing the thermal processing map of the material. The service performance of Ti₂AlNb-base alloy can be obtained by formulating the thermal processing parameters of the alloy reasonably, which provides the basis for the development and application of Ti₂AlNb-base alloy.

1.1 Experimental and Materials

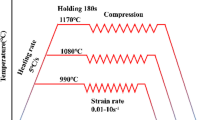
The experimental material is Ti2AlNb-based alloy; the chemical composition of the alloy is given in Table 1. Its nominal composition is Ti-22Al-26Nb-2Ta. The raw alloy was obtained by melting in a vacuum induction furnace. The raw alloy was processed into a cylindrical sample of Φ8mm × 12 mm by wire-cut electrical discharge machining (WEDM), and the perpendicularity of both ends of the samples was also ensured. The detailed dimension of the specimen is shown in Fig. 1a. In addition, both ends of the sample were coated with high-temperature lubricants (glass powder) and padded with graphite flakes to reduce friction. The isothermal and constant strain rate compression experiments were carried out on the Gleeble-3500 thermo-mechanical simulator. The schematic drawing of the experimental set-up is shown in Fig. 1b. The thermal compression process is shown in Fig. 2. The experimental temperatures were 1173, 1223, 1273, 1323, 1373, and 1423 K, and the strain rates were 0.001, 0.01, 0.1, 1, and 10 s−1, respectively. Each deformation condition corresponds to one sample, and a total of 30 tested samples. The maximum deformation degree of the alloy was 70%, and the corresponding maximum true strain was 1.2. The samples were heated to the set experimental temperatures at a heating rate of 5 K/s, and the holding time was 300 s to homogenize the sample temperature. Water quenching was used after compression to retain the deformed structure at high temperatures. Finally, the samples were cut symmetrically along the compression direction, and one sample was inlaid, grounded, and polished in turn. Then, the mixed etching solution HF + HNO3 + H20 (volume percentage 9:27:64) was used for corrosion. The microstructure of the successfully corroded samples was observed by a XJP-6A metallographic microscope. The initial microstructure of the alloy is shown in Fig. 3.

Table 1 The chemical composition (wt%)

Fig. 1

The dimension of specimen a and the schematic drawing of experimental set-up b

Fig. 2

Thermal compression process

Fig. 3

Initial microstructure of Ti-22Al-26Nb-2Ta alloy

2 Results and Discussion

2.1 Flow Behaviors and Deformation Activation Energy of Ti-22Al-26Nb-2Ta Alloy

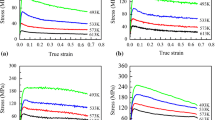
Figure 4a, b show the true stress-true strain curves of Ti-22Al-26Nb-2Ta alloy at a strain rate of 0.001 s⁻¹, deformation temperature in 1173–1423 K, a strain rate of 0.001–10 s⁻¹, and deformation temperature 1323 K. Figure 4a, b show that at the initial stage of deformation, the flow stress increased rapidly with the increase of strain variables, and the average increase was about 92.4%. When the flow stress reached the peak, the flow stress decreased gradually with the continuous increase of strain variables and the average reduction was about 59.8%; when the strain reached 0.8, the flow stress slightly changed with the increase of strain. This phenomenon was because the dislocation density increased sharply in the initial stage of deformation, and the dislocation entanglement led to the blocks of dislocation climbing and sliding, resulting in the work hardening [13,14,15]. The work hardening rate (θ) was changeable during hot deformation; the work hardening rate could be interpreted by the function [15]: $\theta = \left( {\partial \sigma /\partial \varepsilon } \right)_{{T,{\kern 1pt} \dot{\varepsilon }}}$. As a result, the variation of work hardening rate (θ) under different temperatures and strain rates are shown in Fig. 4 (c) and (d). As can be seen from Fig. 4c, d, at this stage (ε = 0 ~ 0.08), the working hardening rate was at a high level (the average value of θ was 2772). Work hardening was dominant, and the corresponding flow stress rose rapidly on the true stress-true strain curves, which was consistent with the above results. When the strain reached the critical strain of dynamic recrystallization, enough energy was accumulated inside the alloy, and the softening effect of dynamic recrystallization was enhanced with the strain increase; the softening effect was not enough to counteract the work hardening effect, and the flow stress increased slowly on the true stress-true strain curve until the flow stress reached the peak value. With the continuous development of strain variables, dynamic softening had a dominant role. The flow softening behavior could be quantified by using flow softening index ($\Delta$), which was calculated as follow [16, 17]:

$$\Delta = \frac{{\sigma_{{\text{p}}} - \sigma_{0.6} }}{{\sigma_{{\text{p}}} }}$$

(1)

where _p is the peak stress (MPa) and _0.6 is the flow stress (MPa) at a strain of 0.6.

Fig. 4

The experimental true stress-true strain curves at different deformation conditions (a $\dot{\varepsilon }$ = 0.001 s⁻¹; b T = 1323 K) and variation curves of work hardening rate (c$\dot{\varepsilon }$ = 0.001 s⁻¹; d T = 1323 K)

Table 2 presents the flow softening index ($\Delta$) at different deformation conditions. Figure 5 a shows the changing curves of the flow softening indexes with temperatures and strain rates according to Table 2. It can be seen from Fig. 5a that under the condition of low strain rates (0.001 ~ 0.01 s⁻¹), the overall flow softening index was relatively large (the average value of $\Delta$ was 0.57), which may be because the low strain rate provided sufficient incubation period for recrystallization, and recrystallization promoted the softening process [16,17,18]; the flow softening degree increased with the increased temperature. When the temperatures were 1323 ~ 1423 K, the flow softening index decreased with the increased of strain rates (0.1 ~ 10 s⁻¹), which was because the higher work hardening rate (Fig. 4d) at high strain rates slowed the dynamic softening. After the flow stress reached peak value on the true stress-true strain curve, the flow stress gradually decreased with the increase of strain until the dynamic balance between work hardening and dynamic softening was reached, which was consistent with the above results. Figure 5b shows the 3D flow stress map of the alloy at T = 1173 ~ 1423 K and $\dot{\varepsilon }$ = 0.001 ~ 10 s⁻¹ under strain 0.6. Figure 5b shows that when the temperature of deformation was constant with the increased strain rate, the flow stress increased, indicating that Ti-22Al-26Nb-2Ta alloy was a positive strain rate-sensitive material; when the strain rate was constant with the increased deformation temperature, the flow stress decreased, indicating that the alloy was also a negative temperature-sensitive material. This effect was because the growth of the strain rate lead to a large number of dislocation proliferation and reduced the occurrence of dynamic recrystallization, thereby increasing the rheological stress. On the contrary, the increased temperature promoted the occurrence of dynamic recrystallization and other thermal activation processes, enhanced the dynamic softening, reduced the processing hardening, and dropped the rheological stress.

Table 2 The flow softening index at different deformation conditions

Fig. 5

The curves of the flow softening indexes at different temperatures and strain rates a and the 3D flow stress map at ε = 0.6 b

The activation energy of hot deformation Q was an important parameter to characterize the difficulty of plastic deformation at high temperature, which was related to the microscopic mechanism that controlled the high-temperature deformation behavior of materials [15]:

$$Q = 1000 \cdot R\left( {\frac{{\partial \ln \dot{\varepsilon }}}{\partial \ln [\sinh (\alpha \sigma )]}} \right)_{T} \left( {\frac{\partial \ln [\sinh (\alpha \sigma )]}{{\partial (1000/T)}}} \right)_{{\dot{\varepsilon }}} {\kern 1pt}$$

(2)

where Q is the hot deformation activation energy (J·mol⁻¹); R is the gas constant (8.314 J·(mol·K)⁻¹); $\dot{\varepsilon }$ is the strain rate (s⁻¹); is the true stress (MPa); T is the temperature (K); the stress level factor α is material constants, and α can be deduced through the two constants (n₁ and β) [19, 20], $\alpha = \beta /n_{1} = (\partial \ln \dot{\varepsilon }/\partial \sigma )/(\partial \ln \dot{\varepsilon }/\partial \ln \sigma )$.

The activation energy at different temperatures, strain rates, and strains can be calculated by the above method, and the corresponding activation energy map can be constructed. Figure 6a and b show 3D activation energy maps at different temperatures and strain rates, as well as at different strains and temperatures. It can be seen from Fig. 6 that the Q value in the entire region was significantly higher than the self-diffusion activation energies of pure α titanium alloy (204 kJ mol⁻¹) and pure β titanium alloy (161 kJ·mol⁻¹) [21]. This means that there were other deformation mechanisms other than high-temperature diffusion during thermal deformation. At that time, the deformation process of the alloy may be affected by the combined effect of the pinning mechanism and the dislocation; larger energy was required to initiate the dislocation [22]. With the increased strain, the deformation activation energy decreased slightly at lower temperatures (1173 ~ 1250 K), increased significantly at 1250 ~ 1330 K, and decreased sharply at 1330 ~ 1423 K. At the same temperature, the deformation activation energy at high strain rates (0.1 ~ 10 s⁻¹) was generally higher (the average value of Q was 614.5 kJ mol⁻¹), and higher than the self-diffusion activation energies of pure α and pure β titanium alloys. This may be because when the strain rate was higher, the driving force required for dynamic softening was smaller, and the densities of vacancies and dislocations between alloy grains were also smaller. At this time, the attraction needed to overcome between atoms at partial recrystallization and the energy consumed was increased, which lead to an increase in the deformation activation energy of the alloy [23]. With the increased temperature, the hot activation energy map generally presented an inverted V shape; the deformation activation energy increased firstly and then decreased. The reason for this phenomenon may be that when deformation was at a higher temperature, the atomic motion ability was enhanced, and the dislocation movement was aggravated, which in turn increased the deformation activation energy. It is also possible that the solute atoms were pinned, resulting in a significant increase in the activation energy. In addition, as the deformation temperature further increased, the dynamic softening effect gradually increased, which makes the deformation easier, resulting in a decreased activation energy [24]. Under different strains, the deformation activation energy at low temperatures was relatively higher, because the deformation at this time was dominated by work hardening, which was consistent with results in Fig. 4c.

Fig. 6

3D deformation activation energy maps at different deformation conditions

2.2 LSSVM Constitutive Model Based on the GA

LSSVM adopts the quadratic programming method to change the inequality constraints into equality constraints in support vector machine (SVM) and transforms the quadratic programming into the problem of solving linear equations [25]. It uses limited sample information to find the optimal balance between model learning ability and complexity, thereby improving the generalization ability of the model, and has good performance in solving nonlinear and high-dimensional aspects. It overcomes the shortcomings of the conventional forecasting methods, such as less original data, rough data and large data volatility.

For the construction of the constitutive model, given a set of n-dimensional vector sample set {(x_i, y_i), i = 1, 2, 3, …, l}, where x_i∈Rⁿ was the input vector (strainε, deformation temperature T, strain rate $\dot{\varepsilon }$ of Ti-22Al-26Nb-2Ta alloy hot compression experiment) and y_i∈R was the output vector (flow stressσ). A nonlinear mapping $\phi ( \cdot )$ was used to map the sample from the original space Rⁿ to the high-dimensional feature space $\phi (x_{i} )$, in which the optimal regression function $f(x) = w\phi (x) + b$ was constructed. According to the principle of structure minimization, the objective function and constraint conditions are set as follows:

$$\left\{ \begin{gathered} \mathop {\min }\limits_{w,b,e} J(w,e) = \frac{1}{2}w^{{\text{T}}} w + \frac{1}{2}\gamma \sum\limits_{i = 1}^{N} {e_{i}^{2} } \hfill \\ {\text{s.t.}}y_{i} = w^{{\text{T}}} \phi (x_{i} ) + b + e_{i} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} ...,{\kern 1pt} {\kern 1pt} {\kern 1pt} l \hfill \\ \end{gathered} \right.$$

(3)

where J(w, e) represents the objective optimization function; w represents the spatial weight coefficient; $\gamma$ represents the penalty coefficient of the loss function, and $\gamma$ ≥ 0; b represents the deviation; e_i represents the training error.

By introducing the Lagrangian function, the optimization problem of formula (3) was converted to the dual space for solution:

$$L(w,b,e,a) = J(w,e) - \sum\limits_{i = 1}^{l} {\left[ {a_{i} w^{{\text{T}}} \phi (x_{i} ) + b + e_{i} - y_{i} } \right]}$$

(4)

where a_i is Lagrange multiplier.

According to the karush-kuhn-tuker (KKT) conditions in the optimization theory, the Lagrange function is used to obtain partial derivatives of w, b, e_i, and a_i in formula (4). The results are as follows:

$$\left\{ \begin{gathered} \frac{\partial L}{{\partial w}} = 0 \to w = \sum\limits_{i = 1}^{l} {a_{i} \phi (x_{i} ),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} ...,{\kern 1pt} {\kern 1pt} {\kern 1pt} l{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } \hfill \\ \frac{\partial L}{{\partial b}} = 0 \to \sum\limits_{i = 1}^{l} {a_{i} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} ...,{\kern 1pt} {\kern 1pt} {\kern 1pt} l} \hfill \\ \frac{\partial L}{{\partial e_{i} }} = 0 \to a_{i} = \gamma e_{i} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} ...,{\kern 1pt} {\kern 1pt} {\kern 1pt} l \hfill \\ \frac{\partial L}{{\partial a_{i} }} = 0 \to w^{{\text{T}}} \phi (x_{i} ) + b + e_{i} - y_{i} = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,{\kern 1pt} {\kern 1pt} 2,{\kern 1pt} {\kern 1pt} {\kern 1pt} ...,{\kern 1pt} {\kern 1pt} {\kern 1pt} l \hfill \\ \end{gathered} \right.$$

(5)

By eliminating w and e_i in formula (5), the following linear equations can be obtained:

$$\left[ {\begin{array}{*{20}c} 0 & {s^{{\text{T}}} } \\ s & {K + \gamma^{ - 1} I} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} b \\ a \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 0 \\ y \\ \end{array} } \right]$$

(6)

where y = [y₁, y₂, …, y_i]^T; I is identity matrix; s = [1, 2, …, l]; a = [a₁, a₂, …, a_l]^T; b = [b₁, b₂, …, b_l]^T; K = $\phi (x_{i} )^{{\text{T}}} \phi (x_{j} )$.

According to Mercer’s theorem, the inner product operation is replaced by the kernel function k(x_i, y_j), and the least square method is used to solve the a and b in formula (6), and the constitutive relationship prediction model of the alloy based on the LSSVM algorithm can be obtained:

$$f(x) = \sum\limits_{i = 1}^{l} {a_{i} } k(x_{i} ,y_{j} ) + b$$

(7)

There are many choices for the kernel function in formula (7), including the linear kernel, polynomial kernel, multi-layer perceptual kernel, radial basis kernel, and so on. In the regression prediction, the radial basis function $k(x_{i} ,x_{j} ) = {\text{exp}}( - \left\| {x_{i} - x_{j} } \right\|^{2} /2\delta^{2} )$ ($\delta$ represents the undetermined width parameter of the kernel function, reflecting the radius contained in the boundary closure) had a better effect. We selected this function as the kernel function of LSSVM to establish the model.

The width parameter $\delta$ of the kernel function and the penalty coefficient $\gamma$ are crucial to the generalization performance of LSSVM: the selection of $\gamma$ will directly affect the calculation complexity and stability of the entire model and $\delta$ controls the radial action range of the entire function. In practical applications, trial-and-error methods or empirical determination of $\delta$ and $\gamma$ are usually used. It is not only time-consuming and labor-intensive, but also easy to choose blindly, and the effect is not good. Therefore, we used a genetic algorithm (GA) to perform global optimization and determined the parameters of LSSVM to improve the predictive ability of the constitutive model. By using MATLAB software and the LSSVM toolbox, the constitutive prediction model of GA-LSSVM was established.

GA is a global probabilistic search algorithm with adaptive capabilities. Its core process of solving problems includes coding (binary), genetic operations (selection, crossover, mutation), and fitness function. LSSVM requires the optimization of two parameters, so the populations dimension d = 2 and other parameter settings of GA-LSSVM are shown in Table 3. The input and output data were selected from T = 1173 ~ 1423 K, $\dot{\varepsilon }$ = 0.001 ~ 10 s⁻¹, and ε = 0 ~ 1.2. Table 4 shows the division of the alloy samples, F represents the data used to train the prediction model, X represents the data used to test the accuracy of the prediction model. The specific steps of GA-LSSVM optimization and flow stress prediction are as follows:

• (1) Input training data.

• (2) Population initialization. The individual coding method uses real coding to encode the sum $\gamma$ and $\delta^{2}$ of LSSVM.

• (3) The fitness value of the individual is calculated. The fitness objective function is calculated to find a set of parameters ($\gamma$, $\delta^{2}$). The LSSVM is trained to calculate the objective function formula (8), global minimum, and the fitness value maximum, and then judge whether the accuracy requirements were met. If so, execute step (7), otherwise execute step (4).

  $$\left\{ \begin{gathered} \min f(\gamma ,\delta^{2} ) = \frac{1}{2l}\sum\limits_{i = 1}^{l} {(y_{i} - y_{i}^{^{\prime}} )^{2} } \hfill \\ {\text{s.t.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma \in {[}\gamma_{{{\text{min}}}} {,}\gamma_{{{\text{max}}}} {],}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta^{2} \in [\delta^{2}_{\min } ,\delta^{2}_{\max } ] \hfill \\ \end{gathered} \right.$$

  (8)

  where y_i and y_i´ are the actual and predicted values of the i-th sample, respectively.

• (4) Selection. Individuals with good fitness are selected and passed on to the next generation to improve global convergence and calculation speed.

• (5) Crossover. Randomly select the genes at position j of the k-th chromosome α_k and the l-th chromosome α_l for the exchange to produce new outstanding individuals:

  $$\left\{ \begin{gathered} \alpha_{kj} = \alpha_{kj} (1 - \beta ) + \alpha_{lj} \beta \hfill \\ \alpha_{lj} = \alpha_{lj} (1 - \beta ) + \alpha_{kj} \beta \hfill \\ \end{gathered} \right.$$

  (9)

  where α_kj represents the gene at position j of the k-th chromosome; α_lj represents the gene at position j of the l-th chromosome; $\beta \in [0,{\kern 1pt} {\kern 1pt} 1]$.

• (6) Variation. Randomly select the j-th chromosome of the i-th individual from the population to mutate into a better individual:

  $$\alpha_{ij} = \left\{ \begin{gathered} \alpha_{ij} + (\alpha_{ij} - \alpha_{\max } )f(g),{\kern 1pt} {\kern 1pt} {\kern 1pt} r \ge 0.5 \hfill \\ \alpha_{ij} + (\alpha_{\min } - \alpha_{ij} )f(g),{\kern 1pt} {\kern 1pt} {\kern 1pt} r < 0.5 \hfill \\ \end{gathered} \right.$$

  (10)

  where α_max and α_min are the upper and lower bounds of the value of gene α_ij; f(g) = r(1-g/G_max)², where g is the current iteration number, G_max is the maximum evolutionary algebra, and r is a random number in the interval [0, 1].

• (7) Stop the cycle and get the best chromosome. The optimal individual obtained by the genetic algorithm optimization is decomposed into $\gamma$ and $\delta^{2}$ as the parameters of the GA-LSSVM constitutive model for prediction.

Table 3 Parameters setting of GA-LSSVM model

Table 4 Specimen division

Finally, the best penalty parameter $\gamma$ = 243.642 and kernel parameter $\delta^{2}$ = 1.731 were determined. After that, the LSSVM model was trained and tested again. The process is shown in Fig. 7. The optimized LSSVM model can quickly reach the target error value of 10^–5, and the training accuracy of the GA-LSSVM algorithm is relatively high (R = 0.99994).

Fig. 7

The training and testing process of GA-LSSVM algorithm constitutive model

Figure 8 shows the experimental values and comparison of fitted flow stress, thereby verifying the applicability of the GA-LSSVM constitutive model at different T,, and $\dot{\varepsilon }$. Besides, the accuracy of the chosen model can be assessed through the following three parameters: R, μ, and MRE. They can be defined as:

$$R = \frac{{\sum\limits_{{{\text{i}} = 1}}^{n} {\left( {F_{{\text{i}}} - \overline{F}} \right)\left( {X_{{\text{i}}} - \overline{X}} \right)} }}{{\sqrt {\sum\limits_{{{\text{i}} = 1}}^{n} {\left( {F_{{\text{i}}} - \overline{F}} \right)^{2} } } \sqrt {\sum\limits_{{{\text{i}} = 1}}^{n} {\left( {X_{{\text{i}}} - \overline{X}} \right)}^{2} } }}$$

(11)

$$\mu {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{F_{{\text{i}}} - X_{{\text{i}}} }}{{F_{{\text{i}}} }}$$

(12)

$$MRE{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{n}\;\sum\limits_{{{\text{i}} = 1}}^{n} {\left| {\frac{{F_{{\text{i}}} - X_{{\text{i}}} }}{{F_{{\text{i}}} }}} \right| \times 100{\kern 1pt} {\kern 1pt} {\kern 1pt} \% }$$

(13)

where F_i and X_i represent the experiment data of the testing and the corresponding predicted data acquired from the constitutive model; n is the number of testing data; $\overline{F}$ and $\overline{X}$ are the average values of F_i and X_i, respectively. The correlation coefficient (R) is usually used to show the linear relations between predicted and experimental data. To evaluate the selected model, average relative error (MRE) and relative error (μ) were considered unbiased statistics for confirming the credibility of the model.

Fig. 8

The fitted values of GA-LSSVM algorithm constitutive model under different deformation conditions are compared with the experimental data (a $\dot{\varepsilon }$ = 0.001 s⁻¹; b T = 1323 K)

It can be seen from Fig. 8 that the true stress–strain curve drawn by the fitted value and the experimental value coincided within the experimental range. The relative error distribution between the experimental data and the fitted data is shown in Fig. 9 (a). The average value of μ was close to 0, and it conformed to a typical normal distribution. It can be seen from Fig. 9 (b) that the relative error of most samples is within 10%, accounting for 93.18%. Furthermore, MRE for all samples is only 6.74%; R is 0.9922, which shows that the GA-LSSVM algorithm constitutive model has a good fitting ability.

Fig. 9

Evaluation of the GA-LSSVM constitutive model

The cross-validation technique [26,27,28,29] was used to evaluate the predictive capability of the constructed GA-LSSVM constitutive model. Fifteen trial data sets were constructed by individually extracting the stress–strain experimental curves tested in the sample division (Table 4), as shown in Table 5. The model was then reconstructed for each trial data set, the excluded conditions were predicted and compared with the experimental values, and the results were shown in Fig. 10; the predicted values of the model and the experimental values were in good agreement (R = 0.9951 and MRE = 6.17%). It is further proved that the GA-LSSVM constitutive model had good accuracy. In general, the GA-LSSVM algorithm constitutive model constructed in this paper was relatively efficient and simple, and provided a new alternative method for predicting flow stress.

Table 5 The excluded conditions in trial data sets

Fig. 10

Comparison between the predicted results of the GA-LSSVM model and the experimental results

3.3 3D processing map.

2.2.1 Processing Map Based on DMM and PRM

The dynamic material model (DMM) was established by Prasad based on system engineering concept and based on the basic principles of continuum mechanics of large strain plastic deformation, irreversible thermodynamics, and physical system simulation [30,31,32]. According to the DMM theory, the total energy P consumed by plastic deformation of the deformable body in the unit time can be divided into two parts: energy G dissipated in the form of thermal energy and energy J consumed in microstructure change:

$$P = \sigma \dot{\varepsilon } = G + J = \int_{0}^{{\dot{\varepsilon }}} {\sigma {\text{d}}\dot{\varepsilon }} + \int_{0}^{\sigma } {\dot{\varepsilon }{\text{d}}\sigma }$$

(14)

where G represents the power dissipation content, which indicates that the viscoplastic heat will be produced by power dissipation during plastic deformation ($G = \int_{0}^{{\dot{\varepsilon }}} \sigma {\text{d}}\dot{\varepsilon } = \sigma \dot{\varepsilon }/(1 + m)$); J represents the co-content of power dissipation that is related to the evolution of microstructure in the process of deformation ($J = \int_{0}^{\sigma } {\dot{\varepsilon }} {\text{d}}\sigma = [m/(1 + m)] \cdot \sigma \dot{\varepsilon }$).

Prasad et al. [33] used cubic spline function to fit the relationship between ln and ln $\dot{\varepsilon }$, and derived the formula of strain rate sensitivity index m:

$$m = \left[ {\frac{\partial J}{{\partial G}}} \right]_{{\varepsilon ,{\kern 1pt} T}} = \left[ {\frac{{\dot{\varepsilon }{\kern 1pt} {\text{d}}\sigma }}{{\sigma {\kern 1pt} {\text{d}}\dot{\varepsilon }}}} \right]_{{\varepsilon ,{\kern 1pt} T}} = \left[ {\frac{{\partial {\text{ln}}\sigma }}{{\partial \ln \dot{\varepsilon }}}} \right]_{{\varepsilon ,{\kern 1pt} T}}$$

(15)

Power dissipation efficiency η:

$$\eta = \frac{J}{{J_{{{\text{max}}}} }} = \frac{2m}{{m + 1}}$$

(16)

where η is a dimensionless parameter, it forms a power dissipation map with the change of strain rate and temperature. The η contour line on the map of power dissipation expresses the relative entropy production rate associated with the evolution of the material’s microstructure.

Meanwhile, Prasad et al. [34, 35] proposed the criteria of plastic instability:

$$\xi (\dot{\varepsilon }) = \frac{{\partial \ln (\frac{m}{m + 1})}}{{\partial \ln \dot{\varepsilon }}} + m < 0$$

(17)

The instability map can be formed through the relationship between value of $\xi (\dot{\varepsilon })$ and strain rate and temperature and calculating the area of $\xi (\dot{\varepsilon })$ < 0. The power dissipation map and the instability map were superimposed to obtain a processing map based on DMM.

Compared with DMM, the polar reciprocity model (PRM) takes into account the dependence between flow stress and processing history. At the same time, the dependence of flow stress on the strain rate is considered as the main rheological characteristic of the workpiece during thermal processing [36,37,38]. In this model, power is divided into two parts: one is the hardening power, expressed by $\dot{W}_{H}$ ($\dot{W}_{H} = \int_{0}^{{\dot{\varepsilon }}} \sigma {\text{d}}\dot{\varepsilon }$); the other part is the dissipative power, expressed by $\dot{W}_{D}$ ($\dot{W}_{D} = \int_{0}^{\sigma } {\dot{\varepsilon }} {\text{d}}\sigma$).

In PRM, an intrinsic hot workability parameter ξ based on hardening power $\dot{W}_{H}$ is defined as: $\xi = \dot{W}_{H} /\dot{W}_{{H_{\min } }} - 1$. When the two convex potential functions have polar reciprocity, there is $\left( {\dot{\varepsilon }^{P} } \right)^{{m^{\prime}}} = F\left( {\dot{\varepsilon }^{P} } \right)$, m´ represents the corrected strain rate sensitivity index. Rajagopalachary et al. [36] used the following constitutive equation:

$$\sigma = C \cdot F\left( {\dot{\varepsilon }^{P} } \right) + H\left( {\varepsilon^{P} } \right)$$

(18)

where C and H(εP) are functions related to the processing history among which: $H{(}\varepsilon^{P} {)} = \sigma \cdot (\int_{0}^{{\varepsilon_{1} }} {\sigma {\kern 1pt} d\varepsilon - \int_{0}^{{\varepsilon_{1} }} {\sigma_{\min } {\kern 1pt} {\kern 1pt} d\varepsilon } } )/(\int_{0}^{{\varepsilon_{1} }} {\sigma {\kern 1pt} d\varepsilon } )$_.

It can be concluded that:

$$\xi = 1 - \left( {\frac{{\sigma - H(\varepsilon^{P} )}}{\sigma }} \right)\left( {\frac{{2m^{^{\prime}} }}{{m^{^{\prime}} + 1}}} \right)$$

(19)

In the processing map based on the PRM theory, there is no need to distinguish between stable and unstable regions. Rajagopalachary and Kutumbarao [36] concluded that it was an unstable situation when ξ approaches 1.

According to formulas (15) ~ (16, 17)), the strain rate sensitivity index m, the power dissipation efficiency η, and the instability parameter $\xi (\dot{\varepsilon })$ were calculated. 3D contour maps of strain rate sensitivity index for true strains of 0.9 and 1.2 were constructed as shown in Fig. 11. Figure 12 shows the constructed 3D relationship map between ε, $\dot{\varepsilon }$, and T and the values of $\xi (\dot{\varepsilon })$ and η. It can be concluded from the 3D power dissipation map (Fig. 12a) that the value of power dissipative efficiency (η = 0.52 ~ 0.80) was higher when T = 1173 ~ 1423 K and $\dot{\varepsilon }$ = 0.001 ~ 0.01 s⁻¹; with the increased strain, the areas of higher power dissipative efficiency gradually decreased. In general, the high η value region corresponded to a better processability region. Power dissipative efficiency (η = 0.081 ~ 0.37) was lower when T = 1173 ~ 1273 K and $\dot{\varepsilon }$ = 0.01 ~ 10 s⁻¹; the areas of lower power dissipative efficiency was maximum when the strain became 0.9. The red area was the stable region and black was unstable in the 3D instability map (Fig. 12 (b)). The range of processing parameters that should be avoided during thermal deformation can be confirmed by the region defined through the unstable parameter $\xi (\dot{\varepsilon })$. From the whole 3D instability map, it can be concluded that instability areas were concentrated in 1173 ~ 1273 K/0.004 ~ 0.1 s⁻¹ and 1323 ~ 1423 K/0.001 ~ 0.01 s⁻¹. The instability areas appeared when the strain became 0.6 and T = 1273 ~ 1303 K and $\dot{\varepsilon }$ = 1 ~ 10 s⁻¹.

Fig. 11

3D contour maps of strain rate sensitivity index (a ε = 0.9; b ε = 1.2)

Fig. 12

3D power dissipation map a and 3D instability map b of Ti-22Al-26Nb-2Ta alloy

In this paper, the intrinsic hot workability parameter ξ was calculated based on the formula (19); the processing maps of the alloy were constructed based on DMM and PRM at true strains 0.9 and 1.2 as shown in Fig. 13. In the processing map based on DMM (Fig. 13a, b), the number on the contour line was the power dissipation efficiency η value, and the regions with higher power dissipation efficiency generally corresponded to a better range of deformation process parameters. The shaded areas were the parameter ranges of rheological instability during thermal deformation. It can be concluded from Fig. 13a, b) that the rheological instability region expanded and then remained stable with the increased strain during T = 1173 ~ 1258 K and $\dot{\varepsilon }$ = 0.004 ~ 0.56 s⁻¹. Within T = 1263 ~ 1303 K and $\dot{\varepsilon }$ = 1 ~ 10 s⁻¹, the flow instability region gradually moved in the direction of increasing strain rate, and the area of the region gradually increased. The area of rheological instability region gradually decreased towards the direction of low strain rate with the increased strain in the region of T = 1333 ~ 1393 K and $\dot{\varepsilon }$ = 0.001 ~ 0.01 s⁻¹. When the strain was 1.2, the material’s power dissipative efficiency was lower under the high deformation rate and was mostly in the instability area. This alloy was not suitable for high strain rate (such as hammer forging). It could also be seen from Fig. 13a, b that there was mainly one peak area of η in the processing map. This region was: T = 1173 ~ 1273 K, $\dot{\varepsilon }$ = 0.001 ~ 0.003 s⁻¹, and the corresponding maximum value of η was 0.78. Judging from the processing map based on DMM, it can be considered that the above regions were suitable for hot deformation process parameters. As shown in Fig. 13c, d (the processing map based on PRM), the values on the contour line in the figure represented intrinsic hot workability parameters. As $\dot{\varepsilon }$ and ε increased and T decreased, ξ slowly decreased. It can be seen from Fig. 13c, d that the ξ maxima (ξ approached 1) region mainly appeared in: T = 1173 ~ 1223 K and $\dot{\varepsilon }$ = 0.001 ~ 0.74 s⁻¹, T = 1248 ~ 1348 K and $\dot{\varepsilon }$ = 0.001 ~ 0.01 s⁻¹, and T = 1273 ~ 1323 K and $\dot{\varepsilon }$ = 5.6 ~ 10 s⁻¹. According to the theory of the PRM, the above-mentioned area was the unstable area of the alloy. The ξ minimum value region was mainly in T = 1173 ~ 1226 K, $\dot{\varepsilon }$ = 0.001 ~ 0.0032 s⁻¹, and the minimum value of ξ was 0.41. Judging from the processing map based on PRM, the above region could be considered as a suitable hot deformation process parameter of the alloy.

Fig. 13

Processing map based on DMM and PRM at different strains (ε = 0.9:a and c; ε = 1.2: b and d)

2.2.2 Verification of Microstructure

The range of process parameters optimized by 3D processing maps also needed to be verified by observation and analysis of the microstructure. Figure 14a (T = 1173 K and $\dot{\varepsilon }$ = 0.01 s⁻¹) and b (T = 1373 K and $\dot{\varepsilon }$ = 0.001 s⁻¹) all have local plastic flow phenomena and diversities in direction. The adiabatic shear phenomenon can be seen in the microstructure of Fig. 14 c (T = 1273 K and $\dot{\varepsilon }$ = 1 s⁻¹). The angle between the direction of the adiabatic shear band and the direction of the compression axis was about 45°. This was because of the low thermal conductivity of titanium alloy, which was easy to produce adiabatic temperature-rise effect during deformation, resulting in adiabatic shear. In addition, the effect may be related to the deformation zone and stress state of the compression specimen. The emergence of local flow and adiabatic shear signify that the material had undergone severe irregular deformation, and these areas should be avoided during actual processing. Figure 14d (T = 1273 K and $\dot{\varepsilon }$ = 10 s⁻¹) can be seen that microstructure had different degrees of cracks, and the formation of the cracks had a negative effect on the comprehensive performance of the alloy, so this area should also be avoided during actual processing. The corresponding deformation conditions in Fig. 14a–c belonged to the instability region in the DMM processing map (T = 1173 ~ 1258 K and $\dot{\varepsilon }$ = 0.004 ~ 0.56 s⁻¹; T = 1263 ~ 1303 K and $\dot{\varepsilon }$ = 1 ~ 10 s⁻¹; and T = 1333 ~ 1393 K and $\dot{\varepsilon }$ = 0.001 ~ 0.01 s⁻¹). In the PRM processing map, the ξ value under these conditions did not approach 1, so the prediction of PRM under these conditions failed. The corresponding deformation conditions in Fig. 14d belonged to the instability region in the DMM processing map (T = 1263 ~ 1303 K and $\dot{\varepsilon }$ = 1 ~ 10 s⁻¹), and the value of ξ in the PRM processing map approached 1. Therefore, the predictions of DMM and PRM under this condition are both accurate.

Fig. 14

Microstructure of deformation instability zone (a T = 1173 K, $\dot{\varepsilon }$ = 0.01 s⁻¹; b T = 1373 K, $\dot{\varepsilon }$ = 0.001 s⁻¹; c T = 1273 K, $\dot{\varepsilon }$ = 1 s⁻¹; d T = 1273 K, $\dot{\varepsilon }$ = 10 s⁻¹)

The microstructure of Ti-22Al-26Nb-2Ta alloy (Fig. 15a–c in the stable region showed that under the condition of a low strain rate (0.001 s⁻¹), the grain size was generally smaller and the deformation was uniform and stable. With the increased temperature, the microstructure became more uniform and equiaxed. The corresponding deformation conditions in Fig. 15a–c belong to the peak region of power dissipation efficiency in the DMM processing map (T = 1173 ~ 1273 K and $\dot{\varepsilon }$ = 0.001 ~ 0.003 s⁻¹), and the corresponding strain rate sensitivity index was 0.64. The deformation conditions corresponding to Fig. 15a, b belonged to the ξ minimum region in the PRM processing map, and the corresponding hot workability parameter was 0.43. The strain rate sensitivity index m reflected the ability of the metal to generate uniform deformation or resist local deformation. It was an important index for judging the mechanism of superplastic deformation. It is generally believed that if the material’s strain rate sensitivity index is greater than 0.3, superplasticity is prone to occur [18, 39, 40]. Kutumbarao et al. [37] studied the modeling of metal hot working behavior and found that superplasticity of the material may occur when the hot workability parameter ξ < 0.5. In the process of superplastic forming, the grain boundary slip was accompanied by diffusion creep. The migration of atoms regulated the grain boundary slip. The grain boundary had high mobility, so the power dissipation efficiency was high, which was consistent with the results of the processing map. For the fine-grained superplasticity, fine structure, equiaxed, and dual-phase are one of the conditions for superplastic forming. If the temperature was in a certain range, the strain rate was low, and the microstructure was fine; it can be roughly considered that superplastic forming occurred easily [18, 41, 42]. The above description was consistent with the stable-zone microstructure of the alloy. According to the analysis of the processing map and microstructure, the deformation mechanism of the corresponding region may be fine-grained superplasticity under the condition of the deformation process parameters. However, the corresponding deformation conditions in Fig. 15 c corresponded to the value of ξ that approached 1 in the PRM processing map, which did not belong to the ξ minimum region, so the prediction of PRM under this condition was invalid.

Fig. 15

Microstructure of deformation stability zone (a T = 1173 K, $\dot{\varepsilon }$ = 0.001 s⁻¹; b T = 1223 K, $\dot{\varepsilon }$ = 0.001 s⁻¹; c T = 1273 K, $\dot{\varepsilon }$ = 0.001 s⁻¹)

In conclusion, the DMM processing map based on the Prasad instability criterion was more accurate than the PRM processing map in optimizing the process parameters of the alloy. By observing microstructure, the 1173 ~ 1273 K/0.001 ~ 0.003 s⁻¹ were the best parameters during the processing of this alloy.

3 Conclusions

The strain rate and deformation temperature had a great influence on the rheological stress of Ti-22Al-26Nb-2Ta alloy. The rheological stress decreases with a decreased strain rate and increased temperature and shows the rheological softening phenomenon. The alloy is a negative temperature-sensitive and a positive strain rate-sensitive material.

The GA-LSSVM algorithm constitutive model can well describe the non-linear relationship between $\dot{\varepsilon }$, T and and stress and has a good predictive ability. The relative error of most samples was within 10%, accounting for 93.18%. The GA-LSSVM algorithm provides a new method to establish the constitutive model of materials at high temperatures.

Through the analysis of Ti-22Al-26Nb-2Ta alloy via the 3D power dissipation map and 3D instability map, it was concluded that the areas with high power dissipation efficiency value mainly concentrated in 1173 ~ 1423 K/0.001 ~ 0.01 s⁻¹; the instability areas mainly concentrated in 1173 ~ 1273 K/0.004 ~ 0.1 s⁻¹ and 1323 ~ 1423 K/0.001 ~ 0.01 s⁻¹.

The comparison and microstructural observation showed that the DMM processing map was more accurate than the PRM processing map in optimizing the hot deformation process parameters of Ti-22Al-26Nb-2Ta alloy. The instability modes in the rheological instability region of the alloy mainly included adiabatic shear, crack, and local flow. The 1173 ~ 1273 K/0.001 ~ 0.003 s⁻¹ were the best parameters during the processing of the alloy.