An equivalent medium model of stress wave propagation through a three-dimensional geo-stressed rock

Abstract

Applying the equivalent medium method, a dynamic constitutive equation of rock with three-dimensional geo-stress is constructed by modifying the Kelvin-Voigt model, and a theoretical model of stress wave propagation through a three-dimensional geo-stressed rock is proposed. Based on the theory of one-dimensional stress wave propagation, the wave equation of the theoretical model is derived, and the analytical formulas of the stress wave propagation velocity, spatial attenuation coefficient and response frequency are obtained by using harmonic solution. Based on stress wave propagation experimental, the proposed theoretical model is verified by comparing the experimental and theoretical results. Based on the validated theoretical model, the effects of three-dimensional geo-stress on stress wave propagation velocity, spatial attenuation coefficient and response frequency are studied by using the parametric study. The results show that the proposed model of stress wave propagation can effectively study the propagation of stress wave in three-dimensional geo-stressed rock. Three-dimensional geo-stress varies the level of a rock porosity and damage, which makes the rock have different equivalent modulus, and then affects the stress wave propagation characteristics. Moreover, the initial porosity, initial elastic modulus, viscosity coefficient of a rock and vibration frequency have significant influence on the stress wave propagation velocity, spatial attenuation coefficient and response frequency.

Introduction

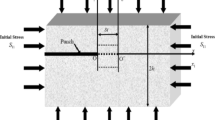
The rock mass is initially subjected to three-dimensional geo-stress (Fan and Sun 2015). In the blasting excavation of underground rock mass engineering, the surrounding rock mass is generally subjected to stress waves produced by dynamic loading (Niu et al. 2020), and there is usually a crucial engineering problem: stability analysis of buildings around explosion source. As shown in Fig. 1, when blasting excavation is carried out in tunnel 1, stress waves pass through the three-dimensional geo-stressed rock mass and then pass through the tunnel 2 and affect it. Simultaneously, the rock is a kind of porous geological material; the pores compaction and damage evolution induced by the three-dimensional geo-stress govern the physical and mechanical properties of a rock (Han et al. 1986; Baud et al. 2014; Xie and Shao 2015; Han et al. 2016; Du et al. 2020a) and significantly influence the properties of stress wave propagation through a rock. Therefore, it is of great significance to study the effects of three-dimensional geo-stress on the properties of stress wave propagation through a rock, which is helpful to the stability analysis of engineering surrounding rock mass and buildings.

Fig. 1

Schematic for stress states of rock mass in underground engineering application

The dynamic properties of a rock include dynamic response and stress wave propagation, both of which are closely related to the geo-stress. Dynamic response characteristics are mainly reflected in the dynamic strength, deformation characteristics, energy dissipation, failure mode and mechanism of a rock (Wang and He 2000; Yin et al. 2012; Zhang et al. 2019a, b; Du et al. 2020b; Yan et al. 2020; Wang et al. 2021; Jiang et al. 2021). Stress wave propagation mainly investigates the propagation and attenuation laws of stress wave in a rock, such as stress wave propagation velocity, amplitude of stress wave, stress wave dispersion characteristics and waveform (Schenk 1971; Proskuryakov et al. 1975; Shkuratnik et al. 2016; Chen et al. 2018; Cheng et al. 2019). There are two main reasons for the attenuation of stress wave amplitude. One of the reasons is that the stress wave dissipates as heat energy on account of the inelastic action of a rock, which is called intrinsic attenuation; the other is that the stress wave scatters in the micro-pores inside a rock, which is called scattering attenuation (Majstorović et al. 2017; Hu et al. 2018). In general, there are two empirical relationships between the wave velocity and stress: quadratic function and power function (Sun and Zhu 2014; Zhu et al. 2020a, b), respectively. At present, the stress wave propagation through a geo-stress rock has been systemically investigated experimentally (Liu et al. 2017; Zhu et al. 2020a; Yuan et al. 2020), which has played a great role in promoting the development of the rock dynamics. However, the results of experimental research have the characteristics of individual cases, while the results of theoretical model research not only have the advantages of generality, but also can characterize the true attribute relations among variables. Therefore, it is particularly urgent to establish a theoretical model of stress wave propagation through a three-dimensional geo-stress rock, which can provide a direct and effective theoretical reference for engineering safety.

The displacement discontinuity method (DDM) and equivalent medium method (EMM) are two typical theoretical approaches to study stress wave propagation through a rock and rock mass. DDM was firstly proposed by Mindlin (1960) and was applied to seismic wave propagation studies by Schoenberg (1980). The basic assumption of the DDM is that the particle displacements along the rock joints are discontinuous, while the stress remains continuous (Niu et al. 2020). DDM has attracted great attention from scholars and has been applied to the propagation of stress wave in various joint rocks, but it is difficult to provide an explicit expression of stress wave propagation (Zhao et al. 2006; Li et al. 2015; Fan et al. 2021). EMM ignores the random distribution of rock pores and takes the porous rock as a whole continuous medium. Simultaneously, EMM uses a representative elementary volume (REV) to obtain the propagation characteristics of stress wave in a rock (Li et al. 2010, 2011; Ma et al. 2013; Jin et al. 2020); the key of the EMM is to extract a reliable equivalent parameter which can characterize the overall dynamic characteristics of a rock. In the scope of existing theoretical research, the propagation laws of stress wave in a rock with macro-joints and micro-cracks is the focus of scholars and established some fruitful models of stress wave propagation based on DDM and EMM (Chai et al. 2016, 2017). However, the stress wave propagation characteristics are also related to the three-dimensional geo-stress that the rock mass subjected to; there are no relevant reports on the theoretical models in this respect. Therefore, it is necessary to put forward a theoretical model of stress wave propagation through a three-dimensional geo-stressed rock and to predict the propagation characteristics of stress wave in a rock; furthermore, the parameters of engineering rock mass can be retrieved.

Based on the EMM, many constitutive models such as Kelvin model, Maxwell model, Generalized Maxwell model, Boltzmann model and Burgers model had been proposed. Kelvin model and Maxwell model are the two most classic constitutive models; they are widely used in many fields of rock engineering (Mogilevskaya and Lecampion 2018; Zhang et al. 2019a, b). Both of the two models abstract a rock into viscous body and damaged body, which can well describe the influence of rock viscosity and damage on its mechanical properties (Du et al. 2021). However, Kelvin model and Maxwell model cannot describe the influence of rock initial pores on mechanical properties of a rock; it is also not possible to characterize the effects of changes in rock porosity on the propagation characteristics of stress waves.

In this paper, a theoretical model of stress wave propagation through a three-dimensional geo-stressed rock is proposed based on EMM. On the basis of the theoretical model, the wave equation of stress wave propagation in three-dimensional geo-stressed rock is derived by combining the one-dimensional stress wave propagation theory. The wave equation is solved by the harmonic method, and the analytical solution of the stress wave propagation velocity, spatial attenuation coefficient and response frequency are obtained. The proposed theoretical model is verified by comparing the experimental and theoretical results. In addition, based on the verified theoretical model, the effects of three-dimensional geo-stress, rock equivalent modulus, initial porosity, viscosity coefficient and vibration frequency on the stress wave propagation characteristics are analysed by detailed parameter study. The innovation of this paper is that a theoretical model of stress wave propagation through a three-dimensional geo-stressed rock is proposed, and the influence characteristics of three-dimensional geo-stress on stress wave in a rock are revealed. The research is helpful to the excavation of underground engineering surrounding rock mass and the inversion of rock parameters.

Establishment of model and solution to wave equation

Abstraction of a rock and modification of Kelvin-Voigt modelling

Based on the equivalent medium method, the rock is abstracted into the equivalent medium composed of three basic elements. To characterize the effects of the rock pores compaction and damage evolution induced by the three-dimensional geo-stress on stress wave propagation, the Kelvin model was modified by adding units of rock void body and skeleton body, that is, the modified model consists of rock void body R_p, skeleton body R_s and viscous body η_v, as shown in Fig. 2.The rock void body R_p, skeleton body R_s and viscous body η_v are, respectively, used to describe the effects of the rock pores compaction, damage evolution and viscosity on the propagation characteristics of the stress wave. In Fig. 2, σ_s, σ_c and σ_d denote the axial static stress, confining pressure and the dynamic stress, respectively.

Fig. 2

Modified Kelvin-Voigt model

Due to the extremely heterogeneous structure within the rock, and considering that rock damage is a continuous and cumulative process, the following basic assumptions are made to facilitate the analysis of the study: (1) A unitary micro-element of rock skeleton, void body and viscous body all assumed to have duality. On the one hand, on the fine view, it is assumed that the size of the micro-elements is large enough to be used as an abstract representation of the rock and thus for mechanical analysis. On the other hand, on the macroscopic side, assuming that the size of the micro-element is small enough, it can be seen as a continuous mass when analysing the damage to the rock. (2) The rock is not viscous under static load, but only under dynamic load with a certain loading rate.

Establishment of the wave equation

As shown in Fig. 2, based on the relationship of the stress balance and strain coordination of the rock void body R_p, skeleton body R_s and viscous body η_v, the stress and strain exhibit the following relationships, respectively:

$$\sigma ={\sigma}_{\mathrm{D}}={\sigma}_{\mathrm{s}}+{\sigma}_{\mathrm{d}}+{\sigma}_{\upeta}$$

(1)

$$\varepsilon ={\varepsilon}_{\mathrm{D}}={\varepsilon}_{\eta }$$

(2)

where σ and ε are the total axial stress and strain of the rock, respectively. σ_D and ε_D are the stress and strain of the damage body that is consisted of the rock skeleton and void, respectively. σ_η and ε_η are the stress and strain of the viscous body, respectively. σ_s and σ_d are the axial static stress and the dynamic stress, respectively.

Assuming that the initial porosity of the rock is γ₀, based on the constitutive model of rock mass (Cao et al. 2016), the stress-strain relationship of the rock skeleton body and the void body under three-dimensional geo-stress as:

$${\varepsilon}_{\mathrm{D}}=\left(1-{\gamma}_0\right){\varepsilon}_D^V+{\gamma}_0{\varepsilon}_D^R$$

(3)

$${\varepsilon}_D^V=1-\exp \left[-\frac{\sigma_{\mathrm{s}}+{\sigma}_{\mathrm{d}}-2{\mu}_1{\sigma}_{\mathrm{c}}}{E_1}\right]$$

(4)

$${\varepsilon}_D^R=\frac{\sigma_{\mathrm{s}}+{\sigma}_{\mathrm{d}}-2{\mu}_2{\sigma}_{\mathrm{c}}}{E_2\left(1-D\right)}$$

(5)

where γ₀ is the initial porosity of the rock; ${\varepsilon}_D^V$ and ${\varepsilon}_D^R$ are the strain of the rock micro-element void body and skeleton body, respectively; μ₁ and E₁ are the Poisson’s ratio and initial elastic modulus of the rock void body; μ₂ and E₂ are the Poisson’s ratio and initial elastic modulus of the rock skeleton body, respectively; and D is the damage value of the rock under static stress coupled with dynamic stress, which lies between 0 and 1.

Substituting Eqs. (4) and (5) into Eq. (3) yields:

$$\varepsilon ={\varepsilon}_{\mathrm{D}}={\gamma}_0\left\{1-\exp \left[-\frac{\sigma_{\mathrm{s}}+{\sigma}_{\mathrm{d}}-2{\mu}_1{\sigma}_{\mathrm{c}}}{E_1}\right]\right\}+\left(1-{\gamma}_0\right)\left[\frac{\sigma_{\mathrm{s}}+{\sigma}_{\mathrm{d}}-2{\mu}_2{\sigma}_{\mathrm{c}}}{E_2\left(1-D\right)}\right]$$

(6)

According to the characteristics of the rock viscous body, the viscous stress σ_η is directly proportional to the strain rate, and its constitutive equation can be expressed mathematically as (Wang 2007):

$${\sigma}_{\eta }=\eta \frac{\partial {\varepsilon}_{\eta }}{\partial t}=\eta \frac{\partial \varepsilon }{\partial t}$$

(7)

where constant η is the viscous coefficient of the viscous body.

By taking the derivative with respect to x, Eqs. (1), (6) and (7) can be transformed into:

$$\frac{\partial \sigma }{\partial x}=\frac{{\partial \sigma}_{\mathrm{d}}}{\partial x}+\frac{{\partial \sigma}_{\eta }}{\partial x}$$

(8)

$$\frac{\partial \varepsilon }{\partial x}=\frac{\gamma_0}{E_1}\exp \left[-\frac{\sigma_{\mathrm{s}}+{\sigma}_{\mathrm{d}}-2{\mu}_1{\sigma}_{\mathrm{c}}}{E_1}\right]\frac{{\partial \sigma}_{\mathrm{d}}}{\partial x}+\frac{\left(1-{\gamma}_0\right)}{E_2\left(1-D\right)}\frac{{\partial \sigma}_{\mathrm{d}}}{\partial x}$$

(9)

$$\frac{{\partial \sigma}_{\eta }}{\partial x}=\eta \frac{\partial^2\varepsilon }{\partial t\partial x}$$

(10)

Substituting Eqs. (9) and (10) into Eq. (8) yields:

$$\frac{\partial \sigma }{\partial x}=\frac{1}{\beta}\frac{\partial \varepsilon }{\partial x}+\eta \frac{\partial^2\varepsilon }{\partial t\partial x}$$

(11)

Among them:

$$\frac{{\partial \sigma}_{\mathrm{d}}}{\partial x}=\frac{1}{\beta}\frac{\partial \varepsilon }{\partial x}$$

(12)

$$\beta =\frac{\gamma_0}{E_1}\exp \left[-\frac{\left({\sigma}_{\mathrm{s}}+{\sigma}_{\mathrm{d}}\right)-2{\mu}_1{\sigma}_{\mathrm{c}}}{E_1}\right]+\frac{\left(1-{\gamma}_0\right)}{E_2\left(1-D\right)}$$

(13)

where β is the reciprocal of equivalent modulus of the stressed rock, and the rest of the symbols are expressed as above.

According to the theory of one-dimensional stress wave propagation, Eq. (13) can be transformed into:

$$\rho \frac{\partial^2u}{{\partial t}^2}=\frac{1}{\beta}\frac{\partial^2u}{{\partial x}^2}+\eta \frac{\partial^3u}{{\partial x}^2\partial t}$$

(14)

Equation (14) is the wave equation in a rock with three-dimensional geo-stress.

Solutions to the wave equation

The surrounding rock mass in the three-dimensional geo-stress environment has different initial porosity. In deep rock engineering, when stress waves generated by earthquakes or artificial blasting pass through the surrounding rock mass, the stress waves produce pore compression and damage evolution on the surrounding rock mass, resulting in changes in the modulus, which in turn affects the stress wave propagation characteristics. Fig. 3 shows the theoretical model of stress wave propagation in a three-dimensional geo-stressed rock constructed in this paper. The stress wave propagates to the left interface of the rock and passes through the rock to produce pore compression and damage evolution, resulting in changes in the propagation characteristics such as stress wave propagation velocity, amplitude spatial attenuation coefficient, and response frequency at the right interface of the rock.

Fig. 3

A theoretical model of stress wave propagation in three-dimensional geo-stressed rocks

In order to characterize the influence of vibration frequency of the source, three-dimensional geo-stress and rock initial parameters on the propagation and attenuation characteristics of stress wave, the harmonic method is adopted to solve Eq. (14) in combination with the characteristics of partial differential equations shown in Eq. (14). Assuming that stress wave is consisted of a series of simple harmonics, the harmonic equation for vibrating particle at a distance x from the seismic source as (Wang 2007):

$$u\left(x,t\right)={u}_0{e}^{i\left({\omega}_1t-{k}_tx\right)}$$

(15)

where u₀, ω₁ and k_t are the amplitude, angular frequency and wave number of the harmonic wave, respectively.

Substituting Eq. (15) into Eq. (14) yields:

$$\rho {\omega}_1^2=\frac{1}{\beta }{k}_t^2+\eta {k}_t^2{\omega}_1i$$

(16)

Because Eq. (16) involves complex numbers, the angular frequency ω₁ should be a complex number when the wave number k_t is a real number, and the angular frequency ω₁ can be defined as:

$${\omega}_1={\omega}_w+{\alpha}_{\mathrm{t}}i$$

(17)

where ω_w is the response frequency and α_t is the time attenuation coefficient.

Substituting Eq. (17) into Eq. (16) yields:

$$\rho \left({\omega}_w^2-{\alpha}_{\mathrm{t}}^2\right)+2\rho {\omega}_w{\alpha}_{\mathrm{t}}i=\eta {k}_t^2{\omega}_wi-\eta {k}_t^2{\alpha}_{\mathrm{t}}+\frac{k_t^2}{\beta }$$

(18)

From Eq. (18), the complex numbers on the left and right sides must have the equal real and imaginary components, so the following equations can be obtained:

$${\alpha}_{\mathrm{t}}=\frac{\eta {k}_t^2}{2\rho }$$

(19)

$${\omega}_w^2=\frac{k_t^2}{\rho \beta}-\frac{\eta^2{k}_t^4}{4{\rho}^2}$$

(20)

Amplitude attenuation and energy dissipation occurred when the stress wave propagates in the rock, where the amplitude attenuation in both time and space forms. Equation (15) essentially considers time attenuation, whereas, if it is taking account of the spatial attenuation of amplitude, assuming that the wave number is a complex number, the corresponding harmonic equation is traced to the following form as:

$$u\left(x,t\right)={u}_0{e}^{-{\alpha}_sx}{e}^{i\left({\omega}_qt-{k}_sx\right)}$$

(21)

where α_s is the spatial attenuation coefficient, ω_q is the vibration frequency and k_s is the spatial response wave number.

Similarly, substituting Eq. (21) into Eq. (14) yields:

$${\rho \omega}_q^2=\frac{\left({k}_s^2-{\alpha}_s^2\right)}{\beta }+2\eta {k}_s{\alpha}_s{\omega}_q+\left[\eta \left({k}_s^2{\omega}_q-{\alpha}_s^2{\omega}_q\right)-\frac{2{k}_s{\alpha}_s}{\beta}\right]$$

(22)

Similarly, according to the left and right sides of Eq. (22), they are equal to each other, which yields:

$$\eta \left({k}_s^2{\omega}_q-{\alpha}_s^2{\omega}_q\right)=\frac{2{k}_s{\alpha}_s}{\beta }$$

(23)

$${\rho \omega}_q^2=\frac{\left({k}_s^2-{\alpha}_s^2\right)}{\beta }+2\eta {k}_s{\alpha}_s{\omega}_q$$

(24)

Spatial response wavenumber k_s and spatial attenuation coefficient α_s can be obtained by solving Eqs. (23) and (24), which yields:

$${k}_s^2=\frac{{\rho \omega}_q^2\beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}+1\right)}{2\left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}$$

(25)

$${\alpha}_s^2=\frac{{\rho \omega}_q^2\beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}-1\right)}{2\left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}$$

(26)

Based on the relations among the wave number, wave velocity and frequency, the specific expression of the stress wave propagation velocity C_q can be obtained as:

$${C}_q^2=\frac{\omega_q^2}{k_s^2}=\frac{2\left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}{\rho \beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}+1\right)}$$

(27)

According to the spatial response wavenumber k_s which is equal to the temporal response wavenumber k_t, substituting Eq. (25) into Eqs. (19) and (20) yields:

$${\omega}_w^2=\frac{{\rho \omega}_q^2\beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}+1\right)}{2\left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}\times \left(\frac{1}{\rho \beta}-\frac{\omega_q^2{\eta}^2\beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}+1\right)}{8\rho \left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}\right)$$

(28)

From Eq. (28), it can be seen that the response frequency changes with the change of vibration frequency. In order to get a clearer picture of the change of response frequency with the vibration frequency, the ratio of response frequency and vibration frequency is defined as the frequency ratio, which yields:

$$\frac{\omega_w}{\omega_q}=\sqrt{\frac{\rho \beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}+1\right)}{2\left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}}\times \frac{1}{\rho \beta}-\frac{\omega_q^2{\eta}^2\beta \left(\sqrt{1+{\beta}^2{\omega}_q^2{\eta}^2}+1\right)}{8\rho \left(1+{\beta}^2{\omega}_q^2{\eta}^2\right)}$$

(29)

Equations (26) to (29) are the harmonic solution of the amplitude spatial attenuation coefficient α_s, the stress wave propagation velocity C_q, the amplitude time attenuation coefficient α_t, the stress wave response frequency ω_w and the frequency ratio ω_w/ω_q, respectively, which are important parameters that together characterize the attenuation properties of stress wave propagation in rock (Wang 2007).

Validation of the theoretical model

In order to verify the correctness and feasibility of the proposed model, this paper uses an improved SHPB impact experimental system; a series of stress wave propagation tests of red sandstone with three-dimensional static stress had been conducted. According to the experimental data, the propagation velocity of the stress wave C_q, spatial attenuation coefficient α_s and response frequency ω_w were obtained.

Rock specimen and experimental system

The uniformly textured red sandstone was selected for the test and was processed into cylindrical. The dimension of rock specimens are ϕ50mm×80mm. To ensure uniform force on the plane and avoid end damage caused by end effect, the bottom surface of the cylindrical rock specimens is flat and parallel.

A modified split Hopkinson pressure bar (SHPB) experimental system in this experiment was adopted, and it consists of an axial precompression stress inducer, a lateral loading confining pressure device, an impact system, an incident bar, a transmission bar and a data acquisition system, as shown in Fig. 4. The data acquisition unit comprises a SDY2017A ultrahigh dynamic strainmeter, a DL850E oscilloscope and a desktop computer. As shown in Fig. 4, strain gauges were affixed to the corresponding positions of the incident bar and transmission bar, and the ultra-dynamic strain gauge and oscilloscope were connected with the bridge box to receive and display the incident, reflected and transmission waves.

Fig. 4

a Schematic diagram of experimental system; b schematic diagram of strain gauge pasting position

The basic physical and mechanical parameters of rock specimens are shown in Table 1, where E₁ and E₂ denote the initial elastic modulus of the void body and the skeleton body of red sandstone, respectively; μ₁ denotes the Poisson’s ratio of the rock void body; the symbols of ρ, γ₀ and η denote the density, porosity and viscosity coefficient of red sandstone, respectively. It is noted that the value of porosity ρ was measured using the method of nuclear magnetic resonance. Based on stress-strain curves of red sandstone under triaxial compression, the values of μ₁, E₁ and E₂ were obtained by using the feasible determining method (Cao et al. 2016), respectively. According to the experimental data of stress wave propagation through red sandstone, the viscosity coefficient ƞ was determined by using the feasible determining method (Niu et al. 2018).

Table 1 Physical and mechanical parameters of red sandstone

Experimental method and results

The purpose of this experiment is to verify the model of stress wave through a rock with three-dimensional geo-stress; the axial static load and confining pressure are applied to rock specimens to simulate the three-dimensional geo-stress that rock subjected to, and the impact load is used to simulate the dynamic load generated by engineering blasting. Many factors were considered in this experiment; therefore, to avoid the influence caused by the change of multiple factors, the impact velocity and axial static stress were fixed, respectively. The axial static stress of the experiment was set to 13.5 MPa, and the confining pressure was set to five levels of 0, 5, 10, 15 and 20 MPa, respectively (Fig. 5).

Fig. 5

Stress waves of rock specimen under different static stress conditions: a σ_s=13.5 MPa, σ_c=0 MPa; b σ_s=13.5 MPa, σ_c=5 MPa; c σ_s=13.5 MPa, σ_c=10 MPa; d σ_s=13.5 MPa, σ_c=15 MPa; e σ_s=13.5 MPa, σ_c=20 MPa

The incident, reflected and transmission waves under different conditions are shown in Fig. 5. The experiment results are shown in Table 2, where ε_I and ε_T denote the absolute value of the incident stress wave amplitude and the transmission stress wave amplitude, respectively; t₁ and t₂ denote the time corresponding to the starting point of the incident and transmission waves, respectively; the remaining symbols are the same as above.

Table 2 Experimental results of stress wave propagation in red sandstone

Based on the incident and transmission waves obtained from the test, the C_q under different static stress conditions can be calculated by Eq. (30):

$${C}_q=\frac{L_s}{t_2-{t}_1-\frac{l_2+{l}_3}{C}}$$

(30)

where L_s denotes the length of the red sandstone specimen and l₂ and l₃ denote the distance between end face of rock specimen and strain gauge, as shown in Fig. 5. The symbol C denotes the velocity of the stress wave propagation in the elastic bar, which is 5130 m/s.

In this paper, the harmonic method was used to solve the wave equation. As can be seen from Eq. (21), the stress wave amplitude presents an exponential function relation with the attenuation of propagation distance, so the amplitudes of the incident and transmission waves under different three-dimensional static stress conditions were fitted with the exponential function to obtain the spatial attenuation coefficient α_s, as shown in Table 2. According to the Fourier transform principle, the incident and transmitted wave signals under different three-dimensional static stress conditions are converted from the time domain to the frequency domain, as shown in Fig. 6.

Fig. 6

Frequency spectra (0–12,000 Hz) of incident and transmission waves (σ_s=13.5MPa, σ_c=5MPa)

From Fig. 6, it can also be obtained that the principal frequencies of the incident and transmitted waves are around 1100 Hz, but since the spectrum curve is an irregular line, the centre-of-mass frequency of its enclosing graph cannot be easily obtained either, and a new method is proposed in this paper on how to obtain the centre-of-mass frequency. The spectrum and its centre-of-mass graph for σ_s = 13.5 MPa and σ_c = 5 MPa are given in this section due to space limitations, as shown in Fig. 7. In Fig. 7a, the spectrum is decomposed into 12 graphs consisting of rectangles of the type ABCD, by making a vertical line of the x-axis at the coordinate points with frequencies of 0, 1, 2, …12 kHz. According to the theorem that the line passing through the location of the centre of mass of any graph must equally divide the area of the graph, so this paper calculates the area of the 12 class rectangles separately and then finds the area of the class rectangles, where the coordinates of the centre-of-mass are located, uses the strip division method to obtain the frequency of the centre-of-mass under each three-dimensional geo-stress condition, and obtains the centre-of-mass frequencies of incident and transmission waves, of which the incident wave is about 2900Hz, and the frequency ratio is shown in Table 2.

Fig. 7

Schematic diagram of centre-of-mass frequency solution

Comparisons between experimental and theoretical results

According to the Eqs. (26)–(29) and the parameter values shown in Table 1, the stress wave value σ_d is the absolute value of the stress wave amplitude of the incident bar, and the theoretical results were obtained. According to the research result (Ye et al. 2009), when the axial static stress is constant, the curve relationship between damage of a rock and confining pressure is similar to exponential function. Therefore, when calculating the theoretical results in this paper, it is tentatively determined that there is an exponential function relationship between damage of a rock and confining pressure: D=A*EXP[B*σ_c)], where the parameters A and B are 0.4673 and −0.039, respectively; the unit of σ_c is MPa. Figure 8 shows the theoretical and experimental results of the stress wave propagation velocity C_q, spatial attenuation coefficient α_s and the ratio of response frequency ω_w to vibration frequency ω_q.

Fig. 8

Comparison of theoretical and experimental results: a stress wave propagation velocity C_q, b spatial attenuation coefficient α_s and c ratio of response frequency ω_w to vibration frequency ω_q

From Fig. 8a, it can be seen that the theoretical curve of stress wave propagation velocity C_q agrees well with the experimental results, and the propagation velocity of stress wave increases with the increase of confining pressure. However, it can also be seen from Fig. 8a that the theoretical and experimental results of stress wave propagation velocity C_q do not exactly overlap. This is because the theoretical value is the result of a single frequency signal, while the actual stress wave is a series of harmonic vibrations. At the same time, the viscosity of rock makes the wave velocity of high frequency wave (short wave) greater than that of low frequency wave (long wave) (Wang 2007). Therefore, the different wave velocities of harmonic components result in the incomplete coincidence between theoretical and experimental results.

From Fig. 8b, it can be seen that the experimental results of the spatial attenuation coefficient α_s are distributed between the theoretical results within a frequency band, and the frequency band is just between the centre-of-mass frequency 2900Hz of the incident wave, so the theoretical results are in good agreement with the experimental results. However, it can also be seen from Fig. 8b that when the vibration frequency is 2650 Hz, the theoretical result is lower than the experimental result, while the vibration frequency is 3100 Hz, and the theoretical result is higher than the experimental result. The possible reason for this phenomenon is that the frequency in the theoretical solution is a single frequency, while the frequency component in the real experimental signal is relatively complex. It is conceivable that the deviations in Fig. 8b will decrease if the bandwidths of the experimental signals narrow gradually.

The theoretical values and experimental results of ω_w/ω_q are shown in Fig. 8c; it can be obtained that the experimental results are distributed between the theoretical values of vibration frequencies ω_q=2650~3100 Hz with a consistent trend. However, it can also be seen from Fig. 8c that the theoretical and experimental results of the ratio of response frequency ω_w to vibration frequency ω_q are not completely consistent, which is because of the singularity of the theoretical solution and the complexity of the experimental signal. However, when the bandwidths of the experimental signals converge to the centre-of-mass frequency, the deviations gradually decrease.

Summing up the above, the theoretical and experimental results of the stress wave propagation velocity C_q, spatial attenuation coefficient α_s and response frequency ω_w are in good agreement; it shows that the proposed model of the stress wave propagation through a three-dimensional geo-stressed rock is feasible and reasonable.

Discussion

Based on the theoretical model that has been verified, parametric studies are conducted to investigate the effects of three-dimensional geo-stress and physical and mechanics parameters of a rock on stress wave propagation characteristics such as the stress wave propagation velocity C_q, spatial attenuation coefficient α_s and response frequency ω_w. For the convenience of analysis, the same exponential function as the third chapter is adopted for rock damage, and the basic parameter values are shown in Table 3.

Table 3 Basic parameter values

Stress wave propagation velocity

According to the parameters in Table 3 and Eq. (27), stress wave propagation velocities C_q of different stress conditions are shown in Fig. 9. From Fig. 9, it can be seen that the curve of the C_q shows an overall trend of “increasing firstly and then basically unchanging” with the increase of the confining pressure. When the confining pressure is small, the C_q is relatively sensitive to the confining pressure, and the C_q increases sharply with the confining pressure; when the confining pressure is large, the confining pressure has little effect on the wave velocity. These phenomena occur, because the confining pressure makes the rock pores closed, and give rise to the density and dynamic elastic modulus increasing. At the same time, the confining pressure limits the initiation and expansion of rock microcracks, and weakens the degree of damage evolution of the rock, which leads to the increase of stress wave propagation velocity when the confining pressure is small. When the confining pressure is large, the initial pores of the rock are basically closed, and the density and dynamic elastic modulus tend to remain unchanged, so the stress wave propagation velocity is basically unchanged.

Fig. 9

Effects of confining pressure on the stress wave propagation velocity considering different parameters: a influence of parameter E₁, b influence of parameter E₂, c influence of parameter γ₀, d influence of parameter η and e influence of parameter ω_q

Fig 9 also reveals that many parameters of a rock have effects on the stress wave propagation velocity. As shown in Fig. 9 a and b, for the same confining pressure, the C_q decreases with the initial modulus of rock void body; on the contrary, the C_q increases with the initial modulus of rock skeleton body. It is consistent with the classical elastic wave theory (Wang 2007); the C_q increases with the increase of rock modulus. As shown in Fig. 9c, for the same confining pressure, an increase of the initial porosity γ₀ results in a decrease in the C_q, which is because the greater the initial porosity γ₀, the smaller the density and modulus of rock, and the smaller the C_q. Similarly, the vibration frequency ω_q and the viscosity coefficient η exert a considerable influence on the C_q. As shown in Fig.9 d and e, the C_q increases with the increase of the η and the ω_q for the same confining pressure, and the relations between the effective velocity and incident wave frequency for in situ stressed rock mass also have similar results (Li et al. 2015).

Spatial attenuation coefficient

According to the parameters in Table 3 and Eq. (26), spatial attenuation coefficient α_s of different stress conditions are shown in Fig. 10. From Fig. 10, it can be seen that the α_s decreases with the increase of confining pressure, and the curve is steeply sloping down in the low confining pressure area and then slowly decreasing and tending to be unchanged. The attenuation of stress wave amplitude is the representation of the dissipation of stress wave energy; the dissipation of stress wave energy is caused by the friction dissipation of stress waves on the surface of microcracks inside rock and the grain boundary of the rock. Therefore, the size and number of the rock pores determine the degree of the attenuation of the stress wave amplitude to a certain extent. With the increase of confining pressure, the microcracks inside the rock close, and the friction force that drives the sliding increases, while the number of microcracks that can slip under the action of stress wave decreases, so the attenuation of stress wave decreases accordingly.

Fig. 10

Effects of confining pressure on the spatial attenuation coefficient ⍺_s considering different parameters: a influence of parameter E₁, b influence of parameter E₂, c influence of parameter γ₀, d influence of parameter η and e influence of parameter ω_q

From Fig. 10, it can be seen and also reveals that many parameters of a rock have effects on the spatial attenuation coefficient α_s. Fig. 10 a and b show that the α_s increases with the E₁ and decreases with the E₂ increase for the same confining pressure. Fig. 10 c shows that the α_s increases with the γ₀ for the same confining pressure. These phenomena are attributed to the fact that the attenuation of stress wave amplitude is related to the porosity of the rock. As shown in Fig. 10 d and e, the spatial attenuation coefficient α_s increases with the increase of viscosity coefficient η and vibration frequency ω_q for the same confining pressure, which is consistent with other studies (Li et al. 2015; Liu and Ahrens 1997).

Response frequency

Similarly, according to the parameters in Table 3 and Eq. (29), the ratio of response frequency ω_w to vibration frequency ω_q under different stress conditions are shown in Fig. 11. From Fig 11, it can be seen that the ratio increases with the increase of confining pressure. As shown in Fig. 11 a and b, the initial elastic modulus E₁ of the rock void body and the initial elastic modulus E₂ of the skeleton body always affect the ratio. The ratio decreases with the increase of the E₁; on the contrary, the ratio increases with the E₂. As in Fig. 11c, the ratio is negatively correlated with the rock porosity γ₀.The influence of the γ₀ is related to the fact that the rock pores is gradually compacted with the increase of the confining pressure. As in Fig. 11 d and e, the effects of viscosity coefficient η and vibration frequency ω_q on the ratio is similar, and the ratio decreases with the increase of the η and ω_q.

Fig. 11

Effects of confining pressure on the ω_w/ω_q considering different parameters: a influence of parameter E₁, b influence of parameter E₂, c influence of parameter γ₀, d influence of parameter η and e influence of parameter ω_q

Conclusions

This paper presents an equivalent medium model of stress wave propagation through a three-dimensional geo-stressed rock. The correctness and reliability of the theoretical model are verified by experiments. Based on the verified theoretical model, a detailed parameter study is carried out, and the effects of three-dimensional geo-stress, physical and mechanical parameters of a rock on the propagation characteristics of stress wave are discussed. The main conclusions are as follows:

• (1) The proposed theoretical model is effective and feasible for investigating the effects of three-dimensional geo-stress on the stress wave propagation through a rock.

• (2) The pores compaction and damage evolution of a rock which caused by three-dimensional geo-stress affect the propagation characteristics of stress wave by changing the equivalent modulus of a rock.

• (3) For a rock subjected to three-dimensional geo-stress, when the axial static stress is constant, the stress wave propagation velocity C_q and response frequency ω_w increase with the confining pressure. On the contrary, the spatial attenuation coefficient α_s is negatively correlated with confining pressure.

• (4) The basic physical and mechanical parameters of a rock have an important effect on the propagation characteristics of stress wave. For the same three-dimensional geo-stress, the stress wave propagation velocity C_q is positively correlated with the parameters E₂, η and ω_q; on the contrary, the C_q decreases with the increase of the parameters E₁ and γ₀. Similarly, the spatial attenuation coefficient α_s is negatively correlated with parameter E₂ and positively correlated with the other parameters. The response frequency ω_w is positively correlated with parameter E₂ and negatively correlated with the other parameters.