Introduction

In recent decades, longer and larger buried depth of tunnels have become the overall tendency with the advancement of construction technologies and methods; however, tunnel engineering still suffering from the facts of changeable geological environments and frequent disasters. In practical underground engineering, stability issue is of invariable essential to safety construction which not only guarantees the project can complete on schedule but also prevents potential risks to workers so as to reduce economic losses, therefore, large quantities of researches have been done by the pioneering scholars to evaluate tunnel stability, until nowadays, several approaches including model tests, numerical simulations and theory analyses are performed to discuss the topic.

The model tests are usually designed to understand the response mechanism of surrounding materials under different external factors, especially with the assistance of modern technologies, e.g., X-ray CT scanner or digital camera recording and imaging, the mechanical behaviors can be visually seen, and therefore, model tests are generally considered to be credible methods to provide verifications for numerical simulations and theoretical analyses. In general, the model tests mainly contain two groups from the literature, 1-g model tests and centrifuge tests under n-g conditions (Sterpi and Cividini 2004; Fellin et al. 2010; Chen et al. 2013; Soranzo, et al. 2015). Idinger et al. (2011) designed a series of centrifuge tests for three overburden-to-diameter ratios to study the influence of various over-burden pressures on support pressure and ground deformation. Berthoz et al. (2012) carried out several tests to compute failure kinematics and limit face pressures. Besides, the limit support pressures to the tunnel face under the seepage condition were also discussed (Lü et al. 2018). Despite the evident advantages of model tests, the size effects in the model tests are domain influence factors which cannot be ignored, the stress and strain usually change due to constrain effects of model boundaries.

In parallel with experimental tests, the advances in computer technologies accelerate numerical simulations to be more universal tools to handle with the complex soil problems in civil engineering, with reference to the aforementioned researches, numerical methods mainly contain two branches, continuum and discrete. The continuum numerical methods can be displayed by finite element method (FEM) or finite difference method (FDM), while discrete element method (DEM) can describe mechanical behaviors of discontinuous media (Mollon et al., 2009a, b, Zhang, et al. 2011, Ibrahim, et al. 2015, Zheng, et al. 2021). As a representative method, finite element method is frequently adopted to analyze tunnel face stability. Alagha and Chapman (2019) designed a series of 3-D finite element simulations to compute required collapse pressure to tunnel face in purely cohesion or \(c^{\prime}\)-\(\varphi ^{\prime}\) soil layer. Besides, the finite element method shows distinct advantages in continuum materials, when encountered non-continuum medium, the discrete element method supposes to be a better decision. When taking the characteristics of granular materials into consideration, Chen et al. (2011) analyzed the failure mechanism, limit support pressure, and soil arch of shallow shield tunnels by PFC3D simulations. However, more attentions should be paid to select appropriate constitutive models and mechanical parameters when numerical simulations are applied to instruct routine design.

In the last few decades, different theoretical methods have been adopted to analyze stability issues in tunnel engineering. The limit equilibrium method was firstly proposed to explain a sliding wedge mechanism and then further developed in many subsequent works (Anagnostou and Kovári 1996; Anagnostou 2012). Apart from the aforementioned method, limit analysis method attracts scholars’ attentions in tunnel stability issues due to more rigorous solutions and less assumption conditions. Especially, according to the upper and lower bound theory of limit analysis, the interval in which the true solution falls can be narrowed by finding the possible larger lower bound solution and smaller upper bound solution (Yang and Yin 2006; Huang and Yang 2011). As a matter of fact, the stability evaluations in underground projects mainly focus on mechanical mechanism of surrounding soils or rocks at top of tunnel or ahead of tunnel face. Mollon et al. (2011) proposed a new 2D kinematically admissible collapse mechanism to confirm collapse pressure to a pressurized tunnel face when taking the spital variability of friction angel \(\varphi\) into consideration. The 3D rotational models were also developed to predict face pressures (Mollon et al. 2010; Pan and Dias 2017), besides, the verifications from experimental tests or numerical simulations prove efficient of these models. For the roof stabilization, Fraldi and Guarracino (2009, 2010) established two-dimension collapse mechanism of deep-buried tunnel in Hoek–Brown rock medium. However, the actual destructive process in practical engineering supposes to be three-dimensional, and two-dimensional collapse feature cannot reflect real geotechnical structure. Yang and Huang (2013) developed three-dimensional failure mechanism of a rectangular cavity. Considering the adverse effect of underground water table, Qin et al. (2015) analyzed 2D and 3D progressive collapse mechanism under varying water table. The above researches were based on the assumption of single ground layer, and roof stability issues in double-layer rock mass were also discussed (Wang et al. 2019; Zhao, et al. 2019).

When taking the uncertainties and variations of mechanical parameters into consideration, reliability analysis gradually becomes an efficient solution to remedy those weakness in deterministic analysis. Mollon et al (2009a, b) displayed tunnel reliability by combining deterministic model and numerical simulations to evaluate ultimate and serviceability limit state. Lü et al (2011) found the support position possessed an evident influence on the three failure models of ground-support interaction by the method of FORM and SORM. Li and Yang (2018) performed tunnel face reliability by considering multiple failure mechanism. The reliability in layered Hoek–Brown rock mass was also investigated (Yang et al 2017). Worthy to attention, despite the collapse mechanism in single soil layer had been discussed (Yu et al. 2019), the failure mechanism and reliability analysis based on nonlinear Mohr–Coulomb failure criterion in double-layered soil stratums still require further research.

This paper is devoted to discuss roof stability of deep-buried tunnel in layered soil mass according to upper bound theory of limit analysis and reliability theorem. The rationality of proposed model is primarily validated by making comparisons with existing research. The numerical analysis is subsequently designed to investigate the impacts of corresponding parameters on potential failure surface. Then, a probabilistic model is proposed by consolidating collapse mechanism into response surface method, by assuming the geotechnical parameters involved in the performance function as random variables, the effects of individual nonrandom variables and cross-correlation of random variables on the failure probability are discussed. Eventually, a reliability-based design is provided to compute the target support pressure to tunnel crown.

2D progressive failure mechanism under varying groundwater tables

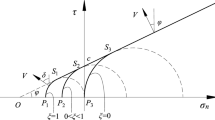
In reality, the strength parameters are severely affected when considering the adverse effects of underground water on the soil properties; hence, it sounds reasonable to put forward a collapse mechanism by consolidating the layered stratums and varying groundwater tables. With reference to the previous studies, the two-dimensional failure mechanism of a deep-buried rectangular tunnel in layered stratums is established. As shown in Fig. 1, the failure mechanism contains three parts when the ground water table in the upper stratum; then, a slide between the collapse block and surrounding soil mass occurs due to the discontinuity of velocity, and a two-dimensional failure mechanism is formed in XOY plane, v is the velocity in the mobile field, h1 denotes the collapse height in stratum 1 and h2 is the thickness of ground layer 2, \(\eta\) is ration of the upper height of roof collapse in layer 1 to the whole height, h1.

Fig. 1
figure 1

Two-dimensional collapse mechanism for deep-buried tunnel in two-layer soil mass

Full size image

Pore water pressure in upper bound theorem of limit analysis

According to the upper bound theorem of limit analysis, when the velocity boundary condition is satisfied, the load derived by equating the external work rate to the rate of energy dissipation in any kinematically admissible velocity field is no less than the actual load. To bring the effect of pore water pressure into the framework of upper bound theorem of limit analysis, Viratjandr and Michalowski (2006) supposed the pore water pressure mainly acted on the soil skeleton and the boundary of velocity field, consequently, the upper bound theorem can be expressed as follows when taking the pore water pressure into consideration.

$$\int_V\sigma_{ij}{\dot\varepsilon}_{ij}dV\geq\int_sT_iv_ids+\int_VX_iv_idV-\int_Vu{\dot\varepsilon}_{ij}dV-\int_sn_iv_iuds$$
(1)

where \(\sigma_{ij}\) and \(\dot{\varepsilon }_{ij}\) are stress tensor and strain rate in the kinematically admissible velocity field, respectively, \(T_{i}\) is the surcharge load on the boundary s, \(X_{i}\) is the body force, V is the volume of the mechanism, \(v_{i}\) is the velocity along the velocity discontinuity line, \(n_{i}\) is the unit normal vector of the curve, and u is the pore water pressure.

Besides, the falling block bounded by the velocity discontinuity line and boundary surface is regarded as rigid material, hence, the strain rate \(\dot{\varepsilon }_{ij}\) in Eq. (1) are equal to zero, this indicates only last term in Eq. (1) consists of the effect of pore water pressure, therefore, the work rate of pore water pressure can be expressed as

$$P_{u} = - \int_{s} {n_{i} } v_{i} uds$$
(2)

Nonlinear Mohr–Coulomb failure criterion

The nonlinear Mohr–Coulomb criterion is used to describe the nonlinear relationship between the principal stress and the shear stress when soil materials yield, and the criterion is widely accepted due to its simple expression and clear physical meaning, the failure criterion is

$$\tau_n=C_0\left(1+\frac{\sigma_n}{\sigma_t}\right)^\frac1m\left\{m\in\left(1,+\infty\right),\sigma_t\geq0,C_0\geq0\right\}$$
(3)

where \(\sigma_{n}\) is the normal stress, \(\tau_{n}\) is the shear stress, \(\sigma_{t}\) is the axial tension stress, \(C_{0}\) is the initial cohesion, and m is the nonlinear coefficient. Equation (3) becomes linear criterion when m = 1.

$$\left\{ {C_{0} = c,\frac{{C_{0} }}{{\sigma_{t} }} = \tan \varphi } \right\}$$
(4)
$$\tau_{n} = C_{0} + \frac{{C_{0} }}{{\sigma_{t} }}\sigma_{n} = c + \sigma_{n} \tan \varphi$$
(5)

According to the associate flow rule, the plastic potential surface is in accordance with the plastic yield surface, and the plastic potential function can be written as

$$f = \tau_{n} - C_{0} \left( {1 + \frac{{\sigma_{n} }}{{\sigma_{t} }}} \right)^{\frac{1}{m}}$$
(6)

In the plastic flow state, there is no direct relationship between the yield stress and plastic strain, and the correlation between yield stress and plastic strain rate can be determined by flow rule.

$$\dot{\varepsilon }_{n} = \lambda \frac{\partial f}{{\partial \sigma_{n} }} = - \frac{{\lambda C_{0} }}{{m\sigma_{t} }}\left( {1 + \frac{{\sigma_{n} }}{{\sigma_{t} }}} \right)^{{\frac{1 - m}{m}}}$$
(7)
$$\dot{\gamma }_{n} = \lambda \frac{\partial f}{{\partial \tau_{n} }} = \lambda$$
(8)

where \(\lambda\) is a scalar parameter.

Besides, the expression of plastic strain rate can be derived by geometric relationship

$$\begin{array}{*{20}c} {\sin \theta = \frac{1}{{\sqrt {1 + f^{\prime}\left( x \right)^{2} } }}} & {\cos \theta = \frac{f^{\prime}\left( x \right)}{{\sqrt {1 + f^{\prime}\left( x \right)^{2} } }}} \\ \end{array}$$
(9)
$$\begin{array}{*{20}c} {\dot{\varepsilon }_{n} = \frac{v}{w}\sin \theta } & {\dot{\gamma }_{n} = - \frac{v}{w}\cos \theta } \\ \end{array}$$
(10)

Submitting Eq. (9) into Eq. (10), the shear and normal stress rate can be expressed as

$$\dot{\varepsilon }_{n} = \frac{v}{{w\sqrt {1 + f^{\prime}\left( x \right)^{2} } }}$$
(11)
$$\dot{\gamma }_{n} = - \frac{vf^{\prime}\left( x \right)}{{w\sqrt {1 + f^{\prime}\left( x \right)^{2} } }}$$
(12)

Combining Eqs. (7), (8), (11), and (12), the expression of \(\sigma_{n}\) is

$$\sigma_{n} = \sigma_{t} \left( {\frac{{m\sigma_{t} }}{{f^{\prime}\left( x \right)C_{0} }}} \right)^{{\frac{m}{1 - m}}} - \sigma_{t}$$
(13)

Upper bound analysis of progressive collapse mechanism

According to the upper bound theorem, the internal energy dissipation at any point on the velocity discontinuous line can be calculated by

$$D = \left( {\sigma_{n} \dot{\varepsilon }_{n} + \tau_{n} \dot{\gamma }_{n} } \right)w = \frac{{ - \sigma_{t} + \left( {1 - m} \right)\sigma_{t}^{{\frac{1}{1 - m}}} \left( {m^{ - 1} } \right)^{{\frac{m}{m - 1}}} C_{0}^{{\frac{m}{m - 1}}} f^{\prime}\left( x \right)^{{\frac{m}{m - 1}}} }}{{\sqrt {1 + f^{\prime}\left( x \right)^{2} } }}v$$
(14)

where w is the thickness of plastic detaching zone, \(f^{\prime}\left( x \right)\) is the first derivative of \(f\left( x \right)\). Based on the roof collapse mechanism shown in Fig. 1, all the internal energy dissipation in the failure of collapsing block occurs within the discontinuity line, and the energy dissipation rate can be derived by integrating Eq. (14) along the whole velocity discontinuity line

$$P_D=P_{D1}+P_{D1w}+P_{D2w}=\int_0^{l_1}\left[-\sigma_{t1}+\left(1-m_1\right)\sigma_{t1}^{\textstyle\frac1{1-m_1}}\left(m_1^{-1}\right)^{\textstyle\frac{m_1}{m_1-1}}C_{0-1}^{\textstyle\frac{m_1}{m_1-1}}f_1^{\prime}\left(x\right)^{\textstyle\frac{m_1}{m_1-1}}f_1^{\prime}\left(x\right){\textstyle\frac{m_1}{m_1-1}}\right]vdx+\int_{l_1}^{l_{1w}}\left[-\sigma_{t2}+\left(1-m_2\right)\sigma_{t2}^{\textstyle\frac1{1-m_2}}\left(m_2^{-1}\right)^{\textstyle\frac{m_2}{m_2-1}}C_{0-1}^{\textstyle\frac{m2}{m_2-1}}f_1^{\prime}\left(x\right)^{\textstyle\frac{m_2}{m_2-1}}f_1^{\prime}\left(x\right){\textstyle\frac{m_1}{m_1-1}}\right]vdx+\int_{l_{1w}}^{l_{2w}}\left[-\sigma_{t3}+\left(1-m_3\right)\sigma_{t3}^{\textstyle\frac1{1-m_2}}\left(m_3^{-1}\right)^{\textstyle\frac{m_3}{m_3-1}}C_{0-3}^{\textstyle\frac{m3}{m_3-1}}g^{\prime}\left(x\right)^{\textstyle\frac{m_3}{m_3-1}}\right]vdx$$
(15)

The work rate done by the gravitation of collapsing block of the two layers can be expressed as

$$P_\gamma=P_{\gamma1}+P_{\gamma1w}+P_{\gamma2w}=\gamma_1\int_0^{l_1}\left[f_1\left(x\right)-f_1\left(l_1\right)\right]vdx+\gamma_1^{\prime}\int_0^{l_1}\left[f_1\left(l_1\right)-f_{1w}\left(l_{1w}\right)\right]vdx+\gamma_2^{\prime}\int_0^{l_1}f_{1w}\left(l_{1w}\right)vdx+\gamma_1^{\prime}\int_{l_1}^{l_{1w}}\left[f_{1w}\left(x\right)-f_{1w}\left(l_{1w}\right)\right]vdx+\gamma_2^{\prime}\int_{l_1}^{l_{1w}}f_{1w}\left(l_{1w}\right)vdx+\gamma_2^{\prime}\int_{l_{1w}}^{l_{2w}}g\mathit{\left(x\right)}vdx$$
(16)

where \(\gamma_{1}\) is the unit weight of stratum 1, \(\gamma_{1} ^{\prime}\) and \(\gamma_{2} ^{\prime}\) denote the buoyant unit weight of stratum 1 and stratum 2 calculated by \(\gamma ^{\prime} = \gamma - \gamma_{w}\), and \(\gamma_{w}\) represents the unit weight of water.

With reference to the previous studies (Saada et al. 2012; Yang et al. 2017), the excess pore water pressure can be expressed as

$$u = p - p_{w} = p - \gamma_{w} h$$
(17)

where p is the pore water pressure defined by \(p = \gamma_{u} \gamma h\), \(\gamma_{u}\) is the pore water pressure coefficient, and h is the vertical distance from the collapse roof to the tunnel border.

The gradient of pore water pressure is

$$\begin{array}{*{20}c} { - grad} & u \\ \end{array} = - \frac{du}{{dy}} = \gamma_{w} - \gamma_{u} \gamma$$
(18)

Consequently, the pore water pressure inducing work rate along the detaching surface is

$$P_u=P_{u1w}+P_{u2w}=\left(\gamma_w-\gamma_u\gamma_1\right)\int_0^{l_1}\left[f_1\left(l_1\right)-f_{1w}\left(l_{1w}\right)\right]vdx+\left(\gamma_w-\gamma_u\gamma_2\right)\int_0^{l_1}f_{1w}\left(l_{1w}\right)vdx+\left(\gamma_w-\gamma_u\gamma_1\right)\int_{l_1}^{l_{1w}}\left[f_{1w}\left(x\right)-f_{1w}\left(l_{1w}\right)\right]vdx+\left(\gamma_w-\gamma_u\gamma_2\right)\int_{l_1}^{l_{1w}}f_{1w}\left(l_{1w}\right)vdx+\left(\gamma_w-\gamma_u\gamma_2\right)\int_{l_{1w}}^{l_{2w}}g\left(x\right)vdx$$
(19)

The work rate of support pressure can be illustrated as

$$P_{q} = ql_{2w} v\cos \pi = - qvl_{2w}$$
(20)

According to the virtual work principle, the work rate of internal energy dissipation equals to the total external work rate.

$$P_{D1} + P_{D1w} + P_{D2w} = P_{\gamma 1} + P_{\gamma 1w} + P_{\gamma 2w} + P_{u1w} + P_{u2w} + P_{q}$$
(21)

To obtain the two-dimensional shape of the collapse body at the roof of the tunnel under the upper bound limit state. It is necessary to establish an analytical expression of the surface equation that constitutes the collapse body in the limit state. The upper bound theorem states that the calculation of optimizing upper solution can be regarded as searching the extremum among these upper solutions. The objective function \(\zeta\) which can be used to determine the optimizing upper solution represented by the difference of the total energy dissipation rate and the whole work rate done by external forces can be written as:

$$\zeta\left[f_1\left(x\right),f_1^{\prime}\left(x\right),f_{1w}\left(x\right),f_{1w}^{\prime}\left(x\right),g\left(x\right),g^{\prime}\left(x\right),x\right]=P_D-P_\gamma-P_u-P_q=\int_0^{l_1}\left[\right.-\sigma_{t1}+\left(1-m_1\right)\sigma_{t1}^\frac1{1-m_1}\left(m_1^{-1}\right)^\frac{m_1}{m_1-1}C_{0-1}^\frac{m_1}{m_1-1}f_1^{\prime}\left(x\right)^\frac{m_1}{m_1-1}-\gamma_1f_1\left(x\right)\left.\right]vdx+\int_{l_1}^{l_{1w}}\left[\right.-\sigma_{t2}+\left(1-m_2\right)\sigma_{t2}^\frac1{1-m_2}\left(m_2^{-1}\right)^\frac{m_2}{m_2-1}C_{0-2}^\frac{m_2}{m_2-1}f_{1w}^{\prime}\left(x\right)^\frac{m_2}{m_2-1}-\left(1-\gamma_u\right)\gamma_1f_{1w}\left(x\right)\left.\right]vdx+\int_{l_{1w}}^{l_{2w}}\left[\right.-\sigma_{t3}+\left(1-m_3\right)\sigma_{t3}^\frac1{1-m_3}\left(m_3^{-1}\right)^\frac{m_3}{m_3-1}C_{0-3}^\frac{m_3}{m_3-1}g^{\prime}\left(x\right)^\frac{m_3}{m_3-1}-\left(1-\gamma_u\right)\gamma_2g\left(x\right)\left.\right]vdx+W=\int_0^{l_1}\psi_1\left[f_1\left(x\right),f_1^{\prime}\left(x\right),x\right]vdx+\int_{l_1}^{l_{1w}}\psi_2\left[f_{1w}\left(x\right),f_{1w}^{\prime}\left(x\right),x\right]+\int_{l_{1w}}^{l_{2w}}\psi_3\left[g\left(x\right),g^{\prime}\left(x\right),x\right]vdx+W$$
(22)

where the specific expression of \(\psi_{1}\), \(\psi_{2}\), \(\psi_{3}\) and W are listed as follows:

$$\psi_1\left[f_1\left(x\right),f_1^{\prime}\left(x\right),x\right]=-\sigma_{t1}+\left(1-m_1\right)\sigma_{t1}^{\textstyle\frac1{1-m_1}}\left(m_1^{-1}\right)^{\textstyle\frac1{m_1-1}}C_{0-1}^{\textstyle\frac1{m_1-1}}f_1^{\prime}\left(x\right)^{\textstyle\frac1{m_1-1}}-\gamma_1f_1\left(x\right)\psi_1\left[f_{1w}\left(x\right),f_{1w}^{\prime}\left(x\right),x\right]=-\sigma_{t2}+\left(1-m_2\right)\sigma_{t1}^{\textstyle\frac1{1-m_2}}\left(m_1^{-1}\right)^{\textstyle\frac1{m_2-1}}C_{0-2}^{\textstyle\frac1{m_2-1}}f_{1w}^{\prime}\left(x\right)^{\textstyle\frac{m2}{m_2-1}}-\left(1-\gamma_u\right)\gamma_1f_{1w}\left(x\right)\psi_3\left[g\left(x\right),g^{\prime}\left(x\right),x\right]=-\sigma_{t3}+\left(1-m_3\right)\sigma_{t3}^{\textstyle\frac1{1-m_3}}\left(m_3^{-1}\right)^{\textstyle\frac{m_3}{m_3-1}}C_{0-3}^{\textstyle\frac{m_3}{m_3-1}}g^{\prime}\left(x\right)^{\textstyle\frac{m_3}{m_3-1}}-\left(1-\gamma_u\right)\gamma_2g\left(x\right)W=2\left(1-\gamma_u\right)\left(\gamma_1-\gamma_1\right)f_{1w}\left(l_{1w}\right)v+\gamma_u\gamma_1f_1\left(l_1\right)v+ql_{2w}v$$
(23)

Evidently, \(\zeta\) is determined by \(\psi\) whose extremum can be derived by variational calculation from Eq. (23). Based on the variational principle, the problem of searching the extreme value of function \(\psi\) is transformed into solving the definite solution problem of the Euler equation under satisfying boundary conditions. Wherein, the variational equation used to derive the Euler’s equation of \(\psi\) is written as

$$\frac{\partial \psi }{{\partial f(x)}} - \frac{d}{dx}\left[ {\frac{\partial \psi }{{\partial f^{\prime}(x)}}} \right] = 0$$
(24)

Submitting Eq. (23) into Eq. (24), the Euler equation of function \(\psi\) is

$$\begin{array}{*{20}c} {\gamma_{1} - \frac{{m_{1} }}{{m_{1} - 1}}\sigma_{t1}^{{\frac{1}{{1 - m_{1} }}}} \left( {m^{ - 1} } \right)^{{\frac{{m_{1} }}{{m_{1} - 1}}}} C_{0 - 1}^{{\frac{{m_{1} }}{{m_{1} - 1}}}} f_{1} ^{\prime}\left( x \right)^{{\frac{{2 - m_{1} }}{{m_{1} - 1}}}} f_{1} ^{\prime\prime}\left( x \right) = 0} \\ {\left( {1 - \gamma_{u} } \right)\gamma_{1} - \frac{{m_{2} }}{{m_{2} - 1}}\sigma_{t2}^{{\frac{1}{{1 - m_{2} }}}} \left( {m_{2}^{ - 1} } \right)^{{\frac{{m_{2} }}{{m_{2} - 1}}}} C_{0 - 2}^{{\frac{{m_{2} }}{{m_{2} - 1}}}} f_{1w} ^{\prime}\left( x \right)^{{\frac{{2 - m_{2} }}{{m_{2} - 1}}}} f_{1w} ^{\prime\prime}\left( x \right) = 0} \\ {\left( {1 - \gamma_{u} } \right)\gamma_{2} - \frac{{m_{3} }}{{m_{3} - 1}}\sigma_{t3}^{{\frac{1}{{1 - m_{3} }}}} \left( {m_{3}^{ - 1} } \right)^{{\frac{{m_{3} }}{{m_{3} - 1}}}} C_{0 - 3}^{{\frac{{m_{3} }}{{m_{3} - 1}}}} g^{\prime}\left( x \right)^{{\frac{{2 - m_{3} }}{{m_{3} - 1}}}} g^{\prime\prime}\left( x \right) = 0} \\ \end{array}$$
(25)

It is observed that the Eq. (25) belongs to a nonhomogeneous second-order linear differential equation with constant coefficients; the analytical solution can be obtained by analytical method.

$$\begin{array}{*{20}c} {f_{1} ^{\prime}\left( x \right) = m_{1} \sigma_{t1} C_{0 - 1}^{{ - m_{1} }} \gamma_{1}^{{m_{1} - 1}} \left( {x + c_{1} } \right)^{{m_{1} - 1}} } \\ {f_{1w} ^{\prime}\left( x \right) = m_{2} \sigma_{t2} C_{0 - 2}^{{ - m_{2} }} \left[ {\gamma_{1} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{2} - 1}} \left( {x + c_{3} } \right)^{{m_{2} - 1}} } \\ {g^{\prime}\left( x \right) = m_{3} \sigma_{t3} C_{0 - 3}^{{ - m_{3} }} \left[ {\gamma_{2} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{3} - 1}} \left( {x + c_{5} } \right)^{{m_{3} - 1}} } \\ \end{array}$$
(26)

Integrating the above equations, the velocity discontinuity line can be expressed as

$$\begin{array}{*{20}c} {f_{1} \left( x \right) = k_{1} \left( {x + c_{1} } \right)^{{m_{1} }} + c_{2} } \\ {f_{1w} \left( x \right) = k_{2} \left( {x + c_{3} } \right)^{{m_{2} }} + c_{4} } \\ {g\left( x \right) = k_{3} \left( {x + c_{5} } \right)^{{m_{3} }} + c_{6} } \\ \end{array}$$
(27)

where \(k_{1} = \sigma_{t1} C_{0 - 1}^{{ - m_{1} }} \gamma_{1}^{{m_{1} - 1}}\), \(k_{2} = \sigma_{t2} C_{0 - 2}^{{ - m_{2} }} \left[ {\gamma_{1} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{2} - 1}}\), \(k_{3} = \sigma_{t3} C_{0 - 3}^{{ - m_{3} }} \left[ {\gamma_{2} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{3} - 1}}\), and c1, c2, c3, c4, c5, c6 are the integration constants. Considering the geometric relationship in Fig. 1, the following boundary conditions are met

$$\left\{ {\begin{array}{*{20}l} {f_{1} \left( {x = 0} \right) = - \left( {h_{1} + h_{2} } \right)} \hfill \\ {f_{1} \left( {x = l_{1} } \right) = - \left[ {\left( {1 - \eta } \right)h_{1} + h_{2} } \right]} \hfill \\ {f_{1w} \left( {x = l_{1} } \right) = - \left[ {\left( {1 - \eta } \right)h_{1} + h_{2} } \right]} \hfill \\ {f_{1w} \left( {x = l_{1w} } \right) = - h_{2} } \hfill \\ {g\left( {x = l_{1w} } \right) = - h_{2} } \hfill \\ {g\left( {x = l_{2w} } \right) = 0} \hfill \\ \end{array} } \right.$$
(28)

In this literature, the final solution is exactly needed, and necessary assumption should be made to derive the results. To make the velocity discontinuity line smooth, an equation between the first derivative of curve function at certain points should be satisfied.

$$\left\{ {\begin{array}{*{20}c} {f_{1} ^{\prime}\left( {x = l_{1} } \right) = f_{1w} ^{\prime}\left( {x = l_{1} } \right)} \\ {f_{1w} ^{\prime}\left( {x = l_{1w} } \right) = g^{\prime}\left( {x = l_{1w} } \right)} \\ \end{array} } \right.$$
(29)

Submitting Eq. (27) into Eqs. (28) and (29), the integration constants can be determined

$$\left\{ {\begin{array}{*{20}l} {c_{1} = 0} \hfill \\ {c_{2} = - \left( {h_{1} + h_{2} } \right)} \hfill \\ {c_{3} = \left( {\frac{{m_{1} k_{1} }}{{m_{2} k_{2} }}} \right)^{{\frac{1}{{m_{2} - 1}}}} l_{1}^{{\frac{{m_{1} - 1}}{{m_{2} - 1}}}} - l_{1} } \hfill \\ {c_{4} = - \left[ {k_{2} \left( {l_{1w} + c_{3} } \right)^{{m_{2} }} + h_{2} } \right]} \hfill \\ {c_{5} = \left( {\frac{{m_{2} k_{2} }}{{m_{3} k_{3} }}} \right)^{{\frac{1}{{m_{3} - 1}}}} \left( {l_{1w} + c_{3} } \right)^{{\frac{{m_{2} - 1}}{{m_{3} - 1}}}} - l_{1w} } \hfill \\ {c_{6} = - k_{3} \left( {l_{2w} + c_{5} } \right)^{{m_{3} }} } \hfill \\ \end{array} } \right.$$
(30)

Combining Eqs. (22), (23), (27), and (30), the total energy loss rate corresponding the Fig. 1 can be illustrated as

$$\begin{gathered} \zeta \left[ {f_{1} \left( x \right),f_{1} ^{\prime}\left( x \right),f_{1w} \left( x \right),f_{1w} ^{\prime}\left( x \right),g\left( x \right),g^{\prime}\left( x \right),x} \right] = \hfill \\ \left\{ {\frac{{\left( {1 - \eta } \right)m_{1} + 1}}{{\left( {m_{1} + 1} \right)\eta }}\sigma_{t1} C_{0 - 1}^{{ - m_{1} }} \gamma_{1}^{{m_{1} }} l_{1}^{{m_{1} + 1}} + \left( {\gamma_{1} h_{2} - \sigma_{t1} } \right)l_{1} + \left\{ {\sigma_{t2} } \right.C_{0 - 2}^{{ - m_{2} }} \left[ {\gamma_{1} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{2} }} \left( {l_{1w} + c_{3} } \right)^{{m_{2} }} } \right. \hfill \\ + \left( {1 - \gamma_{u} } \right)\gamma_{1} h_{2} \left. { - \sigma_{t2} } \right\}\left( {l_{1w} - l_{1} } \right) - \frac{{m_{2} }}{{m_{2} + 1}}\sigma_{t2} C_{0 - 2}^{{ - m_{2} }} \left[ {\gamma_{1} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{2} }} \left[ {\left( {l_{1w} + c_{3} } \right)^{{m_{2} + 1}} - \left( {l_{1} + c_{3} } \right)^{{m_{2} + 1}} } \right] \hfill \\ + \left\{ {\sigma_{t3} } \right.C_{0 - 3}^{{ - m_{3} }} \left[ {\gamma_{2} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{3} }} \left( {l_{2w} + c_{5} } \right)^{{m_{3} }} - \left. {\sigma_{t3} } \right\}\left( {l_{2w} - l_{1w} } \right) - 2\left( {1 - \gamma_{u} } \right)\left( {\gamma_{1} - \gamma_{2} } \right)h_{2} - \gamma_{u} \gamma_{1} h_{2} + ql_{2w} \hfill \\ + \frac{\eta - 1}{\eta }\gamma_{u} \sigma_{t1} C_{0 - 1}^{{ - m_{1} }} \gamma_{1}^{{m_{1} }} l_{1}^{{m_{1} }} \left. { - \frac{{m_{3} }}{{m_{3} + 1}}\sigma_{t3} C_{0 - 3}^{{ - m_{3} }} \left[ {\gamma_{2} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{3} }} \left[ {\left( {l_{2w} + c_{5} } \right)^{{m_{3} + 1}} - \left( {l_{1w} + c_{5} } \right)^{{m_{3} + 1}} } \right]} \right\}v \hfill \\ \end{gathered}$$
(31)

Based on the upper bound theorem of limit analysis, the optimized solution can be derived when the whole internal energy dissipation equals to the external work rate, namely that the total energy loss rate in Eq. (31) equals to zero.

$$\begin{gathered} \frac{{\left( {1 - \eta } \right)m_{1} + 1}}{{\left( {m_{1} + 1} \right)\eta }}\sigma_{t1} C_{0 - 1}^{{ - m_{1} }} \gamma_{1}^{{m_{1} }} l_{1}^{{m_{1} + 1}} + \left( {\gamma_{1} h_{2} - \sigma_{t1} } \right)l_{1} + \left\{ {\sigma_{t2} } \right.C_{0 - 2}^{{ - m_{2} }} \left[ {\gamma_{1} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{2} }} \left( {l_{1w} + c_{3} } \right)^{{m_{2} }} \hfill \\ + \left( {1 - \gamma_{u} } \right)\gamma_{1} h_{2} \left. { - \sigma_{t2} } \right\}\left( {l_{1w} - l_{1} } \right) - \frac{{m_{2} }}{{m_{2} + 1}}\sigma_{t2} C_{0 - 2}^{{ - m_{2} }} \left[ {\gamma_{1} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{2} }} \left[ {\left( {l_{1w} + c_{3} } \right)^{{m_{2} + 1}} - \left( {l_{1} + c_{3} } \right)^{{m_{2} + 1}} } \right] \hfill \\ + \left\{ {\sigma_{t3} } \right.C_{0 - 3}^{{ - m_{3} }} \left[ {\gamma_{2} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{3} }} \left( {l_{2w} + c_{5} } \right)^{{m_{3} }} - \left. {\sigma_{t3} } \right\}\left( {l_{2w} - l_{1w} } \right) - 2\left( {1 - \gamma_{u} } \right)\left( {\gamma_{1} - \gamma_{2} } \right)h_{2} - \gamma_{u} \gamma_{1} h_{2} + ql_{2w} \hfill \\ + \frac{\eta - 1}{\eta }\gamma_{u} \sigma_{t1} C_{0 - 1}^{{ - m_{1} }} \gamma_{1}^{{m_{1} }} l_{1}^{{m_{1} }} - \frac{{m_{3} }}{{m_{3} + 1}}\sigma_{t3} C_{0 - 3}^{{ - m_{3} }} \left[ {\gamma_{2} \left( {1 - \gamma_{u} } \right)} \right]^{{m_{3} }} \left[ {\left( {l_{2w} + c_{5} } \right)^{{m_{3} + 1}} - \left( {l_{1w} + c_{5} } \right)^{{m_{3} + 1}} } \right] = 0 \hfill \\ \end{gathered}$$
(32)

Probability analysis by application of RSM

Failure probability

Probability analysis usually belongs to an efficient solution to deal with the complex problems in civil engineering, and the results can remedy deficiencies and provide references for the deterministic analysis. Until now, several approaches have been developed to compute system reliability, and in which, Monte Carlo simulation (MCS) is considered to be a robust method for verifying different approaches in probability analysis; however, a stable solution usually requires large quantities of repeated numerical computations when using MCS method and which certainly leads to lower efficiency. Besides, the first-order and the second-order reliability method (FORM/SORM) applied in reliability analysis generally demand explicit performance functions; however, in reality, the expressions reflect the relationships between the system reliability and random variables maybe difficult to be determined due to non-linear and complicated characteristics of soil. In this section, the probability analysis is performed by combining the failure mechanism with response surface method (RSM). To maintain the stability of the tunnel roof, the support force should be no less than the weight of collapse block; therefore, the performance function of reliability analysis can be established.

$$G\left( x \right) = ql_{2w} - W_{block}$$
(33)

In which

$$\begin{gathered} W_{block} = \gamma_{1} \int_{{l_{1} }}^{0} {\left[ {f_{1} \left( x \right) - f_{1} \left( {l_{1} } \right)} \right]} vdx + \gamma_{1} \int_{{l_{1} }}^{0} {\left[ {f_{1} \left( {l_{1} } \right) - f_{1w} \left( {l_{1w} } \right)} \right]} vdx + \gamma_{2} \int_{{l_{1} }}^{0} {f_{1w} } \left( {l_{1w} } \right)vdx \hfill \\ + \gamma_{1} \int_{{l_{1w} }}^{{l_{1} }} {\left[ {f_{1w} \left( x \right) - f_{1w} \left( {l_{1w} } \right)} \right]} vdx + \gamma_{2} \int_{{l_{1w} }}^{{l_{1} }} {f_{1w} } \left( {l_{1w} } \right)vdx + \gamma_{2} \int_{{l_{2w} }}^{{l_{1w} }} {g\left( x \right)} vdx \hfill \\ \end{gathered}$$
(34)

And the expression of performance function can be expressed as

$$\begin{gathered} G = ql_{2w} - \left\{ {} \right.\frac{{\gamma_{1} }}{{m_{1} + 1}}k_{1} l_{1}^{{m_{1} + 1}} - \gamma_{1} \left( {h_{1} + h_{2} } \right)l_{1} + \left( {\gamma_{2} - \gamma_{1} } \right)\left[ {k_{2} \left( {l_{1w} + c_{3} } \right)^{{m_{2} }} + c_{4} } \right]l_{1} + \hfill \\ \frac{{\gamma_{1} }}{{m_{2} + 1}}k_{2} \left[ {\left( {l_{1w} + c_{3} } \right)^{{m_{2} + 1}} - \left( {l_{1} + c_{3} } \right)^{{m_{2} + 1}} } \right] + \gamma_{1} c_{4} \left( {l_{1w} - l_{1} } \right) + \left[ {k_{2} \left( {l_{1w} + c_{3} } \right)^{{m_{2} }} + c_{4} } \right]\left( {\gamma_{2} - \gamma_{1} } \right)\left( {l_{1w} - l_{1} } \right) + \hfill \\ \frac{{\gamma_{2} }}{{m_{3} + 1}}k_{3} \left[ {\left( {l_{2w} + c_{5} } \right)^{{m_{3} + 1}} - \left( {l_{1w} + c_{5} } \right)^{{m_{3} + 1}} } \right] + \gamma_{2} c_{6} \left( {l_{2w} - l_{1w} } \right)\left. {} \right\} \hfill \\ \end{gathered}$$
(35)

The failure probability can be computed by

$$P_{f} = \frac{1}{N}\sum\limits_{i = 1}^{N} {I\left( G \right)}$$
(36)

where N represents repeated trials, and I(G) = 0 for G > 0, otherwise I(G) = 1. Hence, the reliability index can be obtained.

$$\Phi \left( \beta \right) = 1 - P_{f}$$
(37)

where \(\Phi \left( \cdot \right)\) represents the cumulative distribution function (CDF) of the standard normal variable.

Probabilistic analysis model

RSM possesses evident advantages to eliminate the obstacles between the deterministic approach and reliability analysis despite of complicated and non-linear soil problems. The key point for RSM analysis is to establish an explicit function to replace the real expression, and the model is started by assuming a second order polynomial with square terms, the expression is illustrated as follows

$$G\left( x \right) = \lambda_{0} + \sum\limits_{i = 1}^{n} {\lambda_{i} } x_{i} + \sum\limits_{i = 1}^{n} {\lambda_{ii} } x_{i}^{2}$$
(38)

where n is the number of random variables, \(\lambda_{0}\), \(\lambda_{i}\), and \(\lambda_{ii}\) are the undetermined coefficients. Hence, there are total 2n + 1 coefficients to be computed to construct the response surface function.

In the design of experiment of RSM, the central composite design (CCD) is usually adopted, and the model can be accomplished by increasing axial and central points under the circumstance of two levels design points (Fig. 2). The specific steps to analyze the reliability by using RSM can be described as follows:

Fig. 2
figure 2

Design of sampling points. a Initial central composite design. b Design of random variables

Full size image
  1. (1)

    Select the \(\mu_{i}\) of each random variables xi as initial sample points, and the design points can be derived by enlarging the initial values with \(f\sigma_{i}\) according to the method of CCD, then, the performance function \(G\left( x \right)\) can be evaluated at the mean value \(\mu_{i}\) and the 2n points each at \(\mu_{i} \pm f\sigma_{i}\), Where \(\mu_{i}\) denote the mean values of random variables, and \(\sigma_{i}\) are standard deviations, f is usually equal to 1, and this parameter may be varied in different cases. And f takes 3.5 in this study.

  2. (2)

    The undetermined coefficients of RSM can be eventually calculated according to the above 2n + 1 values of performance function. This obtains a tentative response surface function.

  3. (3)

    Display the reliability analysis by using FORM method to obtain the reliability index \(\beta\) and design points \(x_{i}^{*}\), subject to the constraint that the tentative response surface \(G\left( x \right)\) = 0.

  4. (4)

    In practical, the iterative method is usually conducted to improve the accuracy of the reliability analysis by updating the sampling points once per round, and as a result, the distance between the limit state surface and the center of sampling points can be narrowed

    $$x_{i} ^{\prime} = \mu_{{x_{i} }} + G\left( {\mu_{{x_{i} }} } \right)\frac{{\left( {x^{*} - \mu_{{x_{i} }} } \right)}}{{G\left( {\mu_{{x_{i} }} } \right) - G\left( {x^{*} } \right)}}$$
    (39)

where \(x_{i} ^{\prime}\) denotes the new sampling points.

Validation

To verify the validity of the proposed model of deep-buried soil tunnel, the numerical results are compared with the solutions computed by Yang and Huang (2013). For deep buried rectangular tunnel, Yang and Huang (2013) calculated the internal energy dissipation with Hoek–Brown failure criterion and derived the three-dimensional failure surfaces in single rock layer. Hence, the difficulty between two proposed models is that the upper solution of Yang and Huang (2013) had not taken the underground water table and multiple stratums into consideration and the failure model supposed to be different when comparing with the mechanism presented in this paper. To overcome this obstacle, when taking one single layer into consideration, the total energy dissipation in the failure surface can be calculated by

$$\frac{1}{m + 1}\sigma_{t} C_{0}^{ - m} \left[ {\gamma \left( {1 - \gamma_{u} } \right)} \right]^{m} L^{m} - \sigma_{t} + q = 0$$
(40)

Correspondingly, the equation of collapse surface can be expressed as

$$f\left( x \right) = \sigma_{t} C_{0}^{ - m} \left[ {\gamma \left( {1 - \gamma_{u} } \right)} \right]^{m - 1} x^{m} - H$$
(41)

When x equals to L, \(f\left( L \right) = 0\), and the height of falling block is

$$H = \sigma_{t} C_{0}^{ - m} \left[ {\gamma \left( {1 - \gamma_{u} } \right)} \right]^{m - 1} L^{m}$$
(42)

The nonlinear Mohr–Coulomb criterion can be transformed into linear Mohr–Coulomb failure criterion when m is taken as a unit, and the radius and height can be simplified as follows when the pore water pressure coefficient \(\gamma_{u}\) is equal to zero.

$$L = \frac{2\tan \varphi }{\gamma }\left( {\frac{c}{\tan \varphi } - q} \right)$$
(43)
$$H = \frac{L}{\tan \varphi }$$
(44)

Meanwhile, the width and height of deep buried rectangular tunnel computed by Yang and Huang (2013) according to the Hoek–Brown failure criterion disregarded the effect of pore water pressure

$$L = \frac{2A}{\gamma }\left[ {\frac{{\left( {1 + 2B} \right)\left( {\sigma_{tm} - q} \right)}}{2B}} \right]^{B} \sigma_{ci}^{{\left( {1 - B} \right)}}$$
(45)
$$H = \frac{1 + 2B}{{\gamma B}}\left( {\sigma_{tm} - q} \right)$$
(46)

Supposing B = 1, A = tan \(\varphi\), \(\sigma_{t} = \frac{c}{\tan \phi }\), an equivalence between the Hoek–Brown and the Mohr–Coulomb can be established, Eq. (45) and Eq. (46) can be simplified by the linear Mohr–Coulomb criterion as

$$L = \frac{3\tan \varphi }{\gamma }\left( {\frac{c}{\tan \varphi } - q} \right)$$
(47)
$$H = \frac{3}{\gamma }\left( {\frac{c}{\tan \varphi } - q} \right)$$
(48)

Eventually, different parameters (c = 10–30 kPa, \(\varphi\) = 15–35°, \(\gamma\) = 15–35 kN/m3, q = 0–20 kPa) are carefully selected to compare the analytical results derived from this paper with the existing researches. As shown in Fig. 3, the evolution rules of width and height of falling block are in accordance with the numerical results proposed by Yang and Huang (2013), and therefore, the model proves to be efficient in analyzing the roof collapse mechanism. The potential range including radius and height demonstrates a positive correlation with cohesion c while decreases as the friction angel φ, unit weight γ, and support pressure q tend to be larger; furthermore, the numerical results computed in this paper are smaller than those of the reference, which indicate the results are more secure.

Fig. 3
figure 3

Comparisons of numerical results with different parameters. a With the effect of cohesion c. b With the effect of friction angel φ. c With the effect of unit weight γ. d With the effect of support pressure q

Full size image

Numerical results and comparisons

The 2D progressive collapse mechanism in layered soil masses of deep-buried tunnel is affected by various parameters of corresponding stratums; therefore, with determinacy of collapse range above the tunnel roof, suitable support measures can be adopted to prevent potential roof collapse, and from this perspective, parametric study contributes to instruct support design. Based on the analytical solution presented in Eq. (32), the collapse curves as functions of different parameters (\(\sigma_{t1}\) = 55–70 kPa, \(\sigma_{t2}\) = 50–65 kPa, \(\sigma_{t3}\) = 40–55 kPa, \(C_{0 - 1}\) = 40–55 kPa, \(C_{0 - 2}\) = 30–45 kPa, \(C_{0 - 3}\) = 20–35 kPa, \(\gamma_{1}\) = 20–26 kN/m3, \(\gamma_{2}\) = 12–18 kN/m3, m1 = 1.5–1.8, m2 = 1.4–1.7, m3 = 1.2–1.5, h2 = 2–5 m, \(\gamma_{u}\) = 0.1–0.7, q = 20–35 kPa, \(\eta\) = 0.3–0.9) are plotted in Fig. 4. The possible range including radius and height of the falling block enlarges as the increases of tensile strength, nonlinear coefficient, underlying stratum thickness, pore water pressure coefficient, and reversely, the extent shows negative correlations with the unit weight, support pressure, the parameter \(\eta\); however, compared with the monotonous evolution rules of other parameters, the initial cohesion presents more complicate effects on the collapse mechanism, and increasing initial cohesion displays two opposite effects on the change rules of collapsing extent, that is, bringing with it a horizon expansion but also a vertical shrinkage. Additionally, the slight fluctuations of pore water pressure and parameter \(\eta\) will result in an evident variation of collapse extent, especially, the higher pore water pressure coefficient and lower \(\eta\) work so greatly to the disadvantage of tunnel stability, and larger support pressure needs to be designed to improve the unfavorable conditions, consequently, one can conclude that underground water including pore water pressure coefficient and water table is the key factor to affect the support design of deep-buried soil tunnel.

Fig. 4
figure 4

2D potential collapse range with different parameters. a With variation of tensile strength \(\sigma_{t}\). b with variation of initial cohesion \(C_{0}\). c With variation of unit weight \(\gamma\). d With variation of nonlinear coefficient m. e With variation of stratum thickness h2. f With variation of pore water coefficient \(\gamma_{u}\). g With variation of support force q. h With variation of parameter \(\eta\)

Full size image

Parametric analysis

Before performing the reliability analysis of deep-buried tunnel, related parameters involved in the performance function \(G\left( x \right)\) should be identified firstly. In this section, the corresponding parameters are divided into two parts, random variables and nonrandom variables. the initial cohesion \(C_{0 - i}\) and tensile strength \(\sigma_{ti}\) are regarded as random variables with mean values and coefficients of variation. The subscript i of these random variables denotes 1, 2, or 3 separately. Their values are listed in Table 1. For the rest parameters, especially in specific underground projects, underlying stratum thickness and underground water table can be determined precisely by drilling data, besides, the pore water pressure coefficient usually displays lower variation due to stable underground water table. Hence, as discussed above, the remaining parameters including nonlinear coefficient \(m_{i}\), unit weight \(\gamma_{i}\), pore water pressure coefficient \(\gamma_{u}\), underlying stratum \(h_{2}\) and the water table \(\eta\) are selected as nonrandom variables (Table 2).

Table 1 Statical values of random variables
Full size table
Table 2 Deterministic values of nonrandom variables
Full size table

In general, normal function is widely adopted to describe the distribution features of random variables, meanwhile, when encountered larger coefficient of variation (COV) of random variable, lognormal distribution is usually recommended in reliability analysis to avoid negative values. Consequently, the choice of lognormal distribution is driven by the strict non-negative of random variables (Li et al 2014). Due to the complicated expression of performance function \(G\left( x \right)\), RSM codes in MATLAB software are used to compute numerical results.

Individual effects of nonrandom variables

Understanding the effects of different nonrandom variables on the tunnel roof failure chances possesses dominant values for the optimization of tunnel support design. Therefore, as parameter settings above, the collapse probability as a function of the support pressure against tunnel roof is plotted in Fig. 5, the individual effects of nonrandom variables (\(m_{1}\), \(m_{2}\), \(m_{3}\), \(\gamma_{1}\), \(\gamma_{2}\), \(\eta\), \(\gamma_{u}\), \(h_{2}\)) are investigated by assigning them different values one by one.

Fig. 5
figure 5

Failure probability versus support pressure. a With variation of pore water pressure coefficient \(\gamma_{u}\). b With variation of \(\eta\). c With variation of stratum thickness h2. d With variation of nonlinear coefficient m. e With the variation of unit weight \(\gamma\)

Full size image

As shown in Fig. 5, the support pressure has a significant influence on the tunnel crown stabilization, the collapse chance decreases evidently when the support force tends to be larger, besides, the increases of pore water pressure coefficient \(\gamma_{u}\), underlying stratum thickness h2, nonlinear coefficient (m1, m2, m3) and unit weight (\(\gamma_{1}\), \(\gamma_{2}\)) promote the failure probability enhancement, while the remaining parameter \(\eta\) displays an opposite impact on the collapse mechanism, the smaller of the \(\eta\) is, the more unstable of the roof stability is. Furthermore, by comparing the difference of failure probability, under the influences of parameters \(\gamma_{u}\) and \(\eta\), the differences of failure probability increase evidently than those of other nonrandom variables when support force becomes larger, this indicates the factor of underground water including pore water pressure coefficient \(\gamma_{u}\) and water table \(\eta\) presents a more essential effect on the collapse mechanism, correspondingly, the ground layer thickness h2 possesses the least influence, and therefore, more attentions should be paid to the ground water when analyzing tunnel reliability.

Cross-correlation of random variables

Worthy to attention, the above analyses are conducted without considering the mutual correlated relationships among the random variables, and in reality, large quantities of researches have been designed to investigate the effects of correlated coefficients of random variables on the engineering structure reliability. Cherubini (2011) found the negative correlation between the effective cohesion and friction angel would result in a higher reliability index of shallow foundations. Therefore, the correlation coefficients \(\rho_{1}\) denotes the cross correlation between the initial cohesion and tensile strength for the upper stratum parameters (\(C_{0 - 1}\), \(\sigma_{t1}\), \(C_{0 - 2}\), \(\sigma_{t2}\)) and \(\rho_{2}\) for the lower stratum (\(C_{0 - 3}\), \(\sigma_{t3}\)) are primarily selected to research their effects on the reliability indexes. Generally, increasing initial cohesion will result in larger tensile strength; this phenomenon can be seen from Eq. (4), and therefore, only positive correlated correlation is considered. As shown in Fig. 6, when taking the correlated coefficients into consideration, the reliability index increases evidently than that of noncorrelated random variables, besides the difference between the reliability curves tends to be larger as the growth of support pressure. Hence, one can be concluded that larger support force to the tunnel roof needs to be designed to meet the safety requirement when ignoring the cross-correlation of random variables.

Fig. 6
figure 6

The reliability index versus the support pressure under different correlated coefficients

Full size image

Furthermore, the COV of random variable also presents a significant influence on the tunnel support stability. And in general, the larger of the COV of the random variable is, the more uncertainties could be encountered in the tunnel support design. When the support pressure remains unchanged, the reliability indexes as functions under cross effects of COV and correlated coefficients of random variables are plotted in Fig. 7. The combined effects of both factors display more complicated impacts on the structure stability, as growth of COVs of random variables, the reliability indexes monotonically decrease when the correlated coefficient is smaller than 0.3, reversely, the reliability indexes increase firstly and then reduce when in the other situation of correlated coefficient is larger than 0.3. The corresponding values of COV to the peak values of reliability indexes gradually grow as then increment of correlated coefficients, and this indicates the growth of COVs in a certain range may be in favor of the tunnel stability. By comparing the differences between the reliability curves, one can conclude that the lower COV of tensile strength while the higher COV of initial cohesion will result in huge fluctuations of reliability indexes.

Fig. 7
figure 7

Comparisons of failure probability with different COVs of random variables in the condition of q = 55 kPa. a \(COV_{{\sigma_{t} }}\) = 0.06. b \(COV_{{C_{0} }}\) = 0.06

Full size image

Reliability analysis of deep-buried tunnel

Reliability index and design points

Reliability index is commonly employed to evaluate safety insurance of engineering projects, to verify the accuracy of proposed model, number of repeated trails N = 5 × 104 for MCSs are designed to calculate the support reliability in condition of normal and lognormal distribution of random variables. When assigning larger values to support force to tunnel crown, the comparison results of two models are listed in Table 3.

Table 3 Reliability indexes and design points for normal and lognormal variables
Full size table

As expected, the support force displays an essential effect on the tunnel stability, the reliability index increases evidently with the enhancement of support force. The maximum differences of reliability indexes \(\beta\) between the proposed model and MCS method are controlled within 0.14 and 0.15 for normal and lognormal distribution variables, which prove the model is effective in computing the reliability index. Besides, the comparison results of normal distribution variables with those of lognormal distribution variables reveal the reliability indexes corresponding to normal parameters are slight smaller than those of lognormal parameters, and this indicates the tunnel reliability design maybe conservative when the random variables obey the lognormal distribution rules.

The design points \(\left({{C}_{0-1}}^{*}, {{\sigma }_{t1}}^{*}, {{C}_{0-2}}^{*}, {{\sigma }_{t2}}^{*}, {{C}_{0-3}}^{*}, {{\sigma }_{t3}}^{*}\right)\) to different support pressures represent the most possible failure points on the limit state surface (LSS), they’re the points where the expanding 6-dimensional dispersion ellipsoid are tangent to the limit state surface. According to the definition of LSS, the whole state can be divided into safe and failure domain, in the failure area, the performance function should be smaller than zero. The reliability index denotes the distance, in units of standard deviations, from the mean value point to the closest points on the LSS which is also regarded as design points. Low and Tang (1997, 2004) recommended an alternative perspective of reliability index according to an expanding ellipsoid in the original space of the basic random variables, finding the design points is equivalent to derive the smallest ellipsoid which is tangent to the limit state surface, and the reliability index can be calculated by the co-directional ratio of the smallest ellipsoid that just touches the LSS to the unit dispersion ellipsoid (Lü and Low 2011). As listed in Table 3, in the circumstance of lower coefficient of variation, the design point \({{C}_{0-1}}^{*}\) decreases while the rest points \(\left({{\sigma }_{t1}}^{*}, {{C}_{0-2}}^{*}, {{\sigma }_{t2}}^{*}, {{C}_{0-3}}^{*}, {{\sigma }_{t3}}^{*}\right)\) increase as the increment of tunnel support pressure, besides, the more remarkable change rates to the design points \({{C}_{0-1}}^{*}\) and \({{\sigma }_{t1}}^{*}\) reveal the upper stratum parameters possess a more dominant effect on the LSS.

Reliability-based design

As discussed above, the reliability of tunnel support design seeks for the optimal issue under the combined effects of multiple factors including the random and nonrandom variables, nevertheless, different stratum combinations between the strong and weak layers may demonstrate reverse influences on the crown stability, therefore, considering the complexity of geological conditions, it is essential to investigate the evolution rules of tunnel reliability under various scenarios. In this section, a series of numerical simulations including four tests are carried out. As listed in Table 4, in case 1, only one layer is considered, the natural and saturated parameters are selected for the ground layer above and under the water table. In cases 2 and 4, strong stratum in the upper layer and weak stratum in the lower layer and vice versa are studied. And finally, the saturated parameters in the upper layer are smaller than that of underlying stratum for case 3. All these random variables are normally distributed with the COVs of 0.04. The numerical results of the four cases are compared in Fig. 8, under the same support pressure, the failure probability of case 4 is apparently larger than those of another three cases, and there is case 1 afterwards, while little difference of failure curves between the case 2 and case 3 possesses the least failure chance which demonstrates the tunnel roof maintains higher stability when the strong stratum in the upper layer no matter whatever combinations of the underlying stratums. Consequently, one can conclude that the strong stratum in the lower layer works so greatly to the disadvantage of the tunnel crown stability; therefore, the roof stability is deeply affected by the layer soil stratum.

Table 4 Mean values of random variables in different scenarios
Full size table
Fig. 8
figure 8

Comparison of the failure chances in different cases

Full size image

Reliability-based design (RBD) gradually becomes an efficient and reliable solution to cope with uncertainty in soil problems, and in general, a target reliability index \(\beta\) of 2.5 or 3 is required in RBD analysis, and correspondingly, the failure chances to them are equal to 0.62% and 0.13%, respectively. As discussed above, compared with the other parameters, the factor of groundwater including the pore water pressure coefficient \(\gamma_{u}\) and the parameter \(\eta\) presents a more significant influence on the tunnel crown failure chance; therefore, the RBD is conducted in this section to compute designed support pressure against tunnel roof with a target reliability index 2.5 by taking the underground water into consideration, and this tunnel pressure may also be called as “probability tunnel pressure.” In the condition of normal distribution of \(C_{0}\) and \(\sigma_{t}\), a set of COVs of random variables are selected to investigate the evolution rules between the designed support pressures and the parameters of \(\gamma_{u}\) and \(\eta\). As shown in Fig. 9, the designed support force increases with the enhancement of pore water pressure coefficient \(\gamma_{u}\) while decreases as the parameter \(\eta\) tends to be larger. Furthermore, the larger force to the roof is required when encountered larger COVs of the both normal distributed random variables, and under the same variations of the COVs to the variables, the change rate under the influence of \(COV_{{\sigma_{t} }}\) displays more obvious effect than that of \(COV_{{C_{0} }}\); therefore, one can conclude that larger COVs of random variables, especially for the tensile strength, works so greatly to the disadvantage of the tunnel reliability, and RBD may be an efficient way to design the tunnel support pressure.

Fig. 9
figure 9

Design roof pressure with different COVs of random variables. a With the parameter \(\eta\). b With the pore water pressure coefficient \(\gamma_{u}\)

Full size image

Conclusion

This paper presents a reliability analysis method for deep-buried tunnel roof in layered soil mass, taking the seepage force into consideration, the upper bound solution of potential collapse range is derived, and the performance function to evaluate support reliability is established, by dividing the corresponding parameters into random and nonrandom variables, the failure probability and reliability index can be obtained to assess roof stability. Detailed conclusions are illustrated as follows.

1. Without regard to multiple layers and underground water, the two-dimensional collapse mechanism in this paper is compared with the model proposed by Yang and Huang (2013), and the results reveal that the evolution rules of radius and height of falling block in this paper consist with those of Yang and Huang (2013); meanwhile, the numerical results in this study are slight smaller than those suggested by Yang and Huang (2013), and therefore, the solutions are more effective and secure. Numerical results reveal that the potential collapse range including radius and height increases as tensile strength, nonlinear coefficient, underlying stratum thickness and pore water pressure coefficient tend to be larger, while decreases as the growth of unit weight, support force and parameter \(\eta\). Increasing initial cohesion possesses two opposite influences on the collapse range, that is, bringing with a horizon expansion but a vertical shrinkage.

2. Parametric analysis is designed to investigate the effects of random and nonrandom variables on the failure probability of tunnel roof. Results show that the failure chance increases when pore water pressure coefficient, underlying stratum thickness, nonlinear coefficient and unit weight tend to be larger, while the tunnel roof maintains higher stability with the growth of parameter \(\eta\). Among all the individual nonrandom variables, underlying stratum thickness owns the least while underground water factor including pore water pressure coefficient and underground water table possesses the most significant effects on the crown stability. Besides, studies on the random variables show that the reliability index evidently enlarges as the growth of correlated coefficients of random variables, however, the evolution rules change when considering the cross effects of COV and correlation coefficient on the roof stability, and the reliability index would increase first and then decrease as the growth of COV and correlated coefficient.

3. The reliability indexes are slightly larger when random variables lognormal distributed; meanwhile, as increment of support force, the reliability index grows, and design points for the upper stratum are more sensitive to support pressure. Among all the possible double stratums combinations, tunnel roof is extremely unstable and requires larger support pressure when encountered with strong underlying stratum. Eventually, reliability-based design is conducted to investigate target support pressure to the tunnel roof, the analysis results reveal that designed support pressure increases as the increase of pore water pressure coefficient while decreases as the growth of parameter \(\eta\). Additionally, increasing coefficients of variation of random variables also requires larger support pressure, and variation of tensile strength has a more obvious effect on the target support force and more attentions should be given so as to reduce potential risks.