Introduction

The rock creep is one of important mechanical properties of rock materials. With the deepening of underground engineering, such as coal mining and underground tunnel excavating, the creep effect on the stability of engineering surrounding rocks is gaining importance (Wang and Li 2008). The landslide due to the rock creep in the Yanchi phosphate mine in Hubei, resulted in heavy casualties (Ma et al. 2011). The rock creep phenomenon is known to have caused numerous problems in sandstone tunnels of the Western Foothill Range in Taiwan, causing significant remediation costs (Tsai et al. 2008). The rock creep has become the focus in materials mechanics, geotechnical engineering, and other disciplines. However, there are numbers of classical combined creep models, such as Burgers model, generalized Kelvin model, and Poynting-Thomson creep model, which are not able to demonstrate either the accelerated creep stage or the plastic creep, obviously, the practical engineering needs are not met.

For this reason, many scholars have made remarkable achievements in the study of rock creep, especially non-linear creep, by improving the combined components or empirical equations. Tomanovic (2006) developed a new visco-elastoplastic model to define the creep behavior after unloading and reloading of marl samples. Ping et al. (2016) proposed a new non-linear creep constitutive model based on the damage creep characteristics, which can work out reasonably explanations for the soft rock creep deformation. Liu et al. (2017) introduced a damage variable and a new non-linear viscous component to improve the Nishihara model for describing the accelerated creep stage. Zhou et al. (2011) replaced the traditional Newton dashpot with the Abel dashpot in the classical Nishihara model and simulated the entire creep process of salt rocks according to the fractional calculus theory. Nedjar and Roy (2013) Coupled the local damage model with the generalized Kelvin-Voigt rheological model based on yield surface theory to describe the long-term creep behavior of gypsum rock materials.

At present, some improved models can simulate the plastic creep and the accelerated creep stage, but most of them still present the following problems: (1) too many coefficients are set and the creep equations are too complex, resulting in the complexity of calculation process and the difficulty in numerical simulation; (2) although the parameters of those new models meet the non-linear relationship with time, and also get a good fitting effect with the accelerated creep experiment data, the inversion parameters cannot meet the non-linear relationship with stress. Under different stress conditions, the parameters of those improved models are very different, so that the model cannot be used in the non-uniform stress field. These problems directly lead to the result that those improved models can only be applied theoretically, not practically.

With the growing function of computer, using the secondary development interface of commercial software to develop the constitutive model has become a trend. Wang et al. (2006) derived a soft matrix for numeral calculations of viscous-elastic-plastic material according to the Mises yield criterion and successfully added to the ADINA finite element program. Wang et al.(2017) developed a new Duncan-Chang to describe the water-rock interaction in FLAC3D by using Visual C ++ language; Xu et al. (2004) introduced the method of developing Duncan-Chang material constitutive model in ABAQUS and improved the application scope of the ABAQUS software in geotechnical engineering. Gao and Chen (2012) proposed a semi-empirical creep model to study the long-term deformation of expanded polystyrene (EPS) composite soil and secondarily developed the semi-empirical creep model based on the user subroutines CREEP of ABAQUS, which provided a powerful finite element approach to the study the creep behavior of EPS composite soil. In order to simulate secondary creep stage at low stress level and calculate unloading and reloading creep deformations, Fahimifar et al. (2015) modified the elasto-viscoplastic model proposed by Sterpi and Gioda (2009) and implemented its governing equations in FLAC3D by using the built-in FISH language.

In view of the defects of classical models and the present improved models, the Poynting-Thomson creep model, one of the classical creep models, is modified based on the creep damage theory and the introduction of the viscoplastic unit in this paper, and a new model named NP-T creep model is obtained. In the Visual C++ language and FISH language environment, the NP-T creep model is secondarily developed by the interface of by FLAC3D (version 3.0). After validating its accuracy and superiority, the NP-T creep model is used to study the influence of soft rock thickness on roadway stability. This work is of great significance for both theoretical research and practical application in geotechnical engineering.

NP-T creep model and its finite difference form

Creep damage effect

Many uniaxial compression experiments results showed that some parameters of rock, such as elastic modulus, strength, and viscosity coefficient, usually decrease with the increase of creep time (Yuan 2012; Yu 1997; Miao and Chen, 1994; Sun 2007). In this paper, the creep parameters are modified by damage factor to characterize the damage evolution process of rock. Based on the damage theory, there are two determination methods of damage factor. The one is the geometrical damage which is defined by the effective load-bearing area of the structure (Kachanov 1992), and the other one is the energy damage which is defined by the change of elastic modulus (Zhang et al. 2009). The second determination methods of damage factor is used in this paper, and according to Yang et al. (2010), the damage factor w is defined as follows:

$$ w=\frac{E_0-{E}_{\infty }}{E_0}\left(1-{e}^{-\alpha t}\right)=\beta \left(1-{e}^{-\alpha t}\right) $$
(1)

where E 0 is the initial elastic modulus of the rock, E ∞ is the long-term modulus of the rock, and α is a coefficient related to the damage degree.

If the damage of viscoelastic parameters is considered and the damage is isotropic, the rock modulus and viscosity coefficient A(t) vary with time as follows:

$$ A(t)={A}_0\left(1-w\right)={A}_0\left[1-\beta \left(1-{e}^{-\alpha t}\right)\right] $$
(2)

In this paper, it is considered that the damage only occurs in the accelerated creep stage, and the damage can be ignored in the decay or steady creep stage (Jiang et al. 2009). The damage condition is that the stress σ is greater than or equal to the yield strength σs, and the equivalent strain \( \varepsilon \mathrm{e}=\sqrt{\varepsilon 1+\varepsilon 2+\varepsilon 3} \) is greater than the strain threshold εt. That is, when σ ≥ σ s,ε e > ε t, the viscoelastic parameters of the rock begin to damage.

Establishment of the NP-T creep model

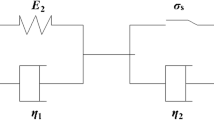
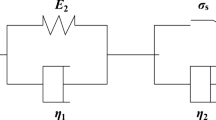
In order to reflect the plasticity of rock and the accelerated creep process, the damage properties of the creep parameters and the Mohr-Coulomb yield criterion are introduced into the Poynting-Thomson creep model (Fig. 1a), and an improved creep damage model defined as NP-T (New Poynting-Thomson) creep model is established (Fig. 1b), where E 1 and E 2 are the elastic moduli of the two Hooke units and η 1 and η 2are the viscosity coefficients of the two dashpots. When the rock reaches the Mohr-Coulomb yield criterion, the viscoplastic unit will produce viscoplastic deformation, and the damage of the E 1, E 2, η 1, and η 2will occur if the rock reaches the damage condition.

Fig. 1
figure 1

Component of the Poynting-Thomson and NP-T creep model. a Poynting-Thomson creep model. b NP-T creep model

Full size image

According to the rheological model theory, the creep equation of the NP-T model under different stress states can be expressed as follows.

  1. (1)

    Whenσ < σs, the model is the classical Poynting-Thomson model, which is composed of a Maxwell unit and a Hooke unit in parallel. The model can describe transient deformation, decay and steady creep, the creep equation is (Wang et al. 2014) as follows:

$$ \varepsilon =\frac{\sigma }{E_2}\left(1-\frac{E_1}{E_1+{E}_2}{e}^{\frac{-{E}_1{E}_2}{\left({E}_1+{E}_2\right){\eta}_1}t}\right) $$
(3)
  1. (2)

    When σ ≥ σs,εe ≤ εt, the Poynting-Thomson model is connected with a viscoplastic unit in series, which obeys the Mohr-Coulomb criterion and will produce viscoplastic deformation. The creep equation is as follows:

$$ \varepsilon =\frac{\left(\sigma -{\sigma}_{\mathrm{s}}\right)}{\eta_2}t+\frac{\sigma }{E_2}\left(1-\frac{E_1}{E_1+{E}_2}{e}^{\frac{-{E}_1{E}_2}{\left({E}_1+{E}_2\right){\eta}_1}t}\right) $$
(4)
  1. (3)

    When σ ≥ σs,εe > εt, the rock reaches the damage condition and the parameters E 1, E 2, η 1, and η 2 will decrease according to Eq. (2), the accelerated creep stage occurs at this time. The creep equation derived from and Eq. (4) is

$$ \varepsilon =\frac{\left(\sigma -{\sigma}_{\mathrm{s}}\right)}{\eta_2\left(1-w\right)}t+\frac{\sigma }{E_2\left(1-w\right)}\left(1-\frac{E_1}{E_1+{E}_2}{e}^{\frac{-{E}_1{E}_2}{\left({E}_1+{E}_2\right){\eta}_1}t}\right) $$
(5)

The constitutive equation in the three-dimensional finite difference form of the NP-T creep model

In the process of the secondary development by the FLAC3D interface, the one-dimensional creep constitutive equation of NP-T creep model must be extended into a three-dimensional central difference form. In three-dimensional stress state, the internal stress tensor of rock can be decomposed into the spherical stress tensor σ m and the deviatoric stress tensor S ij , which is

$$ {\sigma}_{ij}={\sigma}_{\mathrm{m}}{\delta}_{ij}+{S}_{ij} $$
(6)

The total deviatoric strain rate of rock \( {\dot{e}}_{ij} \)consists of the deviatoric strain rate of the Poynting-Thomson unit \( {\dot{e}}_{ij}^P \)and the deviatoric strain rate of viscoplastic unit \( {\dot{e}}_{ij}^{vp} \), which is

$$ {\dot{e}}_{ij}={\dot{e}}_{ij}^{\mathrm{P}}+{\dot{e}}_{ij}^{\mathrm{vp}} $$
(7)

The Poynting-Thomson unit is composed of the Maxwell unit and the Hooke unit in parallel. For the Maxwell unit, the expression is

$$ {\dot{e}}_{ij}^{\mathrm{M}}=\frac{{\dot{S}}_{ij}^{\mathrm{M}}}{2{G}_1}+\frac{S_{ij}^{\mathrm{M}}}{2\eta {\prime}_1} $$
(8)

where \( {S}_{ij}^{\mathrm{M}} \) and \( {\dot{e}}_{ij}^{\mathrm{M}} \) are the deviatoric stress and the deviatoric strain rate of the Maxwell unit, respectively; η′1 is the three-dimensional form of the η 1; and G 1 is the three-dimensional form of the Maxwell unit shear modulus, the incremental difference form are as follows:

$$ \varDelta {e}_{ij}^{\mathrm{M}}=\frac{\varDelta {S}_{ij}^{\mathrm{M}}}{2{G}_1}+\frac{{\overline{S}}_{ij}^{\mathrm{M}}\varDelta t}{2\eta {\prime}_1} $$
(9)
$$ {\overline{S}}_{ij}^{\mathrm{M}}=\frac{S_{ij}^{\mathrm{M},\mathrm{N}}+{S}_{ij}^{\mathrm{M},\mathrm{O}}}{2} $$
(10)

where \( {\overline{S}}_{ij}^{\mathrm{M}} \) is the average deviatoric stress of the Maxwell unit within a time step, \( {S}_{ij}^{\mathrm{M},\mathrm{O}} \) is the deviatoric stress tensor of the Maxwell unit at the time t, and \( {S}_{ij}^{\mathrm{M},\mathrm{N}} \) is the deviatoric stress tensor of the Maxwell unit at the time t + ∆t. From Eq. (9) and Eq. (10), the following equation can be obtained:

$$ {S}_{ij}^{\mathrm{M},\mathrm{N}}=\frac{1}{A}\varDelta {e}_{ij}^{\mathrm{M}}+\frac{B}{A}{S}_{ij}^{\mathrm{M},\mathrm{O}} $$
(11)

where

$$ A=\frac{1}{2{G}_1}+\frac{\varDelta t}{4{\eta}_1^{\prime }} $$
(12)
$$ B=\frac{1}{2{G}_1}-\frac{\varDelta t}{4{\eta}_1^{\prime }} $$
(13)

For Poynting-Thomson unit, since the Maxwell unit and the Hooke unit are in parallel, the following equations can be obtained:

$$ {S}_{ij}^{\mathrm{P},\mathrm{N}}-2{G}_2{e}_{ij}^{\mathrm{P},\mathrm{N}}={S}_{ij}^{\mathrm{M},\mathrm{N}} $$
(14)
$$ {S}_{ij}^{\mathrm{M},\mathrm{O}}={S}_{ij}^{\mathrm{P},\mathrm{O}}-2{G}_2{e}_{ij}^{\mathrm{P},\mathrm{O}} $$
(15)
$$ {e}_{ij}^{\mathrm{P},\mathrm{N}}=\varDelta {e}_{ij}^{\mathrm{P}}+{e}_{ij}^{\mathrm{P},\mathrm{O}}. $$
(16)

From Eq. (11), Eq. (14), Eq. (15), and Eq. (16), the following equations can be obtained:

$$ {S}_{ij}^{\mathrm{P},\mathrm{N}}=\left(\frac{1}{A}+2{G}_2\right)\varDelta {e}_{ij}^{\mathrm{P}}+2{G}_2{e}_{ij}^{\mathrm{P},\mathrm{O}}\left(1-\frac{B}{A}\right)+\frac{B}{A}{S}_{ij}^{\mathrm{P},\mathrm{O}} $$
(17)
$$ \varDelta {e}_{ij}^{\mathrm{P}}=\frac{S_{ij}^{\mathrm{P},\mathrm{N}}-2{G}_2{e}_{ij}^{\mathrm{P},\mathrm{O}}\left(1-\frac{B}{A}\right)-\frac{B}{A}{S}_{ij}^{\mathrm{P},\mathrm{O}}}{\frac{1}{A}+2{G}_2} $$
(18)
$$ {e}_{ij}^{\mathrm{P},\mathrm{N}}=\frac{S_{ij}^{\mathrm{P},\mathrm{N}}+\left(\frac{1}{A}+\frac{B}{A}2{G}_2\right){e}_{ij}^{\mathrm{P},\mathrm{O}}-\frac{B}{A}{S}_{ij}^{\mathrm{P},\mathrm{O}}}{\frac{1}{A}+2{G}_2} $$
(19)

For the viscoplastic unit, the deviatoric strain rate is

$$ {\dot{e}}_{ij}^{\mathrm{vp}}=\frac{H\left\langle F\right\rangle }{2{\eta}_2^{\prime }}\frac{\partial g}{\partial {\sigma}_{ij}}-\frac{1}{3}{\dot{e}}_{vol}^{\mathrm{vp}}{\delta}_{ij} $$
(20)

where

$$ {\dot{e}}_{vol}^{\mathrm{vp}}=\frac{H\left\langle F\right\rangle }{2{\eta}_2^{\prime }}\left[\frac{\partial g}{\partial {\sigma}_{11}}+\frac{\partial g}{\partial {\sigma}_{22}}+\frac{\partial g}{\partial {\sigma}_{33}}\right] $$
(21)

and the\( {\eta}_2^{\prime } \) is the three-dimensional form of the η 2.

The total strain increment of viscoplastic unit is

$$ \varDelta {e}_{ij}^{\mathrm{vp}}=\frac{H\left\langle F\right\rangle }{2{\eta}_2^{\prime }}\frac{\partial g}{\partial {\sigma}_{ij}}\varDelta t $$
(22)

whereH〈F〉 is the switching function, \( H\left\langle F\right\rangle =\left\{{{}_F^0}_{F>0}^{F\le 0}\right. \), F is the yield function, and g is the plastic potential function.

In the plastic mechanics, it is assumed that the spherical stress tensor only produces volume strain and does not produce plastic strain, so the corresponding spherical stress rate \( {\dot{\sigma}}_{\mathrm{m}} \) has the following linear relationship:

$$ {\dot{\sigma}}_{\mathrm{m}}=K\left({\dot{e}}_{vol}-{\dot{e}}_{vol}^{vp}\right) $$
(23)

where K is the volume modulus, \( {\dot{e}}_{vol} \)is the spherical strain rate, and \( {\dot{e}}_{vol}^{vp} \)is the plastic spherical strain rate.

The shear failure yield function f s is \( {\sigma}_1-{\sigma}_3{N}_{\phi }+2C\sqrt{N_{\phi }} \), the potential function g s is σ 1 − σ 3 N φ , where \( {N}_{\phi }=\frac{1+\sin \phi }{1-\sin \phi } \), \( {N}_{\varphi }=\frac{1+\sin \varphi }{1-\sin \varphi } \), ϕ is the internal friction angle, φ is the dilation angle, and C is the cohesion. The tensile failure yield functionf t is σ t − σ 3, the potential function g t is −σ 3, where σ t is the tensile strength, σ 1 and σ 3are the minimum, and the maximum principal stress of the unit, which is agreed that compressive stress is negative.

The incremental form of Eq. (7) is

$$ \varDelta {e}_{ij}=\varDelta {e}_{ij}^{\mathrm{P}}+\varDelta {e}_{ij}^{\mathrm{vp}} $$
(24)

From Eq. (17), Eq. (22), and Eq. (24), the following equation can be obtained:

$$ {S}_{ij}^N={S}_{ij}^{\mathrm{P},\mathrm{N}}=\left(\frac{1}{A}+2{G}_2\right)\left(\varDelta {e}_{ij}-\varDelta {e}_{ij}^{\mathrm{vp}}\right)+2{G}_2{e}_{ij}^{\mathrm{P},\mathrm{O}}\left(1-\frac{B}{A}\right)+\frac{B}{A}{S}_{ij}^{\mathrm{O}}. $$
(25)

When the stress state of the rock reaches the condition of damage, the parameters G 1, G 2, \( {\eta}_1^{\prime } \), an \( {\eta}_2^{\prime } \), and K will weaken according to Eq. (2).

The secondary development of the custom constitutive model

The secondary development of the NP-T creep model is mainly carried out in the software of Visual Studio 2005. The main work includes the setting of the software environment and the modification of head file (.h file) and source file (.cpp file) (Chen and Xu 2013; Gao et al. 2015; Zhao et al. 2014; Liu and Zhao 2010).

In the head file, a derived class statement should be made for the new constitutive model, and the model ID number, model name string, and model output name string have to be modified. It is necessary to redefine the private variables which include the parameters of the model and the intermediate variables required for iteration, such as dBulk (volume modulus) and dHshear (shear modulus of the Hooke unit), dMshear (shear modulus of the Maxwell unit), dMviscosity (viscosity coefficient of the Maxwell unit), dPviscosity (viscosity coefficient of the viscoplastic unit), dCohesion (cohesion of material), dFriction (internal friction angle), dDilation (dilation angle), dTension (uniaxial tensile strength), dMnphi (N ϕ ), and dMnpsi (N φ ).

At the beginning of the source file, some file calls and constant statements are necessary, and the variables of plasticity status indicator should be defined and assigned in hexadecimal format. The two most important functions in the source file are the Initialize () function and the Run () function. The Initialize () function initializes some commonly used variables in the model calculation. When FLAC3D executes run (Solve, Cycle) or performs large strain correction, the Initialize () function executes at a time. The Run () function is used to program the core equations like Eq. (18), Eq. (23), and Eq. (25). The main role is to carry out some important computing links, such as the modulus calculation, the plasticity judgment and correction, and the stress tensor calculation according to strain increment. The Run () function is called in every cycle and subunit in the FLAC3D unit calculation.

The udm project is regenerated after modifying the head file and the source file, when a reminder about the compiled result will appear. If the compiled result does not have any errors, the newly generated file named NP-T.dll in the Release folder should be copied to the FLAC3D installation directory. Therefore, the NP-T model can be called by the “config cppudm” command and the “model load NP-T.dll” command in FLAC3D.

Because the damage factor is difficult to transform into the incremental form about Δt, the damage identification and evolution equations are obtained by the FLAC3D built-in FISH language. Initially, the node traversal statements in the FISH language are used to judge whether the node of the model reaches the damage condition. Additionally, the COMMAND statement is used to reassign parameters as the rule of A(t) = A 0(1 − w) = A 0[1 − β(1 − e−αt)] for the unit where the nodes reach the damage condition, and one step can be solved after that. Finally, the previous statements are put into the LOOP statement where the cycle step length is agreed with the creep step length, the program will reassign parameters and calculate at a time if the creep time increases one step length in each cycle, and the LOOP statement is ended until the creep complete. The evolution and creep calculation are achieved in the whole process. The specific process is shown in Fig. 2.

Fig. 2
figure 2

The flow of creep damage identification and evolution

Full size image

Parameter inversion and model validation

Parameter fitting and inversion

Parametric fitting is one of the most widely used methods to determine the creep parameters of rock. The uniaxial creep tests of argillite in different stress levels were carried out by Xu (1997), the size of test samples is Ø50 × 100, and the test temperature is in the range of 20 ± 3 °C. Based on the test results, the algorithm of Levenberg-Marquardt + Universal Global Optimization (LM-UGO) in the 1stOpt software is used to fit and invert creep parameters of the NP-T creep model. The LM-UGO algorithm overcomes the difficulty of giving an appropriate initial value, which exists in the ordinary iterative method. That is, the user does not need to give the initial value of the parameter and can finally find the optimal solution by the random value of the 1stOpt software and the global optimization algorithm (Cheng et al. 2012). It can be obtained that \( \beta =\frac{E_0-{E}_{\infty }}{E_0}=\frac{E_0-{E}_{\infty }}{E_0}=0.691 \) from Xu (1997). Thus, the inversion results of remaining parameters in the model are shown in Table 1, and the fitting result comparison between the NP-T creep model and the Poynting-Thomson creep model is given in Fig. 3.

Table 1 Inversion results of creep parameters
Full size table
Fig. 3
figure 3

Comparison of fitting results. a Creep experimental curve and fitting curve of the NP-T creep model. b Creep experimental curve and fitting curve of the Poynting-Thomson creep model

Full size image

It can be seen in Table 1 and Fig. 3a that the NP-T creep model has good fitting effect and the fitting correlation coefficients R are all above 0.99. Compared with the Poynting-Thomson model fitting results in the stress states of 13.16, 14.29, and 15.82 MPa which are shown in Fig. 3b, the NP-T creep model can not only reflect the steady-state creep process of rock but also the plastic deformation and accelerated creep process. In addition, the parameters that needed inversion are less than those of other improved models, which shows the advantages of the NP-T creep model. At the same time, it can be seen that the inversion results of creep parameters fluctuate within an order of magnitude under different stress conditions and the NP-T creep model can be applied to the non-uniform stress field.

Validation of the NP-T creep model in the FLAC3D simulation

A cylindrical model is built to simulate the uniaxial creep experiment in FLAC3D. According to the size of the experimental sample (Xu 1997), the diameter and the height are set to be 50 and 100 mm, respectively. The inversion results of parameters in Table 1 are transformed into three-dimensional form (Yang 2011), and Poisson’ ratio and other plastic parameters are assigned according to the parameters of similar soft rock in a mine. The bottom of the model is fixed, and the surface force is imposed on the top of y-axis. The creep calculation is carried out after the initial displacement is confirmed 0, and the creep curves of the center point on the top of the model under the axial stresses of 14.29 and 15.82 MPa are shown in Fig. 4.

Fig. 4
figure 4

Uniaxial creep simulation curve of the NP-T creep model. a Axial stress is 14.29 MPa. b Axial stress is 15.82 MPa

Full size image

According to Fig. 4, the maximum creep deformation is 0.75 mm under the axial stress of 14.29 MPa at the 250 d, and the maximum creep deformation is 1.10 mm under the axial stress of 15.82 MPa at nearly 200 d. In consideration of the model height and the instantaneous strain (\( \varepsilon =\frac{\sigma }{E_1+{E}_2} \)), the maximum strains are 11.18 × 10−3 and 14.71 × 10−3, while the experimental results are 12.90 × 10−3 and 16.87 × 10−3. Compared to experimental results, the simulation results have the deviations of 13.3 and 12.8%. Because the Poisson’s ratio, tensile strength, dilation angle, friction angle, cohesion, and other key parameters of experimental material are not given in the original reference; the similar soft rock parameters of a mine are taken to simulate; and the model will have a certain deviation inevitably in the calculation, iteration, discrimination, and other processes. The simulated curve is close to the experimental curve in shape, so it is considered that simulating the creep behavior of soft rock by the NP-T creep model is feasible.

The influence of the soft rock thickness on roadway stability

Simulation model establishment and numerical calculation

In some underground engineering, such as the III11 mudstone roadway of the Luling coal mine, the creep performance of roadway surrounding rocks is not only related to the lithology but also the thickness of surrounding rocks. Xue et al. (2016) discovered that the creep capability of the surrounding soft rock is weakened along with the decrease of the thickness of the soft rock layer where the roadway was located, and this phenomenon was named as “hesitation effect.” The model is established by FLAC3D as in Fig. 5 to further explain the connection between the soft rock thickness and the roadway stability.

Fig. 5
figure 5

Simulation model and its mesh generation

Full size image

The model size is 50 m × 100 m × 50 m in the X, Y, and Z direction, where a semi-circular arch roadway in the cross section with 4 m in width, 2 m in wall height, and 2 m in arch height is constructed. The horizontal roadway locates in the slanting soft rock layer with thickness of 20 m. The upper and lower layers of soft rock are hard sandstone layers with thickness of 10–20 m. A load of 15 MPa is applied at the top of the model, and based on the Poisson’s ratio, the lateral pressure coefficient λ, which is the ratio of the horizontal compressive stress and the vertical compressive stress, is set to be 0.3 according to the A·H·Gennik equation: \( \lambda =\frac{\mu }{1-\mu } \). The two boundaries on the x-axis are fixed in the X direction, the two boundaries on the y-axis are fixed in the Y direction, and the bottom boundary is fixed in the Z direction. The hard sandstone layers are set to be the Mohr-Coulomb model, the soft rock layer is set to be the NP-T creep model, and the parameters of soft rock are obtained after a three-dimensional transformation according to the average value of the inversion results in Table 1. The specific parameters of each rock layer are shown in Table 2. In this model, the soft rock thickness is invariable along the strike direction; thus, the hesitation effect is avoided. As the hard sandstone layers do not creep, the impact of its thickness on roadway stability is not taken into account. At the roadway roof and floor, monitoring points are set along the strike direction. The thickness of the soft rock above roof monitoring points is defined as H r, and the thickness of the soft rock below floor monitoring points is defined as H f. Since the H r and H f change gradually along the strike direction, the influence of soft rock thickness on roadway stability can be discussed by observing the difference in the displacement of each monitoring points.

Table 2 Parameter values of each rock layer in the model
Full size table

The deformation characteristics of the roadway roof and floor

The deformation of each roof and floor monitoring point in the creep process is compared respectively in Fig. 6a, b, which appears that in the non-supporting condition, the H r and the H f have great influence on roadway stability. For the roadway roof, the value of creep subsidence increases with the increase of H r; the thicker the soft rock is, the stronger the creep capability is. But there is a thickness threshold of H r, when the H r is greater than 9.0 m, the effect of H r on creep capability is weakened, and the difference between H r = 11.5 m and H r = 14.0 m in the value of roof creep subsidence is small. For the roadway floor, there is also a thickness threshold. When the H f is less than 9.5 m, the creep capability of the roadway floor increases with the increase of the H f. When the H f is 9.5 and 12.0 m, the accelerated creep occur at 360 and 386d, respectively; the roadway floor tends to be destroyed, but there is no significant difference between the value of the floor expansion before the accelerated creep. In addition, it can be seen in Fig. 7 that the deflection of the roadway roof also increases with the increase of H r, and the destruction of the roadway roof begins from the center and expands to the two sides. Through observation and analysis, the roadway floor deflection also has the same law as the roadway roof.

Fig. 6
figure 6

Characteristics of roadway creep deformation in different conditions. a Characteristics of roadway roof creep deformation in different H r conditions. b Characteristics of roadway floor creep deformation in different H f conditions

Full size image
Fig. 7
figure 7

Roof deflection in different H r conditions

Full size image

Figure 8a shows the displacement contour in the z-axis direction of the roadway roof at 400 d, and Fig. 8b shows the displacement contour in z-axis direction of the roadway floor at 386 d; they demonstrate the regular impact of H r and H f on the roadway roof and floor clearly. That is, even if the thickness of soft rock layer where the roadway located is the same, the thickness difference of the soft rock above and below the roadway will also produce hesitation effect on the roadway.

Fig. 8
figure 8

The contour of displacement in the z-axis direction. a Roadway roof at 400 d. b Roadway floor at 386 d

Full size image

Conclusions

  1. (1)

    Damage effect is an important factor in rock failure, and the accelerated creep stage is an important part of creep process. Therefore, the time-dependent damage and accelerated creep threshold are introduced to establish the non-linear NP-T creep model, through which the rock creep behavior can be demonstrated more realistically.

  2. (2)

    The NP-T creep model can simulate the plastic deformation and the entire creep process in the non-uniform stress field, and the inversed parameters are less than those of other improved models, so the NP-T creep model can effectively simulate the soft rock creep deformation.

  3. (3)

    When the thickness of the soft rock above roadway roof or below roadway floor is within the threshold, the thicker the soft rock is, the worse the roadway stability is. When the thickness of soft rock is greater than the threshold, the thickness has little effect on roadway stability. Therefore, it is useless to improve the support strength even if the soft rock thickness increases, which is of great significance for the choice of the support way and the support location in underground engineering.