Introduction

Underground excavation, such as tunneling and foundation pit, are the common engineering activities in urban construction, while more and more excavation engineering are located above or beside existing municipal pipelines and subway tunnels. The longitudinal uneven settlements of existing pipelines and tunnels are inevitably caused by adjacent underground excavation, particularly tunneling which are widely constructed by the shield method. According to tunnels in service, it will lead to segment leakage or local damage, and even longitudinal distortion of railway track, which are a fatal threat to the structural safety of tunnels and normal operations of trains. Therefore, it is desirable to develop a theoretical method to predict the deformation behavior of existing pipelines affected by underground excavation in soft clays.

Recently, some attempts have been made for the response of surrounding soils and existing structures induced by adjacent excavation in soft clays. In the in situ monitoring study, Chang et al. (2001), Hsiung (2009), Wang et al. (2010), Kog (2010), and Khoiri and Ou (2013) presented the measured deformation behavior for ground movements and buried structures (pipelines and tunnels). In the experiment study for foundation pit, Kusakabe et al. (1985) carried out centrifuge model tests for the effects of buried pipelines caused by foundation pit. He et al. (2010) presented the simulation of a roadway excavation in the geologically horizontal strata at great depth based on large-scale physical model tests. Lam et al. (2012) developed a new apparatus to simulate deep excavation in geotechnical centrifuge. On the other hand, for tunneling experiments, Kamata and Mashimo (2003) presented typical auxiliary bolting methods using centrifugal models with sandy ground to confirm their strengthening effects on tunnel faces. Vorster et al. (2005a) conducted centrifuge model tests for the effects of adjacent pipelines induced by tunneling. Juneja et al. (2010) investigated the effects of forepoles on stability of tunnel face and unsupported length during tunnel excavation in clay beds using centrifuge model tests. Ng et al. (2013) conducted a centrifuge modeling to investigate the effects of twin tunneling on an existing pile.

In the calculation study, there are two analysis methods. The first one, finite element numerical method, which is to analyze the interaction mechanics between underground excavation and existing structures in its entirety, is often conducted using commercial software. Dolezalova (2001), Sharma et al. (2001), Yoo and Lee (2008), Tang and Kung (2010), Devriendt et al. (2010), and Huang et al. (2013) presented the deformation behavior of surrounding soils and existing tunnels induced by unloading of deep foundation pit based on the finite element numerical method. Yamaguchi et al. (1998), Addenbrooke and Potts (2001), Chehade and Shahrour (2008), Dang and Meguid (2008), and Gui and Chen (2013) used this method to analyze the effect of surrounding soils and existing tunnels caused by new tunnel excavation. Finite element numerical method has an advantage to reasonably simulate the complex construction process and the interaction mechanics between structures and surrounding soils. However, it usually needs professional software to calculate the complex numerical model and it takes very long time to obtain the final results. The other calculation method, a two-stage analysis method, can divide the complex interactional problem into two simple stages. In the first stage, it is to calculate the free soil deformation or stress at the location of existing structures. In the second stage, the free soil deformation or stress is imposed onto existing structures. Yoo and Choi (2006) presented an engineering accident about the rupture of cast iron pipelines caused by deep foundation pit excavation, and finite element method was used to solve the problem in the second stage. Klar et al. (2005) and Vorster et al. (2005b) estimated the free soil deformation based on Peck curves and modified Peck curves in the first stage and then used elastic theory method to consider soil-pipeline interaction in the second stage.

The abovementioned analysis methods are complicated for initial design and construction adjustments. Therefore, a simple analytical method is still needed to analyze the deformation behavior of existing pipelines affected by underground excavation, and there is no doubt that the two-stage method based on Winkler foundation model is a suitable choice. Attewell et al. (1986) and Klar et al. (2005) analyzed the effects of tunneling on buried pipelines based on Winkler foundation model, respectively. In their study, Peck curves were used to simulate the soil displacement field in the first stage and the empirical methods cannot always fit the practical deformation with high precision. In addition, Son and Cording (2005) developed a procedure for estimating damage in nearby structures due to excavation-induced ground movements. The effects of soil-structure interaction were considered using numerical models and correlated with field data and physical model test data. Kung et al. (2007) proposed a simplified semiempirical model to predict the maximum wall deflection, the maximum surface settlement, and the surface-settlement profile due to excavations in soft to medium clays. Schuster et al. (2009) used a simplified model to evaluate the damage potential of a building adjacent to a braced excavation. The abovementioned studies are important references for the interaction mechanism between underground excavation and pipelines.

In the present approach, a simplified displacement-controlled two-stage method and stress-controlled two-stage method using Winkler foundation model are presented for determining the mechanical behavior of buried pipelines induced by underground excavation in soft clays. For the case of tunnel excavation, the displacement-controlled boundary element solution is used to calculate the free soil displacement field. The oval-shaped ground deformation pattern is imposed to the tunnel opening to consider the nonuniform convergence characters. For the case of foundation pit excavation, the free soil stress is calculated based on Mindlin (1936) classical theoretical solution, including the situations that the excavation unloading center is not acting on the pipeline axis and that the excavation boundary and pipeline axis are formed with an arbitrary angle in the horizontal plane. Then, the existing pipelines are considered as Winkler foundation beams with infinite length. The longitudinal deformation equation for soil-pipeline interaction is built, and then, the displacement and internal force of pipelines are obtained finally.

Displacement-controlled two-stage method for tunneling

Based on the different calculation approach that underground excavation influence is exerted on adjacent pipelines by the means of free displacement or free stress, the simplified method can be divided into two categories: displacement-controlled method and stress-controlled method. Because the soil displacement caused by tunnel excavation can be predicted more reasonable, it is more suitable to use displacement-controlled method for tunneling, but for foundation pit excavation, stress-controlled method is adopted more.

Generally speaking, the excavation boundary of tunneling is easier to determine when compared with the one of foundation pit. The nonuniform convergence deformation pattern is imposed as the boundary condition at the tunnel opening in this study. In addition, the deformation models of foundation pit-retaining structure can be divided into four categories: cantilever shape, skirting shape, inward protrusion shape, and compound shape. Because that the deformation models are rather complex, the deformation pattern of the excavation boundary is difficult to acquire by the unified expression. However, according to foundation pit excavation, the unloading can be equal to the rectangular or circular uniform load at the bottom plan. Therefore, the stress-controlled method is more applied to simulate foundation pit excavation.

Free displacement induced by tunneling

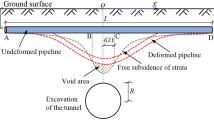
According to the tunnel-soil-pipeline interaction problem as shown in Fig. 1a, Klar et al. (2005) simulated the free soil displacement at the pipeline position using Peck empirical formula. Celestino et al. (2000) and Jacobsz (2002) suggested that Peck formula could not exactly describe the soil settlements induced by tunnel excavation. The boundary element method is a powerful tool to solve the boundary value problems on the condition of given displacement-controlled pattern. In this study, the nonuniform convergence deformation pattern is imposed as the boundary condition at the tunnel opening proposed by Park (2004) as shown in Fig. 1b. The deformation pattern can be written as follows:

Fig. 1
figure 1

Tunnel-soil-pipeline interaction problem: a whole excavation view; b nonuniform convergence pattern

Full size image
$$ {u}_x^j=-\frac{g_0}{2}\left(1- \sin \theta \right) \cos \theta $$
(1)
$$ {u}_z^j=-\frac{g_0}{2}\left(1- \sin \theta \right) \sin \theta $$
(2)

where u j x and u j z are the horizontal and vertical displacements at the boundary node j; g 0 is the equivalent ground loss parameter, that is,

$$ {g}_0=2R\left(\sqrt{1+{\varepsilon}_0}-1\right) $$
(3)

in which ε 0 is the equivalent ground loss ratio, and R is the radius of the tunnel.

In order to reduce the geometric approximate error and improve element interpolation accuracy, the curved conic isoparametric elements are employed, where low-order constant elements are frequently used previously. The interpolation expressions for the coordinates and the functions can be written in terms of the homogeneous coordinate ξ as follows:

$$ \left\{x\right\}={\displaystyle \sum_{k=1}^3{N}_k\left(\xi \right){\left\{x\right\}}_k} $$
(4)
$$ \left\{u\right\}={\displaystyle \sum_{k=1}^3{N}_k\left(\xi \right){\left\{u\right\}}_k} $$
(5)
$$ \left\{t\right\}={\displaystyle \sum_{k=1}^3{N}_k\left(\xi \right){\left\{t\right\}}_k} $$
(6)

in which {x}, {u}, and {t} are the coordinate, displacement, and traction vectors at any node on the element, respectively, i.e., \( \left\{x\right\}={\left[\begin{array}{cc}\hfill x\hfill & \hfill z\hfill \end{array}\right]}^T \), \( \left\{u\right\}={\left[\begin{array}{cc}\hfill {u}_x\hfill & \hfill {u}_z\hfill \end{array}\right]}^T \), and \( \left\{t\right\}={\left[\begin{array}{cc}\hfill {t}_x\hfill & \hfill {t}_z\hfill \end{array}\right]}^T \); {x} k , {u} k , and {t} k are the coordinate, displacement, and traction vectors at the node k on the element, respectively, i.e., \( {\left\{x\right\}}_k={\left[\begin{array}{cc}\hfill {x}_k\hfill & \hfill {z}_k\hfill \end{array}\right]}^T \), \( {\left\{u\right\}}_k={\left[\begin{array}{cc}\hfill {u}_x^k\hfill & \hfill {u}_z^k\hfill \end{array}\right]}^T \), and \( {\left\{t\right\}}_k={\left[\begin{array}{cc}\hfill {t}_x^k\hfill & \hfill {t}_z^k\hfill \end{array}\right]}^T \), k = 1, 2, or 3. N k (ξ) is the interpolation function which is defined as follows:

$$ {N}_1\left(\xi \right)={\scriptscriptstyle \frac{1}{2}}\xi \left(\xi -1\right) $$
(7)
$$ {N}_2\left(\xi \right)=1-{\xi}^2 $$
(8)
$$ {N}_3\left(\xi \right)={\scriptscriptstyle \frac{1}{2}}\xi \left(\xi +1\right) $$
(9)

where − 1 ≤ ξ ≤ 1.

Based on the abovementioned higher-order elements, boundary discretization equations for the arbitrary source node i can be written as follows:

$$ {\displaystyle \sum_{J=1}^N{\displaystyle \sum_{k=1}^3\left({h}_{xx}^{iJk}{t}_x^{Jk}+{h}_{xz}^{iJk}{t}_z^{Jk}\right)}}={\displaystyle \sum_{J=1}^N{\displaystyle \sum_{k=1}^3\left({g}_{xx}^{iJk}{u}_x^{Jk}+{g}_{xz}^{iJk}{u}_z^{Jk}\right)}} $$
(10)
$$ {\displaystyle \sum_{J=1}^N{\displaystyle \sum_{k=1}^3\left({h}_{zx}^{iJk}{t}_x^{Jk}+{h}_{zz}^{iJk}{t}_z^{Jk}\right)}}={\displaystyle \sum_{J=1}^N{\displaystyle \sum_{k=1}^3\left({g}_{zx}^{iJk}{u}_x^{Jk}+{g}_{zz}^{iJk}{u}_z^{Jk}\right)}} $$
(11)

in which J is the element number with the location of the field point, u Jk m and t Jk m are the displacement and traction functions in the m coordinate direction at the node k on the element J, respectively, and m, n = x, z, k = 1, 2, or 3; h iJk mn and g iJk mn are, respectively, the displacement and traction influence coefficient, i.e.,

$$ {h}_{mn}^{iJk}={\displaystyle {\int}_{-1}^1{U}_{mn}^{iJk}\left(\xi \right)}{N}_k\left(\xi \right)\left|\overline{B}\right|d\xi $$
(12)
$$ {g}_{mn}^{iJk}={\displaystyle {\int}_{-1}^1{T}_{mn}^{iJk}\left(\xi \right)}{N}_k\left(\xi \right)\left|\overline{B}\right|d\xi $$
(13)

where U iJk mn and T iJk mn are, respectively, the displacement and traction components in the n coordinate direction at the node k on the element J due to a unit point load in the m direction at the node i. They are defined by the Green’s function solution proposed by Mindlin (1936). \( \left|\overline{B}\right| \) is the Jacobian determinant and represents the transformation from the global coordinate system to the local coordinate system, i.e.,

$$ \left|\overline{B}\right|=\left[{\left({\displaystyle \sum_{k=1}^3\frac{d{N}_k}{d\xi }{x}_k}\right)}^2+{\left({\displaystyle \sum_{k=1}^3\frac{d{N}_k}{d\xi }{z}_k}\right)}^2\right] $$
(14)

In order to obtain the global equation corresponding to the arbitrary node i in discrete form, it is necessary to add the contribution from two adjoining elements, e.g., (j − 1) and (j), into one term, defining the nodal influence coefficient. This will obtain the following equation:

$$ {\displaystyle \sum_{j=1}^{2N}{\left[H\right]}_{ij}{\left\{t\right\}}_j}={\displaystyle \sum_{j=1}^{2N}{\left[G\right]}_{ij}{\left\{u\right\}}_j} $$
(15)

where i and j are the discrete nodes on the boundary; {u} j and {t} j are, respectively, displacement and traction vectors at the node j, i.e., \( {\left\{t\right\}}_j={\left[\begin{array}{cc}\hfill {t}_x^j\hfill & \hfill {t}_z^j\hfill \end{array}\right]}^T \) and \( {\left\{u\right\}}_j={\left[\begin{array}{cc}\hfill {u}_x^j\hfill & \hfill {u}_z^j\hfill \end{array}\right]}^T \). [H] ij and [G] ij are the displacement and traction influence coefficient matrixes, respectively, and the elements of abovementioned matrixes are defined by Eqs. (12) and (13).

When all the nodes are taken into consideration, Eq. (15) produces a 2N × 2N system of equations which can be represented in matrix form as:

$$ \left[H\right]\left\{t\right\}=\left[G\right]\left\{u\right\} $$
(16)

in which [H] and [G] are the global displacement and traction influence coefficient matrixes, and the elements of the matrixes are determined by Eqs. (12) and (13). {t} is the global boundary traction matrix, i.e.,

$$ \left\{t\right\}={\left[\begin{array}{ccccccc}\hfill {t}_x^1\hfill & \hfill {t}_z^1\hfill & \hfill {t}_x^2\hfill & \hfill {t}_z^2\hfill & \hfill \cdots \hfill & \hfill {t}_x^{2N}\hfill & \hfill {t}_z^{2N}\hfill \end{array}\right]}^T, $$

and {u} is the global boundary displacement matrix, i.e.,

$$ \left\{u\right\}={\left[\begin{array}{ccccccc}\hfill {u}_x^1\hfill & \hfill {u}_z^1\hfill & \hfill {u}_x^2\hfill & \hfill {u}_z^2\hfill & \hfill \cdots \hfill & \hfill {u}_x^{2N}\hfill & \hfill {u}_z^{2N}\hfill \end{array}\right]}^T. $$

The given boundary displacement pattern of Eqs. (1) and (2) is imposed into Eq. (16); thus, the unknown boundary traction value {t} can be determined. Finally, the displacement at arbitrary point Q can be calculated:

$$ {\left\{u\right\}}_Q={\displaystyle \sum_{j=1}^{2N}{\left[H\right]}_{Qj}{\left\{t\right\}}_j}-{\displaystyle \sum_{j=1}^{2N}{\left[G\right]}_{Qj}{\left\{u\right\}}_j} $$
(17)

where [H] Qj and [G] Qj are the displacement and traction influence coefficient matrixes, respectively. Actually, the solution for Eq. (17) is the tunneling-induced ground movements in clays based on displacement-controlled boundary element method considering oval-shaped convergence deformation pattern.

Displacement-controlled analysis between pipeline and disturbance soil

The key assumptions are listed as follows: (1) the pipeline is elastic continuous, and (2) the interaction between the pipeline and disturbance soil satisfies the deformation compatibility condition. The existing pipeline can be regarded as a Winkler foundation beam which is affected by excavation-induced free soil displacements. So, the displacement-controlled equation for the deformation behavior of existing pipeline induced by tunneling can be obtained:

$$ EI\frac{d^4{W}_z(x)}{d{x}^4}+K{W}_z(x)=K{U}_z(x) $$
(18)

where W z (x) is the vertical displacement of pipeline caused by adjacent excavation, U z (x) is the free soil displacement due to tunneling and it can be calculated by Eq. (17). K = kD, k is the subgrade modulus, and D is the outer diameter of pipeline. It should be noted that the subgrade modulus k is usually calculated by means of the Vesic (1961) expression, which is given by

$$ k=\frac{0.65{E}_s}{1-{v}^2}\sqrt[12]{\frac{E_s{W}^4}{EI}} $$
(19)

where W is the width of a beam (in this case for the outer diameter of pipeline D). EI is the bending stiffness of the beam. E s and v are the soil elastic modulus and Poisson’s ratio, respectively. According to nonhomogeneous foundation, the soil elastic parameters under the condition of homogeneous foundation are calculated by the means of weighted average proposed by Poulos and Davis (1980). In fact, Vesic (1961) expression essentially allows a beam on a Winkler foundation to exhibit similar displacements and moments to that of a beam on an elastic half-space when loaded with the same load.

The subgrade modulus is important to the analysis for the interaction problem, and the physical meaning of this subgrade modulus is as follows. If this subgrade modulus is used to define the maximum moment in an infinite Winkler beam under a concentrated load P, the moment M can be expressed as follows:

$$ M=\frac{P}{4\sqrt[4]{K/4EI}}=0.37Pb{\left(1-{v}^2\right)}^{0.25}{\left(\frac{EI}{E_s{b}^4}\right)}^{0.27} $$
(20)

where b = W/2.

Biot (1937) presented a solution for the same conditions (concentrated load on an infinite beam), but it is for elastic continuum:

$$ M=\frac{P}{4\sqrt[4]{K/4EI}}=0.37Pb{\left(1-{v}^2\right)}^{0.277}{\left(\frac{EI}{E_s{b}^4}\right)}^{0.277} $$
(21)

In fact, the two abovementioned expressions are practically the same. Equation (21) provides the physical meaning of the Vesic (1961) equation, which is simply an analogue, essentially allowing a beam on a Winkler foundation to exhibit similar displacements and moments to those of a beam on an elastic foundation when loaded with concentrated loads.

Based on the Vesic (1961) expression, the solution of the differential Eq. (18) is

$$ \begin{array}{c}{W}_z(x)=A \sinh \left(\lambda x\right) \sin \left(\lambda x\right)+B \sinh \left(\lambda x\right) \cos \left(\lambda x\right)\\ {}+E \cosh \left(\lambda x\right) \sin \left(\lambda x\right)+F \cosh \left(\lambda x\right) \cos \left(\lambda x\right)+{W}_z^{*}(x)\end{array} $$
(22)

where A, B, E, and F are the integral parameters, which can be determined by the boundary condition of the pipeline. \( \lambda =\sqrt[4]{\frac{K}{4EI}} \), W * z (x) is the corresponding special solution for the item KU z (x) in Eq. (18). A cubic curve function can be used in order to simulate the soil displacements induced by the special solution W * z (x):

$$ {W}_z(x)={\alpha}_0+{\alpha}_1x+{\alpha}_2{x}^2+{\alpha}_3{x}^3 $$
(23)

where α 0, α 1, α 2, and α 3 are the curve parameters and they are determined by introducing the Eq. (23) into Eq. (18).

The bending moment and shear force of the pipeline induced by tunnel excavation can be solved by the following formulas:

$$ \begin{array}{c}{M}_z(x)=-EI\frac{d{W}_z^2(x)}{dx{}^2}=-2{\lambda}^2EI\left[A \cosh \left(\lambda x\right) \cos \left(\lambda x\right)-B \cosh \left(\lambda x\right) \sin \left(\lambda x\right)\right.\\ {}\left.+E \sinh \left(\lambda x\right) \cos \left(\lambda x\right)-F \sinh \left(\lambda x\right) \sin \left(\lambda x\right)\right]-EI\frac{d{W}_z^{*2}(x)}{d{x}^2}\end{array} $$
(24)
$$ {Q}_z(x)=-EI\frac{d{W}_z^3(x)}{d{x}^3}=\left.-2{\lambda}^3EI\left\{A\Big[ \sinh \left(\lambda x\right) \cos \left(\lambda x\right)- \cosh \left(\lambda x\right) \sin \left(\lambda x\right)\right.\right]-B\left. \sinh \left(\lambda x\right) \sin \left(\lambda x\right)+ \cosh \left(\lambda x\right) \cos \left(\lambda x\right)\right]+E\left[ \cosh \left(\lambda x\right) \cos \left(\lambda x\right)- \sinh \left(\lambda x\right) \sin \left(\lambda x\right)\right]\left.\left.-F\Big[ \cosh \left(\lambda x\right) \sin \left(\lambda x\right)+ \sinh \left(\lambda x\right) \cos \left(\lambda x\right)\right]\right\}-EI\frac{d{W}_z^{*3}(x)}{d{x}^3} $$
(25)

Stress-controlled two-stage method for foundation pit

Except for the abovementioned displacement-controlled method, the mechanical behavior of municipal pipelines considering disturbance effects of foundation pit excavation can be estimated by the stress-controlled method.

Free stress induced by foundation pit excavation

For the foundation pit excavation, the unloading can be equal to the rectangular or circular uniform load at the bottom plan. Shown as Figs. 2 and 3, a rectangular foundation pit is conducted and the excavation length, width, and depth are defined as L, B, and d, respectively. The excavation boundary and pipeline axis are formed with an arbitrary angle. The axis depth of pipeline is defined as z 0. The free stress at the location of pipeline axis can be deduced according to the Mindlin (1936) classical theoretical solution.

Fig. 2
figure 2

Foundation pit-soil-pipeline interaction problem

Full size image
Fig. 3
figure 3

Plan view for simplified model of Fig. 2

Full size image

Based on Mindlin (1936) solution, the free vertical stress at the point of pipeline axis (x 1, y 1, z 0) due to the unit loading pdξdη at the point (ξ, η) of excavation bottom can be written as follows:

$$ \begin{array}{l}{\sigma}_z=\frac{p}{8\pi \left(1-v\right)}\left\{\left(1-2v\right)\left({z}_0-d\right){\displaystyle {\iint}_D\frac{d\xi d\eta}{R_1^3}}+3{\left({z}_0-d\right)}^3\right.\\ {}{\displaystyle {\iint}_D\frac{d\xi d\eta}{R_1^5}}-\left(1-2v\right)\left({z}_0-d\right){\displaystyle {\iint}_D\frac{d\xi d\eta}{R_2^3}}+\left[3\left(3-4v\right){z}_0\right.\\ {}\left.{\left({z}_0+d\right)}^2-3d\left({z}_0+d\right)\left(5{z}_0-d\right)\right]{\displaystyle {\iint}_D\frac{d\xi d\eta}{R_2^5}+30d{z}_0{\left({z}_0+d\right)}^3}{\displaystyle {\iint}_D\frac{d\xi d\eta}{R_2^7}}\Big\}\end{array} $$
(26)

where v is the soil Poisson’s ratio, D is the integral domain for the excavation bottom, and the variables R 1 and R 2 are

$$ {R}_1=\sqrt{{\left({x}_1-\xi \right)}^2+{\left({y}_1-\eta \right)}^2+{\left({z}_0-d\right)}^2} $$
(27)
$$ {R}_2=\sqrt{{\left({x}_1-\xi \right)}^2+{\left({y}_1-\eta \right)}^2+{\left({z}_0+d\right)}^2} $$
(28)

When the excavation depth of foundation pit achieves, or even exceed the buried depth of existing pipeline, the free horizontal stress could not be ignored. The free horizontal stress σ H at the point of pipeline axis (x 1, y 1, z 0) due to the unit loading pdξdη at the point (ξ, η) of excavation bottom can be expressed:

$$ \begin{array}{l}{\sigma}_H=\frac{P}{8\pi \left(1-v\right)}\left\{-\left(1-2v\right)\left({z}_0-d\right){\displaystyle {\iint}_D\frac{d\xi d\eta}{R_1^3}}+3\left({z}_0-d\right)\right.\\ {}{\displaystyle {\iint}_D\frac{y_1^2}{R_1^5}} d\xi d\eta -\left(1-2v\right)\left[3\left({z}_0-d\right)-4v\left({z}_0-d\right)\right]{\displaystyle {\iint}_D\frac{d\xi d\eta}{R_2^3}}\\ {}+3\left(3-4v\right)\left({z}_0-d\right){\displaystyle {\iint}_D\frac{y_1^2}{R_2^5}} d\xi d\eta -6d\left({z}_0-d\right)\left[\left(1-2v\right){z}_0-2vd\right]\\ {}{\displaystyle {\iint}_D\frac{d\xi d\eta}{R_2^5}}+30d{z}_0\left({z}_0-d\right){\displaystyle {\iint}_D\frac{y_1^2}{R_2^7}} d\xi d\eta +4\left(1-v\right)\left(1-2v\right)\\ {}\left.{\displaystyle {\iint}_D\frac{1}{R_2\left({R}_2+{z}_0+d\right)}\left[1-\frac{y_1^2}{R_2\left({R}_2+{z}_0+d\right)}-\frac{y_1^2}{R_2^2}\right]} d\xi d\eta \right\}\end{array} $$
(29)

where the variables R 1 and R 2 is the same with Eqs. (27) and (28).

The Eqs. (26) and (29) can be resolved using Gauss-Legendre numerical integration method. In order to obtain the free stress on the condition that the unloading center is not acting on the pipeline axis and the excavation boundary and pipeline axis are formed with an arbitrary angle, the coordinate system can be conversed (Fig. 3). The point (x 0, y 0, z 0) is defined as a point on the longitudinal axis of pipeline which is the closest to the center of rectangular unloading. Then, the origin of ξ − η coordinate system can be transferred to the point (x 0, y 0, 0) on the surface ground. According to the new coordination, the axis x is parallel with the pipeline axis and the axis y is perpendicular with the pipeline axis. The point (x 1, y 1) on pipeline axis in ξ − η coordinate system can be expressed by the point (x, y) in the new coordinate system:

$$ {x}_1=x \cos \beta +S \sin \beta $$
(30)
$$ {y}_1=x \sin \beta -S \cos \beta $$
(31)

where S is the longitudinal coordinate value of unloading center in the new coordinate system, β is the angle between the positive direction of x ‐ axis and positive direction of ξ ‐ axis.

Stress-controlled analysis between pipeline and disturbance soil

The existing pipeline can be regard as a Winkler foundation beam which is affected by excavation-induced free soil stresses. So, the stress-controlled equation for the mechanical behavior of existing pipeline induced by foundation pit excavation can be expressed as follows:

$$ EI\frac{d^4W(x)}{d{x}^4}+KW(x)=P(x) $$
(32)

where W(x) is the vertical or horizontal displacement of pipeline caused by the adjacent excavation, P(x) is the additional loads on the pipeline induced by excavation, and P(x) = σ z D for the vertical loads (or P(x) = σ H D for the horizontal loads); σ z and σ H can be calculated by the Eqs. (26) and (29).

Because solving the fourth-order differential Eq. (32) is difficult, it is the better approach to transform it into a first-order integral equation and get partly analytical solution with certain integral constants, then obtain the final solution by the numerical integration method. Consequently, the pipeline displacement suffering a concentrated force p 0 is obtained:

$$ {W}_0(x)=\frac{p_0\lambda }{2K}{e}^{-\lambda x}\left[ \cos \left(\lambda x\right)+ \sin \left(\lambda x\right)\right] $$
(33)

Assuming that the concentrated force P(ξ)dξ is acted on the point ξ, the pipeline displacement dW(x) induced by the load P(ξ)dξ can be expressed based on Eq. (33):

$$ dW(x)=\frac{P\left(\xi \right)\lambda }{2K}{e}^{-\lambda \left|x-\xi \right|}\left[ \cos \left(\lambda \left|x-\xi \right|\right)+ \sin \left(\lambda \left|x-\xi \right|\right)\right]d\xi $$
(34)

Then, the solution for differential Eq. (32) can be obtained:

$$ W(x)=\frac{\lambda }{2K}{\displaystyle {\int}_{-\infty}^{+\infty }P\left(\xi \right){e}^{-\lambda \left|x-\xi \right|}\left[ \cos \left(\lambda \left|x-\xi \right|\right)+ \sin \left(\lambda \left|x-\xi \right|\right)\right]d\xi } $$
(35)

The bending moment and shear force of the pipeline induced by foundation pit excavation can be written:

$$ M(x)=\frac{\lambda }{4}{\displaystyle {\int}_{-\infty}^{+\infty }P\left(\xi \right){e}^{-\lambda \left|x-\xi \right|}\left[ \cos \left(\lambda \left|x-\xi \right|\right)- \sin \left(\lambda \left|x-\xi \right|\right)\right]d\xi } $$
(36)
$$ Q(x)=-\frac{\lambda^2}{2}{\displaystyle {\int}_{-\infty}^{+\infty }P\left(\xi \right){e}^{-\lambda \left|x-\xi \right|} \cos \left(\lambda \left|x-\xi \right|\right)d\xi } $$
(37)

Examples

Verification for tunnel excavation

Case compared with existing calculation results

Vorster (2005) and Vorster et al. (2005b) presented the influences of underground pipeline caused by tunnel excavation based on elastic theory method. The tunnel is excavated in dry sand (e = 0.67, γ = 16 kN m− 3) with elastic modulus 14.32 MPa and Poisson’s ratio 0.25. The tunnel is perpendicular crossing the pipeline. The outer diameter and the axis depth of the tunnel are 1.5 and 5 m, respectively. Three kinds of pipelines with different materials are selected in this study, and the vertical bending stiffness are 2.625 × 104, 1.05 × 105, and 4.2 × 105 kN m2, respectively. The outer diameters of pipeline are 0.4 m, and the axis depth of pipeline is 1.5 m. The ground loss ratio is 5 %. This example is obtained by reverting from the original normalized data. The schematic representation of centrifuge model test is shown in Fig. 4.

Fig. 4
figure 4

Schematic representation of centrifuge model test for tunneling (unit: m)

Full size image

According to the research of Vorster et al. (2005b), a method based on Mindlin (1936) solution was presented for obtaining an upper approximation of bending moment for pipelines affected by tunnel-induced ground movement. The method is an equivalent linear approach which utilizes a closed form solution of subsoil displacement to derive deviatoric strain. Figures 5 and 6 show the comparisons of pipeline vertical displacements and bending moments of different bending stiffness between Vorster et al. (2005b) and the displacement-controlled two-stage method in this paper. From these pictures, it shows that the calculated pipeline vertical displacements and bending moments are in general consistent with the Vorster et al. (2005b) results, although there are slight differences between the two results. Especially for the small bending stiffness, a good agreement can be obtained between the two different methods. When the pipeline bending stiffness increases, the differences between Vorster et al. (2005b) and the displacement-controlled two-stage method are obvious. In fact, the homogenous elastic foundation model is used by Vorster et al. (2005b). By contrast, this study focused on Winkler foundation model. The reasons may be that the greater the pipeline bending stiffness becomes, the worse the deformation compatibility between pipeline and surrounding soil becomes, and the more obvious the effects of foundation model on the pipeline deformation behavior becomes.

Fig. 5
figure 5

Comparisons of pipeline settlements considering different bending stiffness

Full size image
Fig. 6
figure 6

Comparisons of pipeline bending moments considering different bending stiffness

Full size image

Case compared with engineering project

This case (Jia et al. 2009) involves a 6-m diameter shield-driven tunnel running 14.5 m deep in soft clay, which is part of the subway tunnel link from Yitian Station to Xiangmihu Station in the town of Shenzhen, China. A cable pipeline 3 m in diameter and 12 cm thick exists perpendicular to and above the tunnel, buried 8.7 m below the soil surface. Its bending stiffness is 2.82 × 107 kN m2. Soil properties from the reported ground investigation are listed in Table 1. The schematic representation of soil stratification and tunneling engineering is shown in Fig. 7. Two separate series of points are marked on the east and west walls of the pipe to measure the displacement of the pipeline during tunnel construction.

Table 1 Geological condition of the tunneling site
Full size table
Fig. 7
figure 7

Schematic representation of soil stratification and tunneling engineering (unit: m)

Full size image

The calculated pipeline displacement curve is shown in Fig. 8 with the comparison of observed data. As for the analytical solution, the elastic parameters of homogeneous soil are calculated by the means of weighted average proposed by Poulos and Davis (1980). It is shown that although the calculated sagging of the pipeline displacement is shallower than measured results and that the calculated maximum displacement is smaller, the predictions from the displacement-controlled method are in general consistent with the observed data.

Fig. 8
figure 8

Comparisons of vertical displacements of pipeline

Full size image

Verification for foundation pit excavation

Case compared with centrifuge model test

Kusakabe et al. (1985) conducted a series of centrifuge model tests on the condition of acceleration 50 g to study the influences of existing pipeline caused by adjacent excavation. The excavation depth of the cylindrical foundation pit was 100 mm, and the diameter of excavation bottom was 50 mm. The dry Toyoura sand had a density of 1570 kg/m3, a gravity of 2.66, maximum and minimum void ratios of 0.966 and 0.61, and an effective internal friction angle of 40°. The pipeline model with the depth of 35 mm was placed nearby the excavation site, and it was set with a thickness of 2 mm, an outer diameter of 10 mm, and the bending moment of 20.29 N m2. The distances S 0 between the excavation boundary and the pipeline axis for two cases were 25 and 50 mm, respectively. The schematic representation of centrifuge model test is shown in Fig. 9. Because excavation depth exceeds the buried depth of pipeline, the horizontal deformation of pipeline could not be neglected, the vertical and horizontal bending strain of the pipeline has been determined in the tests.

Fig. 9
figure 9

Schematic representation of centrifuge model test for foundation pit (unit: mm)

Full size image

The curves of vertical bending strain in one section during centrifuge tests (S 0 = 25 mm) are shown in Fig. 10. The tests include three typical phases: first (0~6 min), centrifuge acceleration gradually increases to 50 g; second (6~8 min), foundation pit excavation is completed in the stage of acceleration 50 g; and third (8~20 min), centrifuge acceleration gradually reduces to natural gravity stage. It indicates that the strain almost recovers to the initial value when the centrifuge stops, indicating that the deflections of the pipeline can be considered to be elastic and the simplified two-stage method based on the elastic assumption is suitable to consider this problem.

Fig. 10
figure 10

Vertical bending strain in one section during centrifuge tests (S 0 = 25 mm)

Full size image

Figures 11 and 12 show the comparisons of horizontal and vertical bending moments between the calculation results using the stress-controlled method in this study and the measured data of centrifuge model tests. It can be seen that the calculated pipeline bending moments are in general consistent with the observed data. When the excavation boundary is far from the pipeline (S 0 = 50 mm), the calculation results of vertical and horizontal bending moments are closer to the observed data. However, the excavation boundary is nearer from the pipeline (S 0 = 25 mm), the difference between calculation results and observed data are obvious. The reason may be that the soil nonlinear effects induced by foundation pit excavation are high when the distance between the excavation boundary and the pipeline axis is small. Although the theoretical solution presented in this study is limited in scope, it appears to be useful for a preliminary design of foundation pits to predict the excavation-induced pipeline deformation.

Fig. 11
figure 11

Comparisons of pipeline horizontal bending moments due to foundation pit excavation

Full size image
Fig. 12
figure 12

Comparisons of pipeline vertical bending moments due to foundation pit excavation

Full size image

Case compared with engineering project

The interchange project under Dong-fang Road (Chen 2005) is located in the intersection of Dong-fang Road, Century Avenue, and Zhangyang Road at Pudong New District in Shanghai. The excavation plan is approximately for a rectangular of 26 m long and 18 m wide. The excavation depth of foundation pit is 6.5 m, and the concrete floor with 1.88 m thick is poured its bottom. The metro up-line 2 passes just below the section no.1 of foundation pit with an angle of 45°. The axis horizontal distance between down-line and up-line 2 is 18 m. The outside diameter of tunnel is 6.2 m, and the depth is 12.36 m. The longitudinal bending stiffness is 1.087 × 108 kN m2. Geological condition of the site is shown in Table 2. The schematic representation of soil stratification and foundation pit engineering is shown in Fig. 13. In order to reduce the disturbance of the existing tunnels, the deep mixing pile inserted in the H-shaped steel is set as the retaining walls of the foundation pit. The surrounding soils are excavated along the tunnel axis based on the principle of “division, layering, blocking, symmetry, balancing, and time-limiting.” The soils aside by the middle wall are excavated firstly. Then, the soils aside by the existing tunnels are excavated secondly. Each section excavation is divided into five pieces, in which the width of middle piece is 3.7 m and the width of the other pieces is 3.6 m. In addition, each piece excavation consists of two layers of soil. The soil excavation depth of the first layer is not more than 2 m. When the soils at the bottom of foundation pit, the surrounding soils aside by the tunnels, and the uplift piles meet the design requirements of deformation and strength, the second layer soil will be excavated.

Table 2 Geological condition of the foundation pit site
Full size table
Fig. 13
figure 13

Schematic representation of soil stratification and foundation pit engineering (unit: m)

Full size image

Figures 14 and 15 show the vertical displacements of down-line and up-line 2 induced by foundation pit excavation, which are calculated by the stress-controlled two-stage method. The measured data proposed by Chen (2005) is also shown in Figs. 14 and 15. From the above figures, it can be seen that the calculated vertical displacements of down-line and up-line 2 are in general consistent with the observed shapes, though there are slight differences between the two results. The measured displacements of up-line 2 are smaller than the results of simplified method. That is mainly because reinforcement measures and time-space effect methods are taken in the construction in situ. The applications of these protection measures can effectively reduce the deformation value of tunnels due to adjacent excavation. It should be noted that the section no.1 of foundation pit is just above the up-line 2 and far from the down-line 2. The down-line 2 is weakly influenced by these protection measures. Therefore, some measured displacement value of down-line 2 is bigger than the corresponding calculated value by this simplified method. It should be noted that the objective for this study is to present a simplified approach to analyze the excavation-soil-structure interaction mechanics. As an effective tool at least for a preliminary design, the proposed method in this paper should help engineers rapidly determine the excavation-induced pipeline (tunnel) deformation so that to make the corresponding construction adjustments in a short time.

Fig. 14
figure 14

Comparisons of vertical displacements of up-line tunnel

Full size image
Fig. 15
figure 15

Comparisons of vertical displacements of down-line tunnel

Full size image

Parametric analyses

A series of parametric studies is carried out to investigate systematically the effect of excavation-induced soil unloading on adjacent tunnels. The influence factors include the horizontal distance between the excavation boundary and tunnel axis, the tunnel depth, the tunnel bending stiffness, and the crossing angle between the excavation boundary and tunnel axis. To enable a direct comparison corresponding to different parameters, an assumed example is selected in this study. The length, width, and depth of foundation pit are 170, 58, and 12 m, respectively, which is excavated adjacent the existing tunnel. The tunnel axis is parallel to the long side of excavation boundary. The horizontal distance between the excavation centerline and tunnel axis is 35 m. The tunnel has the outer diameter of 4 m, segment thickness of 0.15 m, bending stiffness of 1.2 × 108 kN m2, buried depth of 15 m. The soil unit weigh, elastic modulus, and Poisson’s ratio are set as 17.5 kN m−3, 4.53 MPa, and 0.32, respectively.

Three cases are considered for the horizontal distance between the excavation centerline and tunnel axis (defined as l i , i = 1, 2, 3), including l 1 = 35 m, l 2 = 40 m and l 3 = 45 m. The plan view for three cases of horizontal distance is shown in Fig. 16. The comparisons of tunnel vertical displacements caused by foundation pit excavation with different horizontal distance l i are shown in Fig. 17, in which the buried depth of tunnel is 15 m. This figure shows that the tunnel vertical deformation decreases gradually with the increase of the horizontal distance. It appears that the distance from the excavation site has a great influence on the deformation of existing structures. According to Shanghai technical code for protection region of urban bridge and tunnels (Shanghai Municipal Standards 2010), constructions nearby the tunnel site cannot be allowed on both outer sides of the range ≤ 3 m.

Fig. 16
figure 16

Plan view for three cases of horizontal distance

Full size image
Fig. 17
figure 17

Vertical displacement curves of tunnel for different horizontal distance with foundation pit

Full size image

In this study, three cases are considered for the buried depth of tunnel (defined as z i , i = 1, 2, 3), including z 1 = 15 m, z 2 = 20 m, and z 3 = 25 m. The section view for three cases of buried depth of tunnel is shown in Fig. 18. The comparisons of tunnel vertical displacements caused by foundation pit excavation with different buried depth of tunnel z i are shown in Fig. 19, in which the horizontal distance between the excavation centerline and tunnel axis is 35 m. This figure shows that the tunnel deformation is quite larger when the buried depth of tunnel is smaller, because the location of excavation unloading is close to the tunnel and the additional free stress suffering on the tunnel is very large. As the buried depth of tunnel increases, the tunnel vertical displacements decrease rapidly. Therefore, the covering thickness is an important index to protect the operation safety for tunnels in the design and construction, which should be bigger than the outer diameter of tunnel based on Japanese Civil Engineering Society regulations (Japanese Civil Engineering Society 2001).

Fig. 18
figure 18

Section view for three cases of buried depth of tunnel

Full size image
Fig. 19
figure 19

Vertical displacement curves of tunnel for different buried depth

Full size image

Three cases are considered for the bending stiffness of tunnel (defined as (EI) i , i = 1, 2, 3), including (EI)1 = 1.2 × 108kN m2, (EI)2 = 2.4 × 108kN m2, and (EI)3 = 4.8 × 108kN m2. The section view for three cases of bending stiffness of tunnel is shown in Fig. 20. When the horizontal distance between the excavation centerline and tunnel axis is 35 m and the buried depth of tunnel is 15 m, the comparisons of tunnel vertical displacements induced by foundation pit excavation with different bending stiffness are shown in Fig. 21. The figure indicates that the value of tunnel displacements decreases with the increase of the bending stiffness. That is to say, structures with higher bending stiffness can resist outside construction disturbance. Therefore, reasonable structural and material parameters of subway tunnel are very important for the segment design.

Fig. 20
figure 20

Section view for three cases of bending stiffness of tunnel

Full size image
Fig. 21
figure 21

Vertical displacement curves of tunnel for different bending stiffness

Full size image

In this study, three cases are considered for the arbitrary crossing angle between the excavation boundary and tunnel axis (defined as β i , i = 1, 2, 3), including β 1 = 0°, β 2 = 60°, and β 3 = 90°. The plan view for three cases of arbitrary crossing angle is shown in Fig. 22. The buried depth of tunnel is 15 m for three cases. According to case one (β 1 = 0°), the horizontal distance between the excavation centerline and tunnel axis is 35 m. According to the other cases (β 2 = 60° and β 3 = 90°), the tunnel location is formed rotating with the same point “o” and it is shown as Fig. 22. It is a crossing point “o” with the original tunnel axis (β 1 = 0°) and the vertical symmetry axis of foundation pit plan. The comparisons of tunnel vertical displacements induced by foundation pit excavation with different arbitrary crossing angle are shown in Fig. 23. It shows that the maximum value of tunnel displacements increases with the increase of the crossing angle. However, the influence range of tunnel caused by foundation pit excavation decreases gradually from the crossing angle 0° to 90°. The tunnel displacement has been changed sharply for different crossing angle. It is indicated that the crossing angle has a greater influence on the tunnel deformation caused by the excavation construction, which should be given to emphatic consideration in the theoretical analyses.

Fig. 22
figure 22

Plan view for three cases of arbitrary crossing angle

Full size image
Fig. 23
figure 23

Vertical displacement curves of tunnel for different crossing angle

Full size image

Conclusions

In this study, the displacement-controlled two-stage method and stress-controlled two-stage method are presented to analyze the deformation behavior of buried pipelines considering disturbance effects of underground excavation in soft clays. At the first analysis stage, the free soil deformation calculated by the displacement-controlled boundary element solution is used to estimate the soil disturbance effects. The oval-shaped ground deformation pattern is imposed to the tunnel opening to consider the nonuniform convergence characters. The free soil stress based on the Mindlin (1936) solution is used to predict the soil disturbance effects of foundation pit excavation. At the second analysis stage, the free soil deformation or free soil stress are imposed onto existing pipelines to consider the interaction between existing pipeline and surrounding soils. The proposed method is verified through comparisons with published solutions by the existing calculation results, centrifuge model tests, and site investigation data. It has been demonstrated that the proposed method provides reliable estimates in rather correct way for the response of existing pipelines affected by underground excavation in soft clays. Furthermore, the parametric analyses for tunnel deformation behavior indicate that the influence factors, including the horizontal distance between the excavation boundary and tunnel axis, the tunnel depth, the tunnel bending stiffness, and the crossing angle between the excavation boundary and tunnel axis, have significant effects on tunnel displacements due to soil excavation. It is also suggested that these influence factors should be fully considered in the design and construction for reducing potential construction risks.

Compared with finite element numerical method, the obvious advantage of the simplified two-stage method is to explicitly point out free soil deformation or free soil stress. The simplified two-stage method can reasonably consider the actual engineering, as long as the suitable calculating formula for free soil deformation and free soil stress is chosen. Furthermore, the two-stage method based on Winker foundation model is simpler than finite element numerical method. The present method can in general give less time to achieve a satisfactory prediction of existing pipeline deformation subjected to underground excavation. It can be used to quickly provide some guidance and advice during urban underground engineering. However, the major limitation of the proposed method stems from the simplified assumptions of linearity and elasticity. Complex stratigraphy condition, such as the nonhomogeneous foundation, and advanced mechanisms, such as relative uplift failure and gapping between the existing pipelines and the surrounding soil, which would contribute additionally to nonlinear soil behavior, should be introduced into the analysis in near future research.