Introduction

The relationship of resistivity index and water saturation is not linear correlation in log-log coordinate which is called as non-Archie phenomenon and exists not only in carbonates, but also in sandstones (Diederix 1982; Swanson 1985; Brown 1988; Worthington et al. 1989; Herrick and Kennedy 1993). This behavior may be the results of conductive mineral, residual water in micro-pore space, roughness of the rock surface and the conductive path, etc., and it turns prediction of water and hydrocarbon saturation of formations into a challenge (Khelil 1971; Herrick 1988; Salem 1994). In order to obtain accurate saturation exponent, the influence factors such as components of rocks, pore structure, and fluid distribution coupled with wettability of rocks have been studied (Donaldson and Siddiqui 1989; Dunlap et al. 1991; Suman and Knight 1997; Küntz et al. 2000).

There have been some attempts to express the relation between n and S w . Wang and Sharma (1988) and Suman and Knight (1997) used a three dimensional pore network model to simulate the effects of wettability, pore structure, and the saturation history on the electrical conductivity of rocks. Their results showed that n was a variable parameter which the wettability was seen to have the most significant effect on the electrical conductivity, hence on n. Yue (2003) and Tao et al. (2004) have studied the electrical transport behavior of porous media and the physical meaning of the Archie’s parameters by 2D lattice gas automata. Their results showed that there existed a power function relationship between n and S w with the exponent related to the porosity. Kumar et al. (2011) coupled 3D imaging, high-resolution SEM analysis, and in situ observations of fluid saturation with numerical simulations to probe the saturation exponent under variable saturation conditions. They found that non-Archie phenomenon mainly occurred at lower S w , and concentration of water film at or on the perimeter of grain contacts and microporosity accounted for most of this phenomenon for the clean water-wet sandstone and carbonate, respectively.

However, due to the technical limitation of pore scale, it is hard to quantify the influence factors of n. Most studies carried out on reservoirs with complex petrophysical properties were based on pore network model or 3D imaging with complicated procedure and high technical requirements, as well as high costs. Most of the results were still qualitative rather than quantitative. The relationship between saturation exponent and water saturation is still unclear. To contribute to the solution of this concern, this paper details an attempt to investigate the saturation exponent by combining the classic capillary theory and Purcell equation with NMR logging and core plugs experiments. This is an attractive alternative to complicated methods for estimating this relationship and provides a better insight into their initial relationship which has a certain theoretical basis.

Derivation of resistivity index from capillary theory and Purcell equation

Formation factor of fully water saturated rock

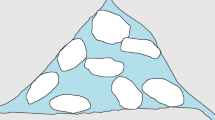
Capillary theory is wildly used in the estimation of formation property (Kozeny 1927; Carman 1937, 1948, 1956; Pape et al. 1999). It describes the pore space of porous rock with cross-section area A and length L by a bundle of parallel fluid saturated bent cylindrical capillary tubes of equal length but random diameters (Fig. 1). The resistance of the rock is equivalent to the parallel connection of resistance of the bundle of capillary tubes (Fig. 2). In terms of Ohm’s law, the resistance of a given water saturated capillary tube can be expressed as

$$ {r}_{\mathrm{i}}={R}_{\mathrm{w}}\frac{L_{\mathrm{c}}}{\pi {r}_{\mathrm{c}\mathrm{i}}^2} $$
(1)

where r i is the resistance of the ith water saturated capillary tube in ohm, R w is the resistivity of saturated water in ohmm, L c is the length of the capillary tube in meter, and r ci is ith capillary tube radius in meter.

Fig. 1
figure 1

The capillary tube model of porous rock which is made up of a number of bent parallel capillary tubes with equal length but random radius (Liu et al. 2007)

Full size image
Fig. 2
figure 2

The parallel connection of resistance of the bundle of capillary tubes (Wang et al. 2014)

Full size image

Purcell (1949) proposed the theoretical equation which related to the permeability of a system of parallel cylindrical capillaries of equal length, but various radii, to the porosity of the system and to the capillary pressures and volumes of its component parts

$$ k=\frac{{\left(\sigma \cos \theta \right)}^2}{2}\phi {{\displaystyle \sum_{\mathrm{i}=1}^N{S}_{\mathrm{i}}\left(\frac{1}{p_{\mathrm{ci}}}\right)}}^2 $$
(2)

where k is the permeability in millidarcy, σ is the interfacial tension in millinewton per meter, θ is the contact angle in degree, ϕ is the porosity in percent, Pci is the ith capillary pressure in megapascal, and S i is the percentage of the cross-section area of capillary tube with r ci   radius in cross-section areas of all the capillary tubes.

Based on the capillary theory and Purcell equation, Wang et al. (2014) have deduced the formation factor equation of fully water saturated rock as

$$ F=\frac{R_0}{R_{\mathrm{w}}}=\frac{1}{\phi^{\mathrm{m}}}=\frac{e^{\prime}\tau {A}_{\mathrm{N}}^{\prime }}{8\pi}\frac{\phi }{k} $$
(3)

where F is the formation factor, R 0 is the resistivity of fully water saturated rocks in ohmm, m is the cementation factor, τ (τ = L c /L) is the tortuosity of capillary tubes, A ′ N (\( {A}_N^{\prime }=A/{\displaystyle \sum_{i=1}^N{D}_i^{\prime }} \), D ′ i is the number of capillary tube with the ith resistance) is apparent average cross-section area in meter squared and e′ is a constant exponent.

Resistivity index of partially water saturated rock

While hydrocarbon charging occurs, water in larger pores will be displaced first. At the end of this proceeding, the larger pores are filled by hydrocarbon and water film, and the remaining are still filled with water. Hydrocarbon and the matrix are seen to be none conductive. The conductivity of hydrocarbon-bearing rock is still contributed by saturated water. According to the parallel connection of resistance of tube bundle model, the resistance of partially water saturated rock can be obtained as

$$ \frac{1}{{\mathrm{r}}_{\mathrm{t}}}={D}_1\frac{1}{{\mathrm{r}}_1}+{D}_i\frac{1}{{\mathrm{r}}_{\mathrm{i}}}+\dots \dots +{D}_{\mathrm{N}}\frac{1}{{\mathrm{r}}_{\mathrm{N}}}={\displaystyle \sum_{i=1}^{\mathrm{N}}{D}_{\mathrm{i}}\frac{1}{{\mathrm{r}}_{\mathrm{i}}}} $$
(4)

where r t is the resistance of partially water saturated rock in ohm.

Substituting Eq. (1) into Eq. (4), this relationship becomes

$$ \frac{1}{{\mathrm{r}}_{\mathrm{t}}}={\displaystyle \sum_{i=1}^{\mathrm{N}}{D}_{\mathrm{i}}\frac{1}{R_{\mathrm{w}}\frac{L_{\mathrm{c}}}{\pi {r}_{\mathrm{c}\mathrm{i}}^2}}} $$
(5)

Carrying out some algebraic transformations, and it becomes

$$ {r}_t=\frac{R_w}{\pi }{L}_{\mathrm{c}}{\left({\displaystyle \sum_{i=1}^N{D}_i{r}_{\mathrm{c}\mathrm{i}}^2}\right)}^{-1} $$
(6)

The form of Ohm’s law for partially water saturated rock is

$$ {r}_{\mathrm{t}}={R}_{\mathrm{t}}\frac{L}{A} $$
(7)

where R t is the resistivity of partially water saturated rocks in ohmm.

Combine Eqs. (7) and (6) and then

$$ {R}_{\mathrm{t}}=\frac{R_{\mathrm{w}}}{\pi}\tau {A}_{\mathrm{N}}{\left({\displaystyle \sum_{i=1}^{\mathrm{N}}{d}_i{r}_{\mathrm{ci}}^2}\right)}^{-1} $$
(8)

where A N is the apparent average cross-section area in partially water saturated rocks in meter squared and is expressed as

$$ {A}_{\mathrm{N}}=A/{\displaystyle \sum_{i=1}^{\mathrm{N}}}{D}_{\mathrm{i}} $$
(9)

and d i is the percentage of the number of capillary tubes with the r ci radius in all the capillary tubes, and is expressed as

$$ {d}_i={D}_i/{\displaystyle \sum_{i=1}^N}{D}_i $$
(10)

P ci in Pucrcell equation (Eq. (2)) can be obtained by

$$ {p}_{\mathrm{ci}}=\frac{2\sigma \cos \theta }{r_{\mathrm{ci}}} $$
(11)

Thus, Pucrcell equation for fully water saturated rock can be expressed as

$$ k=\frac{\phi }{8}{\displaystyle \sum_{i=1}^{\mathrm{N}}{S}_i^{\prime }{r}_{\mathrm{ci}}^2} $$
(12)

From the percolation theory, when two phases (water and oil/gas) coexist in pore space, each phase has its own flow path with a stable interface when this two phase flow steadily (Helba et al. 1992). That means when one phase flows, the other phase can be seen as matrix which has no contribution to the flow. As the same form in Eq. (12), water-phase permeability can be regarded as

$$ {k}_{\mathrm{w}}=\frac{\phi_{\mathrm{w}}}{8}{\displaystyle \sum_{i=1}^{\mathrm{N}}{S}_i{r}_{ci}^2} $$
(13)

where k w is the permeability of water-phase in millidarcy and ϕ w is the porosity of water in percent.

Introducing a constant exponent e to account for the difference between \( {\displaystyle \sum_{i=1}^{\mathrm{N}}{S}_i{r}_{\mathrm{ci}}^2} \) and \( {\displaystyle \sum_{i=1}^{\mathrm{N}}{d}_i{r}_{\mathrm{ci}}^2} \), then yield

$$ {\displaystyle \sum_{i=1}^{\mathrm{N}}{S}_i{r}_{\mathrm{ci}}^2}=e{\displaystyle \sum_{i=1}^{\mathrm{N}}{d}_i{r}_{\mathrm{ci}}^2} $$
(14)

Combine Eqs. (8), (13), (14) and then

$$ \frac{R_t}{R_w}=\frac{\tau {A}_N}{\pi }{\left({\displaystyle \sum_{i=1}^{\mathrm{N}}{d}_i{r}_{\mathrm{ci}}^2}\right)}^{-1}=\frac{e\tau {A}_{\mathrm{N}}}{8\pi}\frac{\phi_{\mathrm{w}}}{k_{\mathrm{w}}} $$
(15)

Eq. (15) divided by Eq. (3) and then

$$ I=\frac{R_t}{R_0}=\left(\frac{e\tau {A}_{\mathrm{N}}}{8\pi}\frac{\phi_{\mathrm{w}}}{k_{\mathrm{w}}}\right)/\left(\frac{e^{\prime}\tau {A}_{\mathrm{N}}}{8\pi}\frac{\phi }{k}\right)=\frac{e}{e\hbox{'}}\frac{\phi_{\mathrm{w}}}{\phi}\frac{k}{k_{\mathrm{w}}}\cong \frac{\phi_w}{\phi}\frac{k}{k_{\mathrm{w}}}={S}_{\mathrm{w}}\frac{k}{k_{\mathrm{w}}} $$
(16)

where I is the resistivity index.

Saturation exponent model from NMR

One of the wildly used two permeability models in NMR log evaluation is SDR model which proposed by Schlumberger Doll Research Center (Kenyon et al. 1988; Kenyon 1997) is

$$ k={C}_1\times {\phi}^{m_1}\times {T}_{2gm}^{n_1} $$
(17)

where T 2gm is the geometric mean of the NMR T2 spectrum of fully water saturated rock in ms, C 1 , m 1 and n 1 are the statistical model parameters which can be acquired from core sample experimental results, while without enough core samples, these three parameters can be assigned to empirical values of 10, 4, and 2, respectively.

When the rock is partially water saturated in laboratory, the water-phase permeability can be gained by

$$ {k}_{\mathrm{w}}={C}_1\times {\phi}_{\mathrm{w}}^{{\mathrm{m}}_1}\times {T}_{2wgm}^{n_1} $$
(18)

where T 2wgm is the geometric mean of the NMR T2 spectrum of partially water saturated rock in ms.

Eq. (17) divided by Eq. (18) and then

$$ \frac{k}{k_{\mathrm{w}}}=\frac{C_1\times {\phi}^{{\mathrm{m}}_1}\times {T}_{2\mathrm{g}\mathrm{m}}^{{\mathrm{n}}_1}}{C_1\times {\phi}_{\mathrm{w}}^{{\mathrm{m}}_1}\times {T}_{2\mathrm{w}\mathrm{g}\mathrm{m}}^{{\mathrm{n}}_1}}={\left(\frac{\phi }{\phi_{\mathrm{w}}}\right)}^{{\mathrm{m}}_1}{\left(\frac{T_{2\mathrm{g}\mathrm{m}}}{T_{2\mathrm{w}\mathrm{g}\mathrm{m}}}\right)}^{{\mathrm{n}}_1}={\left(\frac{1}{S_{\mathrm{w}}}\right)}^{{\mathrm{m}}_1}{\left(\frac{T_{2\mathrm{g}\mathrm{m}}}{T_{2\mathrm{w}\mathrm{g}\mathrm{m}}}\right)}^{{\mathrm{n}}_1} $$
(19)

Combine Eqs. (19) and (16), then

$$ I={S}_{\mathrm{w}}\frac{k}{k_{\mathrm{w}}}={S}_{\mathrm{w}}{\left(\frac{1}{S_{\mathrm{w}}}\right)}^{{\mathrm{m}}_1}{\left(\frac{T_{2\mathrm{g}\mathrm{m}}}{T_{2\mathrm{w}\mathrm{g}\mathrm{m}}}\right)}^{{\mathrm{n}}_1}={S}_{\mathrm{w}}^{\hbox{-} \mathrm{n}} $$
(20)

That means

$$ {\left(\frac{1}{S_{\mathrm{w}}}\right)}^{m_1-1}{\left(\frac{T_{2\mathrm{g}\mathrm{m}}}{T_{2\mathrm{w}\mathrm{g}\mathrm{m}}}\right)}^{n_1}={S}_w^{-n} $$
(21)

Thus, the relation between n and S w was developed, which is expressed in terms of NMR information by

$$ n={m}_1-1-{n}_1\frac{ \ln \left(\frac{T_{2\mathrm{g}\mathrm{m}}}{T_{2\mathrm{w}\mathrm{g}\mathrm{m}}}\right)}{ \ln {S}_{\mathrm{w}}} $$
(22)

T2 spectrum of water

It is wildly accepted that T2 spectrum varies with lithology as seen in complex sandstones, as well as in carbonates where rock properties vary significantly. In addition, there are other parameters that affect the T2 distribution, such as the pore body diameter to pore throat diameter (aspect ratio). Currently, all the variables that influence the T2 distribution are not fully understood or identified.

The laboratory NMR measurements carried out on partially water saturated rocks have shown that as air replaces water in pores, the long T2 components disappear first, corresponding to the draining of the largest pores first, as shown in (Fig. 3). Disappearance of the long T2 components at each increment of centrifuge speed corresponds directly to the loss of water from the largest pores. The air that replaces the water generates no NMR signal since it contains no hydrogen (Straley et al. 1991). Combing percolation theory, the water phase (water/air) T2 spectrum can be obtained by centrifuging (Helba et al. 1992).

Fig. 3
figure 3

T2 spectrum at variable water saturations of sample B8

Full size image

For the given formation, especially the given core samples, the influence factors of NMR T2 spectrum are almost the same except the fluid property. The geometric mean of the T2 spectrum of partially water saturated samples to that of fully water saturated samples may offset many influence factors which hard to be expressed quantitatively.

Case studies

To verify the reliability of the saturation exponent model proposed in Eq. (22), NMR measurements on both fully water saturated and partially water saturated (i.e., under different centrifuge forces) 16 core samples drilled from a reservoir in the Middle East were conducted. To calculate n, five parameters (constant parameters m 1 and n 1 , geometric mean of the NMR T2 spectrum of fully water saturated rocks and partially water saturated rocks T 2gm and T 2wgm , water saturation and S w ) are required.

Calculation of m 1 and n 1

The values of m 1 and n 1 in SDR model can be obtained through combining porosity and permeability measured from core samples in laboratory and NMR T2 spectrum. Fifty core samples were used to calculate them and some of them are shown in Table 1. The values of m 1 and n 1 are 2.00 and 0.69 by regression, respectively, as shown in Table 1.

Table 1 k, ϕ, and T 2gm of some core samples used to regress m 1 and n 1
Full size table

Calculation of n

Sixteen samples have been tested under different centrifuge speeds and the values of T 2gm and T 2wgm can be obtained both. The values of n of all these samples under different water saturations have been calculated through the model which have been inferred by Eq. (22), and only the samples which both NMR and resistivity measurement have been conducted are shown in Table 2. Calculated and experimental values of n are shown in Table 2 and Fig. 4.

Table 2 Calculated and experimental values of n
Full size table
Fig. 4
figure 4

The relationship between S w and n through application of the new model in the Middle East reservoir core samples

Full size image

Saturation exponent values acquired from resistivity experimental measurements and predicted from NMR log information show that:

  1. 1.

    Saturation exponent values decrease as water saturation decreasing, and they obey the law of power function which is in accord with the result of network simulation from Tao et al. (2004)

    $$ n=a{S_{\mathrm{w}}}^{\mathrm{b}} $$
    (23)

    and this can also be a good proof of the reliability of this new model.

  2. 2.

    The calculated saturation exponent values range from 1.782 to 2.522 while the measured values are ranging from 1.747 to 2.911.

Besides, in reservoir with consecutive NMR logs, once the T2 spectrum distribution of water and gas or oil can be distinguished, water saturation can be calculate without the application of Archie equation, hence n and m which are difficult to determine. The S w estimation equation can be gained from Eq. (20) as

$$ {S}_{\mathrm{w}}={\left({\left(\frac{T_{2\mathrm{g}\mathrm{m}}}{T_{2\mathrm{w}\mathrm{g}\mathrm{m}}}\right)}^{n_1}\frac{R_0}{R_{\mathrm{t}}}\right)}^{\frac{1}{m_1-1}} $$
(24)

This will be valuable for the calculation of hydrocarbon and water saturation in complex reservoirs, such as carbonates, so as sandstones.

Conclusions

A new method for probing the saturation exponent under variable water saturations by combining the NMR with capillary theory and Purcell equation has been developed. In the process of derivation of the formula, a key hypothesis which is accepted in percolation theory has been introduced. That is when two phases (water and oil/gas) coexist in pore space, each phase has its own flow path with a stable interface when this two phase flow steadily (i.e., when one phase flow, the other phase can be seen as matrix which has no contribution to the flow). Based on these theories, the proposed new saturation exponent estimator quantitatively reveals that the saturation exponent is not a constant but a variable parameter depends on water saturation and pore structure. NMR measurements on partially water saturated core samples were used to calculate n through this new model. Result shows that n and S w followed a power law which is in accordance with that gained by network model simulation that has been published. And it is also accord with the power law in percolation theory that has been widely proved in transport property of porous media. Water saturation equation is also gained from the T2 spectrum and well logging resistivity without the application of Archie equation, hence n and m which are difficult to determine.

Notice that for the given formation, especially the given core samples, the influence factors of NMR T2 spectrum are almost the same except the fluid property. T2gm/T2wgm may offset many influence factors of T2 spectrum which hard to be expressed quantitatively, and the same case for water saturation equation. But, this saturation exponent model and water saturation equation is based on that T2 spectrum distribution of water and gas or oil can be distinguished. For example, T2 spectrum of high viscosity oil in water-base mud well is often overlapping that of salinity water. Then, this method will be invalid.

Anyhow, the results have a certain practical significance in the evaluation of water saturation, while further study is still required.