Optimal ordering policy for an inventory system with linearly increasing demand and allowable shortages under two levels trade credit financing

Abstract

To reduce default risk, a retailer may offer a partial down-stream trade credit to its credit-risk customers who should pay a portion of their purchasing costs at the time of receiving items as a collateral deposit, and then receive a permissible trade credit on the rest of the outstanding amount. To reflect this fact, we consider an inventory model with linear time dependent demand under two levels of trade credit and allowable shortages. Depending on the relationship between up-stream and down-stream trade credit periods, several cases are considered and the necessary and sufficient conditions are derived for finding the optimal solution. We also present a simple algorithm to determine the optimal solution. Numerical examples are provided to illustrate the solution procedure. Sensitivity analysis of important model-parameters is performed and some relevant managerial implications are discussed.

1 Introduction

In the classical economic order quantity (EOQ) model, it is assumed that the retailer must pay immediately on receiving the items. However, in practice, the manufacturer/supplier or vendor may offer the retailer a delay period (called trade credit) to settle the payment. Supplier uses trade credit to promote sales, increase market share and reduce on-hand stock level. Usually, no interest is charged on the outstanding amount if the payment is settled within the trade credit period. However, if the payment is not paid in full by the end of the permissible delay period, interest is charged on the outstanding amount on previously agreed terms and conditions. The retailer accumulates interest on revenue generated from sales during the credit period. This brings some economic advantage to the retailer. Hence he/she wants to delay the payment up to the end of the permissible period. Trade credit in fact serves as an immediate source of short-term fund, especially to small retailers. Small businesses are frequently financed by their suppliers, rather than by financial institutions (Petersen and Rajan 1997). On the other hand, the policy of granting credit terms to the retailer not only adds an additional cost but also an additional dimension of default risk to the supplier, in the event that the retailer being unable to pay the debt. Similar to the supplier, the retailer may also extend the trade credit offer to his/her customers (down-stream trade credit).

Goyal (1985) first developed an EOQ model under trade credit financing. In his model, he ignored the difference between selling price and purchase price. Dave (1985) and later Teng (2002) corrected Goyal’s (1985) model by addressing the fact that the selling price is necessarily higher than the purchase price. Several authors have extended the model of Goyal (1985) in many directions. Aggarwal and Jaggi (1995) extended Goyal’s (1985) model for deteriorating items. Jamal et al. (1997) further generalized Aggarwal and Jaggi’s (1995) model to allow for shortages. Huang (2003) extended Goyal’s (1985) model in which the supplier provides the retailer a permissible delay period and the retailer in turn provides a trade credit period to his/her customers. Teng and Goyal (2007) addressed the shortcomings of Huang’s (2003) model and proposed a generalized model. Ouyang et al. (2009) developed an EOQ model for deteriorating items with partially delay in payments linked to order quantity. More related articles can be found in Shinn and Hwang (2003), Teng et al. (2005), Ouyang et al. (2006), Huang and Hsu (2008), Teng and Chang (2009), Thangam and Uthayakumar (2010), Giri and Sharma (2014) and their references.

All the above inventory models assumed that the demand rate is constant. From product life cycle perspective, it is only during the maturity stage that the demand is near constant. During the growth stage, the demand increases with time while during the mortality stage, the demand decreases with time. Teng et al. (2012) developed an EOQ model under trade credit financing and assumed that demand rate increases linearly with time. Maihami and Abadi (2012) developed an inventory model for determining the joint optimal pricing and inventory control policy for non-instantaneous deteriorating items where a delay in payment is allowed. The demand is assumed to be dependent on both price and time simultaneously. Khanra et al. (2011) proposed an inventory model with quadratic time varying demand under permissible delay in payments. Teng et al. (2013) developed an inventory model for increasing demand in a supply chain with up-stream and down-stream trade credit. The trade credit offered by the supplier depends on the retailer’s ordering quantity. Recently, Khanra et al. (2013) developed an EOQ model with time varying quadratic demand, shortages and permissible delay in payments.

The above inventory models ignored the default risk incurred by the retailer in offering trade credit to credit-risk customers. In reality, to reduce default risks, a retailer may offer a partial down-stream trade credit to its credit-risk customers who must pay a portion of purchase amount at the time of placing an order as a collateral deposit and then receive a permissible delay on the rest of the outstanding amount. Teng (2009) determined optimal ordering policies for a retailer in an EOQ model who offers distinct trade credit to its good and bad credit customers. Recently, Chen et al. (2013) developed an economic production quantity (EPQ) model for deteriorating items with up-stream full trade credit and down-stream partial trade credit. Wang et al. (2014) developed an EOQ model to determine optimal credit period and replenishment cycle time for a supplier with credit linked demand incorporating maximum lifetime for deteriorating items and credit-linked default risk. In these models, occurrence of shortage in the retailer’s inventory is overlooked. In many cases, occurrence of shortage is unavoidable due to various uncertainties. Furthermore, it is commonly observed that for many products of famous brands or modern goods such as Apple’s iPad and iPhone, other hi-fi equipment or fashionable clothes, customers may prefer to wait for backorders while shortages occur. Shortages in inventory can have significant impact on the retailer’s profit and customer’s service. Therefore, it is worth discussing the impact of shortage in any inventory model.

In this paper, we propose an EOQ model under two levels of trade credit assuming that demand rate is a linear increasing function of time, the retailer offers a partial trade credit to its credit-risk customers to reduce default risk and shortages in the retailer’s inventory are allowed. Our model presents a general framework compared to the previous works done by Goyal (1985), Teng (2002), Huang (2003), Teng and Goyal (2007), Teng (2009), Teng et al. (2012) and others. We derive the necessary and sufficient conditions for finding the optimal solution in different cases depending on the relationship between the up-stream and down-stream trade credits. An algorithm is developed for finding numerical solution of the model. Numerical examples are taken to illustrate the solution procedure. Furthermore, a sensitivity analysis of some important model-parameters is performed to investigate their implications on the optimal solution. Finally, conclusions together with possible future research directions are provided.

2 Notation and assumptions

The following notation and assumptions are used throughout this paper.

2.1 Notation

$A$ :	Ordering cost per order
$c$ :	Unit purchasing cost
$p({>}c)$ :	Unit selling price
$h$ :	Unit stock holding cost per unit time excluding interest charges
$s$ :	Unit shortage cost per unit time
$I_e$ :	Interest earned per dollar per year by the retailer
$I_p$ :	Interest paid per dollar per year by the retailer
$M$ :	Retailer’s trade credit period in years offered by the manufacturer
$N$ :	Customer’s trade credit period in years offered by the retailer
$\alpha$ :	Fraction of purchase cost that a credit-risk customer must pay the retailer at the time of placing an order, where $0\le \alpha \le 1$
$1{-}\alpha$ :	Portion of purchase cost on which the retailer offers its credit-risk customers a permissible delay period $N$
$T_1$ :	Length of stock-end cycle (decision variable)
$T$ :	Length of replenishment cycle (decision variable)
$Q$ :	Order quantity

2.2 Assumptions

• 1. We consider the inventory system for a single starting period over an infinite planning horizon. The demand rate $D(t)$ is linearly increasing in time. We take $D(t)=a+bt$, where $a$ and $b$ are non-negative constants.

• 2. The lead time is negligible.

• 3. Shortages are allowed and are completely backlogged.

• 4. All replenishments are instantaneous.

• 5. The retailer receives a full trade credit period of $M$ years from the manufacturer, and in turn provides a partial trade credit to his/her credit-risk customers who must pay $\alpha$ portion of the total purchasing amount at the time of placing an order as a collateral deposit, and then receive a permissible delay of $N$ years on the outstanding amount (i.e., the customers orders items at time $t$, and must pay the delay amount at time $t+N$). Note that, to good-credit customers, the retailer may provide a full trade credit in which case we simply set $\alpha =0$.

• 6. If $M\ge N$, the retailer uses the sales revenue to accumulate interest in an interest bearing account for time $0$ to $M$ from the portion of immediate payment. From the portion of delayed payment, the retailer earns interest for the time $N$ to $M$. If $M\ge T_1+N$ (the time at which the retailer receives the payment from the last customer), the retailer receives full payment from the customers and hence pays the entire purchase amount to the manufacturer. In case, $M\le T_1+N$, the retailer does not receive the full payment by the time $M$ and hence finances all units sold after time $(M-N)$ at an interest rate of $I_p$ per dollar per year.

• 7. If $M<N$, then the retailer finances and pays the manufacturer the entire amount of delayed payment at the end of the trade credit period $M$, and starts to pay off the loan after time $N$ at which the retailer starts to receive portion of delayed payment from customers. From the portion of immediate payment, the retailer earns interest until the end of permissible delay time $M$. If $T_1\ge M$, the retailer pays the manufacturer the purchase amount of immediate payment at time $M$ and then finances all units sold after time $M$ at an interest rate of $I_p$ per dollar per year.

3 Model formulation

Based on the assumptions made in the previous section, we formulate the model as follows. At the beginning of the cycle, the retailer orders and obtains $Q$ quantity from the manufacturer. Let $I(t)$ denotes the inventory level at any time $t$. During the period $[0, T_1]$, the inventory is depleted due to meeting up customer demand and ultimately it reaches zero at time $t=T_1$. Thereafter, shortages are allowed to occur during the time interval $[T_1, T]$, and are completely backlogged. The behavior of the inventory system at any time $t \in [0, T]$ is shown in Fig. 1.

Fig. 1

Graphical representation of the inventory system

The instantaneous state of $I(t)$ over $[0, T_1]$ is described by the differential equation:

$$\begin{aligned} \frac{dI(t)}{dt}=-D(t)=-(a+bt), \quad 0\le t\le T_1 \end{aligned}$$

(1)

with the boundary condition $I(T_1)=0$.

The solution of (1) is given by

$$\begin{aligned} I(t)=a(T_1-t)+\frac{b}{2}\bigg (T_1^2-t^2\bigg ), \quad 0\le t\le T_1 \end{aligned}$$

(2)

Therefore, the initial level of inventory is $q_0=I(0)=aT_1+\frac{b}{2}T_1^2$.

The maximum backorder level $B=-I(T)=a(T-T_1)+\frac{b}{2}(T^2-T_1^2)$.

Therefore, the retailer’s order quantity per replenishment cycle is $Q=q_0+B=aT+\frac{b}{2}T^2$.

In the following, we now determine the inventory costs and the sales revenue per cycle.

• (a) Ordering cost $=A$.

• (b) Holding cost (excluding interest charges) $=h\int _{0}^{T_1}I(t) \, dt=h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg )$.

• (c) Shortage cost $=-s\int _{T_1}^{T}I(t) \, dt=\frac{s(T-T_1)^2}{6}\bigg [3a+b(T+2T_1)\bigg ]$.

• (d) Purchasing cost $=cQ=c\bigg (aT+\frac{b}{2}T^2\bigg )$.

• (e) Sales revenue $=pQ=p\bigg (aT+\frac{b}{2}T^2\bigg )$.

• (f) Interest earned and interest payable.

In order to calculate the interest earned and interest payable, we consider the two cases:

(1) $M\ge N$ and (2) $M<N$.

Case 1. $M\ge N$

In this case, for the portion of immediate payment, interest earned on the backorder amount is $\alpha I_ep [a(T-T_1)+\frac{b(T^2-T_1^2)}{2} ]M$. For the portion of delayed payment, interest earned on the backorder amount is $(1-\alpha )I_ep [a(T-T_1)+\frac{b(T^2-T_1^2)}{2} ](M-N)$. No interest is required to be paid on the backorder amount in this case.

For further calculation of interest earned and interest payable, based on the values of $M$, $T_1$ and $T_1+N$, three sub-cases are considered: (i) $M\le T_1\le T_1+N$, (ii) $T_1\le M\le T_1+N$ and (iii) $T_1\le T_1+N\le M$. Next, we derive the interest earned and interest payable in each of the above sub-cases.

Sub-case 1(i) $M\le T_1\le T_1+N$

By the time $M$, the retailer has two sources to accumulate revenue and earn interest: portion of immediate payment for time 0 to $M$, and portion of delayed payment for time $N$ to $M$.

Interest earned by the retailer from immediate payment is

$$\begin{aligned} \alpha pI_e\int _{0}^{M}\big [I(0)-I(t)\big ] \, dt=\alpha pI_e\int _{0}^{M}\bigg (at+\frac{bt^2}{2}\bigg ) \, dt=\alpha pI_e\bigg (\frac{aM^2}{2}+\frac{bM^3}{6}\bigg ) \end{aligned}$$

(3)

Interest earned from delayed payment is

$$\begin{aligned}&(1-\alpha )pI_e\int _{N}^{M}\big [I(0)-I(t-N)\big ] \, dt\nonumber \\&\quad =(1-\alpha )pI_e\bigg [\frac{a}{2}(M-N)^2+\frac{b}{6}(M-N)^3\bigg ] \end{aligned}$$

(4)

Since $M\le T_1$, the retailer does not receive total revenue from the customers by the time the retailer’s permissible delay time offered by the manufacturer, $M$ ends. Therefore, the retailer must finance all units sold after time $M$ for the portion of immediate payment and all units sold after time $(M-N)$ for the portion of delayed payment at an interest rate of $I_p$ per dollar per year. The representations of interest earned and interest payable for both immediate and delayed payment are shown in Fig. 2.

Fig. 2

Retailer’s interest earned and interest paid when $M \ge N$ and $M \le T_{1} \le T_{1}+N$. a Immediate payment. b Delayed payment

The interest paid by the retailer for the portion of immediate payment is given by

$$\begin{aligned} \alpha cI_p\int _{M}^{T_1}I(t-M) \, dt=\alpha cI_p\bigg [\frac{a}{2}(T_1^2-M^2)+\frac{b}{6}\big (M^3-3M^2T_1+2T_1^3\big )\bigg ] \end{aligned}$$

(5)

Interest paid for the portion of delayed payment is given by

$$\begin{aligned}&(1-\alpha )cI_p\int _{M}^{T_1+N}I(t-M) \,dt\nonumber \\&\quad =\,(1-\alpha )cI_p\bigg \{\frac{a}{2}\bigg [T_1^2-(M-N)^2\bigg ]+\frac{b}{6}\bigg [(M-N)^3-3(M-N)^2T_1+2T_1^3\bigg ]\bigg \} \end{aligned}$$

(6)

Hence, the retailer’s total profit per unit time is

$$\begin{aligned} TP_1(T_1,T) &= \hbox {sales revenue}-\hbox {purchasing cost}-\hbox {ordering cost}-\hbox {holding cost}-\hbox {shortage cost}\nonumber \\& \quad -\,\hbox {interest paid}+\hbox {interest earned}\nonumber \\& = \frac{1}{T}\bigg \{(p-c)\bigg (aT+\frac{bT^2}{2}\bigg )-A-h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg ) -\frac{s(T-T_1)^2}{6}\bigg [3a+b(T+2T_1)\bigg ]\nonumber \\&\quad -\, \alpha cI_p\bigg [\frac{a}{2}\bigg (T_1^2-M^2\bigg )+\frac{b}{6}\bigg (M^3-3M^2T_1+2T_1^3\bigg )\bigg ]\nonumber \\& \quad -\,(1-\alpha )cI_p\bigg [\frac{a}{2}\bigg (T_1^2-(M-N)^2\bigg )+\frac{b}{6}\bigg ((M-N)^3-3T_1(M-N)^2+2T_1^3\bigg )\bigg ]\nonumber \\& \quad +\,\alpha pI_e\bigg (\frac{aM^2}{2}+\frac{bM^3}{6}\bigg )+(1-\alpha )pI_e\bigg [\frac{a}{2}(M-N)^2+\frac{b}{6}(M-N)^3\bigg ]\nonumber \\& \quad+\,\alpha pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ]M\nonumber \\&\quad + \quad \,(1-\alpha )pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ](M-N) \bigg \} \end{aligned}$$

(7)

The interest earned for the backlogged amount is given by the last two terms in the above expression for the retailer’s total profit per unit time.

Proposition 1

$TP_1(T_1,T)$ is maximum for those values of $T$ and $T_1$ which satisfy the equations:

$$2a\big \{sT-\big (h+cI_p+s\big )T_1-I_ep\big [M-N(1-\alpha )\big ]\big \}+b\big \{2T_1\big [sT-(h+s)T_1-I_ep\big (M-N(1-\alpha ) \big )\big ]+cI_p\big [(M-N)^2-2T_1^2+(2M-N)N\alpha \big ]\big \}=0 \, and \, 6A+3aX_{11}+b\big (X_{12}+cX_{13}\big )=0, $$

provided that the following conditions are satisfied:

$$\big \{3\big [2aX_{21}+b\big (X_{22}-cX_{23}\big )\big ]^2+4\big (aX_{31}+bX_{32}\big )\big [-6A+bX_{41}+3a(X_{42}+cX_{43})\big ]\big \}<0, aX_{31}+bX_{32}>0 \, and \, -6A+bX_{41}+3a(X_{42}+cX_{43})<0,$$

where

$$\begin{aligned} X_{11} & = (h+s)T_1^2-sT^2+cI_p\bigg [T_1^2-(M-N)^2-N(2M-N)\alpha \bigg ]+I_ep\bigg [2M(T_1+(1-\alpha )N)\\& \quad -\,M^2-N(N+2T_1)(1-\alpha )\bigg ]\\ X_{12} & = T^2(3p-2sT)+2(h+s)T_1^3+I_ep\bigg \{3M\big [T^2+T_1^2-N^2(1-\alpha )\big ]-M^3+3M^2N(1-\alpha )\\& \quad +\,N\big [N^2-3(T^2+T_1^2)\big ](1-\alpha )\bigg \}\\ X_{13} & = I_p\bigg \{M^3+2T_1^3-(1-\alpha )\big [N^3+3N^2T_1-3MN(N+2T_1)\big ]-3M^2[T_1+N(1-\alpha )]-3T^2\bigg \}\\ X_{21} & = (h+cI_p+s)T_1+I_ep\bigg [M-N(1-\alpha )\bigg ], \, X_{22}=2T_1\bigg \{(h+s)T_1+I_ep\big [M-N(1-\alpha )\big ]\bigg \}\\ X_{23} & = I_p\bigg [(M-N)^2-2T_1^2+(2M-N)N\alpha \bigg ], \, X_{31}=(h+cI_p+s), \, X_{32}=2(h+cI_p+s)T_1\\&\quad +\,I_ep[M-N(1-\alpha )]-sT\\ X_{41} & = (M-N)^3(pI_e-cI_p)-sT^3+3cI_p(M-N)^2T_1-3I_ep(M-N)T_1^2-2(h+cI_p+s)T_1^3\\&\quad +\,N\bigg [(3M^2-3MN+N^2)(pI_e-cI_p)+3cI_p(2M-N)T_1-3I_epT_1^2\bigg ]\alpha \\ X_{42} & = -(h+s)T_1^2+I_ep\bigg [M^2-2M(N+T_1)+N(N+2T_1)(1-\alpha )+2MN\alpha \bigg ]\\ X_{43} & = I_p\bigg [(M-N)^2-T_1^2+(2M-N)N\alpha \bigg ] \end{aligned}$$

Proof

See Appendix.

Sub-case 1(ii) $T_1\le M\le T_1+N$

In this sub-case, the retailer accumulates revenue and earns interest from the portion of instant payment made during the time 0 to $M$, and from the portion of delayed payment made during the time $N$ to $M$. Hence, the retailer’s annual interest earned for the portion of immediate payment as shown in Fig. 3 is

$$\begin{aligned}&\alpha pI_e\int _{0}^{T_1}\big [I(0)-I(t)\big ] \, dt+\alpha pI_eI(0)(M-T_1)\nonumber \\&\quad =\alpha pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6} +\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1)\bigg ] \end{aligned}$$

(8)

The interest earned for the portion of delayed payment is

$$\begin{aligned} (1-\alpha )pI_e\int _{N}^{M}\big [I(0)-I(t-N)\big ] \, dt=(1-\alpha )pI_e\bigg [\frac{a}{2}(M-N)^2+\frac{b}{6}(M-N)^3\bigg ] \end{aligned}$$

(9)

Since $T_1\le M$, the retailer receives full instant payment by the time $T_1$ and hence no interest is required to be paid for the portion of instant payment. However, the retailer does not obtain full amount of delayed payment by the time $M$ from customers and hence the retailer must finance all units sold after time $(M-N)$ at an interest rate of $I_p$ per dollar per year. Thus, the retailer pays interest for the portion of delayed payment only, which is given by

$$\begin{aligned}&(1-\alpha )cI_p\int _{M}^{T_1+N}I(t-M) \,dt\nonumber \\&\quad =(1-\alpha )cI_p\bigg \{\frac{a}{2}\bigg [T_1^2-(M-N)^2\bigg ]+\frac{b}{6}\bigg [(M-N)^3-3(M-N)^2T_1+2T_1^3\bigg ]\bigg \} \end{aligned}$$

(10)

As a result, the retailer’s total profit per unit time is

$$\begin{aligned} TP_2(T_1,T)= & {} \frac{1}{T}\bigg \{(p-c)\bigg (aT+\frac{bT^2}{2}\bigg )-A-h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg ) -\frac{s(T-T_1)^2}{6}\big [3a+b(T+2T_1)\big ]\nonumber \\&-\,(1-\alpha )cI_p\bigg [\frac{a}{2}\bigg (T_1^2-(M-N)^2\bigg )+\frac{b}{6}\bigg ((M-N)^3-3T_1(M-N)^2+2T_1^3\bigg )\bigg ]\nonumber \\&+\,\alpha pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1)\bigg ]\nonumber \\&+\,(1-\alpha )pI_e\bigg [\frac{a}{2}(M-N)^2+\frac{b}{6}(M-N)^3\bigg ]+\alpha pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ]M\nonumber \\&+\,(1-\alpha )pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ](M-N)\bigg \} \end{aligned}$$

(11)

Fig. 3

Retailer’s interest earned and interest paid when $M \ge N$ and $T_{1} \le M \le T_{1}+N$. a Immediate payment. b Delayed payment

Proposition 2

$TP_2(T_1,T)$ has the maximum value for those values of $T$ and $T_1$ which satisfy the following equations:

$$2a\{sT-(h+cI_p+s)T_1+cI_pT_1\alpha +I_ep[N-M(1-\alpha )-(N+T_1)\alpha]\} +b\{cI_p\left[(M-N)^2-2T_1^2\right](1-\alpha )+2T_1[sT-(h+s)T_1+I_ep (N-M(1-\alpha )-(N+T_1)\alpha )]\}=0$$

and $6A+3aY_{11}+b\big (Y_{12}+cY_{13}\big )=0,$ provided that the following conditions are satisfied:

$$\left [4\left(6A+3aY_{21}+b\left(Y_{22}+cY_{23}\right)\right)\left(-aY_{31}+bY_{32}\right)+3\left(2aY_{41}+b\left(Y_{42}+cY_{43}\right)\right)^2\right]<0,$$

$$-aY_{31}+bY_{32}<0 \; and \; 6A+3aY_{21}+b\left(Y_{22}+cY_{23}\right)>0,$$

where

$$\begin{aligned} Y_{11}& = (h+s)T_1^2-sT^2-cI_p\bigg [(M-N)^2-T_1^2\bigg ]\big (1-\alpha \big )+I_ep\bigg [(M-N-T_1)^2\alpha \\&\quad -\,(M-N)(M-N-2T_1)\bigg ]\\ Y_{12} & = T^2(3p-2sT)+2(h+s)T_1^3-I_ep\bigg \{(1-\alpha )\bigg[ M^3-3M^2N-N^3+3N\left( T^2+T_1^2\right) \bigg] \nonumber \\& \quad -\,2T_1^3\alpha -3M\bigg [T^2+(1-\alpha )\left( T_1^2-N^2\right) \bigg ]\bigg \}\\ Y_{13} & = -3T^2+I_p(1-\alpha )\bigg [(M-N)^3-3(M-N)^2T_1+2T_1^3\bigg ]\\ Y_{21}& = (h+s)T_1^2-cI_p\bigg [(M-N)^2-T_1^2\bigg ](1-\alpha )-I_ep\bigg [(M-N)(M-N-2T_1)-(M-N-T_1)^2\alpha \bigg ]\\ Y_{22}& = sT^3+2(h+s)T_1^3+I_ep\bigg [3(M-N)T_1^2 +(M-N-T_1)^2(M-N+2T_1)\alpha -(M-N)^3\bigg ]\\ Y_{23}& = I_p(1-\alpha )\bigg [(M-N)^3-3(M-N)^2T_1+2T_1^3\bigg ], Y_{31}=h+cI_p+s+\alpha (pI_e-cI_p)\\ Y_{32}& = sT-2(h+cI_p+s)T_1+2cI_pT_1\alpha +I_ep\bigg [N-M(1-\alpha )-(N+2T_1)\alpha \bigg ]\\ Y_{41}& = T_1\bigg [h+s+cI_p(1-\alpha )\bigg ]+I_ep\bigg [M-N+(N-M+T_1)\alpha \bigg ]\\ Y_{42} &= 2T_1\bigg \{(h+s)T_1+I_ep\bigg [M-N+(N-M+T_1)\alpha \bigg ]\bigg \},\\ Y_{43}& = -I_p\bigg [(M-N)^2-2T_1^2\bigg ](1-\alpha )\\ \end{aligned}$$

Proof

The proof follows similarly as in Proposition 1.

Sub-case 1(iii) $T_1\le T_1+N \le M$.

In this sub-case, the retailer obtains the total revenue before the trade credit period $M$ expires, and hence no interest is payable. The representation of interest earned by the retailer is shown in Fig. 4.

Fig. 4

Retailer’s interest earned when $M \ge N$ and $T_{1} \le T_{1}+N \le M$. a Immediate payment. b Delayed payment

From Fig. 4, the interest earned for the portion of immediate payment is

$$\begin{aligned}&\alpha pI_e\int _{0}^{T_1}\big [I(0)-I(t)\big ] \, dt+\alpha pI_eI(0)(M-T_1)\nonumber \\&\quad =\alpha pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1)\bigg ] \end{aligned}$$

(12)

The interest earned for the portion of delayed payment is

$$\begin{aligned}&(1-\alpha )pI_e\int _{N}^{T_1+N}\big [I(0)-I(t-N)\big ] \, dt+(1-\alpha )pI_eI(0)(M-T_1-N)\nonumber \\&\quad =(1-\alpha )pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1-N)\bigg ] \end{aligned}$$

(13)

Hence, the retailer’s total profit per unit time is

$$\begin{aligned} TP_3(T_1,T)= & {} \frac{1}{T}\bigg \{(p-c)\bigg (aT+\frac{bT^2}{2}\bigg )-A-h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg ) -\frac{s(T-T_1)^2}{6}\big [3a+b(T+2T_1)\big ]\nonumber \\&+\,\alpha pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1)\bigg ]\nonumber \\&+\,(1-\alpha )pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1-N)\bigg ]\nonumber \\&+\,\alpha pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ]M\nonumber \\&+\,(1-\alpha )pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ](M-N)\bigg \}\nonumber \\= & {} \frac{1}{T}\bigg \{(p-c)\bigg (aT+\frac{bT^2}{2}\bigg )-A-h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg ) -\frac{s(T-T_1)^2}{6}\big [3a+b(T+2T_1)\big ]\nonumber \\&+\,pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1)\bigg ]-(1-\alpha )pI_eN\bigg (aT_1+\frac{bT_1^2}{2}\bigg )\nonumber \\&+\,\alpha pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ]M\nonumber \\&+\,(1-\alpha )pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ](M-N)\bigg \} \end{aligned}$$

(14)

Proposition 3

$TP_3(T_1,T)$ has the maximum value for those values of $T$ and $T_1$ which satisfy the following equations:

$$(a+bT_1)\big [(h+I_ep)T_1-s(T-T_1)\big ]=0$$

and

$$6A+3a\left[(h+I_ep+s)T_1^2-sT^2\right]+b\left\{2(h+s)T_1^3-3cT^2-2sT^3+p \left[2I_eT_1^3+3T^2(1+I_e(M -N(1-\alpha )))\right]\right\}=0,$$

provided that the following conditions are satisfied:

$$\big \{3(h+I_ep+s)^2T_1^2(a+bT_1)^2+\big [bsT-(h+pI_e+s)(a+2bT_1)\big ]\times \big [6A+bsT^3+ T_1^2(h+I_ep+s)(3a+2bT_1)\big ]\big \}<0,$$

$$bsT<(h+pI_e+s)(a+2bT_1)$$

and

$$6A+bsT^3+(h+pI_e+s)T_1^2(3a+2bT_1)>0.$$

Proof

The proof is omitted as it is similar to that of Proposition 1.

Case 2. $M<N$

In this case, for the backorder amount, the retailer earns interest only for the portion of instant payment which is given by $\alpha I_ep\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ]M$. Since $M<N$, for the portion of delayed payment, interest paid by the retailer for the backorder amount is $(1-\alpha )cI_p\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ](N-M)$.

For calculation of interest earned and interest payable, based on the values of $M$ and $T_1$, we have the following two possible sub-cases: (i) $M\le T_1$ and (ii) $M\ge T_1$. Sub-case 2(i) $M\le T_1$

Since $M<N$, the retailer accumulates revenue and earns interest from the portion of instant payment only. From Fig. 5, the annual interest earned by the retailer is

$$\begin{aligned} \alpha pI_e\int _{0}^{M}\big [I(0)-I(t)\big ] \, dt=\alpha pI_e\int _{0}^{M}\bigg (at+\frac{bt^2}{2}\bigg ) \, dt=\alpha pI_e\bigg (\frac{aM^2}{2}+\frac{bM^3}{6}\bigg ) \end{aligned}$$

(15)

Fig. 5

Retailer’s interest earned and interest paid when $M<N$ and $M\le T_{1}$. a Immediate payment. b Delayed payment

For instant payment, the retailer must finance all units sold after time $M$, and pay off the loan at time $T_1$. For delayed payment, the retailer must finance the entire portion of delayed amount at the end of trade credit $M$, and then pay off the loan at time $(T_1+N)$. Consequently, interest paid by the retailer for the portion of instant payment is

$$\begin{aligned} \alpha cI_p\int _{M}^{T_1}I(t-M) \, dt=\alpha cI_p\bigg [\frac{a}{2}\left( T_1^2-M^2\right) +\frac{b}{6}\left( M^3-3M^2T_1+2T_1^3\right) \bigg ] \end{aligned}$$

(16)

Interest paid for the portion of delayed payment is given by

$$\begin{aligned}&(1-\alpha )cI_p\bigg [I(0)(N-M)+\int _{N}^{T_1+N}\big [I(t-N)\big ] \, dt\bigg ] \nonumber \\&\quad =(1-\alpha )cI_p\bigg [(N-M)\bigg (aT_1+\frac{bT_1^2}{2}\bigg )+\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg )\bigg ] \end{aligned}$$

(17)

Thus, we obtain the retailer’s total profit per unit time as

$$\begin{aligned} TP_4(T_1,T)= & {} \frac{1}{T}\bigg \{(p-c)\bigg (aT+\frac{bT^2}{2}\bigg )-A-h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg ) -\frac{s(T-T_1)^2}{6}\nonumber \\&\times \, \big [3a+b(T+2T_1)\big ]-\alpha cI_p\bigg [\frac{a}{2}\left( T_1^2-M^2\right) +\frac{b}{6}\left( M^3-3M^2T_1+2T_1^3\right)\bigg ]\nonumber \\&-\,(1-\alpha )cI_p\bigg [(N-M)\bigg (aT_1+\frac{bT_1^2}{2}\bigg )+\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg )\bigg ]\nonumber \\&+\,\alpha pI_e\bigg (\frac{aM^2}{2}+\frac{bM^3}{6}\bigg )+\alpha pI_e\bigg [a(T-T_1)+\frac{b\left( T^2-T_1^2\right) }{2}\bigg ]M\nonumber \\&-\,(1-\alpha )cI_p\bigg [a(T-T_1)+\frac{b\left( T^2-T_1^2\right) }{2}\bigg ](N-M)\bigg \} \end{aligned}$$

(18)

The last two terms in the above equation are the expressions for interest earned and interest paid by the retailer respectively for the backlogged amount.

Proposition 4

$TP_4(T_1,T)$ has the maximum value for those values of $T$ and $T_1$ which satisfy the following equations:

$$2(a+bT_1)[sT-(h+cI_p+s)T_1]+M[bcI_pM-2I_ep(a+bT_1)]\alpha =0 $$

$$\begin{aligned} & 6A+3a\{(h+cI_p)T_1^2-s( T^2-T_1^2) -M[cI_pM+I_ep(M-2T_1)]\alpha \} \\ & \quad +\,b\{3pT^2-2sT^3+2(h+s)T_1^3+\alpha I_eMp[3( T^2+T_1^2) -M^2]\\ &\quad +\, c[-3T^2(1-I_p(M-N)(1-\alpha ))+I_p(2T_1^3 +M^2\alpha (M-3T_1))]\}=0,\end{aligned}$$

provided that the following sufficient conditions hold:

$$\begin{aligned} &3 \{2T_1(h+cI_p+s)(a+bT_1)+M\alpha [2pI_e(a+bT_1)-bcI_pM]\}^2\\ & \quad +\,4\{-a(h+cI_p+s)+b[s(T-2T_1)\\ & \quad -\,2(h+cI_p)T_1-pI_e M\alpha ]\}\{6A+3a(h+cI_p+s)T_1^2\\ & \quad -\, 3aM[cI_pM+pI_e(M-2T_1)]\alpha +b [2(h+cI_p)T_1^3+s(T^3+2T_1^3) \\ & \quad +\,M\alpha (cI_pM(M-3T_1)-pI_e\left( M^2-3T_1^2\right) )]\}<0,\end{aligned}$$

$$-a(h+cI_p+s)+b[s(T-2T_1)-2(h+cI_p)T_1-\alpha pI_eM]<0$$

and

$$\begin{aligned} & 6A+3a(h+cI_p+s)T_1^2-3aM[cI_pM+pI_e(M-2T_1)]\alpha +b\{2(h+cI_p)T_1^3\\ & \quad +\, s( T^3+2T_1^3) +M[cI_pM(M-3T_1)-pI_e(M^2-3T_1^2)]\alpha\}>0\end{aligned}$$

Proof

The proof is omitted as it is similar to that in Proposition 1.

Sub-case 2(ii) $T_1\le M$

Similar to the previous sub-case, the retailer here accumulates and earns interest from the portion of instant payment only. The interest earned by the retailer per unit time is given by

$$\begin{aligned}&\alpha pI_e\bigg [\int _{0}^{T_1}\big [I(0)-I(t)\big ] \, dt+I(0)(M-T_1)\bigg ] \nonumber \\&\quad =\alpha pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )\big (M-T_1\big )\bigg ] \end{aligned}$$

(19)

Since $T_1\le M$, the retailer accumulates all returns from the customers before paying off the manufacturer at the end of trade credit period $M$, for the portion of immediate payment. Consequently, no interest is required to be paid for the portion of immediate payment.

For the portion of delayed payment, similar to sub-case 2(i), the retailer must finance and pay the manufacturer the entire amount of delayed payment at the end of trade credit period $M$, and then start to pay off the loan at time $N$ at which the retailer starts to receive sales revenue from its customers. Therefore, interest paid for the portion of delayed payment as shown in Fig. 6, is given by

$$\begin{aligned}&(1-\alpha )cI_p\bigg [I(0)(N-M)+\int _{N}^{T_1+N}\big [I(t-N)\big ] \, dt\bigg ] \nonumber \\&\quad =(1-\alpha )cI_p\bigg [(N-M)\bigg (aT_1+\frac{bT_1^2}{2}\bigg )+\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg )\bigg ] \end{aligned}$$

(20)

Fig. 6

Retailer’s interest earned and interest paid when $M<N$ and $M\ge T_{1}$. a Immediate payment. b Delayed payment

Therefore, the retailer’s total profit per unit time can be written as

$$\begin{aligned} TP_5(T_1,T)= & {} \frac{1}{T}\bigg \{(p-c)\bigg (aT+\frac{bT^2}{2}\bigg )-A-h\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg ) -\,\frac{s(T-T_1)^2}{6}\big [3a+b(T+2T_1)\big ]\nonumber \\&-\,(1-\alpha )cI_p\bigg [(N-M)\bigg (aT_1+\frac{bT_1^2}{2}\bigg )+\bigg (\frac{aT_1^2}{2}+\frac{bT_1^3}{3}\bigg )\bigg ]\nonumber \\&+\,\alpha pI_e\bigg [\frac{aT_1^2}{2}+\frac{bT_1^3}{6}+\bigg (aT_1+\frac{bT_1^2}{2}\bigg )(M-T_1)\bigg ]\nonumber \\&+\,\alpha pI_e\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ]M\nonumber \\&-\,(1-\alpha )cI_p\bigg [a(T-T_1)+\frac{b(T^2-T_1^2)}{2}\bigg ](N-M)\bigg \} \end{aligned}$$

(21)

Proposition 5

$TP_5(T_1,T)$ has the maximum value for those values of $T$ and $T_1$ which satisfy the following equations:

$$(a+bT_1)[T_1(h+cI_p(1-\alpha )+\alpha pI_e)-s(T-T_1)]=0,$$

$$\begin{aligned} &6A+3a[-s(T^2-T_1^2)+T_1^2(h+cI_p(1-\alpha )+\alpha pI_e)] \\ &\quad +\,b\{-2sT^3+2(h+s)T_1^3\,+\,c[-3T^2(1-I_p(M-N)(1-\alpha ))\\ &\quad+2I_pT_1^3(1-\alpha )] \,+\,p[2I_eT_1^3\alpha +3T^2(1+I_eM\alpha )]\}=0,\end{aligned}$$

provided that the following conditions are satisfied:

$$\{3T_1^2(a+bT_1)^2[h+s+\alpha pI_e+cI_p(1-\alpha )]^2+[-a(h+cI_p(1-\alpha )+s+\alpha pI_e)+b(s(T-2T_1)-2T_1(h+cI_p(1-\alpha )+\alpha pI_e))]\times [6A+3aT_1^2(h+cI_p(1-\alpha )+s+\alpha pI_e )+b(s(T^3+2T_1^3)+2T_1^3(h+cI_p(1-\alpha )+\alpha pI_e))]\}<0,$$

$$-a[h+cI_p(1-\alpha )+s+\alpha pI_e]+b\{s(T-2T_1)-2T_1 [h+cI_p(1-\alpha )+\alpha pI_e]\}<0$$

and

$$6A+3aT_1^2[h+cI_p(1-\alpha )+s+\alpha pI_e]+b[s(T^3+2T_1^3)+2T_1^3 (h+cI_p(1-\alpha )+\alpha pI_e)]>0.$$

Proof

The proof is omitted as it is similar to that in Proposition 1.

4 Solution algorithm

Based on the values of $M$ and $N$, we outline the following step by step procedure to determine the optimal solution $(T_1^*,T^*)$ and the corresponding optimal total profit and the EOQ.

• Step 1. Compare the values of $M$ and $N$. If $M\ge N$, then go to Step 2. Otherwise, go to Step 6.

• Step 2. Determine $T^*$ and $T_1^*$ from Proposition 1. If $M\le T_1^*\le T_1^*+N$, evaluate $TP_1(T_1^*,T^*)$ from (7).

• Step 3. Determine $T^*$ and $T_1^*$ from Proposition 2. If $T_1^*\le M^*\le T_1^*+N$, evaluate $TP_2(T_1^*,T^*)$ from (11).

• Step 4. Determine $T^*$ and $T_1^*$ from Proposition 3. If $T_1^*\le T_1^*+N\le M$, evaluate $TP_3(T_1^*,T^*)$ from (14).

• Step 5. Let $\widehat{TP}(\widehat{T_1}^*,\widehat{T}^*)=\hbox {max}_{i=1,2,3}{TP_{i}(T_1^*,T^*)}$. Then $\widehat{T_1}^*$ and $\widehat{T}^*$ are the optimal solution corresponding to the maximum total profit $\widehat{TP}(\widehat{T}^*_1,\widehat{T}^*)$.

• Step 6. Determine $T^*$ and $T_1^*$ from Proposition 4. If $M\le T_1^*$, evaluate $TP_4(T_1^*,T^*)$ from (18).

• Step 7. Determine $T^*$ and $T_1^*$ from Proposition 5. If $T_1^*\le M$, evaluate $TP_5(T_1^*,T^*)$ from (21).

• Step 8. Let $\widetilde{TP}(\widetilde{T_1}^*,\widetilde{T}^*)=\hbox {max}_{i=4,5}{TP_i(T_1^*,T^*)}$. Then $\widetilde{T_1}^*$ and $\widetilde{T}^*$ are the optimal solution corresponding to the maximum total profit $\widetilde{TP}(\widetilde{T_1}^*,\widetilde{T}^*)$.

• Step 9. Compute the optimal order quantity corresponding to the maximum total profit.

5 Numerical examples

In this section, we provide four numerical examples to illustrate the theoretical results and to examine the sensitivity of some key parameters on the optimal solution.

We assume that $f(t)=200+150t$, $A=\$10$ per order, $h=\$0.5$/unit/year, $c=\$2$/unit, $p=\$4$/unit, $I_p=0.06$/dollar/year, $I_e=0.05$/dollar/year, $s=\$1.5$/unit/year, $\alpha =0.5$.

Example 1

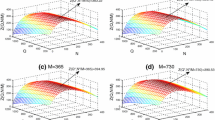
Let $M=1/6$ year, and $N=1/12$ year. Applying the proposed algorithm, we obtain the optimal solution as $T_1^*=2.0323$ years, $T^*=2.8888$ years, and the optimal total profit $TP^*(T_1,T)=TP_1(T_1,T)=\$551.353$. The optimal order quantity is $Q^*=1203.65$ units. Figure 7 gives the graphical representation of total profit of the retailer.

Fig. 7

Graph of the total profit function $TP_{1}(T_{1}, T)$

Example 2

Let $M=1/2$ year and $N=1/12$ year. Then the optimal solution is obtained as $T_1^*=2.0343$ years, $T^*=2.9338$ years and $TP^*(T_1,T)=TP_1(T_1,T)=\$566.255$. The optimal order quantity is $Q^*=1232.30$ units.

Example 3

Let $M=1/12$ year and $N=1/6$ year. Then we obtain the optimal solution as $T_1^*=2.0227$ years and $T^*=2.8642$ years. The optimal total profit is $TP^*(T_1,T)=TP_4(T_1,T)=\$546.237$ and the optimal order quantity is $Q^*=1188.11$ units.

Example 4

Let $M=1/12$ year and $N=1/2$ year. Then the optimal solution is obtained as $T_1^*=1.9950$ years and $T^*=2.8251$ years. The optimal total profit is $TP^*(T_1,T)=TP_4(T_1,T)=\$537.97$ and the optimal order quantity is $Q^*=1163.61$ units.

From the numerical results of Examples 1–4, we have the following observations:

(i):

The longer the up-stream trade credit period $M$, the higher the retailer’s total profit per unit time, the order quantity $Q^*$ and the replenishment cycle time $T^*$.

(ii):

The longer the down-stream trade credit period $N$, the lower the retailer’s total profit per unit time, the order quantity $Q^*$ and the replenishment cycle time $T^*$.

Thus, the retailer will urge the manufacturer to offer a longer trade credit period but he/she will be reluctant to provide a longer trade credit period to his/her own customers.

6 Sensitivity analysis

In this section, we investigate the effects of changes in the values of the parameters $a, b, h, A, s, \alpha , I_p$ and $I_e$ on $T_1^*, T^*, Q^*$ and $TP^*$ based on data given in Example 1. The sensitivity analysis is performed by changing each value of the parameters by $-50$, $-20$, $+20$ and $+50\,\%$, taking one parameter at a time and keeping the remaining parameters unchanged. The computational results are shown in Table 1.

Table 1 Sensitivity analysis

Based on the sensitivity analysis presented in Table 1, we have the following observations:

(i):

The retailer’s total profit per unit time $TP^*(T_1,T)$ increases as one of the parameters $a, b, \alpha$ and $I_e$ increase while it decreases as one of the parameters $h, A, s$ and $I_p$ increase. A simple economic interpretation is as follows: a higher value of $a$ or $b$ causes a higher value of the demand and hence increases the retailer’s annual profit. Likewise, higher values of $I_e$ and $\alpha$ increase the amount of interest earned by the retailer for providing trade credit and thus contribute to increase the retailer’s total profit per unit time. On the other hand, as the values of $h, A, s$ and $I_p$ increase, the total relevant cost of the retailer increases and hence the retailer obtains less profit.

(ii):

When the values of parameters $b, A, \alpha$ and $I_e$ increase, the retailer’s order quantity $Q^*$ increases. This observation can be explained as follows: when $b$ increases, the retailer obtains higher demand and hence increases the order quantity to meet the demand. When ordering cost $A$ increases, retailer places order of higher quantity to minimize the ordering cost. Finally, when the values of $\alpha$ and $I_e$ increase, the retailer obtains a higher value of interest from the sales revenue for providing trade credit and hence orders more quantity to increase his/her interest amount and thereby total profit. However, order quantity $Q^*$ decreases with increase in the values of the parameters $a, h, s$ and $I_p$.

(iii):

The replenishment cycle time $T^*$ increases when the parameters $b, A, \alpha$ and $I_e$ increase while it decreases with increase in the values of the parameters $a, h, s$ and $I_p$.

(iv):

The retailer’s total profit per unit time $TP^*(T_1,T)$ is highly sensitive to changes in values of the parameters $a, b, h$ and $s$; moderately sensitive to parameter $I_p$ while it is weakly sensitive to parameters $A, \alpha$ and $I_e$.

7 Managerial insights

Based on the results of numerical examples and observations from the sensitivity analysis, we have the following managerial insights:

• The retailer’s optimal total profit per unit time is positively correlated with the trade credit period offered by the manufacturer while it is negatively correlated with his/her trade credit period offered to customers.

• The optimal order quantity increases as the up-stream trade credit period $M$ increases, and decreases as the down-stream trade credit period $N$ increases.

• The optimal replenishment cycle time increases as $M$ increases, while it decreases as $N$ increases.

• An increase in one of the parameters $b, A, \alpha$ and $I_e$ increases the optimal order quantity and the optimal replenishment cycle time. On the other hand, the optimal order quantity as well as the optimal replenishment cycle time decreases as one of the parameters $a, h, s$ and $I_p$ increases.

8 Conclusions

Most of the existing inventory models under trade credit financing assumed that the demand rate is known and constant. However, in today’s world, demand of many products especially high-tech products increases significantly during the growth stage. Also, the use of partial down-stream trade credit to reduce default risk from credit-risk customers has received little attention from researchers. In this paper, we have considered an inventory system with increasing demand and allowable shortages over a single period under trade credit financing. The manufacturer offers a full trade credit period (up-stream trade credit) to the retailer but the retailer only offers a partial trade credit to his/her credit-risk customers (down-stream trade credit). Shortages are allowed and are completely backlogged. We have derived the necessary and sufficient conditions to find the optimal solution and then devised a suitable algorithm to locate the optimal solution. Finally, we have used several numerical examples to present all possible relationships between up-stream and down-stream trade credit periods and conduct a sensitivity analysis of important model-parameters to study their influence on optimal solution. The proposed model can be extended in many ways. For example, one can consider deterioration or imperfect items in retailer’s inventory, quantity discount offer by the manufacturer and so on.

Appendix

Proof of Proposition 1

For maximization of $TP_1(T_1,T)$, the necessary conditions are $\frac{\partial TP_1(T_1,T)}{\partial T_1}=0$ and $\frac{\partial TP_1(T_1,T)}{\partial T}=0$ and the sufficient conditions are $\frac{\partial ^2 TP_1(T_1,T)}{\partial T_1^2}<0$, $\frac{\partial ^2 TP_1(T_1,T)}{\partial T^2}<0$ and $\left| \begin{array}{cc} \frac{\partial ^2 TP_1(T_1,T)}{\partial T_1^2} &{} \frac{\partial ^2 TP_1(T_1,T)}{\partial T_1\partial T}\\ \frac{\partial ^2 TP_1(T_1,T)}{\partial T\partial T_1} &{} \frac{\partial ^2 TP_1(T_1,T)}{\partial T^2} \end{array}\right| >0$.

Now,

$$\begin{aligned} \frac{\partial TP_1(T_1,T)}{\partial T_1}= & {} \frac{1}{2T}\bigg\{ 2a\big[ sT-(h+cI_p+s)T_1-I_ep(M-N(1-\alpha ))\big ]+b\big[ 2T_1(sT-(h+s)T_1 \\&-\,\left. I_ep\big (M-N(1-\alpha ))\big )+cI_p\left( (M-N)^2-2T_1^2+(2M-N)N\alpha \right) \right] \bigg\} \\ \frac{\partial TP_1(T_1,T)}{\partial T}= & {} \frac{1}{6T^2}\big [6A+3aX_{11}+b(X_{12}+cX_{13}\big )\big ] \end{aligned}$$

Therefore, $\frac{\partial TP_1(T_1,T)}{\partial T_1}=0$ and $\frac{\partial TP_1(T_1,T)}{\partial T}=0$ give $2a\{sT-(h+cI_p+s)T_1-I_ep[M-N(1-\alpha) ] \}+b \{2T_1 [sT-(h+s)T_1-I_ep (M-N(1-\alpha ))]+cI_p [(M-N)^2-2T_1^2+(2M-N)N\alpha ] \}=0$ and $6A+3aX_{11}+b(X_{12}+cX_{13})=0$.

The optimal values of $T$ and $T_1$ which maximize $TP_1(T_1,T)$ are obtained by solving the above pair of equations, provided that they satisfy the sufficient conditions.

The sufficient conditions are given by

$$\begin{aligned} \frac{\partial ^2 TP_1(T_1,T)}{\partial T_1^2}=-\frac{1}{T}\big [aX_{31}+bX_{32}\big ]<0 \end{aligned}$$

which gives $aX_{31}+bX_{32}>0$,

$$\begin{aligned} \frac{\partial ^2 TP_1(T_1,T)}{\partial T^2}=\frac{1}{3T^3}\big [-6A+bX_{41}+3a\big (X_{42}+cX_{43}\big )\big ]<0 \end{aligned}$$

which gives $-6A+bX_{41}+3a\big (X_{42}+cX_{43}\big )<0$.

and $\left| \begin{array}{cc} \frac{\partial ^2 TP_1(T_1,T)}{\partial T_1^2} &{} \frac{\partial ^2 TP_1(T_1,T)}{\partial T_1\partial T}\\ \frac{\partial ^2 TP_1(T_1,T)}{\partial T\partial T_1} &{} \frac{\partial ^2 TP_1(T_1,T)}{\partial T^2} \end{array}\right| =-\frac{1}{12T^4}\big \{3\big [2aX_{21}+b(X_{22}-cX_{23})\big ]^2+4(aX_{31}+bX_{32})(-6A +bX_{41}+3a(X_{42}+cX_{43}))\big \}>0,$ which gives $\{3[2aX_{21}+b(X_{22}-cX_{23})]^2+4 (aX_{31}+bX_{32} ) (-6A +bX_{41}+3a(X_{42}+cX_{43}) ) \}<0$. This completes the proof.