Understanding Cannibalism Dynamics in Predator–Prey Interactions: Bifurcations and Chaos Control Strategies

Abstract

The occurrence of cannibalism is common in natural colonies and can substantially affect the functional relationships between predators and prey. Despite the belief that cannibalism stabilizes or destabilizes predator–prey models, its effects on prey populations are not well-understood. In this study, we propose a discrete-time prey–predator model to examine the presence and local stability of biologically possible equilibria. We employ the center manifold theorem and normal theory to investigate the various types of bifurcations that arise in the system. The findings of our study reveal that the model exhibits transcritical bifurcation at its trivial equilibrium. In addition, the discrete-time predator–prey system demonstrates period-doubling bifurcation in the vicinity of both its boundary equilibrium and interior equilibrium. Furthermore, we analyze the existence of Neimark–Sacker bifurcation around the interior equilibrium point. We demonstrate that cannibalism in the prey population can lead to periodic outbreaks, but these outbreaks are limited to the prey population and do not affect predation. In order to regulate the periodic oscillations and other bifurcating and fluctuating behaviors of the system, various chaos control strategies are executed. Additionally, extensive numerical simulations are carried out to validate and substantiate the analytical findings. We utilized the software Mathematica 12.3, which is an efficient and effective computing tool that enables symbolic and numerical computations to carry out numerical simulations.

1 Introduction

The inclusion of cannibalism within predator–prey frameworks constitutes a valuable instrument for comprehending ecosystem dynamics. Cannibalism ensures when conspecific individuals are consumed by members of a given species. Despite its apparent paradoxical nature, cannibalism is prevalent within the realm of the animal kingdom, notably observed among aquatic and insect communities. In the realm of predator–prey population models, the incorporation of cannibalism stands to exert influence upon the stability and intricate dynamics of the population under scrutiny. The phenomenon denoting the consumption of conspecific tissue, colloquially termed as cannibalism, has garnered empirical attention as a societal custom within diverse indigenous communities of south America, African tribes, and the populace of New Guinea [1]. In the Northern region of India, there exists a group of ascetics or sorcerers known as ‘‘Aghoris’’ who partake in cannibalism as a part of their pursuit of eternal life. Additionally, cannibalistic behavior has been witnessed among diverse creatures including flour beetles, locusts, non-predatory insects, spiders, and fish, as documented in references [2,3,4,5,6]. Cannibalism is a phenomenon that typically involves individuals of varying stages of development within a species such as adolescents and adults, or immature and mature individuals from different groups. This behavior can be interpreted as a form of predator–prey interaction occurring within the same species. Mathematical models used to describe this relationship differ from those utilized to analyze interactions between different species, as studied in previous research [7, 8]. Investigation of Polis has identified over 1300 species that exhibit cannibalistic behavior [8]. Cannibalism, the act of one organism consuming another of the same species, is frequently employed as a mean of survival, and it can exert an influence on population dynamics via multiple paradoxical mechanisms. For instance, the ‘‘lifeboat’’ mechanism can lead to population persistence in groups doomed for destruction and it can help stabilize cycling populations [9, 10]. Cannibalism appears to be most prevalent in species with limited resources and high population densities [11]. Therefore, it may be a competition-driven behavior.

At the outset, cannibalism was primarily conceptualized as a conduct demonstrated exclusively by predatory species, see [10, 12, 13]. However, this viewpoint contradicts ecological evidence from both experimental studies and field observations, which suggest that cannibalism frequently occurs in prey species [14,15,16]. These empirical observations have made a substantial contribution to the evolution of innovative concepts within contemporary research endeavors. In accordance with an investigation carried out by the investigator [16], an examination was performed on the influence of prey cannibalism on the dynamics of predator–prey relationships. The outcomes suggest that the existence of cannibalism among prey organisms induces density dependent tendencies, thereby engendering intricate nonlinear interactions between predators and prey. The outcomes indicate that the inclusion of prey cannibalism warrants substantial consideration within the investigation of predator–prey interdependencies, owing to its potential to induce noteworthy modifications in ecosystem dynamics. Recent inquiries into cannibalism have delineated the involvement of afflicted predators in prevailing cannibalism frameworks, see [9, 10, 17,18,19,20,21,22]. In a related vein, Zhang et al. [23] demonstrated the overall stability of equilibria and discerned instances of both supercritical and subcritical Hopf bifurcations within the established system. They also identified several quantities with biological meanings that are important for understanding the dynamics of the predator–prey relationship in this system.

In the present manuscript, a comprehensive investigation is conducted on the system under consideration as:

$$ \begin{gathered} u_{n + 1} = ru_{n} \left( {1 - u_{n} } \right) - bu_{n} v_{n}, \hfill \\ v_{n + 1} = du_{n} v_{n}. \hfill \\ \end{gathered} $$

(1.1)

The model (1.1) represents a nonlinear discrete predator–prey system for $n \in N$ and positive parameters $r,a,b,$ which was introduced in [24, 25]. Since its introduction, there have been several studies aimed at investigating various aspects of the system. Recent scientific investigations have been centered on diverse facets of altered versions of the predator–prey dynamic, with a particular emphasis on studying periodic solutions, and dynamical complexity. Amidst these investigations, Liu [26] conducted an inquiry pertaining to the discrete-time semi-ratio-dependent prey and predator interaction with the aim of scrutinizing the existence of periodic solutions. The investigation employed meticulous mathematical and analytical methodologies to deduce findings grounded in the observed phenomena. The ramification of these investigative endeavors could hold significant implications for enhancing our grasp of complex ecological systems and their dynamics. Within the realm of population ecology, a variety of mathematical frameworks have been proposed to investigate the dynamics of predator–prey systems. An illustrative investigation in this context was undertaken by Li et al. [27], focusing on a discrete model incorporating time delay. The outcomes of their analysis indicate the system’s capacity to uphold a consistent population over temporal progression, with said stability being delineated by distinct mathematical attributes. A separate investigation, undertaken by Din [28], centered around the renowned Leslie–Gower mathematical framework, aiming to formulate approaches for averting tumultuous conduct within the system and upholding equilibrium. Furthermore, Gámez et al. [29] employed a discretized rendition of this model to devise a surveillance approach, enabling the tracing of temporal fluctuations in population dynamics. Huang et al. [30], in their study, performed a scientific investigation of a distinct predator–prey model that incorporated a nonmonotonic functional response. The primary objective of their analysis was to determine the presence of various types of bifurcations, such as fold, transcritical, and Neimark–Sacker bifurcation. In addition, [31,32,33,34] conducted scientific studies related to several attractive results concerning the qualitative behavior of difference equations. Their studies were based on rigorous analysis and observation, and the results were reported in scientific publications, see also [35,36,37,38,39,40,41]. Chow and Jang have proposed a discrete-time predator–prey model that incorporates cannibalism. They have studied two-stage population models in which cannibalism occurs.

The objective of this research is to examine the dynamic characteristics of a discrete-time model of predator–prey interactions that incorporates cannibalism as a trait of the prey population.

$$ \begin{gathered} u_{n + 1} = ru_{n} \left( {1 - u_{n} } \right) + cu_{n} - bu_{n} v_{n} - \frac{{\alpha u_{n}^{2} }}{{u_{n} + \beta }}, \hfill \\ v_{n + 1} = du_{n} v_{n} . \hfill \\ \end{gathered} $$

(1.2)

It is noteworthy that the prey species $u_{n}$ is exhibiting intraspecific depredation. Additionally, the prey equation incorporates a cannibalism factor denoted by ${\mathcal{C}}\left( u \right) = \frac{{\alpha u^{2} }}{u + \beta }$. However, we impose the condition $c < \alpha$, as several prey individuals need to be consumed by the cannibal to generate a single new offspring.

The key findings elucidated within this article may be succinctly encapsulated in the ensuing manner:

• In the initial phase, a comprehensive analysis was conducted to assess the existence and robustness of equilibrium states.

• Subsequently, an exploration was undertaken into the conditions governing the orientation and occurrence of Neimark–Sacker bifurcation.

• In the subsequent step, an examination of period-doubling bifurcation and transcritical bifurcation was carried out, employing the center manifold theorem and the theory of normal form.

• Lastly, the manuscript delves into the assessment of the effectiveness of hybrid control and Ott–Grebogi–Yorke (OGY) feedback control strategies in the regulation of bifurcation phenomena within the system.

• In the numerical simulation section serves to collaborate and assess the validity and efficacy of our theoretical and mathematical discourse put forth in our study.

The composition of this article is organized into distinct sections in the subsequent manner. Section 2 of the paper investigates the examination of the presence of biologically viable equilibria, along with the conditions necessary for their local asymptotic stability. Section 3 presents a bifurcation analysis of the system (1.2), demonstrating a transcritical bifurcation of the trivial equilibrium when the prey population's growth parameter "$r$" is used as the bifurcation parameter. Furthermore, the inquiry substantiates that the dynamical system delineated by the formulation (1.2) experiences instances of period-doubling and Neimark–Sacker bifurcations in proximity to its intrinsic equilibrium juncture. In addition, an occurrence of period-doubling bifurcation is observed at the boundary equilibrium point. Section 4 presents a discussion of two chaos control techniques, namely, the OGY method and hybrid control methods. Finally, Sect. 5 presents numerical simulations that provide an illustration of the theoretical discussions.

2 Stability Analysis

Stability analysis is a useful tool to study the dynamics and behavior of predator prey interactions that can have certain biological implications for understanding the factors that affect the population size, growth rate, oscillation, extinction, coexistence, resilience, chaos, adaptation and evaluation of predator–prey species. In order to determine the equilibria of the system (1.2), it is necessary to solve the set of algebraic equations given below.

$$ u = ru\left( {1 - u} \right) + cu - buv - \frac{{\alpha u^{2} }}{u + \beta },\quad v = duv. $$

Through basic computations, the solutions for the algebraic system mentioned above can be derived as $\left( {0, 0} \right)$, $\left( {k,{ }0} \right)$ and $\left( {u^{*} , v^{*} } \right).$ It is evident that a trivial equilibrium point $\left( {0,0} \right)$ always exists. However, a boundary equilibrium point $\left( {k, 0} \right) = \left( {\frac{{r\left( {1 - \beta } \right) - \left( {1 + \alpha } \right) + c + \sqrt {4r\left( {c + r - 1} \right)\beta + \left( {r\left( {1 - \beta } \right) - \left( {1 + \alpha } \right) + c} \right)^{2} } }}{2r},0} \right)$ exists only for $c + r > 1$, and an interior equilibrium point $\left( {u^{*} , v^{*} } \right) = \left( {\frac{1}{d}, \frac{{\left( {1 + d\beta } \right)\left\{ {d\left( {c + r - 1} \right) - r} \right\} - \alpha d}}{{bd\left( {1 + d\beta } \right)}}} \right)$ for system (1.2) exists if and only if $\left( {1 + d\beta } \right)\left( {d + r} \right) + \alpha d < d\left( {1 + d\beta } \right)\left( {c + r} \right)$.

In addition, the Jacobian matrix of model (1.2) computed at $\left( {u,v} \right)$ can be expressed as:

$$ {\mathcal{J}}\left( {u, v} \right) = \left[ {\begin{array}{*{20}l} {c + r - 2ru - bv - \frac{{u\alpha \left( {u + 2\beta } \right)}}{{\left( {u + \beta } \right)^{2} }}} \hfill & { - bu} \hfill \\ {dv} \hfill & {du} \hfill \\ \end{array} } \right] $$

In a state of trivial equilibrium, the variational matrix ${\mathcal{J}}\left( {u, v} \right)$ of system (1.2) undergoes a reduction resulting in the following specific form:

$$ {\mathcal{J}}\left( {0, 0} \right) = \left[ {\begin{array}{*{20}l} {c + r} \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill \\ \end{array} } \right]. $$

The present analysis establishes the following assumptions with clarity: (i) the point $\left( {0,0} \right)$ is a sink if and only if the inequality $0 < c + r < 1$ holds, (ii) the point $\left( {0,0} \right)$ is a saddle point when $c + r$ exceeds 1, and (iii) the point $\left( {0,0} \right)$ is classified as non-hyperbolic if the condition $c + r = 1$ is satisfied.

Here, we present a universal finding concerning the local stability of fixed points within the framework of system (1.2). Assuming that $P^{ * }$ denotes any fixed point of system (1.2), and considering the following conditions:

$$ {\mathcal{J}}\left( {P^{*} } \right) = \left[ {\begin{array}{*{20}l} {e_{11} } \hfill & \quad {e_{12} } \hfill \\ {e_{21} } \hfill & \quad {e_{22} } \hfill \\ \end{array} } \right] $$

If we consider the variational matrix ${\mathcal{J}}$ evaluated at $P^{*} ,$ the characteristic polynomial of ${\mathcal{J}}\left( {P^{*} } \right)$ can be determined as follows:

$$ {\mathbb{H}}\left( \varrho \right) = \varrho^{2} - T_{1} \varrho + D_{1} , $$

In order to examine the stability of a quadratic equation and its root behavior in relation to the unit disk, the ensuing lemma elucidates the optimal correlation between the equation's roots and coefficients. Additional details can be found in reference [42].

Lemma 2.1

Assuming ${\mathbb{H}}\left( 1 \right) > 0$, where ${\mathbb{H}}\left( \varrho \right) = \varrho^{2} - T_{1} \varrho + D_{1}$ and $\varrho_{1} ,\varrho_{2}$ are the roots of ${\mathbb{H}}\left( \varrho \right) = 0$, we present the subsequent conventional findings:

• a. The absolute values of $\varrho_{1}$ and $\varrho_{2}$ are both less than 1 if and only if ${\mathbb{H}}\left( { - 1} \right)$ is greater than 0 and $D_{1}$ is less than 1.

• b. The absolute values of $\varrho_{1}$ and $\varrho_{2}$ are both greater than 1 if and only if ${\mathbb{H}}\left( { - 1} \right)$ is greater than 0 and $D_{1}$ is greater than 1.

• c. Either $\left| {\varrho_{1} } \right|$ is less than 1 and $\left| {\varrho_{2} } \right|$ is greater than 1 or $\left| {\varrho_{1} } \right|$ is greater than 1 and $\left| {\varrho_{2} } \right|$ is less than 1 if and only if ${\mathbb{H}}\left( { - 1} \right)$ is less than 0.

• d. If $\varrho_{1}$ equals -1 and $\varrho_{2}$ is not equal to 1, then H(-1) equals 0 and T_1 is not equal to 0 or 2.

• e. $\varrho_{1}$ and $\varrho_{2}$ are complex conjugates with absolute values of 1 if and only if $T_{1}^{2} - 4D_{1}$ is less than 0 and $D_{1}$ equals 1.

Given that $\varrho_{1}$ and $\varrho_{2}$ are eigenvalues of system (1.2), the stability of $P^{*}$ can be topologically classified based on the following criteria. Specifically, the nature of $P^{*}$ is characterized as a sink if $\left| {\varrho_{1} } \right| < 1$ and $\left| {\varrho_{2} } \right| < 1$, since a sink represents a point of suction that is locally asymptotically stable. Conversely, $P^{*}$ is considered a source if $\left| {\varrho_{1} } \right| > 1$ and $\left| {\varrho_{2} } \right| > 1$, as a source is a repeller and therefore remains unstable. $P^{*}$ is classified as a saddle point if $\left| {\varrho_{1} } \right| < 1$ and $\left| {\varrho_{2} } \right| > 1$, or if $\left| {\varrho_{1} } \right| > 1$ and $\left| {\varrho_{2} } \right| < 1$. If conditions (d) and (e) of Lemma 2.1 are satisfied, then $P^{*}$ is considered a non-hyperbolic point.

The calculation of ${\mathcal{J}}\left( {u, v} \right)$ at the point $\left( {k, 0} \right)$ is carried out as follows:

$$ {\mathcal{J}}\left( {k, 0} \right) = \left[ {\begin{array}{*{20}c} {c + r - 2kr - \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }}} & \quad { - bk} \\ 0 & \quad {dk} \\ \end{array} } \right], $$

where

$$ k = \frac{1}{2r}\left[ {c + r\left( {1 - \beta } \right) - \left( {1 + \alpha } \right) + \sqrt {4r\left( {c + r - 1} \right)\beta + \left( {1 + \alpha - c - r\left( {1 - \beta } \right)} \right)^{2} } } \right], $$

and all parameters are positive along with $c + r > 1$.

Theorem 2.1

The subsequent outcomes are applicable under the presumption of the ensuing condition, $\alpha > 0, \beta > 0, r > 0,$ and $c + r > 1$.

• i. $\left( {k, 0} \right)$ is a sink $\Leftrightarrow 2kr + \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }} < 1 + c + r < 2 + 2kr + \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }}$ and $0 < dk < 1.$

• ii. $\left( {k, 0} \right)$ is a saddle $\Leftrightarrow 2kr + \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }} < 1 + c + r < 2 + 2kr + \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }}$ and $dk > 1.$

• iii. $\left( {k, 0} \right)$ is non-hyperbolic $\Leftrightarrow c + r + 1 = 2kr + \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }} ,$ or $dk = 1.$

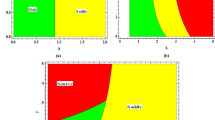
Figure 1 provides an illustration of the local asymptotic stability analysis and topological classification of conducted on boundary equilibrium point using randomly selected biologically suitable numerical values of parameters involve.

Fig. 1

Classification of boundary equilibrium for $d\in \left[0, 5\right], r\in \left[0, 10\right], \alpha =1.3,$ $\beta =0.4, c=0.1.$

Furthermore, for a given positive equilibrium $\left( {u^{*} , v^{*} } \right)$, the Jacobian ${\mathcal{J}}\left( {u, v} \right)$ is evaluated and is given by,

$$ {\mathcal{J}}\left( {u^{*} , v^{*} } \right) = \left( {\begin{array}{*{20}c} {\frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{r}{d}} & \quad { - \frac{b}{d}} \\ {\frac{{\left( {1 + d\beta } \right)\left[ {d\left( {c + r - 1} \right) - r} \right] - \alpha d}}{{b\left( {1 + d\beta } \right)}}} & \quad 1 \\ \end{array} } \right). $$

The characteristic polynomial of ${\mathcal{J}}\left( {u^{*} , v^{*} } \right)$ can be expressed as follows:

$$ {\mathbb{H}}\left( \varrho \right) = \varrho^{2} - \left( {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{r}{d}} \right)\varrho + c + \frac{{\left( {d - 2} \right)r}}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }}, $$

(2.1)

Moreover, through the execution of straightforward algebraic computations and the assumption of the inequality $\left( {1 + d\beta } \right)\left( {d + r} \right) + \alpha d < d\left( {1 + d\beta } \right)\left( {c + r} \right)$, the following is derived:

$$ \begin{aligned} {\mathbb{H}}\left( 1 \right) & = \frac{{\left( {1 + d\beta } \right)\left[ {d\left( {c + r - 1} \right) - r} \right] - \alpha d}}{{d\left( {1 + d\beta } \right)}} \\ {\mathbb{H}}\left( { - 1} \right) & = 3 + c + \frac{{\left( {d - 3} \right)r}}{d} - \frac{{\alpha \left( {1 + 3d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} \\ {\mathbb{H}}\left( 0 \right) & = c + \frac{{\left( {d - 2} \right)r}}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} \\ \end{aligned} $$

(2.2)

Based on the inequality provided in Eq. (2.2), it is evident that ${\mathbb{H}}\left( 1 \right)$ is greater than zero. Hence, by utilizing Lemma 2.1, the ensuing outcomes can be inferred.

Theorem 2.2

Given that $\left( {1 + d\beta } \right)\left( {d + r} \right) + \alpha d < d\left( {1 + d\beta } \right)\left( {c + r} \right)$, and assuming that $\left( {u^{*} , v^{*} } \right)$ denotes the exclusive interior fixed point of the system (1.2), the subsequent outcomes remain valid:

i. $\left( {u^{*} , v^{*} } \right)$ is a sink $\Leftrightarrow \alpha d\left( {1 + 3d\beta } \right) < \left( {1 + d\beta } \right)^{2} \left( {r\left( {d - 3} \right) + d\left( {c + 3} \right)} \right)$ and

$$ d\left( {\alpha \left( {1 + 2d\beta } \right) + \left( {1 + d\beta } \right)^{2} } \right) < \left( {1 + d\beta } \right)^{2} \left( {cd + r\left( {d - 2} \right)} \right) $$

ii. $\left( {u^{*} , v^{*} } \right)$ is a source $\Leftrightarrow \alpha d\left( {1 + 3d\beta } \right) < \left( {1 + d\beta } \right)^{2} \left( {r\left( {d - 3} \right) + d\left( {c + 3} \right)} \right)$ and

$$ d\left( {\alpha \left( {1 + 2d\beta } \right) + \left( {1 + d\beta } \right)^{2} } \right) > \left( {1 + d\beta } \right)^{2} \left( {cd + r\left( {d - 2} \right)} \right) $$

iii. $\left( {u^{*} , v^{*} } \right)$ is a saddle $\Leftrightarrow \left( {1 + d\beta } \right)^{2} \left( {r\left( {d - 3} \right) + d\left( {c + 3} \right)} \right) < \alpha d\left( {1 + 3d\beta } \right).$

iv. Assume that $\varrho_{1} , \varrho_{2}$ be the roots of Eq. (2.1), then

$$ \varrho_{1} = - 1, \left| {\varrho_{2} } \right| \ne 1 \Leftrightarrow c + r \ne \frac{2r}{d} + \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} \pm 1, $$

and

$$ r = \frac{{d\left( {\alpha \left( {1 + 3d\beta } \right) - \left( {3 + c} \right)\left( {1 + d\beta } \right)^{2} } \right)}}{{\left( {d - 3} \right)\left( {1 + d\beta } \right)^{2} }}. $$

v. The roots of Eq. (2.1) exhibit a complex conjugate nature with a unit magnitude, if and only if

$$ \left\{ {{\text{and}} \;\begin{array}{*{20}c} {\left| {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{r}{d}} \right| < 2, } \\ {r = \frac{{d\left( {\left( {1 - c} \right)\left( {1 + d\beta } \right)^{2} + \alpha \left( {1 + 2d\beta } \right)} \right)}}{{\left( {d - 2} \right)\left( {1 + d\beta } \right)^{2} }}.} \\ \end{array} } \right. $$

The asymptotic stability of the unique positive equilibrium point is shown in Fig. 2, using random values of the parameters that are biologically realistic.

Fig. 2

Classification of $\left({u}^{*}, {v}^{*}\right)$ for $d\in \left[0, 5\right], r\in \left[0, 10\right], \alpha =0.16,$ $\beta =0.18,$ $c=0.55.$

3 Bifurcation Analysis

Bifurcation analysis constitites a valuable methodology for the investigation of predator–prey system’s dynamics. Such systems are commonly represented through sets of differential equations, elucidating the temporal evaluation of predator and prey populations. Through the meticulous examination of potential bifurcation points inherent to these equations, profund revelations regarding the enduring dynamics of the system can be attained. Bifurcation analysis is a technique that investigates the qualitative changes in the system’s behavior as a parameter is varied. This technique can reveal the long-term dynamics of the system, such as stability, periodicity, and chaos. This segment is dedicated to the comprehensive investigation of the transcritical bifurcation of the system represented by Eq. (1.2) at the trivial equilibrium point $\left( {0, 0} \right)$, alongside the analysis of the period-doubling bifurcation transpiring at the boundary equilibrium point $\left( {k, 0} \right)$. Furthermore, an in-depth examination will be conducted concerning the period-doubling and Neimark–Sacker bifurcation phenomena exhibited by the model described in Eq. (1.2) when the equilibrium point is situated at $\left( {u^{*} , v^{*} } \right)$.

3.1 Transcritical Bifurcation

During the initial analysis, we investigate the presence of transcritical bifurcation at the trivial equilibrium point $\left( {0, 0} \right)$. To facilitate this, we make the assumption that:

$$ r \equiv r_{0} : = 1 - c. $$

Let us consider the following set,

$$ \Omega_{{T{\mathcal{B}}}} = \left\{ {\left( {r_{0} , b, c, d,\alpha , \beta } \right) \in {\mathcal{R}}_{ + }^{6} :r_{0} : = 1 - c} \right\}. $$

Let $\left( {r_{0} , b, c, d,\alpha , \beta } \right) \in \Omega_{{T{\mathcal{B}}}}$ be under consideration. In such cases, the dynamics governed by the system delineated in Eq. (1.2) can be succinctly represented as a bi-dimensional mapping, as manifested by the subsequent expression:

$$ \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] \to \left[ {\begin{array}{*{20}c} {x\left( {1 - x} \right)\left( {r_{0} + \hat{r}} \right) + cx - bxy - \frac{{\alpha x^{2} }}{x + \beta }} \\ {dxy} \\ \end{array} } \right] $$

(3.1)

Here, $r_{0}$ be a fixed value in a given system, and $\hat{r}$ denote a small perturbation parameter with respect to $r_{0} .$ Applying the Taylor series expansion centered at the origion results in:

$$ \left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] \to \left[ {\begin{array}{*{20}l} {c + \hat{r}} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right] + \left[ {\begin{array}{*{20}l} {{\mathbb{p}}_{0} \left( {x,y,\hat{r}} \right)} \hfill \\ {{\mathbb{q}}_{0} \left( {x,y} \right)} \hfill \\ \end{array} } \right]. $$

(3.2)

whereas,

$$ {\mathbb{p}}_{0} \left( {x,y,\hat{r}} \right) = x\hat{r} - bxy - \left( {\hat{r} + \frac{\alpha }{\beta }} \right)x^{2} + \left( {\frac{\alpha }{{\beta^{2} }}} \right)x^{3} + O\left( {\left( {\left| x \right| + \left| y \right| + \left| {\hat{r}} \right|} \right)^{4} } \right), $$

$$ {\mathbb{q}}_{0} \left( {x,y} \right) = dxy. $$

Given that the linear component of map (3.2) is already in canonical form at $r_{0} : = 1 - c$, and the map is also situated at the origin $\left( {0, 0} \right)$, an approximation for the center manifold of (3.2), $W^{c} \left( {0, 0, 0} \right)$ can be derived as follows:

$$ W^{c} \left( {0, 0, 0} \right) = \left\{ {\left( {x,y, \hat{r}} \right) \in {\mathbb{R}}^{3} : y = h_{1} x^{2} + h_{2} x\hat{r} + h_{3} \hat{r}^{2} + O\left( {\left( {\left| x \right| + \left| {\hat{r}} \right|} \right)^{3} } \right)} \right\}. $$

Let

$$ y = h\left( {x,r} \right) = h_{1} x^{2} + h_{2} x\hat{r} + h_{3} \hat{r}^{2} . $$

Then, from (3.2), we have

$$ {\mathbb{q}}_{0} \left( {x,y} \right) = h\left( {\left( {c + \hat{r}} \right)x + {\mathbb{p}}_{0} \left( {x,h\left( {x,\hat{r}} \right),\hat{r}} \right),\hat{r}} \right). $$

On comparison, we have

$$ h_{1} = h_{2} = h_{3} = 0. $$

In addition, we provide a definition for the subsequent map that is confined to the center manifold $W^{c} \left( {0, 0, 0} \right):$

$$ F:x \to x + \hat{r} + k_{1} x^{2} + k_{2} x\hat{r} + k_{3} \hat{r}^{2} + O\left( {\left( {\left| x \right| + \left| {\hat{r}} \right|} \right)^{4} } \right), $$

where $k_{1} = c - 1 - \frac{\alpha }{\beta },$ $k_{2} = 1,$ $k_{3} = 0.$

In this study, we present the establishment of two nonzero real numbers in the following manner:

$$ {\mathcal{L}}_{1} : = \left( {\frac{{\partial^{2} F}}{{\partial x^{2} }}} \right)_{{\left( {0, 0} \right)}} = 2\left( {c - 1 - \frac{\alpha }{\beta }} \right) \ne 0, $$

$$ {\mathcal{L}}_{2} : = \left( {\frac{{\partial^{2} F}}{{\partial x\partial \hat{r}}}} \right)_{{\left( {0, 0} \right)}} = 1 \ne 0. $$

Based on the analysis conducted, the following outcome regarding transcritical bifurcation for the system (1.2) has been derived.

Theorem 3.1

Assuming that $r = 1 - c$ and $c - 1 - \frac{\alpha }{\beta } \ne 0$, it can be concluded that the system described by Eq. (1.2) will experience a transcritical bifurcation at equilibrium point (0,0).

3.2 Period-Doubling Bifurcation at $\left( {{\varvec{k}},\user2{ }0} \right)$

This section aims to investigate the presence of period-doubling bifurcation in the system (1.2) about steady state $\left( {k,0} \right)$. The corresponding Jacobian matrix of the linearized is provided as:

$$ {\mathcal{J}}\left( {k, 0} \right) = \left[ {\begin{array}{*{20}c} {c + r - 2kr - \frac{{k\alpha \left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }}} & { - bk} \\ 0 & {dk} \\ \end{array} } \right]. $$

Additionally, the circumstance in which one of the eigenvalue equals -1 suggests that,

$$ \alpha : = \frac{{\left( {1 + c + r - 2kr} \right)\left( {k + \beta } \right)^{2} }}{{k\left( {k + 2\beta } \right)}}. $$

Let us assume that

$$ \omega_{{{\mathcal{P}\mathcal{B}}}} = \left\{ {\left( {r, b, c, d,\alpha , \beta } \right) \in {\mathcal{R}}_{ + }^{6} : \alpha : = \frac{{\left( {1 + c + r - 2kr} \right)\left( {k + \beta } \right)^{2} }}{{k\left( {k + 2\beta } \right)}}} \right\}. $$

In the vicinity of $\omega_{{{\mathcal{P}\mathcal{B}}}}$, the boundary equilibrium $\left( {k,0} \right)$ of map (1.2) undergoes a period-doubling bifurcation as the parameters vary. A specific value for $\alpha_{1}$ is given by $\alpha_{1} = \frac{{\left( {1 + c + r - 2kr} \right)\left( {k + \beta } \right)^{2} }}{{k\left( {k + 2\beta } \right)}}$. If the parameters $\left( {\alpha_{1} , r, b, c, d, \beta } \right)$ belong to $\omega_{{{\mathcal{P}\mathcal{B}}}}$, then the map (1.2) can be represented as follows in terms of these parameters:

$$ \left( {\begin{array}{*{20}c} {\mathcal{X}} \\ {\mathcal{Y}} \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {r{\mathcal{X}}\left( {1 - {\mathcal{X}}} \right) + c{\mathcal{X}} - b{\mathcal{X}\mathcal{Y}} - \frac{{\alpha_{1} {\mathcal{X}}^{2} }}{{{\mathcal{X}} + \beta }}} \\ {d{\mathcal{X}\mathcal{Y}}} \\ \end{array} } \right) $$

(3.3)

Given a small bifurcation parameter $\tilde{\alpha }$ and a perturbation of Eq. (3.3), it is feasible to analyze the resulting map:

$$ \left( {\begin{array}{*{20}c} {\mathcal{X}} \\ {\mathcal{Y}} \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {r{\mathcal{X}}\left( {1 - {\mathcal{X}}} \right) + c{\mathcal{X}} - b{\mathcal{X}\mathcal{Y}} - \frac{{(\alpha_{1} + \tilde{\alpha }){\mathcal{X}}^{2} }}{{{\mathcal{X}} + \beta }}} \\ {d{\mathcal{X}\mathcal{Y}}} \\ \end{array} } \right) $$

(3.4)

where the absolute value of $\tilde{\alpha }$ is significantly smaller than 1. This indicates that $\tilde{\alpha }$, which is a parameter representing a small perturbation, has a negligible impact on the system being studied. Thus, the system can be approximated by ignoring the influence of this parameter, leading to simplified mathematical expressions and computational models.

Given the assumption that $x = {\mathcal{X}} - k$ and $y = {\mathcal{Y}}$, the map (3.4) can be transformed into the subsequent expression as:

$$ \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {c_{11} } & {c_{12} } \\ {c_{21} } & {c_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {{\mathbb{p}}_{1} \left( {x, y, \tilde{\alpha }} \right)} \\ {{\mathbb{q}}_{1} \left( {x, y} \right)} \\ \end{array} } \right), $$

(3.5)

where

$$\genfrac{}{}{0pt}{}{{{\mathbb{p}}}_{1}\left(x, y, \widetilde{\alpha }\right)={c}_{13}{x}^{2}+{c}_{14}xy+{c}_{15}{x}^{3}+{c}_{16}x\widetilde{\alpha }+{c}_{17}{x}^{2}\widetilde{\alpha }+O\left({\left(\left|x\right|+\left|y\right|+\left|\widetilde{\alpha }\right|\right)}^{4}\right)}{{{\mathbb{q}}}_{1}\left(x, y, \widetilde{\alpha }\right)={c}_{23}xy.}$$

$$ c_{11} = c + r - 2kr - \frac{{k\tilde{\alpha }\left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }} , \;c_{12} = - bk, c_{21} = 0, \;c_{22} = dk, c_{14} = - b,\; c_{15} = \frac{{\tilde{\alpha }\beta^{2} }}{{\left( {k + \beta } \right)^{4} }} , $$

$$ c_{13} = - \frac{{\beta^{3} r + \tilde{\alpha }\beta^{2} + 3kr\beta^{2} + 3\beta rk^{2} + rk^{3} }}{{\left( {k + \beta } \right)^{3} }},\;c_{16} = - \frac{{k\left( {k + 2\beta } \right)}}{{\left( {k + \beta } \right)^{2} }},\; c_{17} = - \frac{{\beta^{2} }}{{\left( {k + \beta } \right)^{3} }}, \;c_{23} = d. $$

Now, we will introduce the following translation immediately.

$$ \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \mapsto T\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) $$

(3.6)

where $T = \left( {\begin{array}{*{20}c} {c_{12} } & {c_{12} } \\ { - 1 - c_{11} } & {\lambda_{2} - c_{11} } \\ \end{array} } \right)$ be an invertible matrix. The formulation of Translation (3.6) can be expressed with respect to Translation (3.5) in the following manner:

$$ \left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} { - 1} & 0 \\ 0 & {\lambda_{2} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {{\mathbb{p}}_{2} \left( {u, v, \tilde{\alpha }} \right)} \\ {{\mathbb{q}}_{2} \left( {u, v, \tilde{\alpha }} \right)} \\ \end{array} } \right) $$

(3.7)

where

$$ {\mathbb{p}}_{2} \left( {u, v, \tilde{\alpha }} \right) = \left( {\frac{{\left( {\lambda_{2} - c_{11} } \right)c_{15} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }}} \right)x^{3} + \left( {\frac{{\left( {\lambda_{2} - c_{11} } \right)\left( {\tilde{\alpha }c_{17} + c_{13} } \right)}}{{c_{12} \left( {\lambda_{2} + 1} \right)}}} \right)x^{2} + \left( {\frac{{(\lambda_{2} - c_{11} )c_{14} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }} - \frac{{c_{23} }}{{\lambda_{2} + 1}}} \right)xy + \left( {\frac{{\left( {\lambda_{2} - c_{11} } \right)\tilde{\alpha }c_{16} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }}} \right)x + O\left( {\left( {\left| u \right| + \left| v \right| + \left| {\tilde{\alpha }} \right|} \right)^{4} } \right), $$

$$ {\mathbb{q}}_{2} \left( {u, v, \tilde{\alpha }} \right) = \left( {\frac{{\left( {1 + c_{11} } \right)c_{15} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }}} \right)x^{3} + \left( {\frac{{\left( {1 + c_{11} } \right)\left( {\tilde{\alpha }c_{17} + c_{13} } \right)}}{{\left( {\lambda_{2} + 1} \right)c_{12} }}} \right)x^{2} + \left( {\frac{{\left( {1 + c_{11} } \right)c_{14} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }} + \frac{{c_{23} }}{{\lambda_{2} + 1}}} \right)xy + \left( {\frac{{\left( {1 + c_{11} } \right)\tilde{\alpha }c_{16} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }}} \right)x + O\left( {\left( {\left| u \right| + \left| v \right| + \left| {\tilde{\alpha }} \right|} \right)^{4} } \right). $$

$$ x = c_{12} \left( {u + v} \right),\;y = - \left( {1 + c_{11} } \right)u + \left( {\lambda_{2} - c_{11} } \right)v. $$

Furthermore, we postulate that the center manifold of map (3.7) at the origin $\left( {0,0} \right)$ within a limited region of $\tilde{\alpha } = 0$ is ${\mathcal{W}}^{c} \left( {0, 0, 0} \right)$. It follows that an approximation of ${\mathcal{W}}^{c} \left( {0, 0, 0} \right)$ is:

$$ {\mathcal{W}}^{c} \left( {0, 0, 0} \right) = \left\{ {\left( {u, v, \tilde{\alpha }} \right) \in {\mathbb{R}}^{3} :v = \mathcalligra{h}_{1} u^{2} + \mathcalligra{h}_{2} u\tilde{\alpha } + \mathcalligra{h}_{3} \tilde{\alpha }^{2} + O\left( {\left( {\left| u \right| + \left| {\tilde{\alpha }} \right|} \right)^{3} } \right)} \right\}. $$

where

$$ \mathcalligra{h}_{1} = \frac{{\left( {1 + c_{11} } \right)\left( {c_{11} c_{14} - c_{12} c_{13} + c_{12} c_{23} + c_{14} } \right)}}{{\lambda_{2}^{2} - 1}}, \;\mathcalligra{h}_{2} = - \frac{{\left( {1 + c_{11} } \right)c_{16} }}{{\lambda_{2}^{2} - 1}},\;\mathcalligra{h}_{3} = 0. $$

As a result, the mapping that is constrained to ${\mathcal{W}}^{c} \left( {0, 0, 0} \right)$ can be expressed as follows:

$F:u \to - u + \mathcalligra{s}_{1} u\tilde{\alpha } + \mathcalligra{s}_{2} u^{2} + \mathcalligra{s}_{3} u^{2} \tilde{\alpha } + \mathcalligra{s}_{4} u\tilde{\alpha }^{2} + \mathcalligra{s}_{5} u^{3} + O\left( {\left( {\left| u \right| + \left| {\tilde{\alpha }} \right|} \right)^{4} } \right),$ where

$$ \left\{ {\begin{array}{*{20}l} {\mathcalligra{s}_{1} : = \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)c_{16} ,} \hfill \\ {\mathcalligra{s}_{2} : = \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)c_{12} c_{13} + \left( {\frac{{c_{23} }}{{\lambda_{2} + 1}} - \frac{{\left( {\lambda_{2} - c_{11} } \right)c_{14} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }}} \right)\left( {1 + c_{11} } \right)c_{12} ,} \hfill \\ {\mathcalligra{s}_{3} : = \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)2c_{12} c_{13} \mathcalligra{h}_{2} + \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)c_{12} c_{17} + \left( {\frac{{(\lambda_{2} - c_{11} )c_{14} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }} - \frac{{c_{23} }}{{\lambda_{2} + 1}}} \right)(\lambda_{2} - c_{11} )c_{12} \mathcalligra{h}_{2} } \hfill \\ {\quad \quad + \left( {\frac{{c_{23} }}{{\lambda_{2} + 1}} - \frac{{(\lambda_{2} - c_{11} )c_{14} }}{{(\lambda_{2} + 1)c_{12} }}} \right)\left( {1 + c_{11} } \right)c_{12} \mathcalligra{h}_{2} + \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)c_{16} \mathcalligra{h}_{1} ,} \hfill \\ {\mathcalligra{s}_{4} : = \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)2c_{12} c_{13} \mathcalligra{h}_{3} + \left( {\frac{{(\lambda_{2} - c_{11} )c_{14} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }} - \frac{{c_{23} }}{{\lambda_{2} + 1}}} \right)(\lambda_{2} - c_{11} )c_{12} \mathcalligra{h}_{3} } \hfill \\ {\quad \quad + \left( {\frac{{c_{23} }}{{\lambda_{2} + 1}} - \frac{{(\lambda_{2} - c_{11} )c_{14} }}{{(\lambda_{2} + 1)c_{12} }}} \right)\left( {1 + c_{11} } \right)c_{12} \mathcalligra{h}_{3} + \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)c_{16} \mathcalligra{h}_{2} ,} \hfill \\ {\mathcalligra{s}_{5} : = \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)c_{12}^{2} c_{15} + \left( {\frac{{\lambda_{2} - c_{11} }}{{\lambda_{2} + 1}}} \right)2c_{12} c_{13} \mathcalligra{h}_{1} + \left( {\frac{{(\lambda_{2} - c_{11} )c_{14} }}{{\left( {\lambda_{2} + 1} \right)c_{12} }} - \frac{{c_{23} }}{{\lambda_{2} + 1}}} \right)(\lambda_{2} - c_{11} )c_{12} \mathcalligra{h}_{1} } \hfill \\ {\quad \quad + \left( {\frac{{c_{23} }}{{\lambda_{2} + 1}} - \frac{{(\lambda_{2} - c_{11} )c_{14} }}{{(\lambda_{2} + 1)c_{12} }}} \right)\left( {1 + c_{11} } \right)c_{12} \mathcalligra{h}_{1} .} \hfill \\ \end{array} } \right. $$

Herein, we hereby establish the ensuing two non-zero real numbers as follows:

$$ \ell_{1} = \left( {\frac{{\partial^{2} f}}{{\partial u\partial \tilde{\alpha }}} + \frac{1}{2}\frac{\partial F}{{\partial \tilde{\alpha }}}\frac{{\partial^{2} F}}{{\partial u^{2} }}} \right)_{{\left( {0, 0} \right)}} = \frac{{\left( {\lambda_{2} - c_{11} } \right)c_{16} }}{{\lambda_{2} + 1}} \ne 0. $$

$$ \ell_{2} = \left( {\frac{1}{6}\frac{{\partial^{3} F}}{{\partial u^{3} }} + \left( {\frac{1}{2}\frac{{\partial^{2} F}}{{\partial u^{2} }}} \right)^{2} } \right)_{{\left( {0, 0} \right)}} = \mathcalligra{s}_{5} + \mathcalligra{s}_{1}^{2} \ne 0. $$

Through the analysis presented above, the phenomenon of period-doubling bifurcation in System (1.2) has been determined and can be summarized as follows.

Theorem 3.2

In the case where $\ell_{2}$ is not equal to zero, system (1.2) experiences a period-doubling bifurcation at the boundary equilibrium $\left( {k,0} \right)$ as the parameter $\alpha$ undergoes small variations in its neighborhood around $\alpha_{1}$. Moreover, if $\ell_{2}$ is greater than zero, the resulting period-two orbits emerging from $\left( {k,0} \right)$ are stable, while if $\ell_{2}$ is less than zero, these orbits are unstable.

3.3 Period-Doubling Bifurcation at $\left( {{\varvec{u}}^{\user2{*}} ,\user2{ v}^{\user2{*}} } \right)$

In this section, an analysis is conducted to examine the period-doubling bifurcation of system (1.2) at the interior fixed point $\left( {u^{*} , v^{*} } \right) = \left( {\frac{1}{d}, \frac{{\left( {1 + d\beta } \right)\left( {d\left( {c + r - 1} \right)} \right) - \alpha d}}{{bd\left( {1 + d\beta } \right)}}} \right)$. Additionally, the characteristic equation of the Jacobian matrix of the linearized form of system (1.2) evaluated at the point $\left( {u^{*} , v^{*} } \right)$ is provided by

$$ {\mathbb{H}}\left( \varrho \right) = \varrho^{2} - p\left( {u^{*} , v^{*} } \right)\varrho + q\left( {u^{*} , v^{*} } \right).{ } $$

(3.8)

where

$$ \begin{aligned} p\left( {u^{*} , v^{*} } \right) & : = \left( {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{r}{d}} \right), \\ q\left( {u^{*} , v^{*} } \right) & : = c + \frac{{\left( {d - 2} \right)r}}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }}. \\ \end{aligned} $$

Let us consider

$$ \left( {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{r}{d}} \right)^{2} > 4\left( {c + \frac{{\left( {d - 2} \right)r}}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }}} \right), $$

(3.9)

and

$$ {\mathbb{H}}\left( { - 1} \right) = 3 + c + \frac{{\left( { - 3 + d} \right)r}}{d} - \frac{{\alpha \left( {1 + 3d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} = 0, $$

consequently,

$$ r: = \frac{{d\left( {\alpha \left( {1 + 3d\beta } \right) - \left( {3 + c} \right)\left( {1 + d\beta } \right)^{2} } \right)}}{{\left( {d - 3} \right)\left( {1 + d\beta } \right)^{2} }} $$

(3.10)

In accordance with Eq. (3.8), the roots corresponding to ${\mathbb{H}}\left( \varrho \right) = 0$ are $\varrho_{1} = - 1$ and

$$ \varrho_{2} = \frac{{c + 3d - 6 - \alpha - 12d\beta + 2cd\beta + 6d^{2} \beta - d^{2} \alpha \beta - 6d^{2} \beta^{2} + cd^{2} \beta^{2} + 3d^{3} \beta^{2} }}{{\left( {d - 3} \right)\left( {1 + d\beta } \right)^{2} }}. $$

Furthermore, the condition that $\left| {\varrho_{2} } \right| \ne 1$ suggests that

$$ c + \frac{{\left( {d - 2} \right)r}}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} \ne \pm 1. $$

(3.11)

Let us posit that

$$ \Omega_{{{\mathcal{P}\mathcal{B}\mathcal{U}}}} = \left\{ {\left( {r, b, c, d,\alpha , \beta } \right) \in {\mathcal{R}}_{ + }^{6} :\left( {3.9} \right), \left( {3.10} \right) {\text{and}} \left( {3.11} \right){\text{are satisfied}}} \right\}. $$

In the vicinity of $\Omega_{{{\mathcal{P}\mathcal{B}\mathcal{U}}}}$, the interior equilibrium point $\left( {u^{*} , v^{*} } \right)$ of map (1.2) exhibits period-doubling bifurcation. By defining $r_{1} = \frac{{d\left( {\alpha \left( {1 + 3d\beta } \right) - \left( {3 + c} \right)\left( {1 + d\beta } \right)^{2} } \right)}}{{\left( {d - 3} \right)\left( {1 + d\beta } \right)^{2} }}$ and selecting arbitrary parameters $\left( {r_{1} , b, c, d,\alpha , \beta } \right) \in \Omega_{{{\mathcal{P}\mathcal{B}\mathcal{U}}}}$, we can express map (1.2) as a two-dimensional map in terms of these parameters:

$$ \left( {\begin{array}{*{20}c} {\mathcal{M}} \\ {\mathcal{N}} \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {r_{1} {\mathcal{M}}\left( {1 - {\mathcal{M}}} \right) + c{\mathcal{M}} - b{\mathcal{M}\mathcal{N}} - \frac{{\alpha {\mathcal{M}}^{2} }}{{{\mathcal{M}} + \beta }}} \\ {d{\mathcal{M}\mathcal{N}}} \\ \end{array} } \right) $$

(3.12)

By considering a perturbation of map (3.12) and assuming a small bifurcation parameter $\tilde{r}$, we can investigate the resulting map as follows:

$$ \left( {\begin{array}{*{20}c} {\mathcal{M}} \\ {\mathcal{N}} \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {(r_{1} + \tilde{r}){\mathcal{M}}\left( {1 - {\mathcal{M}}} \right) + c{\mathcal{M}} - b{\mathcal{M}\mathcal{N}} - \frac{{\alpha {\mathcal{M}}^{2} }}{{{\mathcal{M}} + \beta }}} \\ {d{\mathcal{M}\mathcal{N}}} \\ \end{array} } \right) $$

(3.13)

where $\left| {\tilde{r}} \right| \ll 1$ is significantly smaller perturbation parameter. By substituting $x = {\mathcal{M}} - x^{*} {\text{and }}y = {\mathcal{N}} - y^{*}$ in the Eq. (3.13), the system can be expressed in the following form:

$$ \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {a_{11} } & \quad {a_{12} } \\ {a_{21} } & \quad {a_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\mathbb{f}_{1} \left( {x, y, \tilde{r}} \right)} \\ {\mathbb{g}_{1} \left( {x, y, \tilde{r}} \right)} \\ \end{array} } \right), $$

(3.14)

$$ {\text{where}},{ }\; \begin{array}{*{20}l} {\mathbb{f}_{1} \left( {x, y, \tilde{r}} \right) = a_{13} x^{2} + a_{14} xy + a_{15} x^{3} + a_{16} x\tilde{r} + a_{17} x^{2} \tilde{r} + O\left( {\left( {\left| x \right| + \left| y \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right),} \hfill \\ {\mathbb{g}_{1} \left( {x, y, \tilde{r}} \right) = a_{23} xy + a_{24} x\tilde{r} + O\left( {\left( {\left| x \right| + \left| y \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right),} \hfill \\ \end{array} $$

$$ a_{11} = \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{{\tilde{r}}}{d}, a_{13} = - \frac{{\beta^{3} d^{3} \tilde{r} + \alpha \beta^{2} d^{3} + 3\beta^{2} d^{2} \tilde{r} + 3\beta d\tilde{r} + \tilde{r}}}{{\left( {1 + \beta d} \right)^{3} }}, $$

$$ a_{21} = \frac{{d\left( { - 1 + c + \tilde{r} - \frac{{\tilde{r}}}{d} - \frac{\alpha }{1 + d\beta }} \right)}}{b}, a_{15} = \frac{{\alpha \beta^{2} d^{4} }}{{\left( {1 + \beta d} \right)^{4} }}, a_{24} = \frac{d - 1}{b}, a_{12} = - \frac{b}{d}, a_{16} = - \frac{1}{d}, $$

$$ a_{14} = - b, a_{23} = d, a_{17} = - 1,{ }a_{23} = d, a_{22} = 1. $$

Furthermore, we have presented the subsequent translation:

$$ \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \mapsto T\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) $$

(3.15)

where $T$ is an invertible matrix defined as, $T = \left( {\begin{array}{*{20}c} {a_{12} } & {a_{12} } \\ { - 1 - a_{11} } & {\varrho_{2} - a_{11} } \\ \end{array} } \right)$. Under map (3.14), the translation shown in Eq. (3.15) can be expressed as follows:

$$ \left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} { - 1} & 0 \\ 0 & {\varrho_{2} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\mathbb{f}_{2} \left( {u, v, \tilde{r}} \right)} \\ {\mathbb{g}_{2} \left( {u, v, \tilde{r}} \right)} \\ \end{array} } \right) $$

(3.16)

$$ \begin{aligned} \mathbb{f}_{2} \left( {u, v, \tilde{r}} \right) & = \frac{{\left( {\varrho_{2} - a_{11} } \right)a_{15} x^{3} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} + \frac{{\left( {\varrho_{2} - a_{11} } \right)\left( {\tilde{r}a_{17} + a_{13} } \right)x^{2} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} + \left( {\frac{{(\varrho_{2} - a_{11} )a_{14} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} - \frac{{a_{23} }}{{\varrho_{2} + 1}}} \right)xy \\ & \quad + \left( {\frac{{\left( {\varrho_{2} - a_{11} } \right)\tilde{r}a_{16} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} - \frac{{\tilde{r}a_{24} }}{{\varrho_{2} + 1}}} \right)x + O\left( {\left( {\left| u \right| + \left| v \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right), \\ \end{aligned} $$

$$ \begin{aligned} \mathbb{g}_{2} \left( {u, v, \tilde{r}} \right) & = \frac{{\left( {1 + a_{11} } \right)a_{15} x^{3} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} + \frac{{\left( {1 + a_{11} } \right)\left( {\tilde{r}a_{17} + a_{13} } \right)x^{2} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} + \left( {\frac{{\left( {1 + a_{11} } \right)a_{14} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} + \frac{{a_{23} }}{{\varrho_{2} + 1}}} \right)xy \\ & \quad + \left( {\frac{{\left( {1 + a_{11} } \right)\tilde{r}a_{16} }}{{a_{12} \left( {\varrho_{2} + 1} \right)}} + \frac{{\tilde{r}a_{24} }}{{\varrho_{2} + 1}}} \right)x + O\left( {\left( {\left| u \right| + \left| v \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right). \\ \end{aligned} $$

$$ x = a_{12} \left( {u + v} \right),\quad y = - \left( {1 + a_{11} } \right)u + \left( {\varrho_{2} - a_{11} } \right)v. $$

In view of the system (3.16), when evaluated at $\left( {0,0} \right)$ in a vicinity of $\tilde{r} = 0$, the center manifold $W^{c} \left( {0, 0, 0} \right)$ can be estimated as follows:

$W^{c} \left( {0, 0, 0} \right) = \left\{ {\left( {u, v, \tilde{r}} \right) \in {\mathbb{R}}^{3} :v = h_{1} u^{2} + h_{2} u\tilde{r} + h_{3} \tilde{r}^{2} + O\left( {\left( {\left| u \right| + \left| {\tilde{r}} \right|} \right)^{3} } \right)} \right\}$, where

$$ h_{1} = \frac{{\left( {1 + a_{11} } \right)\left( {a_{11} a_{14} - a_{12} a_{13} + a_{12} a_{23} + a_{14} } \right)}}{{\varrho_{2}^{2} - 1}},h_{2} = - \frac{{a_{11} a_{16} + a_{12} a_{24} + a_{16} }}{{1 - \varrho_{2}^{2} }}, h_{3} = 0. $$

Thus, the mapping constrained to the central manifold $W^{c} \left( {0, 0, 0} \right)$ can be expressed as follows:

$F:u \to - u + s_{1} u\tilde{r} + s_{2} u^{2} + s_{3} u^{2} \tilde{r} + s_{4} u\tilde{r}^{2} + s_{5} u^{3} + O\left( {\left( {\left| u \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right),$ where

$$ \left\{ {\begin{array}{*{20}l} {s_{1} : = \frac{{{\varrho }_{2} a_{16} - a_{12} a_{24} - a_{11} a_{16} }}{{{\varrho }_{2} + 1}},} \hfill \\ {s_{2} : = \frac{{\left( {{\varrho }_{2} - a_{11} } \right)a_{12} a_{13} }}{{{\varrho }_{2} + 1}} + \left( {\frac{{\left( {{\varrho }_{2} - a_{11} } \right)a_{14} }}{{a_{12} \left( {{\varrho }_{2} + 1} \right)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)\left( { - 1 - a_{11} } \right)a_{12} ,} \hfill \\ {s_{3} : = \frac{{2({\varrho }_{2} - a_{11} )a_{12} a_{13} h_{2} }}{{{\varrho }_{2} + 1}} + \frac{{({\varrho }_{2} - a_{11} )a_{12} a_{17} }}{{{\varrho }_{2} + 1}} + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{14} }}{{a_{12} \left( {{\varrho }_{2} + 1} \right)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)({\varrho }_{2} - a_{11} )a_{12} h_{2} } \hfill \\ {\quad \quad + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{14} }}{{a_{12} ({\varrho }_{2} + 1)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)\left( { - 1 - a_{11} } \right)a_{12} h_{2} + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{16} }}{{a_{12} \left( {{\varrho }_{2} + 1} \right)}} - \frac{{a_{24} }}{{{\varrho }_{2} + 1}}} \right)a_{12} h_{1} ,} \hfill \\ {s_{4} : = \frac{{2({\varrho }_{2} - a_{11} )a_{12} a_{13} h_{3} }}{{{\varrho }_{2} + 1}} + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{14} }}{{a_{12} \left( {{\varrho }_{2} + 1} \right)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)({\varrho }_{2} - a_{11} )a_{12} h_{3} } \hfill \\ {\quad \quad + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{14} }}{{a_{12} ({\varrho }_{2} + 1)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)\left( { - 1 - a_{11} } \right)a_{12} h_{3} + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{16} }}{{a_{12} \left( {{\varrho }_{2} + 1} \right)}} - \frac{{a_{24} }}{{{\varrho }_{2} + 1}}} \right)a_{12} h_{2} ,} \hfill \\ {s_{5} : = \frac{{({\varrho }_{2} - a_{11} )a_{12}^{2} a_{15} }}{{{\varrho }_{2} + 1}} + \frac{{2({\varrho }_{2} - a_{11} )a_{12} a_{13} h_{1} }}{{{\varrho }_{2} + 1}} + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{14} }}{{a_{12} \left( {{\varrho }_{2} + 1} \right)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)({\varrho }_{2} - a_{11} )a_{12} h_{1} } \hfill \\ {\quad \quad + \left( {\frac{{({\varrho }_{2} - a_{11} )a_{14} }}{{a_{12} ({\varrho }_{2} + 1)}} - \frac{{a_{23} }}{{{\varrho }_{2} + 1}}} \right)\left( { - 1 - a_{11} } \right)a_{12} h_{1} .} \hfill \\ \end{array} } \right. $$

In present context, we define two distinct real numbers which are not equal to zero as follows:

$$ l_{1} = \left( {\frac{{\partial^{2} f}}{{\partial u\partial \tilde{r}}} + \frac{1}{2}\frac{\partial F}{{\partial \tilde{r}}}\frac{{\partial^{2} F}}{{\partial u^{2} }}} \right)_{{\left( {0, 0} \right)}} = \frac{{\varrho_{2} a_{16} - a_{12} a_{24} - a_{11} a_{16} }}{{\varrho_{2} + 1}} \ne 0. $$

$$ l_{2} = \left( {\frac{1}{6}\frac{{\partial^{3} F}}{{\partial u^{3} }} + \left( {\frac{1}{2}\frac{{\partial^{2} F}}{{\partial u^{2} }}} \right)^{2} } \right)_{{\left( {0, 0} \right)}} = s_{5} + s_{1}^{2} \ne 0. $$

As a result of the aforementioned investigations, we have derived the following result.

Theorem 3.3

The dynamical system (1.2) undergoes a period-doubling bifurcation at $\left( {u^{*} , v^{*} } \right)$ when the parameter $r$ varies within a small range of $r_{1}$, provided that $l_{2} \ne 0$. Additionally, the resulting period-two orbits are stable if $l_{2} > 0$ and unstable if $l_{2} < 0$.

3.4 Neimark–Sacker Bifurcation

The objective of this section involves an examination into the Neimark–Sacker bifurcation phenomenon exhibited by the system (1.2) at the state $\left( {u^{*} , v^{*} } \right)$, achieved through the utilization of the parameter $r$ in the capacity of the bifurcation parameter. This study entails a comprehensive examination of the bifurcation theory for discrete-time dynamical systems, which builds upon prior research conducted by the authors [42,43,44,45,46]. The Neimark–Sacker bifurcation is a noteworthy phenomenon observed in iterated maps. This transition occurs when the parameter of the system is varied, causing the attracting equilibrium to lose stability and dynamically closed curves to emerge. As a consequence, a small number of isolated periodic orbits and trajectories that densely fill these closed invariant curves have been identified [47]. The properties of system (1.2) have been investigated in the presence of a non-hyperbolic fixed point characterized by a pair of complex conjugate eigenvalues with unit modulus. In light of Eq. (3.8), it can be inferred that ${\mathbb{H}}\left( \varrho \right) = 0$ will possess two complex conjugate roots with a modulus of unity provided that the following conditions hold true.and

$$ r: = \frac{{d\left( {\left( {1 - c} \right)\left( {1 + d\beta } \right)^{2} + \alpha \left( {1 + 2d\beta } \right)} \right)}}{{\left( {d - 2} \right)\left( {1 + d\beta } \right)^{2} }} $$

$$ \left| {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{r}{d}} \right| < 2. $$

(3.17)

Considering the following map:

$$ \Omega_{{{\mathcal{N}\mathcal{B}}}} = \left\{ {\left( {r, b, c, d,\alpha , \beta } \right):\left( {3.17} \right)\;{\text{holds}}\;{\text{with}}\;r: = \frac{{d\left( {\left( {1 - c} \right)\left( {1 + d\beta } \right)^{2} + \alpha \left( {1 + 2d\beta } \right)} \right)}}{{\left( {d - 2} \right)\left( {1 + d\beta } \right)^{2} }} } \right\}. $$

The Neimark–Sacker bifurcation gives rise to the equilibrium point $\left( {u^{*} , v^{*} } \right)$ of system (1.2) for various parametric values in a small neighborhood of the set $\Omega_{{{\mathcal{N}\mathcal{B}}}}$. By selecting arbitrary parameters $\left( {r_{2} , b, c, d,\alpha , \beta } \right)$ from the set $\Omega_{{{\mathcal{N}\mathcal{B}}}}$, where $r_{2} = \frac{{d\left( {\left( {1 - c} \right)\left( {1 + d\beta } \right)^{2} + \alpha \left( {1 + 2d\beta } \right)} \right)}}{{\left( {d - 2} \right)\left( {1 + d\beta } \right)^{2} }}.$ we examine system (1.2) with these parameters and obtain the following map:

$$ \left( {\begin{array}{*{20}c} {\mathcal{M}} \\ {\mathcal{N}} \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {r_{2} {\mathcal{M}}\left( {1 - {\mathcal{M}}} \right) + c{\mathcal{M}} - b{\mathcal{M}\mathcal{N}} - \frac{{\alpha {\mathcal{M}}^{2} }}{{{\mathcal{M}} + \beta }}} \\ {d{\mathcal{M}\mathcal{N}}} \\ \end{array} } \right) $$

(3.18)

Taking the perturbation of map (3.18) with respect to the choice of $\overline{r}$ as a bifurcation parameter yields the following map:

$$ \left( {\begin{array}{*{20}c} {\mathcal{M}} \\ {\mathcal{N}} \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {(r_{2} + \overline{r}){\mathcal{M}}\left( {1 - {\mathcal{M}}} \right) + c{\mathcal{M}} - b{\mathcal{M}\mathcal{N}} - \frac{{\alpha {\mathcal{M}}^{2} }}{{{\mathcal{M}} + \beta }}} \\ {d{\mathcal{M}\mathcal{N}}} \\ \end{array} } \right) $$

In this study, we choose $\left| {\overline{r}} \right| \ll 1$ as a small perturbation parameter.

In this study, we propose the introduction of a set of transformations denoted by $x = {\mathcal{M}} - x^{*}$ and $y = {\mathcal{N}} - y^{*}$. Here, $\left( {x^{*} , y^{*} } \right)$ represents the interior fixed point. Subsequently, the reformulated form of map (3.18) can be expressed as follows:

$$ \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} {m_{11} } & \quad {m_{12} } \\ {m_{21} } &\quad {m_{22} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\mathbb{f}_{3} \left( {x, y} \right)} \\ {\mathbb{g}_{3} \left( {x, y} \right)} \\ \end{array} } \right), $$

(3.19)

where

$$ \mathbb{f}_{3} \left( {x, y} \right) = m_{13} x^{2} + m_{14} xy + m_{15} x^{3} + O\left( {\left( {\left| x \right| + \left| y \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right), $$

$$ \mathbb{g}_{3} \left( {x, y} \right) = m_{23} xy + O\left( {\left( {\left| x \right| + \left| y \right| + \left| {\tilde{r}} \right|} \right)^{4} } \right), $$

and $m_{11} , m_{12} , m_{21} , m_{22} , m_{13} , m_{14} , m_{15}$ and $m_{23}$ are given in (3.14) by replacing $m_{ij} = a_{ij} , i = 1,2 ;j = 1,2,3,4,5$ and $r_{1}$ by $r_{2} + \overline{r}.$ The characteristic equation for the Jacobian matrix of the linearized system represented by Eq. (3.19) can be expressed in the following form when evaluated at the equilibrium point (0,0) is

$$ \varrho^{2} - p\left( {\overline{r}} \right)\varrho + q\left( {\overline{r}} \right) = 0, $$

(3.20)

where

$$ p\left( {\overline{r}} \right) = \left( {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{{r_{2} + \overline{r}}}{d}} \right) {\text{and}} q\left( {\overline{r}} \right) = c + \frac{{\left( {d - 2} \right)(r_{2} + \overline{r})}}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }}. $$

Since $\left( {r_{2} , b, c, d,\alpha , \beta } \right) \in \Omega_{{{\mathcal{N}\mathcal{B}}}} ,$ the solutions of (3.20) are complex conjugate $\varrho_{1} ,\varrho_{2}$ with $\left| {\varrho_{1} } \right| = \left| {\varrho_{2} } \right| = 1.$ Consequently, as a result $\varrho_{1} ,\varrho_{2}$ are

$$ \varrho_{1} ,\varrho_{2} = \frac{{p\left( {\overline{r}} \right)}}{2} \pm \frac{i}{2}\sqrt {4q\left( {\overline{r}} \right) - p^{2} \left( {\overline{r}} \right)} . $$

Subsequently, we acquire

$$ \left| {\varrho_{1} } \right| = \left| {\varrho_{2} } \right| = \sqrt {q\left( {\overline{r}} \right)} ; \left( {\frac{{d\left| {\varrho_{1} } \right|}}{{d\overline{r}}}} \right)_{{\left( {\overline{r} = 0} \right)}} = \left( {\frac{{d\left| {\varrho_{2} } \right|}}{{d\overline{r}}}} \right)_{{\left( {\overline{r} = 0} \right)}} = \frac{d - 2}{{2d\sqrt {c + \frac{{\left( {d - 2} \right)r_{2} }}{d} - \frac{{\alpha \left( {1 + 2d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }}} }}. $$

Additionally, it is assumed that $p\left( 0 \right) = \left( {1 + \frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{{r_{2} }}{d}} \right) \ne 0, - 1.$ Moreover, the parameters $\left( {r_{2} , b, c, d,\alpha , \beta } \right) \in \Omega_{{{\mathcal{N}\mathcal{B}}}}$ indicates that $- 2 < p\left( 0 \right) < 2.$ therefore $p\left( 0 \right) \ne \pm 2, 0, - 1$ implies $\varrho_{1}^{n} , \varrho_{2}^{n} \ne 1$ for all $n = 1, 2, 3, 4$ at $\overline{r} = 0.$ Thus, the roots of Eq. (3.20) are not located within the intersection of the unit circle and the coordinate axes under the condition that $\overline{r} = 0$ and certain criteria are met.

$$ 1 + \frac{{1 + d\beta \left( {2 + d\beta - \alpha } \right)}}{{\left( {1 + d\beta } \right)^{2} }} \ne \frac{{r_{2} }}{d}, 2 + \frac{{1 + d\beta \left( {2 + d\beta - \alpha } \right)}}{{\left( {1 + d\beta } \right)^{2} }} \ne \frac{{r_{2} }}{d}. $$

(3.21)

To discuss the normal form of (3.21) at $\overline{r} = 0,$ we take $\gamma = \frac{p\left( 0 \right)}{2},$ $\delta = \frac{1}{2}\sqrt {4q\left( 0 \right) - p^{2} \left( 0 \right)}$ attains only if we elaborate the following transformation:

$$ \left( {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {m_{12} } & \quad 0 \\ {\gamma - m_{11} } &\quad { - \delta } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right). $$

(3.22)

Upon applying transformation (3.22), it is possible to express the normal form of (3.19) as:

$$ \left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) \mapsto \left( {\begin{array}{*{20}c} \gamma & { - \delta } \\ \delta & \gamma \\ \end{array} } \right)\left( {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {{\tilde{\mathbb{f}}}\left( {u, v} \right)} \\ {{\tilde{\mathbb{g}}}\left( {u, v} \right)} \\ \end{array} } \right). $$

where

$$ {\tilde{\mathbb{f}}}\left( {u, v} \right) = \frac{{m_{15} }}{{m_{12} }}x^{3} + \frac{{m_{13} }}{{m_{12} }}x^{2} + \frac{{m_{14} }}{{m_{12} }}xy + O\left( {\left( {\left| u \right| + \left| v \right|} \right)^{4} } \right), $$

$$ {\tilde{\mathbb{g}}}\left( {u, v} \right) = \frac{{\left( {\gamma - m_{11} } \right)m_{15} }}{{\delta m_{12} }}x^{3} + \frac{{\left( {\gamma - m_{11} } \right)m_{13} }}{{\delta m_{12} }}x^{2} + \left( {\frac{{\left( {\gamma - m_{11} } \right)m_{14} }}{{\delta m_{12} }} - \frac{{m_{23} }}{\delta }} \right)xy + O\left( {\left( {\left| u \right| + \left| v \right|} \right)^{4} } \right), $$

$x = m_{12} u$ and $y = \left( {\gamma - m_{11} } \right)u - \delta v.$ In accordance with established conventions, we hereby define ${\mathcal{L}} \ne 0$ as a member of the set of real numbers.

$$ {\mathcal{L}} = \left( {\left[ { - Re\left( {\frac{{\left( {1 - 2\varrho_{1} } \right)\varrho_{2}^{2} }}{{1 - \varrho_{1} }}\eta_{20} \eta_{11} } \right) - \frac{1}{2}\left| {\eta_{11} } \right|^{2} + \left| {\eta_{02} } \right|^{2} + Re\left( {\varrho_{2} \eta_{21} } \right)} \right]} \right)_{{\overline{r} = 0}} . $$

where

$$ \eta_{11} : = \frac{1}{4}\left[ {{\tilde{\mathbb{f}}}_{uu} + {\tilde{\mathbb{f}}}_{vv} + i\left( {{\tilde{\mathbb{g}}}_{uu} + {\tilde{\mathbb{g}}}_{vv} } \right)} \right]. $$

$$ \eta_{02} : = \frac{1}{8}\left[ {{\tilde{\mathbb{f}}}_{uu} - {\tilde{\mathbb{f}}}_{vv} - 2{\tilde{\mathbb{g}}}_{uv} + i\left( {{\tilde{\mathbb{g}}}_{uu} - {\tilde{\mathbb{g}}}_{vv} + 2{\tilde{\mathbb{f}}}_{uv} } \right)} \right]. $$

$$ \eta_{20} : = \frac{1}{8}\left[ {{\tilde{\mathbb{f}}}_{uu} - {\tilde{\mathbb{f}}}_{vv} + 2{\tilde{\mathbb{g}}}_{uv} + i\left( {{\tilde{\mathbb{g}}}_{uu} - {\tilde{\mathbb{g}}}_{vv} - 2{\tilde{\mathbb{f}}}_{uv} } \right)} \right]. $$

$$ \eta_{21} : = \frac{1}{16}\left[ {{\tilde{\mathbb{f}}}_{uuu} + {\tilde{\mathbb{f}}}_{uvv} + {\tilde{\mathbb{g}}}_{uuv} + {\tilde{\mathbb{g}}}_{vvv} + i\left( {{\tilde{\mathbb{g}}}_{uuu} + {\tilde{\mathbb{g}}}_{uvv} - {\tilde{\mathbb{f}}}_{uuv} - {\tilde{\mathbb{f}}}_{vvv} } \right)} \right]. $$

Upon conducting a detailed investigation as previously mentioned, we have obtained precise results as cited in references [48,49,50,51,52].

Theorem 3.4

Assuming that condition (3.21) is satisfied and ${\mathcal{L}}$ is not equal to zero, the system (1.2) will undergo a Neimark–Sacker bifurcation at the interior equilibrium point $\left( {u^{*} , v^{*} } \right)$ as the parameter $r$ varies within a small vicinity of $r_{2} = \frac{{d\left( {\left( {1 - c} \right)\left( {1 + d\beta } \right)^{2} + \alpha \left( {1 + 2d\beta } \right)} \right)}}{{\left( {d - 2} \right)\left( {1 + d\beta } \right)^{2} }}$. Additionally, if ${\mathcal{L}} < 0$, an attractive invariant closed curve will bifurcate from the equilibrium point when $r$ is less than $r_{2}$, whereas if ${\mathcal{L}}$ is greater than zero, a repelling invariant closed curve will bifurcate from the equilibrium point when $r$ is greater than $r_{2}$.

4 Chaos control

The management of chaos in discrete dynamical systems is an indispensable technique for sustaining or stabilizing unstable and chaotic behavior in intricate systems. Discrete dynamical systems undergo a series of discrete and deterministic steps, and their behavior can exhibit high levels of complexity and unpredictability. Chaos control approaches strive to control the state and parameters of the system to direct it towards the desired state or stabilize chaotic behavior and transform it into a more organized state. In scientific terms, chaos control techniques are employed to circumvent erratic and unfavorable behavior in systems that display chaotic or unstable dynamics. These techniques operate by introducing slight perturbations or manipulating system parameters to stave off the onset of chaos and maintain a more predictable state.

In the present section, we introduce two distinct feedback control approaches intended to facilitate the transition of unstable trajectories towards stable trajectories.

4.1 OGY Control Method

In this section, we utilize the OGY method introduced by Ott et al. [53, 54] to analyze the system (1.2). The OGY method is applied to the system, leading to a modified version expressed as:

$$ \begin{aligned} u_{n + 1} & = ru_{n} \left( {1 - u_{n} } \right) + cu_{n} - bu_{n} v_{n} - \frac{{\alpha u_{n}^{2} }}{{u_{n} + \beta }} = f\left( {u_{n} , v_{n} , r} \right) \\ v_{n + 1} & = du_{n} v_{n} = g\left( {u_{n} , v_{n} , r} \right), \\ \end{aligned} $$

(4.1)

In this study, the variable $r$ is employed as the control parameter. To ensure desired control through the implementation of small perturbations, we limit the range of $r$ to a narrow interval of $r \in \left( {r_{0} - \mu , r_{0} + \mu } \right)$, wherein $r_{0}$ denotes the nominal value within the chaotic region. The objective of our study is to guide the system trajectory towards the desired orbit using a stabilizing feedback control strategy. Additionally, assuming that the system (1.2) exhibits an unstable equilibrium point $\left( {u^{*} , v^{*} } \right)$ in a chaotic region due to the Neimark–Sacker bifurcation, we propose to utilize a linear map to approximate the system (4.1) in the vicinity of the unstable equilibrium $\left( {u^{*} , v^{*} } \right)$ as follows:

$$ \left[ {\begin{array}{*{20}c} {u_{n + 1} - u^{*} } \\ {v_{n + 1} - v^{*} } \\ \end{array} } \right] \approx J\left( {u^{*} , v^{*} , r_{0} } \right)\left[ {\begin{array}{*{20}c} {u_{n} - u^{*} } \\ {v_{n} - v^{*} } \\ \end{array} } \right] + B\left[ {r - r_{0} } \right] $$

(4.2)

where

$$ J\left( {u^{*} , v^{*} , r_{0} } \right) = \left[ {\begin{array}{*{20}c} {\frac{{\partial f\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial u}} & {\frac{{\partial f\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial v}} \\ {\frac{{\partial g\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial u}} & {\frac{{\partial g\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial v}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{{1 + d\beta \left( {2 - \alpha + d\beta } \right)}}{{\left( {1 + d\beta } \right)^{2} }} - \frac{{r_{0} }}{d}} & { - \frac{b}{d}} \\ {\frac{{\left( {1 + d\beta } \right)\left[ {d\left( {c + r_{0} - 1} \right) - r_{0} } \right] - \alpha d}}{{b\left( {1 + d\beta } \right)}}} & 1 \\ \end{array} } \right] $$

and

$$ B = \left[ {\begin{array}{*{20}c} {\frac{{\partial f\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial r}} \\ {\frac{{\partial g\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial r}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{d - 1}{{d^{2} }}} \\ 0 \\ \end{array} } \right] $$

Moreover, the controllable system (4.1) yields the following matrix

$$ C = \left[ {B: JB} \right] = \left[ {\begin{array}{*{20}c} {\frac{d - 1}{{d^{2} }}} & {\left( {\frac{{\partial f\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial u}} \right)\left( {\frac{d - 1}{{d^{2} }}} \right)} \\ 0 & {\left( {\frac{{\partial g\left( {u^{*} , v^{*} , r_{0} } \right)}}{\partial u}} \right)\left( {\frac{d - 1}{{d^{2} }}} \right)} \\ \end{array} } \right] $$

is of rank 2.

Moreover, by choosing $\left[ {r - r_{0} } \right] = - K\left[ {\begin{array}{*{20}c} {u_{n} - u^{*} } \\ {v_{n} - v^{*} } \\ \end{array} } \right],$ where $K = \left[ {\begin{array}{*{20}c} {k_{1} } & {k_{2} } \\ \end{array} } \right],$ then (4.2) can be written as

$$ \left[ {\begin{array}{*{20}c} {u_{n + 1} - u^{*} } \\ {v_{n + 1} - v^{*} } \\ \end{array} } \right] \approx \left[ {J - BK} \right]\left[ {\begin{array}{*{20}c} {u_{n} - u^{*} } \\ {v_{n} - v^{*} } \\ \end{array} } \right] $$

Additionally, the corresponding regulated system for Eq. (1.2) is presented as:

$$ \begin{aligned} u_{n + 1} & = u_{n} \left( {1 - u_{n} } \right)\left[ {r_{0} - k_{1} \left( {u_{n} - u^{*} } \right) - k_{2} \left( {v_{n} - v^{*} } \right)} \right] + cu_{n} - bu_{n} v_{n} - \frac{{\alpha u_{n}^{2} }}{{u_{n} + \beta }} \\ v_{n + 1} & = du_{n} v_{n} . \\ \end{aligned} $$

(4.3)

Furthermore, the asymptotic stability of $\left( {u^{*} , v^{*} } \right)$ is guaranteed when both eigenvalues of '$J - BK$' lie within an open unit disk. The system (4.3) can be expressed in terms of '$J - BK$' as follows:

$$ J - BK = \left[ {\begin{array}{*{20}c} {\omega_{11} } & {\omega_{12} } \\ {\omega_{21} } & {\omega_{22} } \\ \end{array} } \right]. $$

The equation describing the characteristic properties of '$J - BK$' is expressed as follows:

$$ {{\mathbb{p}}}\left( \varrho \right) = \varrho^{2} - \left( {\omega_{11} + \omega_{22} } \right)\varrho + {\Delta } = 0, $$

where

$$ \omega_{11} = \frac{{d\left( { - r_{0} + d\left( {1 + \beta \left( {d^{2} \beta - 2r_{0} - d\left( {\alpha - 2 + r_{0} \beta } \right)} \right)} \right)} \right) - \left( {d - 1} \right)\left( {1 + d\beta } \right)^{2} k_{1} }}{{d^{2} \left( {1 + d\beta } \right)^{2} }}, \omega_{22} = 1, $$

$$ \omega_{12} = \frac{{k_{2} - d\left( {b + k_{2} } \right)}}{{d^{2} }}, \omega_{21} = \frac{{\left( {1 + d\beta } \right)\left[ {d\left( {c + r_{0} - 1} \right) - r_{0} } \right] - \alpha d}}{{b\left( {1 + d\beta } \right)}}. $$

$$ {\Delta } = \omega_{11} \omega_{22} - \omega_{12} \omega_{21} , $$

$$ {\mathbb{L}}_{1} : {{\mathbb{p}}}\left( 1 \right) = 0 \Rightarrow {\Delta } - \omega_{11} = 0 \Rightarrow \omega_{12} \omega_{21} = 0, $$

$$ {\mathbb{L}}_{2} : {{\mathbb{p}}}\left( { - 1} \right) = 0 \Rightarrow 2(1 + \omega_{11} ) - \omega_{12} \omega_{21} = 0, $$

$$ {\mathbb{L}}_{3} : {{\mathbb{p}}}\left( 0 \right) = 1 \Rightarrow {\Delta } = \omega_{11} \omega_{22} - \omega_{12} \omega_{21} = 1. $$

4.2 Hybrid Control Method

In this section, we employ the Hybrid control approach to regulate the chaotic behavior resulting from the bifurcation phenomenon in System (1.2). The Hybrid control technique was initially developed to govern chaos in the presence of period-doubling bifurcation. Additionally, the identical approach is employed to regulate Neimark–Sacker bifurcation, for more details, see [55, 56]. Given that the system represented by Eq. (1.2) experiences a bifurcation at $\left( {u^{*} , v^{*} } \right)$, the modified controlled system can be expressed as:

$$ \begin{aligned} u_{n + 1} & = \rho \left[ {ru_{n} \left( {1 - u_{n} } \right) + cu_{n} - bu_{n} v_{n} - \frac{{\alpha u_{n}^{2} }}{{u_{n} + \beta }}} \right] + \left( {1 - \rho } \right)u_{n} \\ v_{n + 1} & = \rho \left[ {du_{n} v_{n} } \right] + \left( {1 - \rho } \right)v_{n} . \\ \end{aligned} $$

(4.4)

The parameter $\rho$ is confined to the interval $(\mathrm{0,1})$. It is noteworthy that the controlled approach specified in Eq. (4.4) encompasses both feedback control and perturbation parameter. Moreover, through the selection of an appropriate value for the controlled parameter $\rho$, the bifurcation of $\left({u}^{*}, {v}^{*}\right)$ in the controlled system (4.4) can be shifted earlier or postponed, or even eradicated entirely. For further information, please refer to [57,58,59]. The expression denoting the Jacobian matrix of system (4.4), evaluated at the point $\left({u}^{*}, {v}^{*}\right)$, can be represented as follows:

$$ J\left( {u^{*} , v^{*} } \right) = \left[ {\begin{array}{*{20}c} {\delta_{11} } & \quad {\delta_{12} } \\ {\delta_{21} } & \quad{\delta_{22} } \\ \end{array} } \right]. $$

The characteristic equation of the system (4.4) is an essential component that warrants investigation in scientific inquiry and is defined as; ${\varrho }^{2}-\left({\delta }_{22}+{\delta }_{11}\right)\varrho +{\mathbb{D}}=0,$ where

$$ \delta_{11} = 1 - \frac{{\left( {d^{2} \alpha \beta + r\left( {1 + d\beta } \right)^{2} } \right)\rho }}{{d\left( {1 + d\beta } \right)^{2} }}, \delta_{12} = - \frac{b\rho }{d}, \delta_{21} = \frac{{d\left( {c + r - 1 - \frac{r}{d} - \frac{\alpha }{1 + d\beta }} \right)\rho }}{b},\delta_{22} = 1. $$

$$ {\mathbb{D}} = 1 + \frac{{\left( {\left( {1 + d\beta } \right)\left( {c - \alpha - 1 + \left( {c - 1} \right)d\beta } \right)\rho - d\alpha \beta } \right)\rho }}{{\left( {1 + d\beta } \right)^{2} }} + \frac{{r\rho \left( {\left( { - 1 + d} \right)\rho - 1} \right)}}{d}. $$

The subsequent outcome provides criteria for the local asymptotic stability of the positive equilibrium point $\left({u}^{*}, {v}^{*}\right)$ in the controlled system (4.4).

Lemma 4.1

The interior equilibrium point $\left({u}^{*}, {v}^{*}\right)$ of the controlled system (4.4) is locally asymptotically stable, if the following assumption holds:

$$\left|{\delta }_{22}+{\delta }_{11}\right|<1+{\mathbb{D}}<2.$$

5 Numerical Simulation and Discussion

This particular section is devoted to the validation of our theoretical and mathematical conclusions. In this section, we present a series of empirical illustrations to substantiate our aforementioned work. Our aim is to demonstrate the practical relevance and applicability of our theoretical framework through examples. These examples not only serve as a test of the validity of our theory but also provide insights into the potential impact of our research on practical applications. Through the analysis of these instances, an evaluation of the durability and applicability of our theoretical and mathematical frameworks across diverse contexts and scenarios can be undertaken.

Example 5.1

Choosing parameters $\beta =0.18, b=0.2, c=0.56, d=1.5, \alpha =0.5, r\in [2, 3.75]$ and with initial conditions $\left({u}_{0}, {v}_{0}\right)= \left(0.666, 0.01\right),$ then system (1.2) undergoes period-doubling bifurcation as $r\approx 2.998898877797755$. Figure 3a and b portray the bifurcation diagram and Maximum Lyapunov Exponents (MLE) of the dynamic system denoted as (1.2). The bifurcation diagram serves as a visual representation illustrating the dynamic tendencies of the system, with specific focus on its stability characteristics and pivotal bifurcation junctures. Conversely, the MLE quantifies the velocity of divergence among proximate trajectories within the system’s phase space. This metric offers insights into the system’s responsiveness to initial conditions and its propensity for exhibiting chaotic behavior. These graphical representations assume a pivotal role as indispensable analytical tools, facilitating the comprehensive examination and comprehension of the intricate behaviors exhibited by the system. Additionally, the system indexed as (1.2) encompasses an interior equilibrium point, precisely defined as $\left({u}^{*}, {v}^{*}\right)=(0.66666, 0.82966)$. The characteristic equation of the Jacobian matrix evaluated at this equilibrium point is provided as follows:

$$ \varrho^{2} + 0.08296608593217147\varrho - 0.9170339140678279 = 0 $$

(5.1)

Fig. 3

Bifurcation diagram, MLE and controllable region diagrams, when $\beta =0.18, b=0.2, c=0.56, d=1.5, \alpha =0.5, r\in [2, 3.75]$, $\left({u}_{0}, {v}_{0}\right)= \left(0.666, 0.01\right)$. a Bifurcation diagram of prey population b MLE c Stability controlled region for system (5.2)

Furthermore, the solutions of (5.1) are ${\varrho }_{1}=-1$ and ${\varrho }_{2}=0.9170339140678282$ with $\left|{\varrho }_{2}\right|\ne 1.$ Thus the parameters $\left(r, b, c, d,\alpha , \beta \right)=\left(2.998898877797755, 0.2, 0.56, 1.5, 0.5, 0.18\right)\in {\Omega }_{\mathcal{P}\mathcal{B}}.$

The subsequent phase entails the application of the Ott–Grebogi–Yorke (OGY) control methodology to govern the chaotic dynamics arising from the manifestation of period-doubling bifurcation phenomena. In particular, we choose the values of the system parameters as follows: $r=3.7, \beta =0.18, b=0.2, c=0.56, d=1.5, \alpha =0.5,$ we identify a unique positive equilibrium point $\left({u}^{*}, {v}^{*}\right)= \left(0.667, 0.829\right)$ as the target state for our control strategy. Based on these choices, we derive the equivalent controlled system by:

$$ \left. {\begin{array}{*{20}l} {u_{n + 1} = u_{n} \left( {1 - u_{n} } \right)\left[ {3.7 - k_{1} \left( {u_{n} - 0.667} \right) - k_{2} \left( {v_{n} - 0.829} \right)} \right] + 0.56u_{n} - 0.2u_{n} v_{n} - \frac{{0.5u_{n}^{2} }}{{u_{n} + 0.18}}} \hfill \\ {v_{n + 1} = 1.5u_{n} v_{n} . } \hfill \\ \end{array} } \right\} $$

(5.2)

Then, ‘${\text{J}} - {\text{BK}}$’ of the controlled system (5.2) can be evaluated as follows:

$$ J - BK = \left[ {\begin{array}{*{20}c} { - 1.550367 - 0.2222k_{1} } & { - 0.13333 - 0.2222k_{2} } \\ {2.997244094488188} & 1 \\ \end{array} } \right]. $$

Moreover, ${\mathbb{L}}_{1} , {\mathbb{L}}_{2}$ and ${\mathbb{L}}_{3}$ represents the marginal stability lines, which are given by

$$ {\mathbb{L}}_{1} : k_{2} = - 0.599999999999999, $$

$$ {\mathbb{L}}_{2} : k_{2} = 0.667279653224746k_{1} + 1.052618655821837, $$

$$ {\mathbb{L}}_{3} : k_{2} = 0.33363982661237307k_{1} + 3.229067767422276. $$

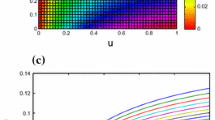
The area enclosed by the marginal lines, which form a triangle, is indicative of the stability region. This region is visually depicted in Fig. 3c.

Bifurcation has important biological implication in predator–prey interactions, as they can indicate the onset of complex dynamics such as oscillations, coexistence and chaos. Period-doubling bifurcation can reflect the phenomenon of population cycles where the prey and predator populations oscillate with a period that doubles as the parameter varies. The occurrence and characteristics of period-doubling bifurcation depend on various factors such as the functional response and environmental parameters. Subsequently, we proceed to once again acquire $\beta =0.18, b=0.2, c=0.56, d=1.5, \alpha =0.5, r\in [2, 3.75]$ and choose initial conditions $\left({u}_{0}, {v}_{0}\right)= \left(0.666, 0.01\right),$ then for the given set of numerical values, the dynamical system described by Eq. (1.2) exhibits period-doubling bifurcation. In order to regulate this bifurcation phenomenon, we employ a hybrid control technique. The resultant system under parallel control can be expressed as follows:

$$ \begin{aligned} u_{n + 1} & = \rho \left[ {2.999u_{n} \left( {1 - u_{n} } \right) + 0.56u_{n} - 0.2u_{n} v_{n} - \frac{{0.5u_{n}^{2} }}{{u_{n} + 0.18}}} \right] + \left( {1 - \rho } \right)u_{n} \\ v_{n + 1} & = \rho \left[ {1.5u_{n} v_{n} } \right] + \left( {1 - \rho } \right)v_{n} . \\ \end{aligned} $$

(5.3)

Table 1 displays the stability interval of the controlled system (5.3) for different values of the bifurcation parameter within the chaotic region. These stability intervals were determined by examining various parametric values.

Table 1 Stability controlled region of system (5.3) where $r$ belongs to chaotic region

In addition, Fig. 5a displays the bifurcation diagrams for system (5.3) under control. It is noteworthy that, while the period-doubling bifurcation is solely discernible in the prey population of system (1.2), it is readily observable in both the prey and predator populations of the controlled system (5.3).

Example 5.2

Let us choose the parameters $\beta =1.2, b=1.2, c=2.6, d=1.51, \alpha =1.61, r\in [1, 2.999]$ and initial conditions $\left({u}_{0}, {v}_{0}\right)= \left(0.667, 1.75\right)$, then the system described by Eq. (1.2), a Neimark–Sacker bifurcation occurs at a critical parameter value of $r\approx 2.029303573581053$. This is demonstrated through the parallel bifurcation diagrams and maximum Lyapunov exponent (MLE) plots shown in Fig. 4a, b, c. Additionally, the system (1.2) possesses a single positive equilibrium point $\left({u}^{*}, {v}^{*}\right)=(0.6211180124, 1.516461115)$. The characteristic equation calculated at $\left({u}^{*}, {v}^{*}\right)$ is given by

$$ \varrho^{2} - 0.37773258620952876\varrho + 1.1974859242784675 = 0 $$

(5.4)

Fig. 4

Selecting $\beta =1.2$, $b=1.2$, $c=2.6$, $d=1.51$, $\alpha =1.61$, $r\in [\mathrm{1,2.999}]$, and initial conditions ${u}_{0}=0.667$, ${v}_{0}=1.75$. a Bifurcation diagram of prey ${u}_{n}$ b bifurcation diagram of predator ${v}_{n}$ c MLE d stability controlled region of system (5.5)

Furthermore, the roots of (5.4) are ${\varrho }_{\mathrm{1,2}}=0.18886629310476438\text{\hspace{0.05em}}\pm 1.0778754323238529i$ with $\left|{\varrho }_{\mathrm{1,2}}\right|=1.$ Thus $\left(r, b, c, d,\alpha , \beta \right)=\left(2.029303573581053, 1.2, 2.6, 1.51, 1.61, 1.2\right)\in {\Omega }_{\mathcal{N}\mathcal{B}}.$

Subsequently, we incorporate the OGY control strategy to manage chaos ensuing from the emergence of the Neimark–Sacker bifurcation. The parameters $r=1.2$, $\beta =1.2$, $b=1.2$, $c=2.6$, $d=1.51$, and $\alpha =1.61$, along with $\left({u}^{*}, {v}^{*}\right)= \left(0.621, 1.516\right)$, are selected to obtain the modified controlled system as follows:

$$ \left. {\begin{array}{*{20}l} {u_{n + 1} = u_{n} \left( {1 - u_{n} } \right)\left[ {1.2 - k_{1} \left( {u_{n} - 0.621} \right) - k_{2} \left( {v_{n} - 1.516} \right)} \right] + 2.6u_{n} - 1.2u_{n} v_{n} - \frac{{1.61u_{n}^{2} }}{{u_{n} + 1.2}}} \hfill \\ {v_{n + 1} = 1.51u_{n} v_{n} . } \hfill \\ \end{array} } \right\} $$

(5.5)

Then, the Jacobian ‘${\text{J}} - {\text{BK}}$’ of the system (5.5) can be expressed in the following form:

$$ J - BK = \left[ {\begin{array}{*{20}c} { - 0.16364003 - 0.2236744k_{1} } & \quad { - 0.7947 - 0.22367k_{2} } \\ {1.802879326695116} & \quad 1 \\ \end{array} } \right]. $$

In addition, the lines of marginal stability denoted as ${\mathbb{L}}_{1} , {\mathbb{L}}_{2}$ and ${\mathbb{L}}_{3}$ are determined by

$$ {\mathbb{L}}_{1} : k_{2} = - 3.552941176470587 - 1.3765 \times 10^{ - 16} k_{1} , $$

$$ {\mathbb{L}}_{2} : k_{2} = 0.5546682937637952k_{1} - 0.6673435991222073, $$

$$ {\mathbb{L}}_{3} : k_{2} = 0.5546682937637952k_{1} - 0.6673439525613608. $$

Figure 4d displays the triangular region of stability defined by ${\mathbb{L}}_{1} , {\mathbb{L}}_{2}$ and ${\mathbb{L}}_{3}$.

Note that the Neimark–Sacker bifurcation can reflect the phenomenon of quasi periodicity where the predator–prey populations oscillate with two or more incommensurate frequencies that are not multiples of each other. Neimark–Sacker bifurcation can lead to irregular chaotic dynamics with implications for population stability, conservation efforts, ecosystem health and the understanding of complex ecological interactions.

Moreover, we once again adopt $\beta = 1.2, b = 1.2, c = 2.6, d = 1.51, \alpha = 1.61, r \in \left[ {1, 2.999} \right]$ with initial conditions $\left( {u_{0} , v_{0} } \right) = \left( {0.667, 1.75} \right)$, then to specific values, the dynamical system described by Eq. (1.2) experiences a Neimark–Sacker bifurcation. To mitigate the chaotic behavior resulting from this bifurcation, we implement a hybrid control strategy. The resulting system is a modified controlled version of the original one.

$$ \begin{gathered} u_{n + 1} = \rho \left[ {2.0293u_{n} \left( {1 - u_{n} } \right) + 2.6u_{n} - 1.2u_{n} v_{n} - \frac{{1.61u_{n}^{2} }}{{u_{n} + 1.2}}} \right] + \left( {1 - \rho } \right)u_{n} \hfill \\ v_{n + 1} = \rho \left[ {1.51u_{n} v_{n} } \right] + \left( {1 - \rho } \right)v_{n} . \hfill \\ \end{gathered} $$

(5.6)

Table 2 displays the stability range of system (5.6) under different parameter values of the bifurcation parameter, obtained by analyzing its behavior in the chaotic region.

Table 2 Stability controlled interval for map (5.6) when $r$ taken from sensitive region

In addition, Fig. 5b illustrates the bifurcation diagrams to the controlled systems (5.6).

Fig. 5

Bifurcation control diagram for maps (5.3) and (5.6). a Bifurcation diagram by using hybrid control method of system (5.3) when $\rho =0.83.$ b Bifurcation diagrams by using hybrid control method of system (5.6) when $\rho =0.812.$

6 Concluding Remarks

Intra-specific predation, colloquially referred to as cannibalism, constitutes a fundamental ecological phenomenon integral to the regulation of population dynamics across a wide spectrum of biological taxa. Extensive investigations have been conducted to elucidate the multifaceted impacts of cannibalism on population dynamics, as documented in previous research [7, 43]. Notably, while cannibalism has the potential to induce population fluctuations [23], it also serves as a mechanism for achieving population equilibrium and management. Given the paramount importance ascribed to cannibalism within prey populations, this study advances and scrutinizes a discrete-time framework that governs the dynamics between predators and prey. The present study utilizes the center manifold theorem and bifurcation theory of normal forms to meticulously examine the dynamics of the mentioned system. This analysis is executed concurrently with the intentional manipulation of the intrinsic prey population growth rate, denoted as $r$, thereby serving as the focal bifurcation parameter. The findings of our investigation incontrovertibly demonstrate the manifestation of transcritical, period-doubling, and Neimark–Sacker bifurcations within the system. Moreover, the results presented in our investigation provide compelling evidence for the significant involvement of cannibalism in the modulation of the cyclic oscillations observed in population dynamics. Through the utilization of numerical simulations, we validate the hypothesis that the incorporation of cannibalistic interactions within the prey population consistently gives rise to periodic epidemic outbreaks. These outbreaks manifest as distinctive recurring patterns exclusively within the prey population, devoid of any discernible impact on the dynamics of the predator population. However, the recurring fluctuations observed in the density of prey populations hold promise for mitigation through the implementation of bifurcation and oscillation control strategies. Employing these methodologies offers the opportunity to regulate the inherent dynamics of the system, thus sustaining its population stability.

In summary, our study underscores the paramount importance of cannibalism as an inherent phenomenon that plays a central role in the regulation of population dynamics. By analyzing the dynamics within a predator–prey system marked by the occurrence of cannibalism, this research demonstrates the emergence of cyclic oscillations in the population density of the prey organisms. Furthermore, it explores strategies aimed at controlling these oscillations. The findings of this investigation have substantial implications for advancing our understanding of the complexities surrounding population dynamics across various biological species, thereby providing insights into their effective management and regulation.

7 Future Directions

We will investigate the corresponding Ordinary Differential Equation (ODE) system of discrete framework discussed above. This analysis will focus on elucidating the influence of cannibalism on the ODE dynamics and conducting a rigorous comparison between the discrete and continuous frameworks to gain deeper insights into cannibalism’s role in population dynamics.