Introduction

The description of the material behavior is a core aspect in the numerical prediction and evaluation of sheet metal forming processes [1]. The plastic flow behavior is classically described by the flow curve and the yield locus together with an appropriate flow rule.

A large number of different tests, e.g. tensile test, plain strain test, layer crush test and hydraulic bulge test, are typically used to identify the model parameters of the flow curve and the yield locus [2]. Each of these tests requires individual sample preparation and tailored evaluation routines [3]. This makes it difficult, in particular for small and medium-sized companies, as well as less well-equipped institutes and laboratories, to acquire their own set of material parameters.

Especially in the field of sheet metal forming up to now only process-specific approaches exist, e.g. [4], which simplify the parameter identification procedures, with regard to sample preparation, measurement technology and laboratory equipment, on the one hand, but do not require complex inverse analysis based on finite element simulations, e.g. [5, 6], on the other hand.

Objective

The aim of this work is to present a fast and cost-effective methodology that allows to identify the material parameters of the flow curve and the yield locus model for sheet metal material with minimal equipment and measurement techniques, efficient sample preparation and without the use of finite element simulations.

To achieve this objective, the three-point bending test is used as an information-rich experiment for data generation. Specimen production and preparation, test execution as well as data recording, i.e. penetration depth and punch force, are all possible with minimal effort and cost. In particular, the limitation of data recording to the integral quantities of force and displacement is helpful in terms of measurement technology and efficient data evaluation, as the recording and evaluation of other (local) measurement quantities in the three-point bending test is a major challenge in itself, see for example [7] with regard to the bending angle, [8] in terms of bendability, and [9] for optical strain measurement.

Fig. 1
figure 1

Parameterization of the bending process according to [13]

Full size image

Approach

The basic approach is to rely on analytical models for parameter identification in order to get by without finite element simulation. Numerous analytical approaches exist for modeling the three-point bending test [10]. Based on analytical models of the three-point bending test for isotropic work hardening materials, e.g. [11, 12], various analytical models have been developed, which can also take into account anisotropy in sheet materials [13, 14].

The approach used in this work is based on the analytical model for analyzing the bending of anisotropic sheet metal materials under plane strain conditions presented in [13], however, due to its generic nature the presented methodology can in principle be used for other analytical models. This also applies to extensions, such as the consideration of kinematic hardening also presented in [13], or the inclusion of tensile stress superposition, see e.g. [15].

The bending process is described in two-dimensional space in cylindrical coordinates, whereby the five radii \(r_i\), \(r_o\), \(r_m\), \(r_u\), and \(r_n\) uniquely define the current state of the bending process for the bending angle \(\alpha \), see Fig. 1. The radius \(r_i\) represents the inner (concave) surface of the sheet metal, the radius \(r_o\) the outer (convex) surface of the sheet metal, the radius \(r_m\) the middle layer, the radius \(r_u\) the unstretched layer and the radius \(r_n\) the neutral layer.

The central equation for describing the three-point bending test according to [13] represents the dimensionless ordinary differential equation

$$\begin{aligned} \frac{d \eta }{d \kappa }=-\frac{\eta }{2 \kappa }\left( e^{-\lambda }-1\right) \end{aligned}$$
(1)

with

$$\begin{aligned} \lambda =\frac{A-B}{C B n}\left( \left( \frac{1+\frac{\kappa }{2}}{\eta }\right) ^{-C n}+2 \rho ^{C n}-2-\left( \frac{1-\frac{\kappa }{2}}{\eta }\right) ^{C n}\right) \end{aligned}$$

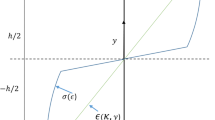
and where \(\eta =t/t_0\) represents the relative thickness, \(\rho =r_n/r_u\) the relative curvature of the neutral layer and \(\kappa =t/r_m\) the relative curvature as a measure for progress in the bending process. Equation 1 was derived using the Voce flow curve model [16] for the true stress \(\sigma \) and true strain \(\varepsilon \) relation with the three parameters A, B, and n

$$\begin{aligned} \sigma =B-(B-A)^{-n \varepsilon } \text { .} \end{aligned}$$

The parameter C in Eq. 1 describes the anisotropy according to [17] and is directly related to the R values, see [13]. For the bending axis along the rolling direction, C reads

$$\begin{aligned} C_0=\sqrt{\frac{\left( 1+R_0\right) \left( \frac{R_{90}}{R_0}+R_{90}\right) }{1+R_0+R_{90}}} \end{aligned}$$
(2)

and

$$\begin{aligned} C_{90}=\sqrt{\frac{\left( 1+R_0\right) \left( 1+R_{90}\right) }{1+R_0+R_{90}}} \end{aligned}$$
(3)

for the bending axis perpendicular to the rolling directions. Since for the bending axis diagonal to the rolling direction quasi-isotopic conditions exits, C reduces to \(C_{45}=2/\sqrt{3}\).

Fig. 2
figure 2

Flow chart of the material parameter identification routine

Full size image

Solving for Eq. 1 given a set of material parameters A, B, n, and C yields the bending moment per unit width for a bending process parameterized by the dimensionless parameter \(\kappa \), see [13]. By introducing the dimensions of the specimen and kinematics of the bending test setup, this further allows to compute punch penetration depth d and by numerical integration over the sheet thickness the bending moment M or punch force F, respectively.

The presented approach for parameter identification only from bending experiments uses the presented model in an optimization routine. Instead of giving a fixed set of material parameters A, B, n, and C, these parameters are identified by means of an optimization with respect to a set of punch displacement and force curves from three-point bending experiments. Here, the bending axis for is oriented parallel (for \(0^{\circ }\) and \(90^{\circ }\) parameters), diagonal (for \(45^{\circ }\) parameters), and perpendicular (for \(0^{\circ }\) and \(90^{\circ }\) parameters) to the rolling direction of the sheet metal to address anisotropy, which yields \(|i|=3\) (\(i=\){\(0^{\circ }\), \(45^{\circ }\), \(90^{\circ }\)}) independent sets of material parameters \(A_i\), \(B_i\), \(n_i\), and \(C_i\). These sets of parameters may be utilized for the flow curve and to derive yield locus parameters based on the contained yield stresses \(A_0 = \sigma _0\), \(A_{45} = \sigma _{45}\), and \(A_{90} = \sigma _{90}\), as well as the R values \(R_0\) and \(R_{90}\) using Eqs. 2 and 3. Since as above-mentioned \(C_{45}=2/\sqrt{3}\), \(R_{45}\) is computed a posteriori using the yield stresses \(\sigma _0\), \(\sigma _{45}\), \(\sigma _{90}\) and the R values \(R_0\) and \(R_{90}\) [18].

In this work, the identified Voce parameters from the three-point bending test with the rolling direction perpendicular to the bending axis is directly used as the flow curve model. Further, the yield stresses and R values are used to calibrate the parameters of the YLD2000-2d yield locus [19].

Fig. 3
figure 3

Experimental results of the conventional characterization. a) Tensile tests, b) Bulge test, c) Plain strain tests, d) Shear tests

Full size image

Optimization

The optimization routine to identify the set of material parameters with respect to the experimental data of the three-point bending experiments uses a least squared error objective function and a sequential quadratic programming algorithm [20]. For experiments with the bending along and perpendicular to the rolling direction the set of optimization variables \(\varphi _i\) has the four elements \(A_i\), \(B_i\), \(n_i\), and \(C_i\) with \(i=\){\(0^{\circ }\), \(90^{\circ }\)}, for experiments with the bending axis diagonal to the rolling direction the three elements \(A_{45}\), \(B_{45}\), and \(n_{45}\). The expression to be minimized with respect to the set of optimization variable \(\varphi _i\) reads

$$\begin{aligned} {\text {argmin}}_{\varphi _i}\left( F_{\text{ exp } }(d)-F_{\text{ mod } }\left( d ; \varphi _i\right) \right) ^2 \text {,} \end{aligned}$$
(4)

where \(F_{\text {exp}}(d)\) represents the experimentally identified punch force with respect to the punch penetration depth d, and \(F_{mod}(d;\varphi _i)\) the model prediction of the punch force for the parameter set \(\varphi _i\). For the computations, an equidistant discretization of d with a step size of \(\Delta d=0.01\) mm has been chosen. The optimization according to Expression Eq. 4 is performed independently for each specimen orientation resulting in three independent optimization runs in the presented work. Figure 2 shows the flow chart of the material parameter identification routine.

Experiments

The material parameter identification in this work was performed for a dual phase steel DP600 with a thickness of 0.83 mm. On the one hand, a conventional material characterization routine has been performed to acquire a reference set of parameters, see Subsection“Conventional characteri-zation”. On the other hand, the material parameters has been identified by the proposed methodology using only the three-point bending test data. The three-point bending test setup is described in Subsection“Three-point bending” along with a finite element simulation of the bending process for a first validation. Both sets of material parameters are then used and compared again in an independent validation experiment, the MUC-test, described in Subsection“Validation experiment”.

Conventional characterization

Material characterization according to the conventional procedure is carried out using quasi-static tensile tests at \(0^{\circ }\), \(45^{\circ }\), and \(90^{\circ }\) with respect to the initial rolling direction, see Fig. 3a). For a more accurate description of the yield locus shear tensile tests (Fig. 3d)) and tensile tests with notched samples (Fig. 3c)) under \(0^{\circ }\), \(45^{\circ }\), and \(90^{\circ }\) with respect to the initial rolling direction were conducted. The geometry of the notched specimen is according to [21, Fig. 4b)], where the geometric parameters are \(\rho =\)1.5mm (notch tip radius), \(a=\)9.0mm (notch depth), \(d=\)18mm (width between notch tips) and \(D=\)36mm (specimen width). The force displacement curves of the tensile tests with notched samples and the shear tensile experiments were used for inverse optimization of the yield locus using FE simulation. The uniaxial flow curve was extrapolated using the bulge test (Fig. 3b)) and the equivalent work method according to DIN EN ISO 16808. The conventional material characterization is also reffered to as reference.

Fig. 4
figure 4

Experimental results, model prediction and simulation outcomes for the different three-point bending experiment configurations

Full size image

Three-point bending

The three-point bending tests were performed on a universal testing machine Z150 from ZwickRoell GmbH & Co. KG, Ulm, Germany. The width of the specimen was 20mm and its length was 100mm. The bending roller radii is 2mm and their distance was set to 30mm. The punch radius is 1mm. The maximum penetration depth during the test was set to 15mm. The specimen was bent with constant punch speed of 1mm/s. For each rolling direction, ten tests have been performed, where in Fig. 4 the mean results are shown.

The simulation of the three-point bending test was carried out in LS-Dyna. For this purpose, the tools were transferred to the simulation as rigid bodies. The mesh size is 0.1mm x 0.1mm for all rigid bodies. The punch speed is taken from the real test and is 1mm/s. The sheet metal was meshed using fully integrated shell elements (Element type 16) and an element size of 0.25mm x 0.25mm. Nine integration points are used across the thickness in order to map the bending stresses over the thickness of the sheet accurately. The material behavior was implemented using the Yld2000-2d yield locus. Figure 4 shows the results for the parameter set identified from conventional material characterization and for the parameter set identified from the optimization using the three-point bending experiment measurements.

Validation experiment

The Material Under Control (MUC) test is designed to validate constitutive models [22, 23]. The advantages of this validation experiment are its low friction effects and its wide deformation range from uniaxial to biaxial strain conditions. The low friction is achieved through the use of a locking bead and a blankholder force of 400kN. This prevents the material from flowing over the bead. Furthermore, its wide deformation range is achieved by the optimized butterfly geometry of the punch. The MUC-test tool offers a high degree of accessibility, allowing the displacements to be recorded and the major- and minor strains to be calculated using a digital image correlation system (DIC). During the experiment, images are recorded at a frequency of 10Hz while the stamp moves continuously at a speed of 1mm/s. The specimens were prepared using guillotine shears, which makes specimen preparation easy. All of these characteristics distinguish it from established validation experiments, such as the cross die. Using a digital twin, the forces and strains of the simulation can be continuously compared and validated with the corresponding experimental step. Three different sample widths at \(0^{\circ }\), \(45^{\circ }\) and \(90^{\circ }\) to the rolling direction are investigated experimentally and compared with the simulations.

The piezoelectric sensor measurements of forming forces were compared with the simulation results to validate the flow curve. The yield locus curve is validated by comparing the strain field of the DIC measurements to the simulation mesh. To ensure consistency in the comparison, the isoparametric approach for shifting the measurement points to the simulation mesh is used. The strain evolution of each shell element in the 1mm mesh of the digital twin are then compared with the major- and minor strain of the DIC measurements.

Results

The results section is split in two subsections. Subsection“Parameter identification” shows the results of the parameter identification methodology, Subsection“Valida-tion” the results of the validation experiment.

Parameter identification

Figure 4 shows the mean experimental data for the three-point bending experiments for each orientation of the rolling direction with respect to the bending axis (\(0^{\circ }\) top, \(45^{\circ }\) middle, and \(90^{\circ }\) bottom), i.e. \(F_{\text {exp}}(d)\) from Expression Eq. 4. Further, Fig. 4 visualizes the optimization result, i.e. \(F_{mod}(d;\varphi _{i,opt})\) using the identified set of material parameters \(\varphi _{i,opt}\) in the prediction model according to Eq. 1. The optimized sets of material parameters \(A_i\), \(B_i\), \(n_i\), and \(C_i\) are summarized in Table 1.

Table 1 Summary of the results for the optimization variables \(A_i\), \(B_i\), \(n_i\), and \(C_i\) for \(i=\){\(0^{\circ }\), \(45^{\circ }\), \(90^{\circ }\)}. RD: rolling direction; BA: bending axis
Full size table
Table 2 Summary of the valuation variables for the experiments, optimized analytical model predictions, and finite element simulations
Full size table

For a first comparison, Fig. 4 also shows the results of finite element simulations of the three-point bending tests, which use on the one hand the reference material parameters identified according to Section“Conventional characteri-zation” \(F_{sim-r}(d;\varphi _{i,ref})\) and on the other hand the parameter sets from the optimization \(F_{sim-b}(d;\varphi _{i,opt})\).

As an integral valuation variable, the bending work per unit width w is utilized.

$$\begin{aligned} w = \int _{d_l}^{d_u} F(d) \text { d}\delta \end{aligned}$$

For the analysis \(d_l\) was set to 1.5 mm and \(d_u\) to 15 mm. The maximum punch force \(F_{x}\) and the penetration depth at the maximum punch force \(d_{x}\) represent the local valuation variables. Table 2 summarizes the valuation variables for each curve shown in Fig. 4.

Fig. 5
figure 5

Comparison of the DP600 reference flow curve with the flow curve from the bending test

Full size image
Fig. 6
figure 6

Comparison of the DP600 reference yield locus YLD2000-2d with the yield locus YLD2000-2d calibrated from the bending test (right: yield locus, left: normalized yield locus)

Full size image

Given the small number of four optimization parameters, the model results obtained generally show good global agreement with the experimental measurements (mean deviation in bending work per unit width \(\bar{w}_{\text {exp}}-\bar{w}_{mod} = 0.002\)Nm with a standard deviation of \(s_{w,mod} = 0.008\)Nm), and higher accuracy compared to both finite element simulations (\(\bar{w}_{\text {exp}}-\bar{w}_{sim-b} = 0.045\)Nm with \(s_{w,sim-b} = 0.117\)Nm, \(\bar{w}_{\text {exp}}-\bar{w}_{sim-r} = -0.113\)Nm with \(s_{w,sim-r} = 0.135\)Nm), for which also the parameter set \(\varphi _{i,opt}\) shows higher accuracy. This was to be expected, since the formulation of the objective function of the optimization, see Expression (4), enforces global agreement of the model prediction and the simulation results have not been optimized to fit the experimental results.

However, also for the local valuation variable, which the set of material parameters in the analytical model has not been explicitly optimized for, are in good agreement with the experimental measurements. Especially the maximum punch forces are predicted with high accuracy (mean deviation in maximum punch force \(\bar{F}_{x,\text {exp}}-\bar{F}_{x,mod} = -1.319\)N with a standard deviation of \(s_{F_x,mod} = 1.078\)N) and show low deviations compared to the finite element simulation results (\(\bar{F}_{x,sim-b}-\bar{F}_{x,sim-b} = -0.942\)N with \(s_{F_x,sim-b} = 9.907\)N, \(\bar{F}_{x,sim-r}-\bar{F}_{x,sim-r} = -15.262\)N with \(s_{F_x,sim-r} = 11.386\)N). For all analyzed virtual models, the values for the penetration depth at maximum punch force are higher compared to the experimental results. The optimized analytical model shows similar results as the simulation using the optimized set of material parameters from the three-point bending experiments (mean deviation in penetration depth at maximum punch force \(\bar{d}_{x,\text {exp}}-\bar{d}_{x,mod} = -0.883\)mm with a standard deviation of \(s_{d_x,mod} = 0.128\)mm, \(\bar{d}_{x,sim-b}-\bar{d}_{x,sim-b} = -0.923\)mm with \(s_{d_x,sim-b} = 0.053\)N). Again, the simulation using the reference material model parameters yields the largest deviations (\(\bar{d}_{x,sim-r}-\bar{d}_{x,sim-r} = -1.952\)N with \(s_{d_x,sim-r} = 0.070\)N).

The results exhibit two major systematic deviations of the optimized analytical model. It predicts the maximum punch force to occur at higher penetration depths compared to the experimental measurements, and it shows differences in slope and curvature of the punch force curves after a penetration depth of  10mm. The shift of the point of maximum punch force to higher penetration depths also occurs for the finite element analysis, even in terms of quantity for the simulation with the material parameter set from the optimization. This suggests that the systematic error originates from the material model and its associated parameters used in the analytical description, see Eq. 1 and during the optimization of Expression (4) the model capabilities are balanced with the accuracy in material parameter identification. This goes hand in hand with the second systematic error that is not present in the finite element analysis, for which the slope and curvature of the punch force curves are similar to the experimental results also after a penetration depth of  10mm. For higher deformation values, i.e. larger punch penetration depth, the Voce flow curve model used in the analytical model, seems less suitable for accurately describing the bending process of the material at hand, see especially the difference in the punch force slopes compared to the experimental and simulated results in Fig. 5. This becomes even clearer, when comparing the conventionally identified flow curve with the reference flow curve that has been identified by conventional material characterization. Figure 5 visualizes the reference flow curve and the flow curve derived from the three-point bending tests.

Figure 6 shows a comparison of the reference yield locus and the yield locus identified based on the three-point bending test data. The yield stresses identified from the bending test are higher than the yield stresses identified by conventional material characterization (see right graph in Fig. 6), however, the general shape of the yield loci show high similarity (see left graph in Fig. 6). Very likely, the higher values for the yield stresses identified by the optimization also originate from the used Voce flow curve model.

Table 3 summarizes the material parameters identified by optimization and the material parameters from conventional material characterization. Since the Voce flow curve model forms also the analytical basis for the determination of the R values, it also has an impact on their optimized values. The overestimation of \(R_0\) is in line with the underestimation of \(R_{90}\), since they are identified based on the bending experiments, where the bending axis is parallel or perpendicular to the rolling direction. These two experiments show a significant difference in the maximum punch force value \(F_x\), see Table 2. The bending experiment performed with the bending axis perpendicular to the rolling direction has an overall flatter appearance compared to the bending experiment performed with the bending axis parallel to the rolling direction. This may be also seen in the valuation variable w, for which the bending experiment performed with the bending axis perpendicular to the rolling direction lies slightly higher compared the experimental value and slightly lower for the bending experiment performed with the bending axis parallel to the rolling direction (see Table 2). Following Eqs. 2 and 3 for the deduction of the actual R values from \(C_{0}\) and \(C_{90}\) (see Table 1), this yields an overestimation of \(R_0\) and an underestimation of \(R_{90}\). The even higher overestimation of \(R_{45}\) originates from the same reason with no opposing coupled influence effect from another experiment in the \(45^{\circ }\) direction.

Validation

Table 3 Material parameters of conventional material characterization method and parameters determined by bending experiments
Full size table
Fig. 7
figure 7

Force-displacement curves of the simulations with the material parameters from the optimization and the material parameters by conventional material characterization (reference), and the MUC-test validation experiment for three different specimen widths in the rolling direction

Full size image

For validation and comparison, the MUC-test has been experimentally performed and simulated using both yield locus functions from Fig. 6 and Table 3, and the corresponding yield curves, see Fig. 5. The result of the digital twin analysis was then compared to the experimental data following the procedure outlined in [22]. The comparison of the force-displacement curves of the two investigated approaches and the experiment is shown in Fig. 7 for three different specimen widths (70mm, 110mm, and 230mm), each in the rolling direction.

In Fig. 7, there is hardly any deviation in the force-displacement curves in the first 75% of the punch stroke. From that point onward, it can be concluded that the deviating flow curve of the bending test for higher strain values takes effect, resulting in larger deviations in the force-displacement curve. This applies also when comparing the specimens at \(45^{\circ }\) and \(90^{\circ }\) to the rolling direction and no other behavior of the force-displacement curves can be determined.

Figure 8 demonstrates the strain distribution for the three experiments from Fig. 7 at 80% of each the punch stroke, so at a point with significant deviation in the force-displacement curve between the experiments and the simulation using the optimized set of parameters. For better illustration, all simulation results in Fig. 8 are shown by their envelope only. The highest deviation is observed for the 70mm specimen width, see also Fig. 9. In this case, the constitutive model derived from of the bending test is unable to accurately simulate especially the high strain region in the uniaxial tension direction. In contrast, the reference constitutive model is capable to model that region. This difference also has its origin in the large deviations of the flow curves, i.e. hardening behavior. The overestimation of the stresses in case of the optimized set of parameters from the bending experiments leads to a damping of larger strain values, especially for higher strained regions, see for example the 230 mm specimen width in the high strain region of the biaxial tension.

In general, the combination of large deviations in the flow curve and hardening behavior for higher strains and the higher yield stress values yield too low major and minor strain values for the optimized set of material parameters. Figure 9 shows the specific deviations for the major and minor strains of the two simulation results.

Fig. 8
figure 8

Distribution of major and minor strain of three different specimen geometries in the rolling direction and the envelope of the simulation points of each specimen geometry for the reference set of material parameters and the set of material parameters calibrated by three-point bending experiments. Strain distribution at 80% punch travel of the MUC-test and the corresponding time step of the simulation

Full size image
Fig. 9
figure 9

Mean deviations of the major and minor strains for the reference set of material parameters (ref) and the set of material parameters calibrated by three-point bending experiments (mod). The MUC-test evaluation results are shown for three different specimen geometries (70mm, 110mm, and 230mm) in three different orientations (\(0^{\circ }\), \(45^{\circ }\), and \(90^{\circ }\) to rolling direction)

Full size image

According to [22], the MUC-test evaluation allows to quantify the deviations of different material parameter sets by a scalar value. For the set of material parameters optimized based on the three-point bending experiments, a total deviation of 1.82 was found. For the reference set of material parameters by conventional material characterization, a total deviation of 1.40 results. The MUC-test analysis of a large number of different material models and materials in [24, p. 128] permit to set these quantities into perspective. For the evaluated mean punch stroke of 21.8mm, the identified set of material parameters from three-point bending experiments may be categorized at the boarder between an average and good material description, where the reference set of material parameters clearly classifies as a very good material description.

Conclusion

The three-point bending test represents an information rich test that allows for a straightforward identification of plastic material parameters of sheet metal based on an analytical model, at least for moderate strain levels. A flow curve and yield locus parameters can be identified with reasonable accuracy, especially with regard to the low sample preparation effort, and the small number of necessary tests and comparatively cheap experimental equipment, respectively.

Two major deviations occur in the set of material parameters calibrated from the three-point bending experiments: overestimation of the yield stresses; overestimation of the flow curve for higher strain values. The results indicate that both deviations can be attributed to the used Voce flow curve model in the analytical description of the bending process.

Outlook

Improvements of the parameter identification results can be expected, especially for higher strains, by adapting the analytical model for the bending process. The highest potential lies in the inclusion of a more flexible flow curve model in the derivation of Eq. 1, e.g. by using a weighted sum approach of a Swift flow curve model [25] and a Hockett-Sherby flow curve model [26]. Since in the proposed approach indirectly couples the flow curve and anisotropy, an increased accuracy regarding the flow curve model is expected to also enhance the determination of the R values.

Next to flow curve and yield locus parameters, the three-point bending test, or cyclic variants of it, offers kinematic hardening information as well, which could be exploited to identify associated parameters following the generic methodology presented in this work.