Analysis, simulation and experimental study of electromagnetic forming of titanium bipolar plate with arc-shaped uniform pressure coil

Abstract

In the electromagnetic forming (EMF) titanium bipolar plates (BPPs), a reasonable coil structure can provide higher forming efficiency and repeatability. An arc-shaped uniform pressure coil (UPC) is proposed, and an efficient and reliable multiphysics sequentially coupled analytical model is established. Through the LS-DYNA numerical model and the fitted current curve obtained from experiments, the predictive capabilities of equivalent circuit parameters and dynamic phenomena are verified, and the rationality of the magnetic shielding assumption and magnetic flux uniform distribution are evaluated. Starting from the durability and forming efficiency of the coil, the optimal coil geometry in analytical form is constructed. The study found that there is an optimal solution for the height of the primary coil, wire thickness, primary and secondary side gap, which are 18.3 mm, 2.7 mm, and 3.2 mm, respectively. Based on this, under the discharge capacitor of 100 μF, acceleration distance of 2 mm, and driven by 0.3 mm thick Cu110, a TA1 titanium BPP with a channel depth-to-width ratio of 0.53 was successfully manufactured. Its maximum thinning rate is 18.2%, the maximum fluctuation rate does not exceed 2.5%, and the filling rate of the channel above 95%. Overall, this study provides theoretical basis and reference for the design of UPC in EMF for BPPs.

Introduction

Titanium bipolar plates (BPPs), as core components of fuel cells, have gradually attracted wide attention due to their high specific strength and corrosion resistance. However, titanium has poor formability and suffers from severe springback. Daehn et al. [1] pointed out that compared to traditional forming processes, electromagnetic forming (EMF) can not only significantly increase the forming limit, reduce wrinkling and springback, but also only require a single-sided die during the forming process. This process utilizes pulse magnetic pressure to shape metal workpieces into desired geometric shapes in a flexible and controllable manner. This indicates the possibility of localized embossing and patterning for forming titanium BPPs with microchannel features.

In EMF, the quality of the coil structure plays a decisive role in forming efficiency. Over the past few decades, numerous studies on coil structures for EMF have been conducted. For instance, Takatsu et al. [2] applied planar circular spiral coils in the forming of circular sheet metal parts, but this approach resulted in uneven force distribution at the center of the workpiece. To overcome this issue, Golovashchenko [3] initially proposed planar square coils, followed by Oliveira et al. [4] proposing parallel square coils. However, these coils can only partially address the problem of low force distribution at the center of the workpiece. Kamal et al. [5] introduced an outer channel and proposed a uniform pressure coil (UPC) that can generate uniform magnetic pressure on a relatively large area of sheet metal. The UPC is stable enough to sustain hundreds of forming operations and provides higher energy efficiency for sheet metal forming compared to other coils. Therefore, based on the background of manufacturing titanium BPPs using uniform force electromagnetic technology, numerous researchers have conducted relevant process studies. Wang et al. [6] obtained a Grade 2 titanium BPP with a channel depth-to-width ratio of 0.22 using a track-shaped UPC with a discharge energy of 8.0 kJ. Wu et al. [7] achieved a maximum channel depth of 0.294 mm for TA1 titanium BPP using an internal field rectangular UPC with a discharge energy of 7.5 kJ. Dong et al. [8] prepared a TA1 titanium BPP with a channel depth-to-width ratio of 0.67 using a wire-wound rectangular UPC in vacuum with a discharge energy of 10.8 kJ.

Like other forming coils, life expectancy and forming efficiency are universal goals in the design and manufacture of UPCs. The life expectancy of forming coils is mainly determined by thermal, deformation, and electrical insulation loads on the coil, which has been discussed in several previous studies. Gies et al. [9] investigated the thermal load on working coils in long-term discharge sequences. They pointed out that approximately 50% of the electrical energy is lost due to Joule heating during electromagnetic sheet forming, leading to an increased thermal load on the working coils and a shortened lifespan. Cao et al. [10] employed a crowbar circuit to control the discharge current in the coil, reducing the Joule heat in the coil from 4.62 kJ to 2.07 kJ. Golovashchenko [3] discussed coil failure modes and preventive measures. He pointed out that common failure modes include coil deformation and short circuits. By reinforcing coil support and insulation, and ensuring the insulation material thickness matches the gap between the coil, coil expansion and rupture can be prevented. Cui et al. [11] analyzed the electromagnetic force distribution on the coil based on the structural parameters of failed coils. The results indicated that the bottom bulging failure of a uniformly compressed coil is caused by a stronger magnetic force in the upper region of the coil compared to the bottom.

Higher energy efficiency can increase the achievable deformation speed at a specific discharge energy and reduce the energy required for forming specific workpieces, thereby improving the lifespan of both the coil and the entire forming system to some extent. Numerous papers have discussed the optimization design of UPC through analysis of geometric shapes and electromagnetic parameters' influence on coil performance. For example, Zhang et al. [12] investigated the effects of discharge capacity and coil length on forming efficiency through analytical and experimental studies. The research revealed that longer coil lengths and smaller capacitor bank capacities result in higher forming efficiency. The maximum forming efficiency is achieved when the skin depth is approximately 0.9 mm. Kamal and Kamal et al. [13] proposed an analytical formula to analyze the basic performance of coils and found that there is an optimal number of turns that results in maximum magnetic pressure and maximum plate velocity. Thibaudeau et al. [14] conducted analytical optimization of the geometric shape and number of turns of a uniform pressure coil, which was validated with experimental results. Kim et al. [15] combined analytical, numerical, and experimental studies to analyze the influence of several key geometric parameters on magnetic pressure. Weddeling et al. [16] proposed an analytical method-based electromagnetic pressure welding process design model for predicting process parameters such as discharge energy. Li et al. [17] compared the forming efficiency of different uniformly compressed coils through theoretical analysis, numerical simulation, and experiments. The study demonstrated that coils with a higher number of turns per unit length exhibit higher forming efficiency. Kinsey et al. [18] developed a semi-analytical model for predicting magnetic pressure distribution, workpiece velocity, and deformation parameters to design coils. Lai et al. [19] claimed that by analytically characterizing the energy efficiency of coils, rectangular uniformly compressed coils exhibit optimal channel height.

Therefore, this study aims to develop an efficient and reliable analytical model for EMF from the perspectives of coil durability and forming efficiency. To achieve this, numerous simplifications and assumptions were made in the model. One of the fundamental assumptions is the magnetic shielding assumption utilized by Al-Hassani et al. and Kinsey et al., which posits that the magnetic field generated by the coil can be completely shielded by conductive pathways and metal workpieces, and it is distributed uniformly along the magnetic path. These assumptions greatly simplify the calculation process of magnetic pressure. However, they are only applicable within limited process parameter boundaries, such as frequency, workpiece resistivity, workpiece thickness, and unit length of turns. For instance, Thibaudeau et al. [14] proposed that the analytical model based on the magnetic shielding assumption is ineffective for thin and low-conductivity workpieces, showing over 100% analysis error. Al-Hassani et al. [20] found that the deformation of a steel tube component at room temperature was overestimated by 200% in EMF, indicating that the magnetic pressure was overestimated by 200%. Jablonski et al. [21] derived from the approximate solution the optimal frequency that can achieve maximum deformation. To ensure the reliability of the analytical model, it is necessary to establish reasonable criteria to evaluate the applicability of the magnetic shielding assumption. For example, Kamal et al. [13] and Thibaudeau et al. [14] widely considered the ratio of workpiece thickness to skin depth α as an evaluation criterion for model applicability. Lai et al. [22] analyzing and modeling track-shaped structure coils, proposed the ratio of secondary side impedance between the conducting channels and the workpiece, denoted as β, and verified β = 8.8 as a general applicable boundary. However, due to the influence of the coil geometric shape on β, the critical value of this ratio is being challenged.

Thus, this study focuses on two main aspects. Firstly, a circular arc type uniform pressure coil(UPC) is proposed as a commonly used driving coil. Among them, the main objective of the work is to develop and validate an efficient and reliable multiphysics analytical model that considers electromagnetic-deformation interactions. Another aspect, by investigating the durability and forming efficiency of the coil, the optimal configuration of the coil geometric structure in analytical form is obtained, facilitating rapid design for Titanium BPP EMF processes and UPCs.

Analytical model

The analytical model introduced should be able to predict the maximum workpiece velocity V_Wmax and displacement S_Wmax under certain parameters of the workpiece and BPP mold. By considering the knowledge of the required impact velocity for specific material combinations in magnetic pulse impacting, these values can estimate whether the collision velocity and acceleration distance after impact form microchannel features in the BPP. The model consists of two parts. First, the discharge current I_c(t) and magnetic pressure P_M(t) in the electromagnetic field are calculated. In the next section, mechanical values describing deformation V_Wmax and S_Wmax are computed.

Prediction of discharge current and applied magnetic pressure

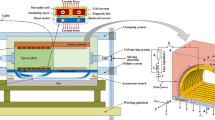
In the electromagnetic field model, Manish et al. [23] and Xu et al. [24] often design the shape of the primary coil in UPC as rectangular or racetrack-shaped, aiming to ensure uniform force on the wires near the workpiece side. Building upon the work of Cui et al. [25, 26] who utilized expandable tubing with circular helical coil winding, this research uses a UPC with a arc-shaped helical coil, and its electromagnetic field model is shown in Fig. 1, with the relevant geometric parameters listed in Table 1.

Fig. 1

The schematic diagram of the UPC electromagnetic field model

Table 1 Geometric parameters of UPC

Figure 2(a) shows the equivalent circuit diagram of the EMF device depicted in Fig. 1, which can be simplified to an RLC circuit in Fig. 2(b). Here, R_eq and L_eq represent the equivalent resistance and equivalent inductance of the system consisting of the primary coil, outer channel, and workpiece. R_i and L_i denote the internal resistance and internal inductance of EMF machine. According to Al-Hassani [20], if the capacitance C, equivalent inductance L_eq, and equivalent resistance R_eq are known, the current I_c(t) in the simplified RLC circuit can be determined using a damped sinusoidal function:

Fig. 2

EMF Equivalent Circuit Diagram. a Circuit with primary and secondary sides; b Simplified circuit with internal parameters

$${I}_{c}\left({\text{t}}\right)=\frac{{U}_{0}}{\omega ({L}_{i}+{L}_{eq})}{e}^{-\alpha t}sin\left(\omega t\right)$$

(1)

In this equation, U₀ represents the initial voltage of the capacitor, and α is the damping coefficient of the circuit:

$$\alpha =\frac{{R}_{i}+{R}_{eq}}{2({L}_{i}+{L}_{eq})}$$

(2)

For the angular frequency ω in Eq. (1), Psyk et al. [27] provided the following expression:

$$\omega =\sqrt{\frac{1}{C({L}_{i}+{L}_{eq})}-{\alpha }^{2}}$$

(3)

Under different conditions, the current in the UPC forming process exhibits varying degrees of skin effect, and the magnetic field experiences shielding or penetration phenomena to different extents. To depict the assumed two-dimensional magnetic field distribution, Fig. 3(a) illustrates the expanded region of the magnetic field. The magnetic field is concentrated between the gap of the primary coil-outer channel-workpiece and inside the primary coil, uniformly distributed on the equivalent cross-sectional areas A_g and A_c of the magnetic path, denoted by B_g and B_c respectively. In order to calculate A_g and A_c, ε_c^mag, ε_ch^mag, and ε_w^mag are used to represent the equivalent magnetic penetration depths in the primary coil, outer channel, and workpiece respectively:

Fig. 3

The expanded region of the electromagnetic field distribution for the UPC. a Magnetic penetration model; b Electrical penetration model

$$\left\{\begin{array}{c}{\varepsilon }_{c}^{mag}=min\left({\lambda }^{mag}\sqrt{2/{\omega \mu }_{0}{\sigma }_{c}},0.5{\uptau }_{c}\right)\\ {\varepsilon }_{ch}^{mag}=min\left({\lambda }^{mag}\sqrt{2/{\omega \mu }_{0}{\sigma }_{ch}},{\uptau }_{ch}\right)\\ {\varepsilon }_{w}^{mag}=min\left({\lambda }^{mag}\sqrt{2/{\omega \mu }_{0}{\sigma }_{w}},{\uptau }_{w}\right)\end{array}\right.$$

(4)

Here, λ^mag is a constant that represents the ratio of magnetic penetration depth to skin depth. Al-Hassani et al. [20] and Weddeling et al. [16] consider its value to be 0.5. σ_c, σ_ch, and σ_w represent the electrical conductivity of the primary coil, outer channel, and workpiece, respectively, while μ₀ denotes the vacuum permeability.

Figure 3(b) illustrates the expanded region of the assumed eddy current distribution. The eddy currents I_ch&w in the outer channel-workpiece are concentrated on the side of the surface adjacent to the primary coil, with path lengths approximated as l_ch and l_w. The currents I_{c_o} and I_{c_i} on the primary coil conductor flow on its inner and outer surfaces, with respective path lengths approximated as l_{c_o} and l_{c_i}. Introducing the concept of electrical penetration depth to characterize the current distribution, the equivalent electrical penetration depths within the primary coil, outer channel, and workpiece are denoted as ε_c^cur, ε_ch^cur, and ε_w^cur respectively. They can be expressed as:

$$\left\{\begin{array}{c}{\varepsilon }_{c}^{cur}=min\left({\lambda }^{cur}\sqrt{2/{\omega \mu }_{0}{\sigma }_{c}},0.5{\uptau }_{c}\right)\\ {\varepsilon }_{ch}^{cur}=min\left({\lambda }^{cur}\sqrt{2/{\omega \mu }_{0}{\sigma }_{ch}},{\uptau }_{ch}\right)\\ {\varepsilon }_{w}^{cur}=min\left({\lambda }^{cur}\sqrt{2/{\omega \mu }_{0}{\sigma }_{w}},{\uptau }_{w}\right)\end{array}\right.$$

(5)

Here, λ^cur is a constant representing the ratio of electrical penetration depth to skin depth. Lai et al. [19] consider its value to be 0.8.

Based on the previous assumptions and according to Ampere's Circuital Law and Gauss's Magnetism Law (see Eqs. (28) and (29) in Appendix A), B_g and B_c satisfy the following relationships:

$$\left\{\begin{array}{c}\frac{{l}_{c}\left({B}_{g}\left({\text{t}}\right)+{B}_{C}\left({\text{t}}\right)\right)}{{\mu }_{0}}=n{I}_{c}\left({\text{t}}\right)\\ {B}_{g}{\left({\text{t}}\right)A}_{g}={B}_{c}{\left({\text{t}}\right)A}_{c}\end{array}\right.$$

(6)

The magnetic energy of the system E_M can be calculated by integrating the energy density over all magnetic paths, which includes two parts: one stored in the gap between the workpiece and the outer channel denoted by E_g, and the other stored inside the primary coil denoted by E_c. It can be expressed as follows:

$${E}_{M}={E}_{g}+{E}_{c}=\frac{{B}_{g}^{2}\left({\text{t}}\right)}{2{\mu }_{0}}{A}_{g}{l}_{c}+\frac{{B}_{c}^{2}\left({\text{t}}\right)}{2{\mu }_{0}}{A}_{c}{l}_{c}=\frac{{\mu }_{0}{n}^{2}{I}_{c}^{2}\left({\text{t}}\right){A}_{c}{A}_{g}}{2{l}_{c}\left({A}_{c}+{A}_{g}\right)}=\frac{1}{2}{L}_{eq}{I}_{c}^{2}\left({\text{t}}\right)$$

(7)

Therefore, the equivalent inductance of the UPC model can be expressed as:

$${L}_{eq}=\frac{{\mu }_{0}{n}^{2}{A}_{c}{A}_{g}}{{l}_{c}\left({A}_{c}+{A}_{g}\right)}$$

(8)

According to Ampere's Circuital Law (see Eq. (28) in Appendix A), the relationship between the eddy current I_ch&w inside the outer channel and the magnetic field B_g in the gap is given by:

$${I}_{ch\&w}\left({\text{t}}\right)=\frac{{B}_{g}\left({\text{t}}\right){l}_{c}}{{\mu }_{0}}=n{I}_{c}\left({\text{t}}\right)\frac{{A}_{c}}{{A}_{c}+{A}_{g}}$$

(9)

The currents I_{c_i} and I_{c_o} on the primary coil satisfy the following two relationships with B_g and B_c:

$$\left\{\begin{array}{c}{I}_{c\_i}\left({\text{t}}\right)=\frac{{B}_{c}{\left({\text{t}}\right)l}_{c}}{{\mu }_{0}}=n{I}_{c}\left({\text{t}}\right)\frac{{A}_{g}}{{A}_{c}+{A}_{g}}\\ {I}_{c\_o}\left({\text{t}}\right)=\frac{{B}_{g}\left({\text{t}}\right){l}_{c}}{{\mu }_{0}}={nI}_{c}\left({\text{t}}\right)\frac{{A}_{c}}{{A}_{c}+{A}_{g}}\end{array}\right.$$

(10)

The Joule losses on the conductor include four parts. Two of them are generated by the outer channel and the workpiece, denoted as Q_ch and Q_w, respectively. The other two parts are generated on both sides of the primary coil conductor, denoted as Q_{c_i} and Q_{c_o}. The total Joule loss Q_T can be expressed as:

$$\begin{array}{c}{Q}_{T}\left({\text{t}}\right)={Q}_{ch}\left({\text{t}}\right)+{Q}_{w}\left({\text{t}}\right)+{Q}_{{c}_{i}}\left({\text{t}}\right)+{Q}_{{c}_{o}}\left({\text{t}}\right)\\ ={I}_{ch\&w}^{2}\left(t\right)\frac{{l}_{ch}}{{\sigma }_{ch}{l}_{c}{\varepsilon }_{ch}^{cur}}+{I}_{ch\&w}^{2}\left({\text{t}}\right)\frac{{l}_{w}}{{\sigma }_{w}{l}_{c}{\varepsilon }_{w}^{cur}}+{I}_{c\_i}^{2}\left({\text{t}}\right)\frac{{l}_{c\_i}}{{\sigma }_{c}{l}_{c}{\varepsilon }_{c}^{cur}}+{I}_{c\_o}^{2}\left({\text{t}}\right)\frac{{l}_{c\_o}}{{\sigma }_{c}{l}_{c}{\varepsilon }_{c}^{cur}}\end{array}$$

(11)

The equivalent resistance of UPC satisfies the following relationship with the total Joule loss:

$${Q}_{T}\left({\text{t}}\right)={R}_{eq}{I}_{c}^{2}\left({\text{t}}\right)$$

(12)

Therefore, the equivalent resistance of the UPC model can be expressed as:

$${R}_{eq}={\left(\frac{n{A}_{c}}{{A}_{c}+{A}_{g}}\right)}^{2}\left[\frac{{l}_{ch}}{{\sigma }_{ch}{l}_{c}{\varepsilon }_{ch}^{cur}}+\frac{{l}_{c\_o}}{{\sigma }_{c}{l}_{c}{\varepsilon }_{c}^{cur}}+\frac{{l}_{w}}{{\sigma }_{w}{l}_{c}{\varepsilon }_{w}^{cur}}\right]+{\left(\frac{n{A}_{g}}{{A}_{c}+{A}_{g}}\right)}^{2}\frac{{l}_{c\_i}}{{\sigma }_{c}{l}_{c}{\varepsilon }_{c}^{cur}}$$

(13)

When the external magnetic field on the outer channel is zero, the magnetic pressure acting on the metal workpiece can be expressed as:

$${P}_{w}\left({\text{t}}\right)=\frac{{B}_{g}^{2}\left({\text{t}}\right)}{2{\mu }_{0}}=\frac{{A}_{c}^{2}{\mu }_{0}{n}^{2}{I}_{c}^{2}\left({\text{t}}\right)}{2{\left({A}_{g}+{A}_{c}\right)}^{2}{l}_{c}^{2}}$$

(14)

Similarly, the magnetic pressure acting on the primary coil wire near the workpiece side is:

$${P}_{c}\left({\text{t}}\right)=\frac{{{B}_{c}^{2}\left({\text{t}}\right)-B}_{g}^{2}\left({\text{t}}\right)}{2{\mu }_{0}}=\frac{\left({A}_{g}-{A}_{c}\right){\mu }_{0}{n}^{2}{I}_{c}^{2}\left({\text{t}}\right)}{2{\left({A}_{g}+{A}_{c}\right)}^{2}{l}_{c}^{2}}$$

(15)

If the magnetic shielding assumption does not hold, amount of magnetic field will penetrate the workpiece, and the magnetic pressure calculated using Eq. (14) will be overestimated. Based on the primary and secondary circuit diagrams in Fig. 1(a), Jablonski et al. [21] suggested that the ratio of resistance R_ch&w and inductance L_ch&w of the secondary side formed by the outer channel and the workpiece, denoted as β, and the value ω/β represent the electromagnetic shielding performance of the outer channel and the workpiece:

$$\frac{\omega }{\beta }=\frac{{\omega L}_{ch\&w}}{{R}_{ch\&w}}\gg 1$$

(16)

The formulas for inductance and resistance on the secondary side can be derived using the same method, as follows:

$${L}_{ch\&w}=\frac{{\mu }_{0}}{{l}_{c}}\left[{A}_{c}+{A}_{g}\right]$$

(17)

$${R}_{ch\&w}={R}_{w}+{R}_{ch}=\frac{{l}_{w}}{{\sigma }_{w}{l}_{c}{\varepsilon }_{w}^{cur}}+\frac{{l}_{ch}}{{\sigma }_{ch}{l}_{c}{\varepsilon }_{ch}^{cur}}$$

(18)

In this case, Lai et al. [22] made appropriate modifications to Eq. (14). The improved magnetic pressure on the workpiece is given by:

$${P}_{w}{'}\left({\text{t}}\right)=\frac{\omega }{10\beta }{P}_{w}\left({\text{t}}\right)=\frac{\omega {A}_{c}^{2}{\mu }_{0}{n}^{2}{I}_{c}^{2}\left({\text{t}}\right)}{2{0\beta \left({A}_{g}+{A}_{c}\right)}^{2}{l}_{c}^{2}}$$

(19)

Determination of velocity and displacement

In the work conducted by Dong et al. [8] on EMF of titanium BPPs, titanium BPP, the thin and low-conductivity titanium sheet needs to be driven by a high-conductivity driver sheet, as shown in Fig. 4. The first step in predicting the workpiece velocity and displacement is to determine the minimum pressure P_pl at which plastic deformation begins. Therefore, consider a fully clamped beam with width d_w and length l_w (see Fig. 4(a)).

Fig. 4

The mold configuration for uniform deformation of the workpiece based on. a mechanical assumptions with; b applied pressures P_M and P_pl

Assuming constant thickness τ_D of the driver sheet and uniform pressure distribution, the elastic bending moment M_el is:

$${M}_{el}=\frac{1}{8}{P}_{pl}{d}_{w}{{l}_{w}}^{2}$$

(20)

Assuming plane stress and no strain hardening, the plastic moment M_pl can be expressed according to Weddeling et al. [28] as follows:

$${M}_{pl}=\frac{1}{2\sqrt{3}}{k}_{T}{d}_{w}{\tau }_{D}^{2}$$

(21)

where k_T represents the yielding stress of the material under pure shear. Considering the limit case where elastic deformation transitions to plastic deformation and equating Eqs. (20) and (21), the expression for P_pl is obtained as:

$${P}_{pl}=\frac{4}{\sqrt{3}}{k}_{T}{\left(\frac{{\tau }_{D}}{{l}_{w}}\right)}^{2}$$

(22)

This pressure counteracts a portion of the deformation in the driver sheet during the forming process. At time point t_s, the magnetic pressure exceeds the value of P_pl, and plastic deformation begins (see Fig. 4(b)). Thibaudeau et al. [14] treated the motion of metal sheets induced by magnetic pressure as approximate rigid body motion. Following similar treatments, under the influence of these two pressures, the form of Newton's second law of motion is as follows:

$${a}_{w}\left({\text{t}}\right)=\frac{{P}_{w}\left({\text{t}}\right)-{P}_{pl}}{{\rho }_{w}{\tau }_{w}+{\rho }_{D}{\tau }_{D}}$$

(23)

Integrating this expression over time gives the velocity V_w(t) of the workpiece:

$${V}_{w}\left({\text{t}}\right)=\frac{1}{{\rho }_{w}{\tau }_{w}+{\rho }_{D}{\tau }_{D}}{\int }_{{t}_{s}}^{t}({P}_{w}-{P}_{pl}){d}_{t}$$

(24)

At time point t_e, the acceleration becomes zero again, and the deceleration of the workpiece starts. Thus, this is the point of maximum velocity V_wmax(t_e) for the workpiece. Further integrating Eq. (24) yields the displacement S_w(t):

$${S}_{w}\left({\text{t}}\right)={\int }_{{t}_{s}}^{t}{v}_{w}{(t)d}_{t}$$

(25)

Kamal et al. [13] suggested that maintaining a certain distance between the workpiece and the mold helps achieve the highest impact velocity. The acceleration distance, which is the thickness τ_s of the acceleration plate, can be effectively estimated by assuming that the thin sheet accelerates to half a period of current at time point t_e.

Calculation Process

The electromagnetic parameters derived in Section “Prediction of discharge current and applied magnetic pressure” are functions of angular frequency ω since ω affects the skin depth for all conductors. Based on the expressions for equivalent inductance and equivalent resistance (Eqs. (8) and (13)), both are functions of angular frequency ω, which, in turn, is determined by the inductance and resistance within the circuit. Therefore, these electromagnetic parameters are implicit functions. Before determining the electromagnetic parameters of the model, the angular frequency is determined using the iterative calculation method previously proposed by Neugebauer et al. [29]. This iteration process is illustrated in Fig. 5. Initially, an initial frequency ω⁽⁰⁾ is substituted into Eqs. (8) and (13) to calculate the equivalent inductance and equivalent resistance, denoted as L_eq⁽⁰⁾ and R_eq⁽⁰⁾, respectively. Then, L_eq⁽⁰⁾ and R_eq⁽⁰⁾ are substituted into Eqs. (1) to (3) to recalculate ω, denoted as ω⁽¹⁾. Next, ω⁽¹⁾ is compared with ω⁽⁰⁾, and the deviation between them is evaluated. If the relative deviation is below the allowed tolerance (e.g., 1%), ω⁽¹⁾ is accepted as the final result; otherwise, the guessed frequency is updated to ω⁽¹⁾, and the above three steps are iterated.

Fig. 5

Iterative process for determining the system angular frequency ω

After obtaining the angular frequency, a coupled analysis is performed on the electromagnetic field and deformation field according to the procedure shown in Fig. 6. In this process, constants circuit parameters are assumed, and the interaction between the circuit and magnetic field is neglected. The gap area A_g is updated based on the workpiece displacement S_w, taking into account the interaction between the electromagnetic field and deformation field. The updated A_g is based on the mold configuration shown in Fig. 4.

Fig. 6

Coupling process of the analytical model

Experimental procedure

The experimental procedure is divided into two parts. In the first part, a titanium BPP EMF experimental setup is constructed to validate the analytical model, and the coil current was measured by a Rogowski probe. In the second part, the EMF titanium BPP is achieved by adjusting the discharge parameters and the thickness of the accelerator board, as shown in Fig. 7(a). For the experiment, a 0.1 mm thick TA1-O titanium strip is used as the experimental material. The workpiece and driver sheet are square blanks matched with the coil, and the material parameters are selected according to Table 2. The experimental equipment used is the EMF-20 machine from Harbin Institute of Technology, and the device parameters are shown in Table 3.

Fig. 7

Experimental setup. a equipment; b mold and coil; c measured coil current distribution

Table 2 Material parameters for different driver sheets or workpieces

Table 3 EMF equipment parameters

Figure 7(b) shows the mold and coil designed based on the reference model in Fig. 8. The mold consists of a multi-channel parallel wave-shaped flow field with a depth-to-width ratio of 0.53 (0.4 mm channel depth/0.75 mm channel width). It contains a total of 20 channels, with a partial area of 335 mm × 82 mm for the channels, and the overall cavity area of the mold is 408 mm × 102 mm. The coil is made by tightly winding inner double glass-fiber-covered flat copper wire and polyimide film, and a center epoxy board is used to support the copper wire. In order to reduce the influence of coil end effects, the coil is centrally placed in the outer channel with 25 mm excess on each end. To mitigate electrical contact issues and reduce energy losses from arcs, the contact surfaces on the outer channel are coated with conductive. Figure 7(c) shows the measured current variation curves under three discharge energies: 4.05 kJ, 7.2 kJ, and 11.25 kJ, as well as the fitted curves calculated using Eqs. (1) to (3). From the graph, it can be observed that the fitted current variation curve matches the measured values well during the first half of the current variation cycle. Therefore, the fitted current variation curve can be directly loaded into the circuit equation as the measured current data to obtain the system's equivalent impedance (R_eq, L_eq).

Fig. 8

Geometric parameters of the UPC. a Dimension of the outer channel; b Dimension of the primary coil; c Assembly diagram of the primary coil and outer channel

Numerical model

The numerical model consists of a three-dimensional electromagnetic-coupled finite element model established in LS-DYNA. This model takes into account the eddy currents in both the driver sheet and the coil and is used to assist in the validation of the analytical model. Figure 9 illustrates the three-dimensional coupled field model of the UPC-EMF titanium BPP. By employing dense meshing on the thickness of the driver sheet, primary coil conductors, and the inner surface of the outer channel, high-gradient electromagnetic fields are captured. To ensure the correct formation of the induced current loop between the driver sheet and the inner surface of the outer channel, the mesh nodes on the contact surfaces of the driver sheet and the outer channel are merged, without considering the contact resistance between them. To meet the magnetic shielding assumption, magnetic field boundary conditions are set by defining segments on the upper surface and side walls of the outer channel and on the back and side of the driver sheet, eliminating the contributions of these segments from the boundary element calculations. The solution for coil currents is achieved using the "*EM_CIRCUIT" keyword, with the input variables being the system's equivalent impedance (R_eq, L_eq) and discharge parameters (C, U₀).

Fig. 9

The finite element models used to validate the analytical model. a representing the electromagnetic field model in the upper part; b representing the deformation field model in the lower part

The material properties of copper driver sheets can be characterized using the Johnson–Cook constitutive model proposed by Johnson and Cook [30], which simultaneously considers strain hardening, strain rate hardening, and adiabatic softening effects of materials. They obtained parameters of this model by Hopkinson bar tensile tests and torsion tests, and the model equation is shown as follows:

$$\sigma \text{=}\left({\text{A}}\text{+}{\text{B}}\cdot \dot{{\varepsilon }^{\text{n}}}\right)\left(\text{1} + {\text{C}}\cdot {\text{ln}}\frac{\dot{\varepsilon }}{{\dot{\varepsilon }}_{0}}\right)\left[{1}-{\left(\frac{{\text{T}}-{\text{T}}_{\text{r}}}{{\text{T}}_{\text{m}}-{\text{T}}_{\text{r}}}\right)}^{\text{m}}\right]$$

(26)

In the Eq. (26), ε denotes the equivalent strain, $\dot{\varepsilon }$ and ${\dot{\varepsilon }}_{0}$ (1.0 s⁻¹) represent the equivalent plastic strain rate and reference strain rate, respectively, A (90 MPa) is the yield stress at room temperature, B (292 MPa) and n (0.31) are the strain hardening parameters and strain hardening exponent, respectively, C (0.025) is the strain rate hardening coefficient, m (1.09) is the thermal softening coefficient, T_r (300 K) and T_m (1356 K) are the room temperature and material melting temperature, respectively.

Since the discharge experiment is conducted at normal temperature and the displacement of the sheet during deformation is small, Cui et al. [31] believe that the adiabatic temperature rise of the sheet caused by this plastic deformation is negligible. The driver sheet and workpiece can also utilize the Cowper-Symonds constitutive model, as shown in Eq. (27), to capture the high strain rate effects of the sheet material during the EMF process. The relevant material properties can be found in Table 2.

$$\sigma ={\sigma }_{ys}\left[1+{\left(\frac{\dot{\varepsilon }}{C}\right)}^\frac{1}{p}\right]$$

(27)

where σ_ys is the initial yield strength, $\dot{\varepsilon }$ is the plastic strain rate, and C and P are the strain rate parameters of the material. For aluminum alloy [32], C and P are 6500 s⁻¹ and 4 respectively. For TA1 materials [8], C and P are 200 s⁻¹ and 15 respectively. For SS316L material [33], C and P are 17 × 10⁶ s⁻¹ and 12, respectively.

Results and discussion

Validation of the analytical model

The proposed analytical model was validated through a four-step process by combining analytical, experimental, and numerical results. First, the ability of the analytical model to predict equivalent circuit parameters was evaluated. Second, the ability of the analytical model to predict dynamic phenomena was evaluated. Finally, the effectiveness of the magnetic shielding assumption and the reasonableness of the assumption of uniform magnetic flux distribution were assessed.

Thibaudeau et al. [14] suggest that the ratio between the workpiece eddy current I_ch&w and the total discharge current nI_c can characterize the magnetic coupling between the coil and the workpiece. Equation (9) clearly reveals how the geometric parameters of the electromagnetic field model affect the coupling coefficient. Figure 10 compares the analytical, numerical, and experimental results of the equivalent inductance, resistance, and coupling coefficient under the driving of a 0.15 mm thick Cu110 driver sheet. The deviations between the analytical and numerical results for these three physical quantities are 5.5%, 14.6%, and 1.2%, respectively, while the deviations between the analytical and experimental results are 34.1%, 6.1%, and 9.8%, showing good agreement. Lai et al. [19] investigated the equivalent inductance, resistance, and coupling coefficient of a 1 mm thick AA6061 workpiece. The research findings reveal that the maximum deviation between analytical and numerical results is 33%, and the maximum deviation between analytical results and experimental results is 30%. They assert that the primary reasons behind these discrepancies are the neglect of coil conductor edge effects and gaps.

Fig. 10

Analytical, numerical and experimental results of equivalent inductance, resistance and coupling coefficient of 0.15 mm Cu110

Figure 11 presents the analytical and numerical results for Cu110 driver sheets of different thicknesses, ranging from 0.1 mm to 1.6 mm. The results indicate that the equivalent inductance and coupling coefficient are insensitive to the thickness variation within the range of 0.1 mm to 1.6 mm, with a maximum variation rate of around 5%. However, the variation rate of the equivalent resistance is approximately 50%, indicating a much higher sensitivity of resistance. The analytical model clearly reproduces the saturation phenomenon of resistance when the thickness increases from 0.8 mm to 1.6 mm. This saturation phenomenon demonstrates the rationality of defining the penetration depth ε_w^cur in a segmented form. Lai et al. [19] discussed the equivalent inductance, resistance, and coupling coefficient of AA1060 workpieces at different thicknesses. Analytical and numerical results show that the saturation phenomenon of resistance occurs as the thickness increases from 1 to 2 mm. The reason for this difference lies in the utilization of different sheet resistivities. When the thickness of the driver sheet exceeds λ^cur $\sqrt{2/{\omega \mu }_{0}{\sigma }_{w}}$, the current density distribution through the thickness of the driver sheet should follow an exponential form. When the thickness of the driver sheet is less than λ^cur $\sqrt{2/{\omega \mu }_{0}{\sigma }_{w}}$, the eddy current tends to have a uniform distribution across the thickness of the driver sheet.

Fig. 11

Equivalent inductance, resistance, and coupling coefficients under different driver thicknesses (0.1 mm ~ 1.6 mm) for analytical and numerical prediction

Figure 12 presents the analytical and numerical results for driver sheets made of six different materials, with varying resistivities ranging from 17.2 nΩ·m to 740 nΩ·m, as shown in Table 2. When the resistivity increases from 17.2 nΩ·m to 740 nΩ·m, the variation rates of the equivalent inductance and coupling coefficient are both below 10%, while the variation rates of the equivalent resistance are 39.8% and 43.5% respectively. This indicates that the resistance is highly sensitive, which is consistent with the predicted results in Fig. 11. Lai et al. [22] analyzed the equivalent inductance, resistance, and coupling coefficient of workpieces with varying resistivities. Analytical and numerical results indicate that the variation rates of resistance are 108% and 104% respectively. The reason for this difference lies in the utilization of different sheet thicknesses. Furthermore, when the resistivity exceeds 117 nΩ·m, the trends of the analytical predictions for the inductance and coupling coefficient noticeably deviate from the numerical predictions. The analytical predictions exhibit a saturation phenomenon within this resistivity range, whereas the numerical predictions show a monotonic trend. The saturation phenomenon in the analytical predictions is due to the segmented definition of the reasonable magnetic penetration depth ε_w^mag. This explanation of the saturation phenomenon aligns with the observed explanation in the resistance results shown in Fig. 11. When the thickness of the driver sheet exceeds λ^mag $\sqrt{2/{\omega \mu }_{0}{\sigma }_{w}}$, the current density distribution through the thickness of the driver sheet should follow an exponential form. When the thickness of the driver sheet is less than λ^mag $\sqrt{2/{\omega \mu }_{0}{\sigma }_{w}}$, the eddy current tends to have a uniform distribution across the thickness of the driver sheet.

Fig. 12

Equivalent inductance, resistance, and coupling coefficients under different driver resistivities (17.2 nΩ·m ~ 740 nΩ·m) for analytical and numerical prediction

Figure 13 depicts the results of driving 0.1 mm TA1 using 0.15 mm Cu110 at three discharge energy levels: 7.2 kJ, 11.25 kJ, and 16.2 kJ, based on the inductance and resistance shown in Fig. 10. Figure 13(a) presents the discharge current of the primary coil. The peak discharge current predicted by the analytical model is about 3.2% higher than that of the numerical model. This can be explained by the 5.5% decrease in inductance and 14.6% increase in resistance shown in Fig. 10. Furthermore, the peak current predicted by the analytical model is higher than the experimentally measured peak current, and the deviation of the peak current increases with the increase of discharge energy. Thibaudeau et al. [14] attribute this phenomenon to the neglect of temperature rise in the primary coil. During the discharge process, the electrical conductivity of the coil decreases with an increase in temperature, leading to a reduction in the discharge current of the primary coil. Figure 13(b) illustrates the magnetic pressure on the driver sheet. At energy levels of 7.2 kJ, 11.25 kJ, and 16.2 kJ, the first peak values of magnetic pressure are 11.14 MPa, 17.29 MPa, and 24.7 MPa, respectively. The ratios of peak pressure to the corresponding discharge energy are 1.547 MPa/kJ, 1.536 MPa/kJ, and 1.524 MPa/kJ. These ratios are very close, which supports the finding from Lai et al. [19] that there exists a proportional relationship between magnetic pressure and discharge energy. The slight decrease in this ratio with the increase of discharge energy reflects the interaction between the magnetic field and the deformation of the workpiece. Figure 13(c) shows the velocity of the workpiece. At the three discharge energies, up to about the first velocity platform, the analytical and numerical speeds match very well throughout the process, well reproducing the workpiece speed in the initial acceleration process, with a maximum deviation of less than 6.3%. Dong et al. [8] established a window of the relationship between the impact velocity of the workpiece (that is, discharge voltage and acceleration distance) and the channel depth. They believed that under the discharge energy of 10.8 kJ and the appropriate acceleration distance (4 mm), the impact velocity in the TD direction should exceed 272 m/s, while the impact velocity in the RD direction should exceed 309 m/s. The channel depth can reach 0.4 mm. From Fig. 13(c), it can be observed that under the three discharge energy levels, the impact velocity of the workpiece can exceed 300 m/s. Figure 13(d) displays the displacement of the workpiece. Similar to the workpiece velocity, at 75 μs, the maximum deviation between the analytical and numerical velocities under the three discharge energy levels is below 6.4%, and the workpiece displacement increases with the increase of discharge energy. This variation is mainly attributed to the increase in magnetic pressure. Additionally, Thibaudeau et al. [14] suggest that the neglect of temperature rise in the driver sheet and workpiece may overestimate the deformation of the workpiece, and thinner plates with higher resistivity may result in higher temperature rise.

Fig. 13

Under three discharge energies (7.2 kJ, 11.25 kJ, and 16.2 kJ). a discharge current; b driver magnetic pressure; c workpiece velocity; d workpiece displacement

Figure 14 presents the results of driving 0.1 mm TA1 using Cu110 driver sheets of three different thicknesses (0.1 mm, 0.2 mm, and 0.3 mm) at a discharge energy of 11.25 kJ, based on the inductance and resistance shown in Fig. 12. Figure 14(a) illustrates the discharge current of the primary coil. The three discharge currents almost overlap, with maximum differences in their amplitudes being below 8.3%. This difference is attributed to the insensitivity of the equivalent inductance and coupling coefficient to the workpiece thickness within the range of 0.1 mm to 0.3 mm, while only the equivalent resistance exhibits some sensitivity. Figure 14(b) displays the magnetic pressure on the driver sheet. The overall trend of peak magnetic pressure increases with an increase in workpiece thickness. The magnetic pressure of the 0.1 mm thick driver sheet is lower than that of the 0.2 mm and 0.3 mm thick driver sheets, and the deviation between them intensifies over time. At the first peak, the magnetic pressure of the 0.1 mm driver sheet is 15.8% lower than that of the 0.3 mm thick workpiece, while at the second peak, the deviation increases to 63.8%. Figure 14(c) shows the velocity of the workpiece. Throughout the process, the proposed analytical results align well with the numerical analysis results, with a deviation of approximately 6.7%. Figure 14(d) presents the displacement of the workpiece. Similar to the numerical model, the analytical model successfully reproduces the initial stage deformation of the 0.1 mm, 0.2 mm, and 0.3 mm workpieces. Contrary to the magnetic pressure on the driver sheet, the final displacement of the workpiece increases as the thickness of the driver sheet decreases. Thibaudeau et al. [14] studied three different thicknesses (0.5 mm, 1 mm, and 2 mm) of AA6061 at a discharge energy of 6 kJ. The results show that the deformation acceleration of the 0.5 mm workpiece is much larger than that of the 1 mm and 2 mm workpieces. Similar to this research, thinner workpieces exhibit more significant deformation, resulting in greater attenuation of magnetic pressure.

Fig. 14

Under three thicknesses of Cu110 driver sheet (0.1 mm, 0.2 mm, and 0.3 mm). a discharge current; b Cu110 driver magnetic pressure; c workpiece velocity; d workpiece displacement

Figure 15 shows the results of driving 0.1 mm TA1 using 0.15 mm thick driver sheets made of two different materials, Cu110 and AA1060, at a discharge energy of 11.25 kJ, as well as the results of formulating 0.1 mm TA1 without a driver sheet, based on the inductance and resistance shown in Fig. 12. Figure 15(a) illustrates the discharge current of the primary coil. The current curves for the analytical and numerical models almost overlap with a maximum deviation of only 2.1%. The amplitude deviation between the two materials, Cu110 and AA1060, used as driver sheets, is around 12%, while without a driver sheet, the deviation increases to about 40%. This is primarily due to the approximately 33.5% increase in the equivalent resistance of TA1. Thibaudeau et al. [14] ignored the differences in the equivalent inductance and equivalent resistance among five different materials (Cu110, AA6061, Cu230, Cu510, SS321). According to the research by Lai et al. [22], this ultimately resulted in a discharge current deviation of around 9%. Figure 15(b) displays the magnetic pressure on the plates. The magnetic pressures for Cu110 and AA1060 driver sheets are 17.4 MPa and 14.2 MPa respectively, with a maximum deviation of 20.2% in the amplitude of the first wave period. In contrast, the peak magnetic pressure for the workpiece without a driver sheet is only 0.27 MPa. This is because the resistivity of TA1 is approximately 32 times that of Cu110. Therefore, it is necessary to use driver sheets with high conductivity to drive the forming process of 0.1 mm TA1 workpieces. Figure 15(c) shows the velocity of the workpieces for the three different materials. Both the analytical and numerical models accurately reproduce the velocity during the initial stage of deformation. At 75 μs, the maximum deviation between the analytical and numerical velocities is below 13.3%. After 75 μs, the deviation gradually decreases to below 11.6%. Figure 15(d) depicts the displacement of the workpieces for the three different materials. When Cu110 and AA1060 are used as driver sheets, in contrast to their magnetic pressure, the displacement decreases as the resistivity of the driver sheet increases. This is because AA1060 has much lower mass density and yield strength than which reduces the energy consumed by the driver sheet in driving the forming process of the workpiece, thereby enhancing the acceleration of the workpiece. When no driver sheet is, the displacement of the workpiece significantly reduces to 0.38 mm.

Fig. 15

Under two driver materials (Cu110 and AA1060) and without the driver sheet. a Discharge current; b magnetic pressure; c workpiece velocity; d workpiece displacement

To assess the validity of the magnetic shielding hypothesis, Fig. 16 compares the analytical and numerical coupling coefficients under different driver sheet thicknesses and resistivities. The analytical results align well with the numerical results in cases of larger thicknesses and smaller resistivities. However, in cases of smaller thicknesses and larger resistivities, the analytical results deviate from the numerical results, indicating a lower limit for the driver sheet thickness and an upper limit for the resistivity in which the applicability of the magnetic shielding hypothesis exists. Using a 5% deviation as a criterion, two critical boundaries can be identified to determine the applicability of the magnetic shielding hypothesis, as shown in Table 4. The calculated critical ω/β values based on the two critical conditions are both 9.5, while Lai et al. [19] employed a track-shaped UPC to obtain a critical ω/β value of 8.8 for evaluating the applicability of the model. This suggests the existence of a relatively good critical ω/β criterion under the current coil structure, which can serve as a judgment criterion for the applicability of the EMF titanium BPP model.

Fig. 16

Analytical and numerical coupling coefficient under. a different driver thicknesses; b different driver resistivities

Table 4 Critical conditions for the applicability of the analytical model

To evaluate the reasonableness of the assumption of uniform magnetic flux distribution along the magnetic path, Fig. 17 demonstrates the analysis process of the magnetic pressure exerted on the driver sheet. Figure 17(a) illustrates the magnetic pressure distribution generated by the coil on the driver sheet. Nine typical points (1–9) are selected in the transverse, longitudinal, and center regions of the sheet deformation area. The red dashed box represents the primary coil, while the white dashed box indicates the region with uniform pressure. Due to the influence of end effects, the periphery of the driver sheet in the coil length direction experiences less force. The temporal variation of the normal magnetic pressure acting on different typical points during the deformation process of the driver sheet is depicted in Fig. 17(b). The analytical results align well with the numerical results, with a maximum deviation of 13.3%. Considering the changes in transverse and longitudinal typical points magnetic pressure, the peak values of the normal magnetic pressure essentially coincide within the primary deformation region. This indicates that the uniformly pressed coil can provide a uniform magnetic pressure, leading to uniform plastic deformation of the driver sheet. Figure 17(c) presents the magnitude of the magnetic pressure exerted on the driver sheet along the coil width and length directions. It can be observed that the magnetic pressure on the driver sheet exhibits relatively low uniformity along the coil length direction, with a value of 82.24%. To mitigate the influence of end effects, it is advisable to confine the forming region within a uniform coil turn range. Despite the slight non-uniformity in the coil length direction, this finding still confirms the validity of the analytical model assumption of a uniformly distributed magnetic flux along the magnetic path.

Fig. 17

Analysis of driver force uniformity. a magnetic pressure nephogram of the driver sheet and positions of typical points; b varying curve of magnetic pressure at typical points; c uniformity of magnetic pressure along the length and width directions of the coil (C = 100μF, U = 18 kV)

Figure 18 depicts a schematic diagram illustrating the impact of the coil conductor cross-section on the magnetic pressure distribution across the driver sheet. From the figure, it can be observed that, with a fixed coil length, the magnitude of the unit length turns n/l_c reflects the effects of the wire gap g_s and the wire width w_s. Thibaudeau et al. [14] argued that increasing the unit length turns n/l_c of the coil can make the magnetic field more uniform, thereby generating a uniform pressure distribution. According to Eq. (14), the magnetic pressure on the driver sheet can be expressed as:

Fig. 18

Schematic diagram illustrating the impact of coil conductor cross-section on the distribution of magnetic pressure on the driver sheet

$${P}_{D}=\frac{1}{2}{\mu }_{0}\cdot {\left(\frac{1}{\frac{{A}_{g}}{{A}_{c}}+1}\right)}^{2}\cdot {\left(\frac{n}{{l}_{c}}\right)}^{2}{I}_{c}^{2}\left({\text{t}}\right)=\frac{1}{2}{\mu }_{0}\cdot {\left(\frac{1}{\frac{{A}_{g}}{{A}_{c}}+1}\right)}^{2}\cdot {\left(\frac{1+\frac{{g}_{s}}{{l}_{c}}}{{w}_{s}+{g}_{s}}\right)}^{2}{I}_{c}^{2}\left({\text{t}}\right)$$

(28)

When considering the impact of the discharge circuit current, it is common to reduce the resistance and inductance of the primary coil in order to increase the discharge current. This requires reducing the unit length turns n/l_c, which means increasing the wire gap g_s or the wire width w_s. However, Kamal et al. [13] argue that this measure may result in a corrugated distribution pattern of magnetic pressure along the coil length direction on the driver sheet surface, thereby reducing the uniformity of the magnetic pressure distribution.

Figure 19 compares the magnetic pressure distribution on the driver sheet for 5 different unit length turns. The dimensional parameters in the planar direction of the coil conductor are presented in Table 5. When keeping the wire width constant and changing the wire gap (2 mm ~ 4 mm), the fluctuation of the magnetic pressure in the numerical results increases with an increase in wire gap, with values of 2.1%, 3.7%, and 6.8%, respectively. When maintaining the wire gap and changing the wire width (5 mm ~ 10 mm), the fluctuation of the magnetic pressure in the numerical results decreases with an increase in wire width, with values of 3.7%, 0.4%, and 0.05%, respectively. When the wire gap is 2 mm to 4 mm and the wire width is 5 mm to 15 mm, the peak magnetic pressure on the drive sheet increases with the decrease of the unit length turns, and the distribution uniformity shows a decreasing-then-increasing trend. Kamal et al. [13] investigated the effect of wire gap using circular cross-sections with different wire center distances (5.4 mm and 10.8 mm). The results showed that, under larger wire gaps, it is not possible to achieve a uniformly distributed pressure. Therefore, in order to maintain a balance between the magnitude and uniformity of the magnetic pressure on the driver sheet, and to ensure electrical insulation requirements, it is advisable to minimize the wire gap of the primary coil as much as possible and increase the width of the square wire.

Fig. 19

Distribution of magnetic pressure on the driver sheet for different numbers of turns per unit length (wire gap of 2 mm ~ 4 mm and wire width of 5 mm ~ 15 mm)

Table 5 Parameter settings that affect the number of turns per unit length

Optimal geometric configuration of the coil

To obtain the optimal height for the primary coil, wire thickness, and primary-secondary gap (primary coil-outer channel/driver sheet), a 0.15 mm thick Cu110 driver sheet is used to drive 0.1 mm TA1 during discharge with an energy of 11.25 kJ. By adjusting the corresponding coil parameters while keeping other parameters of the coil geometry constant, the peak magnetic pressure on the driver sheet and the primary coil are analyzed. The numerical values of the magnetic pressure represent its direction, with positive values indicating pressure along the direction of workpiece forming. Figure 20 compares the analytical and numerical results of different primary coil heights for coil wire thickness of 2 mm and primary and secondary side gap of 3 mm. The parameter settings for the height of the primary coil are based on Table 6. Figure 20(a) displays the variation of the peak magnetic pressure on the driver sheet. The optimum height of the primary coil exists at 13.2 mm, resulting in the maximization of coil forming efficiency. This is similar to the argument made by Lai et al. [19] for the track-shaped UPC. Figure 20(b) illustrates the variation of the peak magnetic pressure on the primary coil. When the coil is not under stress, an optimal solution exists for the initial coil height at 18.3 mm, which maximizes the coil lifespan. On the left side of this height, there is a zone where the coil fails, with wire expansion and damage to the insulation layer gradually occurring. On the right side, there is a safety zone where the primary coil wire is compressed towards the inner diameter of the coil, and the high-strength epoxy support structure inside the coil ensures its longevity. Comparing the optimal solutions for these two scenarios, the optimal height of the primary coil corresponding to the peak magnetic pressure on the driver sheet is 13.2 mm, which falls outside the safety zone of the primary coil height corresponding to the peak magnetic pressure (≥ 18.3 mm). Therefore, the optimal height for the primary coil is 18.3 mm.

Fig. 20

Influence of coil heights. a peak magnetic pressure of driver sheet; b peak magnetic pressure of primary coil

Table 6 Factors influencing the height of the primary coil

On the basis of the obtained optimal height of the primary coil (18.3 mm), while maintaining the primary and secondary side gap of 3 mm, Fig. 21 compares the analytical and numerical results for different wire thicknesses of the primary coil. Figure 21(a) displays the variation of peak magnetic pressure on the driver sheet. The peak magnetic pressure exhibits a monotonically decreasing trend with respect to the height of the primary coil. This indicates that a smaller wire thickness leads to higher forming efficiency of the coil. This argument is supported by the research findings of Kim et al. [15]. However, wires that are too thin may result in lower mechanical strength, higher resistance, increased heat loss, and larger temperature rise during discharge, which restrict the lower limit of wire thickness. Figure 21(b) illustrates the variation of peak magnetic pressure on the primary coil. Similar to the analysis of coil height, when the coil is not under stress, an optimal solution exists for wire thickness at 2.7 mm, maximizing the coil lifespan. On the right side of this thickness lies the zone where the coil fails, while on the left side is the safety zone of the primary coil (≤ 2.7 mm).

Fig. 21

Influence of coil wire thicknesses. a peak magnetic pressure of driver sheet; b peak magnetic pressure of primary coil

On the basis of the obtained optimal height of the primary coil (18.3 mm) and optimal wire thickness of the primary coil (2.7 mm), Fig. 22 compares the analytical and numerical results for different primary-secondary gaps. Figure 22(a) displays the variation of peak magnetic pressure on the driver sheet. exhibits a monotonically decreasing trend with respect to the primary and secondary side gap. This indicates a smaller the primary and secondary side gap leads to higher forming efficiency of the coil. This argument is also supported by the research findings of Kim et al. [15]. However, there are limitations on the lower limit of the primary and secondary side gap due to considerations of ensuring electrical insulation requirements and possible mechanical reinforcement. Figure 22(b) illustrates the variation of peak magnetic pressure on the primary coil. Similar to the analysis of coil height and wire thickness, when the coil is not under stress, an optimal solution exists for the primary and secondary side gap at 3.2 mm, maximizing the coil lifespan. On the right side of this gap lies the zone where the coil fails, while on the left side is the safety zone of the primary and secondary side gap (≤ 3.2 mm).

Fig. 22

Influence of primary and second side gap. a peak magnetic pressure of driver sheet; b peak magnetic pressure of primary coil

EMF Titanium BPP Experiment

Figure 23 demonstrates the forming of TA1 titanium BPPs achieved through the uniform pressure magnetic pulse technology. The channel depth of the titanium BPP reached 0.4 mm under three consecutive 9 kV discharges, a 2 mm acceleration distance, and a 0.3 mm thick Cu110 driver sheet. Figure 24 displays the cross-sections of the BPP channels observed through metallographic microscopy. The section thickness of the BPP is relatively uniform and smooth. Measurements were taken on the channel cross-sections at the surface, upper corner radius, sidewall, lower corner radius, and bottom surface (locations 1–9 in the Fig. 24), revealing a maximum thinning rate of 18.49% for the BPP. Figure 25 presents the measurements of the channel depths along the TD direction on the BPP relative to the die surface using a comprehensive surface profile measurement instrument. Along the TD direction, except for a few channel depths slightly lower than 0.38 mm, the remaining channels fluctuate between 0.38 mm and 0.39 mm. Considering a channel depth is 400 μm, the fluctuation is less than ± 10 μm, corresponding to a fluctuation rate of less than ± 2.5%. This indicates that the electromagnetic force generated by UPC on the driver sheet is sufficiently uniform, resulting in a high consistency of the formed titanium BPP channels, which meets industrial requirements. Figure 26 illustrates the surface profiles of 20 channels along the TD direction on the BPP opposite the die surface. The filling rate of the channels obtained from the forming experiment is above 95%, indicating a high overall filling rate. This suggests that the fit between the BPP channel profile and the mold channel profile is good, accurately reflecting the mold shape.

Fig. 23

Titanium BPPs fabricated by 0.3 mm thick Cu110 driver sheet under three 9 kV continuous discharges and 2 mm acceleration distance

Fig. 24

Thickness change of flow channel section

Fig. 25

Channel depth in TD direction of bipolar plate

Fig. 26

Comparison between the channel profile of BPP and the channel profile of mold

Conclusion

Facing the challenges in forming titanium BPPs, an efficient and reliable multiphysics EMF analysis model was verified and obtained through the combination of experiment and LS-DYNA numerical simulation. Considering the forming efficiency and durability of the coil, the geometric shape of the arc-shaped UPC was optimized. Finally, TA1 titanium BPPs meeting industrial requirements were manufactured using the uniform pressure magnetic pulse technology. The following conclusions can be drawn:

• (1) The equivalent resistance is more sensitive to materials with low thickness and high resistivity for the driver sheet. In comparison to the conductivity of the driver sheet, the difference in mass density exhibits more sensitivity to the acceleration magnitude.

• (2) Based on the ω/β magnetic shielding criterion, ω/β = 9.5 can provide an applicability boundary for the arc-shaped UPC. Reducing the wire gap of the primary coil and increasing the width of the square wire contributes to improving the uniformity of workpiece forming while ensuring electrical insulation requirements.

• (3) To achieve the highest coil forming efficiency without coil failure, the arc-shaped UPC has the best primary coil height, wire thickness and primary and secondary side gap of 18.3 mm, 2.7 mm and 3.2 mm, respectively.

• (4) Under the conditions a discharge capacitor of 100 μF, an acceleration distance of 2 mm, and a 0.3 mm thick Cu110 driver sheet, titanium BPPs with a channel depth-to-width ratio of 0.53 were successfully manufactured through three consecutive 9 kV discharges. The channel depth achieved was 0.4 mm, with a maximum thinning rate of 18.2%, a maximum fluctuation rate not exceeding 2.5%, and a channel filling rate exceeding 95%.

Appendix A: Ampere's circuital law and gauss's magnetism law

The following is the integral form of Ampère's Circuital Law and Gauss's Magnetism Law, which establish the physical foundations for electromagnetic modeling in Section “Prediction of discharge current and applied magnetic pressure”:

$$\oint_{\partial\sum}\text{H}\cdot{\text{d}}_l=\iint_\sum \nolimits\text{J}\cdot{\text{d}}_s$$

(29)

$$\oiint_{\partial\Omega}\text{B}\cdot{\text{d}}_s=0$$

(30)

where H is the magnetic field strength, J is the current density, B is the magnetic induction intensity of the current on a surface S, Σ is the arbitrary fixed surface with closed boundary curve ∂Σ, and Ω is the arbitrary fixed volume with closed boundary surface ∂Ω. And H and B satisfy the following relation:

Here, H represents the magnetic field intensity, J represents the current density, B represents the magnetic induction due to current through the surface S, Σ is an arbitrary fixed surface bounded by the closed curve ∂Σ, and Ω is an arbitrary fixed volume enclosed by the closed surface ∂Ω. Additionally, H and B satisfy the following relationship:

$${\text{B}}={\mu }_{0}H$$

(31)

• Eq. (29) is called Ampère's Circuital Law, which states that the integral of the magnetic field intensity H around the closed curve ∂Σ is proportional to the total current passing through the surface Σ.

• Eq. (30) is called Gauss's Magnetism Law, which states that the total magnetic flux passing through the closed surface ∂Ω is zero.