Introduction

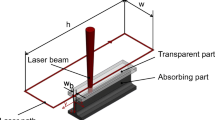
Transmission Laser Welding technique [1] (TLW) presents specific advantages for industrial applications over other conventional technologies: the method is accurate, flexible, small heat affected zone, easy to automate and control and non-contaminant, heat transfer with the ability to optimize the welding temperature (at the interface of the welding zone), absence of vibration during the welding process (contrary to the ultrasonic welding, friction welding), fast welding speed for welding plastic parts with an acceptable welding time. Transmission Laser Welding of composites involves two joining parts. One transparent in the laser wavelength and the other part is absorbent in the same wavelength. The two parts are positioned together before the welding. The laser beam energy is transmitted through the transparent material and is absorbed within the surface of the two materials (Fig. 1). The contact between the parts causes heating of the substrate placed at the interface (through heat transfer via conduction); thus, melting and fusion of the both materials interface occurs (the bonding between the two parts occurs when T>T melt in this area). The extent of the melted material volume depends on the quantity of the energy delivered to the components through the laser beam. The energy is deposited at the interface in a localized volume causing the formation of a weld zone. Comparing with welding traditional techniques, laser welding efficiency strongly depends on the optical properties of the material [2]: absorption, transmission, refraction, reflection, scattering and thermal properties: heat capacity, thermal conductivity and density.

Fig. 1
figure 1

Laser welding system [1]

Full size image

TLW depends on several parameters which are related to the laser beam: laser focusing distance (irradiated laser section area); laser power, velocity and wavelength. Low energy values can lead to a weak joint with low strength, while high energy values may cause degradation and vaporization phenomena; in both cases, a bad joint quality is obtained. Consequently, the energy delivered on the surfaces needs to be optimized for every process application [3]. A growing numbers of applications of composite thermoplastics have lead to an increasing interest in research in the field of laser welding. This is due to the increased need for the structural composite thermoplastic involving oriented continuous fibers tissue. However, some difficulties are experienced during this process: heterogeneous and anisotropic materials; problems of the laser beam transfer caused by the multiplication of fiber-matrix interfaces in materials. This heterogeneity on light scattering should be studied. The literature contains many investigations on the process modeling for the calculation of the temperature field at the interface. The energy input due to the laser is often imposed on the surface. The shape of the laser beam is assumed and is not computed. The absorption phenomenon at the surface of the absorbing material is calculated using the Beer-Lambert law. Labeas et al. [3] assume a heat flux density with Gaussian distribution in order to compute the temperature field. Shanmugam et al. [4] also consider the same assumptions. Grewell and Benatar [5] modeled the amount of scattering intensity diffused in the material using Lambert-Bouger’s law. Authors in [6–8] consider that the laser beam is absorbed in the second material according to the Beer Lambert Law. In [9] a technic called the direct-scattering model (mathematical function) is developed to describe laser beam transmission and absorption in light-scattering polymers. A modified Bouguer-Lambert law is used to describe light intensity distribution in these multi-scattering polymers. Rosenthal [10] develops an analytical solution of heat flow during welding based on conduction heat transfer for predicting the shape and the temperature field for three-dimensional welds. Hou [11] proposed analytical general solutions (both transient and steady state) for the temperature field rise at any point due to stationary or moving plane heat sources of different shapes (elliptical, circular, rectangular, and square) and heat intensity distributions (uniform, parabolic, and normal). The authors [12] also proposed an analytical model the temperature field at a three-dimensional by numerically solving the model using commercially available mathematic software Matlab.

In this study, the purpose is to determine the energy reaching at the interface of the two parts. A macroscopic analytical model is developed and compared to a microscopic numerical model, which is able to simulate and to optimize the laser scattering during the process. This analytical model describes laser beam transmission in light-scattering thermoplastics composites. The radiative energy is estimated at the welding interface of the two materials in order to describe the heat source. This analytical model can be used for FEM computations of the temperature. A correlation between the refraction indexes of fiber and matrix, the fiber volume fraction and the macroscopic light scattering is done. An identification of the main parameters of the analytical model will also be carried using Ray Tracing method.

Analytical model

In thermoplastic composite parts made of polymers and continuous fibers, a scattering occurred during the laser welding. It will therefore be problematic to apply Bouguer-Lambert law to describe light intensity distribution in these multi-scattering thermoplastic composites. It is well-known that fiber increases the scatter of the laser light, which in turn increases the effective beam diameter [13]. In the study, an analytical model is developed to describe laser light path in scattering composites by introducing light scattering ratio and scattering standard deviation. The Fig. 2 sketches the mechanism of light transmission in the transparent composite part. In this study, the absorption is neglected versus the scattering effect.

Fig. 2
figure 2

Light transmission in composite part

Full size image

Due to the light scattering, a collimated beam is requested instead of a focused beam. A well-suited modelling of the laser heat source for the gaussian and rectangular distribution is presented as in [11]. A general solution for various surface heat sources of different heat intensity for different shapes (elliptical, circular, rectangular, and square) is presented. The heat input is distributed on the surface and the surface flux is represented by [14]:

$$ \mathrm{Q}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{I}}_{\mathrm{o}}\times {\mathrm{I}}_{\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right) $$
(1)

Io is the laser power (W), In (x, y) the surface distribution function, which is maximum and centered in (x = 0, y = 0). This function represents a normalized [14, 15] power flux distribution defined as power per unit area so that its integral over the beam area is equal to unity :

$$ {\displaystyle \underset{\mathrm{S}}{\int }{\mathrm{I}}_{\mathrm{n}}}\left(\mathrm{x},\mathrm{y}\right)\mathrm{dxdy}=1 $$
(2)

S is the beam section zone. During the laser welding, the heat flux reaches the higher intensity in the central welding zone. When we keep away from this central zone, the heat flux decreases. It can be assumed that the laser light follows the Gaussian distribution law in the medium (phenomenological approach) [4, 16]. The laser beam can be considered as a sum of beam with an infinitesimal cross section. We call it micro beam. The energy of a micro beam at location (xo, yo) is equal to Io × In(xo,yo), so the sum of the micro beam is equal to Io. Without regarding the shape of the laser beam (Gaussian, Rectangular…), all the micro beams are assumed to be Gaussian. At the incoming surface, the standard deviation of the Gaussian law of the micro beam is equal to zero. The standard deviation is increased with the sample thickness. Each micro beam in the transparent component changes the direction (due to the change of refractive indices between the matrix and the fiber) randomly due to the refraction phenomenon in each matrix-fiber interface. This leads a portion of the laser beam which goes the incoming surface (Backward beam) and a portion of the beam which goes to the welding interface (Inward beam) (Fig. 3).

Fig. 3
figure 3

A micro beam mechanism

Full size image

In each location in the laser beam (xo, yo), we assume that the local energy of the inward beam follow a Gaussian distribution centered in xo, yo and the scattering standard deviation is a function of the thickness. This law is expressed below:

$$ \mathrm{G}\left[\left(\mathrm{x}-{\mathrm{x}}_0\right),\left(\mathrm{y}-{\mathrm{y}}_0\right)\right]=\mathrm{G}\left(\mathrm{x}-{\mathrm{x}}_0\right)\times \mathrm{G}\left(\mathrm{y}-{\mathrm{y}}_0\right) $$
(3)
$$ \mathrm{G}\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}}\right)=\frac{1}{\sqrt{2\pi }{\sigma}_x}{e}^{-\frac{{\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}}\right)}^2}{2{\sigma}_{\mathrm{x}}{}^2}} $$
(4)
$$ \mathrm{G}\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{o}}\right)=\frac{1}{\sqrt{2\pi }{\sigma}_y}{\mathrm{e}}^{-\frac{{\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{o}}\right)}^2}{2{\sigma}_{\mathrm{y}}{}^2}} $$
(5)

x and y are space variables, σ is the spatial distribution parameter of the Gaussian function (scattering standard deviation), xo and yo are centers of each Gaussian micro beam. We assume that the distribution law, which represents the refraction phenomena at the microscopic scale, and the light scattering phenomenon at the macroscopic scale in the composite is a dependent function of the medium thickness (z). It is also depends of the microstructure and physical properties of the composite. The distribution of the total power of the laser beam in the media is expressed by :

$$ \mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)={\mathrm{I}}_{\mathrm{o}}\times \updelta\ \left(\mathrm{z}\right){\displaystyle \underset{\mathrm{S}}{\int }{\mathrm{I}}_{\mathrm{n}}}\left({\mathrm{x}}_{\mathrm{o}},{\mathrm{y}}_{\mathrm{o}}\right)\times \mathrm{G}\left[\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}}\right),\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{o}}\right)\right]{\ \mathrm{dx}}_{\mathrm{o}}{\mathrm{dy}}_{\mathrm{o}} $$
(6)

δ (z) is the light scattering ratio : it is defined as the value of the scattered laser power divided by the total laser power Io. It is a material dependent property, and also a function of the light penetration depth in the composite. In the literature, some studies [5, 17] show that δ  decreases exponentially. The attenuation of the radiation power through a media is due to an extinction phenomenon, wherein the absorption and scattering may also coexist or dominate one another, depending on the optical properties of the media. In this model, only the optical scattering of the laser beam in the transparent part is taking into account (absorption is negligible). δ  might also be expressed by the following relation:

$$ \delta\ \left(\mathrm{z}\right)=\frac{\mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)}{{\mathrm{I}}_{\mathrm{o}}}={\mathrm{e}}^{-\mathrm{Dz}} $$
(7)

The power of the backward micro beam is 1 − δ (z). D is the optical scattering coefficient (m−1). In the case of the laser beam with a Gaussian distribution, the function In(x,y) is given by the following expression:

$$ {\mathrm{I}}_{\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)=\frac{1}{2\pi {\sigma}_0{}^2}{\mathrm{e}}^{-\frac{{\left(\mathrm{x}+\mathrm{y}\right)}^2}{2{\sigma}_0{}^2}} $$
(8)

With σo the spatial shape parameter of the initial laser beam (proportional to the beam diameter). In order to highlight the importance of the knowledge of the composite microstructure on the weldability of two parts, we choose to apply the model for UD composite due to the strong anisotropic microstructure of the composite. The light scattering occurs in the orthogonal plan of the fiber direction (Fig. 4). We note I(x) the intensity distribution. In this case, we can express I(x,y) as the decoupled product of I(x) and I(y) :

Fig. 4
figure 4

Model description

Full size image
$$ \mathrm{I}\left(\mathrm{x}\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\mathrm{G}\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}},0\right)\mathrm{p}\left({\mathrm{x}}_{\mathrm{o}}\right){\mathrm{dx}}_{\mathrm{o}} $$
(9)

Where the expression of p at xo is :

$$ \mathrm{p}\left({\mathrm{x}}_0\right)=\frac{1}{\sqrt{2\pi }{\sigma}_0}{\mathrm{e}}^{-\frac{{\mathrm{x}}_0{}^2}{2{\sigma}_0{}^2}} $$
(10)

We notice that the Eq. (9) represents the convolution product of the two functions (p and G). However, the convolution of two gaussian functions is also a gaussian function. So Eq. (9) can be express using (4) by :

$$ \mathrm{I}\left(\mathrm{x}\right)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\left(\frac{1}{\sqrt{2\pi }{\sigma}_x}{\mathrm{e}}^{-\frac{{\left(\mathrm{x}-{\mathrm{x}}_0\right)}^2}{2{\sigma}_x{}^2}}\frac{1}{\sqrt{2\pi }{\sigma}_o}{e}^{-\frac{{\mathrm{x}}_0{}^2}{2{\sigma}_o{}^2}}\right){\mathrm{dx}}_{\mathrm{o}} $$
(11)

Which leads to:

$$ \mathrm{I}\left(\mathrm{x}\right)=\frac{1}{\sqrt{2\pi \left({\sigma}_{\mathrm{x}}{}^2+{\sigma}_{\mathrm{o}}{}^2\right)}}{\mathrm{e}}^{-\frac{{\mathrm{x}}^2}{2\left({\sigma}_{\mathrm{x}}{}^2+{\sigma}_{\mathrm{o}}{}^2\right)}} $$
(12)

Finally, the expression of I(y) is also the same form with σy → 0 ∀ z ≠ 0 (scattering is anisotropic due to the UD composites) :

$$ \mathrm{I}\left(\mathrm{y}\right)=\frac{1}{\sqrt{2\pi {\sigma}_{\mathrm{o}}{}^2}}{\mathrm{e}}^{-\frac{{\mathrm{y}}^2}{2{\sigma}_{\mathrm{o}}{}^2}} $$
(13)

Therefore, for a gaussian laser beam, the distribution of the total power of the laser inward beam in the UD composite is:

$$ \mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\frac{{\mathrm{I}}_{\mathrm{o}}\times {\mathrm{e}}^{-\mathrm{Dz}}}{2\pi {\sigma}_{\mathrm{o}}\sqrt{\left({\sigma}_{\mathrm{x}}{\left(\mathrm{z}\right)}^2+{\sigma}_{\mathrm{o}}{}^2\right)}}\times {\mathrm{e}}^{-\left(\frac{{\mathrm{x}}^2}{2\left({\sigma}_{\mathrm{x}}{\left(\mathrm{z}\right)}^2+{\sigma}_{\mathrm{o}}{}^2\right)}+\frac{{\mathrm{y}}^2}{2{\sigma}_{\mathrm{o}}{}^2}\right)} $$
(14)

With σx is a function of z, refraction index of matrix and fiber and microstructure.

In the case of the laser beam with a rectangular distribution, the function In(x,y) is given by the following expression

$$ {\mathrm{I}}_{\mathrm{n}}\left(\mathrm{x},\mathrm{y}\right)={\mathrm{I}}_{\mathrm{n}}\left(\mathrm{r}\right)=\mathrm{H}\left(\mathrm{r}-{\mathrm{r}}_{\mathrm{o}}\right) $$
(15)
$$ \mathrm{r}=\sqrt{{\mathrm{x}}^2+{\mathrm{y}}^2} $$
(16)

Where r the polar coordinate, H is the Heaviside function and ro the radius of the spot of the laser beam. Eq. (6) becomes:

$$ \mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)={\mathrm{I}}_{\mathrm{o}}\times \updelta\ \left(\mathrm{z}\right){\displaystyle \underset{\mathrm{S}}{\int}\mathrm{G}}\left[\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}}\right),\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{o}}\right)\right]\times \mathrm{H}\left(\mathrm{r}-{\mathrm{r}}_{\mathrm{o}}\right){\mathrm{dx}}_{\mathrm{o}}{\mathrm{dy}}_{\mathrm{o}} $$
(17)
$$ \begin{array}{c}\hfill \mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)={\mathrm{I}}_{\mathrm{o}}\times \delta\ \left(\mathrm{z}\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\frac{1}{\sqrt{2\pi }{\sigma}_{\mathrm{x}}}{\mathrm{e}}^{-\frac{{\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}}\right)}^2}{2{\sigma}_{\mathrm{x}}{}^2}}\times \frac{1}{\sqrt{2\pi }{\sigma}_{\mathrm{y}}}{\mathrm{e}}^{-\frac{{\left(\mathrm{y}-{\mathrm{y}}_{\mathrm{o}}\right)}^2}{2{\sigma}_{\mathrm{y}}{}^2}}\hfill \\ {}\hfill \times \mathrm{H}\left(\mathrm{r}-{\mathrm{r}}_{\mathrm{o}}\right)\ {\mathrm{dx}}_{\mathrm{o}}{\mathrm{dy}}_{\mathrm{o}}\hfill \end{array} $$
(18)

In the UD case with σy → 0 ∀ z ≠ 0, G(0, y−yo) → ∞, then G (y−yo) represents the Dirac pulse ω(y−yo) and Eq. (18) becomes:

$$ \mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)={\mathrm{I}}_{\mathrm{o}}\times \delta \left(\mathrm{z}\right){\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}}\mathrm{H}\left(\mathrm{r}-{\mathrm{r}}_{\mathrm{o}}\right)\times \omega \left(\mathrm{y}-{\mathrm{y}}_{\mathrm{o}}\right)\times \mathrm{G}\left(\mathrm{x}-{\mathrm{x}}_{\mathrm{o}},0\right){\mathrm{dx}}_{\mathrm{o}}{\mathrm{dy}}_{\mathrm{o}} $$
(19)

Therefore, for a rectangular laser beam, the distribution of the total power of the laser inward beam in the UD composite is :

$$ \mathrm{I}\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)=\frac{{\mathrm{I}}_{\mathrm{o}}\times {\mathrm{e}}^{-\mathrm{Dz}}}{2\pi {\mathrm{r}}^2}\left[-\mathrm{erf}\left(\frac{\sqrt{2}\ \left(\mathrm{x}-\sqrt{{\mathrm{r}}_{\mathrm{o}}{}^2-\mathrm{y}}\right)}{2{\sigma}_{\mathrm{x}}\left(\mathrm{z}\right)}\right)+\mathrm{erf}\left(\frac{\sqrt{2}\ \left(\mathrm{x}+\sqrt{{\mathrm{r}}_{\mathrm{o}}{}^2+\mathrm{y}}\right)}{2{\sigma}_{\mathrm{x}}\left(\mathrm{z}\right)}\right)\right] $$
(20)

Numerical model

Ray Tracing is an optical method used to simulate the radiative transfer in infrared heating problems. This method is very close to the physics of light propagation [18]. It is used to calculate the optical propagation of laser beams in inhomogeneous media with spatially varying dispersion of the refractive index. A ray can be represented by the path of a photon. Ray Tracing allows the simulation of a wide variety of optical effects, such as reflection, refraction and absorption. Snell-Descartes law is applied at each fiber-matrix interface with n1, n2 the refractive indices of the media (Fig. 5).

Fig. 5
figure 5

Ray Tracing method

Full size image

The Ray Tracing can be compared to other numerical methods such as Monte Carlo method for modelling light transport with the Mie theory [19, 20]. Elie et al. [21] use Monte Carlo simulations in order to quantify scattering effects in polymer media with no absorption, and they obtained good agreement with measured profiles of laser beam transmitted through the media. Monte Carlo method can also, as Ray Tracing, predict the quantity and the distribution of the light reaching the interface, as well as the distribution of the light within the transparent part. The Fig. 6 represents a cross section of the type of mesh used for the computation.

Fig. 6
figure 6

Typical mesh used for the computations

Full size image

Data retrieved from the simulation can be used to determine transmission, reflection and the associated distributions of the outgoing light. The propagation of radiation in a scattering medium can be described from the Mie theory, which provides the parameters for single particle scattering and making the switch to a set of particles by a statistical method such as the Monte Carlo method.

Simulations using Ray Tracing allow us to calculate as output the profile of the intensity distribution (Fig. 7) of the laser beam for different shapes (Gaussian and rectangular) at the welding interface (outlet surface).

Fig. 7
figure 7

Intensity distribution of the laser beam at the welding interface (thickness = 1 mm, 40 % fiber)

Full size image

Identification of the macroscopic model parameters (σx and D)

The identification consists to determine the optimal values of the distribution parameters that able analytical models (Gaussian and rectangular shapes) to describe as well as possible Ray Tracing model. The numerical simulation Ray Tracing are accurate as in [18]. The author has developed this method in order to compute the radiative source term in IR heating problem. This method was compared to basic experiments in order to validate some physical assumptions. The final comparison showed the capability of the ray tracing method to predict temperature distribution in the transparent material.

An algorithm (Fig. 8) illustrates the main steps of the procedure for parametric identification. Notice that the refraction of the laser beam in the media is independent of the initial shape. σ and D parameters are identified considering both models (gaussian and rectangular distributions).

Fig. 8
figure 8

Algorithm of the procedure for parametric identification

Full size image

The overall error generated by these two models (double objective error) is obtained by the following expression:

$$ \mathrm{Error}\ \left(\sigma \right)=\sqrt{\frac{{\displaystyle \underset{{\mathrm{R}}^2}{\int }{\left({\mathrm{I}}_{\mathrm{NG}}\left(\mathrm{x},\mathrm{y}\right)-{\mathrm{I}}_{\mathrm{AG}}\left(\mathrm{x},\mathrm{y},\sigma \right)\right)}^2}}{{\displaystyle \underset{{\mathrm{R}}^2}{\int }{\mathrm{I}}_{\mathrm{AG}}{}^2\left(\mathrm{x},\mathrm{y},\sigma \right)}}}+\sqrt{\frac{{\displaystyle \underset{{\mathrm{R}}^2}{\int }{\left({\mathrm{I}}_{\mathrm{NC}}\left(\mathrm{x},\mathrm{y}\right)-{\mathrm{I}}_{\mathrm{AC}}\left(\mathrm{x},\mathrm{y},\upsigma \right)\right)}^2}}{{\displaystyle \underset{{\mathrm{R}}^2}{\int }{\mathrm{I}}_{\mathrm{AC}}{}^2\left(\mathrm{x},\mathrm{y},\sigma \right)}}} $$
(21)

IN(x,y) is the total power of the laser beam of the ray tracing model, IA(x,y) is the analytical total power of the laser beam. G and C are respectively the Gaussian and the rectangular shapes of the laser beam.

The computing time for the Ray Tracing varies between (5 h–10 h) depending on the thickness, CPU Intel Xeon E5450 (8 × 3 GHz). With 200.000 rays and thousands of fibers.

The Table 1 shows the initial values for ray tracing simulation.

Table 1 The initial parameters for the ray tracing simulation
Full size table

Result and analysis

The results of the parametric study are presented depending of the fiber volume fraction (V f ), the thickness (z) and the ratio of refractive indices \( \left(\raisebox{1ex}{$\ {n}_1$}\!\left/ \!\raisebox{-1ex}{${n}_2$}\right.\right) \).

The Fig. 9 highlights the path of each ray of the laser beam in the composite (light scattering). For this the path of 20 rays are launched on the material surface and are followed in the material (depending on thickness). Firstly, it can be noticed, that each ray takes a different path randomly. Then, it can be noticed that in a second time, all rays don’t reach at the welding interface (thickness = 5 mm). Some of the rays rise the incoming surface, a part goes to the side and another arrives at the welding interface. This simulation allows us to show the light scattering phenomenon at the macroscopic scale by introducing light scattering ratio (Table 2) and standard deviation (Table 3).

Fig. 9
figure 9

Path followed by the rays in the composite

Full size image
Table 2 Optical scattering coefficient for different parameters
Full size table
Table 3 σx values for different parameters
Full size table

The light scattering phenomena of the laser beam on a macroscopic scale increases with the thickness of the material (Fig. 10). Figure 10 shows the evolution of σx versus thickness. The nine curves are obtained for different fiber volume fraction (40 % 50 % and 60 %) with each ratio of refractive indices \( \left(\ \raisebox{1ex}{${n}_1$}\!\left/ \!\raisebox{-1ex}{${n}_2$}\right.\ \right) \) (ratio1, ratio2, and ratio3, cf. Table 3).

Fig. 10
figure 10

Evolution of the σx law versus thickness

Full size image

When the laser beam passes through the composite, a portion of the intensity of the beam rise to the incoming surface, another portion passes through the composite (scattering standard deviation σx) and transmitted to the welding interface. This is indeed the amount of energy which is transmitted to the welding interface that is required for weld of the two parts. If the fiber volume fraction is increased, that is to say increasing the number of matrix-fiber interfaces, in the composite then the light scattering increases. Greater is the thickness, higher is the optical scattering coefficient D. The laser beams transmitted to the interface (less energy for welding) will decrease with the thickness, fiber volume fraction and refractive indices ratio.

The values of the error at convergence are less than 10 %. These different parameters affect the light scattering phenomenon of the laser beam at the macroscopic scale and about the refraction phenomenon at the microscopic scale in the composite material.

Figures 11 and 12 show the intensity distribution of the laser beam between the analytical model (Gaussian and rectangular shapes) and the numerical model. These results are obtained for a thickness of 1 mm and 50 % of the fiber volume fraction.

Fig. 11
figure 11

Intensity distribution of the laser beam for different values of y: 0 mm, 0.2 mm and 0.5 mm (Gaussian shape)

Full size image
Fig. 12
figure 12

Intensity distribution of the laser beam for different values of y: 0 mm, 0.2 mm and 0.5 mm (Rectangular shape)

Full size image

Conclusion

The aim of this study is to present an analytical model, able to represent, described and optimize the laser intensity at the welding interface for good weldability. The absorption is neglected in regard of the scattering effect. Light scattering phenomenons are highlighted at the macroscopic scale using the refraction phenomenon at the microscopic scale in an heterogeneous medium. In another future study, we will consider the absorption phenomenon in the model in order to determine the heat source generated at the welding interface and in the volume (first part) and finally to perform a three-dimensional temperature calculation. In the literature, there are several publications dealing with the determination of the temperature field knowing the source of heat at the interface. Moreover, in the proposed model, the distribution of laser beam in the transparent medium and at the welding interface is independent of the shape of the initial laser beam. In addition, temperature measurements will be performed using infrared camera in order to validate both numerical and analytical models.