Introduction

Numerical simulation, mostly using the finite element method (FEM) has been widely used in the forming industry. Enormous amounts of time and money for the prototyping processes can be saved. Nowadays almost every sheet forming process is simulated before the tools for the process are made.

The numerical simulation for the sheet forming processes is of most significance for the correct prediction of possible failures in the processes. Some kinds of failures such as wrinkling and spring back can be directly obtained from the computation. In contrast, some kinds of failure such as rupture can hardly be reasonably computed because the local necking is concentrated in a very narrow region. If the necking or very high deformation gradient should be described with reasonably fine mesh, millions of elements would be necessary for the modelling of the rupture process as it is not foreseen where the rupture appears. An alternative way that is widely used is to perform the task by means of some failure prediction models.

The most widely used method for the necking prediction in the numerical simulation of sheet forming processes is the concept of Forming Limit Curves (FLC) [1]. Nowadays it is almost a standard method in every commercial FE package for the numerical simulation of sheet forming processes. Although it is well known that the FLC is actually rather a band than a curve because of the scatter results due to properties of the sheet metals or due to the errors of measure techniques. Moreover, the FLC is deformation path dependent. For different deformation paths, the deformations achieved before fracture can be quite different. Despite these disadvantages, the FLC is still the most accepted criterion available for sheet forming simulation.

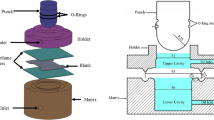
There are different ways to establish a FLC. The primary method is to obtain the curves experimentally. The Nakazima test (Fig. 1) uses a half spherical punch to deform the sheet metals and measures the strains developed in the sheet using optical instruments. Different widths of specimens are used to achieve different strain states. However, this method is very expensive and the measurement also introduces errors.

Fig. 1
figure 1

Nakazima test for the evaluation of FLC

Full size image

Much effort has been put into the theoretical evaluation of forming limit curves. The most famous is the work from Marcinniak and Kuzcynski [2]. It supposes some imperfection of thickness in the sheet and evaluates the deformations in the zones with and without imperfection until no equilibrium state can be found. Practice showed that the imperfection has a strong influence on the obtained forming limit curves. Sufficiently large imperfection is necessary for a reasonable FLC. Unfortunately such imperfection cannot be verified in the real sheet metal.

Early works for the investigation of necking phenomena can be traced to more than half a century ago. Hill, Swift and Hutchinson [3, 4, 6] investigated the necking problems for different deformation states. The forms are still in use in many books about plasticity. Hutchinson and Neale [5] investigated the influence of various factors for the necking as well as for the bifurcation phenomenon.

Actually the necking process has different stages, namely the diffuse necking and localized necking. The condition for a diffuse necking is that the tensile force reaches its maximum value. Mathematically it can be expressed as

$$ dF = 0 $$
(1)

or equivalently

$$ \frac{{d\bar{\sigma }}}{{d\bar{\varepsilon }}} = \bar{\sigma } $$
(2)

where \( \bar{\sigma } \) and \( \bar{\varepsilon } \) are the equivalent stress and equivalent strain respectively.

Because it is derived according to the maximum force condition, it means just the end of the uniform deformation and the beginning of diffuse necking.

Hill [6] derived the condition for the localized necking as:

$$ \frac{{d\bar{\sigma }}}{{d\bar{\varepsilon }}} = \frac{{\bar{\sigma }}}{2} $$
(3)

For the material with the hardening curve of power law type

$$ \bar{\sigma } = A{\bar{\varepsilon }^n} $$
(4)

the critical strain by tensile test is \( {\bar{\varepsilon }_d}{}^{{crit}} = n \) for diffuse necking and \( {\bar{\varepsilon }_n}{}^{{crit}} = 2n \) for the localized necking.

However, the derivations are all based on the assumption that the deformations are under the proportional loading. The process of diffuse necking to the localized necking has not been well investigated.

Using the modern measuring technique, the histories of deformations can be well traced. Figure 2 shows the measurement of deformation histories of steel HC260 in the Nakazima test. It is seen that the deformations are more or less along the linear deformation path until the diffuse necking begins. Upon this point, the component dε 2 decreases and the ratio \( {\sigma_1}/\bar{\sigma } \) increases until the deformation states go to the plane strain state with \( d{\varepsilon_2} \Rightarrow 0 \).

Fig. 2
figure 2

The measured results of the deformation histories in Nakazima test of steel HC260

Full size image

The maximum force criterion reveals the mechanism of the homogenous deformation. Actually the plastic deformations are caused by the movements of the dislocations in the metal materials. Therefore the deformations can only be called uniform deformation in macroscopic sense. Furthermore, many materials even show some softening before rupture. One of the reasons is the activation of new slide systems. During the plastic deformation the grains also undergo rotations. The shear stress on a slide plane changes continuously. As soon as the shear stress exceeds the critical value, dislocations on this plane will be activated. Therefore, decreasing of the tensile force is not a sufficient but a necessary condition for the localization of deformation.

The metal materials in any plastic deformations can show two kinds of behaviour, namely the hardening due to the accumulation of plastic deformation and the softening due to the reduction of the sections as well as the imperfections caused by the deformations inside the materials. So long as the hardening effect is stronger than the softening, the localized necking can be prevented. In other words, if the localized deformation would induce larger force than the force provided by the neighbouring material, the neighbouring material would be forced to deform further. As soon as the maximum force is reached, the deformation cannot be passed to the neighbour material and localized deformation happens.

In the formulation from Swift only the strain hardening effect was included. However, there are more factors which can also have influence on the hardening behaviour and must be taken into account for the investigation of necking process. One of the most important factors is the strain state by necking beside the strain rate and the temperature.

It is well known that the strain state by localized necking is the plane strain state. In a simple tensile test the stress component σ 2 is zero before diffuse necking. It increases during the diffuse necking. As a consequence, the tensile stress σ 1 increases not only because of the hardening effect but also because of the change of the stress state. Before the plane strain state is reached, the material keeps quasi-stable and rupture will not happen. Only when no force reservation exists, the material fails as further deformation will be localized that leads to rupture in the sheet material.

Figure 3 shows the engineering strain–stress diagram obtained from tensile test for a structure steel. It is seen that when the maximum force is reached, no material failure occurs immediately but the deformation goes on. The forming force keeps constant until the localized necking appears. Only the decrease of the loading force indicates the coming of rupture in the specimen. Therefore, the maximum force criterion is not a sufficient condition for the fracture prediction. More factors should be included to get improved precision. Based on the point of view, the Modified Maximum Force Criterion (MMFC) was proposed [7–12].

Fig. 3
figure 3

The engineering strain–stress diagram from tensile test for a structure steel

Full size image

The MMFC model considers the factor that additional tensile stress is induced as the diffuse necking happens. This stress postpones the localized necking or rupture. Since the model considers more factors in the failure processes, higher precision is achieved.

From another point of view, the classic maximum force criterion studies only the effect of hardening behaviours. The influence of yield loci is excluded from the model. In fact, the yield loci, either isotropic or anisotropic, play a very important role in the failure process [13, 14]. Without the consideration of yield loci, the evaluated FLC cannot represent the real material behaviours.

Basic formulation of this model

Observation of the measurement

The deformation states in sheet metal must reach the plane strain state before the rupture occurs. This kind of change of strain states is accompanied by the corresponding change in stress states. The stress transformation provides additional hardening for the force equilibrium and postpones the failure of the material. This kind of effect must be taken into account in order to get accurate failure prediction.

It is well known that the forming limit curves are deformation path dependent. Therefore, the FLC, either calculated or experimentally evaluated, is assumed to be alone a linear deformation path. Actually it is not true. The gradual change to the plane strain state upon uniform deformation exists for all kinds of deformation states except for the plane strain state. The measurement with modern digital technique confirmed this phenomenon (Fig. 2).

Explanation of the phenomenon

As mentioned above, the hardening effect plays the most important role to keep the deformation homogenous. Meanwhile, the section area decreases as the tensile strain increases. The reduction of the section area functions as a softening against the hardening. For most metal materials the hardening rate decreases and softening rate increases as the plastic deformation goes on. The maximal forming force means the transition point from a stable state to an instable state.

If the strain hardening is not sufficient to prevent the localisation of deformation, an additional hardening effect can be activated to postpone the localisation of deformation. The deformation state goes to plane strain state while the maximum tensile stress is accompanied with the plane strain state. During the transformations of stain states and stress states, the forming force keeps at the maximal level and diffuse necking occurs.

The real failure processes in sheet forming processes can be summarised as:

  • The deformations are uniform until the maximum forming force is reached;

  • Upon this point, the deformation states will be gradually transformed to the plane strain state. Additional tensile stress is provided by this state transformation and the fracture is postponed until the strain state is nearly the plane strain state and no more additional stress is available.

Evaluation of FLC using MMFC

The original maximum force criterion is derived from the condition

$$ dF = d({\sigma_1}A) = d{\sigma_1}A + {\sigma_1}dA > 0. $$
(5)

If only the strain hardening effect is considered, it is expressed as

$$ d{\sigma_1} = \frac{{d{\sigma_1}}}{{d{\varepsilon_1}}}d{\varepsilon_1}. $$
(6)

Because most metal materials are incompressible in the forming process, it is obtained that

$$ \frac{{dA}}{A} = - d{\varepsilon_1}. $$
(7)

Substitute (6) and (7) into (5) and take into account that by tensile test \( {\sigma_1} = \bar{\sigma } \) and \( {\varepsilon_1} = \bar{\varepsilon } \), we arrived at the formulation from Swift:

$$ \frac{{d\bar{\sigma }}}{{d\bar{\varepsilon }}} > \bar{\sigma }. $$
(8)

However, we know that the stress σ 11 is not only a function of strain hardening but also the strain ratio \( \beta = d{\varepsilon_2}/d{\varepsilon_1} \). Therefore, the stress increment dσ 11 can be expressed as

$$ d{\sigma_1} = \frac{{\partial {\sigma_1}}}{{\partial {\varepsilon_1}}}d{\varepsilon_1} + \frac{{\partial {\sigma_1}}}{{\partial \beta }}d\beta . $$
(9)

The two terms \( \frac{{\partial {\sigma_1}}}{{\partial {\varepsilon_1}}}d{\varepsilon_1} \) and \( \frac{{\partial {\sigma_1}}}{{\partial \beta }}d\beta \) describe the strain hardening effect and the additional hardening caused by the transformation of stress states. As shown in Fig. 4 where \( \Delta {\sigma_1}^{*} \)denotes the stress increment caused by the work hardening and \( \Delta {\sigma_1}^{{**}} \) represents the stress increment induced by the state transformation.

Fig. 4
figure 4

Different kinds of hardening

Full size image

Substitute (9) into the original form (5) we obtain the expression for the modified maximum force criterion as

$$ \frac{{\partial {\sigma_1}}}{{\partial {\varepsilon_1}}}d{\varepsilon_1} + \frac{{\partial {\sigma_1}}}{{\partial \beta }}d\beta > {\sigma_1}d{\varepsilon_1}. $$
(10)

For the case \( \partial {\sigma_1}/\partial {\varepsilon_1} > {\sigma_1} \), dβ is zero and β keeps constant. It is so called uniform deformation state. As the deformation goes on, the stress increases as the effect of work hardening but the hardening rate \( \partial {\sigma_1}/\partial {\varepsilon_1} \) decreases for most of the metal materials. As soon as the condition \( \partial {\sigma_1}/\partial {\varepsilon_1} > {\sigma_1} \) is violated, β will change correspondently to keep the equilibrium state stable. The influence how the variation of the strain increment ratio affects the stress is determined by the yield locus applicable to the material. The influence of the hardening behaviour and the yield loci are discussed in following sections.

Let \( \beta = \Delta {\varepsilon_2}/\Delta {\varepsilon_1} \)be the strain increment ratio and \( \alpha = {\sigma_2}/{\sigma_1} \)be the stress ratio. Generally the relations \( {\sigma_1} = f(\alpha )\bar{\sigma } \)and \( \Delta \bar{\varepsilon } = g(\beta )\Delta {\varepsilon_1} \)are known so long as the yield function \( F({\sigma_1},{\sigma_2}) = 0 \)is given. The term \( \partial {\sigma_1}/\partial {\varepsilon_1} \) and \( \partial {\sigma_1}/\partial \beta \) can be calculated accordingly as

$$ \frac{{\partial {\sigma_1}}}{{\partial {\varepsilon_1}}} = \frac{{\partial {\sigma_1}}}{{\partial \bar{\sigma }}}\frac{{\partial \bar{\sigma }}}{{\partial \bar{\varepsilon }}}\frac{{\partial \bar{\varepsilon }}}{{\partial {\varepsilon_1}}} = f(\alpha )g(\beta )H'{\text{and}} $$
(11)
$$ \frac{{\partial {\sigma_1}}}{{\partial \beta }} = \frac{{\partial {\sigma_1}}}{{\partial \alpha }}\frac{{\partial \alpha }}{{\partial \beta }} = f'(\alpha )\bar{\sigma }\frac{{\partial \alpha }}{{\partial \beta }} = f'(\alpha )H/(\frac{{\partial \beta }}{{\partial \alpha }}). $$
(12)

In (11) and (12) \( H = H(\bar{\varepsilon }) \) is the hardening function and \( H' \)is the slope of the hardening curve.

From the definition of β, it is clear that \( \beta = \frac{{\partial F}}{{\partial {\sigma_{{22}}}}}/\frac{{\partial F}}{{\partial {\sigma_{{11}}}}} \)can be calculated using an applicable yield locus. Therefore the derivation \( \partial \beta /\partial \alpha \) can also be evaluated easily.

Rewrite (10) as

$$ \frac{{\partial {\sigma_1}}}{{\partial {\varepsilon_1}}} + \frac{{\partial {\sigma_1}}}{{\partial \beta }}\frac{{\partial \beta }}{{\partial {\varepsilon_1}}} > {\sigma_1}, $$
(13)

We obtained the modified formulation of maximum force criterion.

This form can be used for the theoretical evaluation of FLC. However, as mentioned above, the diffuse necking is a nonlinear process. All auxiliary functions as well as the variables α and β vary during the diffuse necking process. The evaluation has to be performed numerically using the diagram shown in Fig. 5.

Fig. 5
figure 5

Diagram for the iterative procedure of FLC evaluation

Full size image

Mathematical expressions for the auxiliary functions

As shown in the previous section, some auxiliary functions are introduced to take the yield locus into account. For a simple yield locus like the yield function from von Mises, the analytical expressions for the auxiliary functions are available.

The case of von Mises yield locus

For example, the yield function according to von Mises for the plane stress states is expressed as

$$ ({\sigma_1}^2 - {\sigma_1}{\sigma_2} + {\sigma_1}^2) - {H^2} = 0. $$
(14)

From the yield function, the functions

$$ f(\alpha ) = \frac{1}{{\sqrt {{1 - \alpha + {\alpha^2}}} }}\,{\text{and}}\,g(\beta ) = \sqrt {{\frac{4}{3}(1 + \beta + {\beta^2})}} $$
(15)

can be derived. It is also an easy task to obtain the expression

$$ \beta = \frac{{2\alpha - 1}}{{2 - \alpha }}\,{\text{and}}\,\beta '(\alpha ) = \frac{3}{{{{(2 - \alpha )}^2}}}. $$
(16)

Although the functions can be analytically well defined, the forming limit curves have to be evaluated numerically since the parameters α and β are not constant. They change in order to provide the additional force increment to keep the force from decreasing.

As the variable α can also be expressed by the variable β, the function

$$ f(\alpha ) = f\left[ {\alpha (\beta )} \right] = f*(\beta ) $$
(17)

can be explicitly written as

$$ f*(\beta ) = \frac{{2 + \beta }}{{\sqrt {{3(1 + \beta + {\beta^2})}} }}. $$
(18)

In this case the derivation \( \frac{{\partial {\sigma_1}}}{{\partial \beta }} = f*'(\beta )\bar{\sigma } \) can be calculated analytically as well.

The auxiliary functions for the formulation of MMFC\( f(\alpha ),g(\beta ),f*(\beta ) \)and the derivation \( f*'(\beta ) \) are shown in Fig. 6.

Fig. 6
figure 6

Auxiliary functions used by MMFC (von Mises)

Full size image

The general cases of yield loci

There have been many models proposed for the yield loci for different metal materials. Most of them are so complex that the auxiliary functions are impossible to be expressed analytically. However, numerical process is applicable so long as the yield locus is derivable.

As discussed in previous sections, the data of a forming limit curve obtained experimentally are not along linear paths as they are supposed to be. If the failure is described correctly, the change of parameter β must be taken into account.

Similar to the analytical process, the numerical process can be used to evaluate the FLC well. The computation starts with a data initialization. The correspondent relations of \( {\alpha_i} \Rightarrow {\beta_i} \) and \( {\beta_i} \Rightarrow {\alpha_i} \) can be established at first. The correspondence must be unique. It is the case by the tensile states with 0 ≤α ≤1.

Provided the data are well initialized, the functions \( g(\beta ),f(\alpha (\beta )) \) and the derivative \( f'(\alpha (\beta )) \) can also be calculated accordingly. It is seen from Fig. 6 that the functions are rather smooth. The numerical calculation delivers usually satisfactory results. For the complex yield functions the function \( g(\beta ) \) might be difficult to obtain. However, considering the plastic work

$$ \Delta W = \Delta {\varepsilon_1}{\sigma_1} + \Delta {\varepsilon_2}{\sigma_2} = \Delta \bar{\varepsilon }\bar{\sigma }, $$
(19)

it is easy to obtain the equation

$$ g(\beta ) = f(\alpha (\beta ))(1 + \alpha \beta ). $$
(20)

A computational example

For a typical mild steel DC04, the harden curve is described with the Ghosh model [15] as

$$ {\sigma_Y} = A{(\bar{\varepsilon } + {\bar{\varepsilon }_0})^n} - C $$
(21)

with A = 600 MPa, \( {\bar{\varepsilon }_0} \) = 0.02, n = 0.27 and C = 0 MPa. Suppose the material obeys von Mises yield condition, the FLC is obtained as shown in Fig. 7. It is also seen from Fig. 8 that the tensile force kept on the maximum value as the effect of transformation of strain states is taken into account.

Fig. 7
figure 7

FLC for DC04 obtained with MMFC

Full size image
Fig. 8
figure 8

a) The change of strain ratio and b) correspondent force by tensile test

Full size image

Influence of hardening curve

As mentioned above, according to the MMFC model, the FLC of any material can be established so long as the hardening curve and yield locus are provided. Generally, higher hardening effects and lower yield stress result in higher forming limit.

It is not a simple task to describe the hardening behaviours of the metal materials properly to large deformations. The data from simple experiments like tensile test are limited to the uniform deformation. It is relatively small in comparison with the deformations resulting in failure. Although this problem has disturbed the simulation technique for decades and many models have been proposed, it is still not very clear how to extrapolate the experimental data properly to the whole deformation range of sheet forming.

Figure 9 shows the approximations of two different models for the same material as an example. The Ghosh model \( {\sigma_Y} = A{(\bar{\varepsilon } + {\bar{\varepsilon }_0})^n} - C \) approximates the hardening behaviour with A = 767.33 MPa, \( {\bar{\varepsilon }_0} \) = 0.0822, n = 0.1897 and C = 180.94 MPa while the model from Hockett-Sherby [16] \( {\sigma_Y} = {\sigma_1} - ({\sigma_1} - {\sigma_0})\exp ( - m{\bar{\varepsilon }^n}) \) describes the hardening curve with σ 1 = 580.34 MPa, σ 0 = 208.42 MPa, m = 3.39 and n = 0.747.

Fig. 9
figure 9

The approximated hardening curves using different models

Full size image

Both functions describe the experimental data excellently. However, for large strains these two curves show remarkable difference. If the hardening curves are used for the evaluation of FLC, we obtain remarkably different results as shown in Fig. 10 because the strains at the critical state are far beyond the uniform deformation measured in tensile test.

Fig. 10
figure 10

The forming limit curves evaluated with different models

Full size image

Nowadays it is possible to use the digital technique to measure the strain by bulge test with sufficient precision. Because the strains obtained from a bulge test is much higher than the strain provided by a tensile test, the bulge test becomes a supplement to the tensile test and delivers very useful information for the description of hardening behaviours. Mostly, the real hardening behaviour lies between the Ghosh and Hockett-Sherby models. A combination of both models results in a better approximation. It also means an improvement for the evaluation of FLCs.

Influence of yield loci

The essential modification of the MMFC model comes from the implementation of the influence of yield loci while the original maximum force criterion considers only the hardening effect. The description of the yield loci is a key point for the estimation of FLCs. Unfortunately it is a very complex topic to describe the yield condition with sufficient accuracy. There have been dozens of models for the yield loci of metal materials beside the classic models from Tresca and von Mises. However, it is still an opened question as to which model should be adopted for which kind of materials. Besides, the parameters in a model for yield condition are generally not constant. For example, in the model from Hill [17] the R-value \( R = \Delta {\varepsilon_2}/\Delta {\varepsilon_3} \) is used. Experiments showed that the R-value changes during the plastic deformation. Furthermore, the material model should include the kinematical hardening effect as the deformations are not exactly along a linear path.

For the illumination of the effect of yield loci, we compare Hill model with R = 1 and R = 2 as an example. The yield loci are plotted in Fig. 11.

Fig. 11
figure 11

Yield loci by Hill 79 R = 1.0 and R = 2.0

Full size image

Of course different yield loci result in different forming limit curves, as shown in Fig. 12. The difference on the right side can be seen immediately. On the left side the curves almost come together. However, the impression that the yield loci don’t have much effect on the results on the left side is incorrect. For tensile test R = 2 results in the strain ratio β = −0.67, the two curves on the left side are also very different if the comparison is made using the same stress states. Generally, increasing R-value increases the forming limit on the left side and reduces the forming limit on the right side.

Fig. 12
figure 12

Forming limit curves evaluated using different yield loci

Full size image

Simplification and explicit expression of MMFC

The MMFC can be well used to establish a forming limit curve numerically provided the hardening curve and the yield locus of a sheet material are known. However, it is favourable to make some simplification to express the criterion in an explicit form which can be applied directly to an arbitrary deformation state.

Interpretation of dβ/dε1

The auxiliary functions \( f(\alpha ),g(\beta ),f*(\beta ) \) and \( \beta (\alpha ) \) are merely defined by the yield locus and the physical meaning of each auxiliary function is very clear. These functions can be evaluated well either analytically or numerically. The term \( \partial {\sigma_1}/\partial \beta \) can be calculated using these functions. In contrast, the term \( \partial \beta /\partial {\varepsilon_{{11}}} \) in diffuse necking is determined by hardening function as well as by yield locus. It is not possible to get an analytical form even for the simplest hardening curve and yield locus.

In our early works [7–9] the following procedure was used for the evaluation of \( \partial \beta /\partial {\varepsilon_{{11}}} \). Since β can also be defined as \( \beta = {\varepsilon_2}/{\varepsilon_1} \) for a linear deformation path, the derivation \( \partial \beta /\partial {\varepsilon_1} = - {\varepsilon_2}/{\varepsilon_1}^2 = - \beta /{\varepsilon_1} \) is obtained and the MMFC was expressed as

$$ H' \leqslant [\frac{1}{{g(\beta )}} + \frac{{f'(\alpha )\beta }}{{f(\alpha )\beta '(\alpha )\bar{\varepsilon }}}]H. $$
(22)

It is actually a rough simplification as shown in Fig. 13. In fact \( \partial \beta /\partial {\varepsilon_{{11}}} \) should be the tangential value of the real process and changes continuously during the diffuse necking. As an improvement, the function can be evaluated using \( \partial \beta /\partial {\varepsilon_{{11}}} \approx - \beta /({\varepsilon_1} - {\varepsilon_1}^{*}) \), where \( {\varepsilon_1}^{*} \) denotes the major strain at the transition from uniform deformation to diffuse necking deformation (Fig. 13). The value \( {\varepsilon_1}^{*} \)is determined by the condition

$$ H'\left( {\varepsilon_1^{*}} \right) = H\left( {\varepsilon_1^{*}} \right)/g(\beta ) $$
(23)

and is a function of parameter β. Since the hardening curve and yield locus are given, it can be very easily evaluated. If the hardening behaviour is described with the Hockett-Sherby model and the material obeys von Mises yield condition, a diagram of \( \varepsilon_1^{*} \) via β is shown in Fig. 14.

Fig. 13
figure 13

Different evaluation methods for \( \partial \beta /\partial {\varepsilon_1} \)

Full size image
Fig. 14
figure 14

A typical \( \beta - {\varepsilon_1}^{*} \)diagram

Full size image

Different explicit expressions

Modification of (22) and using the equivalent strain \( {\bar{\varepsilon }^{*}} = g(\beta ){\varepsilon_1}^{*} \) leads to the explicit expression of MMFC as

$$ H' \leqslant [\frac{1}{{g(\beta )}} + \frac{{f'(\alpha )\beta }}{{f(\alpha )\beta '(\alpha )(\bar{\varepsilon } - {{\bar{\varepsilon }}^{*}})}}]H. $$
(24)

This form can be directly used for the evaluation of FLC or, more generally, used as a judgement for the critical state to monitor the whole forming process.

Approximation of df(α)/dε1

Equivalent expression for Eq. (5) is to introduce the relation \( {\sigma_{{11}}} = f(\alpha )\bar{\sigma } \) directly. We obtain then the forming force is

$$ F = f(\alpha )\bar{\sigma }A. $$
(25)

For the condition

$$ \Delta F = \Delta f(\alpha )\bar{\sigma }A + f(\alpha )\Delta \bar{\sigma }A + f(\alpha )\bar{\sigma }\Delta A > 0 $$
(26)

It comes automatically to the modified maximal force criterion and can be written as

$$ \frac{{\Delta \bar{\sigma }}}{{\Delta {\varepsilon_1}}} > \bar{\sigma }\;\;[1 - \frac{{\Delta f(\alpha )}}{{\Delta {\varepsilon_1}f(\alpha )}}]. $$
(27)

Introducing the yield condition \( \bar{\sigma } = H \) and \( d\bar{\sigma }/d\bar{\varepsilon } = H' \), it is easy to rewrite the condition as

$$ H' > \frac{H}{{g(\beta )}}[1 - \frac{{\Delta f(\alpha )}}{{\Delta {\varepsilon_1}f(\alpha )}}]. $$
(28)

It is an equivalent expression of Eq. (13) and can be used for the evaluation of FLC. The term \( \Delta f(\alpha )/\Delta {\varepsilon_{{11}}} \) can actually not be expressed explicitly as it is not a simple function but the combination of the yield locus as well as the hardening function.

However, during the numerical iteration process, we can plot the development of the function via the deformation. Figure 15 shows the development of the f-function of tensile test for a material obeys von Mises yield function.

Fig. 15
figure 15

Diagram of f-function via strain

Full size image

At the stage of uniform deformation, as the force doesn’t reach the maximal value, the function \( f(\alpha ) \) keeps constant. As soon as the diffuse necking begins, the function changes its value to keep the equilibrium state as far as possible. As can be seen from the plot, it is reasonable to use a linear approximation

$$ \frac{{\Delta f(\alpha )}}{{\Delta {\varepsilon_1}}} \approx \frac{{{f_{{\max }}} - f(\alpha )}}{{{\varepsilon_1} - {\varepsilon_1}^{*}}}. $$
(29)

For the calculation, where f max is the maximal function value by β = 0 and \( {\varepsilon_1}^{*} \) denotes here again the major strain at the transition from uniform deformation to diffuse necking.

The MMFC gets an explicit expression as

$$ H' > \frac{H}{{g(\beta )}}[1 - \frac{{({f_{{\max }}} - f(\alpha ))}}{{f(\alpha )({\varepsilon_1} - {\varepsilon_1}^{*})}}]. $$
(30)

The equivalent form using equivalent strain is

$$ H' > H[\frac{1}{{g(\beta )}} - \frac{{({f_{{\max }}} - f(\alpha ))}}{{f(\alpha )(\bar{\varepsilon } - {{\bar{\varepsilon }}^{*}})}}]. $$
(31)

Now we obtained 3 different formulations for the FLC evaluation, namely the iterative method (Fig. 5) and two explicit formulations (24) and (30) based on some simplifications.

The comparison can be made by recalculating the FLC in Fig 6 with different expressions. The result is shown in Fig. 16. The result obtained with (22) is also plotted as a comparison. It is obvious that the formulation (22) underestimates the FLC, especially on the right side.

Fig. 16
figure 16

Comparison of FLCs obtained using different evaluation methods

Full size image

Consider the factor that the experimental data for FLC are rather scattered and the forming limit is actually more a band than a curve, it is reasonable to say that all the three formulations can perform the task of FLC calculation.

As mentioned in this work, FLCs, either established experimentally using the Nakazima test or calculated iteratively with MMFC, are only along quasi linear deformation paths. As well known, the FLCs are deformation path dependent. If the real deformation paths are not exactly coincided with the paths for FLC, the failure judgement must be made very carefully. Security reservation is often necessary. From this point of view, the formulation (30) might be favourable as it provides a relative conservative evaluation for forming limits.

Discussions

Some critiques as well as discussions have been aroused since the MMFC model was published. One of the most confronted questions is the discussion about the evaluation of\( \partial \beta /\partial {\varepsilon_1} \). This problem is discussed in this work. As shown in Fig. 16, the approach \( \partial \beta /\partial {\varepsilon_1} = - \beta /({\varepsilon_1} - {\varepsilon_1}^{*}) \) uses the average value in the diffuse necking process and delivers approximately the same results as obtained with the iterative procedure.

Another issue was pointed out by Aretz [18] that if the yield locus has a nearly straight line, as in the model Yld2000 proposed by Barlat [14] for the Aluminium alloy AA2090-T3, there would be a singularity in the derivation of the auxiliary functions. This singularity leads to a very strange form of the FLC calculated with MMFC model.

Investigation showed that the problem arises from the derivation of the auxiliary function\( F(\beta ) \), namely \( \partial F(\beta )/\partial \beta \). Figure 17 shows the function and the derivation of this function of different models. The elliptic form of von Mises gives a very smooth derivation. The model proposed by Barlat in 1989 [19] shows moderate deviation from the Mises model. As contrast, the model Yld2000 shows an abrupt jump at \( \beta \approx - 0.1 \). The derivation doesn’t make any sense at this state.

Fig. 17
figure 17

The forms of the auxiliary function \( F(\beta ) \) and its derivation

Full size image

This auxiliary function has a clear physical meaning. It denotes the relation between tensile stress ratio and the strain increment states. An abrupt jump of tensile stress ratio due to a small change of strain ratio is anyway not reasonable by the real materials. Figure 18 illustrated the problem. A straight line in the yield locus means different stress states. If they are mapped with almost the same strain increment, the constitutive equation

$$ d{\sigma_{{ij}}} = {C_{{ijkl}}}d{\varepsilon_{{kl}}} $$
(32)

is singular and delivers indeterminate results. Meanwhile, for the large range −0.1 <β <1, the stress states shrink to a very small zone. Therefore, this type of yield loci causes not only problems for the evaluation of FLC using the MMFC model but also problems in the general constitutive law of the materials.

Fig. 18
figure 18

Analysis of Yield locus for AA2090-T3 according to Yld2000 model

Full size image

In order to avoid the numerical instabilities due to the shape of the yield loci described by high order polynomial models, Comsa et al. proposed an alternate model [20]. Banabic and Soare [21] also discussed this phenomenon and suggested to “wash out” the localized pulse because it is a numerical issue. In this region of yield locus, the condition of unique mapping between strain states and stress states is violated.

To measure the yield loci is also a very complex task. Most models for yield loci describe the yield loci within a relatively small deformation range. For example, ISO 10113–2006 suggests the R-value as average value between 8 and 12% strains. For the aim of the calculation of FLC, however, only yield loci for large strains are useful. Because the theoretical evaluation of FLCs using MMFC is based on the assumption that a yield locus keeps in form and expands with the hardening, the inaccuracy of the description for yield loci at large deformation is obviously an error source for the evaluation.

Benchmark evaluation

In order to verify the model, the examples set as a benchmark test for the conference Numisheet 2008 [22] are used as the evaluation examples.

3 sheet materials were chosen for the benchmark, namely steel sheet with thickness of 0.8 mm and 1.6 mm respectively, and an aluminium sheet with thickness 1.1 mm.

The organizers of the conference provided the material parameters for the hardening curves as well as for the yield loci as input data and the participators should evaluate the forming limit curves accordingly.

The parameters used in this work are listed in Table 1. The Ghosh hardening model and Hill 79 yield locus are used for steel sheets the hardening model from Hockett-Sherby combined with the Barlat 89 yield locus is adopted for the aluminium sheet respectively.

Table 1 The parameters used for the evaluation of Numisheet 2008 benchmark test
Full size table

Different formulations of MMFC are adopted to calculate the FLCs for the materials. Figures 19, 20 and 21 show the results of evaluation. Compared with the experimental data, satisfactory prediction of FLC has been achieved using the MMFC model.

Fig. 19
figure 19

Benchmark test Material 1 for Numisheet 2008

Full size image
Fig. 20
figure 20

Benchmark test material 2 for Numisheet 2008

Full size image
Fig. 21
figure 21

Benchmark test material 3 for Numisheet 2008

Full size image

In order to investigate the influence of the yield loci, the forming limit curves of these materials are also calculated using different yield loci. The parameters are listed in Table 2 and the results are compared in Figs. 22, 23 and 24 for different materials respectively. The iterative procedure (Fig. 5) is used for the FLC evaluation of all materials. Because the parameters for different yield loci are derived from the same R-values provided by the organizers of the bench mark test, generally satisfactory agreement with the experimental data is obtained for different yield loci. However, different yield loci result in different forming limit curves. The comparison shows clearly that the yield function is an essential factor for higher precision of theoretical FLC determination.

Table 2 The parameters used for the comparison of yield loci
Full size table
Fig. 22
figure 22

Benchmark test for Numisheet 2008, material 1 with different yield loci

Full size image
Fig. 23
figure 23

Benchmark test for Numisheet 2008, material 2 with different yield loci

Full size image
Fig. 24
figure 24

Benchmark test for Numisheet 2008, material 3 with different yield loci

Full size image

Conclusions

The rupture or local necking phenomenon is not only determined by the work hardening behaviours but also by the yield locus of the materials. The modified maximum force criterion takes the strain state transformation in diffuse necking into account and improves remarkably the theoretical evaluation of forming limit curves. Experiments verified this model and showed satisfactory agreement between the calculated FLCs and the experimental data. The simplified formulations can provide explicit judgement directly from the simulation results and are very easily implemented into the finite element code.

Because the FLC is the function of hardening behaviour as well as the yield loci, the hardening curves and the yield conditions at high deformation degrees are essential for the evaluation of FLC. The assumption of yield locus is one of the main causes of the deviation of theoretical prediction. Meanwhile, only the tensile test is obviously insufficient to ensure the precision of theoretical FLC evaluation as the tensile test delivers only very limited information for the anisotropic yield loci. Advanced experiments for the yield loci are the base stone for the theoretical calculation of FLCs.

Moreover, the model is built on the assumption that the deformation behaviour of the materials can be described with sufficient accuracy using a function for work hardening combined with a model for yield condition. This assumption is valid for many metallic materials including most steel sheet materials applied in the automobile industry. However, new alloys with very high strength and moderate formability are being developed nowadays. These materials possess more complicated properties as well as the chemical composites. Rupture can occur before the forming force reaches a maximal value and the micro fractures between the crystal grains can also lead to early failure of the materials. As the MMFC model treats the material as homogenous medium, it should be carefully applied with the consideration of basic material properties.