Introduction

When a metal sheet is drawn over a die corner, or through a drawbead, the material is subjected to bending, subsequent unbending, and rebending. In order to perform an accurate simulation of such a sheet metal forming process, it is necessary to have an appropriate constitutive model, which can consider the phenomena that occurs during cyclic loading, such as the Bauschinger effect, the transient behaviour, the permanent softening, and the work-hardening stagnation (see Fig. 1). All these effects can be described by the so-called “hardening law”.

Fig. 1
figure 1

Schematic illustration of the effects occurring during a loading/unloading cycle

Full size image

Many purely phenomenological hardening laws have been proposed in the literature with the purpose of describing the cyclic behavior of metal sheets. The complexity of these models varies within a wide range with respect to number of material parameters and history variables. The material parameters involved have to be determined from some kind of cyclic loading experiment. In theory, the most simple and straight-forward test is a tensile/compression test of a sheet strip. In practice, however, such a test is very difficult to perform, due to the tendency of the strip to buckle in compression. In spite of these difficulties, some successful attempts to perform cyclic tension/compression tests have been reported in the literature; see e.g. Refs. [5–8]. However, common for these attempts is that rather complicated test rigs have been designed and used in the experiments, in order to prevent the sheet strip from buckling.

Another kind of test that frequently has been used for the determination of material hardening parameters is some kind of bending test; see e.g. Refs. [9–12]. The advantage of this kind of tests is that they are simple to perform, and standard test equipments can be used. However, a bending test will involve inhomogeneous stress and strain distributions in the sheet specimen, and the stress-strain response cannot be directly determined from the experiment. This means that the material parameters have to be determined by some kind of inverse approach. Usually, the experiments are simulated by FEM, and the material parameters are identified by means of some optimization technique.

The authors of the present article have recently shown the importance of a proper choice of constitutive model for the hardening behavior [1, 3]. However, a successful constitutive model demands that the material parameters being part of the model can be determined accurately. In the the present study the two material parameter identification strategies above are compared and evaluated. In an ideal world these two methods would yield identical parameter set-ups. However, a few writers have reported that there are substantial differences between hardening parameters determined from bending tests and those from tensile/compression tests [13–15]. These observations have been partly verified by the current investigation.

The purpose of the present study is to try to understand the background of these differences, to find out the influence on the predicted springback, and to determine which of the two methodologies for hardening parameter identification is the most suitable one.

Material data and material characterization

Materials

In this work only one material is accounted for. The reason for this is that the primary aim of the work is to evaluate different methods for the material parameter identification. The considered material is a DP600 steel with the thickness of 1.46 mm.

Material characterization

To determine the parameters for the yield criteria, later discussed in the next chapter yield stresses and Lankford parameters for the rolling, transverse and diagonal directions, respectively, have been determined. These values have been obtained from simple uniaxial tension tests in the directions of interest. The uniaxial tests have been complemented with viscous bulging tests (see Sigvant et al. [37]), aiming at providing plastic hardening data for strain levels much higher than what can be achieved in ordinary tensile tests, and to provide data for the equibiaxial yield stress Y b and r-value r b .

Material properties

In Table 1 the results from the uniaxial tension tests and the viscous bulging tests are presented. In Fig. 2 the plastic hardening curve for the material is shown.

Table 1 Material data for the steel grade included in the current study
Full size table
Fig. 2
figure 2

Plastic hardening curve. Material: TKS-DP600HF

Full size image

Yield criterion and elastic unloading modeling

Introductory remarks

A phenomenological plasticity model is made up by several constituents, which each influences the accuracy of the total model. In order to study the influence of e.g. the hardening model, it is highly essential that the errors from the other constituents of the model are minimized as far as possible. In all the analyses performed within the present study, a yield condition that has turned out to be the most accurate one in a previous comparative study by the authors [4], has therefore been employed. This is the eight parameter yield criterion by Banabic et al. [16], Barlat et al. [17], and Aretz [18]. Another phenomenon that, in many cases, is even more important than the cyclic hardening effects is the degradation of elastic stiffness due to plastic straining. This effect has also been carefully examined by the authors in [4], and the results from that study are implemented in the present one.

The Banabic/Aretz eight parameter model

The eight parameter yield criterion by Banabic et al. [16] (see also Barlat et al. [17], Aretz [18] and Mattiasson and Sigvant [19]) is an extension of the Barlat-Lian (Yld89) criterion such that

$$ \bar{\sigma }\left( {L,K,N,P,Q,R,S,T,{\mathbf{\sigma }}} \right) = {\left[ {\frac{1}{2}\left. {{{\left( {{{\left| {\Gamma + \Psi } \right|}^M} + {{\left| {\Gamma - \Psi } \right|}^M} + \left| {2\Lambda } \right|} \right.}^M}} \right)} \right]^{{\frac{1}{M}}}} $$
(1)

where the functions Γ, ψ and Λ are defined as

$$ \begin{array}{*{20}{c}} {\Gamma = \frac{{L{\sigma_{{xx}}} + K{\sigma_{{yy}}}}}{2}} \\{\Psi = \sqrt {{\frac{{{{\left( {N{\sigma_{{xx}}} - P{\sigma_{{yy}}}} \right)}^2}}}{4} + {Q^2}{\sigma_{{xy}}}{\sigma_{{xy}}}}} } \\{\Lambda = \sqrt {{\frac{{{{\left( {R{\sigma_{{xx}}} - S{\sigma_{{yy}}}} \right)}^2}}}{4} + {T^2}{\sigma_{{xy}}}{\sigma_{{xy}}}}} } \\\end{array} $$
(2)

The coefficients L, K, N, P, Q, R, S and T are material parameters. All these parameters affect the shape of the yield surface. However, the exponent M has most influence on the yield surface shape, even though it is not directly determined from experimental results. The exponent M is related to the crystallographic structure of the material, and it is set to 6 for steel grades and 8 for aluminum alloys according to the work by Logan and Hosford [41]. The eight parameters are determined such that the model reproduces the experimental characteristics of the orthotropic sheet metal as good as possible. Those experimental characteristics are three uniaxial yield stresses (Y 0, Y 45 and Y 90), the equi-biaxial yield stress (Y b), the three anisotropic coefficients (r 0, r 45 and r 90) and, finally, the equi-biaxial r-value (r b) (see Table 1).

Degradation of elastic stiffness due plastic straining

The amount of springback during unloading depends to a great extent on the elastic stiffness of the material. In classic elasticplastic theory, the unloading of a material after plastic deformation is assumed to be linearly elastic with the stiffness equal to Young’s modulus. However, several experimental investigations have revealed that this is an incorrect assumption. The authors have currently studied and discussed this phenomenon extensively [4]. The study confirms earlier investigations from the literature and states that the unloading path is not linear at all and nor is the reloading path. Both the unloading and the reloading paths are slightly curved, and deviate from linearity around an imaginary “mean” line, representing the secant to the curves. Moreover, the slope of this secant is strongly affected by the amount of plastic strain. More precisely, the magnitude of the unloading modulus is decreasing with increasing plastic strain. A schematic illustration of all this can be seen in Fig. 3. The notation E u in the figure represents the slope of the secant to the non-linear unloading path. The authors have chosen to denote this slope the “unloading modulus”. The variable E t in the figure is the slope just in the beginning of the unloading or reloading path. As can be seen in the figure this is also a function of the plastic strain, and it is also smaller than the initial Young’s modulus (E 0 in the figure).

Fig. 3
figure 3

A schematic illustration of the stress-strain relationship of an unloading/reloading cycle

Full size image

The variation of the unloading modulus with plastic strain is here expressed by an analytical function according to Yoshida et al. [5]:

$$ {E_u} = {E_0} - \left( {{E_0} - {E_{{sat}}}} \right) \cdot \left( {1 - {e^{{ - \xi \cdot {{\bar{\varepsilon }}^p}}}}} \right) $$
(3)

where E 0 is the initial Young modulus, E sat is a value that the unloading modulus saturates towards, and ξ is a material parameter. The parameters E sat and ξ have to be determined from some kind of experimental data. In this work results from unloading/reloading tests at various strain levels of uniaxially stretched thin sheet metal strips were used. The strips were stretched to seven different plastic strain levels: 1%, 2%, 4%, 6%, 8%, 11%, and 14%. At each of these unloading/reloading cycles, a stress-strain loop as the one in Fig. 3 is obtained, and the unloading modulus can be determined by measuring the secant slope.

In Fig. 4 the results from measurements of the secant moduli from three specimens of the considered DP-steel are represented by black stars. Based on these experimental points the parameters in Eq. 3 have been determined by least squares fitting to E sat  = 150.8 and ξ = 24.6. The corresponding expression for the unloading modulus is represented by the solid line in Fig. 4.

Fig. 4
figure 4

Unloading modulus as a function of plastic strain. Material: TKSDP600

Full size image

Using a linear unloading modulus as described above is a simplification, since the non-linearity of the unloading path is not considered. However, for the applications in this report, this method has turned out to be sufficiently accurate [1, 3, 4].

Theoretical background of the implemented kinematic hardening laws

Introductory remarks

Numerous phenomenological kinematic hardening laws, for describing the cyclic behavior of metal sheets, have been proposed in the literature. The authors of the present article have recently showed the importance of the choice of kinematic hardening law for accurate springback prediction [1, 3]. This work is focused on the material parameter identification for those models. However, in order to understand the outcome of the identification procedures, it is necessary to have some insight in the theoretical background of the various models. In this work six different hardening laws are studied. They are of various complexities and can simulate one or more of the effects described in Fig. 1. An overview of the characteristics of the considered hardening laws is provided in Table 2. The simplest one of the considered models is the mixed isotropic-kinematic hardening law by Hodge [20] and Crisfield [21]. Then follows in order of increased complexity: the Armstrong-Frederick hardening law [22], the Geng-Wagoner hardening law [23], a three parameter hardening law usually referred to as the nonlinear-linear kinematic hardening law (NLK-LK) [24], and finally two different versions of the Yoshida-Uemori hardening law [25, 26]. Short theoretical backgrounds of these models are outlined in the following sections. For a detailed description of the included hardening laws the reader is referred to earlier works by the authors [1, 3].

Table 2 Characteristics of the different hardening laws
Full size table

Stress update procedure

The various combinations of yield criteria and hardening laws have been implemented in the explicit FE-code LS-DYNA [27] as “User Materials”. The implementation is based on the usual assumption of an additive decomposition of the strain rate tensor into an elastic and a plastic part, together with an associated flow rule. The incremental update of stresses is based on an elastic predictor—plastic corrector procedure. During the plastic corrector phase the stresses are relaxed step-by-step back to the yield surface following a procedure outlined by Ortiz and Simo [28].

Mixed kinematic-isotropic hardening

The simplest hardening law considered in this study is a combination of isotropic and kinematic hardening, where the proportion of the effective plastic strain related to isotropic and kinematic hardening, respectively, is weighted with a scalar m. The basic ideas behind the theory of mixed hardening are usually attributed to Hodge [20]. The theory has been further developed by Crisfield [21], whose representation of the subject is basically followed below. It should, however, be pointed out that the final, resulting equations do not agree with the ones presented by Crisfield [21]. The erroneous results by Crisfield [21] have previously been pointed out by Bathe and Montáns [31].

The scalar m represents the ratio of plastic strain associated to isotropic hardening, whereas the ratio (1-m) is left for the kinematic hardening response. From this it follows that:

$$\begin{array}{*{20}l} {{{\mathop \varepsilon \limits^ \cdot }^{p} = {\mathop \varepsilon \limits^ \cdot }^{p}_{{iso}} + {\mathop \varepsilon \limits^ \cdot }^{p}_{{kin}} = m{\mathop \varepsilon \limits^ \cdot }^{p} + {\left( {1 - m} \right)}{\mathop \varepsilon \limits^ \cdot }^{p} } \hfill} \\ {{0 \leqslant m \leqslant 1} \hfill} \\ \end{array}$$
(4)

By some manipulations of the Ziegler hardening law [30] and Eq. 4, the evolution of the back-stress α can be expressed as:

$$ \mathop{\alpha }\limits^{ \cdot } = \left( {H\prime - \tilde{H}\prime m} \right)\frac{{{{\mathop{{\overline \varepsilon }}\limits^{ \cdot } }^p}}}{{\bar{\sigma }}}\left( {\,\sigma - \alpha } \right) $$
(5)

where:

$$ \begin{array}{*{20}{c}} {H\prime = \frac{{dH\left( {{{\overline \varepsilon }_p}} \right)}}{{d{{\bar{\varepsilon }}_p}}} = \frac{{d{\sigma_Y}\left( {{{\overline \varepsilon }_p}} \right)}}{{d{{\overline \varepsilon }_p}}}} \\{\widetilde{H}\prime = \frac{{dH\left( {m{{\overline \varepsilon }_p}} \right)}}{{d{{\overline \varepsilon }_p}}} = \frac{{d{\sigma_Y}\left( {m{{\overline \varepsilon }_p}} \right)}}{{d{{\overline \varepsilon }_p}}}} \\\end{array} $$
(6)

where now H′ is the current plastic slope (at \( {\overline \varepsilon^p} \)), and \( \widetilde{H}\prime \) is the plastic slope related to the isotropic hardening (at m \( \cdot {\overline \varepsilon^p} \)).

The mixed hardening law is able to consider the Bauschinger effect and the permanent softening behavior. It can be noted that if the scalar m is set to 1, pure isotropic hardening is prevailing.

The Armstrong-Frederick hardening law

The second hardening law considered herein is the classical, nonlinear kinematic hardening law presented by Armstrong and Frederick in 1966, [22], and later on further developed by Chaboche [32, 33]. Armstrong and Frederick added to the hardening law of Prager [29] a recall term, in order to capture the transient behavior during abrupt changes in load paths. The yield function is given by:

$$ f = \Phi \left( {\sigma - \alpha } \right) - {\sigma_{{iso}}} = 0 $$
(7)

where σ iso is the isotropic part of the uniaxial tension curve, such that:

$$ {\sigma_{{iso}}} = {\sigma_Y} - \alpha $$
(8)

where σ Y is the uniaxial yield stress and α is the uniaxial back-stress.

The back-stress evolution is given by

$$ \mathop{\alpha }\limits^{ \cdot } = {C_x}\left( {{\alpha_{{sat}}}\frac{{\left( {\sigma - \alpha } \right)}}{{{\sigma_Y}}} - \alpha } \right){\mathop{{\overline \varepsilon }}\limits^{ \cdot }_p} $$
(9)

where C x and α sat are material parameters.

By integration of Eq. 9, the isotropic part of the tension curve is found to be:

$$ {\sigma_{{iso}}} = {\sigma_Y} - \alpha = {\sigma_Y} - {\alpha_{{sat}}}\left( {1 - {e^{{ - {C_x}{{\overline \varepsilon }^p}}}}} \right) $$
(10)

The Geng-Wagoner hardening law

The third hardening law in this study is a two-surface model by Geng and Wagoner [23], which constitutes an extension of the Armstrong-Frederick hardening law. The Geng-Wagoner model includes a bounding surface, which can expand and translate in the stress space, in order to capture the permanent softening effect.

The evolution of the back stress vector α is given by:

$${\mathop \alpha \limits^ \cdot } = C_{x} {\left[ {\frac{{\alpha _{{sat}} }}{{\overline{\sigma } }}{\left( {\sigma - \alpha } \right)} - {\left( {\alpha - \beta } \right)}} \right]}{\mathop {\overline{\varepsilon } }\limits^ \cdot }^{p} $$
(11)

where the back-stress vector α represents the center of the yield surface, and β is the center of the limiting, bounding surface. The formulation of the active yield surface is similar to the Armstrong-Frederick law, but with the recall term replaced by a vector connecting the centers of the yield and bounding surfaces. The bounding surface develops according to the mixed hardening rule by Hodge [20] and Crisfield [21] (see “Mixed kinematic-isotropic hardening”), rather than by a pure isotropic expansion:

$${\mathop \beta \limits^ \cdot } = \frac{{H\prime - \widetilde{H}\prime m}}{{\sigma _{\beta } }}{\left( {\sigma _{\beta } - \beta } \right)}{\mathop {\overline{\varepsilon } }\limits^ \cdot }^{p} $$
(12)

where \( {\sigma_{\beta }} \) is a measure of the size of the bounding surface, and \( {\sigma_{\beta }} \) is the stress mapping point on the bounding surface. Note that the correct expression for the mixed hardening according to “Mixed kinematic-isotropic hardening” has been used here, and not the erroneous one according to Geng and Wagoner [23] and Crisfield [21]. Mroz [34] and Defalias and Popov [35] proposed the following assumption for the stress mapping:

$$ {\sigma_{\beta }} - \beta = \frac{{{\sigma_{\beta }}}}{{\overline \sigma }}\left( {\sigma - \alpha } \right) $$
(13)

Inserting Eq. 13 into Eq. 12, we obtain the evolution of β as

$${\mathop \beta \limits^ \cdot } = \frac{{H\prime - \widetilde{H}\prime m}}{{\overline{\sigma } }}{\left( {\sigma - \alpha } \right)}{\mathop {\overline{\varepsilon } }\limits^ \cdot }^{p} $$
(14)

The parameter m is the ratio between kinematic and isotropic response for the bounding surface (m = 1 gives purely isotropic behavior and m = 0 purely kinematic behavior) and H′ is the plastic modulus of the monotonic loading curve. A pure isotropic behavior of the bounding surface, i.e. m = 1, returns the Armstrong-Frederick hardening law.

NLK-LK model

The Nonlinear-Linear kinematic hardening (NLK-LK) law is also an extension of the Armstrong-Frederick hardening law, where an additional back-stress term is added. The basic idea of using multiple back-stress terms was first introduced by Chaboche [32, 33]. Several different formulations of the extra back-stress terms have been proposed. However, in the NLK-LK model the simplest possible formulation is used. The only extra back-stress term is purely linear, and includes one extra material parameter. This parameter is called m and accounts for the permanent softening effect. The back-stress evolution is now given by:

$$ \begin{array}{*{20}{c}} {\mathop{\alpha }\limits^{ \cdot } = {{\mathop{\alpha }\limits^{ \cdot } }_1} + {{\mathop{\alpha }\limits^{ \cdot } }_2}} \\{{{\mathop{\alpha }\limits^{ \cdot } }_1} = {C_x}\left( {{\alpha_{{sat}}}\frac{{\left( {\sigma - \alpha } \right)}}{{{\sigma_Y}}} - {\alpha_1}} \right){{\mathop{{\overline \varepsilon }}\limits^{ \cdot } }_p}} \\{{{\mathop{\alpha }\limits^{ \cdot } }_2} = m\frac{{\left( {\sigma - \alpha } \right)}}{{{\sigma_Y}}}{{\mathop{{\overline \varepsilon }}\limits^{ \cdot } }_p}} \\\end{array} $$
(15)

where C x and α sat are the same material parameters as for the Armstorng-Frederick hardening and m is an additional material parameter that accounts for the permanent softening behaviour (see Fig. 1).

The isotropic part of the tension curve is now given by:

$$ {\sigma_{{iso}}} = {\sigma_Y} - \alpha = {\sigma_Y} - {\alpha_{{sat}}}\left( {1 - {e^{{ - {C_x}{{\overline \varepsilon }^p}}}}} \right) - m \cdot {\overline \varepsilon^p} $$
(16)

The Yoshida-Uemori hardening law

The last and most advanced kinematic hardening law included in this study is the Yoshida-Uemori model, presented in 2002 [26, 36]. This model involves three different surfaces in the plane stress space. Besides a yield surface and a bounding surface, there is an additional surface controlling the permanent softening and the work hardening stagnation. In the current model the yield surface can only translate in stress space, i.e. it undergoes a pure kinematic hardening. The bounding surface, on the other hand, can translate as well as expand, i.e. mixed hardening is prevailing. The size of the yield surface is thus constant, and we have σ iso = Y, where Y is the initial, uniaxial yield stress.

The yield function can, thus, be written as

$$ f = \overline \sigma (\sigma - \alpha ) - Y = 0 $$
(17)

The bounding surface is described by the following equation:

$$ F = \overline \sigma (\sigma - \beta ) - (B+R) = 0 $$
(18)

where β is the center of the bounding surface, B is its initial size, and R represents its isotropic hardening. The relative motion of the yield surface with respect to the bounding surface is expressed by

$$ \alpha * = \alpha - \beta $$
(19)

The evolutions of α* and β are given by the equations

$$ \begin{array}{*{20}{c}} { \mathop{\alpha }\limits^{ \cdot } * = {C_x}\left[ {\frac{{B + R\left( {{{\overline \varepsilon }^p}} \right) - Y}}{Y}(\sigma - \alpha ) - \alpha *} \right]\,{{\mathop{{\overline \varepsilon }}\limits^{ \cdot } }^p}} \\{ \mathop{\beta }\limits^{ \cdot } = k\left[ {\frac{b}{{B + R\left( {{{\overline \varepsilon }^p}} \right)}}(\sigma - \beta ) - \beta } \right]{{\mathop{{\overline \varepsilon }}\limits^{ \cdot } }^p}} \\\end{array} $$
(20)

The evolution of R is, furthermore, assumed to be

$${\mathop R\limits^ \cdot }{\left( {\overline{\varepsilon } ^{p} } \right)} = k{\left( {R_{{sat}} - R{\left( {\overline{\varepsilon } ^{p} } \right)}} \right)}{\mathop {\overline{\varepsilon } }\limits^ \cdot }^{p} $$
(21)

The meaning of the various parameters in the above equations is explained graphically for a uniaxial loading case in Fig. 5.

Fig. 5
figure 5

Definition of the parameters in the Yoshida-Uemori hardening model

Full size image

It should be emphasized that in the original form of the Yoshida-Uemori model described above, the uniaxial hardening curve, defined by Eq. 21, is a result of the total optimization process aiming at defining the material parameters. This is in conflict with our demand that the experimentally measured hardening curve should be exactly reproduced in a simulation of a uniaxial tensile test.

In order to meet this demand, we have modified the original Yoshida-Uemori model such that the following relations hold:

$$ \begin{array}{*{20}{c}} {B = Y} \hfill \\{Y + R\left( {{{\overline \varepsilon }^p}} \right) + \beta \left( {{{\overline \varepsilon }^p}} \right) = H\left( {{{\overline \varepsilon }^p}} \right)} \hfill \\\end{array} $$
(22)

where \( H\left( {{{\overline \varepsilon }^p}} \right) \) is the given, experimental plastic hardening curve. The evolution of R is then found to be

$${\mathop R\limits^ \cdot }{\left( {\overline{\varepsilon } ^{p} } \right)} = {\mathop H\limits^ \cdot }{\left( {\overline{\varepsilon } ^{p} } \right)} - {\mathop \beta \limits^ \cdot }{\left( {\overline{\varepsilon } ^{p} } \right)} = \frac{{dH{\left( {\overline{\varepsilon } ^{p} } \right)}}}{{d\overline{\varepsilon } ^{p} }}{\mathop {\overline{\varepsilon } }\limits^ \cdot }^{p} - {\mathop \beta \limits^ \cdot }{\left( {\overline{\varepsilon } ^{p} } \right)}$$
(23)

To be able to model permanent softening, as well as work hardening stagnation (see Fig. 1), Yoshida and Uemori introduced an additional surface g σ in the stress space defined by

$$ {g_{\sigma }} = \overline \sigma (\beta - q) - r = 0 $$
(24)

where r denotes the size of g σ and q its center. The center of the bounding surface, defined by β, is forced to always be situated inside, or on the boundary of g σ . The purpose of this additional surface is to govern the evolution of the parameter R, such that R only evolves when β is situated on the boundary of g σ .

In this work we have used both the original and the modified version of the Yoshida-Uemori hardening. The reason for this is that the two versions differ a lot when it comes to the material parameter identification procedure. The original version must have two target curves in the optimization, a cyclic test and the uniaxial tension curve. The modified version though, only needs one target curve, the cyclic test, since the uniaxial tension curve is given as input to the constitutive model.

Determination of kinematic hardening parameters

Introductory remarks

The unknown material parameters in the kinematic hardening laws have to be determined based on some kind of cyclic experiment. In theory, the most simple and straight-forward test is a tensile/compression test of a sheet strip. In practice, however, such a test is very difficult to perform, due to the tendency of the strip to buckle in compression. However, with rather complicated test rigs, designed in order to prevent the sheet strip from buckling, such a test can be performed.

Another kind of test that frequently have been used for the determination of material hardening parameters is some kind of bending test. The advantage of this kind of tests is that they are simple to perform, and standard test equipments can be used. However, such tests will involve inhomogeneous stress and strain distributions in the sheet specimen, and the stress-strain relationship cannot be directly determined from the experiment. This means that the material parameters have to be determined by some kind of inverse approach. Usually, the experiments are simulated by FEM, and the material parameters are identified by means of some optimization technique.

In this work both a tension/compression test and a three-point bending test are used in order to perform the material parameter identification. A detailed explanation of these methods follows below.

Three-point bending test

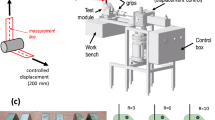
The cyclic three-point bending test is a relatively simple and convenient experiment for determining the kinematic hardening parameters for sheet metals. The test has been suggested in the literature by e.g. Zhao and Lee [38]. The equipment used in the current experiments has previously been described in Omerspahic et al. [10] and Eggertsen and Mattiasson [1–3]. The test set-up is illustrated in Fig. 6. Especially the design of the end supports should be noticed. These provide a moment free support, while the sheet strip is allowed to slip freely between two rollers in the axial direction. The punch in the middle is moved with a prescribed sinusoidal displacement. The distance between the end supports is 100 mm, and the width of the sheet strip was 25 mm. The punch force is measured by means of a load cell. During the test the punch force and punch displacement are recorded. The error in displacement reading is estimated to ± 0.02 mm and in force reading ± 3N.

Fig. 6
figure 6

Experimental set-up used in the three-point cyclic bending test: a a picture of the experimental equipment; b a sketch of the test arrangement

Full size image

Worth mentioning in this context is that at maximum displacement, 20 mm, the strain level at the most strained fibre in the longitudinal direction reaches a value between 2% and 3%.

Optimization procedure

The resulting force-displacement curves from the bending tests were used as target curves in an optimization procedure, where the three-point bending tests were simulated by the FE-method. The parameters in the various hardening laws served as design variables in this optimization procedure, in which the normalized error between the two curves was minimized. The mean squared error (MSE) is defined as

$$ \varepsilon = \frac{1}{P}{\sum\limits_{{p = 1}}^P {{W_p}\left( {\frac{{{f_p}(x) - {G_p}}}{{{s_p}}}} \right)}^2} = \frac{1}{P}{\sum\limits_{{p = 1}}^P {{W_p}\left( {\frac{{{e_p}(x)}}{{{s_p}}}} \right)}^2} $$
(25)

where f p (x), p = 1, ..., P are the values on the computed curve, G p , p = 1, ..., P are the values on the target curve, the Sp, p = 1, ..., P are residual scale factors, and the Wp, p = 1, ..., P are weights applied to the square of the scaled residual (fp - Gp) / sp at point p. That is, the smaller error, the better fit to the experimental data. In this work all parts of the target curve are considered to be of equal importance, and the weight and residual scale factors are therefore set to 1.

The identification of the hardening parameters was performed by means of the optimization code LS-OPT [39] and a Response Surface Methodology (RSM). The RSM is especially advantageous for problems, in which gradients to the object function are difficult to calculate, such as in this highly nonlinear problem.

FE-model

In the inverse approach for determining the hardening parameters, the bending test was simulated by means of the explicit FE-code LS-DYNA [27]. One quarter of the sheet strip was modeled with triangular shell elements. Convergent results were obtained with 160 elements and nine integration points through the thickness. The FE-model is shown in Fig. 7. Special care has been devoted to a correct modeling of the end supports. Just as for the experimental set-up, the support is free to rotate around its own axis. The support was modeled with two rigid plates with a frictionless contact to the specimen, such that the sheet material can slip freely in the longitudinal direction.

Fig. 7
figure 7

FE-model of the three-point bending test

Full size image

Tension/compression test

The experimental test equipment for the tension/compression test, shown in Fig. 8 below, was developed at the Industrial Development Centre in Olofström, Sweden. The test specimen is cut out according to Fig. 8a. The specimen is painted with a randomized dot pattern, which is used for the measurements of strains in the specimen. The specimen is clamped in a specimen holder that is used to prevent buckling of the specimen during the test. The holder has a peek hole that is used for measurements of the strains. A reinforced Teflon film is put between the specimen and the holder in order to eliminate the influence of friction forces. The silicon pieces are used to prevent the specimen to buckle between the specimen holding texture and the chucks. The strain distribution in the specimen is measured by an ARAMIS™ optical measuring system during the whole process.

Fig. 8
figure 8

Experimental equipment used in the tension-compression test: a a picture of the experimental equipment; b a picture of the assembled test equipment

Full size image

Two sets of experiments were performed in this study, in which the specimen was loaded up to 2% and 4%, respectively, in tension, and then reloaded to the corresponding strain levels in compression.

The big advantage with the tension/compression test it that it involves homogeneous stress and strain distributions, and, thus, no inverse modeling is needed.

The identification of the hardening parameters was again performed by means of the optimization code LS-OPT [39] and a Response Surface Methodology (RSM). The resulting stress-strain curves from the tension/compression tests were used as targets and the parameters in the various hardening laws served as design variables in this optimization procedure, in which the normalized error between the two curves was minimized. However, the predicted strain-stress distribution was calculated directly from the constitutive driver instead from a FE-analysis.

Springback prediction

The springback problem chosen in this study is the well known U-bend benchmark from the NUMISHEET’93 conference. The experimental set-up is described in Fig. 9 below.

Fig. 9
figure 9

The NUMISHEET’93 benchmark problem. a Experimental set-up; b Definition of the angles θ 1 and θ 2 , used for the evaluation of the springback

Full size image

Just as for the three-point bending test, the FE-code LS-DYNA was used to solve the problem. The forming step was solved by means of an explicit, dynamic solver, and the springback step with an implicit one. During the springback phase the forming tools were assumed to be removed instantaneously. The symmetry of the problem was utilized, and only one quarter of the model was analyzed. The geometry of the tools is shown in Fig. 9a, and the total size of the blank is 300 × 50 mm. The blankholder force was chosen to be 40 kN. Fully integrated quadrilateral shell elements were utilized in the FE-model. The friction was assumed to be of Coulomb type and of equal magnitude on all contact surfaces. Based on measured punch force and draw-in, a friction coefficient equal to 0.08 was found to be optimal for the studied material.

As shown in the work by Mattiasson et al. (1995) [40], the stress distribution in the workpiece after forming is strongly dependent on the element size in the finite element model of the sheet material. For a too coarse mesh, there is a pronounced stress relaxation after the material has reached its peak stress point at the exit of the die radius. Therefore, a comprehensive mesh convergence study was performed. Convergent results were obtained with a mesh size of 1 × 2 mm and with nine integration points through the sheet thickness.

For the material considered in this study, the most strained fiber in the springback experiment reached a level of about 10%. This can be compared with the 4% of plastic straining that at maximum can be reached in compression in the tension/compression tests. This difference is important to have in mind when we compare predicted and experimental springback in the next chapter.

Results and discussion

Introductory remarks

The U-bend springback example used in this work is commonly used in the literature related to springback predictions. It is a very simple example and the forming procedure consists of bending and subsequent re-bending of the material, i.e. one half cycle of plastic work. Therefore, the optimization of the unknown material hardening parameters is performed on a half cycle both in the three-point bending test and the tension-compression tests. However, in a real industrial application the part geometry often is more complicated, and more than just a half loading cycle can therefore be expected. Because of this reason the optimization procedure is also performed on two whole cycles, both in the three-point bending test and in the tension-compression test. The choice of two cycles is based on the assumption that it can be considered as an upper limit of how many cycles that can be expected in a forming operation in the automotive industry.

Since the different considered hardening laws have different properties, the results are presented individually for each hardening law.

For each hardening law, the results are presented in two tables. The first table describes the result in terms of the obtained material parameters, the obtained MSE-value and the resulting tip deflection in the U-bend springback example. The second table describes how well an optimal solution for a specific experiment suits experimental data for the other experiments, in terms of the MSE-value. A further explanation of how this table should be interpreted follows in the first subchapter below.

Mixed hardening

The mixed hardening law is the simplest kinematic hardening law considered in this work. As can be expected the differences between predicted and experimental results are quite large. This is a consequence of the fact that the mixed hardening law does not account for the transient behavior (see Fig. 1). In Table 3 the value of the material parameter, the MSE-value and the resulting tip deflection of the U-bend springback problem are presented for the three experiments, and for a half and two whole loading cycles, respectively. The resulting tip deflection is compared to the experimental obtained value of 27.3 ± 0.2 mm, where the ± 0.2 mm covers the scatter in experimental values. As also can be seen in the table, the tip deflection of the springback problem is underestimated for all the obtained material parameters. The reason for this can be seen in Fig. 10. As discussed earlier, the U-bend is a very simple example and includes only a half loading cycle. This means that, when comparing an experimental cyclic test with the springback example, only the first half cycle is of interest. Figure 10a shows the experimental curve together with the predicted result with a parameter identified from the 4% tension/compression test for a half cycle. As can be seen, the stress level after a half cycle is under-predicted due to the lack of transient behavior in the predicted result. The under-prediction of the stress is the immediate reason to the under-prediction of the resulting tip deflection. The same effect can be seen even if the parameter is identified from two whole cycles (Fig. 10b). However, in this case the under-prediction is even larger after a half cycle, leading to that the under-prediction of the resulting springback also becomes larger. One other interesting thing that can be seen in Fig. 10b is that the permanent softening effect only works for reverse loading and not for forward loading. As can be seen the stress level after one cycle approaches the same level as pure isotropic hardening. This is a result of that the plastic hardening curve is non-linear. The original mixed hardening model assumes a linear plastic hardening curve, and for such a case the permanent softening effect is predicted in both forward and reverse loading.

Table 3 Material parameters, MSE-Values and resulting springback for the mixed hardening law
Full size table
Fig. 10
figure 10

Predicted and experimental stress-strain relationships for the mixed hardening model: a one half cycle optimized based on the 4% tension/compression test. b two whole cycles optimized based on the 4% tension/-compression test

Full size image

In an ideal world all the considered parameter identification experiments should give the same parameter set-up and equal MSE-value. However, as can be seen in Table 3, this is not the case. Table 4 below shows how the optimized parameters from a certain experiment fits the other experiments. The table should be read row-wise. This means that for the first row the material parameter is optimized from the 2% tension/compression test and for a half cycle. The MSE-value is then 0.01059 and is displayed in the grey shaded cell. The other columns in this row show how well the five other experiments are predicted with this parameter. The percentage values indicate the increase in MSE-value compared to the one in the shaded cell. As an example, if we are using the parameter value optimized from a 2% tension/compression test at a half cycle (m = 0.5972, Table 3), then the MSE-value for a half cycle simulation of the 4% tension/compression test is 30% larger than for the original fit. It should be emphasized that, by presenting the results in this way, one has to be careful when comparing different columns and different materials, since the divergence from the “best” fit is dependent on how good the “best” fit is. This means that even if the divergence is big in terms of percent, the MSE-value in absolute value can still be quite small, if the MSE-value for the “best” fit is sufficiently small.

Table 4 MSE-values for the mixed hardening law
Full size table

As can be seen in Table 4, there is a quite large spread in the MSE-values for the mixed hardening law. This is especially true, when the parameters from the two-cycle tests are used for simulating the half-cycle tests. In some cases the divergence to the “best” fit is hundreds of percents. However, when the parameter from one of the two-cycle tests is applied to simulate the other two-cycle tests, the divergence seems to be quite small. In particular, the correspondence between the bending test and the 2% tension/compression test is very good. This is not so surprising, since both experiments ends up on more or less the same strain level at the most strained fibers.

Armstrong-Frederick hardening

As can be seen in Fig. 10, the mixed hardening does not account for the transient behavior (Fig. 1), which results in quite large deviation between experimental and predicted data. The Armstrong-Frederick hardening law, on the other hand, accounts for both the Bauschinger effect and the transient behavior. This means that smaller deviations (MSE-values) between experimental and predicted data can be anticipated. According to Table 5 this is also the result, especially for the half-cycle tests. In those cases, also the predictions of the tip deflection become very good. For the cases where two whole cycles are considered, the MSE-values are larger, and the accuracy of the springback predictions are worse. The reason for the larger divergence for the two whole cycles cases is related to the fact that the Armstrong-Frederick hardening law cannot account for the permanent softening effect (Fig. 1). An illustration of the fitting for two cycles is shown in Fig. 11b. One of the characteristics of the Armstrong-Frederick model is that the stress at reverse loading always saturates towards the isotropic hardening stress level. However, as can be seen in Fig. 11b, the stress level in the experimental data saturates towards a fixed value of about 700 MPa. This is the reason why the MSE-values and the predicted springback become worse for two-cycles experiments than for the half-cycle ones. In the case shown in Fig. 11b the stress after a half cycle is under-estimated, and, thus, even the springback is under-estimated. Figure 11a shows the predicted and experimental stress-strain relationship based on the 4% tension-compression test for a half cycle. In Table 6 a comparison between the different identification methods is shown in the same manner as for the mixed hardening rule in the previous chapter.

Table 5 Material parameters, MSE-Values and resulting springback for the Armstrong-Frederick hardening law
Full size table
Fig. 11
figure 11

Predicted and experimental stress-strain relationships for the Armstrong-Frederick hardening model: a a half cycle based on the 4% tension compression test. b two whole cycles based on the 4% tension compression test

Full size image
Table 6 MSE-values for the Armstrong-Frederick hardening law
Full size table

Geng-Wagoner hardening law

The Geng-Wagoner hardening law is an extension of the Armstrong-Frederick law, and accounts also for the permanent softening effect. As can seen in Table 7 this seems to work well for the half-cycle tests, where obtained MSE-values are very small. However, for two full cycles the MSE-values are not that good, at least not for the two tension/compression tests. This can be explained by some weaknesses in the theoretical formulation of the Geng-Wagoner hardening law. According to Eq. 14, the permanent softening is governed by the mixed hardening law, Eq. 5. This means that the problems observed for forward loading for the mixed hardening law, also are present for the Geng-Wagoner law. An illustration of this can be seen in Fig. 12b. The figure shows the predicted stress-strain relationship for two whole cycles with parameters obtained from the 4% tension/compression test for just a half cycle. It can be noted that the stress level at forward loading approaches the one for pure isotropic hardening, while the permanent softening effect only is present for reverse loading. An interesting detail for the material parameters obtained from the optimizations based on two whole cycles is that the third parameter, m, is close to 1, which means that there is no permanent softening effect and the Armstrong-Frederick hardening law is recovered.

Table 7 Material parameters, MSE-Values and resulting springback for the Geng-Wagoner hardening law
Full size table
Fig. 12
figure 12

Predicted and experimental stress-strain relationships for the Geng-Wagoner hardening model: a a half cycle based on the 4% tension/compression test. b two whole cycles based on the 4% tension compression test and a half cycle in the optimization

Full size image

When it comes to the predicted tip deflection of the springback problem, it can be observed from Table 7 that the predictions are fairly good. With parameters obtained from experiments with a half loading cycle, both the bending and the 4% tension/compression tests give accurate springback predictions, while the 2% tension/compression test over-predicts the tip deflection. In this case it seems that 2% straining is too small to capture the behavior at the higher strain levels that appears in the springback example. For the two cycles cases there is more spread in the springback predictions, which also can be expected based on the fact that the MSE-values are much higher, and on the consequences related to the discussion on reverse and forward loading above. A comparison between the different identification methods can be found in Table 8.

Table 8 MSE-values for the Geng-Wagoner hardening law
Full size table

NLK-LK

The non-linear kinematic + linear kinematic hardening law is an alternative formulation of the Geng-Wagoner hardening law. Just as the Geng-Wagoner model it accounts for the Bauschinger effect, the transient behavior, and the permanent softening (Table 2, Fig. 1). The permanent softening is included by adding an extra linear backstress term to the Armstrong-Frederick law (Eq. 15). The magnitude of this linear contribution is then dependent on the material parameter m and on the effective plastic strain. This causes some problems for the material parameter identification procedure. According to Table 9 the MSE-values are small both for a half and two whole cycles. However, the predicted tip deflection for the springback problem is far from experimental values in all cases. The reason for this is illustrated in Fig. 13. When the material parameters are identified from e.g. the 2% tension/compression test and two full cycles (Fig. 13a), good agreement with experimental values is achieved. However, as can be seen in Table 9 the parameter m becomes quite large, m = 1325. This fact causes problems when the strain levels become larger, since the linear term that governs the permanent softening effect is dependent on the parameter m and the effective plastic strain. This means that when both the effective plastic strain and the parameter m become large, a large permanent softening effect is obtained. An example of this can be seen in Fig. 13b. In this case the same parameters as in Fig. 13a are used, but now for the 4% tension/compression test. It can be noted that the stress levels are under-estimated. Exactly the same thing happens in the springback example, where the plastic strain levels become even higher for the first reversed loading, and, thus, the stress levels become heavily under-estimated. As can be observed in Table 9, the accuracy of the prediction of the tip deflection is more or less governed by the material parameter m—the larger value of m, the larger deviation from experimental values. If a material parameter identification procedure for this material model could be performed based on experimental values from a test with strain levels near those in the springback example, fairly good springback predictions could be anticipated. Another way to get around the above mentioned problem is to let the parameter m be a function of the effective plastic strain. A comparison between the different identification approaches for the NLK-LK model can be seen in Table 10.

Table 9 Material parameters, MSE-Values and resulting springback for the NLK-LK hardening law
Full size table
Fig. 13
figure 13

Predicted and experimental stress-strain relationships for the NLK-LK hardening model: a two whole cycles based on the 2% tension compression test. b two whole cycles 4% tension-compression with material parameters from the two-cycles 2% tension/compression test

Full size image
Table 10 MSE-values for the NLK-LK hardening law
Full size table

Modified Yoshida-Uemori model

The Yoshida-Uemori hardening model accounts for all the effects described in Fig. 1. Therefore, quite good results can be expected, both for the fit to experimental data, and for the springback prediction. According to the results in Table 11, those expectations are more or less fulfilled. The springback predictions are good in five of six cases, and the MSE-values are quite low in all cases. An explanation of the bad tip deflection prediction for the parameters from the half-cycle, 2% tension/compression test, is simply the fact that this strain level is too low to provide parameters for a case with five times higher strain levels. It can also be observed from Table 12 that the parameters from the half-cycle, 2% tension/compression test yield quite bad results when applied to the five other cases.

Table 11 Material parameters, MSE-Values and resulting springback for the modified Yoshida-Uemori hardening law
Full size table
Table 12 MSE-values for the modified Yoshida-Uemori hardening law
Full size table

Furthermore, for a material parameter identification based on the 4% tension/compression test for two full cycles, the predictions of the other experiments seem to be really good. Even for this material model it can be emphasized that a large deviation in terms of percent can still signify a relatively small MSE-value, since “the best fit” results in low MSE-values for all the experiments.

Original Yoshida-Uemori hardening law

For the original Yoshida-Uemori model the same tendency as for the modified version can be observed. The springback predictions are good in all cases except for the 2% tension/compression test for a half cycle. The explanation of the under-prediction of the tip deflection is of course the same as for the modified version. The strain level of 2% is simply not enough as identification basis when the strain level becomes so much higher in the springback prediction. The MSE-values are slightly higher for the original Yoshida-Uemori model than for the modified model. One reason for this can be that the identification procedure is more complicated for the original version. Firstly, there are six material parameters instead of four. This means that there can be more optimal solutions. The material parameter set-up presented in Table 13 is one optimal solution, but there is no guarantee that it is the best optimal solution. Furthermore, since the plastic hardening curve is not prescribed to the material model for the original version, it has to be a part of the identification procedure. This means that there have to be two target curves in the identification: a cyclic curve and a plastic hardening curve. Of course, this implies that there are even more optimum solutions.

Table 13 Material parameters, MSE-Values and resulting springback for the original Yoshida-Uemori hardening law
Full size table

Table 14 reveals that even for the original version of the Yoshida-Uemori model the 4% tension/compression test used for two full loading cycles seems to give very good results even for the other five experiments.

Table 14 MSE-values for the original Yoshida-Uemori hardening law
Full size table

Summary and conclusions

In the introduction of this paper three tasks were assigned for the present work to investigate. These tasks and the conclusions drawn in relation to them follow below.

  1. 1)

    Explain why different test procedures yield different sets of hardening parameters

    • No hardening law is able to simulate all experiments (type of experiment, number of loading cycles, strain level, etc.) with good accuracy and with the same set of parameters

    • It is, thus, obvious that each experiment yields a unique set of hardening parameters.

    • It has, however, been observed that the more advanced models (more parameters) cover a wider range of strain levels and number of loading cycles.

  2. 2)

    Find out how different test methodologies for determining the hardening parameters influence the predicted springback

    • Parameters determined from bending tests and from tension/compression tests, respectively, seem to yield the same level of accuracy

    • It seems, though, that tests that best resemble the actual springback problem (number of loading cycles, strain level, etc.) result in the most accurate springback predictions

    • In practice, however, it is not possible to adapt the test procedure for the hardening parameter identification for one special springback problem. Instead, the test procedure must be designed so that it covers an as wide spectrum of thinkable springback problems as possible.

  3. 3)

    Determine which of the two test procedures is the “best” one

    • From an accuracy point of view the two test procedures (bending vs. tension/compression) seem to be equally good.

    • Since the methodology based on tension/compression tests does not rely on inverse methods, it is considerably more efficient than the one based on bending tests, and have therefore an advantage.

Besides an increased knowledge of different experimental methods for hardening parameter identification, the present study has also given a deeper understanding of the pros and cons of the various hardening laws. Beyond dispute is that the Yoshida-Uemori model generally is the model that results in the most accurate springback predictions. It is also the model that, with a certain set of hardening parameters, can cover the widest span of loading cycles and strain levels. The disadvantage is that, due its complexity, it is the most demanding model in terms of computational efforts. Another disadvantage in connection to the many material parameters involved in the model is that there exist many local minima in the optimization process for identifying these parameters. There is thus a chance that the global minimum is not found, and that the indentified set of parameters is not the best one.

Even the simplest hardening models can in certain cases produce acceptable springback results. For instance, most of the models can simulate a half loading cycle with decent accuracy. If this resembles the most important deformation mode in the actual springback problem, acceptable springback results can be anticipated.

An important lesson learned from this study is that a good fit to the experimental cyclic data is no guarantee for a good springback prediction. This is especially true if the plastic strain levels reached in the cyclic experiments deviate too much from the strain levels in the springback problem.

Even if it is not obvious from the results in this report, the NLK-LK model can work well for more than a half loading cycle. However, the model is very dependent on that the strain levels in the cyclic experiment are similar in magnitude to those in the springback problem. This is due to the fact that the linear kinematic term is directly dependent on the magnitude of the effective plastic strain. An alternative formulation would be to reformulate the model such that the material parameter associated to the linear kinematic term also is dependent on the effective plastic strain.