1 Introduction

Since the 19th century, linear system theory can no longer meet the needs of reality, thus promoting the rapid development of nonlinear system theory. Among them, nonlinear partial differential equations, as a hotspot in the field of nonlinear scientific research, have been widely used to describe problems in many fields such as mathematics, physics, chemistry, sociology and biology [1,2,3,4]. With the continuous progress of science and technology, many phenomena cannot be described by integer-order differential equations only. For example, in the financial field, stock price fluctuations are affected by a variety of factors, including market sentiment, policy changes, etc. These changes have memory effects and cannot be simply described by integer-order nonlinear differential equations. Thus, the rapid development of fractional order nonlinear differential equations is promoted. Various methodologies for solving fractional partial differential equations have been proposed and developed by scholars both domestically and internationally. These include the first integration method [5], the F-expansion method [6, 7], and the fractional sub-equation method [8, 9], among others.

The Lie symmetry group theory is crucial in analyzing integer-order PDEs, particularly for constructing their exact solutions, and has been extensively developed [10,11,12]. Consequently, many researchers have extended this theory to fractional PDEs. In literature [13,14,15], Professor Zhang and his team studied the symmetry determination and nonlinearization of nonlinear temporal fractional partial differential equations, its local symmetric structure and potential symmetry, and the symmetric structure of multidimensional temporal fractional partial differential equations. These research results are of great significance to the development of symmetry analysis of fractional differential equations. The main idea of the Lie group is that the order of a differential equation can be constructively lowered by 1 place if the equation does not change under the conditions of the Lie transformation. Through this theory, scientists have unified the previous haphazard solution methods and proposed symmetric and group-invariant solutions, simplifying the troubles that existed in the computational process.

Recently, studies [16,17,18] have examined the following dissipative long-wave system:

$$\begin{aligned} \left\{ \begin{array}{llll} u_{t}-u_{xx}-2vu_{x}-2uv_{x}=0, \\ v_{yt}+v_{xxy}-2u_{xx}-2v_{y}v_{x}-2vv_{xy}=0. \\ \end{array}\right. \end{aligned}$$
(1.1)

The (2+1)-dimensional dissipative long-wave system delineates the hydrodynamic water wave model in broad channels or open seas of finite depth. It also serves as an illustrative tool for nonlinear wave propagation in dissipative mediums. In [16], the authors discovered new families of non-traveling wave solutions using an extended projective Riccati equation method. In [17], a set of innovative rational solutions, along with their interactive counterparts, were discovered through the fusion of exponential and quadratic functions. In [18], several fresh exact interaction solutions were explicitly obtained, including trigonometric wave-soliton and soliton-trigonometric wave combinations, achieved through the application of Riccati expansion.

In this paper, we expanded the Lie symmetry analysis to encompass the (2+1)-dimensional time fractional dissipative long-wave system, presented as follows:

$$\begin{aligned} \left\{ \begin{array}{llll} D^{\alpha }_{t}u-u_{xx}-2vu_{x}-2uv_{x}=0, \\ D^{\alpha }_{t}v_{y}+v_{xxy}-2u_{xx}-2v_{y}v_{x}-2vv_{xy}=0.\\ \end{array}\right. \end{aligned}$$
(1.2)

Up to now, most of the types of partial differential equations of fractional order studied using the Lie symmetry method are in the form of pure fractional order of time, pure fractional order of space, or both, while Lie symmetry results for partial differential equations with mixed derivatives of fractional and integer orders are very limited. Moreover, when both spatial and time fractional order derivatives play an important role, the mixed derivatives may have different physical significance. Therefore it is necessary to study this class of equations. The symbol \(D^\alpha _t\) represents the Riemann-Liouville fractional derivative, defined in [19,20,21], namely,

$$\begin{aligned} _{a}D_{t}^\alpha f(t,x) =D_{t}^{n}\ _{a}I_{t}^{n-\alpha } f(t,x)= \left\{ \begin{array}{lll} \frac{1}{\Gamma (n-\alpha )}\frac{\partial ^n}{\partial t^n}\int _a^t {\frac{f(s,x)}{(t-s)^{ \alpha -n+1 }} }\textrm{d}s,\ \ &{} n-1<\alpha <n, n\in \mathbb {N} \\ D_{t}^{n}f(t,x),\ \ &{} \alpha =n\in \mathbb {N} \\ \end{array}\right. \end{aligned}$$

for \(t>a\). We denote the operator \(_{0}D^{\alpha }_{t}\) as \(D^{\alpha }_{t}\) throughout this paper, while \(D^{-\alpha }_{t}=I^{\alpha }_{t}\) is Riemann-Liouville fractional integral.

The objectives of this paper include deriving the symmetry, one-parameter Lie transformation group, exact solutions, optimal system, similarity reduction, and conservation laws for the models under consideration. To the best of the author’s knowledge, these findings have not been reported elsewhere.

2 Lie symmetry analysis of Eq. (1.2)

Drawing upon the Lie group method [22,23,24], we can define a one-parameter Lie group of infinitesimal transformations that operate on both the independent and dependent variables

$$\begin{aligned} \begin{aligned} t^{*}=&t+\epsilon \tau (t,x,y,u,v)+o(\epsilon ^2),\\ x^{*}=&x+\epsilon \xi (t,x,y,u,v)+o(\epsilon ^2), \\ y^{*}=&y+\epsilon \theta (t,x,y,u,v)+o(\epsilon ^2),\\ u^{*}=&u+\epsilon \eta (t,x,y,u,v)+o(\epsilon ^2), \\ v^{*}=&v+\epsilon \zeta (t,x,y,u,v)+o(\epsilon ^2), \end{aligned} \end{aligned}$$
(2.1)

where \(t^*, x^*, y^*, \tau , \xi , \theta , \eta \) and \(\zeta \) represent real functions of t, x, y, u,  and v, while \(\epsilon \) serves as a parameter for the infinitesimal transformation.

The generators of Lie point symmetry for a One-Parameter Lie Group (2.1) can be represented in vector form

$$\begin{aligned} X=\tau \frac{\partial }{\partial t }+\xi \frac{\partial }{\partial x }+\theta \frac{\partial }{\partial y }+\eta \frac{\partial }{\partial u }+\zeta \frac{\partial }{\partial v}, \end{aligned}$$
(2.2)

where \(\tau , \xi , \theta , \eta , \zeta \) meet the following conditions:

$$\begin{aligned} \begin{aligned}&prX(\Delta _1)|_{\Delta _1=0}=0,\\&prX(\Delta _2)|_{\Delta _2=0}=0, \end{aligned} \end{aligned}$$
(2.3)

with

$$\begin{aligned} \begin{aligned}&\Delta _1=D^{\alpha }_{t}u-u_{xx}-2vu_{x}-2uv_{x},\\&\Delta _2=D^{\alpha }_{t}v_{y}+v_{xxy}-2u_{xx}-2v_{y}v_{x}-2vv_{xy}. \end{aligned} \end{aligned}$$
(2.4)

The prolongation of the operator X takes on the following form

$$\begin{aligned} \begin{aligned} prX=&X+\eta ^t_\alpha \frac{\partial }{\partial (\partial ^\alpha _tu)}+\zeta ^{ty}_{\alpha +1}\frac{\partial }{\partial (\partial ^{\alpha }_{t} v_{y})}+\eta ^{x}\frac{\partial }{\partial u_{x}}+\zeta ^{x}\frac{\partial }{\partial v_{x}}+\zeta ^{y}\frac{\partial }{\partial v_y}+\eta ^{xx}\frac{\partial }{\partial u_{xx}}\\&+\zeta ^{xy}\frac{\partial }{\partial v_{xy}}+\zeta ^{xxy}\frac{\partial }{\partial v_{xxy}}, \end{aligned} \end{aligned}$$
(2.5)

where the explicit expressions for \(\eta ^{t}_{\alpha }\), \(\eta ^{x}\), \(\zeta ^x\),\(\zeta ^{y}\), \(\eta ^{xx}\), \(\zeta ^{xy}\), \(\zeta ^{xxy}\) can be found in reference [25, 26]. Given the absence of a chain rule for fractional derivatives, we posit that \(\zeta \) is linear in v. Employing the generalized Leibniz rule [25], we derive the expression for \(\zeta ^{ty}_{\alpha +1}\) as follows

$$\begin{aligned} \begin{aligned} \zeta ^{ty}_{\alpha +1}=&D^\alpha _t[D_y(\zeta -\tau v_t-\xi v_x-\theta v_y)]+\xi \partial ^\alpha _t(v_{xy})+\theta \partial ^\alpha _t(v_{yy})+\tau \partial ^{\alpha +1}_tv_y\\ =&D^\alpha _t[\zeta _y+\zeta _uu_y+\zeta _vv_y-(\tau _y+\tau _uu_y+\tau _vv_y)v_t-(\xi _y+\xi _uu_y+\xi _vv_y)v_x\\&-(\theta _y+\theta _uu_y+\theta _vv_y)v_y]-\sum _{k=1}^{\infty }\left( {\begin{array}{c}\alpha \\ k\end{array}}\right) D^k_t(\xi )D^{\alpha -k}_t(v_{xy})\\&-\sum _{k=1}^{\infty }\left( {\begin{array}{c}\alpha \\ k\end{array}}\right) D^k_t(\theta )D^{\alpha -k}_t(v_{yy})-\sum _{k=0}^{\infty }\left( {\begin{array}{c}\alpha \\ k+1\end{array}}\right) D^{k+1}_t(\tau )D^{\alpha -k}_t(v_y). \end{aligned} \end{aligned}$$
(2.6)

Substituting the expression \(\eta ^{t}_{\alpha }\), \(\eta ^{x}\), \(\zeta ^x\),\(\zeta ^{y}\), \(\eta ^{xx}\), \(\zeta ^{xy}\), \(\zeta ^{xxy}\), and \(\zeta ^{ty}_{\alpha +1}\) into (2.3) and equating the coefficients of various derivatives of u and v to zero, we deduce the infinitesimals as follows

$$\begin{aligned} \tau =c_1t,\ \ \xi =\frac{\alpha }{2 }c_1x+c_2,\ \ \theta =c_3, \ \ \eta =-\frac{\alpha }{2 }c_1u, \ \ \zeta =-\frac{\alpha }{2 }c_1v, \end{aligned}$$
(2.7)

where \(c_1\), \(c_2\) and \(c_3\) are arbitrary constants. So system (1.2) admits the three-dimension Lie algebra spanned by

$$\begin{aligned} X_1=t\frac{\partial }{\partial t }+\frac{\alpha }{2 }x\frac{\partial }{\partial x }-\frac{\alpha }{2 }u\frac{\partial }{\partial u }-\frac{\alpha }{2 }v\frac{\partial }{\partial v },\ \ X_2=\frac{\partial }{\partial x },\ \ X_3=\frac{\partial }{\partial y }. \end{aligned}$$
(2.8)

3 Similarity reductions and invariant solutions of System (1.2)

In this section, reduction equations for System (1.2) are derived using the Lie Symmetry Generators (2.8). These reduction equations enable the construction of analytic solutions for System (1.2).

Case 1: \(X_2=\frac{\partial }{\partial x }\)

The characteristic equation associated with the group generator \(X_2\) is

$$\begin{aligned} \frac{\textrm{d} t }{0}=\frac{\textrm{d}x }{1 }=\frac{\textrm{d} y }{0 }=\frac{\textrm{d}u }{0 }=\frac{dv}{0}. \end{aligned}$$
(3.1)

The subsequent group-invariant solutions can be acquired as follows:

$$\begin{aligned} z_1=t, z_2=y, u=f(z_1,z_2), v=g(z_1,z_2). \end{aligned}$$
(3.2)

By substituting (3.2) into System (1.2), we derive the ensuing reduced system:

$$\begin{aligned} \left\{ \begin{aligned} D^\alpha _tf=0,\\ D^\alpha _tg_y=0, \end{aligned}\right. \end{aligned}$$
(3.3)

from which, we can obtain the following solution:

$$\begin{aligned} u=F_1(y)t^{\alpha -1}, v=F_2(y)t^{\alpha -1}, \end{aligned}$$
(3.4)

where \(F_1(y)\) and \(F_2(y)\) are arbitrary functions about y. Figure 1 illustrates the dynamic behavior of the solution (3.4) under varying parameters.

Fig. 1
figure 1

Contour plot of solution (3.4) for \(F_1(y)=y^2, F_2(y)=sin(y)\)

Full size image

Case 2: \(X_3=\frac{\partial }{\partial y }\)

The characteristic equation corresponding to the group generator \(X_3\) is

$$\begin{aligned} \frac{\textrm{d} t }{0}=\frac{\textrm{d}x }{0 }=\frac{\textrm{d} y }{1 }=\frac{\textrm{d}u }{0 }=\frac{dv}{0}, \end{aligned}$$
(3.5)

By solving the above system, we can obtain the following invariant and invariant solutions

$$\begin{aligned} \psi _1=t, \psi _2=x, u=p(\psi _1,\psi _2), v=q(\psi _1,\psi _2). \end{aligned}$$
(3.6)

By substituting (3.6) into System (1.2), we derive the ensuing reduced system:

$$\begin{aligned} \left\{ \begin{aligned}&D^\alpha _tp-p_{xx}-2qp_x-2pq_x=0,\\&-2p_{xx}=0, \end{aligned}\right. \end{aligned}$$
(3.7)

from which, we can obtain the following solution:

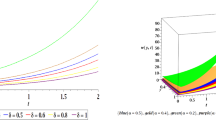
$$\begin{aligned} u=(ax+b)t^{\alpha -1}, v=\frac{H(t)}{ax+b}, \end{aligned}$$
(3.8)

where a, b are arbitrary constants and H(t) is an arbitrary function on t. Figure 2 illustrates the dynamic behavior of the solution (3.8) under varying parameters.

Fig. 2
figure 2

Contour plot of solution (3.8) for \(a=1, b=1, H(t)=t^{0.2},t^{0.4},t^{0.6}\)

Full size image

Case 3:

\(X_1=t\frac{\partial }{\partial t }+\frac{\alpha }{2 }x\frac{\partial }{\partial x }-\frac{\alpha }{2 }u\frac{\partial }{\partial u }-\frac{\alpha }{2 }v\frac{\partial }{\partial v }\)

The characteristic equation associated with the group generator \(X_1\) is as follows:

$$\begin{aligned} \frac{\textrm{d} t }{t }=\frac{\textrm{d}x }{\frac{\alpha }{2 }x }=\frac{\textrm{d}u }{-\frac{\alpha }{2 }u }=\frac{\textrm{d}v}{-\frac{\alpha }{2 }v}. \end{aligned}$$
(3.9)

Hence, we derive the similarity variables as follows \(xt^{-\frac{\alpha }{2 }}\), y, \(ut^{\frac{\alpha }{2 }}\) and \(vt^{\frac{\alpha }{2 }} \). Thus, we deduce the invariant solution of system (1.2) as follows

$$\begin{aligned} u(t,x,y)=t^{-\frac{\alpha }{2 }}f(\omega _1,\omega _2),\ \ v(t,x,y)=t^{-\frac{\alpha }{2 }}g(\omega _1,\omega _2),\ \ \omega _1=xt^{-\frac{\alpha }{2 }},\ \ \omega _2=y.\nonumber \\ \end{aligned}$$
(3.10)

Theorem 3.1

The similarity transformations \(u(t,x,y)=t^{-\frac{\alpha }{2 }}f(\omega _1,\omega _2), v(t,x,y)=t^{-\frac{\alpha }{2 }}g(\omega _1,\omega _2),\) with the similarity variables \(\omega _1=xt^{-\frac{\alpha }{2 }}\), \(\omega _2=y\) reduces system (1.2) to the (1+1)-dimensional fractional partial differential system given by

$$\begin{aligned} \left\{ \begin{aligned}&\left( \mathcal {P}^{1-\frac{3\alpha }{2 },\alpha }_{\frac{2 }{\alpha },\infty }f\right) (\omega _1,\omega _2)-f_{\omega _1\omega _1}-2f_{\omega _1}g-2fg_{\omega _1}=0,\\&\left( \mathcal {P}^{1-\frac{3\alpha }{2 },\alpha }_{\frac{2 }{\alpha },\infty }g_{\omega _2}\right) (\omega _1,\omega _2)+g_{\omega _1\omega _1\omega _2}-2f_{\omega _1\omega _1}-2g_{\omega _1}g_{\omega _2}-2gg_{\omega _1\omega _2}=0, \end{aligned}\right. \end{aligned}$$
(3.11)

where \((\mathcal {P}^{\iota ,\kappa }_{\delta _1,\delta _2})\) is the left-hand Erdélyi-Kober fractional differential operator defined by

$$\begin{aligned}{} & {} \left( \mathcal {P}^{\iota ,\kappa }_{\delta _1,\delta _2}\psi \right) (\omega _1,\omega _2)\!:=\!\prod _{j=0}^{m\!-\!1}(\iota \!+\!j-\frac{1 }{\delta _1}\omega _1\frac{\textrm{d} }{\textrm{d}\omega _1 }\!-\frac{1 }{\delta _2}\omega _2\frac{\textrm{d} }{\textrm{d}\omega _2 })\left( \mathcal {K}^{\iota \!+\!\kappa ,m-\kappa }_{\delta _1,\!\delta _2}\psi \right) (\omega _1,\!\omega _2),\ \kappa >0, \nonumber \\{} & {} \qquad m=\left\{ \begin{array}{lll} [\kappa ]+1,\ \ {} &{}if \ \kappa \notin \mathbb {N}, \\ \kappa ,\ \ {} &{}if \ \kappa \in \mathbb {N}, \end{array}\right. \nonumber \\ \end{aligned}$$
(3.12)

where

$$\begin{aligned} \left( \mathcal {K}^{\iota ,\kappa }_{\delta _1,\delta _2}\psi \right) (\omega _1,\omega _2):=\left\{ \begin{array}{lll} \frac{1 }{\Gamma (\kappa ) }\int _1^\infty (s-1)^{\kappa -1}s^{-(\iota +\kappa )}\psi \left( \omega _1 s^{\frac{1 }{\delta _1 }},\omega _2 s^{\frac{1 }{\delta _2 }}\right) \textrm{d}s,\ \ {} &{}\kappa >0, \\ \psi (\omega _1,\omega _2),\ \ {} &{}\kappa =0, \end{array}\right. \end{aligned}$$
(3.13)

is the left-hand Erdélyi-Kober fractional integral operator.

Proof

For \(0<\alpha <1\), the Riemann–Liouville time fractional derivative of v(t, x, y) can be obtained as follows:

$$\begin{aligned} D^{\alpha }_{t}v_{y}=\frac{\partial ^\alpha }{\partial t^\alpha }(t^{-\frac{\alpha }{2 }}g_{\omega _2}(\omega _1,\omega _2))=\frac{\partial }{\partial t }\Big [\frac{1}{\Gamma (1-\alpha )}\int _0^t (t-s)^{-\alpha }s^{-\frac{\alpha }{2}}g_{\omega _2}(xs^{-\frac{\alpha }{2 }},y)\textrm{d}s\Big ]. \end{aligned}$$

Assuming \(r=\frac{t }{s}\), we have

$$\begin{aligned} \frac{\partial }{\partial t }\Big [\frac{t^{1-\frac{3\alpha }{2 }}}{\Gamma (1-\alpha )}\int _1^\infty (r-1)^{-\alpha }r^{\frac{3\alpha }{2 }-2}g_{\omega _2}(\omega _1 r^{\frac{\alpha }{2 }},\omega _2 )\textrm{d}r\Big ]=\frac{\partial }{\partial t }\Big [t^{1-\frac{3\alpha }{2 }}(\mathcal {K}^{1-\frac{\alpha }{2 },1-\alpha }_{\frac{2 }{\alpha },\infty }g_{\omega _2})(\omega _1,\omega _2)\Big ]. \end{aligned}$$

Because of \(\omega _1=xt^{-\frac{\alpha }{2}}\) and \(\omega _2=y\), the following relation holds:

$$\begin{aligned} t\frac{\partial }{\partial t }g_{\omega _2}(\omega _1,\omega _2)=-\frac{\alpha }{2}\omega _1\frac{\partial }{\partial \omega _1 }g_{\omega _2}(\omega _1,\omega _2). \end{aligned}$$

Hence, we arrive at

$$\begin{aligned} \begin{aligned} D^{\alpha }_{t}v_{y}&=t^{-\frac{3\alpha }{2 }}\Big [(1-\frac{3\alpha }{2 }-\frac{\alpha }{2}\omega _1\frac{\partial }{\partial \omega _1 })(\mathcal {K}^{1-\frac{\alpha }{2 },1-\alpha }_{\frac{2 }{\alpha },\infty }g_{\omega _2})(\omega _1,\omega _2)\Big ] \\&=t^{-\frac{3\alpha }{2 }}(\mathcal {P}^{1-\frac{3\alpha }{2 },\alpha }_{\frac{2 }{\alpha },\infty }g_{\omega _2})(\omega _1,\omega _2). \end{aligned} \end{aligned}$$

Similarly

$$\begin{aligned} D^\alpha _tu=t^{-\frac{3\alpha }{2}}(\mathcal {P}^{1-\frac{3\alpha }{2 },\alpha }_{\frac{2 }{\alpha },\infty }f)(\omega _1,\omega _2). \end{aligned}$$

Meanwhile,

$$\begin{aligned} u_{xx}+2vu_{x}+2uv_x=t^{-\frac{3\alpha }{2 }}(f_{\omega _1\omega _1}+2f_{\omega _1}g+2fg_{\omega _1}),\\ v_{xxy}-2u_{xx}-2v_yv_x-2vv_{xy}=t^{-\frac{3\alpha }{2}}(g_{\omega _1\omega _1\omega _2}-2f_{\omega _1\omega _1}-2g_{\omega _1}g_{\omega _2}-2gg_{\omega _1\omega _2}). \end{aligned}$$

This completes the proof. \(\square \)

Finding exact solutions to the reduced system (3.11) is challenging. Next we use the power series method to derive the power series solution of the reduced system (3.11). Let us assume

$$\begin{aligned} f(\omega _1,\omega _2)=\sum _{n,m=0}^{\infty }a_{n,m} \omega _1^n\omega _2^m,g(\omega _1,\omega _2)=\sum _{n,m=0}^{\infty }b_{n,m}\omega _1^n\omega _2^m, \end{aligned}$$
(3.14)

then

$$\begin{aligned} \begin{aligned} \frac{\partial f}{\partial \omega _1}=&\sum _{n,m=0}^{\infty }(n+1)a_{n+1,m}\omega _1^n\omega _2^m,\\ \frac{\partial g}{\partial \omega _1}=&\sum _{n,m=0}^{\infty }(n+1)b_{n+1,m}\omega _1^n\omega _2^m,\\ \frac{\partial g}{\partial \omega _2}=&\sum _{n,m=0}^{\infty }(m+1)b_{n,m+1}\omega _1^n\omega _2^m,\\ \frac{\partial ^2 f }{\partial \omega _1^2}=&\sum _{n,m=0}^{\infty }(n+2)(n+1)a_{n+2,m}\omega _1^n\omega _2^m,\\ \frac{\partial ^2 g }{\partial \omega _1\partial \omega _2}=&\sum _{n,m=0}^{\infty }(n+1)(m+1)b_{n+1,m+1}\omega _1^n\omega _2^m,\\ \frac{\partial ^3 g }{\partial \omega _1^2\partial \omega _2}=&\sum _{n,m=0}^{\infty }(n+2)(n+1)(m+1)b_{n+2,m+1}\omega _1^n\omega _2^m, \end{aligned} \end{aligned}$$
(3.15)

and

$$\begin{aligned} \begin{aligned} (\mathcal {P}^{1-\frac{3\alpha }{2 },\alpha }_{\frac{2 }{\alpha },\infty }g_{\omega _2})(\omega _1,\omega _2)=&(1-\frac{3\alpha }{2 }-\frac{\alpha }{2}\omega _1\frac{\partial }{\partial \omega _1 })\\&\quad (\frac{1 }{\Gamma (1-\alpha ) }\int _1^\infty (r-1)^{-\alpha }r^{\frac{3\alpha }{2 }-2}g_{\omega _2}(\omega _1 r^{\frac{\alpha }{2 }},\omega _2 )\textrm{d}r)\\ =&(1-\frac{3\alpha }{2 }-\frac{\alpha }{2}\omega _1\frac{\partial }{\partial \omega _1 })(\sum _{n,m=0}^{\infty }\\&\quad \frac{(m+1)b_{n,m+1} \omega _1^n\omega _2^m }{\Gamma (1-\alpha ) }\int _1^\infty (r-1)^{-\alpha }r^{\frac{(n+3)\alpha }{2}-2}\textrm{d}r) \\ =&(1-\frac{3\alpha }{2 }-\frac{\alpha }{2}\omega _1\frac{\partial }{\partial \omega _1 })(\sum _{n,m=0}^{\infty }\\&\quad \frac{(m+1)b_{n,m+1} \omega _1^n\omega _2^m }{\Gamma (1-\alpha ) }B(1-\frac{(n+1)\alpha }{2},1-\alpha ))\\ =&(1-\frac{3\alpha }{2 }-\frac{\alpha }{2}\omega _1\frac{\partial }{\partial \omega _1 })(\sum _{n,m=0}^{\infty }\\&\quad \frac{\Gamma (1-\frac{(n+1)\alpha }{2 })}{\Gamma (2-\frac{(n+3)\alpha }{2 })}(m+1)b_{n,m+1} \omega _1^n\omega _2^m) \\ =&\sum _{n,m=0}^{\infty }\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}(m+1)b_{n,m+1} \omega _1^n\omega _2^m, \end{aligned} \end{aligned}$$
(3.16)

where \(B(p,q)=\int _{0}^{1}x^{p-1}(1-x)^{q-1}dx\) is a beta function, and \(\alpha \) must satisfy \(1-\frac{(n+1)\alpha }{2}>0\) and \(1-\alpha >0\).

Similarly

$$\begin{aligned} (\mathcal {P}^{1-\frac{3\alpha }{2 },\alpha }_{\frac{2 }{\alpha },\infty }f)(\omega _1,\omega _2)=\sum _{n,m=0}^{\infty }\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}a_{n,m}\omega _1^n\omega _2^m. \end{aligned}$$
(3.17)

Substituting (3.15)–(3.17) into the reduced system (3.11) and equating the coefficients of different powers of \(\omega _1^n\omega _2^m\), we can obtain the explicit expressions of \(a_{n,m}\) and \(b_{n,m}\). That is,

$$\begin{aligned} \begin{aligned}&\sum _{n,m=0}^{\infty }\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}a_{n,m} \omega _1^n\omega _2^m-\sum _{n,m=0}^{\infty }(n+2)(n+1)a_{n+2,m}\omega _1^n\omega _2^m\\&-2\sum _{n,m=0}^{\infty }\sum _{l=0}^{n}(l+1)a_{l+1,m}b_{n-l,m}\omega _1^n\omega _2^m\\&-2\sum _{n,m=0}^{\infty }\sum _{l=0}^{n}(n-l+1)a_{l,m}b_{n-l+1,m}\omega _1^n\omega _2^m=0,\\&\sum _{n,m=0}^{\infty }\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}(m+1)b_{n,m+1}\omega _1^n\omega _2^m \\ {}&+\sum _{n,m=0}^{\infty }(n+2)(n+1)(m+1)b_{n+2,m+1}\omega _1^n\omega _2^m\\&-2\sum _{n,m=0}^{\infty }(n+2)(n+1)a_{n+2,m}\omega _1^n\omega _2^m\\&-2\sum _{n,m=0}^{\infty }\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(m-j+1)b_{l+1,j}b_{n-l,m-j+1}\omega _1^n\omega _2^m\\&-2\sum _{n,m=0}^{\infty }\sum _{l=0}^{n}\sum _{j=0}^{m} (l+1)(j+1)b_{l+1,j+1}b_{n-l,m-j}\omega _1^n\omega _2^m. \end{aligned} \end{aligned}$$
(3.18)

For \(n,m\geqslant 0\), we have

$$\begin{aligned} \begin{aligned} a_{n+2,m}=&\frac{1 }{(n+2)(n+1) }\Big [\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}a_{n,m}-2\sum _{l=0}^{n}(l+1)a_{l+1,m}b_{n-l,m}\\&-2\sum _{l=0}^{n}(n-l+1)a_{l,m}b_{n-l+1,m}\Big ], \\ b_{n+2,m+1}=&-\frac{1}{(n+2)(n+1)(m+1)}\\&\Big [\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}(m+1)b_{n,m+1}-2(n+2)(n+1)a_{n+2,m}\\&-2\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(m-j+1)b_{l+1,j}b_{n-l,m-j+1}\\&-2\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(j+1)b_{l+1,j+1}b_{n-l,m-j}\Big ]. \end{aligned} \end{aligned}$$
(3.19)

where \(a_{n,m},b_{n,m},b_{m,0}\ (n=0,1; m=0,1,2,\cdots )\) are arbitrary constants. It means that the power series solution of system (3.11) is

$$\begin{aligned} \begin{aligned} f(\omega _1,\omega _2)=&\sum _{n=0}^{1}\sum _{m=0}^{\infty }a_{n,m} \omega _1^n\omega _2^m+\sum _{n,m=0}^{\infty }\frac{\omega ^{n+2}_1\omega ^{m}_2 }{(n+2)(n+1) }\Big [\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}a_{n,m}\\&-2\sum _{l=0}^{n}(l+1)a_{l+1,m}b_{n-l,m} -2\sum _{l=0}^{n}(n-l+1)a_{l,m}b_{n-l+1,m}\Big ],\\ g(\omega _1,\omega _2)=&\sum _{n=0}^{1}\sum _{m=0}^{\infty }b_{n,m}\omega _1^n\omega _2^m+\sum _{n=0}^{\infty }b_{n,0}\\&\omega _1^n-\sum _{n,m=0}^{\infty }\frac{\omega _1^{n+2}\omega _2^{m+1}}{(n+2)(n+1)(m+1)}\Big [\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}(m+1)b_{n,m+1}\\&-2(n+2)(n+1)a_{n+2,m}-2\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(m-j+1)b_{l+1,j}b_{n-l,m-j+1}\\&-2\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(j+1)b_{l+1,j+1}b_{n-l,m-j}\Big ]. \end{aligned} \end{aligned}$$
(3.20)

Therefore, the power series solution of system (1.2) is

$$\begin{aligned} \begin{aligned} u(t,x,y)=&\sum _{n=0}^{1}\sum _{m=0}^{\infty }a_{n,m} x^ny^mt^{-\frac{(n+1)\alpha }{2}}+\sum _{n,m=0}^{\infty }\frac{x^{n+2}y^{m}t^{-\frac{(n+3)\alpha }{2}} }{(n+2)(n+1) }\Big [\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}a_{n,m}\\&-2\sum _{l=0}^{n}(l+1)a_{l+1,m}b_{n-l,m} -2\sum _{l=0}^{n}(n-l+1)a_{l,m}b_{n-l+1,m}\Big ],\\ v(t,x,y)=&\sum _{n=0}^{1}\sum _{m=0}^{\infty }b_{n,m}x^ny^mt^{-\frac{(n+1)\alpha }{2}}+\sum _{n=0}^{\infty }b_{n,0}x^nt^{-\frac{(n+1)\alpha }{2}}\\&-\sum _{n,m=0}^{\infty }\frac{x^{n+2}y^{m+1}t^{-\frac{(n+3)\alpha }{2}}}{(n+2)(n+1)(m+1)}\\&\times \Big [\frac{\Gamma (1-\frac{(n+1)\alpha }{2})}{\Gamma (1-\frac{(n+3)\alpha }{2})}(m+1)b_{n,m+1} -2(n+2)(n+1)a_{n+2,m}\\&-2\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(m-j+1)b_{l+1,j}b_{n-l,m-j+1}\\&-2\sum _{l=0}^{n}\sum _{j=0}^{m}(l+1)(j+1)b_{l+1,j+1}b_{n-l,m-j}\Big ]. \end{aligned} \end{aligned}$$
(3.21)

Remark

Following the method outlined in [27] and utilizing the explicit function theorem from [28], the power-series solutions provided by system (3.21) are proven to be convergent. The details of the proof are omitted here.

4 Conservation laws of system (1.2)

We utilize the concept of nonlinear self-adjointness to identify conservation laws for system (1.2). A local conservation law of system (1.2) is expressed as follows [11, 12, 29]

$$\begin{aligned} D_t(C^t)+D_x(C^x)+D_y(C^y)=0. \end{aligned}$$
(4.1)

This holds identically for all solutions of system (1.2). Moreover, \((C_t, C_x, C_y)\) is referred to as the conserved current, where \(C_t, C_x\), and \(C_y\) are functions of t, x, y, as well as u, v, and their integer-order derivatives, fractional derivatives, and fractional integrals.

First, we will prove that system (1.2) is nonlinearly self-adjoint, as demonstrated in [29]. Following this, we will construct new, nontrivial conservation laws for system (1.2). We begin by assuming that the formal Lagrangian of system (1.2) is defined as follows

$$\begin{aligned} L=\Phi _1(D^{\alpha }_{t}u-u_{xx}-2vu_{x}-2uv_{x})+\Phi _2(D^{\alpha }_{t}v_{y}+v_{xxy}-2u_{xx}-2v_{y}v_{x}-2vv_{xy}), \end{aligned}$$
(4.2)

where \(\Phi _1\) and \(\Phi _2\) are three newly introduced dependent variables. According to the principle of functional extremum, we know that a necessary condition for the variation of the formal Lagrangian (4.2, \(J [u, v] = \int _{\mathbb {R}} dx \int _{\mathbb {R}} dy \int _{0}^{T} Ldt\), to have an extreme value is that the adjoint equations \( \delta L / \delta u = 0 \) and \(\delta L / \delta v = 0 \), are satisfied, where the Euler-Lagrange operators are defined as follows [30, 31]

$$\begin{aligned} \left\{ \begin{aligned} \frac{\delta }{\delta u}=&^C_t\partial ^\alpha _T\frac{\partial }{\partial (\partial ^\alpha _tu)}+\frac{\partial }{\partial u}-D_x\frac{\partial }{\partial u_x}+D^2_x\frac{\partial }{\partial u_{xx}}+\cdots ,\\ \frac{\delta }{\delta v}=&^C_t\partial ^\alpha _TD_y\frac{\partial }{\partial (\partial ^\alpha _tv_y)}+\frac{\partial }{\partial v}-D_x\frac{\partial }{\partial v_x}-D_y\frac{\partial }{\partial v_y}+D_xD_y\frac{\partial }{\partial v_{xy}}-D^2_xD_y\frac{\partial }{\partial v_{xxy}}+\cdots . \end{aligned}\right. \end{aligned}$$
(4.3)

The adjoint operator of \( \partial _t^\alpha \) is the right Caputo derivative \( ^C_t\partial _T^\alpha \), and system (1.2) is deemed nonlinearly self-adjoint when the adjoint equations, given nontrivial substitutions as \( \Phi _1 = \phi (t,x, y, u, v)\), and \(\Phi _2 = \rho (t,x, y, u, v)\), where \( \Phi _1^2 + \Phi _2^2 \ne 0\), satisfy the following conditions [32]

$$\begin{aligned} \begin{aligned} \frac{\delta L}{\delta u}=&^C_t\partial _T^\alpha (\phi )-2\phi v_x+2D_x(\phi v)-D^2_x(\phi +2\rho )\\ =&^C_t\partial _T^\alpha (\phi )-2\phi v_x+2(\phi _x+\phi _uu_x+\phi _vv_x)v+2\phi v_x\\&-\Big [\phi _{xx}+\phi _{xu}u_x+\phi _{xv}v_x+(\phi _{xu}+\phi _{uu}u_x+\phi _{uv}v_x)u_x+\phi _uu_{xx}\\&+(\phi _{xv}+\phi _{uv}u_x+\phi _{vv}v_x)v_x+\phi _vv_{xx}+2(\rho _{xx}+\rho _{xu}u_x+\rho _{xv}v_x)\\&+2(\rho _{xu}+\rho _{uu}u_x+\rho _{uv}v_x)u_x+2\rho _uu_{xx}+2(\rho _{xv}+\rho _{uv}u_x+\rho _{vv}v_x)v_x+2\rho _vv_{xx}\Big ],\\ =&k_1(t,x,y,u,v)(D^{\alpha }_{t}u-u_{xx}-2vu_{x}-2uv_{x})\\&+k_2(t,x,y,u,v)(D^{\alpha }_{t}v_{y}+v_{xxy}-2u_{xx}-2v_{y}v_{x}-2vv_{xy}),\\ \frac{\delta L}{\delta v}=&^C_t\partial _T^\alpha (\rho _y+\rho _uu_y+\rho _vv_y)-2\phi u_x-2\rho v_{xy}+2(\phi _x+\phi _uu_x+\phi _vv_x)u+2\phi u_x\\&+2(\rho _x+\rho _uu_x+\rho _vv_x)v_y+2\rho v_{xy}+2(\rho _y+\rho _uu_y+\rho _vv_y)v_x+2\rho v_{xy}\\&-2D_x[(\rho _y+\rho _uu_y+\rho _vv_y)v] -2D_x(\rho )v_y-2\rho v_{xy}-D_x^2D_y(\rho ),\\ =&k_3(t,x,y,u,v)(D^{\alpha }_{t}u-u_{xx}-2vu_{x}-2uv_{x})\\&+k_4(t,x,y,u,v)(D^{\alpha }_{t}v_{y}+v_{xxy}-2u_{xx}-2v_{y}v_{x}-2vv_{xy}). \end{aligned} \end{aligned}$$

The functions \(k_i(t, x, y, u, v)( i = 1, 2, 3, 4)\) remain undetermined. By nullifying the coefficients of both the time-fractional derivatives and the integer-order derivatives of u and v, we establish a set of equations to determine \( k_i(t, x, y, u, v)\) for \( i = 1, 2, 3, 4\). Solving this system furnishes the necessary substitutions for nonlinear self-adjointness. It becomes evident that \(\phi (t, x, y, u, v) = c_1\), and \( \rho (t, x, y, u, v) = c_2\), where \( c_1^2 + c_2^2 \ne 0 \), confirming the nonlinear self-adjointness of system (1.2).

We utilize both the Noether identity and the nonlinear self-adjointness method to derive conserved vectors for system (1.2). The Noether identity associated with system (1.2) is represented as

$$\begin{aligned} prX +D_t(\tau )I+D_x(\xi )I+D_y(\theta )I=W_1\frac{\delta }{\delta u}+W_2\frac{\delta }{\delta v}+D_tN^t+D_xN^x+D_yN^y.\nonumber \\ \end{aligned}$$
(4.4)

Here, I represents the identity operator, \(N^t, N^x\), and \(N^y\) denote the Noether operators, PrX is determined by (2.5), and the Euler operators \(\frac{\delta }{\delta u}\) and \(\frac{\delta }{\delta v}\) are defined in (4.3).

To begin, we shift the terms \(W_1 \frac{\delta }{\delta u}\) and \(W_2 \frac{\delta }{\delta v}\) from the right side of Eq. (4.4) to the left side. Then, we apply the identity (4.4) to L, yielding

$$\begin{aligned}{} & {} \Big [prX +D_t(\tau )I+D_x(\xi )I +D_y(\theta )I-W_1\frac{\delta }{\delta u}-W_2\frac{\delta }{\delta v}\Big ]L=\nonumber \\{} & {} \qquad D_t(N^tL)+D_x(N^xL)+D_y(N^yL). \end{aligned}$$
(4.5)

Rephrase prX as follows

$$\begin{aligned} \begin{aligned} prX&=\tau D_t+\xi D_x+\theta D_y+W_1\frac{\partial }{\partial u }+W_2\frac{\partial }{\partial v}\\&\quad +D_t^\alpha (W_1)\frac{\partial }{\partial (\partial ^\alpha _tu)}+D_{t}^{\alpha }D_y(W_2)\frac{\partial }{\partial (\partial ^{\alpha }_{t} v_{y})}+D_x(W_1)\frac{\partial }{\partial u_{x}}+D_x(W_2)\frac{\partial }{\partial v_{x}}\\&\quad +D_y(W_2)\frac{\partial }{\partial v_y}+D^2_x(W_1)\frac{\partial }{\partial u_{xx}} +D_xD_y(W_2)\frac{\partial }{\partial v_{xy}}+D^2_xD_y(W_2)\frac{\partial }{\partial v_{xxy}}, \end{aligned}\nonumber \\ \end{aligned}$$
(4.6)

where \(W_1=\eta -\tau u_t-\xi u_x-\theta u_y, W_2=\zeta -\tau v_t-\xi v_x-\theta v_y\), and \(D^\alpha _t \) is the fractional total derivative.

Lastly, we substitute Eqs. (4.3) and (4.6) into Eq. (4.5), and set \( c_1 = c_2 = 1 \). Then, employing integration by parts,

$$\begin{aligned} D_t(\tau I)=(D_t\tau )I+\tau D_t, D_x(\xi I)=(D_x\xi )I+\xi D_x, D_y(\theta I)=(D_y\theta )I+\theta D_y, \end{aligned}$$

we acquire the following parts

$$\begin{aligned} \begin{aligned} \Pi _1&= D_t(\tau I) + D^\alpha _t(W_1) \frac{\partial }{\partial (\partial ^\alpha _t u)} - W_1 {^C_t\partial ^\alpha _T} \frac{\partial }{\partial (\partial ^\alpha _t u)} \\&= D_t(\tau I) + \left( D_t {_0I^{1-\alpha }_t}(W_1)\right) \frac{\partial }{\partial (\partial ^\alpha _t u)} + W_1 {_t I^{1-\alpha }_T} D_t \frac{\partial }{\partial (\partial ^\alpha _t u)} \\&= D_t \left[ \tau I + {_0I^{1-\alpha }_t}(W_1) \frac{\partial }{\partial (\partial ^\alpha _t u)} + J(W_1, D_t \frac{\partial }{\partial (\partial ^\alpha _t u)})\right] \\ \Pi _2&= D^\alpha _t D_y(W_2) \frac{\partial }{\partial (\partial ^\alpha _t v_y)} - W_2 {^C_t\partial ^\alpha _T} D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} \\&= D_y D_t {_0I_t^{1-\alpha }}(W_2) - W_2 {_t I^{1-\alpha }_T} D_t D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} \\&= D_y \left[ D_t {_0I_t^{1-\alpha }}(W_2) \frac{\partial }{\partial (\partial ^\alpha _t v_y)}\right] \! \!-\! D_t {_0I_t^{1-\alpha }}(W_2) D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} \!-\! W_2 {_t I^{1-\alpha }_T} D_t D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} \\&= D_y \left[ D_t {_0I_t^{1-\alpha }}(W_2) \frac{\partial }{\partial (\partial ^\alpha _t v_y)}\right] - D_t \left[ {_0I_t^{1-\alpha }}(W_2) D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)}\right] \\&\quad + {_0I_t^{1-\alpha }}(W_2) D_t D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} - W_2 {_t I^{1-\alpha }_T} D_t D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} \\&= D_y \left[ D_t^{\alpha }(W_2) \frac{\partial }{\partial (\partial ^\alpha _t v_y)}\right] - D_t \left[ {_0I_t^{1-\alpha }}(W_2) D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)} + J(W_2, D_t D_y \frac{\partial }{\partial (\partial ^\alpha _t v_y)})\right] \\ \Pi _3&= D_x \Bigg [W_1 \frac{\partial }{\partial u_x} + W_2 \frac{\partial }{\partial v_x} + D_x(W_1) \frac{\partial }{\partial u_{xx}} - W_1 D_x \frac{\partial }{\partial u_{xx}} + D_y(W_2) \frac{\partial }{\partial v_{xy}} \\&\quad + D_x D_y(W_2) \frac{\partial }{\partial v_{xxy}} + W_2 D_x D_y \frac{\partial }{\partial v_{xxy}} + \xi I \Bigg ] \\&\quad + D_y \left[ W_2 \frac{\partial }{\partial v_y} - W_2 D_x \frac{\partial }{\partial v_{xy}} - D_x(W_2) D_x \frac{\partial }{\partial v_{xxy}} + \theta I \right] , \end{aligned}\nonumber \\ \end{aligned}$$
(4.7)

where

$$\begin{aligned} J(f(t),g(t))=\frac{1}{\Gamma (1-\alpha )}\int _{0}^{t}d\lambda \int _{t}^{b}\frac{f(\lambda )g(\mu )}{(\mu -\lambda )^\alpha }d\mu , \end{aligned}$$

which satisfies \(D_tJ(f(t),g(t))=f(t)_tI^{1-\alpha }_Tg(t)-g(t)_0I^{1-\alpha }_tf(t)\).

Thus, we can derive the general formula for the conservation law of system (1.2)

$$\begin{aligned} \begin{aligned} C^t=&\tau L+{_0I^{1-\alpha }_t}(W_1) \frac{\partial L}{\partial (\partial ^\alpha _t u)} + J(W_1, D_t \frac{\partial L}{\partial (\partial ^\alpha _t u)})\\&-(_0I_t^{1-\alpha }(W_2)D_y\frac{\partial L}{\partial (\partial ^\alpha _t v_y)}+J(W_2,D_tD_y\frac{\partial L}{\partial (\partial ^\alpha _t v_y)})),\\ C^x=&\xi L+W_1 \frac{\partial L}{\partial u_x} + W_2 \frac{\partial L}{\partial v_x} + D_x(W_1) \frac{\partial L}{\partial u_{xx}} - W_1 D_x \frac{\partial L}{\partial u_{xx}} + D_y(W_2) \frac{\partial L}{\partial v_{xy}} \\&+ D_x D_y(W_2) \frac{\partial L}{\partial v_{xxy}} + W_2 D_x D_y \frac{\partial L}{\partial v_{xxy}},\\ C^y=&\theta L+D_t^{\alpha }(W_2)\frac{\partial L}{\partial (\partial ^\alpha _t v_y)}+W_2 \frac{\partial L}{\partial v_y} - W_2 D_x \frac{\partial L}{\partial v_{xy}} - D_x(W_2) D_x \frac{\partial L}{\partial v_{xxy}}. \end{aligned} \end{aligned}$$
(4.8)

Next, leveraging the conservation law formula from (4.8) and the Lie symmetries outlined in (2.8), we construct several conservation laws for system (1.2).

Case 1: \(X_2=\frac{\partial }{\partial x }\)

The characteristic functions of \(X_2\) is

$$\begin{aligned} W_1=-u_x, W_2=-v_x. \end{aligned}$$
(4.9)

Therefore, for \(0<\alpha <1\),

$$\begin{aligned} \begin{aligned} C^t=&-_0I^{1-\alpha }_t(u_x),\\ C^x=&2u_xv+2uv_x+2v_xv_y+3u_{xx}+2vv_{xy}-v_{xxy},\\ C^y=&-D^\alpha _tv_x, \end{aligned} \end{aligned}$$
(4.10)

which implies \(D_t(C^t)+D_x(C^x)+D_y(C^y)=-D_t(\Delta _1)-D_x(\Delta _2).\) Consequently, \(D_t(C^t+\Delta _1)+D_x(C^x+\Delta _2)+D_y(C^y)=0\) holds true universally, resulting in a trivial conservation law.

Case 2: \(X_3=\frac{\partial }{\partial y}\)

The characteristic functions of \(X_3\) is

$$\begin{aligned} W_1=-u_y, W_2=-v_y. \end{aligned}$$
(4.11)

Therefore, for \(0<\alpha <1\),

$$\begin{aligned} \begin{aligned} C^t=&-_0I^{1-\alpha }_t(u_y),\\ C^x=&2u_yv+2uv_y+2v_y^2+3u_{xy}+2vv_{yy}-v_{xyy},\\ C^y=&-D^\alpha _tv_y, \end{aligned} \end{aligned}$$
(4.12)

which implies \(D_t(C^t)+D_x(C^x)+D_y(C^y)=-D_y(\Delta _1)-D_y(\Delta _2)\). Consequently, \(D_t(C^t)+D_x(C^x)+D_y(C^y+\Delta _1+\Delta _2)=0\) holds true universally, resulting in a trivial conservation law.

Case 3: \(X_1=t\frac{\partial }{\partial t }+\frac{\alpha }{2 }x\frac{\partial }{\partial x }-\frac{\alpha }{2 }u\frac{\partial }{\partial u }-\frac{\alpha }{2 }v\frac{\partial }{\partial v }\)

The characteristic functions of \(X_1\) is

$$\begin{aligned} W_1=-\frac{\alpha }{2}u-tu_t-\frac{\alpha }{2}xu_x,W_2=-\frac{\alpha }{2}v-tv_t-\frac{\alpha }{2}xv_x. \end{aligned}$$
(4.13)

Therefore, for \(0<\alpha <1\),

$$\begin{aligned} \begin{aligned} C^t=&-_0I^{1-\alpha }_t(\frac{\alpha }{2}u+tu_t+\frac{\alpha }{2}xu_x),\\ C^x=&2\alpha uv+2tu_tv+\alpha xu_xv+2tuv_t+\alpha xuv_x+2\alpha vv_y+2tv_tv_y+\alpha xv_xv_y\\&+3\alpha u_x+3tu_{tx}+\frac{3}{2}\alpha xu_{xx}+2tvv_{ty}+\alpha xvv_{xy}-\alpha v_{xy}-tv_{txy}-\frac{\alpha }{2}xv_{xxy},\\ C^y=&-D^\alpha _t(\frac{\alpha }{2}v+tv_t+\frac{\alpha }{2}xv_x). \end{aligned} \end{aligned}$$
(4.14)

These three conserved vectors give a new nontrivial conservation law for system (1.2), that is \(D_t(C^t)+D_x(C^x)+D_y(C^y)=(1-\alpha )\Delta _1+(1-\alpha )\Delta _2=0\), where the multiplier is \((1-\alpha ,1-\alpha )\).

5 Conclusion

Currently, most fractional partial differential equations studied using the Lie symmetry method are either purely of fractional time order or purely of fractional space order, encompassing both forms. However, there are very few results regarding the Lie symmetries of partial differential equations that involve mixed derivatives of fractional and integer orders. In this paper, we conduct Lie symmetry and conservation law analyses for the time-fractional (2+1)-dimensional dissipative long-wave system featuring Riemann-Liouville time-fractional derivatives. We identify explicit Lie symmetries and utilize them to reduce the system. Furthermore, we develop a power series solution and exact solutions. Additionally, we establish a general conservation law formula using the nonlinear self-adjointness method and derive significant conservation law.