1 Introduction

BL Lac objects and flat spectrum radio quasars (FSRQs) form the class of blazars, radio-loud active galactic nuclei (AGN), whose jet is pointing toward us (for recent reviews, see, e.g., Böttcher 2007; Ghisellini et al. 2011; Dermer 2014). FSRQs are powerful sources, with broad emission lines, contrary to BL Lacs, that are less powerful and often line-less. The observational distinction among them is in fact the equivalent width (EW) of their broad emission lines: BL Lacs have EW<5Å (rest frame, Urry and Padovani 1995). This divide is purely observational: objects that do have strong emitting lines could then be classified as BL Lacs if their jet emission is particularly enhanced (see Ghisellini et al. 2011; Sbarrato et al. 2012 for an alternative definition).

Blazars emit most of their electromagnetic power by the synchrotron and the inverse Compton processes. Their spectral energy distribution (SED) is in fact characterized by two broad humps. The SED follows a sequence controlled by the bolometric luminosity: when this is increasing, the peaks of the two main radiation mechanisms shift to smaller frequencies, and the inverse Compton component becomes more dominant (Fossati et al. 1998; Donato et al. 2001; Ghisellini et al. 2017).

At the largest luminosities, the synchrotron peaks in the IR-sub-mm band, and the slope above it is as steep as the slope in the \(\gamma \)-ray band covered by AGILE and Fermi/LAT. This makes the accretion disk clearly visible, and at high redshifts, the observed accretion disk peak falls in the optical band. In these cases, we can directly measure its total luminosity. Otherwise, we have to rely on the observed broad emission lines. Phenomenological relations between their relative weight (Francis et al. 1991; Vanden Berk et al. 2001) allow to calculate the total luminosity emitted by the broad lines. Using an average covering factor of \(\sim \)10, we have an estimate of the accretion disk luminosity.

In addition, from the broad line FWHM and the continuum, we can estimate the black hole mass. This is the so-called virial method, which relies on empirical correlations between the disk luminosity and the distance of the BLR from the central engine. The uncertainties of the method are quite large: a factor between 3 and 4 (Park et al. 2012), and they do not depend on the quality of data, but upon the dispersion of the empirical relations used. Alternatively, we can directly fit the spectrum with a disk model, such as the Shakura and Sunjaev optically thick and geometrically thin accretion disk model (Shakura and Sunyaev 1973; Calderone et al. 2013). This simple model assumes zero black hole spin, and does not take into account relativistic effects. Kerr models including all effects have been studied by, among others, (Li et al. 2005) for binaries, and extended by Campitiello et al. (2018) to AGNs.

Blazars are among the strongest \(\gamma \)-ray emitting sources. The third catalog of AGNs detected by Fermi/LAT lists \(\sim \)1,500 sources, of which the vast majority are blazars (Ackermann et al. 2015). This made possible to make population studies, such as the \(\gamma \)-ray blazar luminosity function and their contribution to the \(\gamma \)-ray background (Ajello et al. 2012, 2014).

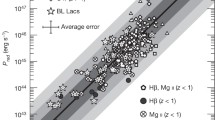
Figure 1 shows the \(\gamma \)-ray luminosities of BL Lacs and FSRQs as a function of their redshift. We have also drawn three lines indicating the approximate limiting sensitivity of EGRET, AGILE and Fermi/LAT. It is approximate, because the same spectral index is used for all sources. This figure shows the improvement that AGILE and especially LAT made possible in our knowledge of blazars. It also makes clear that EGRET could explore only the tip of the iceberg of the entire blazar population. Furthermore, since all blazars vary greatly especially in \(\gamma \)-rays, EGRET probably detected most blazars only when they are in high state. LAT returns instead a more balanced view.

Fig. 1
figure 1

\(\gamma \)-ray luminosity of blazars detected by FERMI/LAT as a function of their redshift. We also plot three solid curves, corresponding (roughly) to the LAT, AGILE, and EGRET sensitivity assuming for simplicity that the \(\gamma \)-ray spectrum is the same

Full size image

2 Comparing jet power and accretion luminosity

The first attempt to derive the relation between the jet and the accretion disk power was made by Rawlings and Saunders (1991). They estimated the average jet power considering the extended radio emission, calculating their minimum energy through equipartition considerations, and estimating their lifetime considering the time needed to expand and the presence of a cooling break in the spectrum. Then, they collected for all the sources the luminosity of the narrow lines. They found a strong correlations between jet power and line luminosity, but this, per se, is not unexpected, since both quantities depend on distance. What is interesting was that the narrow line luminosity was always a factor 100 less that the jet power. Since the covering factor of the narrow lines is \(\sim 10^{-2}\), they concluded that the average jet power energizing the lobes and the accretion luminosity was of the same order.

Stimulated by this result, Celotti and Fabian (1993) tried to improve the estimate of the jet power by considering the jet emission at the parsec (e.g., VLBI) scale to find the number of particles needed to account for the emission and the Lorentz factor needed not to overproduce the X-ray emission through the synchrotron-self-Compton (SSC) process. They confirmed the earlier results. Later, the same was performed using broad line luminosities instead of the narrow ones (Celotti et al. 1997).

At the same time of these pioneering studies, EGRET discovered that blazars are very strong \(\gamma \)-ray emitters and that this emission is the most variable. The first models thought that the \(\gamma \)-rays were SSC emission (Maraschi et al. 1992; Bloom and Marscher 1992; Bloom et al. 1993). Soon, it became clear that variability at different frequencies was correlated, strongly suggesting that the same population of particles, in only one region, was responsible for the emission. This was the birth of the leptonic, one-zone model. The location of this one-zone is still controversial: early suggestions located it close to the accretion disk (Dermer et al. 1992), or within the BLR (Sikora et al. 1994), or beyond the BLR but within the molecular torus size (Sikora et al. 2002). In these models, the seed photons for the inverse Compton process are produced externally to the jet (External Compton, EC for short). This process is highly efficient, since the radiation energy density, as seen in the comoving frame, is enhanced by \(\varGamma ^2\). In general, we have two constraints that limit the location of the emitting region: i) if too close to the disk, the produced \(\gamma \)-rays are absorbed in \(\gamma \)–\(\gamma \) collisions and ii) if very distant from the black hole, the dimension of the emitting region becomes too large to account for the observed short variability. Distances of the order of \(\sim \)10\(^3\) Schwarzschild radii are suggested, see the cartoon in Fig. 2.

The one-zone model had the advantage to greatly simplify the modelling while reducing the number of free parameters. For low power blazars, lacking broad lines, and thermal components, the SSC model is still the leading model, and has the virtue of having no degeneracies: given some basic observables, the solution is unique (Tavecchio et al. 1998). EC models, on the other hand, can offer a unique solution if some extra information is supplied or can be derived from the fitting, such as the black hole mass and the disk luminosity (see Ghisellini and Tavecchio 2009).

Fig. 2
figure 2

Cartoon of the assumed geometry for the model, see (Ghisellini and Tavecchio 2009). At some distance \(R_{\mathrm{diss}}\) from the black hole, the jet produces most of its radiation. This region can be inside the BLR or within \(R_{\mathrm{torus}}\), the dimension of the molecular torus. The radiation energy densities within the BLR and the torus are constant, since both \(R_{\mathrm{BLR}}\) and \(R_{\mathrm{torus}}\) scale as \(L_{\mathrm{d}}^{1/2}\). This structure is valid for FSRQs only, since BL Lacs have a radiatively inefficient disk, unable to photo-ionize the BLR

Full size image

3 Electrons and positrons

If we calculate the jet power estimating how many leptons are necessary to produce the received flux, we face a crucial problem. Any particle distribution fitting the data has to be relatively steep: \(N(\gamma )\propto \gamma ^{-p}\), with \(p\ge 2\), so that the total number of the emitting particles depends strongly on the minimum particle energy, or their minimum random Lorentz factor \(\gamma _{\mathrm{min}}\). The synchrotron emission is self-absorbed for values of \(\gamma {\lesssim }50-100\) and the SSC flux is always hidden by the synchrotron one at low energies. In these condition, we cannot estimate \(\gamma _{\mathrm{min}}\) that corresponds to an uncertainty on the jet power of the order of \(\sim \gamma _{\mathrm{min}}^{p-1}\). However, for powerful blazars, the soft X-ray emission is produced by the EC process. In this case, we do see the effects of changing \(\gamma _{\mathrm{min}}\), since the soft X-ray shape should become harder below \(\nu _{\mathrm{Ly}\alpha } \gamma ^2_{\mathrm{min}}\varGamma ^2 \sim \) 1 keV \(\times \gamma ^2_{\mathrm{min}}(\varGamma /10)^2\). Usually, we do not see a break in the soft X-ray spectrum, corresponding to \(\gamma _{\mathrm{min}}<\) a few. This agrees with the typical values estimated by the radiative cooling occurring in the emitting region.

Fig. 3
figure 3

In the past, there were two major uncertainties concerning the estimate of the jet power. The first was the difficulty to estimate the lowest electron energies, but now, we do have information about it looking at the soft X-rays, where, in the EC scenario, the lowest energy electron contributes to the emission. The second is the importance of pairs. As illustrated in the right panel, if part of the \(\gamma \)-rays do form pairs, we expect that they emit in the X-ray band, filling the “valley” between the synchrotron and the Compton humps

Full size image

The other uncertainty concerns the presence of protons, or, equivalently, the number of electron–positron pairs. This is because, at least in powerful blazars, the bulk motion of protons, even if cold in the comoving frame, dominates the jet power if we assume that there is one proton for emitting electron. If instead, there are no protons, i.e., for a pure pair jet, the jet power estimate is a factor \( \langle \gamma \rangle m_{\mathrm{e}} /m_{\mathrm{p}}\approx 10^{-2}\) smaller. The presence of both protons and pairs corresponds to intermediate values of the jet power. The counter arguments concerning the presence of e\(^-\)–\(e^+\) pairs are:

  • It is not easy to produce pairs in the first place. If we are using even a relatively small fraction of the \(\gamma \)-ray photons produced in the emitting region, we are nevertheless using a large power. The produced pairs, that are born relativistic, emit efficiently, mostly in the X-rays, where the SED of powerful blazars has a “valley” (Ghisellini and Madau 1996), see the right panel of Fig. 3. We do not see any sign of this reprocessed emission.

  • If pairs are produced at the start, very close to the jet apex, there is a maximum number of them that can survive. In fact, if their optical Thomson optical depth is larger than unity and they are cold, they annihilate efficiently until the optical depth is below unity. If they are hot, annihilation is reduced, but they are bound to cool in a short time.

  • Pairs can be the result of hadronic cascades, but in this case, we have to account for the bulk motion of ultra-relativistic protons, and this increases the power demand.

  • In powerful blazars relativistic pairs efficiently cool on external radiation and recoil, braking the jet (Sikora et al. 1996), (Ghisellini and Tavecchio 2010) if there are more than \(\sim \)10–20 pairs per proton.

  • The total power in radiation (integrated over the entire solid angle) often exceeds the power in the relativistic emitting particles, because the radiative cooling time is shorter than the light crossing time. This requires continuous injection of new fresh particles or re-acceleration. If these processes are the result of the dissipation of a fraction of the jet kinetic or magnetic power, they must be larger than the radiated power. The jet Poynting flux is constrained by the observed synchrotron luminosity that is smaller than the inverse Compton one. Bulk motion of protons is, therefore, required.

We conclude that \(e^-\)–\(e^+\) pairs can be present in jets, but their number is severely limited to a be a few per proton. A slightly larger number (i.e., 15 per proton) has been invoked by Sikora (2016) to explain the different median power of a sample of FRII and FSRQs calculated though radio-lobe calorimetry. Such a number of pairs corresponds to a jet kinetic power of the same order of the radiated luminosity, implying that jets are highly efficient radiators. Alternatively, radio-lobes may contain hot protons, not accounted for by calorimetry.

4 Jet power

Jets can carry energy in different forms:

  • Radiation The observed emission has been produced in the jet that spent part of its power to produce it. This is not merely the luminosity measured in the comoving frame, because it needs some extra power to move the emitting particles to blue-shift the photons we receive and to account for the different rate of arrival. Both these effects are measured by the relativistic Doppler factor \(\delta \equiv [\varGamma (1-\beta \cos \theta _{\mathrm{v}})]^{-1}\), where \(\theta _{\mathrm{v}}\) is the viewing angle. The observed (L) and the comoving (\(L^\prime \)) jet bolometric luminosity are linked by \(L =\delta ^4 L^\prime \). If the luminosity is isotropic in the comoving frame, as can be the case for synchrotron and SSC:

    $$\begin{aligned} P_{\mathrm{r}} = 2\times \int _{4\pi } {L^\prime \over 4\pi } \delta ^4 {\text {d}}\varOmega = 2 {L^\prime \over 2\varGamma ^4} \int _{-1}^{1} {{\text {d}}\cos \theta \over (1-\beta \cos \theta )^4} = 2 {\varGamma ^2 L\over \delta ^4} \left( 1+{\beta ^2\over 3}\right) . \end{aligned}$$
    (1)

    The factor 2 accounts for the presence of two jets. If the radiation is not isotropic in the rest frame, as in the EC process, we have (Ghisellini and Tavecchio 2010):

    $$\begin{aligned} P_{\mathrm{r}} = 2\times {\langle L^\prime \rangle \over 4\pi } \int _{4\pi } {\delta ^6\over \varGamma ^2} {\text {d}}\varOmega \sim {32 \over 5} {\varGamma ^4 \over \delta ^6} L \end{aligned}$$
    (2)

    When \(\varGamma =\delta \), implying that the viewing angle \(\theta _{\mathrm{v}}=1/\varGamma \), the two expressions differ by a factor 5 / 12. There is an alternative way to calculate \(P_{\mathrm{r}}\), that is useful also for calculating the other the forms of carried energy. It consists to calculate the flux across a cross section (of radius r) of the jet:

    $$\begin{aligned} P_{\mathrm{r}} = 2\times \pi r^2 \varGamma ^2 U^\prime _{\mathrm{r}} c \sim \pi r^2 \varGamma ^2 {L\over \delta ^4 4\pi r^2 c} c = {\varGamma ^2\over 2 \delta ^4} L. \end{aligned}$$
    (3)

    The reason of the \(\varGamma ^2\) term is due to the transformation of the energy density from the comoving to the observer frame: one term for the blue-shift and the other term for the different number density in the two frames.

  • Magnetic field The Poynting flux is

    $$\begin{aligned} P_{\mathrm{B}} = 2\times \pi r^2 \varGamma ^2 U^\prime _B c, \end{aligned}$$
    (4)

    where \(U^\prime _B\equiv (B^\prime )^2/(8\pi )\) and the factor 2 accounts again for the presence of two jets.

  • Relativistic leptons The power in the bulk motion of relativistic leptons is

    $$\begin{aligned} P_{\mathrm{e}} = 2\times \pi r^2 \varGamma ^2 U^\prime _{\mathrm{e}} \beta c = 2\pi r^2 \varGamma ^2 \beta \, \langle \gamma \rangle \, m_{\mathrm{e}}c^3 \, n^\prime _{\mathrm{e}}, \end{aligned}$$
    (5)

    where \(U^\prime _{\mathrm{e}} =m_{\mathrm{e}} c^2 \int _{\gamma _{\mathrm{min}}}^{\gamma _{\mathrm{max}}} N(\gamma )\gamma {\text {d}}\gamma = \langle \gamma \rangle \, m_{\mathrm{e}}c^2 \, n^\prime _{\mathrm{e}}\). Usually, \(n_{\mathrm{e}}\) and \(\langle \gamma \rangle \) are calculated through the properties of the observed emission. There could be other leptons not participating to the emission and, therefore, not accounted for when we estimate the \(N(\gamma )\) distribution.

  • Protons The power in the bulk motion of protons is

    $$\begin{aligned} P_{\mathrm{p}} = P_{\mathrm{e}} \, {n_{\mathrm{p}}\over n_{\mathrm{e}} }\, { \langle \gamma _{\mathrm{p}} \rangle m_{\mathrm{p}}\over \langle \gamma \rangle m_{\mathrm{e}}}. \end{aligned}$$
    (6)

    If protons are cold, then \(\langle \gamma _{\mathrm{p}} \rangle =1\), but if there is a hot component, possibly highly relativistic, then the power increases. This is indeed a possibility, especially after the discovery of the likely association of one high-energy neutrino detected by Icecube with the BL Lac TXS 0506+056 (Aartsen et al. 2018). For the rest of this paper, we will assume cold protons, and one proton for each emitting electron. With these working assumptions, note that the presence of protons, even if cold, is very important when \(\langle \gamma \rangle \) of the leptons is small, namely, for FSRQs. On the other hand, TeV emitting BL Lacs can have \(\langle \gamma \rangle > m_{\mathrm{p}}/m_{\mathrm{e}}\). In these sources, protons (if cold) do not contribute much to the total jet power.

5 Results

To compare the jet power with the accretion luminosity, we need blazars that have been detected in the \(\gamma \)-ray band and that have been observed spectroscopically, with detected broad emission lines. The high-energy emission allows us to know the entire bolometric luminosity, and the broad emission lines allow us to estimate the disk luminosity.

To this aim, we have used the sample of blazars studied by Shaw et al. (2012) (FSRQs) and Shaw et al. (2013) (BL Lacs). Only very few BL Lacs were selected, only those showing the presence of broad lines. We have collected for all blazars of the total sample the available archival data, and we have applied the one-zone leptonic model described in Ghisellini and Tavecchio (2009). The results concerning the 217 blazars of this sample were presented in Ghisellini et al. (2014) and Ghisellini and Tavecchio (2015).

The SED coverage was much better than in the past, because for all blazars in the sample, we had: i) the spectroscopic data (that are used to find the disk luminosity and the black hole mass); ii) the \(\gamma \)-ray luminosity (used to infer the jet radiated power); iii) the far IR data given by WISE satellite (that help to shape the jet+torus continuum); and iv) the high-frequency radio data from the WMAP and Planck satellites helping to define the synchrotron peak.

Then, we have added a sample of \(z>2\) blazars detected by Swift/BAT (Ghisellini et al. 2010), a sample of \(z>4\) blazars selected from (Sbarrato et al. 2013), and two powerful FSRQs detected by NuSTAR (Sbarrato et al. 2016).

Fig. 4
figure 4

Jet power as a function of the accretion luminosity for different blazar samples. In addition, the BL Lacs shown in this figures had some broad lines in their spectrum. The sources belong to the sample studied by Shaw et al. (2012), Shaw et al. (2013), and Ghisellini et al. (2014); two powerful FSRQs detected by NuSTAR (Sbarrato et al. 2016); a sample of \(z>2\) blazars detected by Swift/BAT (Ghisellini et al. 2010) and a sample of \(z>4\) blazars selected from (Sbarrato et al. 2013). The yellow line is the equality line, and the black line is the best fit

Full size image

We find \(P_{\mathrm{r}} \sim L_{\mathrm{d}}\). These results are model independent, since \(P_{\mathrm{r}} \sim L/\varGamma ^2\), and while \(\varGamma \) is indeed found through modelling, the typical values found agree with independent estimates given by superluminal motion and other beaming indicators (such as the radio brightness temperature).

This is a lower limit to the jet power and does not depend on the uncertainties regarding the particle distribution and the importance of electron–positron pairs. This result is solid.

Then, to go from \(P_{\mathrm{r}}\) to \(P_{\mathrm{j}}= P_{\mathrm{r}} +P_{\mathrm{e}} +P_{\mathrm{p}} +P_{\mathrm{B}}\), we do have to apply a model. We used the model described in Ghisellini and Tavecchio (2009). Figure 4 shows \(P_{\mathrm{j}}\) as a function of \(L_{\mathrm{d}}\) assuming one cold proton per emitting electron. This gives, on average, \(P_{\mathrm{j}} \sim 10 L_{\mathrm{d}}\).

6 Discussion

How can the jet power be proportional to \(L_{\mathrm{d}}\), but larger than it? We have two possibilities. The first, suggested by the fact that the two powers are proportional, is that it is accretion that powers the jet. The gravitational energy dissipated by the accreting \(\dot{M}\) is transformed into heat only partly, while the rest goes to power the jet (Jolley and Kuncic 2008; Jolley et al. 2009). The total accretion efficiency \(\eta \) is used to power the jet with an efficiency \(\eta _{\mathrm{j}}\), and to heat the disk with an efficiency \(\eta _{\mathrm{d}}\):

$$\begin{aligned} P_{\mathrm{j}} = \eta _{\mathrm{j}} \dot{M}c^2; \,\,\,\,\, L_{\mathrm{d}}=\eta _{\mathrm{d}} \dot{M}c^2; \,\,\,\,\, \eta =\eta _{\mathrm{j}}+\eta _{\mathrm{d}}. \end{aligned}$$
(7)

Then, \(P_{\mathrm{j}}= 10 L_{\mathrm{d}}\) requires \(\eta _{\mathrm{j}}= 10 \eta _{\mathrm{d}}\). This has an important consequence: if there is a jet, the disk efficiency can be smaller (even by a factor 10) than what is foreseen for standard accretion models. To produce a given \(L_{\mathrm{d}}\), \(\dot{M}\) must, therefore, be larger, and this helps jetted sources to have black holes that grow faster (especially at large redshifts Ghisellini et al. 2013).

The second possibility is that jets are powered not by accretion, but by the rotational energy of the black hole, by the Blandford–Znajek process (Blandford and Znajek 1977). The total energy that can be extracted by a maximally spinning black hole is 29% of its mass, namely, \(5\times 10^{62}\) erg for a \(10^9 M_\odot \) black hole. This is enough to power a jet with \(P_{\mathrm{j}}=10^{47}\) erg s\(^{-1}\) for 166 million years. As (Cavaliere and D’Elia 2002) and (Ghisellini and Celotti 2002) proposed in 2002, this can be the engine for powering blazars. This has also been confirmed by numerical simulations (Tchekhovskoy et al. 2012) finding an average jet power corresponding to \(\sim \)1.5\( \dot{M} c^2\) that obviously indicates that the power of the jet does not come from direct accretion, but from the rotational black hole energy (in turn originated by the previous accretion, and now released in a efficient way).

The fact that \(P_{\mathrm{j}}\propto L_{\mathrm{d}}\) in this scenario can be explained if the magnetic field energy density necessary to tap the rotational energy of the black hole is proportional to \(\dot{M}\) and hence to \(L_{\mathrm{d}}\). This is possible if \(B^2 \simeq \rho c^2\), where \(\rho \) is the disk density.

Furthermore, when the accretion disk is radiatively efficient, it produces most of its luminosity in the optical-UV, ionizing the gas of the BLR, that can indeed emit broad emission lines, but allows rates of accretion, the disk becomes radiatively inefficient (ADAF (Rees et al. 1982; Narayan and Yi 1994), ADIOS (Blandford and Begelman 1999), and so on), and most of its (already reduced) luminosity is not emitted in the UV (Mahadevan 1997). The clouds of the BLR are not photo-ionized, and no broad line is produced. This explains the divide between FSRQs and BL Lacs (Ghisellini et al. 2009) and possibly their different cosmic evolutions (Cavaliere and D’Elia 2002).