Algorithms for the computation of regular single-valued neutrosophic soft hypergraphs applied to supranational asian bodies

Abstract

The single-valued neutrosophic set efficiently handles the imprecisions of data and makes a simulation of the decision-making method of humans by considering all features of decision (i.e., agree, not sure and disagree). By keeping the benefits of this theory and combining the properties of the parameter-dependent soft set theory, this research article introduces hypergraphs in single-valued neutrosophic soft environment and presents the concept of regularity as well as hyperedge regularity of the proposed hypergraphs. We discuss regular, totally regular, perfectly regular, full regular and perfectly irregular as well as hyperedge regular, totally hyperedge regular, perfectly hyperedge regular, full hyperedge regular and perfectly hyperedge irregular single-valued neutrosophic soft hypergraphs. Moreover, we illustrate that how one can structurally relate the concepts of regularity and hyperedge regularity in a single-valued neutrosophic soft hypergraph. Finally, we describe the proposed model with the help of an application representing the multilateral relationships of the Asian countries through various regional organizations. The proposed hypergraphs are applicable in genetics, human activities and applied sciences.

1 Introduction

Graph theory is a useful mathematical tool that comprises the study of networks and has been developed into a field of mathematical research. The main object of this theory is graph which is being employed to solve many mathematical puzzles of number theory, probability theory, algebra and topology; as well as practical problems of chemistry, transportation engineering, electrical engineering, biology, sociology, economics, etc. Graphs can depict the pairwise association between the constituents of a system. In order to represent the connection between more than two entities of a network, the hypergraphs were suggested by Berge [11, 12]. Hypergraphs are considered to be the most generalized discrete structures. These are used in modeling of databases, satisfiability problems, machine learning, etc. Its applications include image retrieval, detection of money laundering, spectral clustering and bioinformatics. Voloshin [37] and Bretto [13] have discussed some interesting concepts of hypergraphs.

Zadeh [39] is well-known as the pioneer of fuzzy set theory as he introduced mathematical researchers with fuzzy set which handles the statements with the perspective of uncertainty. This set is characterized by a mapping that nominates the real numerical values between the binary values of classical set theory describing the degree of belongingness of each member of fuzzy set. After the acceptance of Zadeh’s fuzzy set, many structures were defined on the basis of this model to deal with uncertainty of actual-world. Fuzzy set clearly explains the truthness of a statement but has no discussion over its falsehood. Atanassov [10] settled this problem and combined the mappings of truth-membership and falsity-membership in his newly defined intuitionistic fuzzy set. He also imposed a constraint that the sum of truth and falsity-membership values of its elements must not exceed one. In 1998, Smarandache [34, 35] presented neutrosophic set based on the concept of neutrosophy. Generalizing the concept of fuzzy set and intuitionistic fuzzy set, this set is defined by three independent mappings: truth, indeterminacy/neutrality and falsity-membership functions. The single-valued neutrosophic set (SNS) was suggested by Wang et al. [38] as a simplified form of neutrosophic set so that various problems of physical world can be solved conveniently.

Molodtsov’s soft set ($\hbox {S}_{f}$S) [25] facilitated us to deal with information from the viewpoint of parametrization. $\hbox {S}_{f}$S model is very convenient to use in decision making as the parameters can be chosen in terms of numbers, variables, functions, etc. Different properties, operations and applications of $\hbox {S}_{f}$Ss are presented in [21, 29]. Various researchers worked over soft set based decision-making with crisp as well as fuzzy information [8, 9, 16, 17]. Maji [22] put forth a hybrid model of $\hbox {S}_{f}$S and neutrosophic set of Smarandache as a neutrosophic soft set ($\hbox {SNS}_{f}$S). Afterwards, Deli and Broumi [15] suggested neutrosophic soft relations on the basis of $\hbox {SNS}_{f}$Ss.

The graphs and hypergraphs are discussed in various generalized models of fuzzy sets. Kaufmann [19] put forth fuzzy graphs as well as fuzzy hypergraphs in order to exhibit the ambiguity in different simple as well as complex networks. These two concepts were explained more adequately by Mordeson and Nair [26]. The connectivity of fuzzy graphs is examined by Mathew and Sunitha [23, 24]. Samanta, with the collaboration of different researchers, studied generalized fuzzy graphs and investigated their completeness and regularity [31, 32]. The intuitionistic fuzzy graphs were suggested by Paravathi and Karunambigai [27]. Ghorai and Pal [18] discussed the concept of faces and dual for m-polar fuzzy planar graphs. Akram [1] described the single-valued neutrosophic graphs (SNGs) and its hybrid models. A lot of researchers made contributions in the study of SNSs as well as SNGs in decision-making [14, 20, 30, 40]. Similar to graphs, fuzzy hypergraphs [26], intuitionistic fuzzy hypergraphs [2, 28] and single-valued neutrosophic hypergraphs (SNHs) [7] are also available in literature.

Graphs were studied in $\hbox {S}_{f}$S theory by Thumbakara and George [36]. Akram and Nawaz [5] introduced fuzzy soft graphs as parameterized fuzzy graphs and also defined their operations. Single-valued neutrosophic soft graphs ($\hbox {SNS}_{f}$Gs) were analyzed by Akram and Shahzadi [6] and defined some operations on them. Zhan et al. [41] proposed a new decision-making method for bipolar neutrosophic data. Furthermore, Shahzadi and Akram [33] proposed the Pythagorean fuzzy soft hypergraphs and illustrated them with results, examples and application. Regular hypergraphs were suggested by Bretto [13]. Akram and Luqman [3, 4] presented valuable contribution on hypergraphs in detail. Our perspective behind the introduction to single-valued neutrosophic soft hypergraphs ($\hbox {SNS}_{f}$Hs) is given below:

• 1. $\hbox {SNS}_{f}$S is a good blend of SNS and $\hbox {S}_{f}$S. It assigns neutrosophic grades to the elements which posses parametric characterization. $\hbox {SNS}_{f}$Gs are able to depict the pairwise relationship between the constituents of a system but cannot represent the connection of more than two components. On the other hand, SNHs can represent multiary relation, however, if the system is parameter-dependent, there is a great chance of information loss. In order to combine the properties of both above discussed models, we put forward the $\hbox {SNS}_{f}$Hs.

• 2. The regularity of hypergraphs has been studied so far in classical set theory as well as in some extensions of fuzzy set theory. But their is no discussion over the degree of a hyperedge or hyperedge regularity of hypergraphs in the literature. This motivated us to initiate the study of hyperedge regularity of hypergraphs.

The usefulness of $\hbox {SNS}_{f}$Ss motivated us to extend the study of hypergraphs in this theory. The proposed $\hbox {SNS}_{f}$Hs are capable to provide the visual representation of parameter-dependent data which carries the imprecision in the grades of truth, indeterminacy as well as falsity. The concept of regularity as well hyperedge regularity of these hypergraphs has been investigated in detail together with their algoritms. It is mentioned that the regularity of a $\hbox {SNS}_{f}$H does not ensure its hyperedge regularity except for some special cases. This article contributes to the current literature in the following way:

• 1. It suggests the $\hbox {SNS}_{f}$Hs that has the ability to exhibit the parameter-dependent connection among any finite number of elements and also presents an application of the proposed model.

• 2. It gives the idea of regular as well as hypeedge regular $\hbox {SNS}_{f}$Hs and explains these concepts with the help of algorithms, numerous results and examples.

• 3. It describes that how these two concepts of regularity and hyperedge regularity are linked with one another in $\hbox {SNS}_{f}$Hs.

The paper is organized in the following manner. Sect. 2 provides the basics about the concept of regularity and also introduces hyperedge regularity of hypergraphs. Sect. 3 is devoted to introduce the $\hbox {SNS}_{f}$Hs. The regularity and hyperedge regularity of $\hbox {SNS}_{f}$Hs with some generalizations, results, examples and algorithms, are described in Sects. 4 and  5, respectively. Sect. 6 relates the regular $\hbox {SNS}_{f}$Hs and hyperedge regular $\hbox {SNS}_{f}$Hs. The application of the suggested model is presented in Sect. 7 which describes multilateral relationship among the Asian countries with the help of regional organizations. Finally, the paper is concluded in Sect. 8.

2 Basic concepts

In this section, we provide some basic definitions that will help in the apprehension of the following research.

Definition 1

[38] Let V be a non-void space of points. A SNS on V, represented by $\mathrm {R}$, is defined by a 3-tuple of mappings $\mathrm {R}=({\mathfrak {t}}_{\mathrm {R}},{\mathfrak {i}}_{\mathrm {R}}, {\mathfrak {f}}_{\mathrm {R}})$, where ${\mathfrak {t}}_{\mathrm {R}}:V\rightarrow [0,1]$, ${\mathfrak {i}}_{\mathrm {R}}:V\rightarrow [0,1]$ and ${\mathfrak {f}}_{\mathrm {R}}:V\rightarrow [0,1]$ denote truth, indeterminacy and falsity membership functions, respectively.

Definition 2

[22] Consider V as a space of points and A as a set of parameters. Let ${\mathcal {P}}(V)$ be an infinite set of all SNSs over V. A $\hbox {SNS}_{f}$S $(\mathrm {R}, A)$ can be defined by the mapping $\mathrm {R}:A \rightarrow {\mathcal {P}}(V)$ which gives the collection of SNSs depending on distinct parameters.

Definition 3

[11, 12] A hypergraph H is defined by the pair $H=(V,E)$, where $V=\{v_{i}:1\le i\le n\}$ is a non-empty set of elements called nodes/vertices and E is a subset of $P(V)\backslash \{\phi \}$ (P(V) denotes the power set of V). The hyperedges of H are the members $E_{j}=\{v_{k}:1\le k\le m, 2\le m\le n\}$ $(1\le j\le t)$ of E which are, in fact, the finite subsets of V.

The order O(H) and size S(H) of H is simply the cardinality of vertex set |V| and cardinality of hyperedge set |E|, respectively. The degree d(v) of a vertex v in H is the number of hyperedges containing v. Moreover, a hypergraph H is called regular of degree r if $d(v)=r$, $\forall v$ [13].

Example 1

Consider a hypergraph $H=(V,E)$ shown in Fig. 1, where $V=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6}\}$ and $E=\{v_{1}v_{2}v_{4},v_{1}v_{6},v_{2}v_{5},v_{3}v_{4},v_{3}v_{5}v_{6}\}$. The order and size of H are $O(H)=6$ and $S(H)=5$, respectively. Moreover, $d(v_{i})=2$, $1\le i\le 6$. Hence, H is regular of degree 2.

Fig. 1

A regular hypergraph H of degree 2

Similar to graphs, one can define the degree of hyperedge as well as the hyperedge regularity of a hypergraph.

Definition 4

The degree $d(E_{j})$ of a hyperedge $E_{j}$ in a hypergraph $H=(V,E)$ is defined as

$$\begin{aligned} d(E_{j})=d(v_{1})+d(v_{2})+...+d(v_{m})-\varepsilon _{j}, \end{aligned}$$

where $\varepsilon _{j}$ denotes the cardinality of $E_{j}$. A hypergraph H is called hyperedge regular of degree k if $d(E_{j})=k$, $\forall j$.

Example 2

Consider a hypergraph $H=(V,E)$ shown in Fig. 2, where $V=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6}\}$ and $E=\{v_{1}v_{3}v_{5},v_{1}v_{4}v_{5},v_{2}v_{3}v_{6},v_{2}v_{4}v_{6}\}$. Note that $d(v_{i})=2$, $1\le i\le 6$. Also, $d(v_1,v_3,v_5)=d(v_1)+d(v_3)+d(v_5)-3=3$. Since degree of all hyperedges in H is 3, therefore H is hyperedge regular of degree 3.

Fig. 2

A hyperedge regular hypergraph H of degree 3

3 Single-valued neutrosophic soft hypergraphs

Throughout the article, V is considered as the universe of discourse and $A\subseteq Z$ is the set of all parameters of elements of V. Further, a $\hbox {SNS}_{f}$H does not contain the loops or multiple hyperedges unless mentioned.

Definition 5

Let us consider a crisp hypergraph $H=(V,E)$. A $\hbox {SNS}_{f}$H $\mathrm {H}$ over H can be represented as an ordered triplet $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$, where

• (1) $(\mathrm {R},A)$ is a $\hbox {SNS}_{f}$S of vertices over V.

• (2) $(\mathrm {S},A)$ is a $\hbox {SNS}_{f}$S over E such that the member $E_{j} (1\le j\le t)$ of $\mathrm {S}({\mathfrak {z}})$ represents the SN hyperedge in the SNH $\mathrm {H}({\mathfrak {z}})=(\mathrm {R}({\mathfrak {z}}),\mathrm {S}({\mathfrak {z}}))$ of $\mathrm {H}$, and its truth-membership, indeterminacy membership and falsity-membership values satisfies

  $$\begin{aligned} {\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})={\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(v_{1}v_{2}...v_{m})\le & {} \min \{{\mathfrak {t}}_{\mathrm {R} ({\mathfrak {z}})}(v_{1}),{\mathfrak {t}}_{\mathrm {R}({\mathfrak {z}})}(v_{2}),..., {\mathfrak {t}}_{\mathrm {R}({\mathfrak {z}})}(v_{m})\},\\ {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})={\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(v_{1}v_{2}...v_{m})\le & {} \min \{{\mathfrak {i}}_{\mathrm {R} ({\mathfrak {z}})}(v_{1}),{\mathfrak {i}}_{\mathrm {R}({\mathfrak {z}})}(v_{2}),..., {\mathfrak {i}}_{\mathrm {R}({\mathfrak {z}})}(v_{m})\},\\ {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})={\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(v_{1}v_{2}...v_{m})\le & {} \max \{{\mathfrak {f}}_{\mathrm {R} ({\mathfrak {z}})}(v_{1}),{\mathfrak {f}}_{\mathrm {R}({\mathfrak {z}})}(v_{2}),..., {\mathfrak {f}}_{\mathrm {R}({\mathfrak {z}})}(v_{m})\},\\ \end{aligned}$$

  respectively, where $2\le m\le n$.

• (3) For all SNHs $\mathrm {H}({\mathfrak {z}})$, the condition $\bigcup _{1\le j\le t}Supp(E_{j})=V$ holds, where $E_{j}$ represents the SN hyperedge in $H({\mathfrak {z}})$.

We can define the order ${\mathcal {O}}(\mathrm {H})$ of a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ as

$$\begin{aligned} {\mathcal {O}}(\mathrm {H})=\sum _{{\mathfrak {z}}\in A}\left( \sum _{v\in V}{\mathfrak {t}}_{\mathrm {R}({\mathfrak {z}})}(v),\sum _{v\in V}{\mathfrak {i}}_{\mathrm {R}({\mathfrak {z}})}(v),\sum _{v\in V}{\mathfrak {f}}_{\mathrm {R}({\mathfrak {z}})}(v)\right) . \end{aligned}$$

Further, the size ${\mathcal {S}}(\mathrm {H})$ of the considered $\hbox {SNS}_{f}$H can be computed by the following expression

$$\begin{aligned} {\mathcal {S}}(\mathrm {H})=\sum _{{\mathfrak {z}}\in A}(\sum _{j}{\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),\sum _j{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),\sum _j{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})). \end{aligned}$$

We now define the degree and total degree for both vertices and hyperedges of a $\hbox {SNS}_{f}$H.

Definition 6

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. The degree ${\mathfrak {d}}(v)$ of its $\hbox {SNS}_{f}$ vertex v is calculated by taking the sum over degrees ${\mathfrak {d}}_{{\mathfrak {z}}}(v)$ of v in all SNHs $\mathrm {H}({\mathfrak {z}})$. That is,

$$\begin{aligned} {\mathfrak {d}}(v)=\sum _{{\mathfrak {z}}\in A}{\mathfrak {d}}_{{\mathfrak {z}}}(v), \end{aligned}$$

where

$$\begin{aligned} {\mathfrak {d}}_{{\mathfrak {z}}}(v)=\left( \sum _{E_{j}\ni v} {\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),\sum _{E_{j}\ni v} {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),\sum _{E_{j}\ni v} {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})\right) . \end{aligned}$$

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. The total degree $\mathfrak {td}(v)$ of its $\hbox {SNS}_{f}$ vertex v is calculated by taking the sum over degrees $\mathfrak {td}_{{\mathfrak {z}}}(v)$ of v in all SNHs $\mathrm {H}({\mathfrak {z}})$. That is,

$$\begin{aligned} \mathfrak {td}(v)=\sum _{{\mathfrak {z}}\in A}\mathfrak {td}_{{\mathfrak {z}}}(v), \end{aligned}$$

where

$$\begin{aligned} \mathfrak {td}_{{\mathfrak {z}}}(v)=\left( \sum _{E_{j}\ni v} {\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})+{\mathfrak {t}}_{\mathrm {R}({\mathfrak {z}})}(v),\sum _{E_{j}\ni v} {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})+{\mathfrak {i}}_{\mathrm {R}({\mathfrak {z}})}(v),\sum _{E_{j}\ni v} {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})+{\mathfrak {f}}_{\mathrm {R}({\mathfrak {z}})}(v)\right) , \end{aligned}$$

or

$$\begin{aligned} \mathfrak {td}_{{\mathfrak {z}}}(v)={\mathfrak {d}}_{{\mathfrak {z}}}(v)+({\mathfrak {t}}_{\mathrm {R}({\mathfrak {z}})}(v),{\mathfrak {i}}_{\mathrm {R}({\mathfrak {z}})}(v), {\mathfrak {f}}_{\mathrm {R}({\mathfrak {z}})}(v)). \end{aligned}$$

Definition 7

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. The degree ${\mathfrak {d}}(E_{j})$ of its $\hbox {SNS}_{f}$ hyperedge $E_{j}$ is calculated by taking the sum over degrees ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j}$ of $E_j$ in all SNHs $\mathrm {H}({\mathfrak {z}})$. That is,

$$\begin{aligned} {\mathfrak {d}}(E_{j})=\sum _{{\mathfrak {z}}\in A}{\mathfrak {d}}_{{\mathfrak {z}}}(E_{j}), \end{aligned}$$

where

$$\begin{aligned} {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})-\varepsilon _{j} ({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})). \end{aligned}$$

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. The total degree $\mathfrak {td}(E_{j})$ of its $\hbox {SNS}_{f}$ hyperedge $E_{j}$ is calculated by taking the sum over total degrees $\mathfrak {td}_{{\mathfrak {z}}}(E_{j}$ of $E_j$ in all SNHs $\mathrm {H}({\mathfrak {z}})$. That is,

$$\begin{aligned} \mathfrak {td}(E_{j})=\sum _{{\mathfrak {z}}\in A}\mathfrak {td}_{{\mathfrak {z}}}(E_{j}), \end{aligned}$$

where

$$\begin{aligned} \mathfrak {td}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})- (\varepsilon _{j}+1)({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})), \end{aligned}$$

or

$$\begin{aligned} \mathfrak {td}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})+({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})). \end{aligned}$$

Example 3

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ on $H=(V,E)$, where $V=\{v_{1},v_{2},v_{3},v_{4},v_{5},v_{6}\}$ and $E=\{v_{1}v_{2}v_{3},v_{1}v_{2}v_{3}v_{5},v_{2}v_{4}v_{5}v_{6},v_{3}v_{4},v_{4}v_{5}v_{6}\}$ such that

$$\begin{aligned} {\mathrm {H}}({\mathfrak {z}}_{1})= & {} (\mathrm {R}({\mathfrak {z}}_{1}),{\mathrm {S}}({\mathfrak {z}}_{1}))=(\{\langle v_{1},(0.5,0.6,0.9)\rangle , \langle v_{2},(0.3,\\&0.7,0.4)\rangle , \langle v_{3},(0.7,0.2,0.8)\rangle , \langle v_{4},(0.9,0.1,0.5)\rangle , \langle v_{5},(0.6,\\&0.8,0.3)\rangle , \langle v_{6},(0.3,0.5,0.8)\rangle \},\{\langle v_{1}v_{2}v_{3},(0.3,\\&0.2,0.7)\rangle , \langle v_{3}v_{4},(0.6,0.1,0.5)\rangle , \langle v_{4}v_{5}v_{6},(0.2,0.1,0.6)\rangle \}),\\ {\mathrm {H}}({\mathfrak {z}}_{2})= & {} (\mathrm {R}({\mathfrak {z}}_{2}),{\mathrm {S}}({\mathfrak {z}}_{2}))=(\{\langle v_{1},(0.4,0.2,0.9)\rangle , \langle v_{2},(0.9,\\&0.3,0.7)\rangle , \langle v_{3},(0.1,0.3,0.8)\rangle , \langle v_{4},(0.6,0.3,0.7)\rangle , \langle v_{5},(0.6,\\&0.7,0.5)\rangle , \langle v_{6},(0.8,0.4,0.5)\rangle \},\{\langle v_{1}v_{2}v_{3}v_{5},(0.1,\\&0.1,0.8)\rangle , \langle v_{3}v_{4},(0.1,0.3,0.7)\rangle , \langle v_{2}v_{4}v_{5}v_{6},(0.5,0.2,0.6)\rangle \}). \end{aligned}$$

Fig. 3

A $\hbox {SNS}_{f}$H $\mathrm {H}$

Figure 3 displays the corresponding $\hbox {SNS}_{f}$H. The order and size of $\mathrm {H}$ are ${\mathcal {O}}(\mathrm {H})=(6.7,5.1,7.8)$ and ${\mathcal {S}}(\mathrm {H})=(1.8,1.0,3.9)$, respectively. The degrees of all vertices of $\mathrm {H}$ are

$$\begin{aligned} {\mathfrak {d}}(v_{1})= & {} (0.4,0.3,1.5),\quad {\mathfrak {d}}(v_{2})=(0.9,0.5,2.1),\quad {\mathfrak {d}}(v_{3})=(1.1,0.7,2.7),\\ {\mathfrak {d}}(v_{4})= & {} (1.4,0.7,2.4),\quad {\mathfrak {d}}(v_{5})=(0.8,0.4,2.0),\quad {\mathfrak {d}}(v_{6})=(0.7,0.3,1.2). \end{aligned}$$

Similarly, the total degrees of all vertices of $\mathrm {H}$ are

$$\begin{aligned} \mathfrak {td}(v_{1})= & {} (1.3,1.1,3.3),\quad \mathfrak {td}(v_{2})=(2.1,1.5,3.2),\quad \mathfrak {td}(v_{3})=(1.9,1.2,4.3),\\ \mathfrak {td}(v_{4})= & {} (2.9,1.1,3.6),\quad \mathfrak {td}(v_{5})=(2.0,1.9,2.8),\quad \mathfrak {td}(v_{6})=(1.8,1.2,2.5). \end{aligned}$$

The degrees of all hyperedges of $\mathrm {H}$ are

$$\begin{aligned} {\mathfrak {d}}(v_{1}v_{2}v_{3})= & {} (0.6,0.1,0.5),\quad {\mathfrak {d}}(v_{3}v_{4})=(1.1,0.6,2.7),\quad {\mathfrak {d}}(v_{4}v_5v_6)=(0.6,0.1,0.5),\\ {\mathfrak {d}}(v_1v_2v_3v_5)= & {} (1.1,0.7,1.9),\quad {\mathfrak {d}}(v_2v_4v_5v_6)=(0.3,0.5,2.3). \end{aligned}$$

Similarly, the total degrees of all hyperedges of $\mathrm {H}$ are

$$\begin{aligned} \mathfrak {td}(v_1v_2v_3)= & {} (0.9,0.3,1.2),\quad \mathfrak {td}(v_3v_4)=(1.8,1.0,3.9),\quad \mathfrak {td}(v_4v_5v_6)=(0.8,0.2,1.1),\\ \mathfrak {td}(v_1v_2v_3v_5)= & {} (1.2,0.8,2.7),\quad \mathfrak {td}(v_2v_4v_5v_6)=(0.8,0.7,2.9). \end{aligned}$$

4 Regular single-valued neutrosophic soft hypergraphs

Definition 8

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H and $\mathrm {H}({\mathfrak {z}})$ be the SNH relative to parameter ${\mathfrak {z}}$. If for all ${\mathfrak {z}}$, $\mathrm {H}({\mathfrak {z}})$ is regular of degree $(r_{1},r_{2},r_{3})$, then $\mathrm {H}$ is also regular of degree $(r_{1},r_{2},r_{3})$.

For the regularity of $\hbox {SNS}_{f}$H, an Algorithm 41 is presented. This algorithm takes $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ as an input, examines the degree of each $\hbox {SNS}_{f}$ vertex of H and then determines the degree of regularity of the considered $\hbox {SNS}_{f}$H if it is regular.

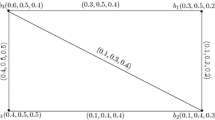
Example 4

Let us consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ presented in Fig. 4. Observe that $\mathrm {H}$ is regular of degree (0.9, 0.4, 0.7) as $\mathrm {H}({\mathfrak {z}}_{i})$, for all $i\in \{1,2\}$ are regular of degree (0.9, 0.4, 0.7).

Fig. 4

A regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Fig. 5

A totally regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Definition 9

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H and $\mathrm {H}({\mathfrak {z}})$ be the SNH relative to parameter ${\mathfrak {z}}$. If for all ${\mathfrak {z}}$, $\mathrm {H}({\mathfrak {z}})$ is totally regular of degree $(s_{1},s_{2},s_{3})$, then $\mathrm {H}$ is also totally regular of degree $(s_{1},s_{2},s_{3})$.

Example 5

Let us consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ presented in Fig. 5. Observe that $\mathrm {H}$ is totally regular of degree (1.7, 1.4, 1.9) as $\mathrm {H}({\mathfrak {z}}_{i})$, for all $i\in \{1,2\}$ are totally regular of degree (1.7, 1.4, 1.9).

Definition 10

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. If $\mathrm {H}$ is both regular as well as totally regular $\hbox {SNS}_{f}$H then $\mathrm {H}$ is a perfectly regular $\hbox {SNS}_{f}$H.

Example 6

Let us consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ presented in Fig. 6. Observe that $\mathrm {H}$ is perfectly regular as it is regular of degree (0.8, 0.4, 1.2) and totally regular of degree (1.5, 0.8, 2.1).

Fig. 6

A perfectly regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Definition 11

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is said to be partially regular if the underlying crisp hypergraphs of each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are regular.

Example 7

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ displayed in Fig. 7. Note that the underlying crisp hypergraphs of both $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are regular of degree 2. Thus, $\mathrm {H}$ is a partially regular $\hbox {SNS}_{f}$H.

Fig. 7

A partially regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Definition 12

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is said to be full regular if $\mathrm {H}$ is both regular as well as partially regular $\hbox {SNS}_{f}$H.

Example 8

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ displayed in Fig. 4. It is regular of degree (0.8, 0.6, 1.2). It is also partially regular as the underlying crisp hypergraphs of both $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are regular of degree 2. So it is full regular $\hbox {SNS}_{f}$H.

Remark 1

A regular $\hbox {SNS}_{f}$H may not be partially regular (or full regular).

The $\hbox {SNS}_{f}$H $\mathrm {H}$, given in Fig. 8, is regular of degree (0.9, 0.6, 1.2). Note that it is not partially regular as the underlying crisp hypergraphs of $\mathrm {H}({\mathfrak {z}}_{1})$ and $\mathrm {H}({\mathfrak {z}}_{1})$ are not regular.

Fig. 8

A regular but not partially regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Remark 2

A partially regular $\hbox {SNS}_{f}$H may not be regular (or full regular).

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}$ displayed in Fig. 7. It is partially regular as the underlying crisp hypergraphs of both $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are regular of degree 2. But it is not a regular $\hbox {SNS}_{f}$H because the degrees of all of its vertices are not equal.

Theorem 1

If $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is a $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are the constant-valued functions. Then $\mathrm {H}$ is a regular $\hbox {SNS}_{f}$H if and only if $\mathrm {H}$ is a partially regular $\hbox {SNS}_{f}$H.

Proof

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ with SNHs $\mathrm {H}({\mathfrak {z}})=(\mathrm {R}({\mathfrak {z}}),\mathrm {S}({\mathfrak {z}}))$ such that ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$, $\forall j, {\mathfrak {z}}$. We will prove that $\mathrm {H}$ is a partially regular $\hbox {SNS}_{f}$H. For this, assume that $\mathrm {H}$ is regular of degree $(r_{1},r_{2},r_{3})$. Using the definition of degree of vertex v in SNH $\mathrm {H}({\mathfrak {z}})$,

$$\begin{aligned} {\mathfrak {d}}_{\mathfrak {z}}(v)= & {} \left( \sum _{E_{j}\ni v} {\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),\sum _{E_{j}\ni v} {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),\sum _{E_{j}\ni v} {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})\right) =d_{{\mathfrak {z}}}(v)(c_{1},c_{2},c_{3})\\ (r_{1},r_{2},r_{3})= & {} d_{{\mathfrak {z}}}(v)(c_{1},c_{2},c_{3}) \\ d_{{\mathfrak {z}}}(v)= & {} \dfrac{(r_{1},r_{2},r_{3})}{(c_{1},c_{2},c_{3})}. \end{aligned}$$

Since v and ${\mathfrak {z}}$ are arbitrary, this shows that the underlying crisp hypergraphs of all $\mathrm {H}({\mathfrak {z}})$ are regular. Hence, $\mathrm {H}$ is a partially regular $\hbox {SNS}_{f}$H.

For the converse part, suppose that $\mathrm {H}$ is a partially regular $\hbox {SNS}_{f}$H. This means that the underlying crisp hypergraphs of $\mathrm {H}({\mathfrak {z}})$ are regular of degree r (say), $\forall {\mathfrak {z}}$. Then for all SN vertices v, ${\mathfrak {d}}_{\mathfrak {z}}(v)=d_{{\mathfrak {z}}}(v)(c_{1},c_{2},c_{3})=r(c_{1},c_{2},c_{3})$. Thus, $\mathrm {H}$ is a regular $\hbox {SNS}_{f}$H.

$\square$

Corollary 1

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. If $\mathrm {H}$ is partially regular $\hbox {SNS}_{f}$H, then $\mathrm {H}$ is full regular $\hbox {SNS}_{f}$H.

Definition 13

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ is said to be neighborly irregular if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are neighborly irregular, i.e., if degrees ${\mathfrak {d}}_{{\mathfrak {z}}}(v)$ of all adjacent SN vertices v of $\mathrm {H}({\mathfrak {z}})$ are distinct.

Example 9

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ given in Fig. 9. Note that the degrees of all adjacent SN vertices are not equal. Thus, $\mathrm {H}$ is neighborly irregular $\hbox {SNS}_{f}$H.

Fig. 9

A neighborly irregular $\hbox {SNS}_{f}$H

Definition 14

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ is said to be totally neighborly irregular if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are totally neighborly irregular, i.e., if total degrees $\mathfrak {td}_{{\mathfrak {z}}}(v)$ of all adjacent SN vertices v of $\mathrm {H}({\mathfrak {z}})$ are distinct.

Example 10

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ given in Fig. 10. Note that the total degrees of all adjacent SN vertices are not equal. Thus, $\mathrm {H}$ is totally neighborly irregular $\hbox {SNS}_{f}$H.

Fig. 10

A totally neighborly irregular $\hbox {SNS}_{f}$H

Definition 15

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ is said to be perfectly irregular if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are perfectly irregular, i.e., if degrees ${\mathfrak {d}}_{{\mathfrak {z}}}(v)$ as well as total degrees $\mathfrak {td}_{{\mathfrak {z}}}(v)$ of all SN vertices v of $\mathrm {H}({\mathfrak {z}})$ are distinct.

Example 11

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ given in Fig. 11. Note that the degrees as well as total degrees of all adjacent SN vertices are not equal. Thus, $\mathrm {H}$ is perfectly irregular $\hbox {SNS}_{f}$H.

Fig. 11

A perfectly irregular $\hbox {SNS}_{f}$H

5 Hyperedge regularity of single-valued neutrosophic soft hypergraphs

Definition 16

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is said to be hyperedge regular of degree $(k_{1},k_{2},k_{3})$ if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are hyperedge regular of degree $(k_{1},k_{2},k_{3})$, i.e., ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})=(k_{1},k_{2},k_{3})$, $\forall j, {\mathfrak {z}}$.

For the hyperedge regularity of $\hbox {SNS}_{f}$H, an Algorithm 51 is presented. This algorithm takes $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ as an input, examines the degree of each $\hbox {SNS}_{f}$ hyperedge of H and then determines the degree of hyperedge regularity of the considered $\hbox {SNS}_{f}$H if it is hyperedge regular.

Example 12

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ shown in Fig. 12. Note that the degree of each SN hyperedge in $\mathrm {H}({\mathfrak {z}}_{i})$ is ${\mathfrak {d}}_{{\mathfrak {z}}_{i}}(E_{j})=(1.2,0.6,1.8)$, $i\in \{1,2\}$. Hence, $\mathrm {H}$ is hyperedge regular of degree (1.2, 0.6, 1.8).

Fig. 12

A hyperedge regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Definition 17

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ over $H=(V,E)$ is said to be totally hyperedge regular of degree $(l_{1},l_{2},l_{3})$ if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are totally hyperedge regular of degree $(l_{1},l_{2},l_{3})$, i.e., $\mathfrak {td}_{{\mathfrak {z}}}(E_{j})=(l_{1},l_{2},l_{3})$ $\forall j,{\mathfrak {z}}$.

Example 13

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ shown in Fig. 13. Note that total degree of each SN hyperedge in $\mathrm {H}({\mathfrak {z}}_{i})$ is $\mathfrak {td}_{{\mathfrak {z}}_{i}}(E_{j})=(2.25,0.9,2.7)$, $i\in \{1,2\}$. Hence, $\mathrm {H}$ is totally hyperedge regular of degree (2.25, 0.9, 2.7).

Fig. 13

A totally hyperedge regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Remark 3

A hyperedge regular $\hbox {SNS}_{f}$H may not be totally hyperedge regular.

Figure 12 represents the (1.2, 0.6, 1.8)-hyperedge regular $\hbox {SNS}_{f}$H. Note that in $\mathrm {H}({\mathfrak {z}}_{1})$, $\mathfrak {td}_{{\mathfrak {z}}_{1}}(v_{1}v_{2}v_{3})=(1.8,0.9,2.7)\ne (1.6,0.8,2.4)=\mathfrak {td}_{{\mathfrak {z}}_{1}}(v_{1}v_{6})$. Similarly, in $\mathrm {H}({\mathfrak {z}}_{2})$, $\mathfrak {td}_{{\mathfrak {z}}_{2}}(v_{1}v_{3}v_{5})=(1.8,0.9,2.7)\ne (1.6,0.8,2.4)=\mathfrak {td}_{{\mathfrak {z}}_{2}}(v_{1}v_{2})$. Thus, the considered $\hbox {SNS}_{f}$H is not totally hyperedge regular.

Remark 4

A totally hyperedge regular $\hbox {SNS}_{f}$H may not be hyperedge regular.

Figure 13 represents the (2.25, 0.9, 2.7)-totally hyperedge regular $\hbox {SNS}_{f}$H. Note that in $\mathrm {H}({\mathfrak {z}}_{1})$, ${\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{1}v_{2})=(1.5,0.7,2.0)\ne (1.45,0.8,1.7)={\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{2}v_{4}v_{5})$. Similarly, in $\mathrm {H}({\mathfrak {z}}_{2})$, ${\mathfrak {d}}_{{\mathfrak {z}}_{2}}(v_{1}v_{3}v_{5})=(1.75,0.7,2.1)\ne (1.5,0.6,1.8)={\mathfrak {d}}_{{\mathfrak {z}}_{2}}(v_{1}v_{2} v_{4}v_{5})$. Thus, the considered $\hbox {SNS}_{f}$H is not hyperedge regular.

Theorem 2

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. Suppose that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. Then the following two statements imply one another:

• 1. $\mathrm {H}$ is hyperedge regular $\hbox {SNS}_{f}$H.

• 2. $\mathrm {H}$ is totally hyperedge regular $\hbox {SNS}_{f}$H.

Proof

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H. Also assume that that for all $j, {\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$, where $c_{1}$, $c_{2}$ and $c_{3}$ are constants from the unit closed interval. Further, suppose that $\mathrm {H}$ is hyperedge regular of degree $(k_{1},k_{2},k_{3})$, i.e., ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})=(k_{1},k_{2},k_{3})$. Moreover, the total hyperedge degree of a SN hyperedge $E_{j}$ in an arbitrary SNH $\mathrm {H}({\mathfrak {z}})$ is computed as $\mathfrak {td}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})+({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))=(k_{1},k_{2},k_{3}) +(c_{1},c_{2},c_{3})=(k_{1}+c_{1},k_{2}+c_{2},k_{3}+c_{3})$, $\forall j$. Consequently, $\mathrm {H}$ is totally hyperedge regular $\hbox {SNS}_{f}$H of degree $(k_{1}+c_{1},k_{2}+c_{2},k_{3}+c_{3})$.

For the converse part, suppose that $\mathrm {H}$ is totally hyperedge regular $\hbox {SNS}_{f}$H of degree $(l_{1},l_{2},l_{3})$. Then

$$\begin{aligned} \mathfrak {td}_{{\mathfrak {z}}}(E_{j})= & {} (l_{1},l_{2},l_{3})\ \\ {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})+({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= & {} (l_{1},l_{2},l_{3})\ \\ {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})+(c_{1},c_{2},c_{3})= & {} (l_{1},l_{2},l_{3})\ \\ {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})= & {} (l_{1}-c_{1},l_{2}-c_{2},l_{3}-{c_{3}}) \end{aligned}$$

for all $j, {\mathfrak {z}}$. Hence, $\mathrm {H}$ is $(l_{1}-c_{1},l_{2}-c_{2},l_{3}-{c_{3}})$-hyperedge regular and the proof ends. $\square$

Theorem 3

If $\mathrm {H}=(\mathrm {R},\mathrm {S}, A)$ is hyperedge regular as well as totally hyperedge regular $\hbox {SNS}_{f}$H then for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions.

Proof

Let $\mathrm {H}=(\mathrm {R},\mathrm {S}, A)$ be a hyperedge regular as well as totally hyperedge regular $\hbox {SNS}_{f}$H of degree $(k_{1},k_{2},k_{3})$ and $(l_{1},l_{2},l_{3})$, respectively. It implies that for all parameters ${\mathfrak {z}}$, the SNH $\mathrm {H}({\mathfrak {z}})=(\mathrm {R}({\mathfrak {z}}),\mathrm {S}({\mathfrak {z}}))$ is hyperedge regular and totally hyperedge regular of degree $(k_{1},k_{2},k_{3})$ and $(l_{1},l_{2},l_{3})$, respectively. Consequently,

$$\begin{aligned} {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})+({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= & {} \mathfrak {td}_{{\mathfrak {z}}}(v) \\ (k_{1},k_{2},k_{3})+({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= & {} (l_{1},l_{2},l_{3}) \\ ({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= & {} (l_{1}-k_{1},l_{2}-k_{2},l_{3}-k_{3}) \\ \end{aligned}$$

for all j, ${\mathfrak {z}}$. Hence, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions, as required. $\square$

Definition 18

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S}, A)$ is said to be perfectly hyperedge regular if it is both hyperedge regular as well as totally hyperedge regular $\hbox {SNS}_{f}$H.

Example 14

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ shown in Fig. 14. Note that the degree and total degree of each hyperedge in $\mathrm {H}({\mathfrak {z}}_{i})$ is ${\mathfrak {d}}_{{\mathfrak {z}}_{i}}(E_{j})=(1.0,0.4,1.2)$ and $\mathfrak {td}_{{\mathfrak {z}}_{i}}(E_{j})=(1.5,0.6,1.8)$, respectively, $i\in \{1,2\}$. Hence, $\mathrm {H}$ is perfectly hyperedge regular.

Fig. 14

A perfectly hyperedge regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Theorem 4

If $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is a perfectly hyperedge regular $\hbox {SNS}_{f}$H, then for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions.

Proof

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a perfectly hyperedge regular $\hbox {SNS}_{f}$H. This means that the degree as well as total degree of each hyperedge in SNH $\mathrm {H}({\mathfrak {z}})$ is same, for all ${\mathfrak {z}}$. Consequently, for all j, ${\mathfrak {z}}$, assume that ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})=(k_{1},k_{2},k_{3})$ and $\mathfrak {td}_{{\mathfrak {z}}}(E_{j})=(l_{1},l_{2},l_{3})$ are the degrees and total degrees of hyperedges, respectively. Using the definition of total degree of a SN hyperedge in SNH $\mathrm {H}({\mathfrak {z}})$,

$$\begin{aligned} \mathfrak {td}_{{\mathfrak {z}}}(E_{j})= & {} {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})+({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S} ({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})) \\ (l_{1},l_{2},l_{3})= & {} (k_{1},k_{2},k_{3})+ {\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S} ({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})) \\ {\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S} ({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= & {} (l_{1}-k_{1},l_{2}-k_{2},l_{3}-k_{3}). \end{aligned}$$

Hence, ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. $\square$

Theorem 5

If $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is a hyperedge regular $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions, then $\mathrm {H}$ is a perfectly hyperedge regular $\hbox {SNS}_{f}$H.

Proof

Straightforward $\square$

Definition 19

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is said to be partially hyperedge regular if the underlying crisp hypergraphs of each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are hyperedge regular.

Example 15

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ displayed in Fig. 15. Note that the underlying crisp hypergraphs of both $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are hyperedge regular of degree 2. Thus, $\mathrm {H}$ is partially hyperedge regular $\hbox {SNS}_{f}$H.

Fig. 15

A partially hyperedge regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Definition 20

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is said to be full hyperedge regular if $\mathrm {H}$ is both hyperedge regular as well as partially hyperedge regular $\hbox {SNS}_{f}$H.

Example 16

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ displayed in Fig. 14. Note that it is hyperedge regular of degree (1.0, 0.4, 1.2). Moreover, it is also partially hyperedge regular as the underlying crisp hypergraphs of both $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are hyperedge regular of degree 2. Consequently, it is full hyperedge regular $\hbox {SNS}_{f}$H.

Remark 5

A partially hyperedge regular $\hbox {SNS}_{f}$H may not be hyperedge regular (or full hyperedge regular).

Consider the $\hbox {SNS}_{f}$H $\mathrm {H}$ given in Fig. 15. It is partially hyperedge regular as the underlying crisp hypegraphs of $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are hyperedge regular of degree 2. But $\mathrm {H}$ is not hyperedge regular $\hbox {SNS}_{f}$H as the degrees of all SN hyperedges are not same.

Theorem 6

If $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is a $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. Then $\mathrm {H}$ is hyperedge regular $\hbox {SNS}_{f}$H if and only if $\mathrm {H}$ is partially hyperedge regular $\hbox {SNS}_{f}$H.

Proof

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ such that ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$, $\forall j, {\mathfrak {z}}$. We will prove that $\mathrm {H}$ is a partially hyperedge regular $\hbox {SNS}_{f}$H. For this, assume that $\mathrm {H}$ is hyperedge regular of degree $(k_{1},k_{2},k_{3})$. Using the definition of degree of SN hyperedge $E_{j}$ in SNH $\mathrm {H}({\mathfrak {z}})$,

$$\begin{aligned} {\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})= & {} {\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})-|\varepsilon _{j}| ({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})) \\ (k_{1},k_{2},k_{3})= & {} (c_{1},c_{2},c_{3})d_{{\mathfrak {z}}}(v_{1})+(c_{1},c_{2},c_{3})d_{{\mathfrak {z}}}(v_{2})+...+(c_{1},c_{2},c_{3})d_{{\mathfrak {z}}}(v_{m})- |\varepsilon _{j}|(c_{1},c_{2},c_{3}) \\= & {} (c_{1},c_{2},c_{3})(d_{{\mathfrak {z}}}(v_{1})+d_{{\mathfrak {z}}}(v_{2})+....+d_{{\mathfrak {z}}}(v_{m})-|\varepsilon _{j}|) \\ (k_{1},k_{2},k_{3})= & {} (c_{1},c_{2},c_{3})d_{{\mathfrak {z}}}(E_{j}) \\ d_{{\mathfrak {z}}}(E_{j})= & {} \dfrac{(k_{1},k_{2},k_{3})}{(c_{1},c_{2},c_{3})}. \end{aligned}$$

Since j and ${\mathfrak {z}}$ are arbitrary, this shows that the underlying crisp hypergraphs of all $\mathrm {H}({\mathfrak {z}})$ are hyperedge regular. Thus, $\mathrm {H}$ is a partially hyperedge regular $\hbox {SNS}_{f}$H.

Conversely, let $\mathrm {H}$ be a partially hyperedge regular $\hbox {SNS}_{f}$H. This means that the underlying crisp hypergraphs of $\mathrm {H}({\mathfrak {z}})$ are hyperedge regular of degree k (say), $\forall {\mathfrak {z}}$. Then for all SN hyperedges $E_{j}$, ${\mathfrak {d}}_{\mathfrak {z}}(E_{j})=d_{{\mathfrak {z}}}(E_{j})(c_{1},c_{2},c_{3})=k(c_{1},c_{2},c_{3})$. Hence, $\mathrm {H}$ is a hyperedge regular $\hbox {SNS}_{f}$H. $\square$

Corollary 2

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. If $\mathrm {H}$ is partially hyperedge regular $\hbox {SNS}_{f}$H, then $\mathrm {H}$ is full hyperedge regular $\hbox {SNS}_{f}$H .

Definition 21

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ is said to be neighborly hyperedge irregular if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are neighborly hyperedge irregular, i.e., if degrees ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})$ of all adjacent SN hyperedges $E_{j}$ of $\mathrm {H}({\mathfrak {z}})$ are distinct.

Example 17

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ shown in Fig. 13. Note that degrees of all adjacent SN hyperedges are distinct. So $\mathrm {H}$ is neighborly hyperedge irregular $\hbox {SNS}_{f}$H.

Definition 22

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ is said to be totally neighborly hyperedge irregular if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are totally neighborly hyperedge irregular, i.e., if total degrees $\mathfrak {td}_{{\mathfrak {z}}}(E_{j})$ of all adjacent SN hyperedges $E_{j}$ of $\mathrm {H}({\mathfrak {z}})$ are distinct.

Example 18

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ shown in Fig. 12. Note that total degrees of all adjacent SN hyperedges are distinct. So $\mathrm {H}$ is totally neighborly hyperedge irregular $\hbox {SNS}_{f}$H.

Definition 23

A $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ is said to be perfectly hyperedge irregular if each of its SNHs $\mathrm {H}({\mathfrak {z}})$ are perfectly hyperedge irregular, i.e., if degrees ${\mathfrak {d}}_{{\mathfrak {z}}}(v)$ as well as total degrees $\mathfrak {td}_{{\mathfrak {z}}}(v)$ of all SN hyperedges $E_{j}$ of $\mathrm {H}({\mathfrak {z}})$ are distinct.

Example 19

Consider a $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R}, \mathrm {S}, A)$ shown in Fig. 16.

Note that degrees as well as total degrees of all adjacent SN hyperedges are distinct. So $\mathrm {H}$ is perfectly hyperedge irregular $\hbox {SNS}_{f}$H.

Fig. 16

A perfectly hyperedge irregular $\hbox {SNS}_{f}$H $\mathrm {H}$

6 Relationship between Regularity and Hyperedge Regularity of $\hbox {SNS}_{f}$Hs

Remark 6

Every regular $\hbox {SNS}_{f}$H may not be hyperedge regular.

Fig. 8 represents the (0.9, 0.6, 1.2)-regular $\hbox {SNS}_{f}$H. Note that in $\mathrm {H}({\mathfrak {z}}_{1})$, ${\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{1}v_{4})=(1.2,0.8,1.6)\ne (1.8,1.2,2.4)={\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{2}v_{4}v_{6})$. Similarly, in $\mathrm {H}({\mathfrak {z}}_{2})$, ${\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{4}v_{5})=(1.2,0.8,1.6)\ne (1.8,1.2,2.4)={\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{2}v_{4}v_{6})$. Thus, the considered $\hbox {SNS}_{f}$H is not hyperedge regular.

Remark 7

Every hyperedge regular $\hbox {SNS}_{f}$H may not be regular.

Fig. 14 represents the (1.0, 0.4, 1.2)-hyperedge regular $\hbox {SNS}_{f}$H. Note that in $\mathrm {H}({\mathfrak {z}}_{i})$, ${\mathfrak {d}}_{{\mathfrak {z}}_{i}}(v_{1})=(1.0,0.4,1.2)\ne (0.5,0.2,0.6)={\mathfrak {d}}_{{\mathfrak {z}}_{i}}(v_{2})$, $i\in \{1,2\}$. Thus, the considered $\hbox {SNS}_{f}$H is not regular.

Theorem 7

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a regular $\hbox {SNS}_{f}$H. Then $\mathrm {H}$ is hyperedge regular if and only if for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions.

Proof

Consider a regular $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ of degree $(r_{1},r_{2},r_{3})$. Then in $\mathrm {H}({\mathfrak {z}})$, ${\mathfrak {d}}_{{\mathfrak {z}}}(v)=(r_{1},r_{2},r_{3})$, for all $v, {\mathfrak {z}}$. Further, assume that $\mathrm {H}$ is hyperedge regular of degree ($k_{1},k_{2},k_{3}$). The definition of degree of SN hyperedge $E_{j}$ in SNH is given by ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1}) +{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})-\varepsilon _{j}({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))$. This implies $(k_{1},k_{2},k_{3})=\varepsilon _{j}(r_{1},r_{2},r_{3})-\varepsilon _{j}({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))$, $\forall j,{\mathfrak {z}}$. As a result, $({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}), {\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))=\frac{(\varepsilon _{j}r_{1}-k_{1},\varepsilon _{j}r_{2}-k_{2}, \varepsilon _{j}r_{3}-k_{3})}{\varepsilon _{j}}$. Hence, for all ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions.

Conversely, suppose that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions, i.e., ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$. Using the definition of degree of SN hyperedge $E_{j}$ in SNH, ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})=\varepsilon _{j}(r_{1},r_{2},r_{3})-\varepsilon _{j}(c_{1},c_{2},c_{3})=\varepsilon _{j}(r_{1}-c_{1},r_{2}-c_{2},r_{3}-c_{3})$. Thus, $\mathrm {H}$ is hyperedge regular $\hbox {SNS}_{f}$H. $\square$

Theorem 8

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. If $\mathrm {H}$ is full regular $\hbox {SNS}_{f}$H then $\mathrm {H}$ is full hyperedge regular $\hbox {SNS}_{f}$H.

Proof

Suppose that $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is a $\hbox {SNS}_{f}$H such that ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$, $\forall j, {\mathfrak {z}}$. Let $\mathrm {H}$ and hence $\mathrm {H}({\mathfrak {z}})$ is full regular, for all ${\mathfrak {z}}$. Then for all SN vertices v, ${\mathfrak {d}}_{{\mathfrak {z}}}(v)=(r_{1},r_{2},r_{3})$ and $d_{{\mathfrak {z}}}(v)=r$. Further, the definition of degree of hyperedge in a hypergraph yields $d_{{\mathfrak {z}}}(E_{j})=d_{{\mathfrak {z}}}(v_{1})+d_{{\mathfrak {z}}}(v_{2})+...+d_{{\mathfrak {z}}}(v_{m})-\varepsilon _{j}=\varepsilon _{j}(r-1)$. So the underlying crisp hypergraph of each $\mathrm {H}({\mathfrak {z}})$ is hyperedge regular. Moreover, using the definition of degree of SN hyperedge, we have ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})- \varepsilon _{j}({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= \varepsilon _{j}(r_{1},r_{2},r_{3})-\varepsilon _{j}(c_{1},c_{2},c_{3})=\varepsilon _{j}(r_{1}-c_{1},r_{2}-c_{2},r_{3}-c_{3})$. Hence, $\mathrm {H}$ is hyperedge regular $\hbox {SNS}_{f}$H. Consequently, $\mathrm {H}$ is full hyperedge regular $\hbox {SNS}_{f}$H. $\square$

Remark 8

The converse of above theorem may not be true.

Figure 17 represent a full hyperedge regular $\hbox {SNS}_{f}$H as it is hyperedge regular of degree (0.6, 0.2, 0.7) and the underlying crisp hypergraphs of both $\mathrm {H}({\mathfrak {z}}_{1})$ as well as $\mathrm {H}({\mathfrak {z}}_{2})$ are 1-hyperedge regular hypergraphs. As ${\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{1})=(0.6,0.2,0.7)\ne (1.2,0.4,1.4)={\mathfrak {d}}_{{\mathfrak {z}}_{1}}(v_{2})$ and ${\mathfrak {d}}_{{\mathfrak {z}}_{2}}(v_{1})=(0.6,0.2,0.7)\ne (1.2,0.4,1.4)={\mathfrak {d}}_{{\mathfrak {z}}_{2}}(v_{3})$, so $\mathrm {H}$ is not regular $\hbox {SNS}_{f}$H and hence $\mathrm {H}$ is not full regular $\hbox {SNS}_{f}$H.

Fig. 17

A full hyperedge regular but not full regular $\hbox {SNS}_{f}$H $\mathrm {H}$

Theorem 9

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a regular $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions. If $\mathrm {H}$ is regular $\hbox {SNS}_{f}$H then $\mathrm {H}$ is perfectly hyperedge regular $\hbox {SNS}_{f}$H.

Proof

Consider a regular $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ such that ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$, for all $j, {\mathfrak {z}}$. Further, assume that $\mathrm {H}$ is $(r_{1},r_{2},r_{3})$-regular $\hbox {SNS}_{f}$H. This implies that ${\mathfrak {d}}_{{\mathfrak {z}}}(v)=(r_{1},r_{2},r_{3})$, $\forall v, {\mathfrak {z}}$. Using definition of degree of SN hyperedge $E_{j}$ in $\mathrm {H}({\mathfrak {z}})$, ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})- \varepsilon _{j}({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= \varepsilon _{j}(r_{1},r_{2},r_{3})-\varepsilon _{j}(c_{1},c_{2},c_{3})=\varepsilon _{j}(r_{1}-c_{1},r_{2}-c_{2},r_{3}-c_{3})$, $\forall j$. So, $\mathrm {H}$ is hyperedge regular. Further, using definition of total degree of SN hyperedge $E_{j}$ in $\mathrm {H}({\mathfrak {z}})$, ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})- (\varepsilon _{j}+1)({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= \varepsilon _{j}(r_{1},r_{2},r_{3})-(\varepsilon _{j}+1)(c_{1},c_{2},c_{3})=\varepsilon _{j}(r_{1}-c_{1},r_{2}-c_{2},r_{3}-c_{3})+(c_{1},c_{2},c_{3})$, $\forall j$. So, $\mathrm {H}$ is totally hyperedge regular and hence perfectly hyperedge regular $\hbox {SNS}_{f}$H. $\square$

Remark 9

The converse of above theorem may not be true.

Consider the $\hbox {SNS}_{f}$H given in Fig. 14. It is perfectly hyperedge regular as it is hyperedge regular of degree (1.0, 0.4, 1.2) and totally hyperedge regular of degree (1.5, 0.6, 1.8). But it is not regular because in $\mathrm {H}({\mathfrak {z}}_{i})$, ${\mathfrak {d}}_{{\mathfrak {z}}_{i}}(v_{1})=(1.0,0.4,1.2)\ne (0.5,0.2,0.6)={\mathfrak {d}}_{{\mathfrak {z}}_{i}}(v_{2})$, $i\in \{1,2\}$.

Theorem 10

If $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ is a perfectly hyperedge regular $\hbox {SNS}_{f}$H, then $\mathrm {H}$ is regular if and only if $\mathrm {H}$ is partially regular.

Proof

Use Theorem 4 and Theorem 1 to get the required result. $\square$

Remark 10

A full regular $\hbox {SNS}_{f}$H need not be perfectly hyperedge regular.

Figure 4 represents the full regular $\hbox {SNS}_{f}$H. But it is not perfectly hyperedge regular as it is neither hyperedge regular nor totally hyperedge regular.

Theorem 11

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a perfectly regular $\hbox {SNS}_{f}$H such that for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions then $\mathrm {H}$ is perfectly hyperedge regular $\hbox {SNS}_{f}$H.

Proof

Let $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ be a perfectly regular $\hbox {SNS}_{f}$H. This means that the degree as well as total degree of each vertex in SNH $\mathrm {H}({\mathfrak {z}})$ is same, for all ${\mathfrak {z}}$. Consequently, for all v, ${\mathfrak {z}}$, suppose that ${\mathfrak {d}}_{{\mathfrak {z}}}(v)=(r_{1},r_{2},r_{3})$ and $\mathfrak {td}_{{\mathfrak {z}}}(v)=(s_{1},s_{2},s_{3})$ are the degrees and total degrees of SN vertices, respectively. Also, according to assumption, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{1}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{2}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j})=c_{3}$, for all $j, {\mathfrak {z}}$. Using definition of degree of SN hyperedge $E_{j}$ in $\mathrm {H}({\mathfrak {z}})$, ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})- \varepsilon _{j}({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= \varepsilon _{j}(r_{1},r_{2},r_{3})-\varepsilon _{j}(c_{1},c_{2},c_{3})=\varepsilon _{j}(r_{1}-c_{1},r_{2}-c_{2},r_{3}-c_{3})$, $\forall j$. So, $\mathrm {H}$ is hyperedge regular. Further, using definition of total degree of SN hyperedge $E_{j}$ in $\mathrm {H}({\mathfrak {z}})$, ${\mathfrak {d}}_{{\mathfrak {z}}}(E_{j})={\mathfrak {d}}_{{\mathfrak {z}}}(v_{1})+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{2})+...+{\mathfrak {d}}_{{\mathfrak {z}}}(v_{m})- (\varepsilon _{j}+1)({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))= \varepsilon _{j}(r_{1},r_{2},r_{3})-(\varepsilon _{j}+1)(c_{1},c_{2},c_{3})=\varepsilon _{j}(r_{1}-c_{1},r_{2}-c_{2},r_{3}-c_{3})+(c_{1},c_{2},c_{3})$, $\forall j$. So, $\mathrm {H}$ is totally hyperedge regular and hence perfectly hyperedge regular $\hbox {SNS}_{f}$H. $\square$

Remark 11

A perfectly regular $\hbox {SNS}_{f}$H in which for all parameters ${\mathfrak {z}}$, ${\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}$, ${\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}$ and ${\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}$ are constant functions may not be partial hyperedge regular.

Consider a regular $\hbox {SNS}_{f}$H $\mathrm {H}=(\mathrm {R},\mathrm {S},A)$ shown in Fig. 18. It is regular of degree (1.0, 0.6, 1.4) and totally regular of degree (1.6, 1.0, 2.2). Moreover, $({\mathfrak {t}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {i}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}),{\mathfrak {f}}_{\mathrm {S}({\mathfrak {z}})}(E_{j}))=(0.5,0.3,0.7)$, for all j and $\mathrm {H}({\mathfrak {z}}_{i}),i\in \{1,2\}$. But $\mathrm {H}$ is not partially hyperedge regular as the degrees of hyperedges in the underlying crisp hypergraphs of $\mathrm {H}({\mathfrak {z}}_{i})$ are not distinct.

Fig. 18

A perfectly regular but not partially hyperedge regular $\hbox {SNS}_{f}$H $\mathrm {H}$

7 Application of proposed model to supranational asian bodies

A union of different countries which surrender their sovereignty of some internal affairs to the association is called supranational organization. These organizations are mostly established to avoid disputes and to assist collaborations among nations. It is done by creating international jurisdictions which affect the natives of all member states accordingly. The politics in these organizations is in the form of multinational/international politics. The association possess the governance over territory of its members in specific domains like trade, business, military affairs, etc. The laws made by association may have a negative impact on the authority of nations even then member states permit the organization to do so through treaties to attain the collective benefits.

7.1 Relationships among the members of various asian regional organizations

An international organization governing more than one country is called regional organization if its member states are geopolitical. These are set up to promote cooperation and dialogue for political or economic integration among countries within geopolitical or geographical premises. The reason the Asian region relies on the global mechanisms of governance is that some participant member states lack trust and confidence among them. This deficiency assembles the state and make it self-sufficient over regional countries. Although, increment in the regional awareness has been observed from past few years, it is not easy to create a deep harmony among Asian regional community.

Regional organization strengthens the trust and confidence among the participant countries. Its purpose is to lessen or eradicate the regional terrorism, cross-border crimes and extremism. It also encourages each pair of member states to join hands for collaboration and cooperation. It aims for the economic, social and cultural development of region by providing beneficial means for investment, trade and tourism. Sometimes, it also helps to diminish the poverty for the prosperity and balanced growth of region. It provides the opportunity to interchange scientific, educational, technical as well as technological expertise. Its agendas also include the disaster relief, energy security and financial stability of region. It also facilitates to conduct military exercises on regular basis among its members against external threats and for the improvement of regional stability. All these objectives can be considered as parameters to get the complete knowledge about the relationships among member countries of regional organizations.

Consider 38 Asian countries: Afghanistan, Azerbaijan, Bahrain, Bangladesh, Bhutan, Brunei Darussalam, Cambodia, China, India, Indonesia, Iran, Japan, Kazakhstan, Republic of Korea, Kuwait, Kyrgyzstan, Lao PDR, Malaysia, Maldives, Mongolia, Myanmar, Nepal, Oman, Pakistan, Palestine, Philippines, Qatar, Russia, Saudi Arabia, Singapore, Sri Lanka, Tajikistan, Thailand, Turkey, Turkmenistan, United Arab Emirates, Uzbekistan and Vietnam. There exist a multilateral relationship among the countries which are the members of same organization. Various regional organizations of Asian continent and their member countries are given in Table 1. The official aims of these regional organizations are overlapping. Each of them lays stress over the cooperation and dialogue for the progress, peace, prosperity and development of region. Consider a set $A=\{{\mathfrak {z}}_{1},{\mathfrak {z}}_{2}\}$ of parameters, where ${\mathfrak {z}}_{1}$ and ${\mathfrak {z}}_{2}$, respectively, stand for trade and culture which are the common objectives of the considered organizations for the development of respective regions. The neutrosophic grades of vertices (countries) and hyperedges represent the extent of presence, indeterminacy and absence of the corresponding parametric characterization and the interaction among them for being participant of a regional organization, respectively. The multilateral relationships among countries for being members of organizations with respect to two parameters are represented graphically as $\hbox {SNS}_{f}$H in Fig. 19.

Table 1 Various asian regional organizations

Fig. 19

A $\hbox {SNS}_{f}$H $\mathrm {H}$

For instance, the neutrosophic grade of Japan relative to parameter ${\mathfrak {z}}_{1}$ is (0.5, 0.6, 0.7) that represents the tendency of its trade, indeterminacy in trade and non-trade orientation. Likewise, the neutrosophic grade of SAARC is (0.6, 0.2, 0.4) which shows the overall extent of trade, neutrality and degree of no trade in this regional organization. This application illustrates that one can easily gather and present all the three types of information with the help of the proposed $\hbox {SNS}_{f}$Hs.

8 Conclusions and future directions

Hypergraphs can successfully represent the relationship among any finite number of components of a system. For being the most generalized discrete structure, hypergraphs are used to design various problems of combinatorics in the areas of bioinformatics, engineering, computer science, artificial intelligence and mathematics. Similar to graphs, different hypergraphs like competition hypergraphs, dual hypergraphs, uniform hypergraphs and regular hypergraphs have been studied so far. We have defined the degree of hyperedge as sum of degree of vertices (in hyperedge) minus the number of vertices in that hyperedge. Moreover, if all hyperedges of a hypergraph have same degree k, we get the hyperedge regular hypergraphs. A $\hbox {SNS}_{f}$S generalizes the concept of fuzzy soft set and intuitionistic fuzzy soft set. It expresses information, relative to each parameter, in the form of a triplet $({\mathfrak {t}},{\mathfrak {i}},{\mathfrak {f}})$, where each ${\mathfrak {t}}$, ${\mathfrak {i}}$ and ${\mathfrak {f}}$ take the numerical values from [0, 1] interval and represent the truth, indeterminacy and falsity of a statement, respectively, with no constraints. In this study, we have presented hypergraphs in $\hbox {SNS}_{f}$ environment. Primarily, the concept of regularity and hyperedge regularity of hypergraphs has been discussed. Afterwards, the regular as well as hyperedge regular $\hbox {SNS}_{f}$Hs have been provided with examples and algorithms. The perfect regularity as well as irregularity for both vertices and hyperedges of $\hbox {SNS}_{f}$Hs has been illustrated. Moreover, we have also established some relationships between regular and hyperedge regular $\hbox {SNS}_{f}$Hs. In the end, we have discussed an application of $\hbox {SNS}_{f}$Hs to illustrate their applicability in real-world systems. We plan to extend our research in following directions: (1) Complex single-valued neutrosophic soft hypergraphs (2) Single-valued neutrosophic soft competition hypergraphs and (3) Regularity of q-rung picture fuzzy soft hypergraphs.