1 Introduction

Rayleigh–Bénard convection in Newtonian liquids is a well studied subject (see Refs.  [18, 27, 47, 69]). In the last few decades there have been a number of studies on thermal convection in a horizontal layer of fluid in the presence of internal heat source. In their studies involving a heat source, Roberts  [50], Thirlby  [70], McKenzie et al.  [41] , Tveitereid and Pahn  [73], and Clever  [14] assumed the internal heat source Q to be uniform. Riahi and Hsui  [49] investigated nonlinear double diffusive convection with local heat source and solute source. Krishnamurti  [37] showed that convection due to the selective absorption of radiation in a viscous liquid can be modeled using an internal heat source.

Due to poor thermal conductivity of liquids, their utility as coolants has not been satisfactory. Enhancement of heat transfer is an important goal in many thermal engineering systems involving liquids as a working media, e.g., heat exchanger systems. Heat transfer enhancement has been attempted in such problems by placement of fins, ventilators and other mechanisms.

In the last several decades attempts have been made to have micron-sized particles in the carrier fluid and such suspensions have been modeled as couple-stress fluids or micropolar fluids or non-Newtonian fluids and there are several works concerning Rayleigh–Benard convection in such fluids ([6, 8, 17, 24, 28, 30, 40, 42, 46, 51,52,53, 57,58,59,60,61, 63, 64] and references therein). The micron-sized particles failed as heat transfer enhancing effects since agglomeration of particles let to settling and abrasion of the surfaces on which they settled.

One other innovative way of heat transfer enhancement is the use of nanoparticles in carrier liquids. The enhancement here is due to the high thermal conductivity of nanoparticles. This concept of using nanoparticles to enhance heat transfer was first introduced by Choi [13]. Many researchers [16, 32, 76, 77] have since published review papers concerning nanoliquids.

To study the heat transfer enhancement by nanoliquids, the following two models are currently available:

  1. (i)

    Buongiorno two-phase model [11],

  2. (ii)

    Modified Buongiorno two-phase model [54, 55] and

  3. (iii)

    Khanafer-Vafai-Lightstone single-phase model [33, 62, 66].

In the single-phase model, particles are in thermal equilibrium with the carrier liquid and in the case of two-phase model this is not so.

Xuan and Roetzel [78] were the first to indicate a mechanism for heat transfer in nanoliquids. Buongiorno [11] conducted an extensive study of convective transport in nanoliquids and explained as to how and why heat transfer enhancement is observed during convective situations. Ruling out dispersion, turbulence and particle rotation as significant agents for heat transfer enhancements, Buongiorno [11] suggested a new model based on the mechanics of nanoparticles/carrier-liquid in terms of their relative velocity. He observed that the absolute velocity of nanoparticles can be taken as the sum total of the carrier-liquid velocity and a slip velocity. He considered seven slip mechanisms- inertia, Brownian diffusion, thermophoresis, diffusophoresis, Magnus effects, liquid drainage and gravity settling in the study. He studied each one of these and concluded that in the absence of turbulent effects, Brownian diffusion and thermophoresis would dominate. Based on these two effects, he derived the conservation equations. With the help of the transport equations of Buongiorno [11], Tzou [74, 75] studied the onset of convection in a horizontal layer of a nanoliquid heated uniformly from below and found that as a result of Brownian motion and thermophoresis of nanoparticles, the critical Rayleigh number was found to be much lower, by one to two orders of magnitude, than that of an ordinary liquid. Kim et al. [34,35,36] also investigated the onset of convection in a horizontal nanoliquid layer and modified the three quantities, namely the thermal expansion coefficient, the thermal diffusivity and the kinematic viscosity that appear in the definition of the Rayleigh number. The role of thermophoresis in laminar natural convection in a Rayleigh–Bénard cell filled with a water-based CuO nanoliquid was studied by Eslamian [20]. Apart from the papers discussed above, there are other related works on this problem ([3, 43, 79, 80]). Nield and Kuznetsov [44] theoretically investigated natural convection induced by a heat source in nanoliquids and this work is similar to the experimental investigation of Tritton and Zarraga [72] in the case of Newtonian liquids without nanoparticles. Unlike previous works using Buongiorno model, the eigenvalue (control parameter) in this problem is internal Rayleigh number.

All the works discussed earlier are based on the Buongiorno model with both the liquid and solid phases playing a distinct role in the heat transfer process. Khanafer et al. [33] has argued in favour of modelling nanoliquids as a single-phase model on the reason that as of now there is no concrete theoretical ground on which enhanced heat transfer in nanoliquids can be explained. It thus becomes clear that in seeking to explain enhanced heat transfer, an alternate way of studying thermoconvective motion in nanoliquids in the form a single-phase model can be quite naturally considered. In this model the liquid and solid phases are in local thermal equilibrium and flow with the same local velocity. This signifies that the nanoparticles and the liquid particles have similar properties so far as flow is concerned but have different thermal properties. Thus in this model nanoliquid behaves more as a liquid rather than as a solid-liquid mixture as assumed in the conventional two-phase model. Since in the single-phase model, properties of nanoliquids have contributions from the solid and liquid phases, the density, thermal expansion coefficient, specific heat, thermal conductivity of the two phases, viscosity of carrier liquid and nanoparticle concentration contribute to the nanoliquid properties. In addition, based on the experimental observation that heat transport is enhanced only when nanoparticle concentration is dilute, nanoparticle volume fractions have to be assumed quite small in this model. Using the Khanafer-Vafai-Lightstone single-phase model, Tiwari and Das [71] investigated natural convection of nanoliquids in an enclosure with heating and cooling at the vertical plates. Simo et al. [67] studied Rayleigh–Bénard convection in a cube with perfectly conducting lateral walls using the Galerkin spectral method. They analysed the stability properties and bifurcations of fixed point and also discussed about chaotic motions. Elhajjar et al. [19] made investigation of Rayleigh–Bénard convection in three water-based nanoliquids in a square enclosure. They incorrectly concluded that nanoparticles stabilize the system. This discrepancy in the results of their paper is due to the improper expressions of equation of state, thermal expansion coefficient and specific heat. Corcione [15] in his paper on Rayleigh–Bénard convection of nanoliquids assumed a single-phase model for nanoliquid. In this paper two empirical equations are adopted from earlier works ([15, 33, 71]) for the evaluation of the effective value of nanoliquid thermal conductivity and dynamic viscosity based on a wide variety of experimental data reported in the literature. The other effective properties are evaluated by the traditional mixing theory. The effect of nanoparticles on chaotic convection in a liquid layer heated from below was studied by Jawdat et al. [31]. Park [45] investigated Rayleigh–Bénard convection of nanoliquids using a single-phase continuum model but with thermophysical properties assumed to be that of nanoliquids rather than that of carrier liquids. The study predicts enhancement of heat transfer. Aghighi et al. [4] obtained a parametric solution for the Rayleigh–Bénard convection problem involving nanoliquids and showed how results for this problem can be obtained from the results of a Newtonian liquid without nanoparticles. The model predictions are thermodynamically correct due to the correct assumptions on thermophysical quantities. The choice of phenomenological relations for thermal consuctivity and dynamic viscosity and the use of results from the mixture theory other thermophysical quantities was scientifically done and thermodynamically correct. Apart from the above works on Rayleigh–Bénard convection, natural convection of nanoliquids inside horizontal cylinder heated from one end and cooled from other has been studied by Putra et al. [48]. A good account of many aspects of enhanced heat transfer in nanoliquids is discussed in the books by Bergman et al. [5] and Bianco et al. [9]. In the absence of experimental works on heat transport by Rayleigh–Bénard convection in nanoliquids, it remains to be seen whether the single-phase or the two-phase model is best suited as a mathematical model for natural convection in nanoliquids. The present paper concentrates on the study of Rayleigh–Bénard convection in nanoliquids in the presence of volumetric heat source. The single-phase model is used for modelling the nanoliquid. This paper is written in the spirit of Magyari [39] whose comments on single-phase model compelled us to leave out many details in the problem. Twenty nanoliquids are considered for investigation.

2 Mathematical formulation

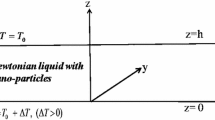
Figure 1 shows an infinite extent horizontal nanoliquid layer of thickness, h, whose lower and upper bounding planes are at \(z = 0\) and \(z = h\) respectively.

Fig. 1
figure 1

Physical configuration

Full size image

The nanoliquid is assumed to be a viscous, Newtonian liquid. The upper and lower boundaries are maintained at constant temperatures \(T_0\) and \(T_0 + \varDelta T\) (\(\varDelta T > 0\) ) respectively. For mathematical tractability we confine ourselves to two-dimensional longitudinal rolls so that all physical quantities are independent of y, a horizontal co-ordinate. The boundaries are assumed to be stress-free and isothermal. In this paper we assume the dynamic coefficient of viscosity of the nanoliquid, \(\mu _{nl}\) , and thermal diffusivity of the nanoliquid, \(\alpha _{nl}\), to be constants. However, these vary with the nanoparticle volume fraction, \(\chi \), the thermal conductivity of the carrier liquid, \(k_l\), the thermal conductivity of the nanoparticle, \(k_{np}\), the density of the carrier liquid, \(\rho _l\), the density of the nanoparticle, \(\rho _{np}\), the heat capacity of the carrier liquid, \((Cp)_l\), and the heat capacity of the nanoparticle, \((Cp)_{np}\). We assume that the Oberbeck-Boussinesq approximation is valid and that there is thermal equilibrium between the Newtonian carrier liquid and the nanoparticles. Before actually writing down the governing equations that are used in the present study, we note that we are essentially using the classical conservation laws of mass, linear momentum and energy, but with thermophysical properties modified due to the presence of nanoparticles (Khanafer et al. [33], Tiwari and Das [71]).

The governing equations describing the Rayleigh–Bénard instability situation in a Newtonian nanoliquid with constant viscosity adopted in the study are:

Conservation of Mass

$$\begin{aligned} \nabla \cdot {\mathbf {q}} = 0, \end{aligned}$$
(1)

Conservation of Linear Momentum

$$\begin{aligned} \rho _{nl}\left[ \dfrac{\partial \mathbf {q}}{\partial t}+(\mathbf {q} . \nabla ) \mathbf {q}\right] =-\nabla p+\mu _{nl} \nabla ^2 \mathbf {q} +\left[ \rho _{nl}-\left( \rho \beta \right) _{nl}(T-T_0)\right] \mathbf {g} , \end{aligned}$$
(2)

Conservation of Energy with temperature-dependent heat source

$$\begin{aligned} \dfrac{\partial T}{\partial t}+(\mathbf {q} . \nabla )T = \alpha _{nl} \nabla ^2 T+Q(T-T_{0}), \end{aligned}$$
(3)

where the nanoliquid properties are obtained from either phenomenological laws or mixture theory as given below:

  1. a.

    Phenomenological laws

    $$\begin{aligned} \dfrac{\mu _{nl}}{\mu _l}= & {} \dfrac{1}{(1-\chi )^{2.5}} \quad \text { (Brinkman model)}\, [10], \end{aligned}$$
    (4)
    $$\begin{aligned} \dfrac{k_{nl}}{k_l}= & {} \frac{\left( \frac{k_{np}}{k_l}+2\right) -2\chi \left( 1-\dfrac{k_{np}}{k_l}\right) }{\left( \dfrac{k_{np}}{k_l}+2\right) +\chi \left( 1-\dfrac{k_{np}}{k_l}\right) } \text { (Hamilton--Crosser model for stagnant conditions )} \, [29].\nonumber \\ \end{aligned}$$
    (5)
  2. b.

    Mixture theory

    $$\begin{aligned} \left. \begin{aligned} \alpha _{nl}=\dfrac{k_{nl}}{(\rho C_p)_{nl}}\\ \dfrac{\rho _{nl}}{\rho _{l}}=(1-\chi )+\chi \dfrac{\rho _{np}}{\rho _{l}}\\ \dfrac{(\rho C_p)_{nl}}{(\rho C_p)_l}=(1-\chi )+\chi \dfrac{(\rho C_p)_{np}}{(\rho C_p)_l}\\ \dfrac{(\rho \beta )_{nl}}{(\rho \beta )_l}=(1-\chi )+\chi \dfrac{(\rho \beta )_{np}}{(\rho \beta )_l}\\ \end{aligned} \right\} . \end{aligned}$$
    (6)

The specific heat and thermal expansion coefficient of nanoliquids are calculated using the following expressions:

$$\begin{aligned} (Cp)_{nl}=\dfrac{(\rho Cp)_{nl}}{\rho _{nl}},\;\;\beta _{nl}=\dfrac{(\rho \beta )_{nl}}{\rho _{nl}}. \end{aligned}$$
(7)

Since there are two phases involved in the system and the present study subscribes to the single-phase model description, thermophysical quantities of the nanoliquids are modelled as is normally done in the case of mixtures. Hence the use of phenomenolgical laws and mixture theory is used to calculate the thermophysical proeprties. In the Eqs. (1)–(6), \(\mathbf {q}=(u, 0, w)\) is the velocity vector, u is the horizontal component of velocity, w is the vertical component of velocity, x is the horizontal coordinate, z is the vertical coordinate, \(\rho _{nl}\) is the density of the nanoliquid at \(T=T_0\), t is the time, p is the hydrostatic pressure, \(\mu _{nl}\) is the dynamic coefficient of viscosity of the nanoliquid, \(\beta _{nl}\) is the coefficient of thermal expansion of the nanoliquid, T is the dimensional temperature, \(\mathbf {g}=(0,0,-g)\) is the acceleration due to gravity, \(\alpha _{nl}\) is the thermal diffusivity of the nanoliquid, \(\mu _{l}\) is the dynamic coefficient of viscosity of the carrier liquid, \(k_{nl}\) is the thermal conductivity of the nanoliquid, \((Cp)_{nl}\) is the heat capacity of the nanoliquid, \(\beta _{l}\) is the coefficient of thermal expansion of the carrier liquid and \(\beta _{np}\) is the coefficient of thermal expansion of the nanoparticle.

The expression for effective viscosity and effective thermal conductivity is applicable for spherical-particles suspended in a carrier liquid. These models are discussed in detail by Khanafer et. al [33]. Taking the velocity, temperature and density fields in the quiescent basic state to be \(q_b (z)=(0,0,0)\), \(T_b (z)\) and \(\rho _b (z)\), we obtain the quiescent state solution in the form:

$$\begin{aligned} \left. \begin{array}{r} q_b =(0,0)\\ T_b = T_0+\varDelta T f(\frac{z}{h})\\ p_b=-\int \rho _b (\frac{z}{h})g dz +C^* \end{array} \right\} , \end{aligned}$$
(8)

where \(f\left( \dfrac{z}{h}\right) =\dfrac{\sin \left[ \sqrt{R_{I_{nl}}}\left( 1-\dfrac{z}{h}\right) \right] }{\sin [\sqrt{R_{I_{nl}}}]}\) and \(C^*\) is the constant of integration. On the quiescent basic state we superimpose perturbations in the form:

$$\begin{aligned} \left. \begin{array}{c} \mathbf {q} = \mathbf {q}_b+\mathbf {q}'\\ T = T_b+T'\\ p = p_b+p' \end{array} \right\} , \end{aligned}$$
(9)

where the prime indicates a perturbed quantity. Since we consider only two-dimensional disturbances, we introduce stream function as follows:

$$\begin{aligned} u'=-\dfrac{\partial \psi '}{\partial z}, w'=\dfrac{\partial \psi '}{\partial x}. \end{aligned}$$
(10)

These satisfy Eq. (1) in the perturbed state. Eliminating the pressure in Eq. (2), incorporating the quiescent state solution and non-dimensionalizing the resulting equations as well as Eq. (3) using the following definition

$$\begin{aligned} (X,Z)=\left( \dfrac{x}{h},\dfrac{z}{h}\right) , \tau =\dfrac{\alpha _l}{h^2}t, \varPsi =\frac{\psi '}{\alpha _l}, \varTheta =\frac{T '}{\varDelta T}, \end{aligned}$$
(11)

we obtain the dimensionless form of the vorticity and heat transport equations as follows (see Siddheshwar and Titus [65], Siddheshwar and Meenakshi [56]) :

$$\begin{aligned} \dfrac{1}{Pr_{nl}}\dfrac{\partial }{\partial \tau }\left( \nabla ^2\varPsi \right) =a_1\nabla ^4 \varPsi +a_1^2R_{nl} \dfrac{\partial \varTheta }{\partial X} - \dfrac{1}{Pr_{nl}} J(\varPsi ,\nabla ^2 \varPsi ), \end{aligned}$$
(12)
$$\begin{aligned} \dfrac{\partial \varTheta }{\partial \tau }=\dfrac{\partial \varPsi }{\partial X} \left[ 1+2\sum _{n=1}^{\infty }\dfrac{R_{I_{nl}}}{R_{I_{nl}}-n^2\pi ^2}\cos ( n\pi Z)\right] + a_1 \nabla ^2 \varTheta + R_{I_{nl}}a_1\varTheta - J(\varPsi , \varTheta ), \end{aligned}$$
(13)

where X is the non-dimensional horizontal coordinate, Z is the non-dimensional vertical coordinate, \(\tau \) is non-dimensional time, \(\varPsi \) is the non-dimensional stream function, \(\varTheta \) non-dimensional temperature and

$$\begin{aligned} \left. \begin{aligned} a_1=\dfrac{\left[ 1-\dfrac{3\chi \left( 1-\dfrac{k_{np}}{k_l}\right) }{\left( \dfrac{k_{np}}{k_l}+2\right) +\chi \left( 1-\dfrac{k_{np}}{k_l}\right) }\right] }{(1-\chi )+\chi \dfrac{(\rho C_p)_{np}}{(\rho C_p)_{l}}} \quad (\text {nanoparticle-related particle}),\\ Pr_{nl}=\dfrac{\mu _{nl}}{\rho _{nl}\alpha _{nl}} \quad (\text {nanoliquid Prandtl number}),\\ R_{nl}=\dfrac{(\rho \beta )_{nl}g\varDelta Th^3}{\alpha _{nl}\mu _{nl}}\quad (\text {Thermal Rayleigh number}),\\ R_{I_{nl}}=\dfrac{Qh^2}{\alpha _{nl}} \quad (\text {Internal Rayleigh number}),\\ J(\varPsi ,...)=\left| \begin{array}{cc} \dfrac{\partial \varPsi }{\partial X} &{} \dfrac{\partial \varPsi }{\partial Z} \\ \\ \dfrac{\partial }{\partial X}(...) &{} \dfrac{\partial }{\partial Z}(...) \\ \end{array} \right| . \end{aligned} \right\} .\nonumber \\ \end{aligned}$$
(14)

Equations (12) and (13) are solved using the boundary conditions

$$\begin{aligned} \varPsi= & {} \frac{\partial ^2}{\partial Z^2}\left( \dfrac{\partial \varPsi }{\partial X}\right) = \varTheta = 0 \quad \mathtt {at} \quad Z = 0,1, \nonumber \\ \varPsi \left( X\pm \dfrac{2\pi }{\pi \kappa _c},Z\right)= & {} \varPsi (X,Z), \varTheta \left( X\pm \dfrac{2\pi }{\pi \kappa _c},Z\right) =\varTheta (X,Z), \end{aligned}$$
(15)

where \(\pi \kappa _c\) is the critical wave number. In the X-direction one has periodicity conditions on \(\varPsi \) and \(\varTheta \). In the next section we discuss the linear stability analysis which is of great utility in the local nonlinear stability analysis to be discussed further on.

3 Linear stability analysis

It can be easily proved that the principle of exchange of stabilities (PES) is valid and hence we consider only the marginal stationary state. In order to make a linear stability analysis we consider the linear and steady-state version of Eqs. (12) and (13) and assume the solutions to be periodic waves of the form (Chandrasekhar [12])

$$\begin{aligned} \varPsi (X,Z)= & {} \dfrac{\sqrt{2}}{\pi ^2\kappa }\left( \eta _1^2-R_{I_{nl}}\right) \varPsi _0\sin (\pi \kappa X)\sin \pi Z, \end{aligned}$$
(16)
$$\begin{aligned} \varTheta (X,Z)= & {} \dfrac{4\sqrt{2}\pi }{r_{nl}\left( 4\pi ^2-R_{I_{nl}}\right) }\varTheta _0\cos (\pi \kappa X)\sin (\pi Z), \end{aligned}$$
(17)

where

$$\begin{aligned} r_{nl}=\dfrac{R_{nl}}{R_{nlc}}, \end{aligned}$$
(18)

and the critical Rayleigh number, \(R_{nlc}\), is:

$$\begin{aligned} R_{nlc}= & {} \dfrac{\eta _1^6}{\pi ^2\kappa _c^2}\left[ 1-\dfrac{R_{I_{nl}}}{\eta _1^2}\right] \left[ 1-\dfrac{R_{I_{nl}}}{4\pi ^2}\right] , \end{aligned}$$
(19)

with the critical wave number \(\kappa _c^2=\dfrac{-R_{I_{nl_{s}}}+\sqrt{R_{I_{nl_{s}}}^2+8R_{I_{nl_{s}}}}}{4}\), \(R_{I_{nl_{s}}}=1-\dfrac{R_{I_{nl}}}{\pi ^2}\) and \(\eta _1^2=\pi ^2 (\kappa _c^2+1).\)

The normal mode solutions (16) and (17) satisfy the boundary conditions in Eq. (15). In Eqs. (16) and (17), \(\pi \kappa \) is the horizontal wave number. The quantities \(\varPsi _0\) and \(\varTheta _0\) are, respectively, amplitudes of the stream function and temperature. It is apt to mention here that in the case of nanochannels the size of the cells may vary in the z-direction also (Sofos et al. [68]). Since we are considering macro channels this aspect does not play a role in the results of this paper.

The linear theory predicts only the condition for the onset of convection and is silent about the heat transport. We now embark on a weakly non-linear analysis by means of a truncated representation of Fourier series for velocity and temperature fields to find the effect of various parameters on steady finite amplitude convection and to know the amount of heat transfer. Specifically we consider three modes for studying nonlinear instability. We note that the results obtained from such an analysis can serve as starting values while solving a more general nonlinear convection problem. We now present a weakly nonlinear analysis of the problem for three modes.

4 Local nonlinear stability analysis and heat transport with minimal modes (three modes)

A local nonlinear stability analysis is reliant on the description of quantities in the nonlinear convective regime in terms of quantities associated with the linear regime that is seen at onset of convection. We may thus use the double Fourier series to make a weakly nonlinear study of the system as done by Lorenz [38] in his pioneering work on atmospheric convection. It is impossible or rather difficult to make a study using a large number of modes. Based on the findings of Siddheshwar and Meenakshi [56], we take a stand that the most minimal number of modes in the Fourier expansion captures all essential features of the full system of Eqs. (12) and (13). So we consider only three modes in the study.

The first effect of nonlinearity is to distort the temperature field through the interaction of \(\varPsi \) and \(\varTheta \). The distortion of temperature field will correspond to a change in the horizontal mean, i.e., a component of the form \(sin (2 \pi z)\) will be generated. A minimal double Fourier series which describes the steady finite amplitude convection in a Newtonian nanoliquid is given by

$$\begin{aligned}&\displaystyle \varPsi (X,Z,\tau ) =\frac{\sqrt{2}}{\pi ^2\kappa _c}\left( \eta _1^2-R_{I_{nl}}\right) A(\tau )\sin (\pi \kappa _c X)\sin \pi Z, \end{aligned}$$
(20)
$$\begin{aligned}&\displaystyle \varTheta (X,Z,\tau ) =\frac{4\pi }{r_{nl}\left( 4\pi ^2-R_{I_{nl}}\right) }\left[ \sqrt{2}B(\tau )\cos (\pi \kappa _c X)\sin (\pi Z)-C(\tau )\sin (2\pi Z)\right] .\nonumber \\ \end{aligned}$$
(21)

4.1 Lorenz model

Substituting Eqs. (20) and (21) into Eqs. (12) and (13) and adopting the standard orthogonalization procedure for the Galerkin expansion, the following system of nonlinear equations is obtained:

$$\begin{aligned} \dfrac{dA}{d\tau _1}= & {} a_1Pr_{nl}[a_1B-A], \end{aligned}$$
(22)
$$\begin{aligned} \dfrac{dB}{d\tau _1}= & {} (1-R_{I_{nl}}\eta _1^{-2})\left[ r_{nl}A-a_1B-AC\right] , \end{aligned}$$
(23)
$$\begin{aligned} \dfrac{dC}{d\tau _1}= & {} (1-R_{I_{nl}}\eta _1^{-2})\left[ AB-a_1bC\right] , \end{aligned}$$
(24)

where

$$\begin{aligned} \tau _1= \eta _1^2\tau , \;\; b=\dfrac{4 \pi ^2}{\eta _1^2}\left[ \dfrac{1-\dfrac{R_{I_{nl}}}{4\pi ^2}}{1-\frac{R_{I_{nl}}}{\eta _1^2}}\right] , \end{aligned}$$
(25)

and \(A_1, B_1\) are amplitudes in normal mode solution and C is the amplitude of convective mode. It is well known in the problems as these that the trajectories of the solution of the Lorenz model in phase-space remain within a bounded region. In the next section we show that this trapping region is, in fact, an ellipsoid for the three modes.

4.2 Trapping region

Multiplying Eqs. (22) and (23) by A and B respectively, we get

$$\begin{aligned} A\dfrac{dA}{d\tau _1}= & {} -a_1Pr_{nl}A^2+a_1^2Pr_{nl}AB, \end{aligned}$$
(26)
$$\begin{aligned} B\dfrac{dB}{d\tau _1}= & {} (1-R_{I_{nl}}\eta _1^{-2})\left[ r_{nl}AB-a_1B^2-ABC\right] . \end{aligned}$$
(27)

Multiplying Eq. (26) by \((1-R_{I_{nl}}\eta _1^{-2})\) and adding the resultant equation with Eq. (27), we get

$$\begin{aligned} (1-R_{I_{nl}}\eta _1^{-2})A\dfrac{dA}{d\tau _1}+_1\dfrac{dB}{d\tau _1}= & {} (1-R_{I_{nl}}\eta _1^{-2})(-a_1Pr_{nl}A^2+a_1^2Pr_{nl}AB)\nonumber \\&+\,(1-R_{I_{nl}}\eta _1^{-2})\left[ r_{nl}AB-a_1B^2-ABC\right] .\qquad \quad \end{aligned}$$
(28)

To get an equation of an ellipsoid, we have to eliminate the terms involving AB and ABC from Eqs. (24) and (28) . To that end we multiply Eq. (24) by \((C-a_1^2Pr_{nl}-r_{nl})\) and add the resulting equation to Eq. (28) to get

$$\begin{aligned} \dfrac{dE}{d\tau _1}=(1-R_{I_{nl}}\eta _1^{-2})A\dfrac{dA}{d\tau _1}+B\dfrac{dB}{d\tau _1} +(C-a_1^2Pr_{nl}-r_{nl})\dfrac{d}{d\tau _1}\left( C-a_1^2Pr_{nl}-r_{nl}\right) . \end{aligned}$$
(29)

Integrating the above equation, we get the trapping region in the form

$$\begin{aligned} E=\dfrac{1}{2}\left[ (1-R_{I_{nl}}\eta _1^{-2})A^2+B^2+(C-a_1^2Pr_{nl}-r_{nl})^2\right] . \end{aligned}$$
(30)

From Eq. (30), we infer that the post-onset trajectories of the Lorenz system (22)–(24) enter and stay within an ellipsoid given by

$$\begin{aligned} A^2+\dfrac{B^2}{\left( 1-R_{I_{nl}}\eta _1^{-2}\right) }+\dfrac{\left( C-a_1^2Pr_{nl}-r_{nl}\right) ^2}{\left( 1-R_{I_{nl}}\eta _1^{-2}\right) } =\dfrac{\left( \sqrt{2}\right) ^2}{\left( 1-R_{I_{nl}}\eta _1^{-2}\right) }. \end{aligned}$$
(31)

The Lorenz model in Eqs. (22)–(24) is, in general, not analytically tractable. However the system of nonlinear ODEs may be solved in a semi-analytical, semi-numerical way using the Adomian decomposition method ([1, 2, 21,22,23]). We now move on to derive the analytically tractable Ginzburg–Landau equation from the tri-modal Lorenz model.

4.3 Ginzburg–Landau amplitude equation

From the Eqs. (22) and (23), B and C can be obtained in terms of A as:

$$\begin{aligned} B= & {} \dfrac{1}{a_1}\left[ \dfrac{1}{a_1Pr_{nl}}\dfrac{dA}{d\tau _1}+A\right] , \end{aligned}$$
(32)
$$\begin{aligned} C= & {} \dfrac{1}{A}\left[ (r_{nl}-1)A-\left( \dfrac{1}{Pr_{nl}a_1}+\dfrac{1}{a_1(1-R_{I_{nl}}\eta _1^{-2})}\right) \dfrac{dA}{d\tau _1}\right. \nonumber \\&\left. -\dfrac{1}{Pr_{nl}a_1^2 (1-R_{I_{nl}}\eta _1^{-2})}\dfrac{d^2A}{d\tau _1^2}\right] . \end{aligned}$$
(33)

Substituting Eqs. (32) and (33) in (24), we get a third order differential equation in A. Neglecting terms of the type \(\left( \dfrac{dA}{d\tau _1}\right) ^2, \left( \dfrac{dA}{d\tau _1}\right) \left( \dfrac{d^2A}{d\tau _1^2}\right) ,\) and \(A\left( \dfrac{d^2A}{d\tau _1^2}\right) \), we get the Ginzburg–Landau model in the form

$$\begin{aligned} \dfrac{dA}{d\tau _1}=\left( \dfrac{Pr_{nl}}{(1-R_{I_{nl}}\eta _1^{-2})+Pr_{nl}}\right) \left( \dfrac{1-R_{I_{nl}}\eta _1^{-2}}{b}\right) \left[ a_1b(r_{nl}-1)A-\dfrac{1}{a_1}A^3\right] .\quad \end{aligned}$$
(34)

Eq. (34) is a Bernoulli equation in A which can be solved using an initial condition \(A(0)=A_0\) and the solution is given by

$$\begin{aligned} A(\tau _1)=\dfrac{A_0a_1\sqrt{b(r_{nl}-1)}e^{\frac{Pr_{nl}(1-R_{I_{nl}}\eta _1^{-2})a_1(r_{nl}-1)\tau _1}{Pr_{nl}+1-R_{I_{nl}}\eta _1^{-2}}}}{\sqrt{A_0^2e^{\frac{2Pr_{nl}(1-R_{I_{nl}}\eta _1^{-2})a_1(r_{nl}-1)\tau _1}{Pr_{nl}+1-R_{I_{nl}}\eta _1^{-2}}}+a_1^2b(r_{nl}-1)-A_{0}^{2}}}. \end{aligned}$$
(35)

It is one of the intentions of the paper to study the pre-onset and post-onset critical points of the tri-modal Lorenz model. The same is discussed below.

4.4 Steady finite amplitude convection

We note that the nonlinear system of autonomous differential equations (22)–(24) is not amenable to analytical treatment for the general time-dependent variables and it is to be solved by means of a numerical method. However, in the case of steady motions, these equations can be solved in closed form.

The solution of the system (22)–(24) with left hand sides omitted is

$$\begin{aligned} (0,0,0), (\pm a_1\sqrt{b(r_{nl}-1)},\pm \sqrt{b(r_{nl}-1)},(r_{nl}-1)). \end{aligned}$$
(36)

These are the post-onset critical points of the dynamical system (22)–(24). The solution \(A=B=C=0\) of the Lorenz model represents the state of no convection and non-zero values represent the convective state. In the next section we quantify the heat transport in terms of the Nusselt number within a wave-length distance in the horizontal direction at the lower boundary.

4.5 Nano-particle-enhanced heat transport

The horizontally-averaged Nusselt number, \(Nu_{nl}\), for the stationary mode of convection (the preferred mode in this problem) in a nanoliquid is given by

$$\begin{aligned} Nu_{nl}= & {} \dfrac{\text {Heat transport by (conduction+convection)}}{\text {Heat transport by conduction}}, \end{aligned}$$
(37)
$$\begin{aligned}= & {} 1+\dfrac{k_{nl}}{k_l}\left[ \dfrac{\int _{0}^{\frac{2}{\kappa _c}}\left( \dfrac{\partial \varTheta }{\partial Z}\right) dX}{\int _{0}^{\frac{2}{\kappa _c}}\left( \dfrac{d\varTheta _b}{dZ}\right) dX}\right] _{Z=0}, \end{aligned}$$
(38)

where \(\varTheta _b=\dfrac{T_b-T_0}{\varDelta T}\).

In the conduction state there will be equilibrium between the liquid and solid phases and thus thermal conductivity can be taken to be that of the liquid phase. In the convective state the thermal conductivity of the nanoliquid is to be assumed [39]. It is on this reason that the ratio \(\dfrac{k_{nl}}{k_l}\) appears in the expression for the Nusselt number in Eq. (38).

Substituting Eqs. (8) and (21) in Eq. (38) and completing the integration, we get

$$\begin{aligned} Nu_{nl}(\tau _1)=1+\dfrac{2}{r_{nl}\left( 1-\dfrac{R_{I_{nl}}}{4\pi ^2}\right) }\dfrac{\tan {\sqrt{R_{I_{nl}}}}}{\sqrt{R_{I_{nl}}}}\left[ a_1a_2\right] C(\tau _1), \end{aligned}$$
(39)

where

$$\begin{aligned} a_2=(1-\chi )+\chi \dfrac{(\rho C_p)_{np}}{(\rho C_p)_l}, \end{aligned}$$
(40)

and how \(C(\tau _1)\) is obtained is discussed in what follows. Substituting \(\dfrac{dA}{d\tau _1}\) and its derivative from Eq. (34) in Eq. (33), we get C in terms of A as:

$$\begin{aligned} C(\tau _1)=-\dfrac{1}{\left[ (1-R_{I_{nl}}\eta _1^{-2})+Pr_{nl}\right] ^2}\left( P_1+P_2A^{2}+P_3A^{4}\right) , \end{aligned}$$
(41)

where

$$\begin{aligned} P_1= & {} Pr_{nl}(1-R_{I_{nl}}\eta _1^{-2})(r_{nl}-1)^2, \end{aligned}$$
(42)
$$\begin{aligned} P_2= & {} -\left( \dfrac{4(r_{nl}-1)Pr_{nl}(1-R_{I_{nl}}\eta _1^{-2})+\left[ (1-R_{I_{nl}}\eta _1^{-2})+Pr_{nl}\right] ^2}{a_{1}^{2}b}\right) , \end{aligned}$$
(43)
$$\begin{aligned} P_3= & {} \dfrac{3Pr_{nl}(1-R_{I_{nl}}\eta _1^{-2})}{a_{1}^{4}b^2}. \end{aligned}$$
(44)

For steady, finite amplitude convection, we get C in the form

$$\begin{aligned} C=r_{nl}-1. \end{aligned}$$
(45)

Using Eq. (45) in (39), we get

$$\begin{aligned} Nu_{nl}=1+\dfrac{2}{\left( 1-\dfrac{R_{I_{nl}}}{4\pi ^2}\right) }\dfrac{\tan {\sqrt{R_{I_{nl}}}}}{\sqrt{R_{I_{nl}}}} \left[ a_1a_2\right] \left[ 1-\dfrac{1}{r_{nl}}\right] . \end{aligned}$$
(46)

The next section presents a detailed discussion on tri-modal analysis and comes up with a few conclusions as well.

5 Results and discussion

Various combinations of the four carrier liquids, viz., water, ethylene glycol, engine oil and glycerine with five nanoparticles, viz., copper, copper oxide, silver, alumina and titania are considered in studying heat transport by Rayleigh–Bénard convection in nanoliquids. The range of thermal conductivity of the carrier liquids considered is from 0.144 to 0.163  W/m-K and the range of thermal conductivity in the case of the considered nanoparticles is from 8.9538 to 401  W/m-K. The dynamic viscosity of the considered carrier liquids ranges from 0.00089 to 0.799 kg/m-s. Thermophysical properties at 300\(^{\circ }\)K of carrier liquids and of nanoparticles considered in this paper assume values as reported in Siddheshwar and Meenakshi [56]. The problem presents a wide range of Prandtl numbers from 2.91 to 8400.76. In arriving at the results reported in the paper, the values of thermophysical quantities of carrier liquids and nanoparticles are extracted from experimental works or from books concerned with various aspects of nanoliquids (Siddheshwar and Meenakshi [56]). Using these values and for a 10% volume fraction of nanoparticles, the values of thermophysical quantities of nanoliquids (carrier liquids+nanoparticles) are evaluated using phenomenological laws or mixture theory as documented in Sect. 2. The choice of \(\chi =0.1\) is guided by the fact that enhanced heat transfer has been observed experimentally only for small volume fractions ([15, 25, 26]). Since small volume fractions of nanoparticles are considered agglomeration is not a phenomenon that can be observed.

The essential difference between the classical Rayleigh–Bénard convection in Newtonian liquids without nanoparticles and with heat source and the corresponding problem in Newtonian nanoliquids is that the classical parameters get redefined in terms of nanoliquid properties rather than in terms of carrier liquid properties. Buckingham-\(\varPi \)-theorem applied to the two problems results in the same number of non-dimensional parameters which in turn means the results on nanoliquids can be obtained from the corresponding problem in carrier liquids without nanoparticles. In view of this fact together with the observation that the treatment here is analytical, essential details are given in the paper regarding the considered problem.

Unconsidered aspects of Rayleigh–Bénard convection with heat source in nanoliquids are the following:

  1. (i)

    Actual values of the thermophysical properties.

  2. (ii)

    The connection between the weakly nonlinear approaches of Lorenz model and Ginzburg–Landau model.

  3. (iii)

    The explanation of the phenomenon of “enhanced heat transport situation” in nanoliquids in terms of the “enhanced thermal conductivity phenomenon” in carrier liquids due to the presence of nanoparticles.

Some of the aspects considered in the paper are new for Newtonian carrier liquids without nanoparticles as well. It is appropriate to recollect here a very apt comment made by Magyari [39] that results in respect of nanoliquids can be obtained from the corresponding results of carrier liquids by suitable redefinition of parameters. We now move on to the discussion of results. The critical Rayleigh number at which convection starts is shown in Fig. 2. From the figure it is clear that critical Rayleigh number decreases with increase in internal Rayleigh number. This means that heat source advances the onset of convection where as heat sink delays the convection.

Fig. 2
figure 2

Variation of critical Rayleigh number, \(R_{nl_c},\) with internal nanoliquid Rayleigh number, \(R_{I_{nl}}\)

Full size image
Fig. 3
figure 3

Variation of nanoliquid Nusselt number, \(Nu_{nl},\) with \(R_{I_{nl}},\) for different volume fraction, \(\chi \), for engine-oil-silver and water-titania nanoliquids

Full size image

There are two types of results on Nussselt number presented through Figs. 3 and 4 and Tables 1, 2, 3, 4 and 5.

Fig. 4
figure 4

Variation of \(Nu_{nl},\) with \(R_{I_{nl}}\) for different scaled nanoliquid Rayleigh number, \(r_{nl}\), for engine-oil-silver and water-titania nanoliquids

Full size image

The two figures and Tables 1, 2, 3 and 4 concern marginal, stationary Rayleigh–Bénard convection. The last table pertains to unsteady regime. It can be easily observed from the two figures that heat source enhances heat transport where as heat sink diminishes it. Heat source adds to the energy of the system and hence an advanced onset is observed in this case compared to the problem with no heat source. In the case of heat sink, however, heat is drawn from the system leading to delay in onset. Advanced onset and delayed onset correspond to enhanced heat transfer and diminished heat transfer respectively. This thermodynamically correct result is depicted by the two figures. Figure 3 demonstrates increase in heat transfer with increase in nanoparticle concentration. A little explanation is required here regarding the value of Prandtl number used. From the definition of \(Pr_{nl}\) in Eq. (14), in conjunction with the phenomenological laws and mixture theory representations of Eqs. (4)–(6), it becomes pretty obvious that \(Pr_{nl}\) varies with \(\chi \). This is an essential departure from the usage of the classical definition of Prandtl number. Figure 4 is basically a reiteration of a classical result. It merely states that \(Nu_{nl}\) increases with increase in \(r_{nl}\) for all values of \(R_{I_{nl}}\). Though the results are shown for \(\chi =0.1\) only, we have observed that this result is true for all \(\chi \) and for dilute concentration. It has been found that amongst the twenty nanoliquids considered water-titania transports least heat and engine oil-silver transports the maximum.

5.1 Highlights of the present study

Valuable information is provided by the problem on onset of convection and heat transfer in twenty nanoliquids and the experimenter thereby has vital information that helps in picking and choosing an appropriate nanoliquid for a desired thermal engineering problem addressing heat removal.

Table 1 Values of \(Nu_{nl}\) in the steady state for \(\chi =0.1\) and different \(R_{I_{nl}}\), for water-based nanoliquids
Full size table
Table 2 Values of \(Nu_{nl}\) in the steady state for \(\chi =0.1\) and different \(R_{I_{nl}}\), for glycerine-based nanoliquids
Full size table
Table 3 Values of \(Nu_{nl}\) in the steady state for \(\chi =0.1\)and different \(R_{I_{nl}}\), for ethylene glycol-based nanoliquids
Full size table
Table 4 Values of \(Nu_{nl}\) in the steady state for \(\chi =0.1\)and different \(R_{I_{nl}}\), for engine oil-based nanoliquids
Full size table
Table 5 Values of \(Nu_{nl},\) for different times, \(\tau _1\), for \(\chi =0.1, r_{nl}=3\), initial amplitude, \(\bar{A_0}=1\)
Full size table

The following are the highlights of the findings of the present study:

  1. 1.

    Half-range Fourier cosine series expansion for the basic nonuniform temperature gradient facilitates obtaining an analytical expression for the critical Rayleigh number.

  2. 2.

    Heat source (\(R_{I_{nl}}>0\)) advances the onset of convection while heat sink (\(R_{I_{nl}}<0\)) diminishes the same.

  3. 3.

    Heat source is shown to enhance the heat transport and heat sink diminishes the same.

  4. 4.

    Amongst the twenty nanoliquids considered, it is found, in general, that engine-oil-silver has the most enhanced heat transport while water-titania has the least. However, all nanoliquids transport more heat compared to a Newtonian liquid without nanoparticles. Thus the following is true:

    \(Nu_{nl}>\) \(Nu_{l}\).

  5. 5.

    There is a definite connection between the Lorenz and Ginzburg–Landau models.

  6. 6.

    In the absence of experimental works on heat transport in nanoliquids by Rayleigh–Bénard convection, it remains to be seen whether the single-phase or the two-phase model is best suited as a mathematical model for studying heat transfer in nanoliquids.