Abstract
This paper describes how drivers’ rules according to EU social legislation can be formally modelled using the resource concept and how ‘legal’ vehicle routes and schedules can be computed by exact and heuristic labelling algorithms for solving the elementary shortest path problem with resource constraints.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This paper presents a comprehensive approach for considering current EU legislation on drivers’ working hours. The paper describes how drivers’ rules according to EU social legislation can be formally modelled using the resource concept and how ‘legal’ vehicle routes and schedules can be computed by exact and heuristic labelling algorithms in the context of the elementary shortest path problem with resource constraints (ESPPRC). The contribution of the paper is twofold: (1) It highlights important properties of driver’s rules and their algorithmic consequences and (2) it presents an algorithm for constructing legal routes and for checking their feasibility/legality. The algorithms presented in this paper can be used as subroutines in exact or heuristic procedures for solving vehicle routing problems with drivers’ rules.
We consider rules contained in Regulation (EC) No 561/ 2006 of the European Parliament and of the Council of 15 March 2006 on the harmonization of certain social legislation relating to road transport and amending Council Regulations (EEC) No 3821/85 and (EC) No 2135/98 and repealing Council Regulation (EEC) No 3820/85 [8] and refer to these as drivers’ rules.
Note This is an OR paper, not a juristic text. It is explicitly stated that none of the algorithms presented in this paper is guaranteed to determine a ‘legal schedule’ for a vehicle route, because there is no precise mathematical definition of the term ‘legal schedule’. The determination of a legal schedule for a vehicle route is not a question of mathematics or computer science, but solely a juristic one. The pertinent regulations give abundant room for interpretation, so that any dispute concerning the legality of a route will eventually have to be settled in court.
The paper is structured as follows. Sect. 2 defines the necessary vocabulary. The relevant drivers’ rules are laid down in Sect. 3. The existing literature is reviewed in Sect. 4. Section 5 discusses some fundamental observations related to drivers’ rules. In Sect. 6, the resources and resource extension functions (REFs) used to model drivers’ rules exactly and heuristically within a dynamic-programming-based solution framework for the elementary shortest path problem with resource constraints are described. Sect. 7 presents and discusses the results of computational experiments performed with implementations of the proposed REFs. The paper ends with a conclusion in Sect. 8.
2 Important terms
For the purposes of this paper, the following definitions apply:
-
Driving time is the time a driver is actually operating a vehicle, sitting behind the steering wheel. The vehicle does not necessarily need to move nor does the motor need to be running; waiting in traffic congestion is also counted as driving time.
-
Other work is any working activity other than driving; this comprises but is not limited to, loading and unloading of vehicles and vehicle maintenance.
-
Break time is time where a driver neither drives nor performs other work.
-
A rest period is a period where a driver neither drives nor performs other work but may freely dispose of his time.
-
A (calendar) week is the time from Monday 0:00 hours to Sunday 24:00 hours.
-
A driving time interval is the time between two long breaks or rest periods. A driving time interval ends after a long break.
-
A short break is a break time of at least 15 and at most 45 min.
-
A long break is a break time of at least 45 min or at least 30 min if a short break has already been taken since the last long break or rest period.
-
A vehicle route is called feasible if it respects all resource constraints, except for the drivers’ rules.
-
A feasible vehicle route is said to have a legal schedule or, for simplicity, is called legal if it complies with the drivers’ rules as specified in Sect. 3.
-
A short arc is an arc with a travel time of at most 270 min. Long arcs are defined correspondingly.
3 Relevant rules
We consider the following rules:
-
Interval driving time
A driver must not drive for more than 4 h 30 min (270 min) consecutively.
-
Daily driving time
The driving time between two daily rest periods (see below) must not exceed 10 h. At most twice in a calendar week, the driving time between two daily rest periods may exceed 9 h.
-
Weekly driving time
The driving time within a calendar week must not exceed 56 h.
-
Fortnightly driving time
The driving time in two consecutive calendar weeks must not exceed 90 h.
-
Breaks
After 4 h 30 min of driving, the driver must take a break of at least 45 min. The break may be split into two interruptions of at least 15 and at least 30 min in this order.
Note The aforementioned rule does not mean that there can be at most 4 h 30 min of driving in each interval of 5 h 15 min. Consider the following example. It is legal for a driver to start his working day by driving for 1 h 30 min, then take a break of 15 min, drive for an additional 3 h, take a break of 30 min, and then drive for another 4 h 30 min. At the end of these 4 h 30 min of driving, the driver has been driving for 7 h 30 min in the last 8 h.
-
Daily rest periods
There are two different rules determining when a daily rest period is necessary:
-
Within 24 h after the end of the last daily or weekly rest period, there must be a daily rest period of at least 9 h.
-
Additionally, when the daily driving time is exhausted, a daily rest period must be taken before the driver may continue driving.
Between two weekly rest periods, there may be at most three daily rest periods of less than 11 h (660 min). A daily rest period may be split into two periods of at least 3 h (180 min) and at least 9 h (540 min) in this order.
-
-
Weekly rest periods
There are also two different rules determining when a weekly rest period is necessary:
-
After at most 144 h after the end of a weekly rest period, there must be an uninterrupted weekly rest period of at least 24 h. If the duration of the weekly rest period is less than 45 h, the difference between 45 h and the actual duration of the weekly rest period must be added as an additional uninterrupted rest period to an uninterrupted rest period of at least 9 h within three calendar weeks after the calendar week where the thus shortened weekly rest period ends.
-
If the weekly or fortnightly driving time is exhausted, a rest must be taken until the end of the current calendar week, even if this is longer than 45 h.
-
The requirement that shortened weekly rest periods be made up for within the subsequent 3 weeks would, in effect, require the planning horizon of an instance to cover at least 3 weeks. This is impossible. (Still worse, the regulation on working hours [7] states in Article 4 (a) that ‘the ... maximum weekly working time may be extended to 60 h only if, over four months, an average of 48 h a week is not exceeded’. This would require a planning horizon of at least 8 months.) Hence, some decisions on the available driving and working time and the required break and rest time of a driver have to be taken outside of the planning algorithm. They constitute assumptions, are exogenous to the instance to be solved, and enter the instance as data. The values of the corresponding resource variables are determined in a preprocessing step. In the end, this means that such decisions exclude certain legal routes in an instance. In the context of empty (vehicle or container) repositioning, [6], p. 3401, state that ‘it is extremely difficult, if not impossible, to determine the appropriate amount of empty travel’. This discussion shows that an analogous statement holds for the balancing rules in EU social legislation. Therefore, we consider the rules on balancing weekly rest periods heuristically as follows. The duration of the weekly rest period for each driver is specified as input data, where the duration is always at least 24 h. If the planning horizon is such that at most one weekly rest is necessary, the duration of the weekly rest period may include balancing periods of previous weeks. This means that the option to add such a balancing period to a daily rest period is excluded. For instances where the planning horizon is at most 24 h, these assumptions are not restrictive. What is more, the weekly rest period rules themselves need not be considered if at most one calendar week is considered and if it is assumed that the previous weekly rest period of each vehicle ends no earlier than at the beginning of the considered calendar week. In this case, as a week has 168 h and as the minimum weekly rest period is 24 h, the vehicle is available during the complete planning horizon (144 + 24 = 168).
Note A daily rest period also resets the interval driving time, and a weekly rest period also resets the daily and the interval driving time (mind the ‘at leasts’ above).
We consider neither multi-manning, i.e. the case that there are at least two drivers in the vehicle to do the driving, nor issues related to multi-modal traffic, such as breaks and rest periods on trains or ferries. Furthermore, we assume that the rules apply to the complete instance, i.e. that each visited customer is located within the area of application of the rules.
One important rule stated in the regulation on working hours [7] is that after at most 6 h of work (driving or other work), a break of at least 30 min is required. It can be assumed that in many cases this rule will automatically be complied with, because in most practical situations, most of the working time will be driving time, and because the rules in Regulation (EC) No 561/2006 etc. require breaks to be taken earlier and more frequently than the rules in the regulation on working hours.
Another rule stated in the regulation on working hours limits the working time per calendar day to 10 h (with exceptions). However, as this regulation is overruled by Regulation (EC) No 561/2006 etc., driving time during a calendar day may exceed 10 h, whereas driving time + other work may not. In principle, overall daily working time can easily be counted (in a resource variable), but it is not done here for simplicity.
4 Literature review
The monographs by [13] and [20] consider drivers’ rules from a juristic perspective and offer a wealth of comments on and explanations of the above-mentioned regulations as well as numerous examples for legal and illegal schedules. It is noteworthy that these authors do not completely agree on the interpretation of the rules.
In the OR literature, there are different approaches for the consideration of drivers’ rules:
-
by means of appropriate variables and constraints in an MIP model [17, 25]
An LP-based algorithm is not an option for the constructive solution of practical problems. However, it may be fast enough to check the feasibility/legality of given routes. Moreover, the development of MIP models fosters the understanding of the problem and facilitates and accelerates the development of practically relevant models and algorithms.
-
by means of increasing the allowed driving times of drivers and travel times of arcs [3]
These authors consider daily driving and break regulations by increasing the maximal daily driving time,
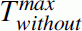 , of 9 h by the required break time of 45 min to
, of 9 h by the required break time of 45 min to  and by increasing the travel time of each arc by the factor \(T_{with}^{max}/T_{without}^{max}\). They write on p. 184: ‘With this approach some slack is implicit in the schedule which may accommodate the real breaks that can be introduced in the final stage of the scheduling.’
and by increasing the travel time of each arc by the factor \(T_{with}^{max}/T_{without}^{max}\). They write on p. 184: ‘With this approach some slack is implicit in the schedule which may accommodate the real breaks that can be introduced in the final stage of the scheduling.’ -
by means of constructing an extended, multi-stage network with a duplicate of the original network on each stage, where the connecting arcs between the stages correspond to breaks ([4], p. 180 f.)
-
by means of introducing artificial customers (vertices) corresponding to breaks or rest periods (Scheuerer (2007): personal communication)
-
by means of resource variables and extension functions in dynamic-programming-based labelling algorithms or in local-search-based heuristics (Grünert (2002): personal communication); [10, 16, 18, 24]
The algorithm by [16] is remarkable in two respects. First, this approach also considers the working time regulations stated in [7]. Second, it uses heuristic dynamic programming by restricting the state space in two ways: (1) by limiting the number of labels (states) to be considered in the next iteration of the algorithm, and (2) by limiting the number of new labels to be constructed from one existing label. In this way, the time complexity of the algorithm does not increase when optional rules, such as splitting breaks, are considered.
-
by means of resource variables and constraints in constructive heuristics such as insertion procedures [1, 9]
[1] consider the drivers’ rules relevant in the USA. These rules, however, are very simple compared with the EU rules. The rules simply require that the minimum rest time after at most 11 h of driving and at most 14 h on duty (driving and waiting) is 10 h. Nevertheless, the algorithm developed in the paper is highly complicated and sophisticated. For a given route, the algorithm determines, in \({\mathcal{O}}(n^3)\) time, whether or not there exists a schedule respecting drivers’ rules. The algorithm is based on a backward search principle. It starts at the last vertex in the route with the heuristic assumption to take rests as late as possible, i.e. as early as possible in a forward direction. The authors describe several issues arising when drivers’ rules are to be considered, but, as similar driving time limits constitute a subset of the EU rules, all of these issues were discovered independently by the authors of the present paper.
[19] use a tree search algorithm for checking the legality of a given route. These authors also consider the whole set of drivers’ rules as described in Sect. 3 within a large neighbourhood search algorithm where the route reconstruction operator is based on heuristic branch-and-price; columns are generated heuristically by tabu search.
Further publications considering drivers’ rules are [6, 23], and [2]. [23] considers the rules on interval breaks in a routine for computing a schedule for a given route. The arrival time at each stop of the route is first computed without taking into account necessary breaks and is then shifted by 45 min for each necessary break. (Besides presenting a labelling algorithm as mentioned earlier, [24] also describe an approach similar to the one by [23] but consider the rules relevant in the USA.) [6] use a depth-first recursive procedure to compute legal duties for drivers within a heuristic for assigning vehicles and drivers to scheduled trips of an LTL carrier in the USA. [2] consider the European rules in an application to road feeder service planning in air cargo transportation. Given scheduled vehicle trips, the task is to assign vehicles and drivers to the trips. To this end, the authors develop a sophisticated recursive procedure for determining the time since the last daily rest. (The break requirements are only approximately considered (similar to the approach by [3] mentioned previously). The daily rests, however, are considered for the single- and double-manning case.) This procedure is embedded in a column generation heuristic and a metaheuristic based on large neighbourhood search for solving the overall problem.
Very recent papers are [9, 12], and [11]. In [9], based on his earlier work [10], the author develops a formal algorithmic framework for considering all rules contained in Regulation (EC) No 561/2006 etc., including weekly rules and multi-manning regulations. [12] develop a polynomial algorithm for the legality test of the rules relevant in the United States, and [11] describe a polynomial algorithm for the legality test of double-manned routes considering the EU rules. No computational tests with implementations of these algorithms are presented.
It must be noted that no paper presents an algorithm implementation for considering weekly rules.
5 Fundamental observations concerning drivers’ rules
This section describes some fundamental observations relevant for the consideration of drivers’ rules. In this section, service times are assumed to be zero.
The first observation shows that the maximum attainable driving time within a calendar day or any 24-h period is considerably longer than what might be expected.
Observation 1
The maximum attainable driving time within a calendar day or any 24-h period is 13 h 45 min.
Example 1
The following example of a feasible schedule for a driver shows the maximum attainable driving time within a calendar day (or any 24-h period):
-
1 min driving at 23:44 hours
-
15 min break at 23:45 hours
-
4 h 29 min driving at 0:00 hours
-
30 min break at 4:29 hours
-
4 h 30 min driving at 4:59 hours
-
9 h daily rest at 9:29 hours
-
4 h 30 min driving at 18:29 hours
-
45 min break at 22:59 hours
-
16 min driving at 23:44 hours
Observation 2
To make a correct decision as to which break or rest periods to take between two vertices, it is necessary to consider the complete route.
This means that it is not sufficient to consider only the partial route from the start vertex to the current vertex and the direct successor of the current vertex. Example 2 illustrates this observation.
Example 2

When at vertex i and when the decision which breaks or rests to take only takes into account the travel time between i and j and the time window at j, no break will be taken. Then, a daily rest is necessary between j and d and the time window at d is missed. To avoid this, it is necessary to consider the travel time between j and d and the time window at d already when planning the breaks or rests to take between i and j.
Observation 3
It is generally sensible to start a new driving time interval, i.e. to reset the interval driving time, after each break or rest period of at least 45 min, whether or not the interval driving time is already exhausted.
This is true because by doing so, additional flexibility is gained, and the rules do not limit the number of driving time intervals between two daily rest periods.
Observation 4
For legality reasons, it may be necessary to take a break or rest period, even when no driving time limit is reached.
In Example 2, it is possible to reach d within its time window only when a (reduced) daily rest is taken before j, although neither the interval nor the daily driving time is exhausted when arriving at j.
Observation 5
Split breaks and split daily rest periods are only useful when waiting time is possible, which of course is always possible when time windows are present.
The following example shows that splitting a break may be the only way to get a feasible schedule.
Example 3

In order to reach vertex j in time and in compliance with drivers’ rules, it is sufficient to take a break of 45 min after 270 min of driving, somewhere between vertices i and j. The beginning of service at j is then 330. Due to the time windows, this means a waiting time of 5 min before the service at j can begin. In order to comply with the drivers’ rules, an additional break of 45 min is necessary before reaching vertex d. The arrival time at d is then 655, which lies after the end of the time window at d. If an additional break of 15 min is taken before j (transforming the 5 min waiting time into break time, which is possible), a break of 30 min between j and d is sufficient with regard to the drivers’ rules and d can be reached in time.
Example 3 also demonstrates the following observation.
Observation 6
It may be sensible to take a break or rest period directly before a vertex with waiting time, even when the waiting time is shorter than the break or rest period into which it is transformed.
In Example 3, there is a waiting time of 5 min before vertex j, which are used to take a split break of 15 min.
It is easy to see that, when there are no drivers’ rules, the overall duration of a route cannot be reduced by finishing the route later than the earliest possible time. When drivers’ rules are present, however, this is no longer true.
Observation 7
To minimize overall route duration, it is not generally sensible to try to also minimize route completion time (end of service at last node). In other words, when drivers’ rules are considered, minimizing route duration and minimizing route completion time are conflicting goals.
This observation is illustrated in Example 4.
Example 4

Observation 8
Whereas it is always sensible to extend a daily or weekly rest period such that no waiting time remains at the next vertex, it may be sensible to extend a daily or weekly rest period further, such that the service at the next vertex may begin later than the earliest possible time.
This quite counterintuitive observation is demonstrated in the following example.
Example 5

Due to the rule that a daily rest period must have been taken not more than 24 h after the end of the preceding daily rest period (cf. Sect. 3), holding other things equal, it is sensible to let a daily or weekly rest period end as late as possible without delaying the beginning of service at any subsequent vertices. This means that if waiting time remains before a vertex after taking a daily or weekly rest period, this waiting time can and should be used to extend the daily or weekly rest period. In Example 5, the earliest point in time when vertex k can be reached is 585. Then, there is a waiting time of 675 min. Therefore, a daily rest period must be taken before beginning the service at k. A weekly rest period is not necessary yet and is also not possible due to the time window at k. A daily rest period need not take longer than 660 min. However, in the depicted situation, the daily rest period can be extended by 15 min, and the service at k can still start as early as possible (270 + 45 + 270 + 660 + 15 = 1260). By doing so, after leaving k, the time since the end of the last daily rest is shorter (0 compared to 15), and more flexibility is gained in this respect for the rest of the route (which might continue beyond l). Unfortunately, if the daily rest period ends at time 1260, a break of 45 min is necessary between k and l, and l is not reached in time (1260 + 270 + 45 + 30 = 1605 > 1590). Hence, the best way to obtain a legal schedule for the route in Example 5 is to take a daily rest period 1 min before reaching k, thereby resetting the interval driving time, go on driving for 1 min until k is reached, and then take a split break of 15 min. Then, the time window at k is maintained, a break of 30 min en route between k and l is sufficient and also l is reached within its time window. A similar example can be constructed for weekly rest periods.
For the situation of Example 5, the legal status is unclear: the rules do not specify whether a split break or a split daily rest may be taken only after a strictly positive amount of driving time, or if after driving 0 min in the current driving time interval or the current daily driving period, a split break of 15 min or a split daily rest period of 180 min may already be taken. Assuming that there must be a positive amount of driving time between two consecutive breaks or rests [Rang (2008): personal communication], the following observation can be made.
Observation 9
During a waiting time, up to three different break or rest times may have to be taken.
This can be seen as follows. If waiting time before a vertex is to be transformed into break or rest time, and if the waiting time is at least 1 min longer than the break or rest time into which it is to be transformed, but less than 15 min longer, it may be sensible to drive until 1 min before reaching the vertex where the waiting time occurs, take the break or rest time, then drive the final minute until the vertex is reached, and then take a split break. If the waiting time is at least 15 min longer than the break or rest time into which it is to be transformed, it is always sensible to do so. The situation is similar with regard to the usefulness of taking a split daily rest. Moreover, if the first break or rest time during a waiting time is at least a shortened daily rest period, it may even be sensible to drive until 2 min before the vertex is reached, take the daily rest period, drive for another minute, take a split daily rest, drive the final minute, and then take a split break.
Observation 9 leads to the final observation, which is a really remarkable one.
Observation 10
There may be up to four breaks or rest periods even on a short arc with a travel time of not more than 4 min.
Example 6
Assume that a driver is supposed to drive a route from o to d with i, j, k, l, and d being the last five vertices of the route (in this order, see the following figure). Further assume that the driver reaches vertex i at time zero (for simplicity) having a remaining daily driving time of 1 min and having already taken three reduced daily rests since the last weekly rest period and two extended daily driving times in the current calendar week.

To drive this route, the following sequence of activities is possible:
-
1 min driving at time 0
-
660 min daily rest at time 1
-
1 min driving at time 661
-
660 min daily rest at time 662
-
1 min driving at time 1322
-
180 min split daily rest at time 1323
-
1 min driving at time 1503
-
15 min split break at time 1504
-
269 min driving at time 1519
-
30 min break at time 1788
-
1 min driving at time 1818
-
268 min driving at time 1819
-
135 min waiting time at time 2087
-
540 min daily rest at time 2222
-
1 min driving at time 2762
Without taking four breaks or rests between i and j, vertex d cannot be reached within its time window. In particular, if the two daily rests taken between i and j were merged into one rest of 1320 min after driving for 1 min, the end of the last daily rest before j would be at time 1321. Then, due to the 24-h rule, the daily rest of 540 min would have to start at time 2221 and the time window at l would be missed. Furthermore, also if the last daily rest was not split so that at time 2222 a rest of 540 min is sufficient, d could not be reached within its time window.
Note that, except for Observations 1 and 3, all of the aforementioned observations or rather complications arise only when there are time windows.
6 A labelling algorithm for the elementary shortest path problem with resource constraints and drivers’ rules (ESPPWDR)
The standard solution technique for (E)SPPRCs is a labelling algorithm based on dynamic programming. In principle, such an algorithm works similar to a labelling algorithm for shortest path problems without resource constraints, e.g. the well-known Dijkstra algorithm. The basic concepts used in such an algorithm are the following (cf. [15]). A resource is an arbitrarily scaled one-dimensional quantity that can be determined or computed at the vertices of a directed walk in a network. Examples are cost, time, load, or the accumulated interval driving time. The value of a resource at a vertex is stored in a resource variable. An arbitrarily scaled resource is constrained if there is at least one vertex in the network where the associated resource variable must not take all possible values. A cardinally scaled resource is constrained if there is at least one vertex in the network with a finite upper or lower bound on the value of the resource. The resource window of a nominally scaled resource r at a vertex is the set of allowed values of r at this vertex. The resource window of a cardinally scaled resource r at a vertex i is the interval \([lb^r_i,ub^r_i]\; \subseteqq\;]-\infty,\; +\; \infty[\). A resource extension function (REF) is defined on each arc in a network for each resource considered. An REF for a resource r maps the set of all possible vectors of resource values at the tail of an arc to the set of possible values of r at the head of the arc. More precisely, let R: = (σ1, \(\ldots\), σ|R|)T be a vector of (values of) resource variables. Then, an REF for a resource r is a function \(f^r:A\times{\mathbb{R}}^{|R|}\mapsto{\mathbb{R}}\). An REF for a cardinally scaled resource r indicates (lower bounds on) the consumptions of r along the arcs. When seeking a path from an origin vertex o to a destination vertex d, partial paths from o to a vertex i≠d are extended along all arcs (i, j) emanating from i to create new, extended paths. For each o-i-path, there is a corresponding label l resident at i that stores the values of all resource variables at i for its path, along with the information on how it was created: the arc (h, i) over which i was reached and (a reference to) the label of the o-h-path whose extension along (h, i) yielded the o-i-path. (This makes it easy to reconstruct the path corresponding to a label.) Initially, there is exactly one label corresponding to the path (o). W.l.o.g., the values of the resource variables of the initial label are all set to the lower bounds of their respective resource windows at o. A label l is feasible if and only if the value of each resource variable in l is within the resource window of its respective resource. If a label is not feasible, it is discarded. An extension of a path/label along an arc (i, j) is feasible if the resulting label at j is feasible. An h-j-path is feasible if, for each arc (i, i′) in the path, a feasible label at i exists which can be extended along (i, i′) to a feasible label at i′. To keep the number of labels as small as possible, it is decisive to perform a dominance procedure to eliminate feasible but unnecessary labels. A label l 1 dominates a label l 2 if both reside at the same vertex, if the value of the resource variable of each nominally scaled resource in l 1 is equal to the corresponding value in l 2, if the value of the resource variable of each cardinally scaled resource in l 1 is ‘better’ (less or greater, depending on the resource) than or equal to the corresponding value in l 2, and if the value of the resource variable of at least one cardinally scaled resource in l 1 is strictly ‘better’ than the corresponding value in l 2. Dominated labels are discarded as well.
For a labelling algorithm, Observations 2 and 10 mean that several new labels have to be created when extending a label along an arc; one label for each potentially sensible sequence of decisions on breaks or rests along an arc.
Creating several new labels from an existing one is, in principle, equivalent to introducing parallel arcs. However, an approach using parallel arcs has several serious drawbacks:
-
The structure of the underlying graph must be modified.
-
The break or rest times that generally need to be considered are 0, 15, 30, 45, 180, 540, 660, and n minutes, where \(1440\leqq n\leqq 2700\), and n is specified as input data. This means that there are at least 87 = \(2{,}097{,}152\) possible combinations of breaks and rest periods even on a short arc. Though most of these combinations are never relevant, the number of relevant combinations is considerable and becomes intractable on long arcs.
-
Due to the previous item, it is clear that long arcs have to be split, i.e. each parallel arc has to be split into two or more consecutive arcs.
-
Along all but one arc of a set of parallel arcs, the resources which are independent of drivers’ rules are updated redundantly.
-
Many new labels are created in the first place and then eliminated in the dominance step. It is much more efficient not to create these labels at all.
An alternative approach is to use vertices corresponding to breaks or rest periods by introducing one artificial vertex for each break or rest period, two antiparallel arcs between each original vertex and each artificial vertex, and between each pair of artificial vertices. This approach avoids the aforementioned drawbacks; most notably, it is not necessary to explicitly determine all relevant combinations of breaks or rest periods—these combinations are determined by the algorithm. However, this approach may lead to the generation of an excessive number of labels by cycling between the break or rest vertices, and it may be difficult to consider the extension of daily and weekly rests. Therefore, using break or rest vertices was also not pursued here.
6.1 Underlying network
In practice, it is common that upon arrival at a customer location, a driver has to perform some active service (tasks such as manoeuvring or paperwork at the local dispatching office), followed by passive service (time spent doing nothing when customer staff is responsible for loading or unloading), again followed by active service (tasks such as cleaning the cargo area on the lorry, checking cargo security, or paperwork). In models for routing problems, service time at a customer location is usually simply added to the travel times of the arcs emanating from the vertices corresponding to the locations. This is obviously not possible when drivers’ rules are considered. To account for service times and to be able to distinguish between active service times such as times for loading or unloading performed by the driver (which have to be counted as other work) and passive service times (which may be counted as break or rest time, because the driver can dispose freely of this time), we use the following approach. With each customer location v c, a possibly empty ordered sequence of active and passive service times is associated. In the digraph used to represent the real-world network, each v c with \(n_c^{ast}\) active and \(n_c^{pst}\) passive service times is represented by a sequence of vertices \(v^{c,in}, v^{c,intermediate,1}, \ldots, v^{c,intermediate,{n_c^{ast}}-2}, v^{c,out}\). These vertices are linked by service arcs with zero travel time to form an elementary path from v c,in to v c,out. Service arcs represent active service times, i.e. time-consuming processes at the same physical location. Passive service times are essentially equivalent to waiting times and are considered at vertices. It is assumed that waiting and passive service times are additive, i.e. it is assumed that waiting and passive service times merge seamlessly. In other words, passive service times are waiting times which start only after the beginning of the time window of the respective vertex. v c,in is the head of all travel arcs representing movements in space and time from other locations to v c, and v c,out is the tail of all arcs representing movements in space and time from v c to other locations.
No vertices are introduced to model locations where breaks or rests can be taken, i.e. it is assumed that breaks and rests can be taken anywhere on a route. This is a considerable simplification, but the alternative, to have a vertex for every parking place, roadhouse, and side street in the geographical region defined by the customer locations, is not an option.
Formally, we consider an ESPPRC instance defined on a digraph D = (V, A) with V = {o, 1, \(\ldots\), n, d}. o is the origin vertex, d is the destination vertex. For each \(i\in V, [a^{service}_i, b^{service}_i]\) is the service time window of \(i, [a^{departure}_i,b^{departure}_i]\) is the departure time window of i, and \(\tau^{service\_passive}_i\) is the passive service time at i. For each arc a ∈ A, if the tail vertex of a is i and the head vertex is j, the notation ij is used to designate a. c ij denotes the cost of traversing \(ij, \tau^{travel}_{ij}\) is the travel time needed for traversing ij, and \(\tau^{service\_active}_{ij}\) is the active service time along ij. For each arc ij, either \(\tau^{travel}_{ij}>0\) and \(\tau^{service\_active}_{ij}=0\) or vice versa.
The service time window of a vertex specifies the interval when the service at that vertex may begin. With \(t^{arrival}_i\) denoting the arrival time at a vertex i (before transforming any waiting time into break or rest time), beginning of the (passive) service at i is possible no earlier than at \(\max\{a^{service}_i,\) \(t^{arrival}_i\},\) and no later than at \(b^{service}_i.\) Departure is possible no earlier than \(\max\{a^{departure}_i,\) \(t^{arrival}_i\}\), and no later than \(b^{departure}_i\).
The relevant standard resources in the ESPPRC are cost and time.
The objective is to compute an elementary shortest path from o to d and a corresponding legal schedule while respecting the resource constraint for capacity and the time windows at the vertices. At d, the labels with minimal cost are considered optimal. If there is more than one label with minimal cost, labels with minimal duration among all labels with minimal cost are preferred.
Note that, contrary to the approaches by [1] and [19], the procedures presented in this section are not only able to compute a legal schedule for a given route but also to simultaneously create a route and compute a legal schedule for it.
6.2 Resources
To consider the standard resource constraints and the drivers’ rules mentioned in Sect. 3, the following resource variables are needed within a label or resource vector l i resident at a vertex i:
-
c i : cost of the partial path up to i
-
t i : point in time where the service at i begins
-
pred i : predecessor arc
-
pred label : predecessor label
-
\(\tau^{drive,cur\_interval}_i\): accumulated driving time in the current driving time interval
-
\(\tau^{drive,daily}_i\): accumulated driving time since the last daily rest period
-
\(\tau^{drive,cur\_calendar\_week}_i\): accumulated driving time in the current calendar week
-
\(\tau^{drive,cur\_calendar\_fortnight}_i\): accumulated driving time in the current calendar fortnight
-
\(\tau^{since\_last\_daily\_rest}_i\): accumulated time since the end of the last daily rest period
-
\(\tau^{max\_ext\_of\_last\_daily\_rest}_i\): maximum amount by which the end of the last daily rest period may be extended without violating the time windows of subsequent vertices
-
\(\tau^{since\_last\_weekly\_rest}_i\): accumulated time since the end of the last weekly rest period
-
\(\tau^{max\_ext\_of\_last\_weekly\_rest}_i\): maximum amount by which the end of the last weekly rest period may be extended without violating the time windows of subsequent vertices
-
\(\tau^{since\_start\_of\_calendar\_week}_i\): elapsed time since Monday, 0:00 h, in the current calendar week
-
\(n^{ext\_ddt}_i\): number of extended daily driving times in the current calendar week
-
\(\beta^{split\_break}_i\): boolean variable specifying whether there has already been a split break of 15 min in the current driving time interval (\(\beta^{split\_break}_i=1\)) or not (\(\beta^{split\_break}_i=0\))
-
\(\beta^{split\_rest}_i\): boolean variable specifying whether there has already been a split daily rest of 180 min during the current daily driving time (\(\beta^{split\_rest}_i=1\)) or not (\(\beta^{split\_rest}_i=0\))
-
\(\beta^{ddt\_extended}_i\): boolean variable specifying whether the current daily driving time has been extended (\(\beta^{ddt\_extended}_i=1\)) or not (\(\beta^{ddt\_extended}_i=0\))
-
\(n^{red\_daily\_rests\_since\_last\_weekly\_rest}_i\): number of reduced daily rest periods since the end of the last weekly rest period
-
XAT i : latest arrival time at i when starting at the predecessor vertex h on the current partial path at t h , if there were no time windows at i
-
LAT i : latest arrival time at i when time windows are considered
-
Duration i : minimal duration of the partial path up to i
These resource variables specify the value of the respective resource at the moment when the service at i begins.
The resource variables XAT i , LAT i , and Duration i are due to [19]. Alternative resources that could have been used here for minimizing route duration were developed by [14, 21, 22], and [5].
6.3 Overall resource extension function
The decisive point that makes the consideration of drivers’ rules difficult is that it is not possible to say at a certain point in time where a break or rest period is necessary or where a wait occurs which break or rest to take without considering the rest of the route. As stated elsewhere, the method chosen here for coping with this difficulty is to create several new labels when extending one old label. For an exact labelling algorithm, this means that when extending a label along an arc, it is necessary to consider all sensible combinations of breaks and rest periods. (Exact means that the algorithm will find a legal schedule if one exists.) To do this correctly, a label is extended iteratively: resources may be updated several times along an arc. The whole procedure is very lengthy and intricate and cannot be described in full detail here, but the principle is as follows. At each iteration, the extension process moves in time (and, where applicable, in space) along the arc until one of the time resources reaches a limit. Then, all break or rest periods that can be taken at the current point in time are identified. For each such break or rest period, the resources are updated accordingly via the REFs, and a tentative label is created and stored for later extension. The old label is then considered extended. This process is repeated until the end vertex of the arc is reached. Depending on the resulting waiting time, additional breaks or rest periods are taken by transforming waiting time and passive service time completely or partially into break or rest time. (This is the reason why passive service time is stored at vertices rather than along arcs: passive service time is not accounted for iteratively; it is always considered all at once.) The labels resulting from this last step are then returned to the labelling algorithm as the result of extending one label along an arc. This overall resource extension process is formalized in the algorithmic description depicted in the following table:
6.4 Exact resource extension
The table on the next page specifies the potentially relevant combinations of break or rest times that can be created by transforming waiting and passive service time (if the sum of these times is at least 1 min) and the conditions when each combination has to be considered. τrem indicates the remaining arc travel time until the head of the arc is reached.
When a time limit expires along an arc, the situation is similar to the one in the above table, but simpler: in this case, no combinations of breaks and/or rest times are necessary.
Along service arcs, only daily and weekly rest periods have to be considered. At the end of service arcs, no waiting occurs.
The REFs for cost, predecessor arc, and predecessor label are straightforward. The difficulty with the other resources introduced in the preceding section is that they are strongly interdependent. In essence, to update one such resource, all other resources have to be considered, too. This is because the old resource levels of all resources related to drivers’ rules are needed to determine which (combinations of) break and/or rest times are relevant, and these times, in turn, are relevant to compute the new values of these resources. Moreover, due to the iterative nature of the algorithm just described, the resources related to drivers’ rules are updated several times. All this leads to the fact that the updating mechanisms for the resources related to drivers’ rules are quite complicated. It is beyond the scope of this paper to specify them all in complete detail. As an example, a verbal description of the REF for the interval driving time is given subsequently.
\(\tau^{drive,cur\_interval}\) is set to zero,
-
if, at the head vertex, at least one break of at least 45 min is taken, or
Overall resource extension function
Input: a Pareto-optimal label l, an arc ij with tail i and head j, where l resides at i, and an empty list \(L^{new\_labels}\) for storing the new labels to be created.
Let \(L^{tentative\_labels}\) be an empty FIFO-list of tentative labels.
Insert l into \(L^{tentative\_labels}\) .
While \(L^{tentative\_labels}\) is not empty
Let l cur be the first element of \(L^{tentative\_labels}\) .
Remove l cur from \(L^{tentative\_labels}\) .
Compute the following values for subsequent use:
• τremaining: remaining travel or active or passive service time along ij
• \(\tau^{break\_accumulated}\): accumulated break or rest times on the current path
• \(\tau^{drive\_remaining,cur\_interval}\): remaining interval driving time
• \(\tau^{drive\_remaining,daily}\): remaining daily driving time
• \(\tau^{drive\_remaining,weekly}\): remaining weekly driving time
• \(\tau^{until\_next\_daily\_rest}\): remaining time until start of next daily rest
• \(\tau^{until\_next\_weekly\_rest}\): remaining time until start of next weekly rest
• \(\tau^{drive\_remaining\_min}\): minimal remaining driving time; takes into account the preceding five resources
• \(\tau^{cur\_extension\_of\_last\_daily\_rest}\): maximal amount of time by which the last daily rest can be extended such that the service at j can still begin as early as possible
• \(\tau^{cur\_extension\_of\_last\_weekly\_rest}\): maximal amount of time by which the last weekly rest can be extended such that the service at j can still begin as early as possible
• \(\beta^{do\_not\_take\_break}\): boolean value indicating whether after \(\tau^{drive\_remaining\_min}\) time units, a break is sufficient to continue working
• \(\beta^{do\_not\_take\_daily\_rest}\): boolean value indicating whether after \(\tau^{drive\_remaining\_min}\) time units, a daily rest is sufficient to continue working
If j can be reached without exceeding any time limit
Compute the sum of waiting and passive service time \(\tau^{wait+service\_passive}_j\) for l cur at j.
Determine the relevant combinations of break or rest times that can be created by transforming the waiting and the passive service time.
For each such combination
Create from l cur a new label l new corresponding to the current combination.
Compute the resource values for l new using the values just computed and insert l new into \(L^{new\_labels}\) .
else
Move along ij until a time limit is reached.
Determine the relevant combinations of break or rest times that can be used to reset all exhausted time resources.
For each such combination
Create a new tentative label \(l^{new\_tentative}\) corresponding to the current combination.
Compute the resource values for \(l^{new\_tentative}\) using the values just computed and insert it into \(L^{tentative\_labels}.\)
\(L^{new\_labels}\) now contains zero or more new labels residing at j.
Return value: the number of new labels.
-
if there has already been a split break in the current driving time interval and one of the break or rest periods taken at the head vertex is at least 30 min long.
Otherwise, the interval driving time is the driving time since its last reset, which may have occurred on a previous arc or which occurs on the current arc
-
if one of the break or rest periods taken along the arc, before reaching the head vertex, is at least 45 min long, or
-
if there has already been a split break in the current driving time interval and one of the break or rest periods taken along the arc is at least 30 min long, or
Potentially relevant combinations of break or rest times for exact resource extension
Break/rest time of
if
15
\(\beta^{do\_not\_take\_break}=0\) and \(\beta^{split\_break}_j=0\) and \(\tau^{drive\_remaining\_min}>\tau^{rem}\)
30
\(\beta^{do\_not\_take\_break}=0\) and \(\beta^{split\_break}_j=1\)
30+15
\(\beta^{do\_not\_take\_break}=0\) and \(\beta^{split\_break}_j=1\) and \(\tau^{wait+service\_passive}_j>30\)
45
\(\beta^{do\_not\_take\_break}=0\) and \(\beta^{split\_break}_j=0\)
45+15
\(\beta^{do\_not\_take\_break}=0\) and \(\beta^{split\_break}_j=0\) and \(\tau^{wait+service\_passive}_j>45\)
180
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{drive\_remaining\_min}>\tau^{rem}\) and \(\min\{\tau^{drive\_remaining\_daily},\tau^{until\_next\_daily\_rest}\}>\tau^{rem}\)
180+15
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>180\) and \(\min\{\tau^{drive\_remaining\_daily},\tau^{until\_next\_daily\_rest}\}>\tau^{rem}\)
540
\(\beta^{do\_not\_take\_daily\_rest}=0\)
540+15
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>540\)
540+180
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>720\)
660
\(\beta^{do\_not\_take\_daily\_rest}=0\)
660+15
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>660\)
660+180
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>840\)
540+180+15
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>735\)
660+180+15
\(\beta^{do\_not\_take\_daily\_rest}=0\) and \(\tau^{wait+service\_passive}_j>855\)
weekly rest
(in any case)
weekly rest + 15
\(\tau^{wait+service\_passive}_j\) > weekly rest duration
weekly rest + 180
\(\tau^{wait+service\_passive}_j\) > weekly rest duration
weekly rest + 180 + 15
\(\tau^{wait+service\_passive}_j\) > weekly rest duration + 180 min
0
no other break or rest time considered except for weekly rest
or \(\tau^{wait+service\_passive}_j\) < shortest break
or rest time already considered
-
if, along the arc, a break or rest period of at least 15 and a break or rest period of at least 30 min are taken in this order.
The other REFs for the exact algorithm are described in the Appendix.
6.5 Dominance
The dominance procedure depicted on the next page is used (where (a ? b : c) returns b if a is true and c otherwise).
As is usual, the above-mentioned procedure checks whether l 1 dominates l 2, and if so, i.e. if the procedure returns true, discards l 2. If the procedure returns false, this does not mean that l 2 dominates l 1. Therefore, the procedure may have to be called twice for each pair of labels.
Considering the number of resources and their intricate interdependencies, it is not surprising that the aforementioned dominance procedure is rather complicated yet extremely weak. Indeed, the procedure is too weak: it will unnecessarily often return false, i.e. it will not recognize all dominated labels. This is necessary for the overall labelling algorithm to be exact, as the development of an exact dominance procedure is out of the question, because the underlying logic quickly becomes intractable.
Dominance function |
Input: two labels l 1 and l 2 both residing at the same vertex j. |
If c(l 2) < c(l 1) |
return false |
If \(\tau^{since\_start\_of\_calendar\_week}(l_1)\ne\tau^{since\_start\_of\_calendar\_week}(l_2)\) |
return false |
If \(n^{red\_daily\_rests\_since\_last\_weekly\_rest}(l_1)\leqq n^{red\_daily\_rests\_since\_last\_weekly\_rest}(l_2)\) |
or \(n^{ext\_ddt}(l_1)\leqq n^{ext\_ddt}(l_2)\) |
or \(\tau^{since\_last\_weekly\_rest}(l_1)\leqq\tau^{since\_last\_weekly\_rest}(l_2)\) |
or \(\tau^{since\_last\_daily\_rest}(l_1)\leqq\tau^{since\_last\_daily\_rest}(l_2)\) |
or \(\tau^{drive,cur\_calendar\_fortnight}(l_1)\leqq\tau^{drive,cur\_calendar\_fortnight}(l_2)\) |
or \(\tau^{drive,cur\_calendar\_week}(l_1)\leqq\tau^{drive,cur\_calendar\_week}(l_2)\) |
or \(Duration(l_1){\leqq}Duration(l_2)\) |
If \(\tau^{drive,daily}(l_1)\leqq\tau^{drive,daily}(l_2)\) |
If \(\tau^{drive,cur\_interval}(l_1)\leqq\tau^{drive,cur\_interval}(l_2)\) and \(t(l_1)\leqq t(l_2)+(\beta^{split\_break}(l_2) ? 30 : 45)\) |
or \(t(l_1)+(\beta^{split\_break}(l_1) ? 30 : 45)\leqq t(l_2)\) |
or \(\tau^{drive,cur\_interval}(l_1)\leqq\tau^{drive,cur\_interval}(l_2)\) and \(t(l_1){\leqq}t(l_2)\) |
If \(\beta^{split\_break}(l_1)\) and \(\beta^{split\_rest}(l_2)\) |
or \(\beta^{split\_break}(l_1)=\beta^{split\_break}(l_2)\) and \(\beta^{split\_rest}(l_1)\) |
or \(\beta^{split\_rest}(l_1)=\beta^{split\_rest}(l_2)\) and \(\beta^{split\_break}(l_1)\) |
or \(\beta^{split\_break}(l_1)=\beta^{split\_break}(l_2)\) and \(\beta^{split\_rest}(l_1)=\beta^{split\_rest}(l_2)\) |
or \(\beta^{split\_rest}(l_1)=\beta^{split\_rest}(l_2)\) and \(Duration(l_1)+15{\leqq}Duration(l_2)\) |
or \(\beta^{split\_rest}(l_1)=0\) and \(\beta^{split\_rest}(l_2)=1\) |
and \((n^{red\_daily\_rests\_since\_last\_weekly\_rest}(l_1)<n^{red\_daily\_rests\_since\_last\_weekly\_rest}(l_2)\) and \(Duration(l_1)+540{\leqq}Duration(l_2)\) |
or \(Duration(l_1)+660{\leqq}Duration(l_2))\) |
return true |
else if \(t(l_1)+(\beta^{split\_rest}(l_1) ? 540 : 660)\leqq t(l_2)\) |
return true |
return false |
One reason why the dominance procedure is so weak is the check, at the beginning of the routine, whether both labels have the same value for \(\tau^{since\_start\_of\_calendar\_week}\). This check is necessary because, on the one hand, the earlier the time, the more flexibility there is to visit additional customers, but on the other hand, the later the time, the sooner the calendar week will be over and the sooner the driving time in a calendar week or fortnight and the number of enlarged daily driving times are reset. To evaluate the importance of this check, computational tests were also performed with a dominance procedure without this check.
6.6 Heuristic resource extension
The REF described earlier leads to a non-polynomial algorithm (as the algorithm presented in [19], too). However, as the most important area of application of a code for considering drivers’ rules is as a subroutine within a surrounding vehicle routing (meta)heuristic, fast heuristic algorithm is necessary. A heuristic algorithm must not return an illegal schedule as legal, although it may erroneously return that no legal schedule exists. This is similar to test procedures in software development: if such a routine works correctly, then, if it returns that there is an error, there is one, but if the routine does not find an error, this is not a guarantee that there is none.
The objective pursued with a heuristic algorithm is, in the first place, to obtain a legal schedule as often as possible and, in the second place, to obtain as short as possible a duration.
There are many different strategies that can be used when pursuing this objective. In this paper, two possible strategies for speeding up the algorithm by (over-)simplifying the resource update are proposed:
-
A moderate strategy:
-
After 4 h 30 min of driving, take a break of 45 min unless the remaining time until the daily or weekly driving time expires is not more than 45 min. If this is the case, take a daily or weekly rest of 11 h or 24 h respectively. However, take a daily or weekly rest only if the time window of the next customer permits and if a daily or weekly rest becomes necessary before the next customer can be reached.
-
After 9 h of driving, take a daily rest of 11 h unless the remaining time until the next weekly rest becomes necessary is not more than 11 h. If this is the case, take a weekly rest of 24 h. However, take a weekly rest only if the time window of the next customer permits and if a weekly rest becomes necessary before the next customer can be reached.
-
144 h after the end of the last weekly rest, take a weekly rest of 24 h.
-
After 56 h of driving within one calendar week and after 90 h of driving within one calendar fortnight, wait until the end of the calendar week.
-
Extend the daily driving time to 10 h if the time window of the next customer does not allow taking a (possibly reduced) daily rest and if the customer can be reached when the daily driving time is extended. Furthermore, extend the daily driving time to 10 h if there will be no more than two daily driving periods and daily rests in the current calendar week or the planning horizon.
-
Use the possibility to reduce the daily rest period to 9 h in a similar way.
-
When there is waiting time,
-
transform the waiting time into a break of 15 min if it is not longer than 15 min and if there has not yet been a break of 15 min in the current driving time interval;
-
otherwise, transform it into a break of 30 or 45 min if it is not longer than 60 min;
-
otherwise, transform it into a split daily rest of 180 min if it is not longer than 180 min or if the time window does not permit taking a daily rest of 11 h;
-
otherwise, transform it into a daily rest of 11 h if it is not longer than 22 h or if the time window does not permit taking a weekly rest of 24 h;
-
otherwise, transform it into a weekly rest of 24 h;
-
Perform these transformations only if the time window at the subsequent vertex permits; otherwise, transform the waiting time into the next shortest break or rest time that maintains the time window at the subsequent vertex;
-
If waiting time remains, consider adding a split daily rest of 180 min and/or a split break of 15 min;
-
-
Shift the end of the last daily and weekly rest as much as possible.
-
-
An aggressive strategy:
-
Always use the shortest possible break or rest time.
-
Enlarge the daily driving times on the first two occasions per week.
-
Reduce the daily rest periods on the first three occasions per week.
-
Transform waiting time into break or rest time only if the resulting break or rest time does not exceed the waiting time.
-
Perform transformations of waiting into break or rest time only if the time window at the subsequent vertex permits; otherwise, transform the waiting time into the next shortest break or rest time that maintains the time window at the subsequent vertex.
-
If waiting time remains, consider adding a split daily rest of 180 min and/or a split break of 15 min.
-
Shift the end of the last daily and weekly rest as much as possible.
-
In both strategies, only one new label will result from extending an existing label along an arc. This means that when performing a legality check along a given path, there will always be only one label at a time and thus the dominance check is inapplicable. When using the heuristic algorithm as part of an otherwise heuristic or exact path construction procedure, then of course there may be more than one label at a vertex at the same time and the dominance check is still necessary.
6.7 Separating path and schedule construction?
If it were possible to first solve the ESPPRC without drivers’ rules, i.e. to determine all Pareto-optimal paths of the problem when drivers’ rules are disregarded, and only afterwards check the Pareto-optimal paths for compliance with drivers’ rules, this would facilitate matters considerably: The ESPPRC is much easier to solve when drivers’ rules are ignored, and the ESPPWDR is easier to solve on a graph corresponding to an otherwise feasible elementary path than on a general graph. (Solving the ESPPWDR on an elementary path is effectively a legality check.)
It is of course possible that a dominated path is legal. It is of course also possible that no Pareto-optimal path is legal, because there is no legal path at all. Then, the instance is simply infeasible. However, it must be ensured that
-
there is no legal dominated path while at the same time there is no legal Pareto-optimal path and
-
the consideration of drivers’ rules does not make a previously dominated path dominate all previously Pareto-optimal paths.
When solving an ESPPWDR instance without time windows with a labelling algorithm, if a path P dominates a path P′, P does by definition not have a higher consumption of the time resource. Consequently, along P, there will not be more breaks or rest periods than along P′. This means that any schedule which is legal for P′ will also be legal for P. This means that in the absence of time windows, the above two conditions are met.
However, it is easy to see that when there are time windows, which is usually the case, both conditions may be violated: there may be a legal dominated path while all Pareto-optimal paths may be illegal, because a necessary break or rest period may lead to the violation of a time window. Similarly, there may be a dominated path where taking the necessary break or rest periods does not increase the overall time of the path (perhaps because of a very long waiting time at a vertex towards the end of the path), whereas the consideration of break or rest periods incurs a significant increase in overall time for all Pareto-optimal paths. In conclusion, the hoped for two-stage procedure does not generally work.
7 Computational experiments
7.1 Test instances
A considerable difficulty when implementing an algorithm considering drivers’ rules is the debugging and testing for correctness. There are no benchmark instances in the literature. Therefore, to debug and test the algorithms described above, 50 test instances were developed by hand, each of which constitutes an elementary path and tests certain aspects of drivers’ rules. For each of these instances, the legal schedule(s) were identified by inspection, and the algorithms and their implementations were adapted where necessary to return correct results. ‘Correct’ means that for all instances where there is no legal schedule, the algorithms must never return a schedule as legal. Moreover, for all instances where there is a legal schedule, an exact algorithm must find one.
To test the computational behaviour of the algorithms, a set of random test instances also constituting elementary paths was created. To create the instances, the road distances and pure (without breaks) driving times between the 25 biggest German cities were used to model full truckload (FTL) long distance road transports by lorry. The velocity profile used is shown in the following table.
Type of road | Velocity profile of road [km/h] | ||
|---|---|---|---|
Fast | Medium | Slow | |
Autobahn (motorway) | 75 | 65 | 60 |
Bundesstraße (A-road) | 45 | 42 | 40 |
Landstraße (country road) | 40 | 35 | 30 |
Stadtstraße (urban road) | 30 | 20 | 15 |
The objective function of the shortest path algorithm used was the weighted sum of distance and travel time, where the weight for distance was 0.1 and the weight for travel time was 0.9. This is a usual setting in routing systems.
The average driving time was 314 min. Assuming that the vehicle is at the first pickup location at the beginning of the planning horizon and that the route is perfect, i.e. that the pickup of request i + 1 is at the same location as the delivery of request i, between ten and eleven pickup-and-delivery requests can be performed within a six-day working week. Therefore, two sets of test instances were created. The first set has six locations/vertices and a planning horizon of 4320 min (\(\widehat{=}\) 3 days); the second has twelve locations/vertices and a planning horizon of 8640 min (\(\widehat{=}\) 6 days).
At each vertex, except for the first one, passive service times ranging randomly between 15 and 120 min were assigned. Active service times were not considered for simplicity. They are modelled as arcs where only a subset of the resources related to drivers’ rules are extended, where no resources are extended that are not also extended along travel arcs and where there are no waiting times at the end vertices. Hence, they add nothing of computational relevance to the problem.
One hundred random feasible instances of each type were generated. For each instance, six and twelve cities respectively were selected, and the selection sequence defined the visiting sequence. Also for each instance, six and twelve random time windows [a, b] were created with \(0\leqq a \leqq b\leqq 4320(8640)\) . The time windows were sorted by increasing a and accordingly assigned to the cities in the instance. During instance generation, instances without a feasible schedule when disregarding drivers’ rules were discarded.
Instances representing short-haul lorry transports with short distances between customers and a large amount of service time compared to driving time were also not created, particularly because, as stated in the introduction, rules on working hours as stated in [7], which are potentially more relevant in short-haul transport, are not considered here.
7.2 Computational results
The instances were tackled with five different approaches:
-
1.
without drivers’ rules
-
2.
with exact consideration of drivers’ rules
-
3.
with the conservative heuristic approach of considering drivers’ rules
-
4.
with the aggressive heuristic approach of considering drivers’ rules
-
5.
with the REF from Sect. 6.4 and the dominance procedure from Sect. 6.5 without the check whether
$$ \tau^{since\_start\_of\_calendar\_week}(l_1) \ne\tau^{since\_start\_of\_calendar\_week}(l_2) $$
The dominance procedure described in Sect. 6.5 for the exact algorithm is both very weak and rather time-consuming. Therefore, some computational tests were also performed for the exact algorithm without using any dominance at all.
The computational experiments were conducted to answer the following questions:
-
How do the computation times of the different approaches compare?
-
How many of the instances do not have a legal schedule?
-
For how many instances with a legal schedule do the heuristic approaches find a legal schedule?
-
How do the resulting schedule durations computed by the different approaches compare?
-
Which of the heuristic strategies is better? Does one strategy dominate the other?
The results of the computational experiments are depicted on the below tables. The first two tables refer to the instances with six locations; the second two tables refer to the instances with twelve locations. The first and the third table show absolute values of the respective data; the second and the fourth table show the percentage, i.e. relative, increase of the respective data compared to the solution approach disregarding drivers’ rules. Each row in each table refers to a particular solution approach as indicated in the leftmost columns of each table. The second columns indicate the number of feasible schedules obtained. The third columns indicate the minimal, average, and maximal arrival time at the end vertex of an instance. Similarly, the fourth columns indicate the minimal, average, and maximal durations of schedules. In both columns, the absolute values are given in minutes. The fifth columns indicate the CPU times (where the absolute values are given in seconds). The sixth columns show the number of Pareto-optimal solutions generated by the shortest path algorithm, and the rightmost columns show the number of generated labels. As in the previous columns, also in columns 6 and 7, the minimal, average, and maximal values of the respective data are given. The running times for the exact approach for the instances with twelve locations were limited to 300 s; only instances where the algorithm terminated within this time limit were considered to yield a feasible schedule.
The tables below allow the following conclusions:
-
For most instances, there is no legal schedule at all. This means that in practice, to serve the customers of such instances, more than one vehicle is necessary.
-
The heuristic approaches of Sect. 6.6 (the moderate and the aggressive strategy) find legal schedules for only about half the instances for which a legal schedule exists. This is unacceptable and clearly underlines the importance of Observation 2: in a labelling algorithm, decisions are taken without considering the rest of the route and this leads to wrong decisions in many cases.
Computational results
6 Locations, absolute
No. feasible
Arrival time
Duration
Running time
No. Pareto-opt. sols.
No. generated labels
No drivers’ rules
100
1731/2971/4240
1694/2206/3945
0/0/0
1/1/1
6/6/6
Exact
50
2887/3393/4240
2784/3011/3718
0/0.1/1.2
4/520/3354
120/2975/15,720
Heuristic moderate
16
3341/3641/4149
3192/3425/4041
0/0/0
1/1/1
6/6/6
Heuristic aggressive
36
2917/3447/4240
2891/3132/3783
0/0/0
1/1/1
6/6/6
Heuristic dominance
50
2887/3393/4240
2784/3011/3718
0/0/0
2/46/157
116/896/2215
6 Locations, relative
No. feasible
Arrival time
Duration
Running time
No. Pareto-opt. sols.
No. generated labels
No drivers’ rules
0
0/0/0
0/0/0
0/0/0
0/0/0
0/0/0
Exact
− 50
0/11/70
1/40/72
∞/∞/∞
300/51,924/335,300
1900/49,488/261,900
Heuristic moderate
− 84
2/19/59
5/61/88
∞/∞/∞
0/0/0
0/0/0
Heuristic aggressive
− 64
0/10/50
1/47/75
∞/∞/∞
0/0/0
0/0/0
Heuristic dominance
− 50
0/11/70
1/40/72
∞/∞/∞
100/4508/15,600
1833/14,838/36,817
12 Locations, absolute
No. feasible
Arrival time
Duration
Running time
No. Pareto-opt. sols.
No. generated labels
No drivers’ rules
100
4061/6724/8262
3579/5561/8019
0/0/0
1/1/1
12/12/12
Exact
5
6776/7117/7526
6610/6726/6952
6.3/7.2/301.6
95/5045/15,911
41,120/185,940/414,857
Heuristic moderate
2
7294/7550/7806
7182/7400/7618
0/0/0
1/1/1
12/12/12
Heuristic aggressive
2
7388/7553/7718
6803/7047/7290
0/0/0
1/1/1
12/12/12
Heuristic dominance
16
6632/7351/8182
6520/6851/7954
0/1.5/5.3
7/337/1592
5934/28,066/77,521
12 Locations, relative
No. feasible
Arrival time
Duration
Running time
No. Pareto-opt. sols.
No. generated labels
No drivers’ rules
0
0/0/0
0/0/0
0/0/0
0/0/0
0/0/0
Exact
− 95
0/15/31
16/52/79
∞/∞/∞
9400/504,400/1,591,000
342,567/1,549,398/3,457,042
Heuristic moderate
− 98
6/10/15
58/61/64
∞/∞/∞
0/0/0
0/0/0
Heuristic aggressive
− 98
0/12/23
41/50/59
∞/∞/∞
0/0/0
0/0/0
Heuristic dominance
− 84
0/6/31
8/39/79
∞/∞/∞
600/33,588/159,100
49,350/233,781/645,908
-
The exact REF together with the heuristic dominance finds more legal schedules than any other approach. (This is due to the computation time limit, which hinders the exact approach from finding at least as many legal schedules.)
-
The routines were used here to check given routes for the existence of legal schedules. Such a legality check (within a surrounding vehicle routing (meta)heuristic) will probably be the most common use of any drivers’ rules algorithm. To this end, it is decisive that the algorithms run fast, because they will be called very often. The moderate and aggressive heuristic strategies fulfil this requirement (but, as stated before, lack the necessary solution quality). The exact REF, heuristic dominance strategy is a compromise between solution quality and running time, but the running time is acceptable only for short routes. The exact algorithm, of course, has much too high running times to be used as a subroutine in a (meta)heuristic. However, in practice, there are applications where the length of the routes to be checked will be short, i.e. in most cases not more than half a dozen stops, and to support a human dispatcher by checking the legality of a route devised by hand, the running times even of the exact algorithm are acceptable.
The computational results for the exact algorithm without using any dominance at all clearly showed that a dominance procedure is absolutely vital and that even the weak dominance procedure from Sect. 6.5 allows the solution of many instances that would otherwise be intractable.
8 Conclusion
This paper has described an exact and two heuristic labelling algorithms for considering EU drivers’ rules in shortest path problems with resource constraints. It has highlighted several properties of legal schedules, has described the resources, the resource extension functions, and the dominance procedure used in the algorithms, and has presented the results of computational experiments.
The central points of the paper can be summarized as follows.
-
The observations in Sect. 5 show that the consideration of drivers’ rules is non-trivial. This is mainly due to the fact that it is not possible to say at a certain point in time where a break or rest is necessary or where a wait occurs which break or rest to take without considering the rest of the route.
-
The basic ideas of the labelling algorithms are:
-
More than one new label can be created from an old one.
-
Labels are extended iteratively along arcs.
-
-
The resources used are strongly interdependent; all resources are needed to identify the relevant break or rest times, and these times, in turn, determine how the resources are updated.
-
The distinguishing features of the presented algorithms are:
-
The algorithms can construct a route, and not only check the legality of a given route.
-
The algorithms are able to check feasibility and legality of a route simultaneously.
-
They are able to consider arbitrarily long routes, i.e. routes including one or several calendar weeks and weekly rest periods.
-
The network model used as input to the algorithms considers active and passive service times, i.e. non-driving time that must be counted as working time or may be considered as break or rest time respectively. The algorithms are able to consider arbitrary sequences of active and passive service times at customer locations. Hence, the algorithms offer sufficient flexibility to accommodate most, if not all, practically relevant situations.
-
The algorithms output a concrete schedule.
-
New heuristic strategies can be easily implemented.
-
-
The computational experiments show the following:
-
The exact algorithm is useful only for checking the legality of very short routes. Such a use case may be routes devised by human dispatchers for long-haul transports at forwarding companies, where the planning situation is usually highly dynamic and only the next few stops of each vehicle en route are known.
-
The heuristic approaches are fast enough to be used as subroutines for feasibility/legality checks in vehicle routing (meta)heuristics but exhibit a rather moderate solution quality due to the lack of a backtracking option to correct unfavourable decisions on breaks or rests.
-
Overall, the results presented in this paper are such that further consideration of the described approach is worthwhile. Future research concerning the algorithms described in this paper should consider, for example, the solution of the vehicle routing problem with time windows and the pickup-and-delivery problem with time windows with drivers’ rules by branch-and-price, where the subproblems are to be solved by the exact and the heuristic labelling algorithms.
The paper closes with an invitation to the scientific community to prove or falsify the following conjecture:
Decision problem LEGAL-ROUTE-DR
Input: An instance of the elementary shortest path problem with time windows and a feasible solution p. Question: Is there a legal schedule for p?
Conjecture
Decision problem LEGAL-ROUTE-DR is \({\mathcal{NP}}\)-complete.
References
Archetti C, Savelsbergh M (2007) The trip scheduling problem. Tech. rep., School of Industrial and Systems Engineering, Georgia Institute of Technology
Bartodziej P, Derigs U, Malcherek D, Vogel U (2009) Models and algorithms for solving combined vehicle and crew scheduling problems with rest constraints: an application to road feeder service planning in air cargo transportation. OR Spectrum 31:405–429
Brandão J, Mercer A (1997) A tabu search algorithm for the multi-trip vehicle routing and scheduling problem. Eur J Oper Res 100:180–191
Cordeau J, Desaulniers G, Desrosiers J, Solomon M, Soumis F (2002) VRP with time windows. In: Toth P, Vigo D (ed) The vehicle routing problem. SIAM Monographs on Discrete Mathematics and Applications, Philadelphia, pp. 157–193
Desaulniers G, Villeneuve D (2000) The shortest path problem with time windows and linear waiting costs. Trans Sci 34:312–319
Erera A, Karacık B, Savelsbergh M (2008) A dynamic driver management scheme for less-than-truckload carriers. Comput Oper Res 35:3397–3411
European Union (2002) Directive 2002/15/EC of the European Parliament and of the Council of 11 March 2002 on the organisation of the working time of persons performing mobile road transport activities. Available at eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=CELEX:32002 L0015:EN:HTML. Accessed 20th August 2009
European Union (2006) Regulation (EC) No 561/2006 of the European Parliament and of the Council of March 15, 2006 on the harmonisation of certain social legislation relating to road transport and amending Council Regulations (EEC) No 3821/85 and (EC) No 2135/98 and repealing Council Regulation (EEC) No 3820/85. Available at eur-lex.europa.eu/LexUriServ/LexUriServ.do?uri=CELEX:32006 R0561:EN:HTML. Accessed 20th August 2009
Goel A (2009a) Truck driver scheduling and regulation (EC) no 561/2006. Tech. rep., Zaragoza Logistics Center, Zaragoza
Goel A (2009b) Vehicle scheduling and routing with drivers’ working hours. Trans Sci 43:17–26
Goel A, Kok L (2009a) Efficient scheduling of team truck drivers in the European Union. Tech. rep., Operational Methods for Production and Logistics, University of Twente
Goel A, Kok L (2009b) Efficient truck driver scheduling in the United States. Tech. rep., Operational methods for production and logistics, University of Twente
Humphreys G (2007) Tachobook. Foster Tachographs, Preston
Ioachim I, Gélinas S, Soumis F, Desrosiers J (1998) A dynamic programming algorithm for the shortest path problem with time windows and linear node costs. Networks 31:193–204
Irnich S, Desaulniers G (2005) Shortest path problems with resource constraints. In: Desaulniers G, Desrosiers J, Solomon M (eds) Column generation. Springer, New York, pp. 33–65
Kok A, Meyer C, Kopfer H, Schutten J (2009) Dynamic programming algorithm for the vehicle routing problem with time windows and EC social legislation. Tech. Rep. 270, Operational methods for production and logistics, University of Twente
Kopfer H, Meyer C, Wagenknecht A (2007) Die EU-Sozialvorschriften und ihr Einfluß auf die Tourenplanung. Logistik Manag 9:32–47
Meyer C, Kopfer H, Kok A, Schutten M (2009) Distributed decision making in combined vehicle routing and break scheduling. Tech. Rep. 271, Operational methods for production and logistics, University of Twente
Prescott-Gagnon E, Desaulniers G, Drexl M, Rousseau L-M (2009) European drivers rules in vehicle routing with time windows. Tech. rep., École Polytechnique de Montréal and GERAD
Rang C (2008) Lenk- und Ruhezeiten im Straßenverkehr. Vogel, München
Savelsbergh M (1985) Local search in routing problems with time windows. Annl Oper Res 4:285–305
Savelsbergh M (1992) The vehicle routing problem with time windows: minimizing route duration. ORSA J Comput 4:146–154
Stumpf P (1998) Tourenplanung im speditionellen Güterfernverkehr. Gesellschaft für Verkehrsbetriebswirtschaft und Logistik (GVB) e.V., Nürnberg
Xu H, Chen Z, Rajagopal S, Arunapuram S (2003) Solving a practical pickup and delivery problem. Trans Sci 37:347–364
Zäpfel G, Bögl M (2008) Multi-period vehicle routing and crew scheduling with outsourcing options. Int J Prod Econ 113:980–996
Acknowledgments
The authors are grateful to Mr Christoph Rang for his very helpful advice on the legal aspects of drivers’ rules. This research was funded by the Bundesministerium für Wirtschaft und Technologie (German Federal Ministry of Economics and Technology) under grant no. 19G7032A (M. Drexl).
Author information
Authors and Affiliations
Corresponding author
Appendix: Resource extension functions
Appendix: Resource extension functions
Note The subscripts indicating the vertex are suppressed, as the update of the resource variables is also performed on arcs, not only at the end vertex of each arc.
τdrive,daily is set to zero,
-
if, at the head vertex, at least one rest period of at least 660 min is taken, or
-
if there has already been a split daily rest in the current daily driving time interval and one of the break or rest periods taken at the head vertex is at least 540 min long, or
-
if it is still possible to take a reduced daily rest period in the current calendar week and one of the break or rest periods taken at the head vertex is at least 540 min long.
Otherwise, the daily driving time is the driving time since its last reset, which may have occurred on a previous arc or which occurs on the current arc
-
if one of the break or rest periods taken along the arc, before reaching the head vertex, is at least 660 min long, or
-
if there has already been a split daily rest in the current daily driving time interval and one of the break or rest periods taken along the arc is at least 540 min long, or
-
if it is still possible to take a reduced daily rest period in the current calendar week and one of the break or rest periods taken along the arc is at least 540 min long.
\(\tau^{drive,cur\_calendar\_week}\) is set to zero if the weekly or fortnightly driving time limit is reached. Otherwise, it is set to the total driving time since its last reset, which may have occurred on a previous arc or which occurs on the current arc if the weekly or fortnightly driving time limit is reached.
\(\tau^{drive,cur\_calendar\_fortnight}\) is set to zero if the fortnightly driving time limit is reached. Otherwise, it is set to the total driving time since its last reset, which may have occurred on a previous arc or which occurs on the current arc if the fortnightly driving time limit is reached.
If either the weekly or the fortnightly driving time limit is reached when travelling along an arc, a break or rest period is taken until the end of the current calendar week.
The update of \(\tau^{since\_last\_daily\_rest}\) is equivalent to that of τdrive,daily, except that not only the driving time is counted, but also the waiting, break, and rest time and the active and passive service time.
Every time a daily or weekly rest ends, the value of \(\tau^{max\_ext\_of\_last\_daily\_rest}\) is set to the maximum amount of time by which the last daily rest can be extended such that no time windows of subsequent vertices are violated. Before each vertex, \(\tau^{max\_ext\_of\_last\_daily\_rest}\) is set to\( \max\left\{\tau^{max\_ext\_of\_last\_daily\_rest}-\tau^{cur\_extension\_of\_last\_daily\_rest},0\right\}. \)
The update of \(\tau^{since\_last\_weekly\_rest}\) is equivalent to that of \(\tau^{since\_last\_daily\_rest}.\)
The update of \(\tau^{max\_ext\_of\_last\_weekly\_rest}\) is equivalent to that of \(\tau^{max\_ext\_of\_last\_daily\_rest}.\)
\(\tau^{since\_start\_of\_calendar\_week}\) is increased by the driving, waiting, break, and rest time and by the active and passive service time, and it is reset when it exceeds 168 h.
\(n^{ext\_ddt}\) is increased by one each time the decision to extend the daily driving time to 10 h is taken until \(n^{ext\_ddt}=2\) . It is reset to zero whenever \(\tau^{since\_start\_of\_calendar\_week}\) is reset.
\(\beta^{split\_break}\) is set to one if a split break of 15 min is taken. It is reset to zero after the next break or rest period of at least 30 min.
\(\beta^{split\_rest}\) is set to one if a split daily rest of 180 min is taken. It is reset to zero after the next rest period of at least 540 min.
\(\beta^{ddt\_extended}\) is set to one if the daily driving time is extended to 10 h. It is reset to zero after the next daily rest period.
\(n^{red\_daily\_rests\_since\_last\_weekly\_rest}\) is increased by one each time the decision to take a reduced daily rest periods is taken until \(n^{red\_daily\_rests\_since\_last\_weekly\_rest}=3\) . It is reset to zero whenever \(\tau^{since\_last\_weekly\_rest}\) is reset.
For the update of XAT, LAT, and Duration, the reader is referred to [19].
Rights and permissions
About this article
Cite this article
Drexl, M., Prescott-Gagnon, E. Labelling algorithms for the elementary shortest path problem with resource constraints considering EU drivers’ rules. Logist. Res. 2, 79–96 (2010). https://doi.org/10.1007/s12159-010-0022-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12159-010-0022-9





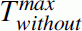 , of 9 h by the required break time of 45 min to
, of 9 h by the required break time of 45 min to  and by increasing the travel time of each arc by the factor
and by increasing the travel time of each arc by the factor