1 Introduction

The session initiation protocol (SIP) is an application layer signaling protocol for creating, modifying, and terminating multimedia sessions among one or more participants [1]. SIP was developed by the Internet Engineering Task Force (IETF) in 1996. With the widespread application of the Voice over IP (VoIP) in Internet [2–4] and mobility management [5–8], SIP has been receiving a lot of attention and the security of SIP is becoming increasingly important [9]. When a user wants to access a SIP service, he or she has to perform an authentication process from the remote server. Thus, authentication is one of the most important issues for SIP. Various authentication schemes ((e.g., [10–24])), especially based on Elliptic Curve Cryptography (ECC), have been proposed to provide security for SIP for a decade [25–32].

In 2005, Yang et al. [33] indicated that the original SIP authentication scheme is vulnerable to off-line password guessing attack and server-spoofing attack. To overcome the attacks, Yang et al. proposed a modified scheme based on Diffie-Hellman key exchange protocol. However, Huang et al.[34] pointed out that the Yang et al.’s scheme may not be suitable for users with limited computational power and further proposed a new scheme. In [35], Jo et al. demonstrated that the schemes by Yang et al. and Huang et al. are both vulnerable to off-line password guessing attack.

Based on Yang et al.’s scheme, Durlanik et al. [36] introduced an efficient authentication scheme for SIP by using Elliptic Curve Diffie-Hellman (ECDH) key exchange protocol. Because of the adoption of elliptic curves, Durlanik et al.’s scheme reduced the total execution time and the requirements for memory in comparison with Yang et al.’s scheme. However, Yoon et al. [37] indicated that Durlanik et al.’s scheme still suffered from off-line password guessing and Denning-Sacco attacks, and projected an improved scheme to overcome the weaknesses. However, Liu et al. [38] demonstrated that Yoon et al.’s scheme still puts up with off-line password guessing and insider attacks.

In 2009, Tsai [39] proposed an efficient authentication protocol based on random nonce, in which one-way hash functions and exclusive-or operations were only utilized for computing all the communication messages. As a result, the computation cost was very low and it was suitable for low computation equipments. However, it was still defenseless to off-line password guessing, Denning-Sacco and stolen-verifier attacks, furthermore, it did not provide any key agreement, known-key secrecy and perfect forward secrecy (PFS) [40–42]. To deal with the problems, Arshad et al. proposed an ECC-based authentication scheme [42]. But, Tang et al. [43] demonstrated the vulnerability of Arshad et al.’s scheme to off-line password guessing attack and introduced an improved scheme to overcome the weakness.

In 2010, Yoo et al. [44] also proposed an authentication scheme based on ECC to deal with the problems in Tsai et al.’s scheme. In 2012, Xie [45] pointed out that Yoo et al.’s scheme still suffers from stolen-verifier and off-line password guessing attacks and proposed an improved scheme. However, Farash and Attari [46] show that Xie’s scheme is also insecure and proposed an enhanced scheme. Recently, Zhang et al. [47] proposed a new password-based authenticated protocol, but Tu et al. [48] foun out thet it is insecure against impersonation attacks. Tu et al. proposed an improved authentication protocol for session initiation protocol using smart card to overcome the security flaws of Zhang et al.’s protocol. They claimed that their protocol satisfies all the security requirements for such protocols. However, this paper indicates that Tu et al.’s protocol is also vulnerable to impersonation attack. To remedy this problem, we proposed an improved protocol by taking a slight change in Tu et al.’s protocol. The security of the improved protocol is proved in the random oracle model.

The rest of this paper is organized as follows. We review Tu et al.’s protocol in Section 2. In Section 3, we propose the security weaknesses of Zhang et al.’s protocol. Our improved protocol and its security proof are proposed in Sections 4 and 5, respectively. A comparison between our improved protocol and the related protocols is proposed in Section 6. Finally, we conclude our paper in Section 7.

2 Review of Tu et al.’s protocol

In this Section, we review Tu et al.’s password-based authenticated key agreement protocol [48] using the notations shown in Table 1). This protocol has four phases: setup, registration, authentication, and password changing phases.

Table 1 The notations
Full size table

2.1 Setup phase

In this phases, the server chooses the following items:

  • The elliptic curve E over the finite field F q ,

  • the additive group \(\mathbb {G}\) generated by the base point P with the prime order p,

  • three one-way hash functions \(h: \{0,1\}^{*} \rightarrow \{0,1\}^{k}\), \(h_{1}:\mathbb {G} \times \{0,1\}^{*} \times \{0,1\}^{*} \rightarrow \{0,1\}^{k}\), and \(h_{2}:\mathbb {G} \times \mathbb {G} \times \{0,1\}^{*} \times \{0,1\}^{*} \rightarrow \{0,1\}^{k}\), and

  • the random number \(s \in \mathbb {Z}^{*}_{p}\) as the server’s secret key.

Finally, the server publishes the public parameters \(\{E(F_{q}),P,p,\mathbb {G},h,h_{1},h_{2}\}\), and maintains the secret key s.

2.2 Registration phase

In this phase, the user U who wants to become a legal user of a remote server performs the following steps over a secure channel:

  • U freely chooses the password PW U and the random number \(a_{U} \in \mathbb {Z}^{*}_{p}\), computes h(PW U ∥a U ), and sends the messages {h(PW U ∥a U ), username U } to the remote server.

  • After receiving the message {h(PW U ∥a U ), username U }, the server computes R U = (h(PW U ∥a U ) + h(username U ||s))P, stores R U in a smart card, and finally delivers the smart card to U.

  • Upon receiving the smart card, U inserts the random numbers a U in the memory of the smart card and memorizes the password PW U in his/her mind.

2.3 Authentication phase

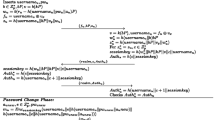
When the user U wants to login to the remote server, he/she inserts his/her smart card to a card reader and inputs his/her username and password PW U . Then, the smart card and the remote server perform as follows, shown in Fig. 1:

Step A1.:

The smart card randomly chooses \(b \in {\mathbb {Z}}^{*}_{p}\) and computes

$$\begin{array}{@{}rcl@{}} V &=& bP,\\ V^{\prime} &=& b(R - h(PW_{U}\|a_{U})P), \\ W &=& h(username_{U}||V||V^{\prime}). \end{array} $$

The smart card then sends REQUEST{username U , V,W} to the remote server.

Step A2.:

Upon receiving REQUEST{username U , V,W}, the remote server firstly computes\(V^{\prime \prime }\hspace *{-.2pt}=\hspace *{-.2pt} h\) (username U ||s)V and \(W^{\prime } = h(username_{U}||V||V^{\prime \prime })\), then it checks if \(W = W^{\prime }\). If it holds, the remote server selects the random numbers \(c,r \in {\mathbb {Z}}^{*}_{p}\) and computes C = cP, K = cV = cbP, SK = h 1(K∥r∥username U ) and \(Auth_{s} = h_{2}(K\|W^{\prime }\|r\|SK)\). Finally, the remote server sends the message CHALLENGE{realm,Auth s ,C,r} to U.

Step A3.:

Upon receiving the message CHALLENGE {realm,Auth s ,C,r}, U computes K = bC = bcP and SK = h 1(K∥r∥username U ). Then he/she verifies Auth s = h 2(K∥W∥r∥SK). If it holds, the smart card computes Auth u = h 2(K∥W∥r+1∥SK) and sends the message RESPONSE{realm,Auth u } to the remote server.

Step A4.:

Upon receiving the message RESPONSE {realm,Auth u }, the remote server checks if \(Auth_{u} = h_{2}(K\|W^{\prime }\|r+1\|SK)\). If it holds, the remote server confirms that the claimant U is a legal user.

Fig. 1
figure 1

The authentication phase of Tu et al.’s protocol [48]

Full size image

2.4 Password changing phase

The user U can change his/her password freely in this phase. To do so, he/she firstly executes the login and authentication phase with his/her username U and the old password PW U . After receiving the successful authentication and sharing the session key SK, the user U does as follows:

Step C1. :

U freely selects the new password \(PW^{*}_{U}\) and the random number \(N,a^{*}_{U} \in \mathbb {Z}^{*}_{p}\). U then computes \(C_{1}=Enc_{SK}(username_{U}\|N\| h(PW^{*}_{U}\|a^{*}_{U})\|h(username_{U}\|\) \(N\| h(PW^{*}_{U}\|a^{*}_{U})))\). Next, U sends {username U ,C 1,N} to the server.

Step C2. :

Upon receiving the message {username U , C 1,N}, the server decrypts C 1 and verifies the integrity of \(h(username_{U}\|N\| h(PW^{*}_{U}\|a^{*}_{U}))\). If it is valid, the server computes \(R^{*}_{U} = h(PW^{*}_{U}\|a^{*}_{U}) - h(username_{U}||s)P\), encrypt it as \(C_{2} = Enc_{SK}(R^{*}_{U}\|h(username_{U}\|N+1\|R^{*}_{U}))\), and sends C 2 to U.

Step C3. :

Upon receiving the message, U decrypts the message and checks the integrity of it. If it is valid, U stores \((PW^{*}_{U}\|a^{*}_{U})\) in the smart card.

3 Cryptanalysis and improvement of Tu et al.’s protocol

In this section, we find out that an active adversary can mount an impersonation attack on Tu et al.’s protocol [48]. We show that an active attacker can masquerade as the remote server to make a session key with users. The details of this attack, shown in Fig. 2, are as follows:

Step I1. :

When the user U wants to login to the remote server, by computing

$$\begin{array}{@{}rcl@{}} V &=& bP, \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} V^{\prime} &=& b(R - h(PW_{U}\|a_{U})P), \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} W &=&h(username_{U}||V||V^{\prime}), \end{array} $$
(3)

and sending the request messageREQUEST {username U ,V,W} to the server, the attacker \(\mathcal {A}\) intercepts and records it.

Step I2. :

\(\mathcal {A}\) then selects random numbers \(c,r \in {\mathbb {Z}}^{*}_{p}\), computes

$$\begin{array}{@{}rcl@{}} &C=cP, \end{array} $$
(4)
$$\begin{array}{@{}rcl@{}} &{\kern28pt}K=cV = cbP, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} &SK=h_{1}(K\|r\|username_{U}),{} \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} &Auth_{s} = h_{2}(K\|W\|r\|SK),{} \end{array} $$
(7)

and sends the message CHALLENGE{realm, Auth s ,C,r} to U.

Step I3. :

Upon receiving the message CHALLENGE {realm,Auth s ,C,r}, U computes

$$\begin{array}{@{}rcl@{}} K^{\prime} &=& bC = bcP, \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} SK^{\prime} &=& h_{1}(K^{\prime}\|r\|username_{U}). \end{array} $$
(9)

Then he/she verifies

$$ Auth_{s} = h_{2}(K^{\prime}\|W\|r\|SK^{\prime}). $$
(10)

If it holds, U believes that the received message was generated by the legal server. Then U computes \(Auth_{u} = h_{2}(K^{\prime }\|W\|r+1\|SK^{\prime })\) and sends the message RESPONSE{realm,Auth u } to the remote server.

Step I4. :

\(\mathcal {A}\) intercepts the response message RESPONSE {realm,Auth u }.

Fig. 2
figure 2

The server impersonation attack on Tu et al.’s protocol

Full size image

Proposition 1

At the end of the proposed impersonation attack, the attacker \(\mathcal {A}\) has accepted as the legal server by the user U.

Proof

As mentioned in Step I3, U ensures that the received message was generated by the legal server if the Eq. 10 holds. In the other hand, the Eq. 10 holds if the \(K = K^{\prime }\) and \(SK^{\prime } = SK\). According to the Eqs. 1, 4, 5 and 8, it is clear that K and \(K^{\prime }\) are same as follows:

$$\begin{array}{@{}rcl@{}} K^{\prime} &=& bC \\ &=& bcP \\ &=& cV \\ &=& K. \end{array} $$

Resultantly, in respect to the Eqs. 6 and 9, the equality \(K = K^{\prime }\), \(SK^{\prime }\) and SK are equal as follows:

$$\begin{array}{@{}rcl@{}} SK^{\prime} &=& h_{1}(K^{\prime}\|r\|username_{U})\\ &=& h_{1}(K\|r\|username_{U}) \\ &=& SK. \end{array} $$

Thus, the verification Eq. 10 holds as follows:

$$\begin{array}{@{}rcl@{}} h_{2}(K^{\prime}\|W\|r\|SK^{\prime}) &=& h_{2}(K\|W\|r\|SK)\\ &=& Auth_{s}. \end{array} $$

Therefore, \(\mathcal {A}\) has succeeded to masquerade as the remote server and share the session key SK = h 1(K∥r∥username U ) with U. □

4 Our improvement

The security flaw of Tu et al.’s protocol [48] is due to this fact that the value of Auth s is computed using the public parameters W, V and username U , and the random numbers r and c. A straightforward solution to overcome the problem is to use a secret parameter for computing Auth s . As can be seen in the original protocol, the parameter \(V^{\prime } = b(R - h(PW_{U}\|a_{U})P) = h(username_{U}||s)V = V^{\prime \prime }\) is a secret parameter for both the user and the remote server. Thus, we improve the the parameter Auth s as \(h_{2}(K\|V^{\prime \prime }\|r\|SK)\) for the server side. Therefore, if the adversary \(\mathcal {A}\) wants to impersonate the remote server, he can not compute Auth s since \(V^{\prime \prime }\) is unknown for him. Note that, this improvement does not impose extra cost to the original protocol.

The details of our improvement on the authentication phase of Tu et al.’s protocol, outlined in Fig. 3, are as follows:

Fig. 3
figure 3

Our improved protocol

Full size image

When the user U wants to login to the remote server, he/she inserts his/her smart card to a card reader and inputs his/her username and password PW U . Then, the smart card and the remote server perform as follows, shown in Fig. 1:

Step A1. :

The smart card randomly chooses \(b \in {\mathbb {Z}}^{*}_{p}\) and computes

$$\begin{array}{@{}rcl@{}} V &=& bP, \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} V^{\prime} &=& b(R - h(PW_{U}\|a_{U})P), \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} W &=& h(username_{U}||V||V^{\prime}). \end{array} $$
(13)

The smart card then sends REQUEST{username U , V,W} to the remote server.

Step A2. :

Upon receiving REQUEST{username U , { V,W}, the remote server firstly computes

$$\begin{array}{@{}rcl@{}} V^{\prime\prime} &=& h(username_{U}||s)V, \end{array} $$
(14)
$$\begin{array}{@{}rcl@{}} W^{\prime} &=&h(username_{U}||V||V^{\prime\prime}). \end{array} $$
(15)

then it checks if \(W = W^{\prime }\). If it holds, the remote server selects the random numbers \(c,r \in {\mathbb {Z}}^{*}_{p}\) and computes

$$\begin{array}{@{}rcl@{}} C &=& cP, \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} K &=& cV, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} SK &=& h_{1}(K\|r\|username_{U}), \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} Auth_{s} &= h_{2}(K\|V^{\prime\prime}\|r\|SK). \end{array} $$
(19)

Finally, the remote server sends the message CHALLENGE{realm,Auth s ,C,r} to U.

Step A3. :

Upon receiving the message CHALLENGE {realm,Auth s ,C,r}, U computes

$$\begin{array}{@{}rcl@{}} K &=& bC, \end{array} $$
(20)
$$\begin{array}{@{}rcl@{}} SK &=& h_{1}(K\|r\|username_{U}). \end{array} $$
(21)

Then he/she verifies

$$ Auth_{s} = h_{2}(K\|W\|r\|SK). $$
(22)

If it holds, the smart card computes

$$ Auth_{u} = h_{2}(K\|W\|r+1\|SK), $$
(23)

and sends the message RESPONSE{realm,Auth u } to the remote server.

Step A4. :

Upon receiving the message RESPONSE {realm,Auth u }, the remote server checks if

$$ Auth_{u} = h_{2}(K\|V^{\prime}\|r+1\|SK). $$
(24)

If it holds, the remote server confirms that the claimant U is a legal user.

5 Security analysis of the improved protocol

In this section, we show that our protocol is secure in the random oracle model. We start with the formal security model and the algorithm assumption that will be used in our proof.

5.1 Security model

In order to make our scheme resist the known attacks to the authentication protocols, we use the method of provable security. The security proof is based on the model proposed by Abdalla and Pointcheval [49]. The model that we use is as follows:

5.1.1 Participants

An authentication protocol Π runs in a network of a number of interconnected participants where each participant is either a client \(U \in \mathcal {U}\) or a trusted server \(S \in \mathcal {S}\). The set \(\mathcal {S}\) is assumed to involve only a single server for simplicity. Each of the participants may have several instances called oracles involved in distinct executions of the protocol Π. We refer to i-th instance of U (resp. S) in a session as \({{\Pi }^{i}_{U}}\) (resp. \({{\Pi }^{i}_{S}}\)). Every instance \({{\Pi }^{i}_{U}}\) (resp. \({{\Pi }^{j}_{S}}\)) has a partner ID \(pi{d^{i}_{U}}\) (resp:\(pi{d^{j}_{S}}\)), a session ID \(si{d^{i}_{U}}\) (resp:\(si{d^{j}_{S}}\)), and a session key \(s{k^{i}_{U}}\) (resp:\(s{k^{j}_{S}}\)). \(pi{d^{i}_{U}}\) (resp:\(pi{d^{j}_{S}}\)) denotes the set of the identities that are involved in this instance. \(si{d^{i}_{U}}\) (resp:\(si{d^{j}_{S}}\)) denotes the flows that are sent and received by the instance \({{\Pi }^{i}_{U}}\) (resp. \({{\Pi }^{j}_{S}}\)). An instance \({{\Pi }^{i}_{U}}\) (resp. \({{\Pi }^{i}_{S}}\)) is said to be accepted if it holds a session key \(s{k^{i}_{U}}\) (resp:\(s{k^{j}_{S}}\)), a session identifier \(si{d^{i}_{U}}\) (resp:\(si{d^{j}_{S}}\)), and a partner identifier \(pi{d^{i}_{U}}\) (resp:\(pi{d^{j}_{S}}\)). Two instances \({{\Pi }^{i}_{U}}\) and \({{\Pi }^{j}_{S}}\) are considered partnered if and only if (1) both of them have accepted, (2) \(pi{d^{i}_{U}} = pi{d^{j}_{S}}\), (3) \(si{d^{i}_{U}} = si{d^{j}_{S}}\), (4) \(s{k^{i}_{U}} = s{k^{j}_{S}}\).

5.1.2 Long-lived keys

Each client \(U \in \mathcal {U}\) holds a password pw U . Each server \(S \in \mathcal {S}\) holds a vector \(pw_{S}= \langle pw_{U} \rangle _{U \in \mathcal {U}}\) with an entry for each client.

5.1.3 Adversary model

The communication network is assumed to be fully controlled by an adversary \(\mathcal {A}\), which schedules and mediates the sessions among all the parties. The adversary \(\mathcal {A}\) is allowed to issue the following queries in any order:

Execute(\({{\Pi }^{i}_{U}}\), \({{\Pi }^{j}_{S}}\))::

This query models passive attacks in which the attacker eavesdrops on honest executions among the client instance \({{\Pi }^{i}_{U}}\) and trusted server instance \({{\Pi }^{j}_{S}}\). The output of this query consists of the messages that were exchanged during the honest execution of the protocol Π.

SendClient(\({{\Pi }^{i}_{U}}\), m)::

The adversary makes this query to intercept a message and then modify it, create a new one, or simply forward it to the client instance \({{\Pi }^{i}_{U}}\). The output of this query is the message that the client instance \({{\Pi }^{i}_{U}}\) would generate upon receipt of message m. Additionally, the adversary is allowed to initiate the protocol by invoking SendClient(\({{\Pi }^{i}_{U}}\), Start).

SendServer(\({{\Pi }^{i}_{S}}\), m)::

This query models an active attack against a server. The adversary makes this query to obtain the message that the server instance \({{\Pi }^{i}_{S}}\) would generate on receipt of the message m.

Reveal(\({{\Pi }^{i}_{U}}\))::

This query models the known session key attack. The adversary makes this query to obtain the session key of the instance \({{\Pi }^{i}_{U}}\).

Corrupt(U)::

This query returns to the adversary the long-lived key pw U for participant U.

Test(\({{\Pi }^{i}_{U}}\))::

Only one query of this form is allowed to be made by the adversary to a fresh oracle. To respond to this query, a random bit b∈{0, 1} is selected. If b = 1, then the session key held by \({{\Pi }^{i}_{U}}\) is returned. Otherwise, a uniformly chosen random value is returned.

5.1.4 Fresh oracle

An oracle \({{\Pi }^{i}_{U}}\) is called fresh if and only if the following conditions hold: (1) \({{\Pi }^{i}_{U}}\) has accepted, and (2) \({{\Pi }^{i}_{U}}\) or its partner (if exists) has not been asked a Reveal query after their acceptance.

5.1.5 Protocol Security

The security of an authentication protocol Π is modeled by the game \(Game({\Pi },\mathcal {A})\). When playing this game, the adversary \(\mathcal {A}\) can make many queries mentioned earlier to \({{\Pi }^{i}_{U}}\) and \({{\Pi }^{j}_{S}}\). If \(\mathcal {A}\) asks a single query, Test(\({{\Pi }^{i}_{U}}\)), where \({{\Pi }^{i}_{U}}\) has accepted and is fresh, then \(\mathcal {A}\) outputs a single bit \(b^{\prime }\). The aim of \(\mathcal {A}\) is correctly guessing the bit b in the test session. More precisely, we define the advantage of \(\mathcal {A}\) as follows:

$$Adv_{\Pi,D}(\mathcal{A})=|2Pr[b^{\prime}=b]- 1|. $$

The protocol Π is said to be secure if \(Adv_{\Pi ,D}(\mathcal {A})\) is negligible.

5.2 Computational assumption

We define the decisional Diffie-Hellman (DDH) assumption which we use in the security proof of our scheme.

Definition 1

The DDH assumption can be precisely defined by two experiments, \(Exp^{ddh-real}_{P,p} (W)\) and \(Exp^{ddh-rand}_{P,p} (W)\). An adversary W is provided with uP, vP and uvP in the experiment \(Exp^{ddh-real}_{P,p} (W)\), and uP, vP and wP in the experiment \(Exp^{ddh-rand}_{P,p} (W)\), where u, v and w are drawn at random from \(\mathbb {Z}^{*}_{p}\). Define the advantage of W in violating the DDH assumption, \(Adv^{ddh}_{P,p} (W)\), as follows:

$$\begin{array}{@{}rcl@{}} Adv^{ddh}_{P,p} (W) &=& \max \{| Pr[Exp^{ddh-real}_{P,p} (W) = 1]\\ &-& Pr[Exp^{ddh-rand}_{P,p} (W) = 1]|\}. \end{array} $$

5.3 Security proof

Theorem 1

Let D be a uniformly distributed dictionary of passible passwords with size |D|. Let Π describes the improved authentication protocol defined in Fig. 3 . Suppose that DDH assumption holds, Then,

$$\begin{array}{@{}rcl@{}} Adv_{\Pi,D}(\mathcal{A}) \leq \frac{{q^{2}_{h}} + q^{2}_{h1} + q^{2}_{h2}}{2^{k}} + \frac{(q_{s}+q_{e})^{2}}{p^{2}}\\ + 2q_{e} \cdot Adv_{P,p}^{DDH}(W) +2\max\{\frac{q_{h1}}{2^{k}}, \frac{q_{s}}{|D|}\}, \end{array} $$

where q s denotes the number of Send queries; q e denotes the number of Execute queries; q h , q h1 and q h2 denotes the number of hash queries to h, h1 and h2, respectively.

Proof

This proof consists of a sequence of hybrid games, starting at the real attack G 0 and ending up at game G 4 where the adversary has no advantage. For each game G i (0≤i≤4), we define Succ i as the event that \(\mathcal {A}\) correctly guesses the bit b in the test session.

Game G 0.:

This game is the real protocol, in the random-oracle model. In this game, all the instances of U and the trusted server S are modeled as the real execution in the random oracle. By definition of event Succ i , which means that the adversary correctly guesses the bit b involved in the Test-query, we have

$$ Adv_{\Pi,D}(\mathcal{A})=2|\Pr[Succ_{0}]- \frac{1}{2}|. $$
(25)
Game G 1.:

This game is as the same as the game G 0 except that we simulate the hash oracles h, h 1 and h 2 as usual by maintaining hash lists h List , h1 List and h2 List with entries of the form (Inp, Outp). On hash query for which there exists a record (Inp, Outp) in the hash list, return Outp. Otherwise, randomly choose Outp ∈{0, 1}k, send it to \(\mathcal {A}\) and store the new tuple (Inp, Outp) into the hash list. We also simulate all the instances, as the real players would do, for the Send-query and for the Execute, SendClient, SendServer, Reveal, Corrupt and Test queries. From the viewpoint of the adversary, we easily see that the game is perfectly indistinguishable from the real attack. Hence,

$$ \Pr[Succ_{1}]=\Pr[Succ_{0}]. $$
(26)
Game G 2.:

In this game, we simulate all the oracles in game G 1, except we cancel the game in which some collisions appear on the partial transcripts (V,C) and on hash values. According to the birthday paradox, the probability of collisions in output of hash oracles are at most \({{q^{2}_{h}}}/{2^{k+1}}\), \({q^{2}_{h1}}/{2^{k+1}}\) and \({q^{2}_{h1}}/{2^{k+1}}\) where q h , q h1 and q h2 denote the maximum number of hash queries. Similarly, the probability of collisions in the transcripts is at most (q s +q e )2/(2p 2), where q s represents the number of queries to the SendClient and SendServer oracles and q e represents the number of queries to the Execute oracle. So we have

$$\begin{array}{@{}rcl@{}} |\Pr[Succ_{2}]-\Pr[Succ_{1}]|\leq \frac{{q^{2}_{h}} + q^{2}_{h1} + q^{2}_{h2}}{2^{k+1}} + \frac{(q_{s}+q_{e})^{2}}{2p^{2}} .\end{array} $$
(27)
Game G 3.:

In this game, we change the simulation of queries to the SendClient oracle. First, we randomly select a session executed by partner instances \({{\Pi }^{i}_{U}}\) and \({{\Pi }^{j}_{S}}\).

  • When SendClient(\({{\Pi }^{i}_{U}}, Start\)) is asked, we choose random values u∈[1,p+1] and compute V = uP, \(V^{\prime } = u(R_{U} - h(PW_{U}\|a_{U})P\) and \(W = h(username_{U}||V||V^{\prime })\), and return {username U ,V,W} to \(\mathcal {A}\).

  • When SendClient \(({{\Pi }^{i}_{U}}\), (username U , V, W) is asked, we choose random values v,r∈[1,p+1] and compute V = vP, SK and Auth s like the real protocol and return {realm,Auth s ,C,r} to \(\mathcal {A}\).

So, it can be easily seen that this game is perfectly indistinguishable from the previous game G 2. Hence,

$$ \Pr[Succ_{3}]=\Pr[Succ_{2}]. $$
(28)
Game G 4.:

In this game, we once again change the simulation of queries to the SendClient oracle for the selected session in game G 3. This time, we change the way we compute K so that it become independent of password and ephemeral keys. When SendServer \(({{\Pi }^{j}_{S}}\), (username U , V, W)) and SendClient \(({{\Pi }^{i}_{A}}\), (realm,Auth s ,C,r)) are asked, we set K = wP, where w is selected from \(\mathbb {Z}^{*}_{p}\) at random. The difference between the game G 4 and the game G 3 is as follows:

$$\begin{array}{@{}rcl@{}} |\Pr[Succ_{4}]-\Pr[Succ_{3}]|\leq q_{e} \cdot Adv_{P,p}^{DDH}(W). \end{array} $$
(29)

By assuming a successful adversary \(\mathcal {A}\) to distinguish G 3 and G 4, we construct a DDH solver W.

In game G 4, the Diffie-Hellman key K is random and independent with the user’s password and ephemeral keys. So, there are three possible cases where the adversary distinguishes the real session key SK and the random key as follows:

Case 1.:

the adversary queries (K,r,username U ) to h 1. The probability that this event occurs is q h1/2k.

Case 2.:

the adversary asks SendClient query except SendClient(\({{\Pi }^{j}_{S}}\), m) and successfully impersonates U to S. The adversary is not allowed to reveal static key PW U of U. Thus, in order to impersonate A, the adversary has to obtain some information of the password PW A of A. The probability is 1/D. Since there are at most q s sessions of this kind, the probability that this event occurs is lower than q s /|D|

As a conclusion,

$$ \Pr[Succ_{4}]=\frac{1}{2}+\max\{\frac{q_{h1}}{2^{k}}, \frac{q_{s}}{|D|}\}. $$
(30)

Combining the Eqs. 25, 26, 27, 28, 29 and 30 one gets the announced result as follows:

$$\begin{array}{@{}rcl@{}} Adv_{\Pi,D}(\mathcal{A})&=&2|\Pr[Succ_{0}]- \frac{1}{2}|\\ &=&2|\Pr[Succ_{0}]- \Pr[Succ_{4}]+\max\left\{\frac{q_{h1}}{2^{k}}, \frac{q_{s}}{|D|}\right\}|\\ &\leq &2(|\Pr[Succ_{0}]- \Pr[Succ_{4}]|+\max\left\{\frac{q_{h1}}{2^{k}}, \frac{q_{s}}{|D|}\right\})\\ &\leq &2(|\Pr[Succ_{1}]- \Pr[Succ_{2}]| + |\Pr[Succ_{3}]\\-\Pr[Succ_{4}]|+\max\left\{\frac{q_{h1}}{2^{k}}, \frac{q_{s}}{|D|}\right\}){}\\ &\leq &\frac{{q^{2}_{h}} + q^{2}_{h1} + q^{2}_{h2}}{2^{k}} + \frac{(q_{s}+q_{e})^{2}}{p^{2}} + 2q_{e} \cdot Adv_{P,p}^{DDH}(W) \\+2\max\{\frac{q_{h1}}{2^{k}}, \frac{q_{s}}{|D|}\}.{} \end{array} $$

□

6 Computation comparison

To estimate the computation cost of our scheme, the following notations are defined: PM is the time complexity of scalar point multiplication, PA is the time complexity of elliptic curve point addition, H is time complexity of hash function and I is time complexity of modular inversion. The computation cost of the proposed protocol and a comparison with Zhang et al.’s protocol [47] and Tu et al.’s protocol [48] are summarized in Table 2. As can be seen, the computation cost of our improved protocol is same as Tu et al.’s protocol.

Table 2 Computation comparisons
Full size table

7 Conclusions

In this paper, we analyzed Tu et al.’s password-based authenticated key agreement protocol. We pointed out that Tu et al.’s protocol suffers from impersonation attack by which an attacker can masquerade as a legal server to share common session keys with legal users. Moreover, we proposed an improvement of Tu et al.’s protocol to overcome the security problem. The security of the improved protocol was proved in the random oracle model. Our improvements did not change the computational and communication cost of the original protocol.