Design of a pharmaceutical supply chain in uncertain conditions considering financial strategies and environmental concerns

Abstract

One of the most pressing concerns of patients is the timely delivery of required medicines at the appropriate time and location, as a lack of medicines can have a direct impact on their health. A multi-product and multi-period integer programming model is presented in this paper to design a pharmaceutical supply chain network with different layers: supplier, manufacturer, distributor, and customer. The proposed model's main goal is to maximize profits across the entire pharmaceutical supply chain. Revenues come from the sale of pharmaceuticals both domestically and internationally. Expenses include transportation, production, the procurement of materials, manufacturer establishment, distribution center establishment, inventory holding, medicines expiration, ordering, and loans. In the suggested model, import and export, customs tariffs, loans, and currencies are all presented. Environmental concerns about greenhouse gas emissions from transportation throughout the supply chain are also considered. A case study for the province of Fars is presented to evaluate the efficiency of the proposed model. While numerical results confirm the model's effectiveness, they also show that as the level of uncertainty increases, profitability decreases; however, profitability can be enhanced by carefully regulating characteristics such as fixed cost of manufacturer construction and fixed cost of distribution center construction.

1 Introduction

A supply chain (SC) is typically thought of as a unified process. Suppliers, manufacturing centers, distribution centers (DCs), and retailers are among the companies that strive to convert raw resources into finished goods and distributing them to end users in this process. Designing a SC network in such a way that it performs well has a significant impact on SC performance (Beamon 1998). SC management, as well as the effective and efficient management of financial information and materials in all network components, are critical factors in maximizing total profit and customer satisfaction (Faisal et al. 2006). As a result, the main goal of SC design is to maintain effectiveness to meet customer demand.

The pharmaceutical SC (PSC) is one of the most important networks in healthcare systems (Weraikat et al. 2016a, b). It will be impossible to improve society's health indicators unless this chain is properly managed and planned at the strategic and operational levels. The main goal of PSC is to get the drug to the patient at the appropriate time and location. Different issues such as facility location, drug corruption, inventory control, financial approaches, suppliers, and end customers must all be considered when designing an efficient PSC. It should be noted that if the order does not arrive on time, the risk to the patient's health increases, in addition to the possibility of losing the customer and increasing the costs of medication shortages. On the other hand, if the order quantity of pharmaceutical products is expected to be higher than usual, there is a risk that the drugs will expire during storage, as most pharmaceutical products have limited expiration dates. As a result, solutions must be devised that account for crucial parameters such as cost, quantity, and expiration date to deliver medication to the patient when he or she requires it (Darestani and Hemmati 2019). Many differences can be seen when comparing the supply of pharmaceutical products to the supply of other goods. For example, while other products (such as food) can be substituted, drug substitution is difficult in the pharmaceutical industry due to the direct link between these products and patient health. To avoid drug shortages, hospitals must store large quantities of pharmaceutical products. As a result, higher holding costs may be incurred (Shah 2004).

The PSC is divided into three sections: drug production, distribution, and sale to the end-user. The drug production sector consists of several steps, including initial drug research and development, the legal process for obtaining a drug license, and drug commercialization. The steps taken in the field of drug production differ from one country to the next. The drug distribution industry is in charge of getting drugs from manufacturers or importers to retailers. The tasks of the drug distribution sector can vary depending on where manufacturers and importers are located, as well as where end customers are located. Transferring drugs to rural and remote areas, for example, is more difficult than in urban areas. One of the things that makes the distribution problem more difficult is keeping track of drug storage temperatures. The final step in the PSC is to sell drug to the end customer, who must receive the medicine at the appropriate time and location. The drug is delivered to the end customer from retailers such as pharmacies, hospitals, and in some countries, physicians (Sousa et al. 2005).

A new complex integer programming model is presented in this paper for designing a multi-period and multi-commodity PSC network under uncertainty and profit maximization. Real-world constraints, such as drug expiration dates, production, and storage, are taken into account in this model. Environmental concerns about greenhouse gas emissions caused by transportation in the SC are also taken into account. Given that the initial budget may not be sufficient to construct the necessary factories and DCs, additional funding can be obtained through loans. The raw materials required to manufacture the drug can be obtained from both domestic and international sources. Furthermore, the manufactured drugs can be sent to both domestic and international customers. The model also includes financial parameters such as customs duty for raw material imports, and loan interest. The key parameters of the system are considered uncertain because many parameters of the PSC are uncertain in real world. The chance constrained fuzzy programming method is utilized to cope with uncertainty. Finally, the suggested model's efficacy is assessed using a case study.

In this article, in the second section, a brief overview of the history of similar research is provided. The problem is defined and explained in detail in the third section. The fourth section introduces the problem modelling, followed by directions on how to linearize the model and deal with uncertainty. The model's performance is examined using a case study in the fifth section. Finally, the findings are summarized and concluded.

2 Literature review

Previous studies on the design of PSC networks are reviewed in this section. Levis and Papageorgiou (2004) proposed a two-step scenario-oriented mathematical model for capacity planning in the pharmaceutical industry in uncertain condition. Amaro and Barbosa-Póvoa (2008) proposed a reverse flow modeling approach for planning and scheduling of SC. Both operational and marketing conditions were taken into account and the proposed methodology was validated through a genuine pharmaceutical case. Sousa et al. (2011) investigated a dynamic allocation-planning model in the global SC at a pharmaceutical company. This model examines production and distribution costs as well as tax rates in various locations to maximize the company's net profit value. Masoumi et al. (2012) have investigated a generalized network oligopoly model for SCs of pharmaceutical products. This model addresses the competition among producers as they seek to determine their optimum profit streams while taking into account the interests of consumers. Susarla and Karimi (2012) addressed a complex model for large-scale multi-period global PSC by integrating procurement, production, and distribution decisions. Uthayakumar and Priyan (2013) have created an inventory model that incorporates the continuous assessment of production and distribution in a SC, which includes a pharmaceutical company and a hospital. In this model, a method is presented for determining the ideal inventory amount, transfer time, and number of deliveries to the chosen hospitals, all while keeping the total cost to a minimum.

Guerrero et al. (2013) presented a method for determining the best inventory control policies for a real-world pharmaceutical system. New criteria have been considered in this system, including random demand, unique factors for regulating health care such as emergency delivery, needed service charges, and a new limitation in the order policy. Meiler et al. (2015) proposed a new density pattern-based method for SC planning in the pharmaceutical industry, and found near-optimal solutions for establishing a schedule that coordinates production operations while taking network flows into account. Mousazadeh et al. (2015) created a robust possibilistic optimization model for designing a PSC network. Their suggested model aids several decisions such as the location of manufacturing centers and DCs and optimal material flows. Weraikat et al. (2016a) investigated a decentralized negotiation process for coordinating undesired substances in customer areas for a reverse PSC. Weraikat et al. (2016b) looked at the impact of persuading customers to return leftover drugs. The goal of returning the remaining pharmaceuticals is to strengthen the reverse PSC's stability. They assessed the model’s effectiveness after providing an acceptable coordination technique between the medication manufacturer and those in charge of collecting drugs from consumer locations. Chung and Kwon (2016) established a framework for the integrated SC management for the consideration of the influence of large-scale production, which comprises manufacturers, distribution hubs, wholesalers, and demand markets. Nematollahi et al. (2017) have studied the simultaneous coordination in the visit time interval and the level of services in the PSC with random demand. In this arrangement, a drug supplier visits a shop regularly and then delivers the order when a certain amount of time has passed.

Zahiri et al. (2017) established a possibilistic-stochastic mathematical model for constructing a PSC network in a multi-period planning horizon by taking into account the effects of environmental challenges. Pariazar et al. (2017) looked at the impact of linked suppliers' failures, as well as an inspection to find these failures in the food and pharmaceutical SCs. A two-stage stochastic model was suggested to investigate the relationship between costs and risk when constructing a supply network. Martins et al. (2017) proposed a method based on optimization and simulation to handle network redesign of pharmaceutical wholesalers, trading off operational costs and customer service level. Marques et al. (2017) proposed a new method that combines an integer linear programming model with a Monte Carlo simulation method to handle integrated design and production decisions under uncertain conditions. A pharmaceutical business was used to validate the suggested methodology. Zahiri and Jula (2018) proposed a model for creating a PSC network with the goals of minimizing overall cost and lowering the maximum unmet demands. They took into account the product's flexibility, replaceability, quantitative discount, and uncertainty. Nematollahi et al. (2018) have examined how coordination in the PSC, according to the level of services, through a participatory decision model. A two-level PSC with stochastic demand has been explored in this model, which consists of a drug distributor and a store. The balance between goals and Pareto optimum solutions was addressed in this study.

Savadkoohi et al. (2018) created a model for a multi-level PSC network design. To reduce the overall network cost, the model calculates the location of production centers and DCs, as well as material flows and the best inventory policy based on the expiration date. A possibilistic approach has been offered to handle the uncertainty of parameters. Sabouhi et al. (2018) proposed a flexible SC in which the efficiency of possible suppliers is first analyzed using a data envelopment analysis model, and then a possibilistic-stochastic model for selecting operational risks is built utilizing the productivity acquired. Marques et al. (2018) presented a new model to make effective strategic decisions, such as process design and capacity investment, in the face of uncertainty. Campelo et al. (2019) suggested a model for vehicle routing in the PSC. An instance size reduction algorithm and a programming-based mathematical analysis method have been presented to solve this problem. Roshan et al. (2019) looked into PSC crisis management and examined three objective functions, each to lower the network's overall cost, lowering the unsatisfied demand, and increase satisfaction with social considerations. Weraikat et al. (2019) investigated how to improve the PSC sustainability. An analytical model has been given in this work to explore the impact of establishing a vendor-managed inventory system on reducing the number of expired pharmaceuticals in hospitals. They have also run a series of Monte Carlo simulations to consider the problem in the event of demand uncertainty. Kees et al. (2019) proposed a novel multi-period model to formulate management strategies that incorporates financial considerations into the hospital SC. This problem is modeled as a mixed integer linear programming (MILP) problem with two opposing goals: total cost and total product scarcity. Fuzzy restrictions are used to account for data unpredictability.

Akbarpour et al. (2020) addressed an issue of designing integrated relief network for pharmaceutical cases. The suggested approach addresses the issue of pharmaceutical item vulnerability, as well as enhancing the mobility of relief facilities and the advantages of adopting the participatory coverage method. To deal with demand uncertainty, they used a robust optimization method. Franco and Alfonso-Lizarazo (2020) investigated a stochastic sample optimization strategy in the PSC to improve tactical and operational choices. This method concentrates on the pharmacy-hospital level and takes into account the unpredictability of demand, prices, and medicines. Goodarzian et al. (2020) developed a multi-period PSC network under uncertainty by considering routing, producing, distributing, ordering, and inventory holding issues. To handle uncertainty, a robust fuzzy programming method has been created. Several multi-objective meta-heuristic algorithms have been presented to discover the best solutions. Abbasi et al. (2021) examined the problem of designing a pharmaceutical logistics network considering the dangers of product disruption and congestion. Their model determines the position and quantity of primary and backup hubs and DCs, backup facility locations, perishable product inventories, and product reordering. Fatemi et al. (2021) introduced a model for designing a PSC with the goals of lowering overall costs, unmet demands, and waiting times. Goodarzian et al. (2021) addressed a model for the PSC network's construction, with the goal of reducing pharmaceutical costs and delivery times to hospitals and pharmacies while maximizing transportation system dependability. For the suggested model, different heuristic and meta-heuristic algorithms are suggested. Ahmad et al. (2021) have set sustainability targets in the context of PSC optimization. Under the uncertainty of the exchange between social, economic, and environmental goals, numerous restrictions have been discovered by assuring the best allocation of different goods between different levels. To confirm the model and optimization technique, an industry case study from a pharmaceutical business is provided. Nasrollahi and Razmi (2021) provided a multi-objective model for optimizing utilization and lowering overall expenses that takes into account various hospitals with varying capacities for different medications. This article considers a multi-layer SC that includes suppliers, distribution facilities, hospitals, and physicians. Rekabi et al. (2021) created a multi-objective stochastic model to improve patient medicine delivery delays and SC operating costs. This research also looks at ways to reduce greenhouse gas emissions. Santos et al. (2022) presented an inventory routing model with the goals of minimizing the costs of ordering, holding, transportation, shortage and overflow. They used a genetic algorithm to solve the model and validated their model using a real case study in a pharmaceutical industry.

Table 1 summarizes recent studies on the subject of the PSC that used mathematical modeling. As can be seen, this table compares the research done on inventory control, customs tariffs, export, import, currency, loan, environmental concerns, capacity of facilities, period, uncertainty, solution methods, and case study. Table 1 shows that only a small percentage of the publications in question have addressed the topic of imports. The implications of foreign currencies and export are not discussed in these publications. The problem of customs tariffs has only been covered in one of these articles. The issue of loan has been discussed in a few of these articles, but it is vital to address it in order to provide the necessary investment in practical conditions. Environmental issues are rarely explored in these studies, and they deserve further attention and study. This study fills in all of these gaps in the literature.

Table 1 A specification of related literature

3 Problem definition

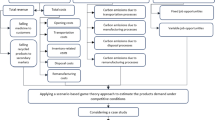
A mathematical model for designing a PSC network that considers financial approaches is presented in this paper. This model's schematic diagram is shown in Fig. 1. As can be seen, the first level of the PSC consists of suppliers who may be located within or outside of the country. The manufacturers at the second level of the chain are responsible for turning the incoming raw materials into drugs. DCs, which are responsible for drug storage and delivery, make up the third level of the chain. Customers, who can be domestic or international, make up the fourth level of the chain. According to the objective function, the model in question determines where and when DCs will be built. In addition, after constructing the production centers, the model decides what medicine to send from the manufacturer to the DCs based on factors such as demand, expiration date, inventory, and order point.

Fig. 1

A schematic of the studied PSC network

Due to a lack of space, pharmacies and hospitals are unable to store large amounts of drug inventory and goods corruption is uncommon in these facilities. As a result, DCs are primarily responsible for keeping drugs in the chain. Due to the large volume of drugs stored in DCs, there is a risk of drug corruption in these facilities. Therefore, policies such as not sending expired drugs or sending drugs according to the expiration date have been considered in inventory control in this model to reduce the effects of this problem. Each time a drug is ordered, an ordering fee must be paid. Furthermore, due to their perishability and increased storage costs, large quantities of drugs cannot be ordered. As a result, this model attempts to select the best option among these possibilities. Because each expired product has a cost in the model, the model attempts to reduce the number of expired drugs by considering demand and inventory control, as well as timely delivery of medicine from the manufacturer to the distributor and from the distributor to the customer. Transporting raw materials and drugs emits greenhouse gases. Given the importance of environmental issues, it is considered that the total greenhouse gases across the network should not exceed a certain amount.

Financial strategies have also been used in this model. The financial strategies in question can be classified into two groups. The first set of strategies looks at how and under what conditions loans are distributed. The total budget limitation has also been considered in the proposed model. Any manufacturer must have a sufficient budget, which can be funded either from the overall budget or through a loan. The model in question decides which manufacturer to establish in which period, as well as which manufacturer to use the loan, based on the optimization policies. Getting a loan is only possible during certain periods due to the model's planning horizon and the guarantee of loan repayment, and the proposed model regulates the rules of loan reception according to the restrictions provided. The second category of strategies examines how to provide foreign currency for the import of raw materials in accordance with Iranian laws, using the Nima system and the Central Bank. It should be noted that each country has its own set of currency rules, so the problem's assumptions and limitations can be written differently depending on the circumstances of each country.

Some of the raw materials needed to make medicine are not always available in the country, and the manufacturer must source some of them from outside the country. Sometimes this is done to diversify the raw material supply basket to prevent monopolies or to make the supply of raw materials from abroad to the country more economical. Providing foreign currency for the import of raw materials has become one of the most difficult tasks for manufacturers today. One option is to provide the necessary currency through the free market, which is neither cost-effective nor efficient and raises production costs. Another option is to prepare the required currency through revenue from medicine exports. Exporters of goods must offer the currency obtained from their exports in the Nima currency system, according to Central Bank instruction (CBI 2018). The Central Bank's directive divides the exchange earnings from exports into four categories.

• First category: less than 1 million euros. Goods exporters are not needed to register for currency sales through the Nima system. The exporter of goods is able to import the materials and services needed for the manufacturing of the exported items or trade cycle in exchange for the export revenue. A goods exporter can also register with the foreign exchange monitoring system, Sana system, to give his foreign currency income to approved banks and exchange offices.

• Second category: between 1 to 3 million euros. Goods exporters are obliged to register 50% of their export revenue to the Nima system, and they are free from selling foreign currency in the Nima system for up to one million euros. Goods exporters must return the rest of their currency to the economic cycle in one of two ways: (a) they can use the desired currency in exchange for importing materials and services required by their production or trade cycle, after registering the order, or (b) they can offer this currency in the form of remittances or banknotes to authorized banks and exchange offices, after registering the order in the Sana system.

• Third category: between 3 to 10 million euros. Exporters are free to sell foreign currency in the Nima system for up to one million euros, and they are required to register in the Nima system 70% of the export currency. Exporters are obliged to reintegrate the remaining money into the economy by utilizing it to import goods and services necessary for their trade or production cycle.

• The fourth category: more than ten million euros. In the Nima system, the exporters are required to register 90% of the export currency, and they are free from selling foreign currency in the Nima system for up to one million euros. Exporters are required to use the money that is left over to import the goods and services that are essential to their trade or production cycle in order to reintegrate it into the economy.

The extra export currency from the first and second categories in the proposed model is recorded in the Sana system after the import cost is subtracted, as only the first and second categories are required to be registered in the Sana system. Additionally, 50% of the second category's export money is also registered in the Nima system. It should be mentioned that selling more currency than the allotted percentage for each category is feasible under the Nima system. Therefore, in the suggested model, after subtracting the import costs of raw materials, the extra export currency is also recorded in the Nima system, in addition to the defined proportion of the export currency that must be registered for the third and fourth categories.

The proposed PSC design problem shares some similarities with traditional SC network design problems. The common SC layers like suppliers, manufacturers, distributors, and customers are included in the suggested model. Thus, like any traditional SC network design, several strategic and tactical decisions are considered, such as supplier selection, manufacturer and distributor locations, material flows between suppliers and manufacturers, product flows between manufacturers and distributors, and product flows between distributors and customers. Certain traditional SC models, such as the PSC model under consideration, also account for the uncertainty of inherent parameters. There are some distinctions between the proposed model and traditional SC problems as well. First, the proposed model takes into account the environmental aspect of sustainable development goals by limiting the harmful environmental effects reflected in greenhouse gas emissions from transportation between different SC layers. Second, since internal suppliers might not have all the materials needed to produce drugs, the model takes importing raw materials along with customs tariffs into account. Third, taking into account the perishability of the drugs, the lifetime of drugs, and the ideal inventory policy as represented by the order quantity and reorder point in the mathematical model are taken into account. Fourth, the distribution of manufactured drugs to both domestic and foreign consumers is taken into account. Fifth, the financial strategy for providing the necessary budget for installing manufacturers is considered. Moreover, because of the planning horizon of the model and loan repayment guarantee, obtaining loans are only feasible during specific times. Sixth, in light of the Central Bank of Iran's regulations, the financial plan for supplying foreign currency for the import of raw materials that can be obtained from the currency obtained from the exports is taken into consideration.

3.1 Assumptions

• All customers' demand must be met in full during each period.

• A maximum of one manufacturer and distributor can be established for each period in each specified area.

• Medicines have a finite lifetime.

• Each producer is permitted to take out a loan for the construction of a manufacturer only once.

• After the planning horizon has ended, loan repayment is not possible.

• The cost of purchasing raw materials has not been directly considered in the objective. Instead, the cost is deducted from export earnings in foreign currency.

• It is not permitted to send a customer expired medicine.

• There is no limit to the number of drug orders.

4 Mathematical model

PSC modeling with the goal of maximizing profits is described in this section. Sets, indices, parameters, and decision variables that are required for modeling are introduced in this section.

4.1 Sets

$I$:

Candidate locations for the establishment of a drug manufacturing plant

$J$:

Candidate locations for establishing a drug DC

$K$:

Internal customers (hospitals, clinics, and pharmacies)

${K}^{\prime}$:

Foreign customers (hospitals, clinics, and pharmacies)

$P$:

Manufactured drugs

$T$:

Time periods

$S$:

Internal suppliers

${S}^{\prime}$:

Foreign suppliers

$M$:

Raw materials

$N$:

Loan courses

$W$:

Drug lifetimes

4.2 Parameters

${{\text{cm}}}_{msit}$:

Cost of transporting each unit of raw material m from internal supplier s to manufacturer i in time t

${{{\text{cm}}}^{\prime}}_{ms^{\prime}it}$:

Cost of transporting each unit of raw material m from foreign supplier sꞌ to manufacturer i in time t

${\widetilde{{\text{C}}}}_{pijt}$:

Cost of transporting each unit of drug p from manufacturer i to DC j in time t

${\widetilde{{\text{Ca}}}}_{pjkt}$:

Cost of transporting each unit of drug p from DC j to internal customer k in time t

${\widetilde{{\text{Cb}}}}_{pj{k}^{\prime}t}$:

Cost of transporting each unit of drug p from DC j to foreign customer k' in time t

${\widetilde{{\text{f}}}}_{ipt}$:

Fixed installation cost of manufacturer i to produce drug p in time t

${\widetilde{{\text{g}}}}_{jt}$:

Fixed installation cost of DC j in time t

${\widetilde{\uprho }}_{pit}$:

Cost of producing each unit of drug p in manufacturer i in time t

${\widetilde{{\text{C}}}}_{pjt}^{in}$:

Cost of maintaining each unit of drug p in DC j in time t

${\widetilde{{\text{C}}}}_{pt}^{e}$:

Cost of each unit of expired drug p in time t

${\widetilde{{\text{C}}}}_{pjt}^{\pi }$:

Cost of ordering drug p from DC j in time t

${\widetilde{\uplambda }}_{mst}$:

Purchase price of each unit of raw material m from internal supplier s in time t

${\widetilde{\uplambda }^{\prime}}_{ms^{\prime}t}$:

Purchase price of each unit of raw material m from foreign supplier sꞌ in time t

${{\text{Pr}}}_{pkjt}$:

Price of each unit of drug p purchased by internal customer k from DC j in time t

${{\text{Pr}}^{\prime}}_{pk^{\prime}jt}$:

Price of each unit of drug p purchased by foreign customer k' from DC j in time t

${\widetilde{\uptau }}_{ip}$:

Capacity of manufacturer i to produce drug p

${\widetilde{\updelta }}_{j}$:

Storage capacity of DC j

${{\text{RF}}}_{p}$:

Lifetime of drug p

${\widetilde{{\text{d}}}}_{kpt}$:

Demand of internal customer k for drug p in time t

${\widetilde{{\text{d}}^{\prime}}}_{k^{\prime}pt}$:

Demand of foreign customer k' for drug p in time t

${{\text{gm}}}_{msi}$:

Greenhouse gas emissions for shipment each unit of raw material m from internal supplier s to manufacturer i

${{\text{gm}}^{\prime}}_{ms^{\prime}i}$:

Greenhouse gas emissions for shipment each unit of raw material m from foreign supplier s' to manufacturer i

${{\text{gh}}}_{pij}$:

Greenhouse gas emissions for shipment each unit of drug p from manufacturer i to DC j

${{\text{gn}}}_{pjk}$:

Greenhouse gas emissions for shipment each unit of drug p from DC j to internal customer k

${{\text{g}}n^{\prime}}_{pjk^{\prime}}$:

Greenhouse gas emissions for shipment each unit of drug p from DC j to foreign customer ${k}^{\prime}$

${\text{GHG}}$:

Maximum allowable emissions in the entire SC

${{\text{h}}}_{mp}$:

Quantity of raw material m needed to make each unit of drug p

${\uptheta }_{m}$:

Customs tariff for each unit of raw material m imported

${{\text{r}}}_{t}$:

Loan interest rate in time t

${\text{A}}$:

Maximum number of allocated loans

${\text{B}}$:

Very large number

${\text{BU}}$:

Total budget

${\text{BoundA}}$:

The first limit of export value

${\text{BoundB}}$:

The second limit of export value

${\text{BoundC}}$:

The third limit of export value

${\text{EN}}$:

The maximum export earnings that can be excluded from the Nima system registration

${\text{rb}}$:

The percentage of export earnings from the second category that must be entered into the Nima system

${\text{rc}}$:

The percentage of export earnings from the third category that must be entered into the Nima system

${\text{rd}}$:

The percentage of export earnings from the fourth category that must be entered into the Nima system

${\text{nima}}$:

Exchange rate in the Nima system

${\text{sana}}$:

Exchange rate in the Sana system

4.3 Variables

${x}_{ipt}$:

If a manufacturer is established at location i to produce drug p in time t 1, otherwise 0

${y}_{jt}$:

If a DC is established at location j in time t 1, otherwise 0

${\upmu }_{pjt}$:

If the stock of drug p in DC j in time t is less than the reorder point 1, otherwise 0

${{\text{O}}}_{pjkt^{\prime}t}^{w}$:

Amount of drug p with a lifetime w that reaches at DC j in time ${t}^{\prime}$ and is delivered to internal customer k in time t

${\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t}^{w}$:

Amount of drug p with a lifetime w that reaches DC j in time ${t}^{\prime}$ and is delivered to foreign customer ${k}^{\prime}$ in time t

${u}_{pijt}^{w}$:

Amount of drug p shipped with lifetime w from manufacturer i to DC j in time t

${{\text{q}}}_{msipt}$:

Amount of raw material m sent from internal supplier s to manufacturer i to produce drug p in time t

${q^{\prime}}_{ms^{\prime}ipt}$:

Amount of raw material m sent from foreign supplier sꞌ to manufacturer i to produce drug p in time t

${{\text{ma}}}_{ipt}$:

Amount of budget allocated to build manufacturer i to produce drug p in time t

${{\text{mma}}}_{jt}$:

Amount of budget allocated to build DC j in time t

${{\text{in}}}_{pjt}$:

Inventory of drug p in DC j in time t

${e}_{pjt^{\prime}t}$:

Amount of drug p received in DC j at the beginning of time ${t}^{\prime}$ and expired at the end of time t

${\uppi }_{pj}$:

Reorder point of drug p in DC j

${{\text{l}}}_{nipt}$:

If a loan is approved with the maturity of n time to establish manufacturer i to produce drug p in time t 1, otherwise 0

${{\text{l}}}_{iptn}^{a}$:

Amount of loan allocated for the establishment of manufacturer i for the production of drug p in time t with maturity of n time

${{\text{l}}}_{iptn}^{ir}$:

Interest on the loan allocated for the establishment of manufacturer i for the production of drug p in time t with maturity of n time

${{\text{AA}}}_{t}$:

If in time t, the export value is less than the first limit (in the first category) 1, otherwise 0

${{\text{BB}}}_{t}$:

If in time t, the export value is more than the first limit and less than the second limit (in the second category) 1, otherwise 0

${{\text{CC}}}_{t}$:

If in time t, the export value is more than the second limit and less than the third limit (in the third category) 1, otherwise 0

${{\text{DD}}}_{t}$:

If in time t, the value of exports is more than the third limit (in the fourth category) 1, otherwise 0

${Vsec}_{t}$:

Revenue from the sale of currency from the second category in the Nima system in time t

${{\text{Vthi}}}_{t}$:

Revenue from the sale of currency from the third category in the Nima system in time t

${{\text{Vfor}}}_{t}$:

Revenue from the sale of currency from the fourth category in the Nima system in time t

${{\text{Vex}}}_{t}$:

Revenue from the sale of excess currency after deducting import costs in the Nima system in time t

${\Omega }_{t}$:

Total Revenue from the sale of currency in the Nima system in time t

${\Gamma }_{t}$:

Total Revenue from the sale of currency in the Sana system in time t

4.4 Formulation

Using the introduced assumptions and symbols, a mathematical model of the problem is presented.

$$\begin{aligned}{\text{max}}TB=&\sum_{j}\sum_{k}\sum_{p}\sum_{t}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}P{r}_{pkjt}{O}_{pjkt^{\prime}t}^{w} +\sum_{t}{\Gamma }_{t}+\sum_{t}{\Omega }_{t}\\& -\sum_{s}\sum_{i}\sum_{m}\sum_{t}\sum_{p}\left(c{m}_{msit}+{\widetilde{\lambda }}_{mst}\right){q}_{msipt}-\sum_{i}\sum_{j}\sum_{p}\sum_{t}\sum_{w=1}^{{RF}_{p}}{\widetilde{C}}_{pijt}{u}_{pijt}^{w}\\&- \sum_{p}\sum_{j}\sum_{k^{\prime}}\sum_{t}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}{\widetilde{{\text{Cb}}}}_{pj{k}^{\prime}t}{\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t}^{w}-\sum_{p}\sum_{j}\sum_{k}\sum_{t}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}{\widetilde{{\text{Ca}}}}_{pjkt}{{\text{O}}}_{pjkt^{\prime}t}^{w}\\&- \sum_{i}\sum_{j}\sum_{p}\sum_{t}\sum_{w=1}^{{RF}_{p}}{\widetilde{\rho }}_{pit}{u}_{pijt}^{w}-\sum_{j}\sum_{t}{\widetilde{g}}_{jt}({y}_{jt}-{y}_{j,t-1})-\sum_{i}\sum_{p}\sum_{t}{\widetilde{f}}_{ipt}\left({x}_{ipt}-{x}_{ip,t-1}\right)\\&- \sum_{j}\sum_{p}\sum_{t}\sum_{t^{\prime}}{\widetilde{C}}_{pt}^{e}{ e}_{pjt^{\prime}t}-\sum_{p}\sum_{j}\sum_{t}{\widetilde{C}}_{pjt}^{in}i{n}_{pjt}-\sum_{j}\sum_{p}\sum_{t}{\widetilde{C}}_{pjt}^{\pi }{\mu }_{pjt}-\sum_{i}\sum_{p}\sum_{t}\sum_{n}{l}_{iptn}^{ir}\end{aligned}$$

(1)

$$\sum\limits_{j}\sum\limits_{w=1}^{{RF}_{p}}{u}_{pijt}^{w}\le {\widetilde{\tau }}_{ip}{x}_{ipt} \quad \forall i,p,t$$

(2)

$$\sum\limits_{k}\sum\limits_{t=t^{\prime}}^{T}{{\text{O}}}_{pjkt^{\prime}t}^{w}+\sum\limits_{k^{\prime}}\sum\limits_{t=t^{\prime}}^{T}{\mathrm{O^{\prime}}}_{pjk{^\prime}t^{\prime}t}^{w}\le \sum\limits_{i}{u}_{pijt^{\prime}}^{w} \quad \forall p,j,t^{\prime},1\le w\le {RF}_{p}$$

(3)

$${u}_{pijt}^{w}\le B{x}_{ipt} \quad \forall i,j,p,t,1\le w\le {RF}_{p}$$

(4)

$${u}_{pijt}^{w}\le B{y}_{jt} \quad \forall i,j,p,t,1\le w\le {RF}_{p}$$

(5)

$${{\text{O}}}_{pjkt^{\prime}t}^{w}\le B{y}_{jt} \quad \forall j,p,k,t^{\prime},{\text{t}},1\le w\le {RF}_{p}$$

(6)

$${\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t}^{w}\le B{y}_{jt} \quad \forall j,p,k^{\prime},t^{\prime},{\text{t}},1\le w\le {RF}_{p}$$

(7)

$$\begin{array}{l}\sum\limits_{s}\sum\limits_{i}\sum\limits_{m}\sum\limits_{t}\sum\limits_{p}g{m}_{msi}{q}_{msipt}+\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{t}\sum\limits_{p}{{\text{g}}m^{\prime}}_{ms^{\prime}i}{q^{\prime}}_{ms^{\prime}ipt}+\sum\limits_{i}\sum\limits_{j}\sum\limits_{p}\sum\limits_{t}\sum\limits_{w=1}^{{RF}_{p}}g{h}_{pij}{u}_{pijt}^{w}\\ +\sum\limits_{j}\sum\limits_{k}\sum\limits_{p}\sum\limits_{t}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}g{n}_{pjk}{{\text{O}}}_{pjkt^{\prime}t}^{w}+\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}g{n^{\prime}}_{pjk^{\prime}}{\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t}^{w}\le GHG\end{array}$$

(8)

$$\sum\limits_{s}{q}_{msipt}+\sum\limits_{s^{\prime}}{q^{\prime}}_{ms^{\prime}ipt}=\sum\limits_{j}\sum\limits_{w=1}^{{RF}_{p}}{h}_{mp}{u}_{pijt}^{w} \quad \forall m,i,p,t$$

(9)

$${x}_{ip,t-1}\le {x}_{ipt} \quad \forall i,p,t$$

(10)

$$\sum\limits_{i}\sum\limits_{p}\sum\limits_{w=1}^{{RF}_{p}}{u}_{pijt}^{w}+\sum\limits_{p}i{n}_{pj,t-1}\le {\widetilde{\delta }}_{j}{y}_{jt} \quad \forall j,t$$

(11)

$${y}_{j,t-1}\le {y}_{jt} \quad \forall j,t$$

(12)

$${e}_{pjt^{\prime}t}=\sum\limits_{i}{u}_{pijt}^{w=t-t^{\prime}+1}-\sum\limits_{k}\sum\limits_{t^{\prime\prime}=t^{\prime}}^{t}{{\text{O}}}_{pjkt^{\prime}t^{\prime\prime}}^{w=t-t^{\prime}+1}-\sum\limits_{k^{\prime}}\sum\limits_{t^{\prime\prime}=t^{\prime}}^{t}{\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t^{\prime\prime}}^{w=t-t^{\prime}+1} \quad \forall j,p,1\le t^{\prime}\le t\le T$$

(13)

$$i{n}_{pjt}=\sum\limits_{i}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{w=1}^{{RF}_{p}}{u}_{pijt^{\prime}}^{w}-\sum\limits_{k}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{t^{\prime\prime}=t^{\prime}}^{t}\sum\limits_{w=1}^{{RF}_{p}}{{\text{O}}}_{pjkt^{\prime}t^{\prime\prime}}^{w}-\sum\limits_{k^{\prime}}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{t^{\prime\prime}=t^{\prime}}^{t}\sum\limits_{w=1}^{{RF}_{p}}{\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t^{\prime\prime}}^{w}-\sum_{t^{\prime}=1}^{t}\sum_{t^{\prime\prime}=t^{\prime}}^{t}{e}_{pjt^{\prime}t^{\prime\prime}} \quad \forall j,p,t$$

(14)

$$\sum\limits_{k}\sum\limits_{t=t^{\prime}+w}^{T}{{\text{O}}}_{pjkt^{\prime}t}^{w}=0 \quad \forall j,p,1\le w\le {RF}_{p},1\le t^{\prime}\le T$$

(15)

$$\sum\limits_{k^{\prime}}\sum\limits_{t=t^{\prime}+w}^{T}{\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t}^{w}=0 \quad \forall j,p,1\le w\le {RF}_{p},1\le t^{\prime}\le T$$

(16)

$$i{n}_{pj,t-1}-{\pi }_{pj}+1\le B(1-{\mu }_{pjt}) \quad \forall j,p,t$$

(17)

$${\pi }_{pj}-i{n}_{pj,t-1}\le B {\mu }_{pjt} \quad \forall j,p,t$$

(18)

$$\sum\limits_{i}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{w=1}^{{RF}_{p}}{u}_{pijt^{\prime}}^{w}\le B {\mu }_{pjt} \quad \forall j,p,t$$

(19)

$$\sum\limits_{j}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{w=1}^{{RF}_{p}}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w}\ge {\widetilde{d^{\prime}}}_{k^{\prime}pt} \quad \forall k^{\prime},p,t$$

(20)

$$\sum\limits_{j}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{w=1}^{{RF}_{p}}{{\text{O}}}_{pjkt^{\prime}t}^{w}\ge {\widetilde{d}}_{kpt} \quad \forall k,p,t$$

(21)

$$A{A}_{t}+B{B}_{t}+C{C}_{t}+D{D}_{t}=1 \quad \forall t$$

(22)

$$\begin{array}{l}\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}{Pr^{\prime}}_{pk^{\prime}jt}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w}\le BoundA A{A}_{t}+BoundB B{B}_{t}+BoundC C{C}_{t}\\+B(1-A{A}_{t}-B{B}_{t}-C{C}_{t})\end{array} \quad \forall t$$

(23)

$$BoundA B{B}_{t}+BoundB C{C}_{t}+BoundC D{D}_{t}\le \sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w} \quad \forall t$$

(24)

$$\begin{array}{l}\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\le\\\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w}+B\left(1-A{A}_{t}\right)\end{array} \quad \forall t$$

(25)

$$\begin{array}{l}\\\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\le\\\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rb\right)+EN+B\left(1-B{B}_{t}\right)\end{array}\quad \forall t$$

(26)

$$\begin{array}{l}\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\le \\ \sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rc\right)+EN+B\left(1-C{C}_{t}\right) \end{array} \quad \forall t$$

(27)

$$\begin{array}{l}\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\le \\ \sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rd\right)+EN+B\left(1-D{D}_{t}\right) \end{array} \quad \forall t$$

(28)

$$\begin{array}{l}{\Gamma }_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}-\\\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}\left[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}\left(1+{\theta }_{m}\right)\right]{q^{\prime}}_{ms^{\prime}ipt}) sanaA{A}_{t}+ \end{array} \quad \forall t$$

(29)

$$\begin{array}{l}(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}\left(1-rb\right)+EN-\\\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}\left[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}\left(1+{\theta }_{m}\right)\right]{q^{\prime}}_{ms^{\prime}ipt})sanaB{B}_{t}\end{array}$$

$${\Omega }_{t}=V{{\text{sec}}}_{t}+Vth{i}_{t}+Vfo{r}_{t}+Ve{x}_{t} \quad \forall t$$

(30)

$$V{{\text{sec}}}_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}rb-EN) B{B}_{t} nima \quad \forall t$$

(31)

$$Vth{i}_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}rc -EN)C{C}_{t} nima \quad \forall t$$

(32)

$$Vfo{r}_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}rd-EN) D{D}_{t} nima \quad \forall t$$

(33)

$$\begin{aligned}Ve{x}_{t}=&[\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rc\right) C{C}_{t} \\ & + \sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rd\right)D{D}_{t}+EN\left(C{C}_{t}+D{D}_{t}\right)\\&-\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}\left[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}\left(1+{\theta }_{m}\right)\right]{q^{\prime}}_{ms^{\prime}ipt}\left(C{C}_{t}+D{D}_{t}\right)]nima\end{aligned}\quad \forall t$$

(34)

$$m{a}_{ipt}\le B{x}_{ipt} \quad \forall i,p,t$$

(35)

$$mm{a}_{jt}\le B{y}_{jt} \quad \forall j,t$$

(36)

$$\sum_{i}\sum_{p}\sum_{t}m{a}_{ipt}+\sum_{j}\sum_{t}mm{a}_{jt}\le BU$$

(37)

$${l}_{nipt}\le B{x}_{ipt} \quad \forall i,p,n,t$$

(38)

$${l}_{iptn}^{a}\le B{l}_{nipt} \quad \forall i,p,n,t$$

(39)

$${l}_{nipt}=0 \quad \forall i,p,n,t\;(t+n-1>T)$$

(40)

$$\sum\limits_{n}{l}_{nipt}\le 1 \quad \forall i,p,t$$

(41)

$${l}_{iptn}^{ir}=\frac{{l}_{iptn}^{a}[{{r}_{t}\left({1+r}_{t}\right)}^{n}]}{{\left({1+r}_{t}\right)}^{n}-1} \quad \forall i,p,n,{\text{t}}$$

(42)

$$\sum_{n}\sum_{i}\sum_{p}\sum_{t}{l}_{nipt}\le A$$

(43)

$$\sum_{i}\sum_{p}\sum_{t}{\widetilde{f}}_{ipt}({x}_{ipt}-{x}_{ip,t-1})\le \sum_{i}\sum_{p}\sum_{t}m{a}_{ipt}+\sum_{i}\sum_{p}\sum_{t}\sum_{n}{l}_{iptn}^{a}$$

(44)

$$\sum_{j}\sum_{t}{\widetilde{g}}_{jt}({y}_{jt}-{y}_{j,t-1})\le \sum_{j}\sum_{t}mm{a}_{jt}$$

(45)

$${x}_{ipt},{y}_{jt},{\mu }_{pjt},{l}_{nipt},A{A}_{t},B{B}_{t},C{C}_{t},D{D}_{t}\in \left\{\mathrm{0,1}\right\} \quad \forall i,j,p,t,n$$

(46)

$$\begin{array}{l}{u}_{pijt}^{w},{O}_{pjkt^{\prime}t}^{w},{O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w},{q}_{msipt},{q^{\prime}}_{ms^{\prime}ipt},{l}_{iptn}^{a},{l}_{iptn}^{ir},mm{a}_{jt},m{a}_{ipt},i{n}_{pjt},{e}_{pjt^{\prime}t},{\pi }_{pj},V{{\text{sec}}}_{t},Vth{i}_{t},Vfo{r}_{t},Ve{x}_{t},\\{\Omega }_{t},{\Gamma }_{t}\ge 0 \quad \forall s,s^{\prime},i,j,k,k^{\prime},m,p,w,n,t,t^{\prime}\end{array}$$

(47)

Total profit is maximized as expressed in Eq. (1). The sections that are displayed with a positive coefficient represent income and the sections that are displayed with a negative coefficient represent expenses. Incomes include: the sale of drug to domestic consumers, the sale of currency in the Sana system, and the sale of currency in the Nima system. The costs include: the cost of supplying and transporting raw materials from the domestic suppliers, the cost of drug transportation from manufacturers to DCs, the cost of drug transfer from the DCs to the foreign and domestic customers, the cost of drug production, the cost of establishing DCs, the cost of establishing manufacturers, the cost of expiration drugs, the cost of keeping the drugs, the cost of ordering the drugs via DCs, and the cost of the loan. Due to the limitation in financial resources, it has been tried to provide some of the budget for the construction of the manufacturer through loans. The total income from the sale of drug to foreign consumers and the total cost of supplying raw materials from foreign suppliers are included in the calculations of the Sana and Nima systems. The currency obtained from exports can be sold in the Central Bank's Nima and Sana system and earn money from its sale.

Constraint (2) ensures that the maximum delivery capacity of drug p is equal to or less than the total capacity of the manufacturer built for that drug during each time. Constraint (3) states that the quantity of drugs sent from the DC to domestic and foreign customers is less than or equal to the quantity of drugs sent from the manufacturers to that DC. Constraints (4) and (5) state that no goods can be transferred from the manufacturer to DCs until the DC or manufacturer is established. Constraints (6) and (7) state that no drug will be transferred to domestic or foreign customers until the DC is established. According to constraint (8), the total amount of greenhouse gases produced across the transportation activities between various SC layers must not go over a specific threshold. The total amount of greenhouse gases produced includes the amount of greenhouse gases produced in the transportation of raw materials from domestic suppliers to manufacturers, the amount of greenhouse gases produced in the transportation of raw materials from foreign suppliers to manufacturers, the amount of greenhouse gases produced in the transportation of drugs from manufacturers to DCs, and the amount of greenhouse gases produced in the transportation of drugs from DCs to the domestic and foreign customers. Note that this constraint assesses the effects of the proposed model's suggested carbon cap policy in order to investigate the environmental side of sustainability. A company's carbon usage is capped at the specified amount under the carbon cap policy. Constraint (9) shows the balance between the raw materials and the manufactured drugs. Constraint (10) ensures that the established manufacturer would remain operational by the completion of the planning horizon. Constraint (11) ensures that in each time, the maximum storage capacity of drug p is equal to or less than the total capacity of the DC built. Constraint (12) guarantees that the DC that has been created will continue to function by the end of the planning horizon. In constraint (13), the amount of drugs that may expire at the conclusion of each time period is calculated. The quantity of inventory is expressed at the conclusion of each time period in constraint (14). The amount of inventory for a given time is equal to the total items received from the first time to the conclusion of that time period after deducting items sent to customers and goods expired during all of these times. It is prohibited to send expired drugs from the DC to domestic customers, according to constraint (15). It is forbidden to send an expired drug from the DC to foreign customers, according to constraint (16). The relationship between current inventory and the status of orders over a specific time period is covered by constraints (17) through (19). In more specific terms, if the inventory level of drug p at the beginning of a given period is smaller than the reorder point for DC j, the order for this drug will be placed in the same time period. Constraints (20) and (21) ensure that the external and internal demands for each drug are satisfied in each time period.

According to the problem definition, the Central Bank of Iran has divided the income obtained from exports into four categories and established regulations for each category. Therefore, constraint (22) specifies that export earnings can only be obtained in one of the four categories during each time. Export revenue is classified as the first category if it is less than one million euros, $BoundA$. When export revenue ranges from 1 to 3 million euros, it falls into the second category (e.g. between $BoundA$ and $BoundB$). Export revenue falls into the third category when it ranges from 3 to 10 million euros (e.g. between $BoundB$ and $BoundC$). Finally, if the income exceeds 10 million euros,$BoundC$, it falls into the fourth category. Therefore, constraints (23) and (24) determine the upper and lower bounds of the export earning, respectively. Constraints (25) to (28) also indicate the maximum import amount for each specified category, since the currency needed for import is supposed to be provided from the currency obtained from drug export. The total revenue obtained from the sale of currency in the Sana system is determined in constraint (29). The total earnings from the sale of currency in the Nima system is calculated in constraint (30). The earning from the sale of currency in the Nima system is calculated according to the second, third, and fourth categories determined in the Central Bank's instructions in constraints (31) to (33), respectively. Note that these export revenues must be registered in the Nima system and the rest can be attributed to the import of raw materials. After subtracting the cost of raw material imports, the additional export revenue from the third and fourth categories in the Nima system is calculated in constraint (34). Constraints (35) and (36) state that if there is no need to build a manufacturer and a DC, no funds will be allocated to them. The total budget allocated to manufacturers and DCs can only be as much as the total budget, according to constraint (37). If there is no need to build a manufacturer, constraint (38) states that no loan will be allocated to that manufacturer. Constraint (39) states that the amount of a loan allocated to the establishment of manufacturers is zero until it is not approved. Constraint (40) states that the repayment times of a loan cannot be longer than the remaining times of the planning horizon in order to ensure repayment. Constraint (41) states that a maximum of one loan is granted per time for the construction of manufacturer i for the production of drug p. The loan interest is calculated according to constraint (42). The maximum number of approved loans in the entire SC is indicated by constraint (43). The cost of constructing manufacturers must be equal to or less than the total allocated loan and budget for their establishment, according to constraint (44). According to constraint (45), construction costs for DCs must be equal to or less than the entire budget allotted for their establishment. The types of decision variables are also indicated by constraints (46) and (47).

4.5 Linearization

Constraints (29) and (31) to (34) in the above model are nonlinear since they are calculated using two continuous and binary variables multiplied together, which can be made linear using the following method. Assume ${{\text{X}}}_{1}$ is a binary variable and ${{\text{X}}}_{2}$ is a continuous variable.

$$Z={X}_{1}\times {X}_{2}$$

(48)

For linearization, the method proposed by Chang and Chang (2000) has been used.

$$Z\le {X}_{2}$$

(49)

$$Z\le B\times {X}_{1}$$

(50)

$$Z\ge {X}_{2}-B(1-{X}_{1})$$

(51)

Nonlinear expressions in the proposed model can be transformed to linear expressions using the method outlined above. Constraint (29) has been linearized using constraints (52) to (64). It should be noted that ${\varphi }_{ms^{\prime}ipt}={q^{\prime}}_{ms^{\prime}ipt}A{A}_{t}$,${\vartheta }_{ms^{\prime}ipt}={q^{\prime}}_{ms^{\prime}ipt}B{B}_{t}$, ${\delta }_{pjk^{\prime}t^{\prime}t}^{w}=A{A}_{t}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}$, and ${\tau }_{pjk^{\prime}t^{\prime}t}^{w}= {BB}_{t}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}$.

$$\begin{aligned}{\Gamma }_{t}=&(\sum_{j}\sum_{k^{\prime}}\sum_{p}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ \delta }_{pjk^{\prime}t^{\prime}t}^{w} \\& -\sum_{s^{\prime}}\sum_{i}\sum_{m}\sum_{p}\left[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}\left(1+{\theta }_{m}\right)\right]{\varphi }_{ms^{\prime}ipt}) sana \\&+(\sum_{j}\sum_{k^{\prime}}\sum_{p}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ \tau }_{pjk^{\prime}t^{\prime}t}^{w}\left(1-rb\right)+EN{BB}_{t} \\&-\sum_{s^{\prime}}\sum_{i}\sum_{m}\sum_{p}\left[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}\left(1+{\theta }_{m}\right)\right]{\vartheta }_{ms^{\prime}ipt})sana\end{aligned} \quad \forall t$$

(52)

$${\varphi }_{ms^{\prime}ipt}\le {q^{\prime}}_{ms^{\prime}ipt} \quad \forall m,s^{\prime},i,p,t$$

(53)

$${\varphi }_{ms^{\prime}ipt}\le BA{A}_{t} \quad \forall m,s^{\prime},i,p,t$$

(54)

$${\varphi }_{ms^{\prime}ipt}\ge {q^{\prime}}_{ms^{\prime}ipt}-B(1-A{A}_{t}) \quad \forall m,s^{\prime},i,p,t$$

(55)

$${\vartheta }_{ms^{\prime}ipt}\le {q^{\prime}}_{ms^{\prime}ipt} \quad \forall m,s^{\prime},i,p,t$$

(56)

$${\vartheta }_{ms^{\prime}ipt}\le B{BB}_{t} \quad \forall m,s^{\prime},i,p,t$$

(57)

$${\vartheta }_{ms^{\prime}ipt}\ge {q^{\prime}}_{ms^{\prime}ipt}-B(1-{BB}_{t}) \quad \forall m,s^{\prime},i,p,t$$

(58)

$${\delta }_{pjk^{\prime}t^{\prime}t}^{w}\le { O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w} \quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(59)

$${\delta }_{pjk^{\prime}t^{\prime}t}^{w}\le BA{A}_{t} \quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(60)

$${\delta }_{pjk^{\prime}t^{\prime}t}^{w}\ge { O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w}-B\left(1-A{A}_{t}\right)\quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(61)

$${\tau }_{pjk^{\prime}t^{\prime}t}^{w}\le { O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}\quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(62)

$${\tau }_{pjk^{\prime}t^{\prime}t}^{w}\le B{BB}_{t}\quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(63)

$${\tau }_{pjk^{\prime}t^{\prime}t}^{w}\ge { O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}-B\left(1-{BB}_{t}\right)\quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(64)

Constraints (31) to (34) are also linearized using the method proposed by Chang and Chang (2000). Note that ${{\pounds }}_{pjk^{\prime}t^{\prime}t}^{ w}={CC}_{t}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}$, ${\varepsilon }_{pjk^{\prime}t^{\prime}t}^{w}{=DD}_{t}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}$, ${\eta }_{ms^{\prime}ipt}={q^{\prime}}_{ms^{\prime}ipt}{CC}_{t}$,and ${\zeta }_{ms^{\prime}ipt}={q^{\prime}}_{ms^{\prime}ipt}{DD}_{t}$.

$$V{{\text{sec}}}_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} { \tau }_{pjk^{\prime}t^{\prime}t}^{w}rb-EN{BB}_{t}) nima \quad \forall t$$

(65)

$$Vth{i}_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {{\pounds }}_{pjk^{\prime}t^{\prime}t}^{ w}rc -EN{CC}_{t}) nima \quad \forall t$$

(66)

$$Vfo{r}_{t}=(\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} { \varepsilon }_{pjk^{\prime}t^{\prime}t}^{w}rd-EN{DD}_{t}) nima \quad \forall t$$

(67)

$$\begin{aligned}Ve{x}_{t}=&[\sum\limits_{j}\sum\limits_{k^{\prime}}\sum_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {{\pounds }}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rc\right) \\&+\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt}{ \varepsilon }_{pjk^{\prime}t^{\prime}t}^{w}\left(1-rd\right)+EN\left(C{C}_{t}+D{D}_{t}\right)\\-&\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}\left[c{m^{\prime}}_{ms^{\prime}it}+{\widetilde{\lambda ^{\prime}}}_{ms^{\prime}t}\left(1+{\theta }_{m}\right)\right]\left({\eta }_{ms^{\prime}ipt}+{\zeta }_{ms^{\prime}ipt}\right)]nima\end{aligned}\quad \forall t$$

(68)

$${{\pounds }}_{pjk^{\prime}t^{\prime}t}^{ w}\le { O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w} \quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(69)

$${{\pounds }}_{pjk^{\prime}t^{\prime}t}^{ w}\le B{ CC}_{t} \quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(70)

$${{\pounds }}_{pjk^{\prime}t^{\prime}t}^{ w}\ge { O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w}-B\left(1-{CC}_{t}\right) \quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(71)

$${\upvarepsilon }_{pjk^{\prime}t^{\prime}t}^{w}\le { O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w} \quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(72)

$${\upvarepsilon }_{pjk^{\prime}t^{\prime}t}^{w}\le B {DD}_{t}\quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(73)

$${\upvarepsilon }_{pjk^{\prime}t^{\prime}t}^{w}\ge { O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{w}-B\left(1-{DD}_{t}\right)\quad \forall p,j,k^{\prime},t^{\prime},t,1\le w\le {RF}_{p}$$

(74)

$${\eta }_{ms^{\prime}ipt}\le {q^{\prime}}_{ms^{\prime}ipt}\quad \forall m,s^{\prime},i,p,t$$

(75)

$${\eta }_{ms^{\prime}ipt}\le B{CC}_{t}\quad \forall m,s^{\prime},i,p,t$$

(76)

$${\eta }_{ms^{\prime}ipt}\ge {q^{\prime}}_{ms^{\prime}ipt}-B(1-{CC}_{t})\quad \forall m,s^{\prime},i,p,t$$

(77)

$${\zeta }_{ms^{\prime}ipt}\le {q^{\prime}}_{ms^{\prime}ipt}\quad \forall m,s^{\prime},i,p,t$$

(78)

$${\zeta }_{ms^{\prime}ipt}\le B{DD}_{t}\quad \forall m,s^{\prime},i,p,t$$

(79)

$${\zeta }_{ms^{\prime}ipt}\ge {q^{\prime}}_{ms^{\prime}ipt}-B(1-{DD}_{t})\quad \forall m,s^{\prime},i,p,t$$

(80)

4.6 Chance constrained fuzzy programming model

The majority parameters in the proposed model like costs, demands, and capacity are subjected to the uncertainty. Usually, historical data in real-world situations is insufficient to exactly characterize probability distributions of uncertain parameters or the problem conditions do not meet probability theory's presumptions (Zarrinpoor and Pishvaee 2021). Under such circumstances, field experts' judgmental data can be used to estimate input parameters by considering possibility distributions in the form of triangular or trapezoidal fuzzy numbers (Kabak and Ülengin 2011). To deal with uncertain parameters in objective function and constraints, a chance constrained fuzzy programming is applied. This fundamental approach is based on certain profound mathematical notions like the expected value of a fuzzy number, as well as necessity (Nec) of satisfying the constraint. The necessity measure indicates the minimum possibility level of occurring an uncertain event and allows the decision-maker to manage the constraint's conservative degree. This method can also be applied to various types of fuzzy numbers, including triangular and trapezoidal numbers (Pishvaee et al. 2012; Inuiguchi and Ramık 2000). These advantages make the chance constrained fuzzy programming method to be used as a powerful tool in complex decision-making and in situations where there is uncertainty and ambiguity.

To begin, the application of the method to a simple linear programming problem is demonstrated. Assume that the fixed costs vector f is a certain parameter. In addition, the parameters c, d and N are all uncertain.

$$\mathrm{Min }Z=fy+cx$$

(81)

$$\begin{array}{l}{\text{s}}.{\text{t}}.\\Ax\ge d\\Sx\le Ny\\y\in [\mathrm{0,1}],x\ge 0\end{array}$$

The objective's uncertain parameters are modeled using the expected value, and the chance restrictions are modeled using the Nec metric. The Nec metric is directly utilized to turn the chance's fuzzy constraints to certain constraints. A trapezoidal fuzzy distribution with four points $\widetilde{\theta }=\left({\theta }_{\left(1\right)},{\theta }_{\left(2\right)},{\theta }_{\left(3\right)},{\theta }_{\left(4\right)}\right)$ has been used in this paper.

According to the above, for an uncertain model, its certain equivalent is defined as follows:

$$Min E[Z]=E[f]y+E[\widetilde{c}]x$$

(82)

$$\begin{array}{l}{\text{s}}.{\text{t}}.\\Nec\{Ax\ge \widetilde{d}\}\ge \alpha\\Nec\{Sx\le \widetilde{N}y\}\ge \alpha\\y\in [\mathrm{0,1}],x\ge 0\end{array}$$

Given that the minimum satisfaction level ($\alpha$) must be considered when considering constraints with uncertain parameters, the certain model can be defined as follows:

$$MinE[Z]=fy+\left(\frac{{c}_{(1)}+{c}_{(2)}+{c}_{(3)}+{c}_{(4)}}{4}\right)x$$

(83)

$$\begin{array}{l}{\text{s}}.{\text{t}}.\\Ax\ge (1-\alpha ){d}_{(3)}+\alpha {d}_{(4)}\\Sx\le [(1-\alpha ){N}_{(2)}+\alpha {N}_{(1)}]y\\y\in [\mathrm{0,1}],x\ge 0\end{array}$$

Using chance constrained fuzzy programming, the certain equivalent of the uncertain suggested model is obtained, as shown below. Note that the expected values of the second and third terms of the objective function are not included in the objective function for the purpose of brevity.

$$\begin{aligned}{\text{max}}E\left[TB\right]=&\sum_{j}\sum_{k}\sum_{p}\sum_{t}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}P{r}_{pkjt} {O}_{pjkt^{\prime}t}^{w}+\sum_{t}{E[\Gamma }_{t}]+\sum_{t}{E[\Omega }_{t}]\\ &-\sum_{s}\sum_{i}\sum_{m}\sum_{t}\sum_{p}\left((c{m}_{msit}+\frac{{\lambda }_{mst(1)}+{\lambda }_{mst(2)}+{\lambda }_{mst(3)}+{\lambda }_{mst(4)}}{4}){q}_{msipt}\right)\\& -\sum_{i}\sum_{j}\sum_{p}\sum_{t}\sum_{w=1}^{{RF}_{p}}\left(\frac{{C}_{pijt(1)}+{C}_{pijt(2)}+{C}_{pijt(3)}+{C}_{pijt(4)}}{4}{u}_{pijt}^{w}\right)\\& -\sum_{p}\sum_{j}\sum_{k^{\prime}}\sum_{t}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}\left(\frac{{{\text{Cb}}}_{pjk^{\prime}t(1)}+{{\text{Cb}}}_{pjk^{\prime}t(2)}+{{\text{Cb}}}_{pjk^{\prime}t\left(3\right)+}{{\text{Cb}}}_{pjk^{\prime}t(4)}}{4}{\mathrm{O^{\prime}}}_{pjk^{\prime}t^{\prime}t}^{w}\right)\\& -\sum_{p}\sum_{j}\sum_{k}\sum_{t}\sum_{t^{\prime}}\sum_{w=1}^{{RF}_{p}}\left(\frac{{{\text{Ca}}}_{pjkt(1)}+{{\text{Ca}}}_{pjkt(2)}+{{\text{Ca}}}_{pjkt(3)}+{{\text{Ca}}}_{pjkt(4)}}{4}{{\text{O}}}_{pjkt^{\prime}t}^{w}\right)\\& -\sum_{i}\sum_{j}\sum_{p}\sum_{t}\sum_{w=1}^{{RF}_{p}}\left(\frac{{\rho }_{pit(1)}+{\rho }_{pit(2)}+{\rho }_{pit(3)}+{\rho }_{pit(4)}}{4}{u}_{pijt}^{w}\right)\\& -\sum_{j}\sum_{t}\left(\frac{{g}_{jt(1)}+{g}_{jt(2)}+{g}_{jt(3)}+{g}_{jt(4)}}{4}\left({y}_{jt}-{y}_{j,t-1}\right)\right)\\ &-\sum_{i}\sum_{p}\sum_{t}\left(\frac{{f}_{ipt(1)}+{f}_{ipt(2)}+{f}_{ipt(3)}+{f}_{ipt(4)}}{4}\left({x}_{ipt}-{x}_{ip,t-1}\right)\right)\\ &-\sum_{j}\sum_{p}\sum_{t}\sum_{t^{\prime}}\left(\frac{{C}_{pt(1)}^{e}+{C}_{pt(2)}^{e}+{C}_{pt(3)}^{e}+{C}_{pt(4)}^{e}}{4}{e}_{pjt^{\prime}t}\right)\\& -\sum_{j}\sum_{p}\sum_{t}\left(\frac{{C}_{pjt(1)}^{in}+{C}_{pjt(2)}^{in}+{C}_{pjt(3)}^{in}+{C}_{pjt(4)}^{in}}{4}i{n}_{pjt}\right)\\ &-\sum_{j}\sum_{p}\sum_{t}\left(\frac{{C}_{pjt(1)}^{\pi }+{C}_{pjt(2)}^{\pi }+{C}_{pjt(3)}^{\pi }+{C}_{pjt(4)}^{\pi }}{4}{\mu }_{pjt}\right)\\& -\sum_{i}\sum_{p}\sum_{t}\sum_{n}{l}_{iptn}^{ir}\end{aligned}$$

(84)

s.t. (3)–(10), (12)–(19), (22)–(24), (35)–(43), (46), (47), (53)–(64), (Undefined control sequence \pounds 69)–(80)

$$\sum\limits_{j}\sum\limits_{w=1}^{{RF}_{p}}{u}_{pijt}^{w}\le \left((1-\alpha ){\tau }_{ip(2)}+\alpha {\tau }_{ip(1)}\right){x}_{ipt}\quad \forall i,p,t$$

(85)

$$\sum\limits_{i}\sum\limits_{p}\sum\limits_{w=1}^{{RF}_{p}}{u}_{pijt}^{w}+\sum\limits_{p}i{n}_{pj,t-1}\le \left((1-\alpha ){\delta }_{j(2)}+\alpha {\delta }_{j(1)}\right){y}_{jt}\quad \forall j,t$$

(86)

$$\sum\limits_{j}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{w=1}^{{RF}_{p}}{ O^{\prime} }_{pjk^{\prime}t^{\prime}t}^{w} \ge (1-\alpha ){d^{\prime}}_{k^{\prime}pt(3)}+\alpha {d^{\prime}}_{k^{\prime}pt(4)}\quad \forall k^{\prime},p,t$$

(87)

$$\sum\limits_{j}\sum\limits_{t^{\prime}=1}^{t}\sum\limits_{w=1}^{{RF}_{p}}{O}_{pjkt^{\prime}t}^{w}\ge (1-\alpha ){d}_{kpt(3)}+\alpha {d}_{kpt(4)}\quad \forall k,p,t$$

(88)

$$\begin{array}{l}\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w} +B(1-A{A}_{t})\\\ge \sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+\left((1-\alpha ){\lambda ^{\prime}}_{ms^{\prime}t(3)}+\alpha {\lambda ^{\prime}}_{ms^{\prime}t(4)}\right)(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\end{array}\quad \forall t$$

(89)

$$\begin{array}{l}\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w} \left(1-rb\right)+EN+B(1-B{B}_{t})\ge \\\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+\left((1-\alpha ){\lambda ^{\prime}}_{ms^{\prime}t(3)}+\alpha {\lambda ^{\prime}}_{ms^{\prime}t(4)}\right)(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\end{array}\quad \forall t$$

(90)

$$\begin{array}{l}\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rc\right)+EN+B\left(1-C{C}_{t}\right)\ge\\\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+\left((1-\alpha ){\lambda ^{\prime}}_{ms^{\prime}t(3)}+\alpha {\lambda ^{\prime}}_{ms^{\prime}t(4)}\right)(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt}\end{array} \quad \forall t$$

(91)

$$\begin{array}{l}\sum\limits_{j}\sum\limits_{k^{\prime}}\sum\limits_{p}\sum\limits_{t^{\prime}}\sum\limits_{w=1}^{{RF}_{p}}P{r^{\prime}}_{pk^{\prime}jt} {O^{\prime}}_{pjk^{\prime}t^{\prime}t}^{ w}\left(1-rd\right)+EN+B\left(1-D{D}_{t}\right)\ge \\\sum\limits_{s^{\prime}}\sum\limits_{i}\sum\limits_{m}\sum\limits_{p}[c{m^{\prime}}_{ms^{\prime}it}+\left((1-\alpha ){\lambda ^{\prime}}_{ms^{\prime}t(3)}+\alpha {\lambda ^{\prime}}_{ms^{\prime}t(4)}\right)(1+{\theta }_{m})]{q^{\prime}}_{ms^{\prime}ipt} \end{array} \quad \forall t$$

(92)

$$\sum_{i}\sum_{p}\sum_{t}m{a}_{ipt}+\sum_{i}\sum_{p}\sum_{t}\sum_{n}{l}_{iptn}^{a}\ge \sum_{i}\sum_{p}\sum_{t}\left((1-\alpha ){f}_{ipt(3)}+\alpha {f}_{ipt(4)}\right)({x}_{ipt}-{x}_{ip,t-1})$$

(93)

$$\sum_{j}\sum_{t}mm{a}_{jt}\ge \sum_{j}\sum_{t}\left((1-\alpha ){g}_{jt(3)}+\alpha {g}_{jt(4)}\right)({y}_{jt}-{y}_{j,t-1})$$

(94)

5 Case study

To test the validity of the suggested model, a case study on drug manufacturing and distribution in Fars province is presented in this section and the model is then tested on it.

5.1 Case description

Fars province is one the most populous province of Iran, with a population of 5,130,927 inhabitants. This province has 37 counties and is located in the south of Iran. The counties of Fars province are also ranked and numbered by population in Table 2 (SCI 2023). All the counties are regarded as potential locations for manufacturers. However, only the ten counties have been chosen to build DCs. These candidate locations include Shiraz, Marvdasht, Kazerun, Fasa, Darab, Jahrom, Larestan, Firuzabad, Mamasani, and Neyriz. A number of factors, such as geographic and climatic conditions, distances from human habitation, population, communication routes, and faults, are taken into account when choosing potential sites for DCs. Furthermore, all counties are considered as customers.

Table 2 Ranking of counties in Fars province based on their population

On the map of the province of Fars, Fig. 2 depicts the locations of all of the province's counties. The rank of counties according to their population is also written on this map. These 37 counties are all referred to as domestic customers. In addition, four countries have been chosen as foreign customers: Iraq, Afghanistan, Uzbekistan, and Azerbaijan. Real data is applied to solve the suggested model, and the locations of manufacturers and DCs are identified.

Fig. 2

The geographic map of Fars province

Four drugs are chosen for this study to evaluate the efficiency of the model in question: half-liter sugar serum, vitamin B6 tablets, dextrose serum, and distilled water ampoules. Figure 3 depicts these drugs.

Fig. 3

Intended drugs

In emergency cases where the body is deficient in fluid and calories, the sugar serum is used to replenish calories and body fluids. The 20 percent sugar serum solutions are used in situations where we need to provide the body with the most calories for the least amount of water. Hypoglycemia caused by high insulin intake is treated with 50 percent sugar serum solutions (DS 2019). Vitamin B6, is one of the B vitamins that can help the nervous system function more efficiently. This vitamin aids in the production of neurotransmitters in a significant and efficient manner. Vitamin B6 belongs to the water-soluble vitamin family. Because the body does not store this vitamin and it is excreted in the urine, it should be consumed on a daily basis. Dextrose serum is injected and used as a source of calories and fluids. This medication is easily metabolized, slows protein and nitrogen breakdown, and increases glycogen formation (IPA 2018). Because each gram of glucose releases 3/4 cal of energy, this drug aids in the supply of energy to the body. Injectable solutions are also made with the ampoule of distilled water (CT 2019).

Drugs demand is sourced from the Food and Drug Organization of Iran's website, covering years from 2018 to 2022 (FDO 2022). Using the linear regression approach, these data are used to predict the requests for these pharmaceutical items for the planning horizon. The Ministry of Industry, Mines, and Trade's website is served as a valuable resource for accessing crucial cost-related information. Data concerning transportation costs, an integral component of the PSC, is also obtained from this source (MIMT 2023). Moreover, the economic condition of Iran is taken into account to determine fixed costs associated with the construction of manufacturers and DCs. Transportation of materials from local suppliers to manufacturers and transportation of drugs to DCs and internal customers are done with truck with 10 ton capacity. According to Fattahi and Govindan (2018), 0.2002 kg CO2 are emitted during the transportation of each ton of goods per kilometer. Therefore, the related environmental parameters (e.g. ${{\text{gm}}}_{msi}$, ${{\text{gh}}}_{pij}$, and ${{\text{gn}}}_{pjk}$) are determined as the multiplication of 0.2002 in the distance between two locations.

The financial indicators that are essential for the comprehensive analysis of the pharmaceutical industry within the province of Fars is retrieved from the Central Bank's website. According to the Central Bank of Iran, the restrictions for the various export earning categories are $BoundA=\mathrm{1,000,000}$, $BoundB=\mathrm{3,000,000}$, and $BoundC=\mathrm{10,000,000}$ euros. Regulations issued by the Central Bank of Iran stipulate that $rb$, $rc$, and $rd$ have respective values of 50%, 70%, and 90%. The maximum export earnings that can be excluded from the Nima system registration for the second, third, and fourth categories (e.g. EN) is also set to 1,000,000 euros based on these regulations. The interest rate for loans provided by the National Development Fund is set in the range of 12% to 14%. The repayment period for these loans is up to 8 years, providing applicants with the flexibility to repay the loan amount comfortably. Additionally, the maximum number of loans allocated to each production unit is limited and determined based on conditions set by the National Development Fund. This measure is aimed at creating a balance in the allocation of financial resources and enhancing the capabilities of manufacturers for industrial growth and development in the country (NDF 2023).

5.2 Experimental results

This subsection presents the numerical results of solving the proposed model. To solve this model, the GAMS 23.4.3 optimization software has been used. To perform the calculations, a computer with 4GB of RAM, which contains a Core i5 processor is used. Since the problem is a linearized MIP, the CPLEX solver is used to solve all instances.

Figure 4 shows diagrams of the proposed PSC network in the uncertain condition for the first to fourth time periods, respectively. As shown in Fig. 4(a), the model in question has chosen Shiraz city as the construction site for manufacturers related to drugs 2 and 4, and Firuzabad for manufacturers related to drugs 3 and 4, for the first time period. The counties of Jahrom, Kazerun, Mamasani, and Larestan are also chosen to construct the manufacturers for drugs 4, 2, and 1. Shiraz, Neyriz, Jahrom, and Mamasani counties have also been chosen to build DCs. The connections between the manufacturers and DCs are as follows in the first time period and for the uncertain state. Drug 2 is manufactured in Shiraz and delivered to DCs in Shiraz and Mamasani. Drug 4 in Shiraz’s manufacturer is sent to the Shiraz’s DC. Drugs 3 and 4 are produced in Firuzabad and delivered to the DCs in Jahrom and Mamasani, respectively. Drugs produced in Mamasani, Jahrom, Larestan and Kazerun are delivered to DCs in Mamasani, Jahrom, Neyriz, and Shiraz. To prevent overcrowding the maps, only the flow of drugs to internal and foreign customers is displayed. As is evident, drug flows during various time periods are not exactly the same. For example, in the first period, a drug DC situated in Jahrom sent drugs to Uzbekistan and Iraq. In the second period, it sent drugs to Jahrom, Ghir and karzin, Lamerd, Evaz, Gerash, Khonj, Mohr, Kharameh, Khafr, Firuzabad, Fasa, Darab, Estahban, Juyom, Zarrin Dasht, and Larestan.

Fig. 4

PSC network design under uncertainty

As shown in Fig. 5(a), the model in question has chosen Shiraz city as the construction site for manufacturers for drugs 3 and 4, and Firuzabad as the construction site for manufacturers for drugs 1 and 4 in the deterministic condition. Jahrom and Neyriz have been chosen as manufacturers for drugs 3 and 2, respectively. Shiraz, Firuzabad, Jahrom, and Fasa have also been chosen as locations for DCs. The connections between the manufacturers and the DCs in the first time are as follows. Drug 4 is sent from Shiraz's manufacturer to the Shiraz's DC. Drug 3 is manufactured in Shiraz and delivered to DCs in Shiraz and Firuzabad. Drugs 1 and 4 are manufactured in Firuzabad and distributed through the same town's DCs. Drug 3 is manufactured in Jahrom and delivered to DCs in Jahrom and Fasa. Drug 2 in Neyriz’s manufacturer is distributed to Shiraz and Fasa DCs. It's worth noting that the locations chosen to build manufacturers and DCs for deterministic and uncertain conditions are different over time. Table 3 depicts the manufacturer construction sites and the DC construction locations for both deterministic and uncertain states.

Fig. 5

PSC network design in the deterministic condition

Table 3 The optimal locations of manufacturers and DCs in deterministic and uncertain conditions

The objective function values for the deterministic model, Z_det, as well as the chance constrained fuzzy programming model, Z_fcc, are displayed in Table 4. The values related to Z_fcc are listed in this table for various confidence levels. The objective function values of Z_det and Z_fcc differ from one another, as shown in this table. As seen in Figs. 4 and 5, the number of manufacturers and DCs rises when uncertainty is taken into consideration in compared to the deterministic model to protect the system from the risk that uncertainty brings. Given that factors such as costs, capacity, and demand uncertainty are included, the model needs to generate solutions that guard against parameter uncertainty in order to satisfy both local and international demands. Because of this, additional facilities are needed to meet demand in unpredictable circumstances. In comparison to the deterministic model, the cost of production and the supply of raw materials both rise in the uncertain condition. Additionally, there is a rise in the flow of drugs between the various PSC tiers, which drives up transportation expenses. In order to develop solutions that are optimal in high degrees of uncertainty, the system profit reduces in uncertain conditions relative to deterministic situations, and the danger of restrictions being unfeasible in uncertain conditions decreases as well. In addition, the value of Z_fcc, the system profit, decreases as α increases. Overall, it can be concluded that taking uncertainty into account has a significant impact on the design of the PSC network and the system's profit, and thus it should not be overlooked. Even though the model takes into account a variety of real-world constraints, such as environmental concerns, financial strategies to provide the necessary budget for locating manufacturers through loans, the import of raw materials, the export of drugs, financial strategies to provide the currency for import, the perishability of the drugs, the lifetime of drugs, the inventory policies, and the uncertainty of the parameters, the CPLEX solver can find the optimal solutions for each instance of the problem in a reasonable amount of time because the model is solved using real-world parameters. Moreover, the CPU time never goes above 721 seconds in any instance. As a result of using real-world parameters, a gap-free solution is also obtained.

Table 4 The objective's value in the certain and uncertain conditions

5.3 Sensitivity analysis

The objective’s values are shown in Fig. 6, based on changes in the two parameters α and ${\widetilde{d^{\prime}}}_{k^{\prime}pt}$. To meet the growing demand, manufacturers will need to raise their manufacturing capacity, while DCs will need to increase their storage capacity. If the capacity of installed manufacturers and DCs is insufficient to meet the heightened demand, more facilities will need to be built, which will raise the fixed installation costs. In addition, there is an increase in the cost of production, raw material supply, and transportation. On the other hand, additional revenue is possible due to the selling of more drugs to foreign customers. An increase in international demands has the potential to boost system profit since income growth is more substantial than system cost growth. Additionally, it can be inferred that the system will need to pay much more to get more reliable results with higher degrees of confidence, and as a result, the profit of the system would decline as α rises.

Fig. 6

Objective values according to changes in α and ${\widetilde{d^{\prime}}}_{k^{\prime}pt}$

In Fig. 7, the values of the objective are calculated with respect to the changes of the two parameters α and ${\widetilde{f}}_{ipt}$. As can be seen, in all cases, the value of the objective decreases with increasing values of α and ${\widetilde{f}}_{ipt}$. It is impossible to reduce the number of manufacturers in order to satisfy domestic and international demand when there is an increase in the fixed installation costs of manufacturers. Consequently, an increase in the fixed installation costs results in an increase in the system cost. Additionally, because the fixed installation cost is entered with a negative coefficient in the objective, an increase in its value causes a large loss in the total profit. Based on the findings, the system designer should first ascertain the appropriate value for the capacity of the manufacturers in order to minimize the need for additional facility installations later on in the planning horizon. This will prevent the system from incurring additional costs for installation, which will also have little effect on the system's profitability.

Fig. 7

Objective values according to changes α and ${\widetilde{f}}_{ipt}$

In Fig. 8, the values of the objective are calculated with respect to the changes of the two parameters α and ${\widetilde{g}}_{jt}$. As can be seen, the value of the objective decreases with increasing values of α and ${\widetilde{g}}_{jt}$. The system profitability will decline as a result of an increase in the overall system cost caused by the fixed installation cost of DCs. As the medications are shipped from the DCs to both domestic and international clients, it is essential to set them up with adequate storage space so they can meet demand in highly uncertain scenarios. Furthermore, since the number of installed DCs does not need to be increased, the system will not become significantly more expensive, and its profitability will not drop.

Fig. 8

Objective values according to changes in α and ${\widetilde{g}}_{jt}$

6 Conclusion

A new mathematical model is presented in this paper for designing a multi-period and multi-product PSC network under uncertainty in order to maximize profits. Several real constraints, such as drug expiration dates, production constraints, and storage constraints, are taken into account in the proposed model. Environmental issues are also considered in this model to produce fewer greenhouse gases. The proposed model determines the location of new manufacturers and DCs across a multi-period planning horizon. The quantity of drug transmitted from the manufacturer to the DC, as well as from the DC to the customer, is also determined. The amount of loan required to build the manufacturer based on the number of repayment periods is among the determining factors in each period. The amount of drug required to export to a foreign customer is determined by the amount of currency required in this model. The level of inventory in DCs is also taken into account. Demand, fixed costs of building the manufacturers and DCs, production costs, holding costs, expired medicines costs, order costs, raw material costs, production capacity, and storage capacity are all considered uncertain parameters in the PSC. The chance constrained fuzzy programming is used to account for the uncertainty of the parameters. The suggested model's efficiency is investigated using a case study and numerical examples in the next step of the calculations, and the profit sensitivity of the PSC is also examined. According to the numerical results, uncertainty has a significant impact on the PSC's profitability, so taking it into account reduces the system's profitability. Managers and designers of the PSC can predict the profitability of the chain by properly managing the factors that cause uncertainty in the parameters. According to the model's sensitivity analysis, demand and the initial cost of building the manufacturer and DC are among the factors that have a significant impact on the system's profitability.

Finally, the following points can serve as suggestions and guidance for researchers interested in this topic. Other objective functions, such as social functions, can be introduced into the model. Other uncertainty programming methods, such as robust optimization or stochastic programming, can be looked into as well. Since decision makers determine the confidence level in the chance constrained fuzzy programming, solving the model with different confidence levels is time consuming. Therefore, consideration of the confidence levels as a decision variable can be another avenue for future research, as it guarantees that the value selected for each confidence level is the best one available. The unused budget in the PSC should be invested in the bank, and interest on the deposit should be considered. One suggestion for lowering drug production costs is to consider setting up a temporary warehouse within the manufacturer. To expedite the delivery of drug, sending the drug directly from the manufacturer to the customer is also one of the options that can be considered.