1 Introduction

Two-dimensional assemblies of magnetic nanoparticles (MNPs) have received significant attention due to their exciting properties and numerous technological applications [1,2,3,4,5,6,7,8,9,10]. These applications include magnetic hyperthermia mediated cancer therapy, targeted drug delivery, magnetic resonance imaging, data storage, etc. The magnetic properties of these systems are complex and extremely sensitive to various parameters of interest, such as particle shape and size, anisotropy strength, spatial distribution, dipolar interaction, etc. [11,12,13]. The understanding of magnetic relaxation characteristics are of paramount importance for their efficient usages in such applications [14,15,16]. The Néel relaxation time is one of the essential quantifiers of magnetic relaxation. The precise knowledge of relaxation time is also of great significance in various applications, such as data storage, magnetic hyperthermia, etc.

The Néel–Brown theory of superparamagnetism correctly explains the relaxation properties in the case of single nanoparticle or extremely dilute assembly [17, 18]. However, the dipolar interaction strongly affects the magnetisation dynamics behaviour in sufficiently dense assembly [19, 20]. The dipolar interaction is long ranged and anisotropic in nature. As a consequence, it can induce ferromagnetic or antiferromagnetic coupling depending on the relative position of the nanoparticle in an assembly. Therefore, the relaxation characteristics are severely affected because of the dipolar interaction [21,22,23,24,25,26,27,28]. For example, Denisov and Trohidou [22] investigated the dipolar interaction dependence of magnetic relaxation in two-dimensional ensembles of MNPs using mean-field approximations. They observed two distinct relaxation time because of dipolar interaction. Hiroi et al [23] studied the magnetisation dynamics in an assembly of hematite (Fe\(_2\)O\(_3\)) as a function of interparticle separation or dipolar interaction strength. The system exhibits super spin glass-like properties for sufficiently large interaction strength. Kesserwan et al [24] investigated the effect of dipolar interaction on the magnetisation dynamics in MNP ensembles using the Fokker–Planck formalism. The dipolar interaction is found to induce fastening in magnetisation relaxation. Kuncser et al [25] analysed the magnetic relaxation as a function of dipolar interaction. The energy barrier gets enhanced due to the dipolar interaction and hence the relaxation time. Shtrikmann and Wohlfarth [26] investigated the dipolar interaction dependence of the relaxation time. They observed an enhancement in relaxation time with an increase in interaction strength. Mørup et al [27] and Dormann et al [28] also found an elevation in relaxation time because of the dipolar interaction.

The influence of dipolar interaction on relaxation characteristics also depends strongly on the spatial distribution of nanoparticles. For instance, the energy barrier gets enhanced and hence the relaxation time due to the dipolar interaction [29, 30]. On the other hand, the dipolar interaction increases the relaxation rate in the square assembly of MNPs [31]. Patrick Ilg [32] studied the magnetisation relaxation of multicore nanoparticles dispersed in viscous solvent using computer simulations. In dense random cluster of MNPs, the magnetic relaxation curve follows exponentially decaying function for moderate interaction strength. López et al [33] analysed the relaxation mechanism in the polycrystalline sample of La\(_{0.5}\)Ca\(_{0.5}\)MnO\(_3\). The magnetisation decay curve is found to follow the logarithmic function. Osaci et al [34] investigated the relaxation properties as a function of dipolar interaction strength using numerical simulations. The relaxation time gets enhanced with an increase in interaction strength. The orientations of anisotropy axes also play important roles in determining the magnetic behaviour in MNP ensembles [35,36,37,38,39,40]. Sharma et al [41] investigated the effect of orientation of the anisotropy axes on the hysteresis properties in ordered MNP assembly. The coercive field and remanence magnetisation get enhanced in the highly anisotropic system. Usov et al [42] also observed larger coercivity for aligned anisotropy axes. Conde-Leborán et al [43] probed the hysteresis characteristics of interacting nanoparticles as a function of the degree of collinearity of anisotropy axes. They found the maximum heat dissipation in the case of aligned anisotropy axes. In a recent work, we have shown that the relaxation time can be modulated by just varying the angle between the anisotropy axis and chain axis of MNPs [44]. In another study, we have shown that the Néel relaxation time can be enhanced or decreased by varying the anisotropy axes in the perfectly ordered system [45].

Fig. 1
figure 1

(a) Schematic of the two-dimensional ensemble of magnetic nanoparticles assembled in the xy-plane. l is the lattice constant and D is the particle diameter. The anisotropy axes are denoted by dashed lined arrows, making an angle \(\alpha \) with the y-axis. (b) Schematic of the nanoparticle assembly with the out-of-plane disorder. A few nanoparticles are dispersed normal to the xy-plane.

Full size image

This discussion clearly shows that the dipolar interaction and anisotropy axes orientation play crucial roles in determining various magnetic properties of interest in MNPs ensembles. Therefore, the precise control over dipolar interaction strength and orientation of anisotropy axes can be of great importance in tuning diverse systematic properties. They found significant usages in various applications, such as plasmonics, data storage, sensors, photovoltaics, etc. [46,47,48]. Therefore, the fabrications of such systems with a high degree of structural and orientational order have gained momentum in recent years [49,50,51]. However, such experimentally fabricated MNP ensembles are found to have various types of defects, which further complicates the magnetic response. Of all possible defects, the out-of-plane positional disorder is the defect often observed in these fabricated samples. In such a situation, all the constituent MNPs do not lie in a single plane. Some of them also scatter normal to the plane of sample. Consequently, the complex and unexpected systematic properties are observed due to interplay among the anisotropy axes orientation, dipolar interaction and out-of-plane disorder. Therefore, it is essential to understand the magnetic properties of such systems and provide a theoretical framework to explain such unexpected behaviour. These studies can be extremely useful in controlling and modulating the systematic properties of such systems to harness their unique anisotropic properties of technological importance. Thus motivated, we investigate the magnetic relaxation in two-dimensional assembly of MNPs as a function of system size and aspect ratio, dipolar interaction, anisotropy axes orientations and out-of-plane disorder strength using kinetic Monte Carlo (kMC) simulations.

The rest of the article is organised as follows. In §2, we present and discuss our theoretical framework and relevant energy terms. We also briefly discuss the procedures of numerical simulations. In §3, we describe the numerical results. Finally, in §4, we provide the summary of the present work.

2 Theoretical framework

We consider a two-dimensional (\(l_x\times l_y\)) ensemble of spherical and monodisperse nanoparticles in the xy-plane with some of them dispersed normal to the sample plane (along z-axis) as depicted in figure 1. Let the particle diameter be D and the lattice spacing be l. Let the magnetocrystalline anisotropy constant be \(K_{\textrm{eff}}\) and particle volume \(V=\pi D^{3}/6\). So, the anisotropy energy of a single particle can be expressed as [52, 53]

$$\begin{aligned} E=K_\textrm{eff} V\sin ^2\Psi . \end{aligned}$$
(1)

Here \(\Psi \) is the angle between the anisotropy or the easy axis and the magnetic moment \(\mu =M_sV\) where \(M_s\) is the saturation magnetisation. The above energy function is a symmetric double well with two minima \(E^{0}_1\) (say) and \(E^{0}_2\) (say) at \(\Psi =0\) and \(\Psi =\pi \), respectively. These are separated by an energy maximum \(E^{0}_3 (\textrm{say})= K_\textrm{eff} V\) at \(\Psi =\pi /2\). The latter is also termed as the energy barrier. In the presence of sufficient temperature T, each magnetic moment associated with a nanoparticle fluctuates between these two minima with oppositely directed magnetisation by surmounting the energy barrier \(K_\textrm{eff} V\). Such magnetisation fluctuation is characterised by a time scale known as the Néel relaxation time \(\tau ^{0}_\textrm{N}\), which is given by the Arrhenius relation [44, 53]

$$\begin{aligned} \tau ^{0}_N=\tau _0\exp (K_\textrm{eff}V/k_\textrm{B}T), \end{aligned}$$
(2)

where \(\tau _0\) is the microscopic limiting relaxation time usually related to the attempt frequency \(\nu _0\approx 10^{10}\) s\(^{-1}\) as \(\tau _0=(2\nu _0)^{-1}\). \(k_\textrm{B}\) is the Boltzmann constant. Equation (2) correctly estimates the relaxation time of single-particle or weakly interacting nanoparticle ensembles.

In an assembly of MNPs, the single-particle energy barrier gets drastically modified because of the dipolar interaction. The corresponding interaction energy \(E_{\textrm{dipolar}}\) can be evaluated using the following expression [54, 55]:

$$\begin{aligned} E_{\textrm{dipolar}}= & {} \frac{\mu _0 \mu ^{2}}{4\pi l ^3}\nonumber \\{} & {} \times \!\sum _{i, j,\ j\ne i}\!\left[ \frac{\hat{\mu _{i}}\cdot \hat{\mu _{j}}\!-\!3(\hat{\mu _{i}}\cdot {\hat{r}}_{ij})(\hat{\mu _{j}}\!\cdot \!{\hat{r}}_{ij})}{(r_{ij}/l)^3}\right] \!. \end{aligned}$$
(3)

\(\mu _{0}\) is the permeability of free space. \(\hat{\mu _{i}}\) and \(\hat{\mu _{j}}\) are the unit vectors for the magnetic moments at the ith and jth positions, respectively. \(r_{ij}\) is the distance between \(\hat{\mu _{i}}\) and \(\hat{\mu _{j}}\). The corresponding dipolar field \(\mu _0\vec {H}_{\textrm{dipolar}}\) can be expressed as [56, 57]

$$\begin{aligned} \mu _{0}\vec {H}_{\textrm{dipolar}}=\frac{\mu _{0}\mu }{4\pi l^3}\sum _{j,j\ne i}\frac{3({\hat{\mu }}_j \cdot {\hat{r}}_{ij}){\hat{r}}_{ij}-\hat{\mu _j} }{(r_{ij}/l)^3}. \end{aligned}$$
(4)

It is evident from eqs (3) and (4) that the long-ranged dipolar interaction varies as \(1/r^{3}_{ij}\). Therefore, we can model the variation of dipolar interaction strength by introducing a control parameter \(h_d=D^{3}/l^{3}\) [58]. The physics of non-interacting particles can be modelled with \(h_d=0.0\). On the other hand, \(h_d=1.0\) represents the strongest interacting system. The total energy of the system can be calculated using the following expression [44, 56]:

$$\begin{aligned}{} & {} E=K^{}_{\textrm{eff}}V\sum _{i}\sin ^2 \Psi ^{}_i+\frac{\mu _0\mu ^2}{4\pi l^3}\nonumber \\{} & {} \qquad \times \sum _{i,j,\ j\ne i}\left[ \frac{\hat{\mu _{i}}\cdot \hat{\mu _{j}}-{3(\hat{\mu _{i}}\cdot {\hat{r}}_{ij})(\hat{\mu _{j}}\cdot {\hat{r}}_{ij})}}{(r_{ij}/l)^3}\right] . \end{aligned}$$
(5)

The dipolar interaction significantly modifies the single-particle energy function (eq. (1)). Consequently, the functional form of the energy barrier becomes asymmetric. The energy extrema also gets modified because of dipolar interaction. Let the new energy minima be \(E_1\) and \(E_2\). Let us also assume the modified energy maxima to be \(E_3\). In such a case, the rate \(\nu _1\) with which the magnetic moment changes its orientation from \(E_1\) to \(E_2\) by surmounting \(E^{}_3\) can be computed using the following formula [59]:

$$\begin{aligned} \nu _1=\nu ^{0}_{1}\exp \bigg (-\frac{E_3-E_1}{k_\textrm{B}T}\bigg ). \end{aligned}$$
(6)

Similarly, the following relation gives the jump rate \(\nu _2\) to switch the direction of the magnetic moment from \(E_2\) to \(E_1\) [59]:

$$\begin{aligned} \nu _2=\nu ^{0}_2\exp \bigg (-\frac{E_3-E_2}{k_\textrm{B}T}\bigg ), \end{aligned}$$
(7)

where \(\nu ^{0}_{1}=\nu ^{0}_{2}=\nu _{0}\).

We investigate the magnetic relaxation in two-dimensional assembly (\(l_x\times l_y\)) of MNPs as a function of anisotropy axis orientation, out-of-plane disorder, dipolar interaction strength \(h_d\) and aspect ratio \(A_r=l_y/l_x\) using numerical simulations. The anisotropy axis of each constituent nanoparticle in the assembly is assumed to make an angle \(\alpha \) with the y-axis as shown in figure 1. We define a control paramater \(\Delta \) to model the effect of the variation of the out-of-plane disorder strength on the magnetisation dynamics. It is defined as \(\Delta (\%)=n_z/N\), where N is the total number of MNPs in the assembly and \(n_z\) is the number of particles dispersed normal to the sample plane (along the z-axis). The kMC algorithm is implemented for computer simulations. It is described in greater detail in Tan et al [56] and Anand et al [44]. Therefore, we do not reiterate it here to avoid duplication. We have also described the implemented kMC algorithm in our recent works [54, 60]. We now describe the protocol used for the investigation of the magnetic relaxation. We apply extremely large constant magnetic field of strength of 30 T along the y-axis to saturate the magnetisation. We then divide the total simulation time into 2000 equal step. The external biasing magnetic field is switched off at time \(t=0\). Thereafter, we study the magnetisation dynamics using the kMC algorithm. The simulated magnetisation decay \(M(t)/M_s\) vs. t curve is then fitted with \(M(t) = M_s \exp (-t/\tau _\textrm{N})\) to extract the effective Néel relaxation time \(\tau _\textrm{N}\) of the underlying system.

3 Simulations results

We have considered the following values of system parameters for numerical simulations: \(D=8\) nm, \(K_{\textrm{eff}}=13\times 10^{3}\) \(\mathrm {Jm^{-3}}\), \(M_s=4.77\times 10^{5}\) \(\mathrm {Am^{-1}}\). The total number of nanoparticles is taken as \(N=400\). We have taken five typical values of system sizes \(l_x\times l_y=20\times 20\), \(10\times 40\), \(4\times 100\), \(2\times 200\) and \(1\times 400\). These correspond to the aspect ratio \(A_r(=l_y/l_x)\): 1.0, 4.0, 25.0, 100.0, 400.0, respectively. We have varied the out-of-plane disorder strength \(\Delta \) from 0 to 50%. The dipolar interaction strength \(h_d\) is changed between 0.0 and 1.0. We have also varied the orientation of anisotropy axis \(\alpha \) from 0 to \(90^\circ \) and T is taken as 300 K.

Fig. 2
figure 2

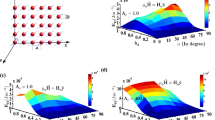
Magnetisation decay curve as a function of t and \(\alpha \) with \(A_r=1.0\). We have considered three representative values of \(h_d\): 0.2 [(a)–(d)], 0.6 [(e)–(h)] and 1.0 [(i)–(l)]. Four typical values of \(\Delta (=10\%\), 20%, 40% and 50%) are also considered. The magnetic relaxation is perfectly exponentially decaying for \(h_d=0.2\), irrespective of \(\alpha \) and \(\Delta \). The magnetisation decays rapidly for large \(h_d\) and negligible \(\Delta \).

Full size image

We first study the magnetic relaxation behaviour in square arrays of nanoparticles as a function of dipolar interaction strength, out-of-plane disorder strength and anisotropy axis orientation. In figure 2, we plot the magnetisation decay \(M(t)/M_s\) vs. t curve as a function of \(h_d\), \(\alpha \) and \(\Delta \) with \(A_r=1.0\). We have considered three representative values of \(h_d=0.2\), 0.6 and 1.0. We have also taken four typical values of \(\Delta =10\%\), 20%, 40% and 50%. \(\alpha \) is varied from 0 to \(90^\circ \). There is a smooth decay of magnetisation for weakly interacting MNPs (\(h_d=0.2\)). In such a case, the functional form of the time evolution of the magnetisation decay exponentially decays and depends weakly on \(\alpha \) and \(\Delta \). On the other hand, the magnetic relaxation characteristics depend strongly on the anisotropy axes orientation and out-of-plane disorder strength for strongly dipolar interacting MNPs. Remarkably, the magnetisation decays rapidly with large dipolar interaction strength and negligible value of disorder. Such rapid decay of magnetisation does not depend on \(\alpha \) because the dipolar interaction of sufficient strength induces antiferromagnetic coupling in square ensembles of MNPs, resulting in faster magnetisation decay. These observations are in perfect qualitative agreement with the work of De’Bell et al [61]. In contrast, there is a slowing down of the magnetisation relaxation for considerable disorder strength. Notably, the magnetisation ceases to relax for \(\alpha \le \alpha ^{\star }\). On the other hand, there is a fastening in the magnetisation relaxation for \(\alpha >\alpha ^{\star }\). Surprisingly, there is an increase in \(\alpha ^{\star }\) with \(\Delta \). It can be explained by the fact that the out-of-plane disorder of significant strength instigates magnetic moments to interact ferromagnetically even in the square assembly of MNPs. Consequently, the magnetisation ceases to relax in such cases.

Fig. 3
figure 3

Magnetic relaxation as a function of t and \(\alpha \) with \(A_r=4.0\). Three representative values of \(h_d\): 0.2 [(a)–(d)], 0.6 [(e)–(h)] and 1.0 [(i)–(l)] are considered. Four typical values of \(\Delta (=10\%\), 20%, 40% and 50%) are also considered. The functional form of the magnetisation decay depends weakly on \(\alpha \) and \(\Delta \) for \(h_d=0.2\). The magnetisation relaxes slowly for \(\alpha <75^\circ \) and moderate \(h_d\).

Full size image

Next, we investigate the magnetisation decay characteristics in the rectangular arrays of MNPs. Figure 3 shows the time evolution of the magnetisation decay \(M(t)/M_s\) vs. t curve with \(A_r=4.0\). We have used the same set of values for \(\alpha \), \(h_d\) and \(\Delta \) as in figure 2. In the case of small dipolar interaction strength (\(h_d=0.2\)), the magnetisation decays smoothly even with the rectangular assembly of MNPs. In this case, the functional form of the magnetisation relaxation also depends very weakly on \(\alpha \) and \(\Delta \). Interestingly, the magnetisation ceases to relax for \(\alpha \le 75^\circ \) even with a moderate value of interaction strength \(h_d=0.6\) and a small value of \(\Delta =10\%\). On the other hand, there is a rapid magnetisation decay for \(\alpha >75^\circ \), irrespective of \(\Delta \). It is because the antiferromagnetic coupling is very large in such a case. Remarkably, the slowing down of the magnetic relaxation shifts to a lower value of \(\alpha =\alpha ^{\star }\) with the largest dipolar interaction strength \(h_d=1.0\). The out-of-plane disorder enhances the value of \(\alpha ^\star \) by increasing the ferromagnetic coupling among the magnetic moments.

Fig. 4
figure 4

Magnetisation relaxation as a function of t and \(\alpha \) with \(A_r=25.0\). We consider three representative values of \(h_d\): 0.2 [(a)–(d)], 0.6 [(e)–(h)] and 1.0 [(i)–(l)]. Four typical values of \(\Delta (=10\%\), 20%, 40% and 50%) are also taken. The magnetisation decay depends weakly on \(\alpha \) and \(\Delta \) for \(h_d=0.2\). The magnetic relaxation slows down for \(\alpha \le 75^\circ \) for \(h_d=0.6\), even with small \(\Delta \).

Full size image
Fig. 5
figure 5

Magnetisation decay \(M(t)/M_s \) vs. t and \(\alpha \) with \(A_r=100.0\). We have considered three representative values of \(h_d\): 0.2 [(a)–(d)], 0.6 [(e)–(h)] and 1.0 [(i)–(l)]. Four typical values of \(\Delta (=10\%\), 20%, 40% and 50%) are also considered. The magnetic relaxation depends weakly on \(\alpha \) and \(\Delta \) for small \(h_d\), while for significant \(h_d\) and \(\Delta \), the magnetisation relaxation depends strongly on \(\alpha \).

Full size image
Fig. 6
figure 6

The magnetisation relaxation \(M(t)/M_s \) vs. t and \(\alpha \) with \(A_r=400.0\). We have taken three typical values of \(h_d\): 0.2 [(a)–(d)], 0.6 [(e)–(h)] and 1.0 [(i)–(l)]. Four representative values of \(\Delta (=10\%\), 20%, 40% and 50%) are also considered. When \(h_d\) is small, the magnetisation decay depends weakly on \(\alpha \) and \(\Delta \). There is a rapid decay of magnetisation for \(\alpha >60^\circ \) and significant \(h_d\).

Full size image
Fig. 7
figure 7

The variation of \(\tau _\textrm{N}\) as a function of \(\alpha \) and \(\Delta \). We have considered two values aspect ratio \(A_r=1.0\) [(a)–(d)] and 4.0 [(e)–(h)]. We have also considered four values of \(h_d(=0.2\), 0.4, 0.6 and 1.0). There is a weak dependence of \(\tau _\textrm{N}\) on \(\alpha \) and \(\Delta \) with small \(h_d\). \(\tau _\textrm{N}\) increases with \(\alpha \) (\(\le 45^\circ \)) for moderate \(h_d\) and for \(A_r=1.0\).

Full size image
Fig. 8
figure 8

The variation of \(\tau _\textrm{N}\) as a function of \(\alpha \) and \(\Delta \). We have considered two values of aspect ratio \(A_r=100.0\) [(a)–(d)] and 400.0 [(e)–(h)]. We have also considered four typical values of \(h_d=0.2\), 0.4, 0.6 and 1.0. \(\tau _\textrm{N}\) decreases slowly with \(\alpha \) for \(h_d=0.2\). There is an enhancement in \(\tau _\textrm{N}\) with \(\alpha \) up to particular \(\alpha \) for large \(h_d\) and \(\Delta \).

Full size image

We then analyse the magnetisation decay behaviour in a system with a huge aspect ratio. We plot the time evolution of the magnetisation decay \(M(t)/M_s\) vs. t curve as a function of \(\alpha \) for \(A_r=25.0\) and 100.0 in figures 4 and 5, respectively. Even with a highly anisotropic system, the magnetisation decays smoothly for weakly interacting MNPs, irrespective of \(\alpha \) and \(\Delta \). For moderate dipolar interaction strength (\(h_d=0.6\)), the magnetic relaxation slows down for \(\alpha <75^\circ \) even with small out-of-plane disorder strength \(\Delta \) because the ferromagnetic coupling is enhanced because of out-of-plane disorder strength. In the case of the largest dipolar interaction strength (\(h_d=1.0\)), the slowing down of magnetisation decay occurs relatively for smaller \(\alpha \) with \(A_r=25.0\) compared to \(A_r=100.0\). It can be explained by the fact that the shape anisotropy becomes prominent in the highly anisotropic system, which strengthens the ferromagnetic coupling. Consequently, the magnetic moments tend to align along the long axis of the system, resulting in prolonged magnetisation decay even with a large value of \(\alpha \).

In figure 6, we study the magnetic relaxation characteristics in a highly anisotropic system \(A_r=400.0\). It corresponds to a one-dimensional chain of MNPs. Such a system is highly important due to its immense application in digital data storage. In the case of small dipolar interaction strength (\(h_d=0.2\)), the function form of the relaxation curve is exponentially decaying, irrespective of the orientation of anisotropy axis and disorder strength \(\Delta \). Interesting physics unfolds with large dipolar interaction strength. The magnetisation ceases to relax for anisotropy orientational angle \(\alpha <60^\circ \) and \(h_d=0.6\) even with small \(\Delta \) because the shape anisotropy in such a case is the maximum that promotes ferromagnetic coupling among the magnetic moments. The out-of-plane disorder further enhances such ferromagnetic interactions. Interestingly, there is a rapid decay of magnetisation for \(\alpha >60^\circ \), irrespective of \(\Delta \). In such cases, the majority of magnetic moments momentarily changes their directions by \(180^\circ \), resulting in negative averaged magnetisation. It can be explained by the fact that the dipolar field and anisotropy axis are directed antiparallel to each other. As a result, magnetisation prefers to align antiparallel to the anisotropy axis for large dipolar interaction strength. The strong dependence of the magnetic relaxation with \(\alpha \) and \(h_d\) is in qualitative agreement with the work of Laslett et al [62] and Hovorka et al [63] for perfectly ordered system (\(\Delta =0\)).

Finally, we analyse the effective Néel relaxation time \(\tau _\textrm{N}\) as a function of \(\alpha \) and \(\Delta \) for various values of \(h_d\) and \(A_r\) of the system in figures 7 and 8. In the square-like MNP assembly, there is a weak dependence of \(\tau _\textrm{N}\) on \(\alpha \) and \(\Delta \) with \(h_d=0.2\). Remarkably, \(\tau _\textrm{N}\) increases with \(\alpha \) (\({\le }45^\circ \)) for moderate dipolar interaction strength \((h_d=0.4\) and 0.6), irrespective of \(\Delta \). In contrast, \(\tau _\textrm{N}\) decreases with \(\alpha \) (\({>}45^\circ \)) in such cases. It is because of the dominance of antiferromagnetic coupling in square-like MNPs ensemble with the negligible positional disorder. Interestingly, \(\tau _\textrm{N}\) increases with \(\alpha \) provided \(\alpha <45^\circ \) and \(\Delta \) is significant. In such cases, the out-of-plane disorder tends to instigate ferromagnetic coupling resulting in the enhancement of \(\tau _\textrm{N}\). Remarkably, the antiferromagnetic coupling prevails for smaller \(\Delta \) and \(\alpha >45^\circ \), which diminishes the value of \(\tau _\textrm{N}\). In a highly anisotropic system (huge \(A_r\)), \(\tau _\textrm{N}\) decreases slowly with \(\alpha \) even for weakly interacting MNPs \((h_d=0.2)\). Notably, there is an increase in \(\tau _\textrm{N}\) with \(\alpha \) (\({\le }30^\circ \)) even for moderate interaction strength \(h_d\). On the other hand, \(\tau _\textrm{N}\) starts to decrease for \(\alpha >30^\circ \). The decrease of \(\tau _\textrm{N}\) occurs relatively at a smaller value of \(\alpha \) (\({\le }15^\circ \)) for large \(h_d\). It is because the dipolar field and anisotropy are antiparallel to each other in such cases, resulting in a decrease in relaxation time. The variation of \(\tau _\textrm{N}\) with \(\alpha \) and \(h_d\) for \(A_r=400.0\) is in agreement with our earlier work [44].

4 Summary and conclusion

In summary, we have performed kMC simulations to investigate magnetic relaxation behaviour in the two-dimensional assembly of MNPs with aligned anisotropy axes and positional defects. Such anisotropic systems has many applications, such as novel magnetic composite materials, sensors, spintronics-based applications, etc. [64,65,66]. The variation of the orientation of anisotropy axes and disorder strength are controlled by \(\alpha \) and \(\Delta \), respectively. We have also investigated the relaxation properties as a function of \(h_d\) and \(A_r\) of the underlying system. The magnetisation decays smoothly for weakly interacting MNPs (\(h_d=0.2\)), irrespective of \(A_r\). In such cases, the functional form of the time evolution of the magnetisation decay is also exponentially decaying and depends weakly on \(\alpha \) and \(\Delta \). In contrast, there is a strong dependence of relaxation characteristics on the anisotropy axes orientation, out-of-plane disorder strength and aspect ratio for strongly dipolar interacting MNPs. In the square arrays of MNPs and irrespective of \(\alpha \), the magnetisation decays rapidly for considerable dipolar interaction strength and negligible \(\Delta \) because the dipolar interaction of enough strength promotes antiferromagnetic coupling among the magnetic moments in square ensembles of nanoparticles, resulting in faster magnetisation decay. It is in perfect qualitative agreement with the work of MacIsaac et al [67], while with significant values of \(\Delta \), the magnetisation ceases to relax. Consequently, there is a prolonged magnetisation decay for large \(\Delta \). The out-of-plane disorder of sufficient strength induces ferromagnetic interaction even in a system with \(A_r=1.0\). In a system with a large \(A_r\), the magnetisation decays extremely slowly for \(\alpha <\alpha ^\star \) even with moderate \(h_d\). Interestingly, the slowing down of the magnetic relaxation shifts to a lower value of \(\alpha ^{\star }\) with the most considerable dipolar interaction strength \(h_d=1.0\). Unusual magnetic relaxation behaviour is observed in the highly anisotropic system (\(A_r=400\)) due to the interplay among the anisotropy axis orientation, shape anisotropy and disorder strength. Even in a perfectly ordered system, there is a prolonged magnetisation decay for \(\alpha \le 60^\circ \) and moderate interaction strength \(h_d=0.6\). In such a case, the shape anisotropy alone can induce sufficient ferromagnetic interaction among the magnetic moments. Remarkably, the magnetisation decays rapidly for \(\alpha >60^\circ \), independent of the value of \(\Delta \). Most of the magnetic moment reverses its direction by \(180^\circ \), resulting in the negative averaged magnetisation in these cases. The dipolar field gets aligned antiparallel to the anisotropy axis for large \(\alpha \) in such cases [44]. Consequently, the magnetic moment tends to get aligned along the dipolar field, resulting in negative magnetisation.

The effective Néel relaxation time \(\tau _\textrm{N}\) also depends strongly on these parameters. There is weak dependence of \(\tau _\textrm{N}\) on \(\alpha \) and \(\Delta \) in a system with small dipolar interaction (\(h_d\le 0.2\)) irrespective of the value of \(A_r\). Notably, there is an enhancement in \(\tau _\textrm{N}\) with \(\alpha \) (\({\le }45^\circ \)) for moderate \(h_d\) and for \(A_r=1.0\). On the other hand, \(\tau _\textrm{N}\) decreases with \(\alpha \) for significant \(h_d\) provided \(\alpha \) is greater than \(45^\circ \). Such behaviour can be explained by the fact that the antiferromagnetic coupling is dominant in square arrays of MNPs in the presence of sufficiently sizeable dipolar interaction strength and negligible positional disorder. In a highly anisotropic system, there is an increase in \(\tau _\textrm{N}\) with \(\alpha \) (\({\le }30^\circ \)) even with moderate values of \(h_d\), while for \(\alpha >30^\circ \), \(\tau _\textrm{N}\) decreases with \(\alpha \). The lowering of \(\tau _\textrm{N}\) occurs relatively at smaller \(\alpha \) with a large \(h_d\) because the dipolar field gets aligned antiparallel to the anisotropy axes for large \(\alpha \). Consequently, the magnetisation tends to get aligned along the dipolar field for a significantly large \(\alpha \), resulting in a decrease in \(\tau _\textrm{N}\). The observations made in the present work clearly indicate that we can tune the relaxation behaviour and effective Néel relaxation time by carefully manoeuvring the system parameters, such as anisotropy axes, positional disorder, aspect ratio and dipolar interaction strength. These results are beneficial in various applications, such as smart materials, sensors, spintronics-based applications, etc.