1 Introduction

Lubricants and coolant liquids are utilised in various industrial applications. The efficiency and development of heat transport devices mainly depend on thermal conductivity of these liquids. This is the most significant goal for these technologies to be financially and energetically viable. Furthermore, in the available literature, there are various procedures that enhance the heat transport coefficient of the flow and improve the efficiency of the solar collector. Solid nanoparticles have higher thermal conductivity when compared to base liquids. Therefore, the idea of adding solid nanoparticles into base liquid was considered. Nanoliquids are utilised inside an absorber and serve as heat transfer liquids. Nanoliquids possess superior thermal features and enhance the performance of the solar system. Khan et al [1] considered the impact of nanoparticles on an Oldroyd-B fluid in the presence of a heat sink–source. Gupta and Ray [2] inspected the features of squeezing the time-dependent flow between parallel plates in the presence of nanoparticles. Sheikholeslami and Ellahi [3] studied the characteristics of cubic cavity for three-dimensional (3D) flow of the magnetonanofluid. Khan and Khan [4] performed the analysis of Burgers’ fluid in the presence of nanoparticles. Sandeep et al [5] investigated the impact of convective heat / mass transfer mechanisms on non-Newtonian magnetonanofluid. Khan and Khan [6] deliberated the impact of the no-mass flux condition on the power law of nanofluids. Haq and Khan [7] considered a two-phase model with water and ethylene glycol-based Cu nanoparticles under suction–injection. A steady-state two-dimensional (2D) flow of Burgers’ fluid in the presence of nanoparticles was demonstrated by Khan and Khan [8]. Zero mass flux relation has been employed by Khan et al [9] to visualise the behaviour of Burgers’ fluid in the presence of nanoparticles. Rahman et al [10] reported nanofluid flow for Jeffrey fluid. Raju et al [11] studied the magnetonanofluid flow in the presence of a rotating cone with temperature-dependent viscosity. Recently, several researchers published their work on heat transport [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

Fig. 1
figure 1

Flow geometry.

Full size image

Chemical reactions can be categorised into different types such as homogeneous / heterogeneous reactions, catalytic / non-catalytic reactions, single-step / multistep reactions, etc. Mostly, the reactions are complex in nature; they proceed through a reaction mechanism or just a mechanism consisting of a number of chemical reaction steps, or the so-called elementary steps. To reduce the complexity of complex reactions, mathematical modelling is essential. Mathematical chemistry deals with the mathematical modelling of chemical phenomena while computational chemistry applies computer techniques to assist in solving chemical problems. It is necessary in today’s science to study chemical processes and reaction rates, to analyse the structures and properties of atoms and molecules, to simulate, optimise and control the processes. In fact, it allows us to study different factors affecting the speed of chemical reactions and gives information about the whole mechanism and transition states. Today we can talk about the microscopic or molecular level of each reaction, i.e. activation energy, atomic collision, at different stages during the reaction. An analysis of the detailed reaction mechanism of the complete interaction between the heat transfer behaviour and cracking reactions offers deep insights. Khan et al [32] analysed the chemical phenomenon for the 3D flow of a non-Newtonian nanofluid. Khan et al [33] investigated the characteristics of chemical processes on 3D flow of Burgers’ fluid. Khan et al [34] explored the features of convective flow in the presence of a surface with variable thickness. Khan et al [35] inspected the aspects of chemical mechanisms by utilising a revised relation. Khan et al [36] scrutinised the impact of chemical reactions on generalised Burgers’ nanofluid. Mustafa et al [37] examined the characteristics of activation energy and chemical mechanisms on the magnetonanofluid. Khan et al [38] studied the aspects of autocatalysis chemical reaction in nonlinear radiative 3D flow of the cross magnetofluid.

Based on the aforementioned literature reviews, we perceived that scant consideration has been paid to the 3D flow of a cross nanofluid over a bidirectional stretched surface. Mathematical modelling of the presented physical model is conducted by considering the aspects of no-flux condition at the boundary. Moreover, heat–mass transport mechanisms are carried out by utilising characteristics of activation energy and Lorentz’s forces. MATLAB function bvpc scheme is implemented to obtain numerical solutions of the presented physical model. The impacts of the involved physical parameters on the flow and heat–mass transport characteristics are presented using tables and graphs.

2 Modelling

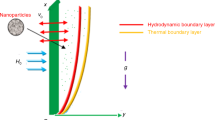
Three-dimensional flow of an incompressible cross fluid in the presence of nanoparticles is reviewed. The configuration of the present physical model is presented in figure 1. Moreover, the flow through the medium is caused by a stretched surface and restricted in the domain, \(z>0\). Heat sink–source mechanisms are carried out in current physical situation which has some engineering applications, such as dissociating fluid. Heat–mass transport mechanisms are examined using variable diffusivity and variable conductivity. A non-uniform magnetic field is applied in the z direction. Moreover, simulation is performed by assuming low Reynolds number. Convective heat transport and no-mass flux conditions are encountered. The governing equations under the above stated assumptions are as follows:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$
(1)
$$\begin{aligned}&u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\nonumber \\&\quad =-\frac{1}{\rho _{f} }\frac{\partial P}{\partial x} +\nu \frac{\partial }{\partial z}\left[ {\frac{\left( {\partial u/\partial z} \right) }{1+\left\{ {\Gamma \left( {\partial u/\partial z} \right) } \right\} ^{n}}} \right] -\frac{\sigma ^{*}B_0^2 u}{\rho _{f} },\nonumber \\ \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\nonumber \\&\quad =-\frac{1}{\rho _{f} }\frac{\partial P}{\partial y} +\nu \frac{\partial }{\partial z}\left[ {\frac{\left( {\partial v/\partial z} \right) }{1+\left\{ {\Gamma \left( {\partial v/\partial z} \right) } \right\} ^{n}}} \right] -\frac{\sigma ^{*}B_0^2 v}{\rho _{f} },\nonumber \\ \end{aligned}$$
(3)
$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\&\quad = \frac{1}{\left( {\rho c} \right) _{f} }\frac{\partial }{\partial z}\left( {k(T)\frac{\partial T}{\partial z}} \right) \nonumber \\&\qquad +\,\tau \left[ {D_B \frac{\partial C}{\partial z}\frac{\partial T}{\partial z}+\frac{D_T }{T_\infty }\left( {\frac{\partial T}{\partial z}} \right) ^{2}} \right] \nonumber \\&\qquad +\,\frac{Q_0 }{(\rho c)_{f} }(T-T_\infty ), \end{aligned}$$
(4)
$$\begin{aligned}&u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}\nonumber \\&\quad = \frac{\partial }{\partial z}\left( {D_{B} \left( C \right) \frac{\partial C}{\partial z}} \right) +\frac{D_T }{T_\infty }\frac{\partial ^{2}T}{\partial z^{2}}\nonumber \\&\qquad -\,k_c^2 \left( {C-C_\infty } \right) \left( {\frac{T}{T_\infty }} \right) ^{m} \exp \left( {-\frac{E_a }{KT}} \right) \end{aligned}$$
(5)

with

$$\begin{aligned}&u= U_w =ax,\quad v=V_w =by,\quad w=0, \nonumber \\&-k\frac{\partial T}{\partial z}= h_{f} [T_f -T],\quad \nonumber \\&D_B \frac{\partial C}{\partial z} +\frac{D_T }{T_\infty }\frac{\partial T}{\partial z}=0\quad \hbox { at }\quad z=0, \end{aligned}$$
(6)
$$\begin{aligned}&u\rightarrow 0,\quad v\rightarrow 0,\quad T\rightarrow T_\infty ,\quad \nonumber \\&C\rightarrow C_\infty \quad \hbox { as }\quad z\rightarrow \infty , \end{aligned}$$
(7)

where

$$\begin{aligned}&k(T)=k_\infty \left( {1+\varepsilon _1 \left( {\frac{T-T_\infty }{T_f -T_\infty }} \right) } \right) , \end{aligned}$$
(8)
$$\begin{aligned}&D(C)= k_\infty \left( {1+\varepsilon _2 \left( {\frac{C-C_\infty }{C_\infty }} \right) } \right) , \end{aligned}$$
(9)

Utilising eqs (8) in (4) and eqs (9) in (5), we get

$$\begin{aligned}&u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\&\quad = \frac{1}{\left( {\rho c}\right) _{f} }\frac{\partial }{\partial z}\left( {k(T)\frac{\partial T}{\partial z}} \right) \nonumber \\&\qquad +\,\tau \left[ {D_B \frac{\partial C}{\partial z}\frac{\partial T}{\partial z}+\frac{D_T }{T_\infty }\left( {\frac{\partial T}{\partial z}} \right) ^{2}} \right] \nonumber \\&\qquad +\,\frac{Q_0 }{(\rho c)_f }(T-T_\infty ). \end{aligned}$$
(10)

Consider

$$\begin{aligned}&u= ax{f}^{\prime }(\eta ),\quad v=ay{g}^{\prime }(\eta ),\nonumber \\&w=-(a\nu )^{1/2}\left[ {f(\eta )+g(\eta )} \right] , \nonumber \\&\theta (\eta )= \frac{T-T_\infty }{T_f -T_\infty },\quad \varphi (\eta )=\frac{C-C_\infty }{C_\infty },\nonumber \\&\eta =z\sqrt{\frac{a}{\nu }}. \end{aligned}$$
(11)

The requirement of continuity equation is automatically fulfilled by utilising transformation (11), whereas eqs (2)–(7), (9) and (10) take the form

$$\begin{aligned}&\left[ {1+\left( {1-n} \right) \left( {\hbox {We}_1 f^{\prime \prime }} \right) ^{n}} \right] {f}^{\prime \prime \prime }-\left[ {1+\left( {\hbox {We}_1 f^{\prime \prime }} \right) ^{n}} \right] ^{2}\nonumber \\&\quad \times \,\left[ {f^{\prime 2}-\left( {f+g} \right) f^{\prime \prime }+M^{2}f^{\prime }} \right] =0,\end{aligned}$$
(12)
$$\begin{aligned}&\left[ {1+\left( {1-n} \right) \left( {\hbox {We}_2 g^{\prime \prime }} \right) ^{n}} \right] {g}^{\prime \prime \prime }-\left[ {1+\left( {\hbox {We}_2 g^{\prime \prime }} \right) ^{n}} \right] ^{2}\nonumber \\&\quad \times \left[ {g^{\prime 2}-\left( {f+g} \right) g^{\prime \prime }+M^{2}g^{\prime }} \right] =0, \end{aligned}$$
(13)
$$\begin{aligned}&\left( {1+\varepsilon _1 \theta } \right) \theta ^{\prime \prime }+\varepsilon _1 \theta ^{\prime 2}+ {\Pr } [(f+g)\theta ^{\prime }+N_b \theta ^{\prime }{\varphi }^{\prime } \nonumber \\&\quad {+}N_t \theta ^{\prime 2}]+{\Pr }\,\lambda \theta =0, \end{aligned}$$
(14)
$$\begin{aligned}&\left( {1+\varepsilon _2 \varphi } \right) \varphi ^{\prime \prime }+\varepsilon _2 \varphi ^{\prime 2}+\hbox {Le}\,{\Pr }(f+g)\varphi ^{\prime } \nonumber \\&\quad -\hbox {Le}\,{\Pr }\,\sigma \varphi \left( {1+\delta \theta } \right) ^{m}\exp \left( {-\frac{E}{1+\delta \theta }} \right) +\frac{N_t }{N_b }\theta ^{\prime \prime }= 0, \nonumber \\ \end{aligned}$$
(15)
$$\begin{aligned}&f= 0,\quad g=0,\quad f^{\prime }=1,\quad g^{\prime }=\alpha , \nonumber \\&\theta ^{\prime }(0)= -\gamma [1-\theta (0)],\nonumber \\&N_b {\varphi }^{\prime }(0) +N_t {\theta }^{\prime }(0)=0\quad \hbox {at}\quad \eta =0, \end{aligned}$$
(16)
$$\begin{aligned}&{f}^{\prime }\rightarrow 0,\quad g^{\prime }\rightarrow 0,\quad \theta \rightarrow 0,\quad \varphi \rightarrow 0,\quad \hbox {as}\quad \eta \rightarrow \infty .\nonumber \\ \end{aligned}$$
(17)

Dimensionless physical parameters are defined as

$$\begin{aligned}&\hbox {We}_1 = \Gamma ax\sqrt{\frac{a}{\nu }},\quad \hbox {We}_2 =\Gamma ay\sqrt{\frac{a}{\nu }},\quad \alpha =\frac{b}{a},\nonumber \\&M=\frac{\sigma ^{*}B_0^2 }{\rho _{f} a},\quad N_b = \frac{\tau D_B C_\infty }{\nu },\nonumber \\&N_t =\frac{\tau D_T (T_f -T_\infty )}{\nu T_\infty },\quad \lambda =\frac{Q_0 }{a(\rho c)_{f} },\nonumber \\&{\Pr } = \frac{\nu }{\alpha _1 }, \quad \hbox {Le}=\frac{\alpha _1 }{D_{B} }, \quad \sigma =\frac{k_c^2 }{a}, \nonumber \\&E=\frac{E_a }{k_\infty T_\infty }, \quad \delta =\frac{T_f -T_\infty }{T_\infty }. \end{aligned}$$
(18)
Table 1 Comparison of surface drag forces for the Newtonian liquid (\(\hbox {We}_1 =\hbox {We}_2 =M=0)\).
Full size table
Fig. 2
figure 2

Illustration of \(g^{\prime }(\eta )\) for various values of M for (a) shear-thinning and (b) shear-thickening liquids.

Full size image

3 Quantities of interest

Mathematically, the expression for surface drag forces and heat transport rate are defined as

$$\begin{aligned} C_{f_x }= & {} \frac{2\tau _{xz} }{\rho _{f} U_w^2 },\quad C_{f_y } =\frac{2\tau _{yz} }{\rho _{f} U_w^2 },\end{aligned}$$
(19)
$$\begin{aligned} \hbox {Nu}_x= & {} -\frac{x}{\left( {T_f -T_\infty } \right) }\left. {\left( {\frac{\partial T}{\partial z}} \right) } \right| _{z=0}. \end{aligned}$$
(20)
Fig. 3
figure 3

Illustration of \(f^{\prime }(\eta )\) for various values of M for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 4
figure 4

Illustration of \(\theta (\eta )\) for various values of \(\alpha \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 5
figure 5

Illustration of \(\theta (\eta )\) for various values of \(\varepsilon _1 \) for (a) shear-thinning (b) and shear-thickening liquids.

Full size image
Fig. 6
figure 6

Illustration of \(\theta (\eta )\) for various values of \(N_t \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 7
figure 7

Illustration of \(\theta (\eta )\) for various values of \(\lambda \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 8
figure 8

Illustration of \(\theta (\eta )\) for various values of \(\gamma \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 9
figure 9

Illustration of \(\varphi (\eta )\) for various values of E for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 10
figure 10

Illustration of \(\varphi (\eta )\) for various values of m for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 11
figure 11

Illustration of \(\varphi (\eta )\) for various values of \(N_b \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Fig. 12
figure 12

Illustration of \(\varphi (\eta )\) for various values of \(N_t \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image

In dimensionless form, one has

$$\begin{aligned}&C_{f_x } \left( {\hbox {Re}_x } \right) ^{1/2}=\frac{2f^{\prime \prime }\left( 0 \right) }{\left[ {1+\left( {\hbox {We}_1 f^{\prime \prime }\left( 0 \right) } \right) ^{n}} \right] }, \nonumber \\&C_{f_y } \left( {\hbox {Re}_y } \right) ^{-{1/2}}=\frac{2V_w g^{\prime \prime }\left( 0 \right) }{U_w \left[ {1+\left( {\hbox {We}_2 g^{\prime \prime }\left( 0 \right) } \right) ^{n}} \right] }, \end{aligned}$$
(21)
$$\begin{aligned}&\left( {\hbox {Re}_x } \right) ^{-{1/2}}\hbox {Nu}_x = -{\theta }^{\prime }(0), \end{aligned}$$
(22)

where

$$\begin{aligned} \hbox {Re}_x =\frac{ax^{2}}{\nu }. \end{aligned}$$

4 Solution of the proposed problem

The nonlinear ODEs along with the associated conditions are integrated by utilising MATLAB tool bvp4c. The ruling ODEs are converted into first-order ODEs and MATLAB software bvp4c is implemented for the step by step integration.

4.1 Verification of numerical outcomes

Table 1 provides a comparison of the current numerical data with the existing literature for the Newtonian fluid tabulated by Ariel [39]. The numerical data for \(-f^{\prime \prime }\left( 0 \right) \) and \(-g^{\prime \prime }\left( 0 \right) \) are computed and the legitimacy of the work is ensured.

5 Discussion

The main theme here is to mark the physical interpretation of the behaviour of various physical parameters which arise in the flow, heat and mass transport of the cross magnetonanofluid past a bidirectional stretched surface. The numerical technique, namely, bvp4v is employed to integrate the governing physical model. The main motivation behind the current research work is to investigate the aspects of all the involved physical parameters such as velocity, temperature and nanofluid concentration profiles. Moreover, flow and heat transport mechanisms are probed by computing the value of drag forces and Nusselt number.

Fig. 13
figure 13

Illustration of \(\varphi (\eta )\) for various values of \(\varepsilon _2 \) for (a) shear-thinning and (b) shear-thickening liquids.

Full size image
Table 2 Numerical values of the rate of heat transport \(\left( {\mathrm{Re}_x } \right) ^{-{1/2} }\hbox {Nu}_x \) for distinct values of escalating parameters when \(M=0.8, \quad \hbox {We}_1 =\hbox {We}_2 =2.2, \hbox {Le}=2.0, N_b =0.2, \alpha =0.3\) and \(\gamma =0.5\).
Full size table

5.1 Nanofluid velocity profiles

Figures 2a, 2b and 3a, 3b demonstrate the impact of M on the velocity of the cross nanofluid. For a stretched surface, increasing M leads to the deterioration of the velocity of the cross fluid. Physically, as we increase M Lorentz’s force is enhanced, due to which the velocity of the cross fluid decreases.

5.2 Nanofluid temperature profiles

Figures 4–8 illustrate the aspects of various physical parameters on the temperature of the cross nanofluid for \(n<1\) and \(n>1\). Figures 4a and 4b represent the impacts of \(\alpha \) on the temperature profile of the cross nanofluid. Through graphical data, the deteriorating behaviour of the cross fluid is detected while sketching the temperature profile. For constant values of the involved physical parameters, a variation in the temperature of the cross nanofluid with variable conductivity \(\varepsilon _1 \) is presented in figures 5a and 5b. Graphical data show that the cross nanofluid temperature increases with increasing \(\varepsilon _1 \). Figures 6a and 6b demonstrate the effects of \(N_t \) on the dimensionless temperature profile of the cross nanofluid. These figures show that the augmentation in \(N_t \) has the tendency to increase the temperature of the nanofluid. This mechanism of the cross nanofluid is physically practical because increasing the estimation of the \(N_t \) difference of the nanofluid temperature between the nanofluid at infinity and the heated fluid behind the sheet increases. The non-dimensional temperature of the cross nanofluid is sketched in figures 7a and 7b with the rising values of \(\lambda \). As revealed from the graphical data, \(\lambda \) has a great impact on the temperature of the nanofluid, i.e. the temperature of the nanofluid is increased by an increase in \(\lambda \). Figures 8a and 8b show the characteristics of \(\gamma \) on the temperature of the nanofluid. It is perceived from our graphical outcomes that for specific values of the involved physical parameter, a significant raise in temperature of the nanofluid is exhibited for augmented values of \(\gamma \). The physical reason behind this trend of \(\gamma \) is that less resistance is faced by the thermal wall which causes an enhancement in convective heat transfer to the fluid.

5.3 Nanofluid concentration profiles

Figures 9–13 demonstrate the impact of non-dimensional physical parameters on the concentration of the nanofluid. Characteristics of nanofluid concentration corresponding to activation energy E are shown in figures 9a and 9b. It is remarkable that an increment E has a tendency to increase the nanofluid concentration. The variations in nanofluid concentration distribution are plotted in figures 10a and 10b for distinct values m. It is observed in these figures that an augmentation in m provides a deterioration in nanofluid concentration. Most significant features of figures 11a, 11b and 12a, 12b are to bring out aspects of \(N_b \) and \(N_t \) for the concentration of the nanofluid. We inferred that an increase in \(N_t \) increases the nanofluid concentration while a reverse trend is detected for \(N_b \). Moreover, it is perceived that physically, an increase in the magnitude of \(N_b \) corresponds to the rise in the rate at which nanoparticles in the base liquid move in random directions at different velocities. This movement of nanoparticles augments the transfer of heat, and therefore, declines the concentration profile. To investigate the aspects of \(\varepsilon _2 \) on the concentration profile, we have plotted figures 13a and 13b. These figures reveal that the concentration profile enhances as the value of \(\varepsilon _2 \) is increased.

5.4 Quantity of physical interest

Table 2 is presented to determine the achieved outcomes of the heat transport rate for the cross nanofluid. Table 2 reveals that the magnitude of the heat transport rate deteriorates for augmented values of \(\delta , \varepsilon _1 , \varepsilon _2 , \sigma \) and \(N_t \) while it rises for \(\Pr \) and E.

6 Main outcomes

A detailed characterisation of boundary layer flow, heat and mass transport of the cross nanofluid is studied here to elucidate the aspects of the chemical process. Moreover, variable diffusivity phenomenon is utilised to describe the mass transport mechanism. Numerical computation is employed for the modelled equations. Outcomes of this work are presented in the form of graphical and tabular data. The findings can be summarised as follows:

  • Temperature of the cross nanofluid is an increasing function of \(N_t\).

  • Higher estimation of \(\lambda \) provides larger temperature of the cross nanofluid.

  • An increment in \(\alpha \) demonstrates decays in \(\theta (\eta )\).

  • \(\varphi (\eta )\) is increased with increasing values of M.

  • Concentration of the cross magnetonanofluid increases for increasing values of E.

  • \(\varphi (\eta )\) decays via m.

  • Profiles of concentration decrease for escalating values of m and \(\sigma \).