1 Introduction

Analysis of thermal stratification is very essential in situations where heat transfer is predicted. Temperature stratification arising due to temperature variations, concentration differences or the presence of different fluids of different density causes free convection in many industrial and engineering processes. Thermal stratification within very large batteries could produce internal leakage or self-discharge. Design of nuclear reactors requires comprehensive understanding of thermal stratification that occurs in a reactor vessel, as they may lead to serious accidents in reactors. With a better stratification such situations can be avoided and higher energy efficiency can be achieved in many energy processes. Chen and Eichhorn [1] investigated natural convection heat transfer from a vertical plate in a linearly stratified fluid by employing a local non-similarity technique. Kulkarni et al [2] investigated the problem of natural convection from an isothermal flat plate suspended in a linearly stratified fluid medium using Von Karman–Pohlhausen method. Srinivasan and Angirasa [3] solved the boundary layer partial differential equations with the explicit finite difference method. Saha and Hossain [4] examined combined buoyancy effects due to thermal and mass diffusion in thermally stratified media. Furthermore, natural convection from a vertical surface has many applications in various industries. Ostrach [5] analysed the laminar free convective flow about a flat plate. An integral method was applied by Siegel [6] to study the transient free convective flow past a semi-infinite vertical plate. An explicit finite difference method which is conditionally stable and convergent was employed by Hellums and Churchill [7]. Gebhart and Pera [8] considered an approximate method to study this problem. Soundalgekar and Ganesan [9] have studied transient free convection past an isothermal plate by employing an implicit finite difference method which is unconditionally stable and convergent. Transient free convection past a semi-infinite vertical plate with variable surface temperature was studied by Takhar et al [10].

Choi [11] introduced nanofluids which are smart fluids and which can technologically handle energy resources in this new age of energy awareness. As the environment of nanofluids is thermally stratified in many branches of science and engineering, study of heat transfer in their presence is important. Kuznetsov and Nield [12] investigated the natural convective boundary layer flow of a nanofluid past a vertical plate. The Cheng-Minkowycz problem for natural convection boundary layer flow in a porous medium saturated by nanofluids is studied by Nield and Kuznetsov [13]. Khan and Pop [14] reported the boundary layer flow of nanofluid past a stretching sheet. Hamad et al [15] investigated the magnetic field effects on the free convection flow of a nanofluid past a semi-infinite vertical flat plate. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids was reported by Ahmed and Pop [16]. Steady MHD free convective flow of a nanofluid past a vertical plate is investigated by Chamkha and Aly [17]. Recently, thermal stratification effects on Heimenz flow of nanofluid over a porous wedge sheet have been investigated by Kandasamy et al [18].

Considering the importance of thermal stratification and nanofluids in the study of convective heat transfer, the present article analyses the effects of thermal stratification and volume fraction of the nanoparticles on the transient natural convective flow of Al 2 O 3, Cu, TiO 2 and Ag water nanofluids past an isothermal semi-infinite vertical plate. The present study may be useful in all those processes which are highly affected by the heat transfer.

2 Mathematical model

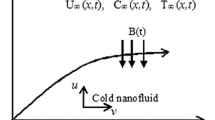
An unsteady, incompressible, two-dimensional flow along a semi-infinite isothermal vertical plate embedded in a thermally stratified nanofluid is considered. The flow is along the x-axis, which is taken along the plate in the vertical upward direction, and the y-axis is normal to the surface of the plate. Initially, the plate and the fluid are at the same temperature. The temperature of the plate is increased to T w at time t ′ > 0. In the ambient, the temperature increases linearly with height, where T ∞,0 corresponds to the temperature at x=0. Stable stratification is ensured by increasing the ambient temperature with height x. The top of the plate is at a temperature above that of the surrounding fluid at the same elevation. The plate starts to act as a cooler, when the wall temperature T w is equal to the ambient temperature T ∞,x . To avoid flow separation, the plate is considered to be of finite length. The fluids are water-based nanofluids containing nanoparticles of aluminium oxide (Al 2 O 3), copper (Cu), titanium oxide (TiO 2) and silver (Ag).

In this study, nanofluids are assumed to behave as single phase fluids with local thermal equilibrium between the base fluid and the nanoparticles suspended in them so that no slip occurs between them [19]. A schematic representation of the physical model and the coordinate system is depicted in figure 1.

Figure 1
figure 1

Schematic diagram.

Full size image

The basic unsteady momentum and thermal energy equations for nanofluids satisfying the Boussinesq approximation [20] are as follows:

$$\begin{array}{@{}rcl@{}} &&{}\frac{\partial u}{\partial x}\! +\! \frac{\partial v}{\partial y}\! =\! 0 \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} &&{}\frac{\partial T}{\partial t^{\prime}}\! +\! u \frac{\partial T}{\partial x}\! +\! v \frac{\partial T}{\partial y}\! =\! \frac{\kappa_{\text{nf}}}{(\rho c_{p})_{\text{nf}}} \frac{\partial^{2} T}{\partial y^{2} } \end{array} $$
(2)
$$\begin{array}{@{}rcl@{}} &&{}\frac{\partial u}{\partial t^{\prime}}\! +\! u \frac{\partial u}{\partial x}\! +\! v \frac{\partial u}{\partial y}\! =\! v_{\text{nf}}\frac{\partial^{2} u}{\partial y^{2} }\! +\!\frac{(\rho\beta)_{\text{nf}}}{\rho_{\text{nf}}}g(T\! -\! T_{\infty,x}). \end{array} $$
(3)

The initial and boundary conditions are:

$$\begin{array}{@{}rcl@{}} &&{}t^{\prime} \,=\, 0 ,~~~ u\! =\! 0, ~~~ v\! =\! 0, ~~~ T\! =\! T_{\infty,x},~\text{for~all~} x~\text{and}~y, \\ &&{}t^{\prime}\! > \! 0 , \quad u\! =\! 0, \quad v\! =\! 0, \quad T\! =\! T_{\infty,0},\; \quad \text{at}\; x = 0,\\ &&{}u \! = \! 0, \quad v\! =\! 0, \quad T\! =\! T_{\mathrm{w}},\; \quad \text{at}\; y \! =\! 0,\\ &&{}u \! \rightarrow\! 0, \quad v \! \rightarrow\! 0, \quad T\! \rightarrow\! T_{\infty, x}, \quad \text{as}\, y\! \rightarrow\! \infty, \end{array} $$
(4)

where u is the velocity component along the plate and v is the velocity component normal to the plate.

For nanofluids, the expression of density (ρ nf), thermal expansion coefficient (ρ β)nf and heat capacitance (ρ c p )nf are given by

$$\begin{array}{@{}rcl@{}} &&{}\rho_{\text{nf}} = (1-\varphi)\rho_{f}+\varphi \rho_{s}\\ &&{}(\rho\beta)_{\text{nf}} = (1-\varphi)(\rho\beta)_{f}+ \varphi (\rho\beta)_{s}\\ &&{}(\rho c_{p})_{\text{nf}} = (1-\varphi)(\rho c_{p})_{f}+ \varphi(\rho c_{p})_{s}. \end{array} $$
(5)

The effective thermal conductivity of the nanofluid according to Hamilton and Crosser [21] model is given by

$$ \frac{\kappa_{\text{eff}}}{\kappa_{f}}=\frac{\kappa_{s}+(n-1)\kappa_{f}-(n-1)\varphi (\kappa_{f}-\kappa_{s})}{\kappa_{s}+(n-1)\kappa_{f}+\varphi(\kappa_{f}-\kappa_{s})}, $$
(6)

where n is the empirical shape factor for the nanoparticle. In particular, n=3 for spherical nanoparticles and n=3/2 for cylindrical ones, while φ is the volume fraction of the nanoparticles, μ is the dynamic viscosity, ν is the kinematic viscosity, β is the thermal conductivity. Here the subscripts n f,f and s respectively represent the thermophysical properties of the nanofluids, base fluid and the solid nanoparticles respectively.

Introducing non-dimensional quantities in eqs (1)–(3):

$$\begin{array}{@{}rcl@{}} X&=&\frac{x}{L},~~ Y=\frac{y\text{Gr}^{1/4}}{L}, ~~~ U = \frac{uL\text{Gr}^{-1/2}}{\nu_{f}},\\ V&=&\frac{vL\text{Gr}^{-1/4}}{\nu_{f}},~~~ t=\frac{t^{\prime} \nu_{f}\text{Gr}^{1/2}}{L^{2}},\\ \theta\! &=&\! \frac{T - T_{\infty,x}}{T_{\text{w}} - T_{\infty,0}}, ~~~ \text{Pr}\! =\! \frac{\nu_{f}}{\alpha_{f}}, ~~~ \text{Gr} \! =\! \frac{g\beta L^{3}(T_{\text{w}} - T_{\infty})}{\nu_{f}},\\ S&=&\frac{{\text{d}T_{\infty,x}}/{\text{d}X}}{T_{\text{w}} - T_{\infty,0}} \end{array} $$

where Gr is the Grashof number, S is the thermal stratification parameter and Pr is the Prandtl number.

Now eqs (1)–(3) become

$$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0 $$
(7)
$$\begin{array}{@{}rcl@{}} \frac{\partial \theta}{\partial t}\! +\! U \frac{\partial \theta}{\partial X} \! +\! V \frac{\partial \theta}{\partial Y}\! +\! SU\! \! &=&\!\! \frac{1}{({}1\! -\! \varphi\! +\! \varphi{{\kern-.5pt}({\kern-.5pt}({\kern-.5pt}\rho c_{p}{\kern-.5pt})_{s}}{\kern-.5pt}/{\kern-.5pt}{({\kern-.5pt}\rho c_{p}{\kern-.5pt})_{f}}{\kern-.5pt})}\\ &&\times \left( \frac{\kappa_{\text{nf}}}{\kappa_{f}}\frac{1}{\text{Pr}} \frac{\partial^{2} \theta}{\partial Y^{2} } \right) \end{array} $$
(8)
$$\begin{array}{@{}rcl@{}} \frac{\partial U}{\partial t}\! +\! U \frac{\partial U}{\partial X} \! +\! V \frac{\partial V}{\partial Y} \! &=&\! \frac{1}{(1\! -\! \varphi+\varphi({\rho_{s}}/{\rho_{f}}))}\\ &&\! \times\! \left( \frac{1}{(1\! -\!\ \varphi)^{2.5}}\frac{\partial^{2} U}{\partial Y^{2} }\right.\\ &&\! +\! \left.\left( 1\! -\!\varphi+\varphi\frac{(\rho\beta)_{s}}{(\rho\beta)_{f}}\right) \theta \right). \end{array} $$
(9)

The transformed initial and boundary conditions are:

$$\begin{array}{@{}rcl@{}} &&{}t = 0 , \quad U = 0, \quad V = 0, \quad \theta=0, \; \text{for\; all}\;x\;\text{and}\; y, \\ &&{}t > 0 , \quad U = 0, \quad V = 0, \quad \theta=0, \; \text{for}\; x = 0, \\ &&{}U = 0, \quad V = 0, \quad \theta = 1 - SX, \; \quad \text{for}\; Y = 0, \\ &&{}U \rightarrow 0, \quad V\rightarrow 0, \quad \theta \rightarrow 0, \quad \;\text{as} \;Y\; \rightarrow \infty. \end{array} $$
(10)

The governing boundary layer partial differential equations under the initial and boundary conditions are solved using an implicit finite difference scheme of Crank–Nicolson-type given as follows:

$$\begin{array}{@{}rcl@{}} &&{}\frac{(U_{i,j}^{n+1}-U_{i-1,j}^{n+1}+U_{i,j}^{n}-U_{i-1,j}^{n}+U_{i,j-1}^{n+1}-U_{i-1,j-1}^{n+1}+U_{i,j-1}^{n}-U_{i-1,j-1}^{n})}{4{\Delta} X}\\ &&\quad+\frac{V_{i,j}^{n+1}-V_{i,j-1}^{n+1}+V_{i,j}^{n}-V_{i,j-1}^{n}}{2{\Delta} Y }= 0 \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} &&{}\frac{(\theta_{i,j}^{n+1}-\theta_{i,j}^{n})}{\Delta t} + U_{i,j}^{n}\frac{(\theta_{i,j}^{n+1}-\theta_{i-1,j}^{n+1}+ \theta_{i,j}^{n}-\theta_{i-1,j}^{n})}{2{\Delta} X}+ V_{i,j}^{n}\frac{(\theta_{i,j+1}^{n+1}-\theta_{i,j-1}^{n+1}+ \theta_{i,j+1}^{n}-\theta_{i,j-1}^{n})}{4{\Delta} Y}\\ &&\quad= E_{3} \frac{(\theta_{i,j-1}^{n+1}-2\theta_{i,j}^{n+1}+ \theta_{i,j+1}^{n+1}+\theta_{i,j-1}^{n}-2\theta_{i,j}^{n}+\theta_{i,j+1}^{n})}{2({\Delta} Y)^{2}}-s \left( \frac{U_{i,j}^{n+1}+U_{i,j}^{n}}{2}\right). \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} &&{}\frac{(U_{i,j}^{n+1}-U_{i,j}^{n})}{\Delta t} + U_{i,j}^{n}\frac{(U_{i,j}^{n+1}-U_{i-1,j}^{n+1}+ U_{i,j}^{n}-U_{i-1,j}^{n})}{2{\Delta} X}+ V_{i,j}^{n}\frac{(U_{i,j+1}^{n+1}-U_{i,j-1}^{n+1}+ U_{i,j+1}^{n}-U_{i,j-1}^{n})}{4{\Delta} Y}\\ &&\quad= E_{1} \frac{(U_{i,j-1}^{n+1}-2U_{i,j}^{n+1}+U_{i,j+1}^{n+1}+U_{i,j-1}^{n}-2U_{i,j}^{n}+U_{i,j+1}^{n})}{2({\Delta} Y)^{2}} + E_{2}\left( \frac{\theta_{i,j}^{n+1}+\theta_{i,j}^{n}}{2}\right). \end{array} $$
(13)

3 Results and discussion

The results are illustrated graphically and the associated boundary conditions are also satisfied. The volume fraction of the nanoparticles is considered in the range of 0 ≤ φ ≤ 0.04, as sedimentation takes place when the volume fraction of the nanoparticles exceeds 8%. In this study, spherical nanoparticles with thermal conductivity and dynamic viscosity are considered. The nanofluids containing nanoparticles of aluminium oxide (Al 2 O 3), copper (Cu), titanium oxide (TiO 2) and silver with water as a base fluid are investigated. The Prandtl number of the fluid is taken as 6.2. In order to verify the accuracy of the result, the present result is compared with the available result in the literature (figures 2 and 3).

Figure 2
figure 2

Comparison of temperature profiles.

Full size image
Figure 3
figure 3

Comparison of velocity profiles.

Full size image

In figures 4 and 5, the velocity and temperature profiles of silver–water nanofluid have been shown for various values of the stratification parameter S with volume fraction of the nanoparticles φ=0 (water) and φ= 0.04. An increase in thermal stratification reduces the temperature difference between the ambient and the surface. This decreases the thermal buoyancy, and hence reduces the velocity of the flow.

Figure 4
figure 4

Velocity profiles for S.

Full size image
Figure 5
figure 5

Temperature profiles for S.

Full size image

The temperature at the lower end of the vertical wall, X=0, is always 1 irrespective of the stratification parameter S. The temperature along the vertical surface varies from 𝜃=1 at the lower end, X=0, to the temperature 𝜃=0 at the upper end, X=1, for S=1. The temperature in the ambient equals the surface temperature at X=1 for S=1 and a portion at the top of the surface will have a temperature less than the ambient for a value of S>1.

In figure 6, effects of volume fraction of the nanoparticles φ on temperature distribution of copper–water nanofluid are shown. For an increase in volume fraction of the nanoparticles within the range 0≤φ≤0.04, the thermal boundary layer increases continuously. This agrees with the physical behaviour that when the volume fraction of the nanoparticles increases, the thermal conductivity of the nanofluid increases, and hence the thickness of the boundary layer increases. It is observed that in the presence of thermal stratification the temperature of the nanofluid increases with volume fraction of the nanoparticles. Figure 7 shows that a change in nanoparticle volume fraction leads to a change in heat tranfer properties.

Figure 6
figure 6

Temperature profiles for φ.

Full size image
Figure 7
figure 7

Velocity profiles for different φ.

Full size image

Figure 7 shows the effect of volume fraction of the nanoparticles φ on the velocity distribution of silver–water nanofluid. It is observed that an increase in the volume fraction of the nanoparticles decreases the velocity of the nanofluid.

Figures 8 and 9 depict the velocity and temperature profiles of silver–water nanofluid at different time in the presence of thermal stratification. It is observed that the velocity and temperature profiles increase with the time t, reach temporal maximum and after certain time-step the profiles decrease gradually to attain steady state. Thus, during transient flow the boundary layer thickness exceeds the value at steady state.

Figure 8
figure 8

Transient velocity profiles.

Full size image
Figure 9
figure 9

Transient temperature profiles.

Full size image

Figures 10 and 11 show the temperature and velocity distributions for different nanofluids when S=0.1, φ=0.04 and Pr =6.2. We observe that the velocity and temperature profiles decrease gradually far away from the surface of the plate for different nanoparticles. It is also noticed that the addition of different nanoparticles to the base fluid causes changes in the velocity and temperature distributions. It can be concluded that nanofluids will be important in cooling and heating processes.

Figure 10
figure 10

Temperature profiles of nanofluids.

Full size image
Figure 11
figure 11

Velocity profiles of nanofluids.

Full size image

Figures 12 and 13 show that an increase in thermal stratification increases the local Nusselt number and average Nusselt number of the copper–water nanofluid. From figure 5, it is clear that the temperature decreases with an increasing stratification parameter. Thus, the temperature gradient along the wall increases and hence there is an increase in the Nusselt number as observed from these figures. Furthermore, it is also noticed that changes in the volume fraction of the nanoparticles lead to a change in heat transfer rates of the nanofluids.

Figure 12
figure 12

Local Nusselt number.

Full size image
Figure 13
figure 13

Average Nusselt number.

Full size image

From figure 14, it is noted that an increase in the thermal stratification parameter S decreases the local skin friction. This is because, the velocity of the fluid decreases by increasing the stratification parameter as depicted in figure 5. Therefore, there is a reduction in the shear stress along the wall and hence a decrease in the skin friction. Furthermore, it is observed from figure 15 that the average skin friction increases with volume fraction of the nanoparticles φ.

Figure 14
figure 14

Local skin friction.

Full size image
Figure 15
figure 15

Average skin friction.

Full size image

4 Conclusion

The conclusions are as follows:

  1. (1)

    An increase in thermal stratification parameter decreases the velocity and temperature profiles.

  2. (2)

    An increase in volume fraction of the nanoparticles φ increases the temperature of the nanofluid which leads to an increase in the heat transfer rates.

  3. (3)

    The dimensionless surface velocity of the fluid decreases with an increase in volume fraction of the nanoparticles φ, which in turn increases the skin friction.

  4. (4)

    During the transient flow development, the momentum and thermal boundary layer thickness, for a certain time, exceeds the steady state.

  5. (5)

    An increase in the thermal stratification parameter decreases local and average skin friction. However, an opposite effect is observed for local and average Nusselt number.